Application of Response Surface Methodology to Optimize Solid-Phase Extraction of Benzoic Acid and Sorbic Acid from Food Drinks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents and Solutions Preparation
2.2. Apparatus
2.3. Solid-Phase Extraction Procedure
2.4. Experimental Design
2.5. Application of BBD for the Optimization of Percolation and Elution Steps
2.6. Sample Preparation
2.7. Comparative Study
3. Results and Discussion
3.1. Effect of Experimental Parameters on Retention Yields
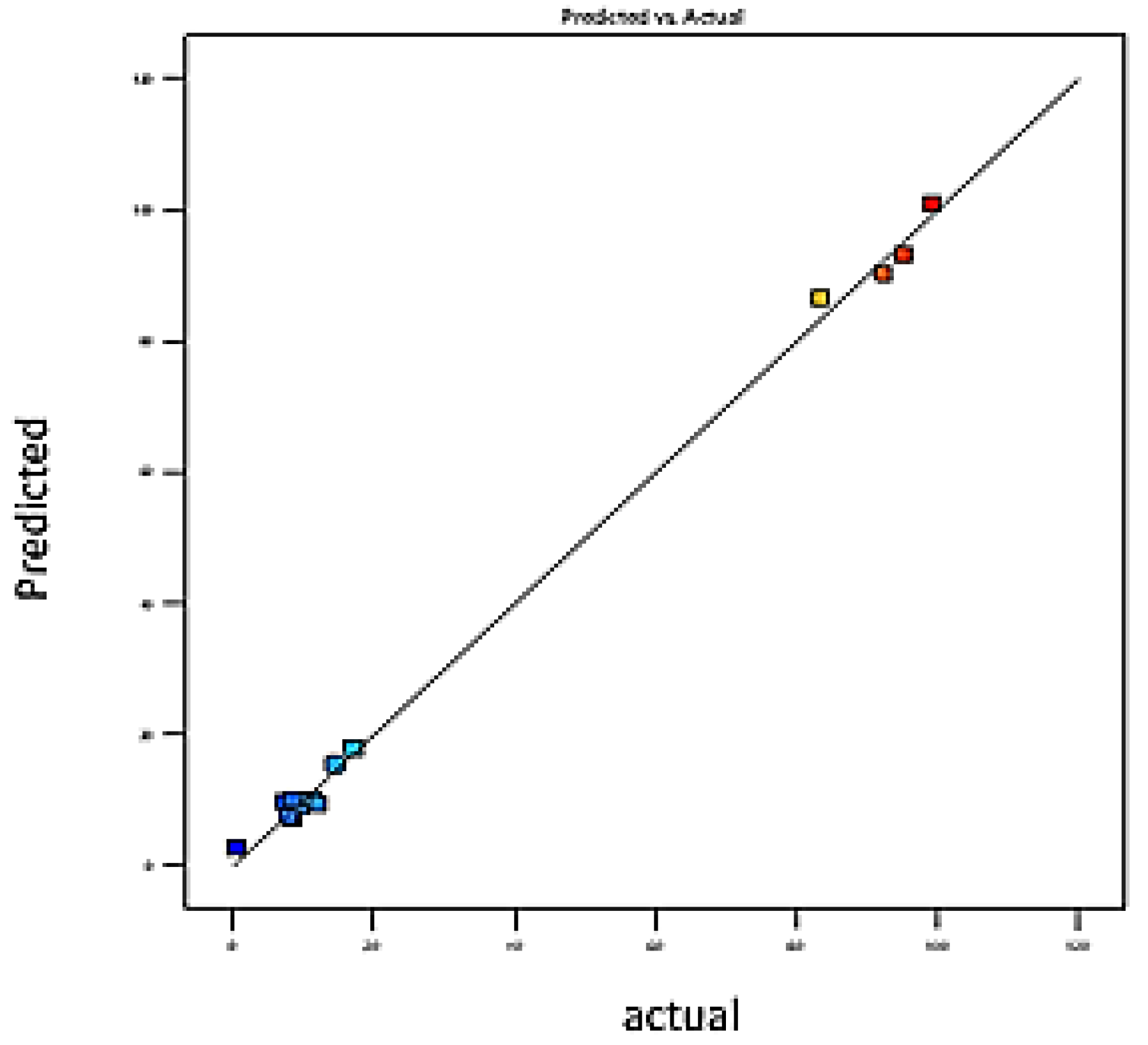
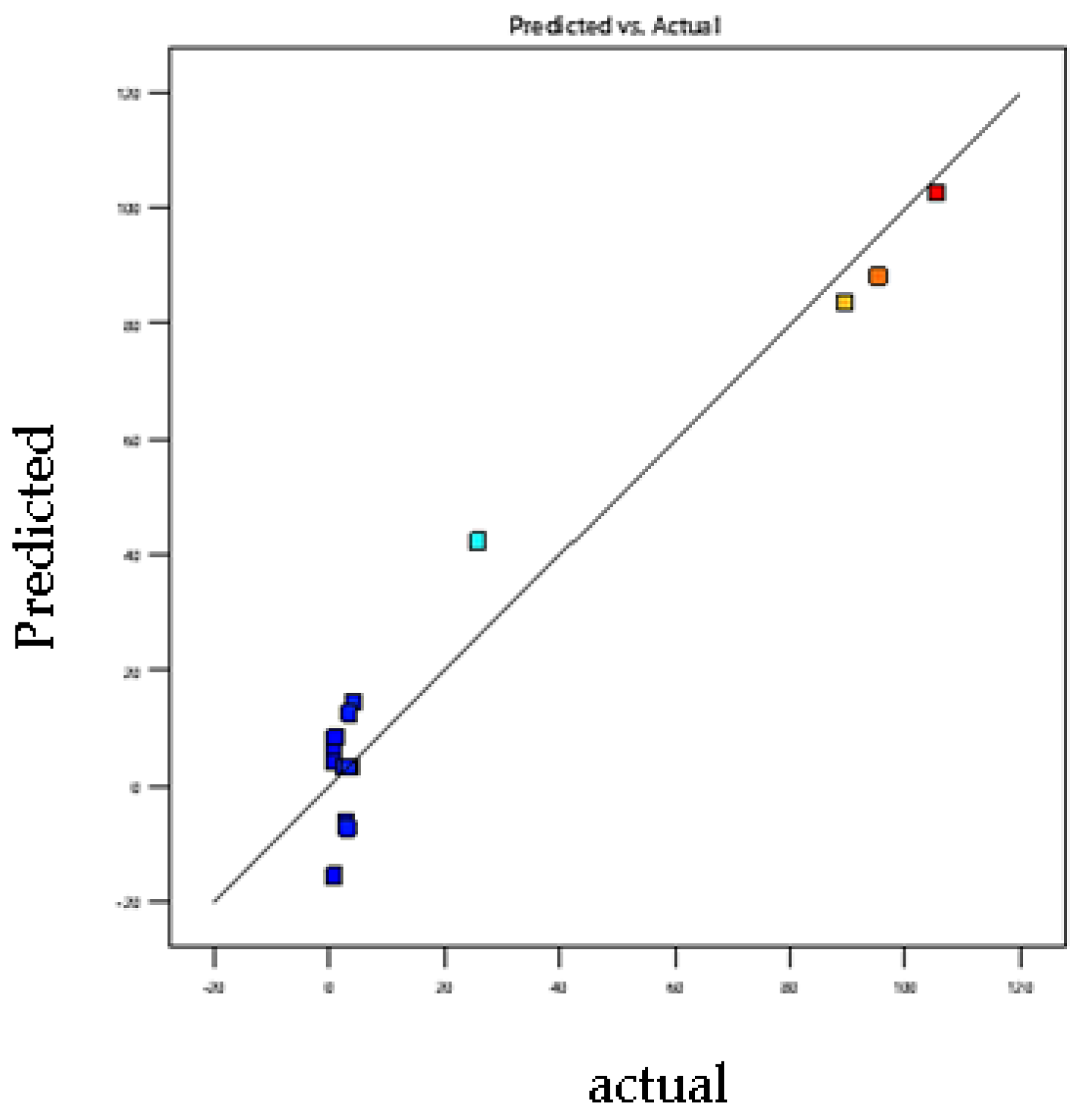
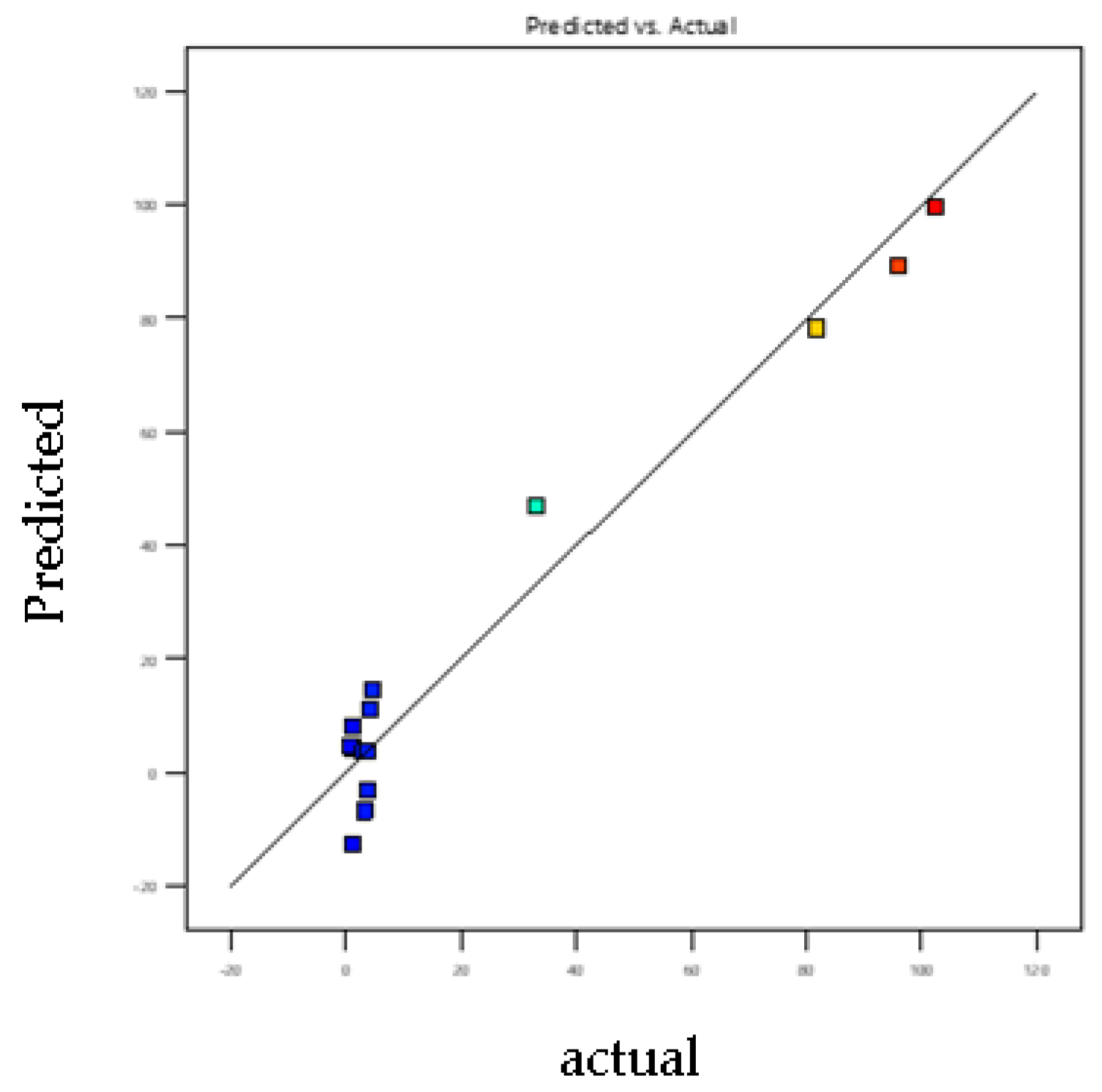
3.2. Model-Fitting and Statistical Analysis
3.3. Analysis of Significant Factors
3.4. Mathematical Models
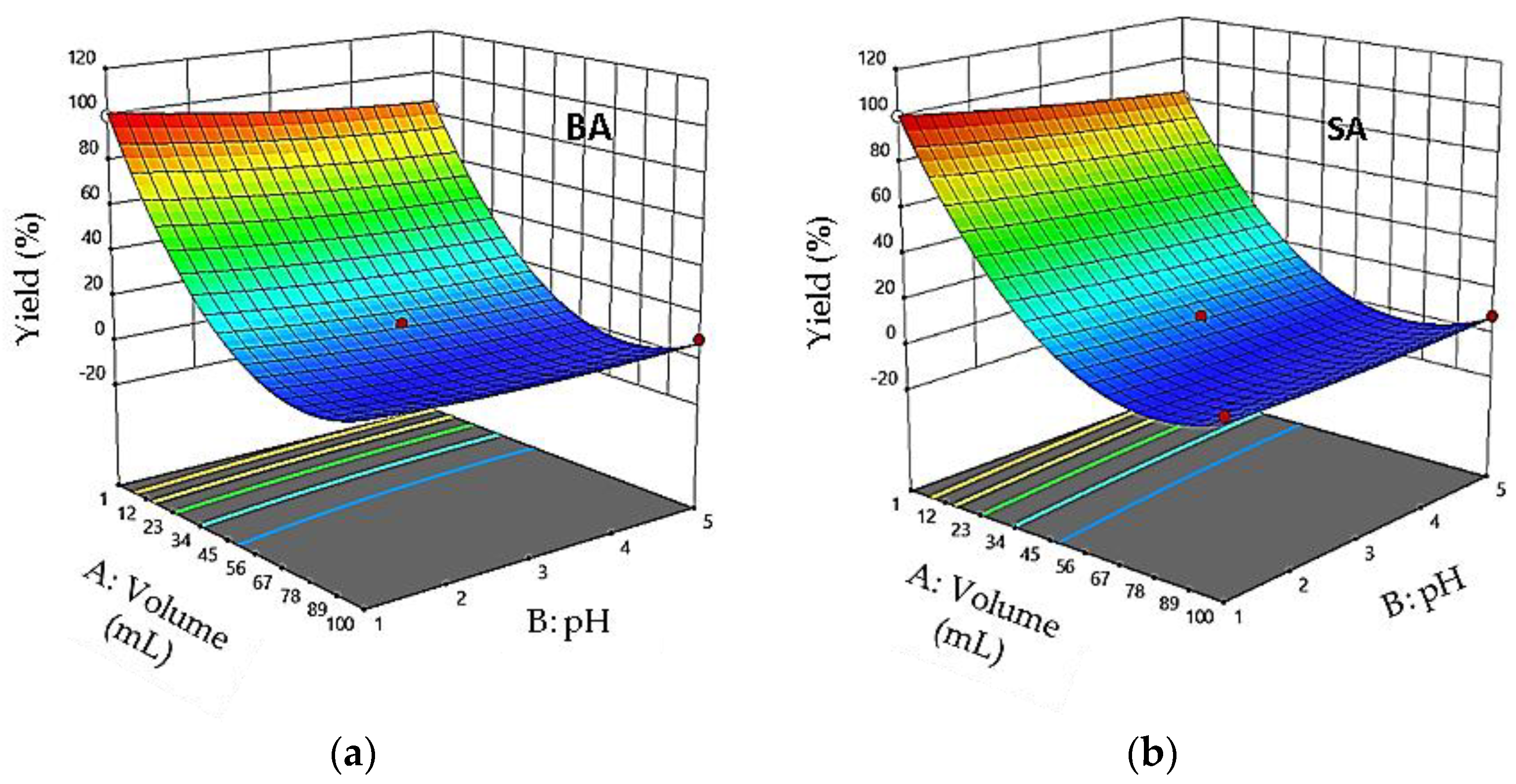
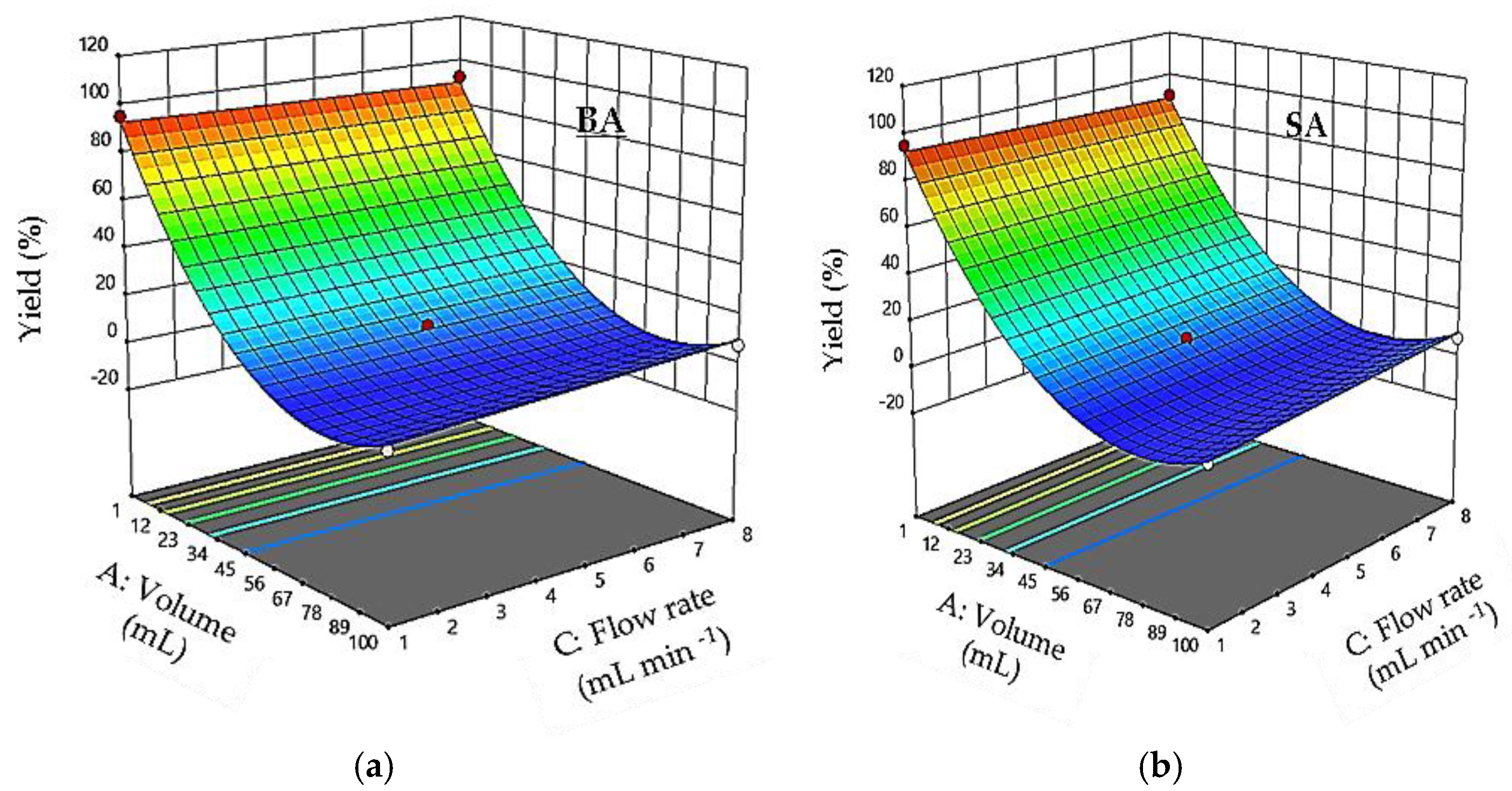
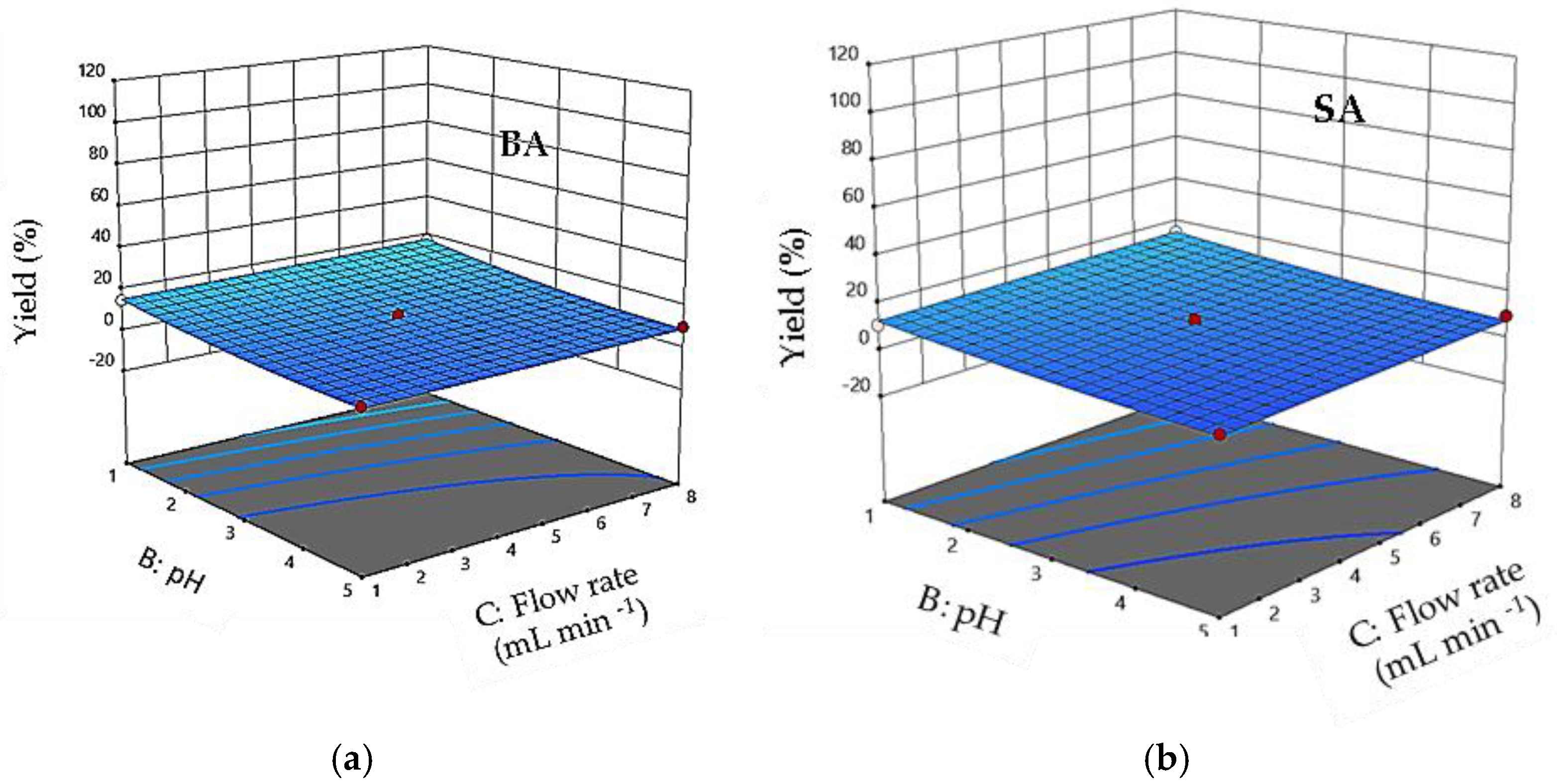
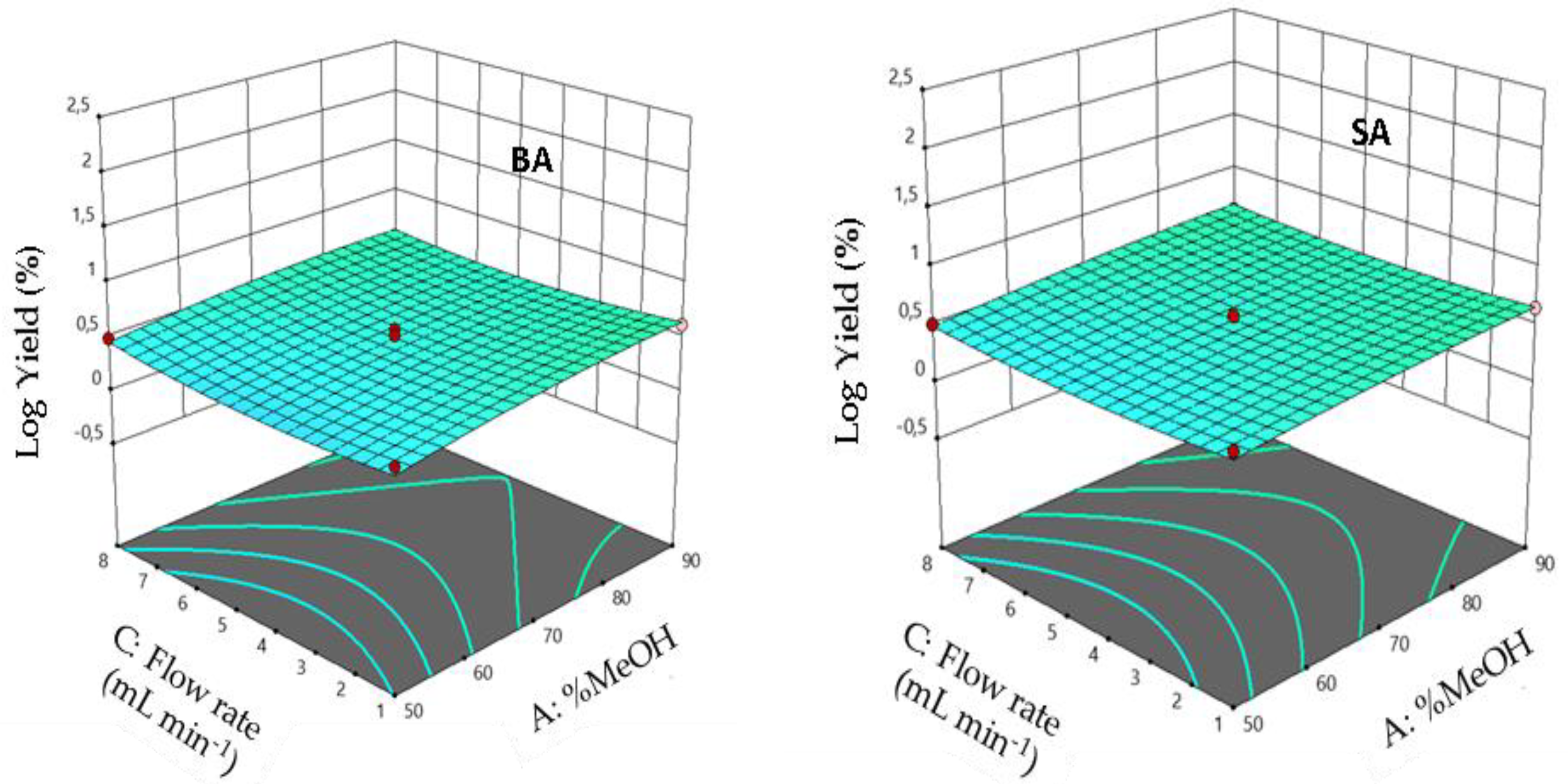
3.5. Effect of Interaction between Factors
3.6. Effect of Experimental Parameters on Elution Yield
3.7. Model Adjustment
3.8. Analysis of Significant Factors
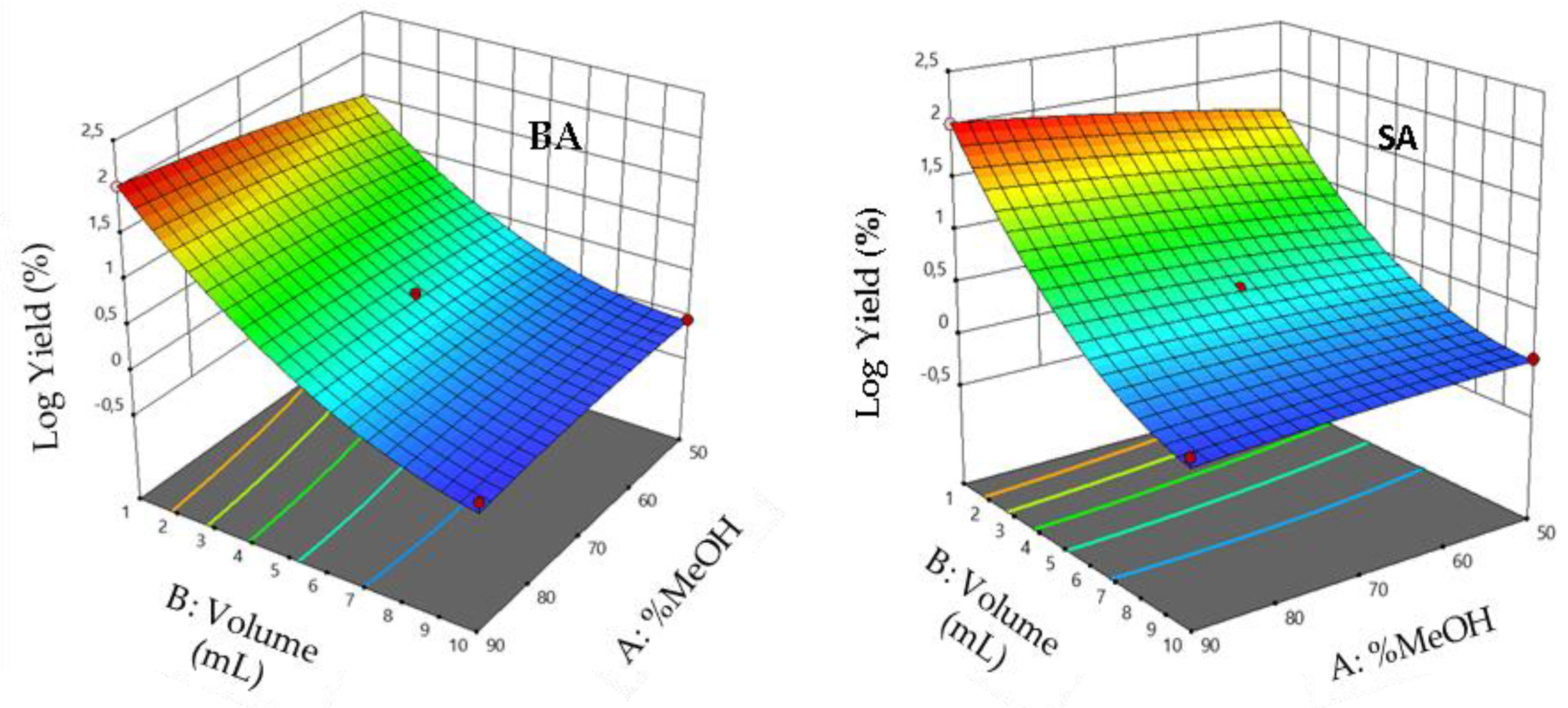
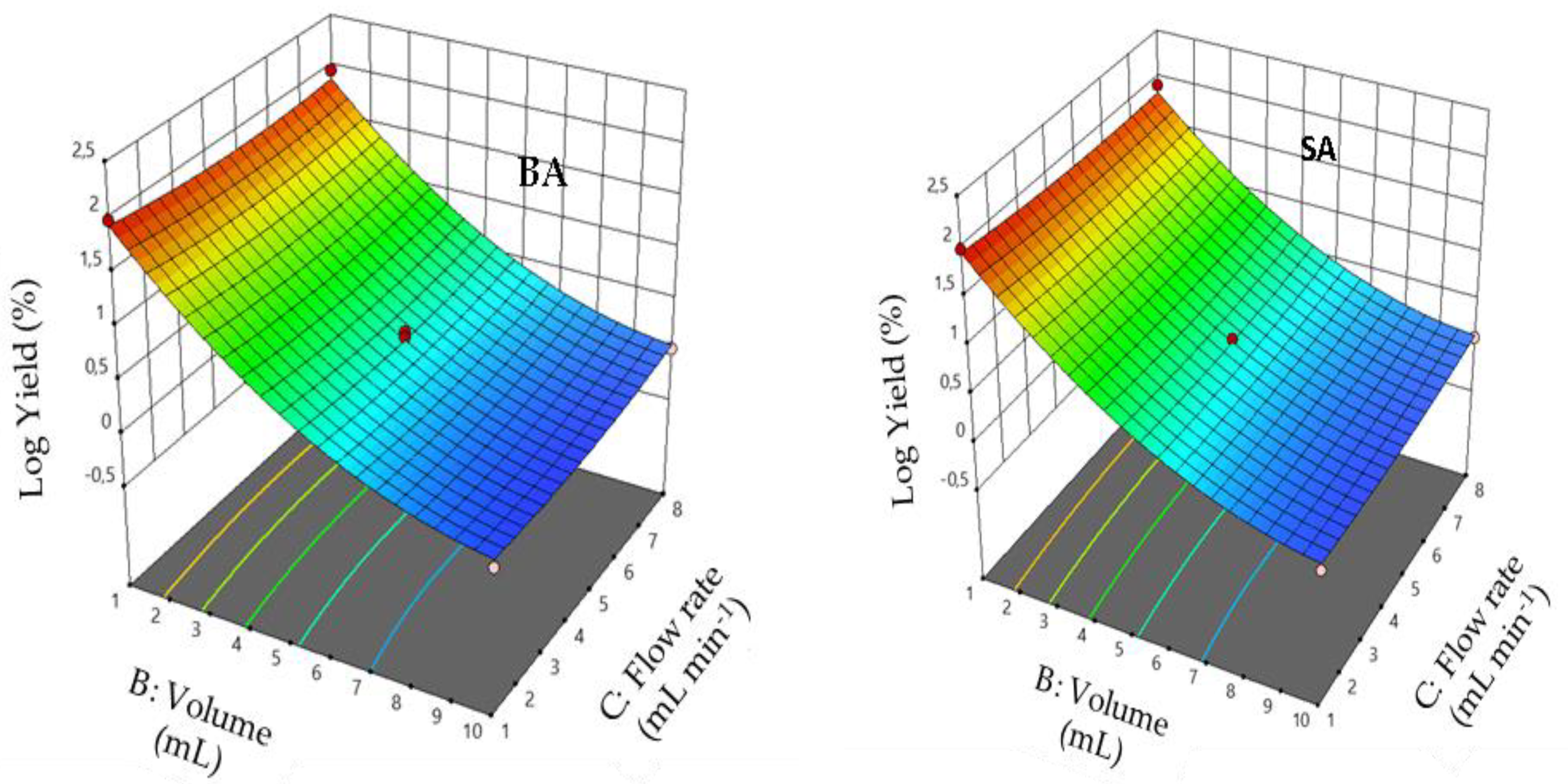
3.9. Mathematical Models
3.10. Interaction Effects
3.11. Determination of Optimal Conditions
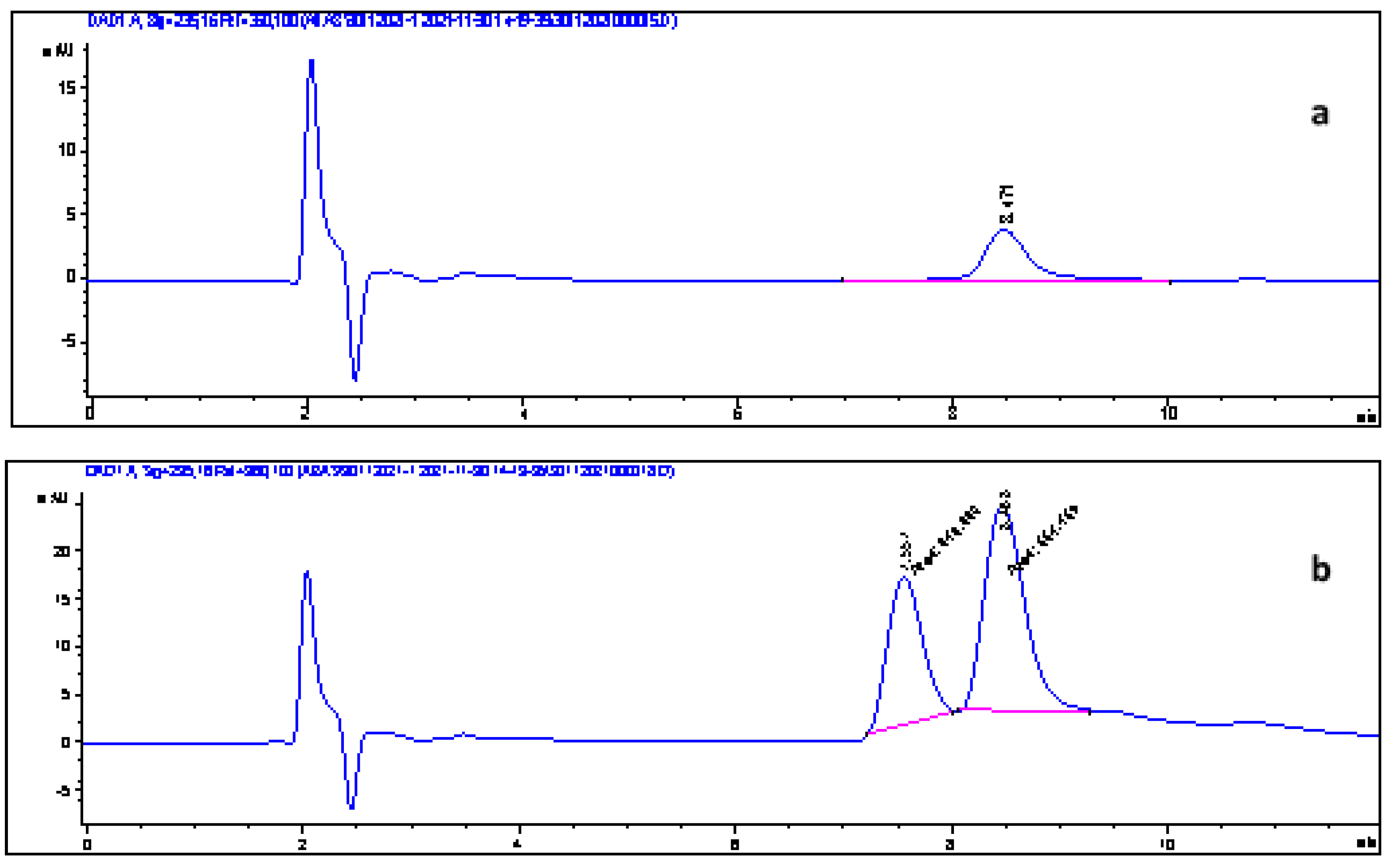
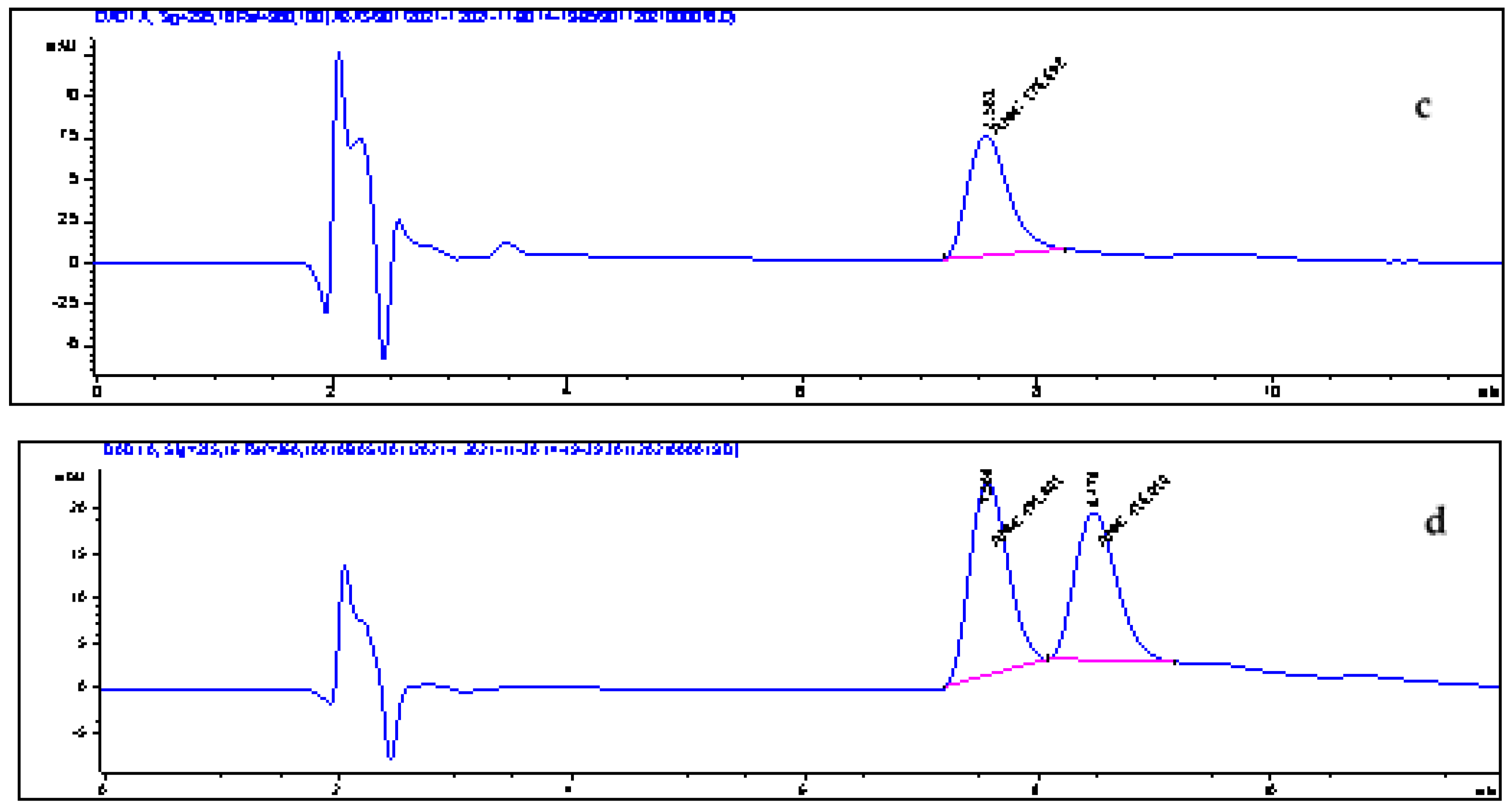
3.12. Method Validation
3.13. Application to Real Samples
3.14. Comparison Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kobylewski, S.; Jacobson, M.F. Food Dyes, A Rainbow of Risks; Centre for Science in the Public Interest: Washington, DC, USA, 2010; Available online: https://cspinet.org/resource/food-dyes-rainbow-risks (accessed on 23 January 2022).
- Pandey, R.M.; Upadhyay, S.K. Food Additive. In Food Additive; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Karunaratne, D.N.; Pamunuwa, G.K. Introductory Chapter: Introduction to Food Additives. In Food Additives; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Vaclavik, V.A.; Christian, E.W. Essentials of Food Science, 3rd ed.; Heldman, D.R., Ed.; Springer: New York, NY, USA, 2008; ISBN 978-0-387-69939-4. [Google Scholar]
- Gómez, H.C.; Serpa, A.; Velásquez-Cock, J.; Gañán, P.; Castro, C.; Vélez, L.; Zuluaga, R. Vegetable nanocellulose in food science: A review. Food Hydrocoll. 2016, 57, 178–186. [Google Scholar] [CrossRef]
- Zengin, N.; Yüzbaıoglu, D.; Unal, F.; Yilmaz, S.; Aksoy, H. The evaluation of the genotoxicity of two food preservatives: Sodium benzoate and potassium benzoate. Food Chem. Toxicol. 2011, 49, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Yadav, A.; Kumar, A.; Das, M.; Tripathi, A. Sodium benzoate, a food preservative, affects the functional and activation status of splenocytes at non-cytotoxic dose. Food Chem. Toxicol. 2016, 88, 40–47. [Google Scholar] [CrossRef] [PubMed]
- European Commossopm, Commission Regulation (EU) No 1129/2011 of 11 November 2011 Amending Annex II to Regulation (EC) No 1333/2008 of the European Parliament and the Council by Establishing a Union List of Food Additives. Off. J. Eur. Union. 2011, L295, 1–177.
- Xu, C.; Liu, J.; Feng, C.; Lv, H.; Lv, S.; Ge, D.; Zhu, K. Investigation of benzoic acid and sorbic acid in snack foods in Jilin province, China. Int. J. Food Prop. 2019, 22, 670–677. [Google Scholar] [CrossRef]
- Akbari-Adergani, B.; Eskandari, S.; Bahremand, N. Determination of Sodium Benzoate and Potassium Sorbate in “Doogh” Samples in Post Market Surveillance in Iran 2012. J. Chem. Health Risks 2013, 3, 65–71. [Google Scholar]
- Dong, C.; Wang, W. Headspace Solid-Phase Microextraction Applied to the Simultaneous Determination of Sorbic and Benzoic Acids in Beverages. Anal. Chim. Acta 2006, 562, 23–29. [Google Scholar] [CrossRef]
- Bajcic, A.; Petronijevic, R.B.; Sefer, M.; Trbovic, D.; Djordjevic, V.; Ciric, J.; Nikolic, A. Sorbates and benzoates in meat and meat products: Importance, application, and determination. IOP Conf. Ser. Earth Environ. Sci. 2021, 854, 012005. [Google Scholar] [CrossRef]
- Yu, H.H.; Chin, Y.W.; Paik, H.D. Application of Natural Preservatives for Meat and Meat Products against Food-Borne Pathogens and Spoilage Bacteria: A Review. Foods 2021, 10, 2418. [Google Scholar] [CrossRef]
- Marrone, R.; Smaldone, G.; Ambrosio, R.L.; Festa, R.; Ceruso, M.; Chianese, A.; Anastasio, A. Effect of beetroot (Beta vulgaris) extract on black Angus burgers shelf life. Ital. J. Food Saf. 2021, 10, 9031. [Google Scholar] [CrossRef]
- Sirhan, A.Y. Optimization and Validation of an HPLC-UV Method for Determination of Benzoic Acid and Sorbic Acid in Yogurt and Dried-Yogurt Products Using a Design of Experiment. Indones. J. Chem. 2018, 18, 522–530. [Google Scholar] [CrossRef]
- Li, M.; Luo, S.; Di, X.; Cui, Y. Ultrasound-assisted extraction coupling to high-performance liquid chromatography for enantiomerically quantitative analysis of two preservatives in cosmetics and the potentially cytotoxic study. Microchem. J. 2022, 172, 106937. [Google Scholar] [CrossRef]
- Carrascal, J.J.; Pinal, R.; Carvajal, T.; Pérez, L.D.; Baena, Y. Benzoic acid complexes with Eudragit E100®: New alternative antimicrobial preservatives. Int. J. Pharm. 2021, 607, 120991. [Google Scholar] [CrossRef] [PubMed]
- Ammen, E.W.; Al-Salihi, S.; Al-Salhi, R. Gas Chromatography—Mass Spectrometry Combined with Successive Dilution for the Determination of Preservatives in Pharmaceuticals. J. Anal. Chem. 2021, 76, 621–629. [Google Scholar] [CrossRef]
- Guarneri, F.; Corazza, M.; Stingeni, L.; Patruno, C.; Napolitano, M.; Pigatto, P.D.M.; Gallo, R.; Cristaudo, A.; Romita, P.; Offidani, A.; et al. Myroxylon pereirae (balsam of Peru): Still worth testing? Contact Dermat. 2021, 85, 269–273. [Google Scholar] [CrossRef]
- Aerts, O.; Goossens, A. Contact Allergy to Preservatives. In Contact Dermatitis; Springer: Berlin/Heidelberg, Germany, 2020; pp. 835–876. [Google Scholar]
- Arnau, A.M.G.; Deza, G.; Bauer, A.; Johnston, G.A.; Mahler, V.; Schuttelaar, M.L.; Sanchez-Perez, J.; Silvestre, J.F.; Wilkinson, S.M.; Uter, W. Contact allergy to preservatives: ESSCA* results with the baseline series, 2009–2012. J. Eur. Acad. Dermatol. Venereol. 2016, 31, 664–671. [Google Scholar] [CrossRef]
- Cruz-Vera, M.; Lucena, R.; Cárdenas, S.; Valcárcel, M. Sample treatments based on dispersive (micro)extraction. Anal. Methods 2011, 3, 1719–1728. [Google Scholar] [CrossRef]
- Lyn, J.A.; Ramsey, M.H.; Fussell, R.J.; Wood, R. Measurement uncertainty from physical sample preparation: Estimation including systematic error. Analyst 2003, 128, 1391–1398. [Google Scholar] [CrossRef]
- Wang, J.; Hansen, E.H. Development of an automated sequential injection on-line solvent extraction-back extraction procedure as demonstrated for the determination of cadmium with detection by electrothermal atomic absorption spectrometry. Anal. Chim. Acta 2002, 456, 283–292. [Google Scholar] [CrossRef]
- Batterham, G.J.; Parry, D.L. Improved dithiocarbamate/oxine solvent extraction method for the preconcentration of trace metals from seawater using metal exchange back-extraction. Mar. Chem. 1996, 55, 381–388. [Google Scholar] [CrossRef]
- Ndung’U, K.; Franks, R.P.; Bruland, K.W.; Flegal, A. Organic complexation and total dissolved trace metal analysis in estuarine waters: Comparison of solvent-extraction graphite furnace atomic absorption spectrometric and chelating resin flow injection inductively coupled plasma-mass spectrometric analysis. Anal. Chim. Acta 2003, 481, 127–138. [Google Scholar] [CrossRef]
- Zhang, W. Determination of Nine Preservatives in Food Samples by Solid Phase Extraction coupled with Capillary Electrophoresis. Int. J. Electrochem. Sci. 2021, 16, 21022. [Google Scholar] [CrossRef]
- Du, J.; Zhao, F.; Zeng, B. Preparation of functionalized graphene and ionic liquid co-doped polypyrrole solid phase microextraction coating for the detection of benzoates preservatives. Talanta 2021, 228, 122231. [Google Scholar] [CrossRef] [PubMed]
- Setyaningsih, W.; Saputro, I.E.; Carrera, C.A.; Palma, M.; Garcia-Barroso, C. Fast Determination of Phenolic Compounds in Rice Grains by Ultraperformance Liquid Chromatography Coupled to Photodiode Array Detection: Method Development and Validation. J. Agric. Food Chem. 2019, 67, 3018–3027. [Google Scholar] [CrossRef] [PubMed]
- Kefi, B.B.; El Atrache, L.L.; Kochkar, H.; Ghorbel, A. TiO2 nanotubes as solid-phase extraction adsorbent for the determination of polycyclic aromatic hydrocarbons in environmental water samples. J. Environ. Sci. 2011, 23, 860–867. [Google Scholar] [CrossRef]
- El Atrache, L.L.; Ben Sghaier, R.; Kefi, B.B.; Haldys, V.; Dachraoui, M.; Tortajada, J. Factorial design optimization of experimental variables in preconcentration of carbamates pesticides in water samples using solid phase extraction and liquid chromatography–electrospray-mass spectrometry determination. Talanta 2013, 117, 392–398. [Google Scholar] [CrossRef]
- El Atrache, L.L.; Hachani, M.; Kefi, B.B. Carbon nanotubes as solid-phase extraction sorbents for the extraction of carbamate insecticides from environmental waters. Int. J. Environ. Sci. Technol. 2016, 13, 201–208. [Google Scholar] [CrossRef] [Green Version]
- International Standard ISO 22855-2008; Fruit, and Vegetable Products—Determination of Benzoic Acid and Sorbic Acid Concentrations—High-Performance Liquid Chromatography Method. ISO: Geneva, Switzerland, 2008.
- Ferreira, S.L.C.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandão, G.C.; da Silva, E.G.P.; Portugal, L.A.; dos Reis, P.S.; Souza, A.S.; et al. Box-Behnken design: An alternative for the optimization of analytical methods. Anal. Chim. Acta. 2007, 597, 179–186. [Google Scholar] [CrossRef]
- Megahed, S.M.; Habib, A.A.; Hammad, S.F.; Kamal, A.H. Experimental design approach for development of spectrofluorimetric method for determination of favipiravir; a potential therapeutic agent against COVID-19 virus: Application to spiked human plasma. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 249, 119241. [Google Scholar] [CrossRef]
- Islam, M.A.; Alam, M.R.; Hannan, M.O. Multiresponse optimization based on statistical response surface methodology and desirability function for the production of particleboard. Compos. Part B Eng. 2012, 43, 861–868. [Google Scholar] [CrossRef]
- Sanahuja, A.B.; Landete, M.P.; Martínez, M.I.D.; Moya, M.S.P.; García, A.V. Optimization of Volatile Compounds Extraction from Industrial Celery (Apium graveolens) By-Products by Using Response Surface Methodology and Study of Their Potential as Antioxidant Sources. Foods 2021, 10, 2664. [Google Scholar] [CrossRef] [PubMed]
- El-Sheikh, A.H.; Sweileh, J.A.; Al-Degs, Y.S.; Insisi, A.A.; Al-Rabady, N. Critical evaluation and comparison of enrichment efficiency of multi-walled carbon nanotubes, C18 silica and activated carbon towards some pesticides from environmental waters. Talanta 2008, 74, 1675–1680. [Google Scholar] [CrossRef] [PubMed]
- Ferrone, V.; Todaro, S.; Carlucci, M.; Fontana, A.; Ventrella, A.; Carlucci, G.; Milanetti, E. Optimization by response surface methodology of a dispersive magnetic solid phase extraction exploiting magnetic graphene nanocomposite coupled with UHPLC-PDA for simultaneous determination of new oral anticoagulants (NAOs) in human plasma. J. Pharm. Biomed. Anal. 2020, 179, 112992. [Google Scholar] [CrossRef]
- Chávez-Moreno, C.A.; Hinojosa-Reyes, L.; Ruiz-Ruiz, E.J.; Hernández-Ramírez, A.; Guzmán-Mar, J.L. Optimization of solid-phase extraction of parabens and benzophenones in water samples using a combination of Plakett-Burman and Box-Behnken designs. J. Sep. Sci. 2018, 41, 4488–4497. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, C.; Wang, L.; Chen, S.; Xu, Y. Optimization and validation of a head space solid-phase microextraction-arrow gas chromatography-mass spectrometry method using central composite design for determination of aroma compounds in Chinese liquor (Baijiu). J. Chromatogr. A 2020, 1610, 460584. [Google Scholar] [CrossRef] [PubMed]
- Carasek, E.; Pawliszyn, J. Screening of Tropical Fruit Volatile Compounds Using Solid-Phase Microextraction (SPME) Fibers and Internally Cooled SPME Fiber. J. Agric. Food Chem. 2006, 54, 8688–8696. [Google Scholar] [CrossRef]
- Cecchi, L.; Ieri, F.; Vignolini, P.; Mulinacci, N.; Romani, A. Characterization of Volatile and Flavonoid Composition of Different Cuts of Dried Onion (Allium cepa L.) by HS-SPME-GC-MS, HS-SPME-GC×GC-TOF and HPLC-DAD. Molecules 2020, 25, 408. [Google Scholar] [CrossRef] [Green Version]
- Gaggiotti, S.; Mascini, M.; Pittia, P.; della Pelle, F.; Compagnone, D. Headspace Volatile Evaluation of Carrot Samples—Comparison of GC/MS and AuNPs-hp DNA-Based E-Nose. Foods 2019, 8, 293. [Google Scholar] [CrossRef] [Green Version]
- Dias, A.N.; Da Silva, A.C.; Simão, V.; Merib, J.; Carasek, E. A novel approach to bar adsorptive microextraction: Cork as extractor phase for determination of benzophenone, triclocarban and parabens in aqueous samples. Anal. Chim. Acta 2015, 888, 59–66. [Google Scholar] [CrossRef]
- Shrivastava, A.; Gupta, V.B. Methods for the determination of limit of detection and limit of quantitation of the analytical methods. Chron. Young Sci. 2011, 2, 21–25. [Google Scholar] [CrossRef]
- Taverniers, I.; de Loose, M.; van Bockstaele, E. Trends in quality in the analytical laboratory. II. Analytical method validation and quality assurance. TrAC Trends Anal. Chem. 2004, 23, 535–552. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, W.; Xiao, J.; Wang, J.; Liu, G.; Shi, Q.; Guo, G. Comparison of the Enrichment Efficiency of Multiwalled Carbon Nanotubes, C18 Silica, and Activated Carbon as the Adsorbents for the Solid Phase Extraction of Atrazine and Simazine in Water Samples. Mikrochim. Acta 2006, 152, 215–224. [Google Scholar] [CrossRef]

| Factor | Level | |||
|---|---|---|---|---|
| Percolation | ||||
| −1 | 0 | +1 | ||
| X1 | Sample volume (mL) | 1 | 50.5 | 100 |
| X2 | pH | 1 | 3 | 5 |
| X3 | Flow rate (mL min−1) | 1 | 4.5 | 8 |
| Elution | ||||
| X1 | Percentage of MeOH (%) | 50 | 70 | 90 |
| X2 | Solvent elution volume (mL) | 1 | 5.5 | 10 |
| X3 | Flow rate (mL min−1) | 1 | 4.5 | 8 |
| Trial Run | X1 | X2 | X3 |
|---|---|---|---|
| 1 | −1 | −1 | 0 |
| 2 | +1 | −1 | 0 |
| 3 | −1 | +1 | 0 |
| 4 | +1 | +1 | 0 |
| 5 | −1 | 0 | −1 |
| 6 | +1 | 0 | −1 |
| 7 | −1 | 0 | +1 |
| 8 | +1 | 0 | +1 |
| 9 | 0 | −1 | −1 |
| 10 | 0 | +1 | −1 |
| 11 | 0 | −1 | +1 |
| 12 | 0 | +1 | +1 |
| 13 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 |
| Experiment | Experimental Plan | BA | Rr (%) | ||
|---|---|---|---|---|---|
| X1 (mL) | X2 | X3 (mL min−1) | SA | ||
| 1 | 1 | 1 | 4.5 | 99.41 ± 5.57 | 99.99 ± 5.68 |
| 2 | 100 | 1 | 4.5 | 12.24 ± 0.23 | 9.05 ± 0.42 |
| 3 | 1 | 5 | 4.5 | 83.54 ± 3.24 | 81.34 ± 4.73 |
| 4 | 100 | 5 | 4.5 | 8.59 ± 0.12 | 7.46 ± 0.11 |
| 5 | 1 | 3 | 1 | 95.20 ± 5.01 | 95.10 ± 5.13 |
| 6 | 100 | 3 | 1 | 0.56 ± 0.01 | 0.00 ± 0.00 |
| 7 | 1 | 3 | 8 | 92.45 ± 4.72 | 90.33 ± 4.35 |
| 8 | 100 | 3 | 8 | 7.38 ± 0.11 | 7.59 ± 0.13 |
| 9 | 50.5 | 1 | 1 | 14.64 ± 0.18 | 10.75 ± 0.62 |
| 10 | 50.5 | 5 | 1 | 7.97 ± 0.10 | 5.26 ± 0.46 |
| 11 | 50.5 | 1 | 8 | 17.20 ± 0.25 | 14.74 ± 0.22 |
| 12 | 50.5 | 5 | 8 | 9.75 ± 0.45 | 9.44 ± 0.42 |
| 13 | 50.5 | 3 | 4.5 | 10.20 ± 0.53 | 9.43 ± 0.40 |
| 14 | 50.5 | 3 | 4.5 | 11.46 ± 0.72 | 10.26 ± 0.68 |
| 15 | 50.5 | 3 | 4.5 | 8.48 ± 0.11 | 6.85 ± 0.51 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| BA | Model | 20,379.64 | 9 | 2264.40 | 242.09 | <0.0001 |
| X1—Volume | 14,607.23 | 1 | 14,607.23 | 1561.70 | <0.0001 | |
| X2—pH | 141.43 | 1 | 141.43 | 15.12 | 0.0115 | |
| X3—Flow | 8.85 | 1 | 8.85 | 0.9465 | 0.3753 | |
| X1X2 | 37.34 | 1 | 37.34 | 3.99 | 0.1022 | |
| X1X3 | 22.90 | 1 | 22.90 | 2.45 | 0.1784 | |
| X2X3 | 0.1561 | 1 | 0.1561 | 0.0167 | 0.9023 | |
| X1² | 5530.76 | 1 | 5530.76 | 591.31 | <0.0001 | |
| X2² | 17.81 | 1 | 17.81 | 1.90 | 0.2261 | |
| X3² | 0.0810 | 1 | 0.0810 | 0.0087 | 0.9295 | |
| Error | 46.77 | 5 | 9.35 | |||
| Lack of Fit | 42.29 | 3 | 14.10 | 6.30 | 0.14 | |
| Pure Error | 4.48 | 2 | 2.24 | |||
| SA | Model | 20,702.25 | 9 | 2300.25 | 272.02 | <0.0001 |
| X1—Volume | 14,677.20 | 1 | 14,677.20 | 1735.67 | <0.0001 | |
| X2—pH | 120.29 | 1 | 120.29 | 14.22 | 0.0130 | |
| X3—Flow | 15.09 | 1 | 15.09 | 1.78 | 0.2391 | |
| X1X2 | 72.70 | 1 | 72.70 | 8.60 | 0.0326 | |
| X1X3 | 38.19 | 1 | 38.19 | 4.52 | 0.0869 | |
| X2X3 | 0.0088 | 1 | 0.0088 | 0.0010 | 0.9755 | |
| X1² | 5734.84 | 1 | 5734.84 | 678.18 | <0.0001 | |
| X2² | 5.34 | 1 | 5.34 | 0.6312 | 0.4629 | |
| X3² | 0.0000 | 1 | 0.0000 | 5.390 | 0.9982 | |
| Error | 42.28 | 5 | 8.46 | |||
| Lack of Fit | 35.96 | 3 | 11.99 | 3.80 | 0.21 | |
| Pure Error | 6.32 | 2 | 3.16 |
| Experiment | X1 (%) | Experimental Plan | Log (Re) | ||
|---|---|---|---|---|---|
| X2 (mL) | X3 (mL min−1) | BA | SA | ||
| 1 | 70 | 5.5 | 4.5 | 0.57 ± 0.023 | 0.58 ± 0.033 |
| 2 | 50 | 5.5 | 8 | 0.49 ± 0.012 | 0.50 ± 0.027 |
| 3 | 90 | 1 | 4.5 | 2.02 ± 0.032 | 2.01 ± 0.034 |
| 4 | 70 | 5.5 | 4.5 | 0.52 ± 0.013 | 0.58 ± 0.016 |
| 5 | 70 | 10 | 8 | 0.01 ± 0.009 | 0.09 ± 0.004 |
| 6 | 50 | 10 | 4.5 | 0.04 ± 0.007 | 0.04 ± 0.001 |
| 7 | 50 | 1 | 4.5 | 1.41 ± 0.017 | 1.52 ± 0.023 |
| 8 | 90 | 5.5 | 8 | 0.54 ± 0.013 | 0.60 ± 0.011 |
| 9 | 90 | 5.5 | 1 | 0.61 ± 0.017 | 0.65 ± 0.013 |
| 10 | 70 | 1 | 8 | 1.95 ± 0.027 | 1.91 ± 0.024 |
| 11 | 50 | 5.5 | 1 | 0.47 ± 0.012 | 0.56 ± 0.017 |
| 12 | 90 | 10 | 4.5 | −0.05 ± 0.008 | 0.02 ± 0.004 |
| 13 | 70 | 5.5 | 4.5 | 0.40 ± 0.011 | 0.50 ± 0.012 |
| 14 | 70 | 10 | 1 | −0.10 ± 0.007 | 0.06 ± 0.013 |
| 15 | 70 | 1 | 1 | 1.97 ± 0.014 | 1.98 ± 0.028 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| BA | Model | 7.89 | 9 | 0.8762 | 62.90 | 0.0001 |
| X1—% MeOH | 0.0784 | 1 | 0.0784 | 5.63 | 0.0437 | |
| X2—Volume | 7.13 | 1 | 7.13 | 512.08 | <0.0001 | |
| X3—Flow Rate | 0.0001 | 1 | 0.0001 | 0.0097 | 0.9254 | |
| X1X2 | 0.0971 | 1 | 0.0971 | 6.97 | 0.0460 | |
| X1X3 | 0.0024 | 1 | 0.0024 | 0.1744 | 0.6936 | |
| X2X3 | 0.0053 | 1 | 0.0053 | 0.3840 | 0.5626 | |
| X1² | 0.0080 | 1 | 0.0080 | 0.5707 | 0.4840 | |
| X2² | 0.5376 | 1 | 0.5376 | 38.59 | 0.0016 | |
| X3² | 0.0222 | 1 | 0.0222 | 1.59 | 0.2626 | |
| Error | 0.0696 | 5 | 0.0139 | |||
| Lack of Fit | 0.0568 | 3 | 0.0179 | 2.27 | 0.3207 | |
| Pure Error | 0.0158 | 2 | 0.0079 | |||
| SA | Model | 7.35 | 9 | 0.8164 | 102.17 | <0.0001 |
| X1—% MeOH | 0.0539 | 1 | 0.0539 | 6.75 | 0.0484 | |
| X2—Volume | 6.69 | 1 | 6.69 | 837.35 | <0.0001 | |
| X3—Flow Rate | 0.0000 | 1 | 0.0000 | 0.0028 | 0.9595 | |
| X1X2 | 0.0652 | 1 | 0.0652 | 8.16 | 0.0356 | |
| X1X3 | 0.0000 | 1 | 0.0000 | 0.0059 | 0.9416 | |
| X2X3 | 0.0128 | 1 | 0.0128 | 1.60 | 0.2612 | |
| X12 | 0.0024 | 1 | 0.0024 | 0.2945 | 0.6107 | |
| X22 | 0.5108 | 1 | 0.5108 | 63.93 | 0.0005 | |
| X32 | 0.0109 | 1 | 0.0109 | 1.36 | 0.2958 | |
| Error | 0.0399 | 5 | 0.0080 | |||
| Lack of Fit | 0.0357 | 3 | 0.0119 | 5.56 | 0.1562 | |
| Pure Error | 0.0043 | 2 | 0.0021 |
| Factor | Optimal Value | R% | |
|---|---|---|---|
| Percolation Step | Sample volume (mL) | 1 | ~99 |
| pH | 1 | ||
| Flow rate (mL min−1) | 4.5 | ||
| Elution Step | MeOH percentage (%) | 90 | ~95 |
| Eluent volume (mL) | 1 | ||
| Flow rate (mL min−1) | 4.5 |
| Linear Range (µg mL−1) | Calibration Equation Y = ax + b | R2 | LDD (µg mL−1) | LDQ (µg mL−1) | |
|---|---|---|---|---|---|
| BA | 1–5 | y = 27.537x + 0.2850 | 0.9646 | 0.177 | 0.592 |
| 5–15 | y = 65.889x − 92.109 | 0.9889 | |||
| 25–45 | y = 43.030x − 65.610 | 0.9890 | |||
| SA | 1–5 | y = 36.852x + 3.561 | 0.9938 | 0.502 | 0.873 |
| 5–15 | y = 115.01x − 185.44 | 0.9760 | |||
| 25–45 | y = 80.260x − 251.2 | 0.9851 |
| Sample | BA | SA | |
|---|---|---|---|
| Fruit Juice | Sample 1 | 92.26 ± 1.02 | 82.99 ± 1.13 |
| Sample 2 | 90.58 ± 0.95 | 81.78 ± 1.04 | |
| Sample 3 | 97.42 ± 2.04 | 94.57 ± 2.41 | |
| Soft Drink | Sample 1 | 74.43 ± 0.56 | 81.18 ± 1.01 |
| Sample 2 | 99.51 ± 2.54 | 96.13 ± 2.72 | |
| Sample 3 | 98.21 ± 2.23 | 96.87 ± 2.91 |
| AC | MWCNT | Silica-Based C18 | ||||
|---|---|---|---|---|---|---|
| R (%) | RSD (%) | R (%) | RSD (%) | R (%) | RSD (%) | |
| BA | 67.62 | 1.85 | 75.25 | 5.67 | 98.23 | 1.64 |
| SA | 54.38 | 2.57 | 69.81 | 6.85 | 95.13 | 1.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kefi, B.B.; Baccouri, S.; Torkhani, R.; Koumba, S.; Martin, P.; M’Hamdi, N. Application of Response Surface Methodology to Optimize Solid-Phase Extraction of Benzoic Acid and Sorbic Acid from Food Drinks. Foods 2022, 11, 1257. https://doi.org/10.3390/foods11091257
Kefi BB, Baccouri S, Torkhani R, Koumba S, Martin P, M’Hamdi N. Application of Response Surface Methodology to Optimize Solid-Phase Extraction of Benzoic Acid and Sorbic Acid from Food Drinks. Foods. 2022; 11(9):1257. https://doi.org/10.3390/foods11091257
Chicago/Turabian StyleKefi, Bochra Bejaoui, Sana Baccouri, Rachel Torkhani, Sidrine Koumba, Patrick Martin, and Naceur M’Hamdi. 2022. "Application of Response Surface Methodology to Optimize Solid-Phase Extraction of Benzoic Acid and Sorbic Acid from Food Drinks" Foods 11, no. 9: 1257. https://doi.org/10.3390/foods11091257
APA StyleKefi, B. B., Baccouri, S., Torkhani, R., Koumba, S., Martin, P., & M’Hamdi, N. (2022). Application of Response Surface Methodology to Optimize Solid-Phase Extraction of Benzoic Acid and Sorbic Acid from Food Drinks. Foods, 11(9), 1257. https://doi.org/10.3390/foods11091257








