Analytical Rheology of Honey: A State-of-the-Art Review
Abstract
1. Introduction
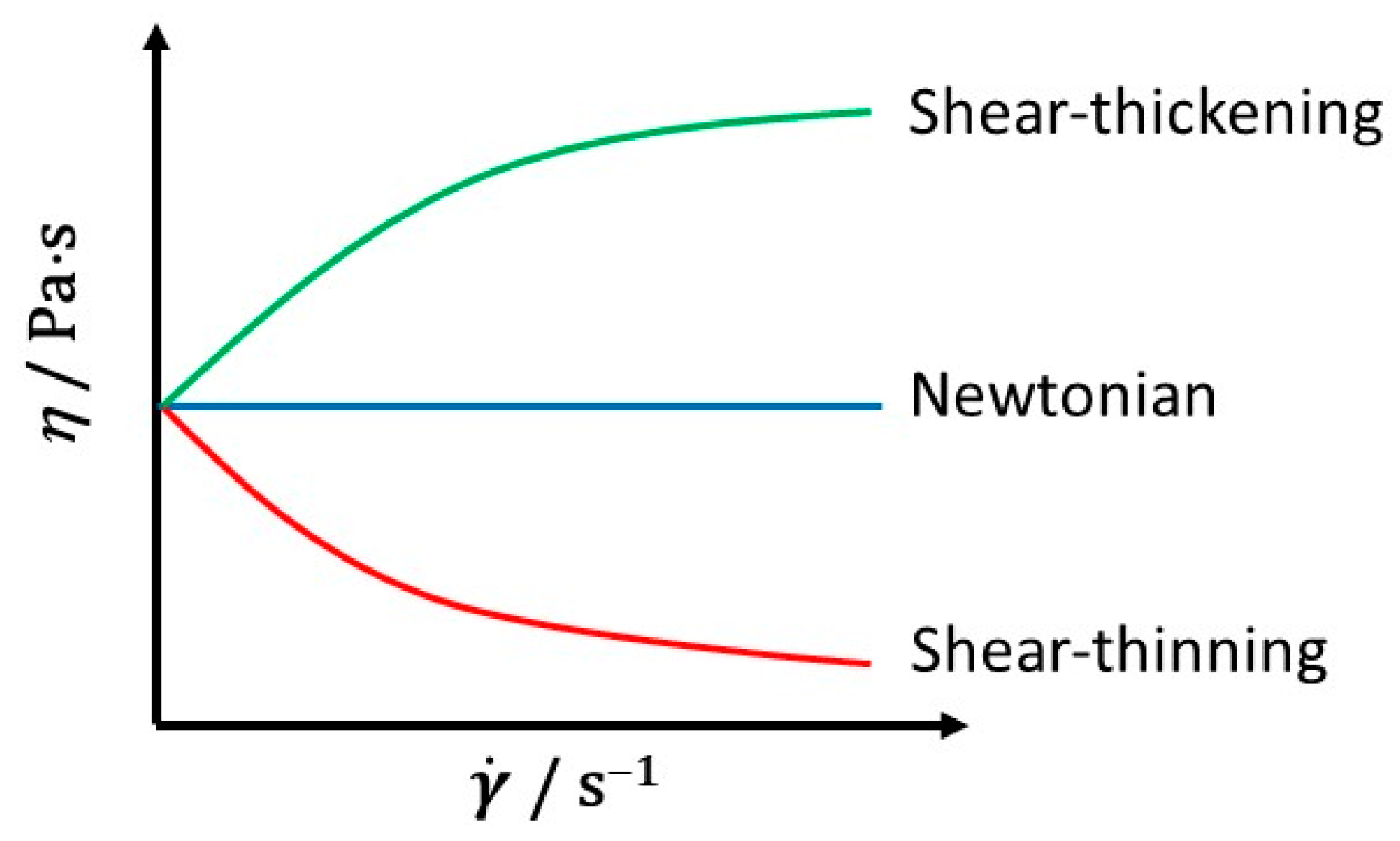
2. Rheological Models
3. Rheological Dependence on Temperature and Honey Composition
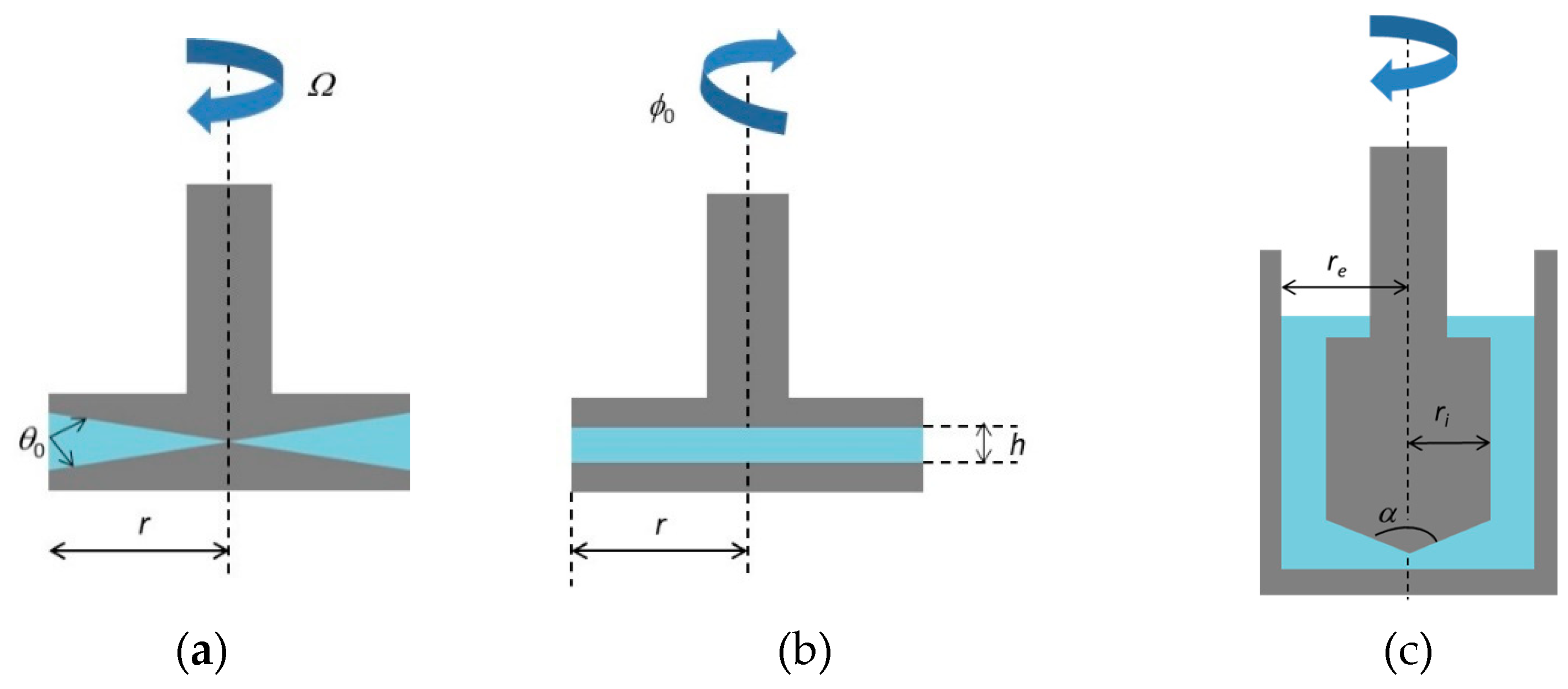
4. Rheological Measurements
5. Rheological Properties of Honey
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Codex Alimentarius. International Standard for Honey CXS 12-1981; Adopted in 1981; Amended in 2019; FAO: Rome, Italy, 1981; pp. 1–8. [Google Scholar]
- Gómez-Díaz, D.; Navaza, J.M.; Quintáns-Riveiro, L.C. Rheological behaviour of Galician honeys. Eur. Food Res. Technol. 2006, 222, 439–442. [Google Scholar] [CrossRef]
- Puscion-Jakubik, A.; Borawska, M.H.; Socha, K. Modern Methods for Assessing the quality of Bee Honey and Botanical Origin Identification. Foods 2020, 9, 1028. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q.X. Chemical composition, characterization, and differentiation of honey botanical and geographical origins. Adv. Food Nutr. Res. 2011, 62, 89–137. [Google Scholar] [CrossRef] [PubMed]
- Faustino, C.; Pinheiro, L. Antimicrobial properties and therapeutic benefits of honey in the quest for more efficient antimicrobial agents. In The Battle Against Microbial Pathogens: Basic Science, Technological Advances and Educational Programs; Méndez-Vilas, A., Ed.; Formatex: Badajoz, Spain, 2015; Volume 1, pp. 98–108. ISBN 978-84-942134-6-5. [Google Scholar]
- Gonçalves, J.; Ribeiro, I.; Marçalo, J.; Rijo, P.; Faustino, C.; Pinheiro, L. Physicochemical, Antioxidant and Antimicrobial Properties of selected Portuguese Commercial Monofloral Honeys. J. Food Nutr. Res. 2018, 6, 645–654. [Google Scholar] [CrossRef]
- Steffe, J.F. Rheological Methods in Food Process Engineering, 2nd ed.; Freeman Press: East Lansing, MI, USA, 1996; ISBN 0963203614. [Google Scholar] [CrossRef]
- Sopade, P.A.; Halley, P.; Bhandari, B.; D’Arcy, B.R.; Doebler, C.; Caffin, N. Application of the Williams-Landel-Ferry model to the viscosity-temperature relationship of Australian honeys. J. Food Eng. 2003, 56, 67–75. [Google Scholar] [CrossRef]
- Rao, M.A. Rheology of Fluid and Semisolid Foods, 2nd ed.; Food Engineering Series; Springer: New York, NY, USA, 2007; ISBN 978-1-4614-9230-6. [Google Scholar] [CrossRef]
- Fischer, P.; Windhab, E.J. Rheology of food materials. Curr. Opin. Colloid Interface Sci. 2011, 16, 36–40. [Google Scholar] [CrossRef]
- Bakier, S.; Miastkowski, K.; Bakoniuk, J.R. Rheological Properties of Some Honeys in Liquefied and Crystallised States. J. Apic. Sci. 2016, 60, 153–166. [Google Scholar] [CrossRef]
- Ahmed, J. Advances in rheological measurements of food products. Curr. Opin. Food Sci. 2018, 23, 127–132. [Google Scholar] [CrossRef]
- Kabbani, D.; Sepulcre, F.; Wedekind, J. Utrasound-assisted liquefaction of rosemary honey: Influence oh rheology and crystal content. J. Food Eng. 2011, 107, 173–178. [Google Scholar] [CrossRef]
- Ahmed, J.; Ptaszek, P.; Basu, S. Food rheology: Scientific development and importance to food industry. In Advances in Food Rheology; Ahmed, J., Ptaszek, P., Basu, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 1–4. ISBN 9780081004319. [Google Scholar] [CrossRef]
- Escriche, I.; Oroian, M.; Visquert, M.; Gras, M.L.; Vidal, D. Rheological Properties of Honey from Burkina Faso: Loss Modulus and Complex Viscosity Modelling. Int. J. Food Prop. 2016, 19, 2575–2586. [Google Scholar] [CrossRef]
- Nguyen, H.T.L.; Katopo, L.; Pang, E.; Mantri, N.; Kasapis, S. Structural variation in gelatin networks from low to high-solids systems effected by honey addition. Food Res. Int. 2019, 121, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Rao, M.A. Flow and Functional Models for Rheological Properties of Fluid Foods. In Rheology of Fluid, Semisolid and Solid Foods, 3rd ed.; Rao, M.A., Ed.; Springer: New York, NY, USA, 2014; pp. 27–61. [Google Scholar] [CrossRef]
- Recondo, M.P.; Elizalde, B.E.; Buera, M.P. Modeling temperature dependence of honey viscosity and of related supersatured model carbohydrate systems. J. Food Eng. 2006, 77, 126–134. [Google Scholar] [CrossRef]
- Bakier, S. Rheological properties of honey in a liquid and crystallized state. In Honey Analysis; de Toledo, V.A.A., Ed.; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Cohen, I.; Weihs, D. Rheology and microrheology of natural and reduced-calorie Israeli honey as a model for high-viscosity Newtonian liquids. J. Food Eng. 2010, 100, 366–371. [Google Scholar] [CrossRef]
- Dobre, I.; Georescu, L.A.; Alexe, P.; Escuredo, O.; Seijo, M.C. Rheological behaviour of different honey types from Romania. Food Res. Int. 2012, 49, 126–132. [Google Scholar] [CrossRef]
- Junzheng, P.; Changying, J. General rheological model for natural honeys in China. J. Food Eng. 1998, 36, 165–168. [Google Scholar] [CrossRef]
- Juszczak, L.; Fortuna, T. Rheology of selected Polish honeys. J. Food Eng. 2006, 75, 43–49. [Google Scholar] [CrossRef]
- Lazaridou, A.; Billiaderis, C.G.; Bacandritsos, N.; Sabatini, A.G. Composition, thermal andrheological behaviour of selected Greek honeys. J. Food Eng. 2004, 64, 9–21. [Google Scholar] [CrossRef]
- Nayik, G.A.; Dar, B.N.; Nanda, V. Physico-chemical, rheological and sugar profile of different unifloral honeys from Kashmir valley of India. Arab. J. Chem. 2019, 12, 3151–3162. [Google Scholar] [CrossRef]
- Oroian, M.; Amariei, S.; Escriche, I.; Leahu, A.; Damian, C.; Gutt, G. Chemical composition and temperature influence on the rheological behaviour of honeys. Int. J. Food Prop. 2014, 17, 2228–2240. [Google Scholar] [CrossRef]
- Ahmed, J.; Raghavan, G.S.V.; Ngadi, M. Physico-chemical, rheological, calorimetric and dielectric behaviour of selected Indian honey. J. Food Eng. 2007, 79, 1207–1213. [Google Scholar] [CrossRef]
- Al-Mahasneh, M.A.; Rababah, T.M.; Amer, M.; Al-Omoush, M. Modeling physical and rheological behaviour of minimally processed wild flowers honey. J. Food Process. Preserv. 2014, 38, 21–30. [Google Scholar] [CrossRef]
- Karasu, S.; Toker, S.O.; Yilmaz, M.T.; Karaman, S.; Dertli, E. Thermal loop test to determine structural changes and thermal stability of creamed honey: Rheological characterization. J. Food Eng. 2015, 150, 90–98. [Google Scholar] [CrossRef]
- Smanalieva, J.; Senge, B. Analytical and rheological investigations into selected unifloral German honey. Eur. Food Res. Technol. 2009, 229, 107–113. [Google Scholar] [CrossRef]
- Yanniotis, S.; Skaltsi, S.; Karaburnioti, S. Effect of moisture content on the viscosity of honey at different temperatures. J. Food Eng. 2006, 72, 372–377. [Google Scholar] [CrossRef]
- Witczak, M.; Juszczak, L.; Gałkowska, D. Non-Newtonian behaviour of heather honey. J. Food Eng. 2011, 104, 532–537. [Google Scholar] [CrossRef]
- Boussaid, A.; Chouaibi, M.; Rezig, L.; Missaoui, R.; Donsí, F.; Ferrari, G.; Hamdi, S. Physicochemical, Rheological, and Thermal Properties of Six Types of Honey from Various Floral Origins in Tunisia. Int. J. Food Prop. 2015, 18, 2624–2637. [Google Scholar] [CrossRef]
- Mehryar, L.; Esmaiili, M.; Hassanzadeh, A. Evaluation of some Physicochemical and Rheological Properties of Iranian Honeys and the effect of Temperatureon its Viscosity. J. Agric. Environ. Sci. 2013, 13, 807–819. [Google Scholar] [CrossRef]
- Al-Malah, K.I.M.; Abu-Jdayil, B.; Zaitoun, S.; Ghzawi, A.-M. Application of WLF and Arrhenius kinetics to rheology of selected dark-colored honey. J. Food Process. Eng. 2001, 24, 341–357. [Google Scholar] [CrossRef]
- Zaitoun, S.; Ghzawi, A.-M.; Al-Malah, K.I.M.; Abu-Jdayil, B. Rheological properties of selected light colored Jordanian honey. Int. J. Food Prop. 2001, 4, 139–148. [Google Scholar] [CrossRef]
- Abu-Jdayil, B.; Ghzawi, A.-M.; Al-Malah, K.I.M.; Zaitoun, S. Heat effect oh rheology of light- and dark-colored honey. J. Food Process. Eng. 2002, 51, 33–38. [Google Scholar] [CrossRef]
- Oroian, M.; Amariei, S.; Escriche, I.; Gutt, G. Rheological Aspects of Spanish Honeys. Food Bioprocess Technol. 2013, 6, 228–241. [Google Scholar] [CrossRef]
- Da Silva, V.M.; de Almeida Torres Filho, R.; de Resende, J.V. Rheological properties of selected Brazilian honeys as a function of temperature and soluble solid concentration. Int. J. Food Prop. 2017, 20, S2481–S2494. [Google Scholar] [CrossRef]
- Afonso, M.J.; Magalhães, M.; Fernandes, L.; Castro, M.; Ramalhosa, E.C.D. Temperature Effect on Rheological Behaviour of Portuguese Honeys. Pol. J. Food Nutr. Sci. 2018, 68, 217–222. [Google Scholar] [CrossRef]
- Maldonado, G.E.; Navarro, A.S.; Yamul, D.K. A comparative study of texture and rheology of Argentinian honeys from two regions. J. Texture Stud. 2018, 49, 424–433. [Google Scholar] [CrossRef]
- Elenany, Y.E. Physiochemical Parameters and Rheological Properties of Citrus, Clover and Marjoram Egyptian Bee Honeys. J. Entomol. 2019, 16, 17–22. [Google Scholar] [CrossRef]
- Maieves, H.A.; Zuge, L.C.B.; Teixeira, G.L.; Cámara, M.; Ribani, R.H.; Sánchez-Mata, M.C. Chemical properties, rheological behaviour, and Melissopalynological Analysis of Selected Brazilian Honey from Hovenia dulcis Flowering. Braz. Arch. Biol. Technol. 2020, 63, e20190743. [Google Scholar] [CrossRef]
- Stanciu, I. Influence of Temperature on the rheological Behaviour of Orange Honey. Orient J. Chem. 2021, 37, 440–443. [Google Scholar] [CrossRef]
- Přidal, A.; Trávníček, P.; Kudělka, J.; Nedomová, S.; Ondrušíková, S.; Trost, D.; Kumbár, V. A Rheological Analysis of Biomaterial Behaviour as a Tool to Detect the Dilution of Heather Honey. Materials 2021, 14, 2472. [Google Scholar] [CrossRef] [PubMed]
- Trávníček, P.; Vítěz, T.; Přidal, A. Rheological Properties of Honey. Sci. Agric. Bohem. 2012, 43, 160–165. [Google Scholar] [CrossRef]
- Ribeiro, G.P.; Villas-Bôas, J.K.; Spinosa, W.A.; Prudêncio, S.H. Influence of freezing, pasteurization and maturation on Tiúba honey quality. LWT Food Sci. Technol. 2018, 90, 607–612. [Google Scholar] [CrossRef]
- Faustino, C.; Bettencourt, A.F.; Alfaia, A.; Pinheiro, L. Introducing Students to Rheological Classification of Foods, Cosmetics, and Pharmaceutical Excipients Using Common Viscous Materials. J. Chem. Educ. 2015, 92, 936–939. [Google Scholar] [CrossRef]
- Kamboj, U.; Mishra, S. Prediction of Adulteration in Honey Using Rheological Parameters. Int. J. Food Prop. 2015, 18, 2056–2063. [Google Scholar] [CrossRef]
- Oh, J.-H.; Yoo, B. Effect of Temperature on the Relationship between Moisture Content and Dynamic Rheological Properties of Korean Honey. Food Sci. Biotechnol. 2011, 20, 261–265. [Google Scholar] [CrossRef]
- Oroian, M.; Ropciuc, S.; Paduret, S.; Todosi, E. Rheological analysis of honeydew honey adulterated with glucose, fructose, inverted sugar, hydrolysed inulin syrup and malt wort. LWT Food Sci. Technol. 2018, 95, 1–8. [Google Scholar] [CrossRef]
- De Silva, V.M.; de Carvalho, L.A.; de Oliveira, N.L.; de Almeida Torres Filho, R.; de Resende, J.V. Rheological and thermal properties of selected Brazilian honeys from various floral origins. J. Texture Stud. 2016, 47, 208–219. [Google Scholar] [CrossRef]
- Yoo, B. Effect of temperature on dynamic rheology of Korean honeys. J. Food Eng. 2004, 65, 459–463. [Google Scholar] [CrossRef]
- Oroian, M.; Amariei, S.; Escriche, I.; Gutt, G. A Viscoelastic Model for Honeys Using the Time-Temperature Superposition Principle (TTSP). Food Bioprocess Technol. 2013, 6, 2251–2260. [Google Scholar] [CrossRef]
- Nobile, M.A.D.; Chillo, S.; Mentana, A.; Baiano, A. Use of the generalized Maxwell model for describing the stress relaxation behaviour of solid-like foods. J. Food Eng. 2007, 78, 978–983. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Tatlisu, N.B.; Toker, O.S.; Karaman, S.; Dertli, E.; Sagdic, O.; Arici, M. Steady, dynamic and creep rheological analysis as a novel approach to detect honey adulteration by fructose and saccharose syrups: Correlations with HPLC-RID results. Food Res. Int. 2014, 64, 634–646. [Google Scholar] [CrossRef]
- Bakier, S. The influence of temperature and water content on the rheological properties of Polish honeys. Pol. J. Food Nutr. Sci. 2007, 57, 17–23. [Google Scholar]
- Gómez-Díaz, D.; Navaza, J.M.; Quintáns-Riveiro, L.C. Effect of temperature on the viscosity of honey. Int. J. Food Prop. 2009, 12, 396–404. [Google Scholar] [CrossRef]
- Saxena, S.; Panicker, L.; Gautam, S. Rheology of Indian Honey: Effect of Temperature and Gamma Radiation. Int. J. Food Sci. 2014. [Google Scholar] [CrossRef] [PubMed]
- Nayik, G.A.; Dar, B.N.; Nanda, V. Rheological behaviour of high altitude Indian honey varieties as affected by temperature. J. Saudi Soc. Agric. Sci. 2018, 17, 323–329. [Google Scholar] [CrossRef]
- Ashokan, B.K.; Kokini, J.L. Determination of the Wlf constants of cooked soy flour and their dependence on the extent of cooking. Rheol. Acta 2005, 45, 192–201. [Google Scholar] [CrossRef]
- Nguyen, H.T.L.; Panyoyai, N.; Paramita, V.D.; Mantri, N.; Kasapis, S. Physicochemical and viscoelastic properties of honey from medicinal plants. Food Chem. 2018, 241, 143–149. [Google Scholar] [CrossRef]
- Kedzierska-Matysek, M.; Florek, M.; Wolanciuk, A.; Skatecki, P. Effect of freezing and room temperatures storage for 18 months on quality of raw rapeseed honey (Brassica napus). J. Food Sci. Technol. 2016, 53, 3349–3355. [Google Scholar] [CrossRef] [PubMed]
- Oroian, M.; Ropciuc, S.; Paduret, S. Honey authentication using rheological and physicochemical properties. J. Food Sci. Technol. 2018, 55, 4711–4718. [Google Scholar] [CrossRef]
- Al-Mahasneh, M.A.; Rababah, T.M.; Ma’Abreh, A.S. Evaluating the combined effect of temperature, shear rate and water content on wild-flower honey viscosity using adaptive neural fuzzy inference system and artificial neural networks. J. Food Process. Eng. 2013, 36, 510–520. [Google Scholar] [CrossRef]
- Naila, A.; Flint, S.H.; Sulaiman, A.Z.; Ajit, A.; Weeds, Z. Classical and novel approaches to the analysis of honey and detection of adulterants. Food Control. 2018, 90, 152–165. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, J.; Wang, Y. Classification of monofloral honeys from different floral origins and geographical origins based on rheometer. J. Food Eng. 2010, 96, 469–479. [Google Scholar] [CrossRef]
- Oroian, M. Influence of temperature, frequency and moisture content on honey viscoelastic parameters—Neural networks and adaptive neuro-fuzzy inference system prediction. LWT Food Sci. Technol. 2015, 63, 1309–1316. [Google Scholar] [CrossRef]
- Escriche, I.; Tanleque-Alberto, F.; Visquert, M.; Oroian, M. Physicochemical and rheological characterization of honey from Mozambique. LWT Food Sci. Technol. 2017, 86, 108–115. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahd, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- De Silva, V.M.; Lacerda, W.S.; de Resende, J.V. Artificial Neural Network and Regression models to evaluate rheological properties of selected Brazilian Honeys. J. Apic. Sci. 2020, 64, 219–228. [Google Scholar] [CrossRef]
- Carmona, J.A.; Ramírez, P.; Calero, N.; Munoz, J. Large amplitude oscillatory shear of xanthan gum solutions. Effect of sodium chloride (NaCl) concentration. J. Food Eng. 2014, 126, 165–172. [Google Scholar] [CrossRef]
- Dealey, J.; Plazek, D. Time-temperature superposition—A users guide. Rheol. Bull. 2009, 78, 16–31. [Google Scholar]
- Oroian, M.; Paduret, S.; Amariei, S.; Gutt, G. Chemical composition and temperature influence on honey texture properties. J. Food Sci. Technol. 2016, 53, 431–440. [Google Scholar] [CrossRef]
- Belay, A.; Haki, G.D.; Birringer, M.; Borck, H.; Addi, A.; Baye, K.; Melaku, S. Rheology and botanical origin of Ethiopian monofloral honey. LWT Food Sci. Technol. 2017, 75, 393–401. [Google Scholar] [CrossRef]
- Determination of the Mechanical and Thermal Stability of Skin Cream with Oscillation and Freeze-Thaw Cycle Tests. Available online: https://www.anton-paar.com (accessed on 16 April 2021).
- Fakhlaei, R.; Selmat, J.; Khatib, A.; Razis, A.F.A.; Sukor, R.; Ahmad, S.; Babadi, A.A. The Toxic Impact of Honey Adulteration: A Review. Foods 2020, 9, 1538. [Google Scholar] [CrossRef]
- Amiry, S.; Esmaiili, M.; Alizadeh, M. Classification of adulterated honeys by multivariate analysis. Food Chem. 2017, 224, 390–397. [Google Scholar] [CrossRef]
- Wu, L.; Du, B.; Heyden, Y.V.; Chen, L.; Zhao, L.; Wang, M.; Xue, X. Recent advancements in detecting sugar-based adulterants in honey—A challenge. TrAC Trends Anal. Chem. 2017, 86, 25–38. [Google Scholar] [CrossRef]
- Venir, E.; Spaziani, M.; Maltini, E. Crystallization in ‘‘Tarassaco” Italian honey studied by DSC. Food Chem. 2010, 122, 410–415. [Google Scholar] [CrossRef]
- Scripcă, L.A.; Amariei, S. The use of Ultrasound for Preventing Honey Crystallization. Foods 2021, 10, 773. [Google Scholar] [CrossRef]
- Önür, İ.; Misra, N.N.; Barba, F.J.; Ptutnik, P.; Lorenzo, J.M.; Gökmen, V.; Alpas, H. Effects of ultrasound and high pressure on physicochemical properties and HMF formation in Turkish honey types. J. Food Eng. 2018, 219, 129–136. [Google Scholar] [CrossRef]
- Ouchemoukh, S.; Lovaileche, H.; Scheitzer, P. Physicochemical characteristics and pollen Spectrum of some Algerian honeys. Food Control. 2007, 18, 52–58. [Google Scholar] [CrossRef]
- Trávníček, P.; Přidal, A. Thixotropic behaviour of Honey from Eucalyptus spp. J. Food Process. Preserv. 2017, 41, e13094. [Google Scholar] [CrossRef]
- Silva, K.F.N.L.; Santos, D.C.S.; Silva, C.T.S.; Queiroz, A.J.M.; Lima, A.O.N. Comportamento reológico do mel de Apis mellifera do município de Tabuleiro do Norte-CE. Rev. Bras. Tecnol. Agroind. 2010, 4, 52–57. [Google Scholar] [CrossRef][Green Version]
- Kamboj, R.; Nayik, A.; Bera, M.B.; Nanda, V. Sugar profile and rheological behaviour of four different Indian honey varieties. J. Food Sci. Technol. 2020, 57, 2985–2993. [Google Scholar] [CrossRef]
- Xia, Q.; Xiao, H.; Pan, Y.; Wang, L. Microrheology advances in methods and insights. Adv. Colloid Interface Sci. 2018, 257, 71–85. [Google Scholar] [CrossRef] [PubMed]
- Orczykowska, M.; Olejnik, T.P.; Rosicka-Kaczmarek, J.; Miskiewicz, K.; Kowalska, G. Use of phenomenological rheology methods to analyze the viscoelastic properties of bee honeys. J. Food Process. Eng. 2021, 44, e13637. [Google Scholar] [CrossRef]
| Honey Variety and Geographical Origin | Viscometer/Rheometer Measuring Geometries | Rheological Methods and Variables Range | Measured Rheological Parameters | Main Outcomes | Ref. |
|---|---|---|---|---|---|
| Argentina: multifloral north (MFN), central (MFC) | Rheometer PP (gap 1.0 mm) | Preheating: 45 °C, 1 h SSF : 0.1–400 s−1 T: 283.15–323.15 K DS—SAOS Frequency sweep: 0.4–600 rad s−1, γ 0.5% (LVR) T: 293.15 K | η, σ G′, G′′, η* | σ vs. —Newtonian behaviour. G′′ >> G′: viscous nature (except at very high frequencies, G′′ = G′′). η ≅ η* (Cox-Merz rule verified). η, G′′, η* (MFN) > η, G′′, η* (MFC). η vs. T (Arrhenius): Ea: 79.61 (MFN)—82.09 (MFC). η vs. T (WLF, r2 ≥ 0.81 MFN, ≥ 0.91 MFC); C1, C2—“universal” constants: Tg: 224.59 K (MFN), 220.41 K (MFC) (matching Tg from DSC); ηg: 1.32 × 1011 (MFN), 1.18 × 1011 (MFC). η vs. T (WLF with varying C1 and C2 constants and Tg from DSC, r2 ≥ 0.97 MFN; ≥ 0.96 MFC); C1: 13.75 (MFN), 14.63 (MFC); C2: 24.76 (MFN), 27.01 (MFC); ηg: 1.95 × 1018 (MFN)—1.66 × 1020 (MFC). Agreement between rheology and back extrusion assays: hardness (MFC) > hardness (MFN); same consistency and adhesivity (MFN and MFC). Cluster analysis (rheological and textural parameters): weak classification of honeys. | [41] |
| Argentina: “algarrobo” | Rotational viscometer | SSF T: 278.15–343.15 K | η | Newtonian behaviour. η vs. T (Arrhenius, r2 = 0.994): Ea: 82.8. η vs. T (WLF, r2 = 0.996); C1 (13.8), C2 (50); ηg: 7.4 × 107; Tg: 227.95 K. η vs. T (VTF, r2 = 0.996); B: 1535. η vs. T (P-L, r2 = 0.998); K: 2.9 × 1014; m: 7.5. WFL equation with C1 and C2 calculated by reduced variables method: the most suitable for modelling viscosity-temperature dependence. | [18] |
| Australia: tulsi (TUL), manuka1 (MH1); USA: alfalfa (ALF); New Zealand: manuka2 (MH2) | Rheometer PP (ϕ 5 mm; gap 1 mm) | DS Samples equilibrated: 15 °C, 10 min; cooled (sub-zero region), 1 °C/min, 1 rads−1, γ = 0.01% Frequency sweeps: 0.1–100 rad s−1. T: 213.15–253.15 K | G′, G′′, aT, Tg, fg, αf, Ea | TTSP: production of a set of aT. log aT vs. T (Arrhenius-type fit), Ea = 108 (TUL), 86 (ALF), 81 (MH1), 99 (MH2). At upper temperature of the glass transition, log aT vs. T (WLF fit, modelling free volume): C1 = 10,70 (TUL), 10.85 (ALF), 11.43 (MH1), 11.13 (MH2); C2 = 50; Tg = 226.15 K (TUL), 228.15 K (ALF), 229.15 K (MH1), 227.15 K (MH2); (Tg,DSC = 226.15 K). fg = 0.040 (TUL, ALF), 0.038 (MH1, MH2); αf = 8.0 × 10−4 (TUL, ALF), 7.6 × 10−4 (MH1, MH2). Hbs in intermolecular association amongst monosaccharides generated a semi-crystalline system which allowed the prediction of mechanical Tg, that define the passage liq-like to sol-like at sub-zero temperatures. WLF eq. allowed estimation of free volume parameters for honey vitrification. | [62] |
| Australia: blue top iron bark (BTIB), bloodwood (BDW), gum top (GT), heath (H), narrow leafed iron bark (NLIB), stringy bark NT (STB), tea tree (TT), yapunyah (YAP), yellow box (YB) | Rheometer with Couette geometry (ϕcup 34 mm; ϕbob 32 mm; Lbob 34 mm; | Preheating 55 °C, kept 30 °C SSF T: 275.15–313.15 K ~0.01–100 s−1 | η | η = 1.0 (STB, 313.15 K)–410.7 (YAP, 275.15 K). η vs. T (Arrhenius, r ≥ 0.987): Ea: 99.6 (TT)–106.0 (BDH); ηg: 9.0 × 105 (NLIB)—2.0 × 106 (BTIB, BDW, H, STB). η vs. T (WLF, r ≥ 0.997); C1 (13.7–21.1), C2 (55.9–118.7); ηg: 4.0 × 107 (NLIB)–4.0 × 1020 (YAP). η vs. T (VTF, r ≥ 0.898); B: 4.5 (NLIB)–13.5 (YAP). η vs. T (P-L, r ≥ 0.951); K: 1.1 × 103 (STB)–8.0 × 103 (YAP); m: −2.3 (YAP)–2.2 (BDW). WLF: the most suitable model for viscosity-temperature dependence; constants C1 and C2 calculated from non-linear regression analysis, are valuable for adequate rheology modelling of honeys. | [8] |
| Brazil: Hovenia dulcis from Apis mellifera (Hd1) and Tetragonisca angustula (Hd2) bees | Rotational viscometer, cylindrical spindles, sample chambers | SSF : 0–2.5 s−1 T: 303.15–333.15 K | η, σ | η (0.1 s−1): 0.08 (Hd2, 333.15 K)–45.50 (Hd1, 303.15 K). η vs. T (Arrhenius): Ea: 52.65 (Hd2)–125.91 (Hd2). σ vs. (P-L), r2 ≥ 0.99; K: 5.22 (Hd2)–421.98 (Hd1); n: 0.88 (Hd1)–1.02 (Hd2). σ vs. (CA), r2 ≥ 0.98; KC: 2.36 (Hd2)–18.96 (Hd1); σC < 1.34. Hd1: Newtonian behaviour (303.15 K); non-Newtonian, shear thinning behaviour (313.15–333.15 K). Hd2: Newtonian behaviour (303.15 K); non-Newtonian, shear-thickening (313.15 K, 323.15 K), shear thinning behaviour (333.15 K). | [43] |
| Brazil: “assa-peixe” (AP), “cipó-uva” (CU), eucalyptus (EU), orange blossom (OB), multifloral—southeast (MF1), south (MF2), northeast (MF3), mid-west (MF4) | Rheometer PP (ϕ 1 mm; gap 35 mm) | Preheating 55 °C, kept 30 °C, 48 h SSF : 0.1–100 s−1, 3 cycles T: 238.15–333.15 K DS—SAOS Stress sweeps, 1 Hz f: 0.1–10 Hz T: 283.15–333,15 K | η G′, G′′, η* | η: 147.3 (CU, 283.15 K)–0.35 (MF4, 333.15 K). η*: 151.33 (CU, 283.15 K)–0.42 (MF4, 333.15 K). η vs. η*: α ~ 1 (Cox-Merz rule verified), except: OB, MF1. η or η* vs. T (Arrhenius, r2 ≥ 0.994): Ea (η): 84.97 (CU)–92.53 (MF4); Ea (η*): 85.60 (EU)–100.40 (OB). η or η* vs. T (WLF, r2 ≥ 0.9999); with fixed C1 and C2 universal constants); ηg (η) 7.4 × 1011 (MF4)–1.09 × 1012 (CU); Tg (η) 210.47 K (MF4)–215.70 (CU); ηg (η*) 4.98 × 1011 (MF3)–1.63 × 1012 (AP); Tg (η*) 210.44 K (EU)–220.27 (OB); η or η* vs. T (VTF, r2 ≥ 0.9986); B (η): 1352.83 (MF4)–1465.71 (CU); B (η*): 1361.68 (EU)–1581.04 (OB). η or η* vs. T (P-L, r2 ≥ 0.9990); K (η): 1.83 × 1015 (MF4)—1.39 × 1016 (OB), m (η): 7.65 (MF4)–7.98 (OB); K (η*): 3.15 × 1015 (MF4)–6.34 × 1017 (MF1), m (η): 7.53 (EU)–8.63 (OB). η* independent of ω: liquid-like, Newtonian behaviour (293.15–333,15 K). Non-Newtonian, shear-thinning (283.15–288,15 K): WLF: best predictor model for OB, MF1, MF2. Increase in TSS concentration → increase in Ea, Tg (WLF), B (VTF), m (P-L) coefficients. Selection of adequate T and TSS conditions, during processing and storage, are decisive for honey stability. ANN-MLP, input layers T, ω: η (model 1); G′, G′′, η* (model 2-heating; model 3-cooling). Input layers T, w, ω:); G′, G′′, η* (model 4). Potential application of the models (except for G´ in models 3 and 4), for the processing of honey and honey-based products. | [39,52,71] |
| Burkina Faso (north- and central-eastern) | Rheometer PP (ϕ 60 mm; gap 0.5 mm) | Preheating 55 °C, kept 30 °C DS Stress sweep, 1 Hz Frequency sweep: 0.62–62.83 rad s−1, 1 Pa (LVR) T: 278.15–313,15 K | G′, G′′, η*, δ | G′′ >> G′: viscous nature. η* vs. ω: constant function; δ ~90°: Newtonian behaviour. η* vs. T: Ea = 41.07–48.58. G′′ vs. T: Ea = 24.09–48.11. Ea (η*) ≅ Ea (G′′): Newtonian behaviour. Prediction of G′′ and η*: negative linear influence of fructose and temperature, positive linear influence of glucose. | [15] |
| Czech Rep.: blossom-honeydew (BHD), blossom honeydew lime (BHL), blossom honey nectar (BHN) | Rheometer CP, (ϕ 50 mm; angle 1°). | Preheating: 55 °C, 1 h; kept: 30 °C, 48 h SSF : 0–100 s−1, T: 287.15–323.15 K | η, σ | σ vs. (Newton model): linear function. η (BHL) > η (BHD) > η (BHN) η vs. T (Arrhenius, r2 ≥ 0.9945); Ea: 102.07 (BHN), 104.85 (BHD), 105.9 (BHL). | [46] |
| Egypt: citrus (CIT), clover (CLO), marjoram (MAR) | Viscometer CC | SSF : 6.12–122 s−1 T: 298.15 K | η, σ | η vs. : shear-thinning behaviour. η: 22.75 (MAR, w 18.10%, F/G 1.33); 12.50 (CLO, w 19.42%, F/G 1.27); 11.40 (CIT, w 19.74%, F/G 1.32). | [42] |
| Ethiopia: acacia (AC), Becium grandiflorum (BG), Croton macrostachyus (CM), Eucalyptus globulus (EUG), Hypoestes (H), Leucas abyssinica (LA), Schefflera abyssinica (SCA), Syzygium guineense (SG), Vernonia amygdalina (VA) | Rotational viscometer CC (ϕint 10.61 mm) | Preheating: 45 °C, 3 h + 50 °C, 30 min SSF : 2.58–258.1 s−1 T: 298.15–318.15 K | η | σ vs. (Newton, r2 ≥ 0.96), η: 4.73 (CM, 318.15 K)–29.21 (EUG, 298.15 K) Newtonian behaviour. η vs. T (Arrhenius, r2 ≥ 0.96): Ea: 9.859 (VA)–60.042 (EUG). η vs. t: constant function. | [75] |
| Germany: false acacia (FA), heather (H), sunflower (SF), lime (L), rape (R) | Rheometer CC | SSF : 0.2–60 s−1 T: 283.15–323.15 K DS γ: 10−3 T: 273.15–348.15 K–273.15 K Heating/cooling rate: 1 K/min | η, σ G′, G′′, tanδ | σ vs. (Newton, FA), η = 0.841(323.15 K)–2.31 (313.15 K) σ vs. (P-L), K: 0.69 (SF, 323.15 K)–172.66 (L, 293.15 K); n: 0.800 (R, 303.15 K)–1.002 (R, 313.15 K). σ vs. (HB), K: 13.39 (H, 293.15 K)–620.06 (R, 283.15 K); n: 0.378 (R, 293.15 K)–1.001 (FA, 283.15 K); σy: 0.15 (H, 293.15 K)–137.26 (R, 283.15 K). Newtonian (FA); Non-Newtonian (H, SF, L, R). G′′ >> G′ (FA, SF, L, R): viscous nature. G′ > G′′ (H): viscoelastic nature; heather honey: gel-like system after heating (>1.6% proteins in colloidal form). T = 338.79 K: G′ = 14.31; G′′ = 14.69; tanδ = 2.24. Crystallization of honeys is depended on botanic origin, temperature and storage time. | [30] |
| Greece: pine honeydew (PHD), fir honeydew (FHD), thymus (THY), orange blossom (OB), helianthus (HEL), cotton (COT) | Rotational viscometer CC, CC (ϕint 19.36 mm; Lint 58.08 mm; ϕext 21 mm | Preheating: 45 °C, 3 h + 50 °C, 30 min SSF : 5–100 s−1 T: 298.15–318.15 K | η, σ | σ vs. —linear regression: Newtonian behaviour. η: 0.421 (COT, 318.15 K, w 21%)–26.52 (FHD, 303.15 K, w 15%). η vs. T (Arrhenius, r2 ≥ 0.9951): Ea: 70.8 (COT, w 21%)–96.3 (FHD, w 15%). | [31] |
| Greece: pine honeydew (PHD), fir honeydew (FHD), multifloral (MF), orange blossom (OB) | Rheometer CC (ϕcup 28.92 mm; ϕbob 26.66 mm) | Preheating 50 °C, 1 h SSF T: 293.15–333.15 K : 0.1–500 s−1 DS γ: 0.1% ω: 3–300 rad s−1 T: 293.15 K | η, σ G′, G′′, η* | η (293.15 K) = 9.9 (PHD)–200 (FHD). σ vs. , constant viscosity: Newtonian behaviour. G′′ >> G′: viscous nature. G′: 0.15 (OB)–19.10 (FHD). G′′: 64 (OB)–1701 (FHD). η*: 7.7 (PHD)–167.0 (FHD). η and G′′ inversely related to the water content of honey. η vs. T (Arrhenius, r2 > 0.95), Ea: 72.69 (PHD)–93.75 (FHD). η vs. T (WLF with fixed C1 and C2 universal constants, r2 = 0.95–0.99); ηg: 3.3 × 1011 (PHD)—7.8 × 1011 (FHD); Tg: 209.88 K (OB)–230.53 (FHD). η vs. T (WLF with varying C1 and C2 constants and Tg from DSC, r2 = 0.95–0.99); C1: 17.20 (OB)–25.18 (PHD), C2: 13.95 (OB)–30.90 (PHD); ηg: 7.1 × 1012 (OB)–5.2 × 1021 (PHD); Tg (DSC): 225.85 K (PHD)–238.40 (FHD). | [24] |
| India: cotton (COT), coriander (COR), dalbergia (DAL), murraya (MUR) | Rheometer PP, (ϕ 50 mm; gap 0.5 mm) | Preheating: 50 °C, 1 h; kept: 30 °C DS Frequency sweep: 0.63–63 rad s−1, γ 0.5% (LVR) T: 278.15–303.15 K | η, σ G′, G′′ | η: 3.89 (MUR)–185.13 (COR). η vs. T (Arrhenius, r2 ≥ 0.99); Ea: 94.51 (COT)– 100.19 (COR). G′′: 227.4 (MUR, 303.15 k)–10.553 (COR, 278.15 K). G′′>>G′: viscous nature. G vs. T (Arrhenius; r2≥ 0.99); Ea: 94.27 (COT)– 99.66 (COR). G′′ vs. ω (P-L), r2≥ 0.99; K′′: 3.70 (MUR, 303.15 K)–169.25 (COR, 278.15 K); n′′: 0.99–1. Newtonian behaviour. | [86] |
| India (Kashmir): saffron (SA), apple (AP), cherry (CH), Plectranthus rugosus (PR) | Rheometer PP, (ϕ 50 mm; gap 0.5 mm) | Preheating: 50 °C, 1 h, kept 30 °C DS Frequency sweep: 0.63–63 rad s−1, γ 3% (LVR) T: 273.15–303.15 K | η, G′, G′′ | η: 0.35 (SA, 303.15 K)–21.97 (PR, 273.15 K). G′′ >> G′, K′′ >> K′: viscous nature. G′: 0.009 (AP, 303.15 K)–85.95 (CH, 273.15 K). G′′: 0.23 (SA, 303.15 K)–1382 (PR, 273.15 K). G′′ vs. ω (P-L), r2 ≥ 0.97; K′′: 0.37 (SA, 303.15 K)–22.02 (PR, 273.15 K); n′′: 0.96 (SA, 303.15 K)–1.00 (PR, 273.15 K). Newtonian behaviour. η vs. T (Arrhenius, r2 = 0.99): Ea: 77.18 (PR)–85.59 (SA); G′′ vs. T (Arrhenius, r2 = 0.99): Ea: 77.80 (PR)–86.88 (SA). | [25] |
| India: acacia (AC), pine honeydew (PHD), multifloral (MF) | Rheometer PP, (ϕ 50 mm; gap 0.5 mm) | Preheating: 50 °C, 1 h, kept 30 °C SSF ~0–1.8 s−1 T: 273.15–303.15 K DS Frequency sweep: 0.63–63 rad s−1, γ 3% (LVR) T: 273.15–303.15 K | η, σ G′, G′′ | σ vs. : Newtonian behaviour. η: 0.27 (AC, 303.15 K)–17.27 (MF, 273.15 K). G′′ >> G′, K′′ >> K′: viscous nature. G′: 0.01 (AC, 303.15 K)–15.3 (MF, 273.15 K). G′′: 0.19 (AC, 303.15 K)–1085.49 (MF, 273.15 K). G′′ vs. ω (P-L), r2: 0.99; K′′: 0.28 (AC, 303.15 K)–17.30 (MF, 273.15 K); n′′: 1. Newtonian behaviour. η vs. T (Arrhenius, r2 = 0.99): Ea: 62.10 (PHD)–75.87 (AC). | [60] |
| India: multifloral honey, adulterated with jaggery (5–30%, w/w) | Rheometer PP, (ϕ 20 mm; gap 1 mm) | SSF : 0–20 s−1, T: 298.15 K σ: 10 Pa, T: 278.15–303.15 K DS Frequency sweep: 0.1–40 Hz, σ 10 Pa, γ 0.409 (LVR) T: 298.15 K | ηapp, σ G′, G′′ | ηap: 2.48 (5%)–4.83 (30%). σ vs. (Bingham model). Pure honey: Newtonian. Adulterated honey: non-Newtonian, Bingham plastic, anti-thixotropic. ηapp vs. T (Arrhenius); Ea: 35.48 (0%)–38.48 (30%). G′′>>G′: viscous nature. Adulteration only affected the viscous properties. | [49] |
| Iran: pure honey adulterated with data syrup (DS) and invert sugar syrup (IS)–7%, 15%, 30% | Rotating viscometer, and spindle Texture analyser; cylindrical probe (ϕ 25 mm; ϕ 6 mm; for adhesion-cohesion) | SSF T: 293.15 K : 10 rpm T: 295.15 K | η, Fmax, adhesiveness, stringiness, Surface stickiness, tStart-Stringiness tstringiness | Samples classification by PCA, LDA. LDA model based on rheological properties, detected and classified correctly 67.65% of honey samples adulterated with complex sugars. | [78] |
| Israel: citrus flower (CIT), wildflower (WF), wildflower-based light (WF-BL), field-flower-based light (FF-BL) | Rheometer CP, (ϕ 60 mm; angle 4°). | Preheating: 55 °C, 3 h; kept: 30 °C SSF > 0.001 s−1 M ≤ 40 T: 278.15–308.15 K VPT micro-rheology: Fluorescent, carboxyl-modified, polystyrene particles (ϕ 200 mm) embedded within honey samples | η | η vs. –constant function: Newtonian behaviour η (natural honeys): 5.0 (WF, 308.15 K)–558.3 (CIT, 278.15 K). η (reduced calories honeys): 4.2 (FF-BL, 308.15 K)–193.8 (WF-BL, 278.15 K). η vs. T (Arrhenius, r2 ≥ 0.98); Ea: 84.7 (FF-BL)–96.9 (CIT). >90% particles: diffusive motion, αMSD = 1. ηmicrorheology–calculated using the Stokes-Einstein relation. η () matched ηmicrorheology–Newtonian behaviour in both length scales. | [20] |
| Jordan: common black horehound (CBH), globe thistle (GT), squill (Sq) | Rotational viscometer, CC (ϕ 15.2 mm; L 60 mm; gap width 5.8 mm | SSF : 2.2–219.8 s−1 T: 293.15–323.15 K | η, σ | σ vs. (Newton, r2= 0.999), η = 0.84 (GT, 323.15 K)–52.12 (CBH, 293.15 K). η vs. T (Arrhenius, r ≥ 0.998)—Ea: 95.64 (Sq), 97.56 (GT), 97.69 (CBH). η vs. T (WLF, r > 0.9995); C1, C2–“universal” constants: Tg: 223.83 (Sq), 225 (GT), 228.44 (CBH); ηg: 2.21 × 1011 (GT), 2.37 × 1011 (Sq), 2.62 × 1011 (CBH). | [35] |
| Mozambique (south-western): honeydew honey | Rheometer PP (ϕ 60 mm; gap 0.5 mm) | DS Stress sweeps, 1 Hz Frequency sweeps: 0.1–10 Hz, 1 Pa (LVR) T: 293.15–313,15 K | G′, G′′, η* | G′′ >> G′: viscous nature. G* vs. ω: constant function: Newtonian behaviour. ANN best models for the prediction of rheological parameters as a function of temperature, frequency, and chemical composition: MLP–for G′′ and η* (r2 > 0.950); PNN–for G′(r2 = 0.758). Sensitivity: G′′ and G′ to frequency and moisture; η* to moisture and temperature. | [69] |
| Norway: heather (H) Czech Rep.: lime (L) (H diluted with L, 10–80% w/w) | Rheometer, CP (ϕcone 50 mm; angle 1°, gap 0.103 mm) | SSF : 1–100 s−1 T: 298.15 K DS Frequency sweep: 0.1–10 rad s−1, γ 1% (LVR) T: 298.15 K | η, σ G′, G′′, η* | σ vs. (P-L), r2 ≥ 0.999; K: 7.91 (L)–74.50 (H); n: 0.9924 (L)–0.6745 (H). σ vs. (HB), r2 ≥ 0.999; K: 8.0 (L)–61.0 (H); n: 0.989 (L)–0.713 (H) σy: (-)1.15 (L)–44.94 (H). σ vs. t (Weltman), r2: 0.55–0.84; B: [-]4.5 (L)–28.0 (H). ϕ ( 50 s−1): 1.0534 (L)–0.7054 (H). C (Equation (35)): [-]1.93 (L)–[-]15.7 (H). Non-linear dependence of rheological parameters (K, n (P-L), K, n (HB), σy, B, ϕ, C) on the degree of dilution with a step change between 40% and 60% (w/w): possible use in the identification of adulterated heather honeys. | [45] |
| Poland: buckwheat (BW), clover (CLO), honeydew (HD) | Rheometer PP, (ϕ 50 mm; gap 0.5 mm) | Preheating: 50 °C, 3 h; kept: 30 °C, 24–48 h DS Frequency sweep: 0.1–100 rad s−1, γ 1% (LVR) T: 253.15–343.15 K | η, G′, G′′ | η (343.15 K): 13.5 (BW, wt 10.21)–324 (HD, wt 16.72). BW: G′ > G′′ (303.15 K, 313.15 K); G′′ > G′ (263.15 K, 343.15 K); G′ = G′′ (253.15 K, 258.15 K, 283.15 K, 293.15 K, 323.15 K, 333.15 K). CLO: G′′ > G′ (263.15 K, 293.15 K, 333.15 K, 343.15 K); G′ > G′′ (313.15 K, 323.15 K); G′ = G′′ (253.15 K, 258.15 K, 283.15 K, 303.15 K). HD: G′′ > G′ (268.15–293.15 K, 343.15 K); G′ > G′′ (323.15 K, 333.15 K); G′ = G′′ (253.15–263.15 K, 303.15–313.15 K). Rheological parameters of the phenomenological method: Ge, Je, , τm,τ0, ω0, k. High values of (~101−107), ω0 (~10−2−102), k (~100−104): honeys with structure of quasi-solid bodies, tending to form a pseudo-gel (high total elasticity, high cross-linking density and capacity); structure able to damp mechanical vibrations; structure sensitive to changes caused by temperature; structure able to slow down the physical aging of honey systems over time. Usefulness in the design and prediction of processing steps. | [88] |
| Poland: rape (R), multifloral (MF), buckwheat (BW). a) liquefied (55 ºC, 24 h + cooling, RT); b) crystallised | Rheometer CC (ϕint 26.652 mm; ϕext 28.905 mm; gap 1.127 mm | T: 293.15 K (a) liquefied SSF—σ: 0–500 Pa DS—ω: 0–250 s−1 (b) crystallised SSF : 0–450 s−1 t: 0–180 s (up- and downward) DS–(the same as in the liquefied samples) | η G*, δ, η* η, σ G*, δ, η* | (a) liquefied σ vs. (Newton, r2 = 0.999), η = 6.66 (R), 5.02 (MF), 3.18 (BW). G* vs. ω (r2 > 0.995), G* = 6.889ω (R), 4.794ω (MF), 2.894ω (BW). (b) crystallised Hysteresis area: large (R, MF), insignificant (BW). σ vs. (P-L, r2 ≥ 0.98): K = 36.696 (R), 15.945 (MF), 6.2218 (BW); n = 0.623 (R), 0.706 (MF), 0.854 (BW). G*(MF) > G*(R) > G*(BW). η* vs. (P-L, r2 ≥ 0.900): K = 374.86 (MF), 252.06 (R), 193.81 (BW). SSF results differ from DS measurements. Structural and rheological properties of the final product may be modelled by controlling the crystallization process. | [11] |
| Poland: rape-seed (stored for 18 months) | Universal Testing Machine with back extrusion cell (ϕ 50 mm; L 60 mm) | 4 cycles: 50–400 mm/min (a) CON; (b) RT, (c) FRO | η | η = 33.6 (CON), 78.0 (RT), 280.5 (FRO) Storage temperatures influenced honey viscosity. The higher viscosity of FRO honey is probably a result of a crystallized structure formed by fine crystals. | [63] |
| Poland: heather | Rheometer PP (ϕ 35 mm; gap 0.5 mm) | Preheating 40 °C SSF :1–100 s−1 (up- and downward), t = 180 s T: 283.15–313.15 K DS T: 283.15–313,15 K ω: 1–100 rad s−1 γ: 0.03 | η, σ G′, G′′, η* | σ vs. (HB), r2 ≥ 0.999; K: 2.0–108.6; n: 0.66–0.90; σy: 2.3–142.2 K vs. T (Arrhenius)—Ea: 47.7–71.7. σ vs. t (Weltman), r2 ≥ 0.96; B [[–]: 10.7–56.7. G′′>>G′: viscous nature. G′′ vs. ω (P-L), r2 ≥ 0.9990; K′′: 2.6–163.4; n′′: 0.78–0.94. η vs. η* (P-L); K: 0.017–0.264; β: 1.39–2.11. Significant dependence of η* on ω: viscoelastic nature. Non-Newtonian, shear-thinning, tendency to yield stress, thixotropic. | [32] |
| Poland: acacia (AC), buckwheat (BW), linden (LI), multifloral (MF), rape (R), honeydew (HD), nectar-honeydew (NHD) | Rheometer (ϕcup 15.8 mm; ϕbob 14.00 mm) | Preheating 50 °C, 3 h SSF T: 283.15–313.15 K : 1–100 s−1 Time effect: T: 293.15 K, : 50 s−1 | η | η = 1.8 (BW, MF, R–313.15 K)–252.6 (NHD, 283.15 K). η vs. T (Arrhenius, r2 ≥ 0.997): Ea: 92.34 (BW)–105.25 (NHD). η vs. T (WLF, r2 > 0.999); universal constants C1, C2; ηg: 1.88 × 1011 (R)–2.86 × 1011 (BW) Tg: 220.34 K (BW)–228.39 (NHD). | [23] |
| Portugal: heather (H), rosemary (ROM) multifloral (MF) | Rotational viscometer, CC, spindles (ϕ 1.18 cm; ϕ 0.94 cm) | SSF ~ 0.2–60 s−1 Up- and downward T: 303.15–368.15 K | η, σ | σ vs. (HB), r2 ≥ 0.976; K: 0.05 (H, 368.15 K)–136 (MF, 303.15 K); n: 0.852 (ROM,368.15 K)–1.68 (H, 368.15 K); σy < 8.5 (insignificant effect of microparticles (crystals) in honey. σ vs. (P-L), r2 ≥ 0.956; K: 1.23 (ROM, 343.15 K)–139.8 (MF, 303.15 K); n: 0.849 (ROM,368.15 K)–1.105 (MF, 303.15 K). η = 74 (MF, 368.15 K)–13,678 (MF, 303.15 K). η* vs. T (Arrhenius, r ≥ 0.946), Ea: 57.7 (ROM)–74.5 (MF). η* vs. T ( fit, r2 ≥ 0.9999). Newtonian behaviour, except ROM 368.15 K (slightly shear-thinning). | [40] |
| Romania: honeydew (HD), adulterated with fructose (F), glucose (G), hydrolysed inulin (I), malt wort (M), inverted sugar (IS), (5–50%, w/w). | Rheometer PP, (ϕ 60 mm; gap 1 mm) | SSF : 0–100 s−1 (up- and downward) T: 293.15 K DS Stress sweeps: 1 Hz, σ 1 Pa (LVR) ω: 0.62–62.83 rad s−1 T: 293.15 K | η, σ G′, G′′ | σ vs. (Newton, r2 ≥ 0.999), Newtonian behaviour. η (HD): 16.64; η (5–50%)—HD+F: 16.02–11.58; HD+G: 17.02–21.94; HD+I: 16.24–21.22; HD+M: 16.64–16.71; HD+IS: 16.63–16.56. η vs. , thixotropic area: increased by M, G, S, IS (highest, HD+M); decreased by F. G′′ >> G′: viscous nature. G′′ vs. ω (P-L), r2 ≥ 0.999; K′′; n′′: 16.78; 0.991 (HD); 16.27–11.76; 0.990–0.988 (HD+F); 17.25–22.15; 0.991–0.993 (HD+G); 16.62–21.40; 0.994–0.995 (HD+I); 17.47–22.92; 0.986–0.951 (HD+M); 16.85–16.70; 0.991–0.996 (HD+IS). Creep phase: 0–180 s. J vs. t (Burgers model, r2 ≥ 0.983): significative influence of F, G, I on η0 (~103–107). Creep start point: F increases, IS decreases. Recovery phase: 180–360 s; J vs. t: Newtonian behaviour; no influence of the adulterants. Honey authentication: PCA (rheological parameters + sugar composition): 100% explanation of total variance. | [51] |
| Romania: linden (LI), black locust (BL), rape (R), sunflower (SF), honeydew (HD), multifloral (MF) | Rheometer, PP (ϕ 40 mm; angle 2°, gap 1 mm) | SSF : 0.1–500 s−1 (up- and downward) T: 283.15–313.15 K DS Frequency sweep: 3–300 rad s−1, γ: 3% (LVR) T: 293.15 K | η, σ G′, G′′, δ | σ vs. —Newtonian behaviour: LI, BL, SF, MF; non-Newtonian with thixotropy: R, HD. η (293.15 K): 17.2 (HD)–2.7 (LI). G′′ >> G′: viscous nature. G′: 13.8 (LI)–315.6 (SF). G′′: 610 (LI)–2229 (SF). tanδ: 55–161. LDA to predict viscosity based on carbohydrate composition, p-value < 0.05: glucose and fructose; correct classification of 78.8% samples. | [21] |
| Spain: eucalyptus (EU), honeydew (HD), orange (OB), multifloral (MF), rosemary (ROM), summer savoury (SS) | Rheometer CC. Rheometer PP, (ϕ 60 mm; gap 0.5 mm) | Preheating: 55 °C; kept: 30 °C SSF : 0–100 s−1 T: 298.15–323.15 K DS Stress sweeps: 1 Hz Frequency sweep: 0.628–62.8 rad s−1, σ 1 Pa (LVR) T: 298.15–323.15 K | η, σ η* | σ vs. (Newton, r2 ≥ 0.99), Newtonian behaviour. η: 0.462 (ROM, 323.15 K)–13.970 (HD, 298.15 K). η vs. and η* vs. : constant functions–Newtonian behaviour. η vs. η*, Cox-Merz rule verified (α~1): all honeys at 313.15–323.15 K; except 298.15–303.15 K (α > 1). Prediction of η and η* from each other, through a modified Cox-Merz rule. η vs. T (Arrhenius, r2 ≥ 0.998); Ea: 84.07 (ROM)–91.35 (HD). η vs. T (VTF), r2 = 0.999); B: 1595 (OB)–1954 (HD). η vs. °Brix and T: P-L and exponential models (r2: 0.733, 0.822); Ea: 73.317, 82.773. | [38] |
| Spain: honeydew (HD), orange (OB), multifloral (MF), rosemary (ROM) | Rheometer PP, (ϕ 60 mm; gap 0.5 mm) | Preheating: 55 °C; kept: 30 °C DS Stress sweeps: 1 Hz Frequency sweep: 0.1–10 Hz, σ 1 Pa (LVR) T: 278.15–313.15 K | G′, G′′, η* | G′′>>G′: viscous nature. η* vs. ω: constant function–Newtonian behaviour. G′′ vs. ω (P-L), r2 ≥ 0.99; K′′: 1.13 (ROM, 313.15 K)–215.74 (HD, 273.15 K); n′′: 0.99–1.05. Application of TTSP to viscoelastic properties: obtention of a viscoelastic model (4th grade polynomial equation, r2 > 0.99), suitable for all honeys. | [54] |
| Spain: rosemary (RO) (a) liquefaction by heating (HT) (b) liquefaction by ultrasound (US)+HT | Viscometer, disc-type | HT: 313.15–333.15 K, 60 min US: 40 Hz, 313.15–333.15 K, 60 min. : 2.5–20 rpm t: 20–60 min | η | σ vs. , constant viscosity: Newtonian behaviour. η (HT) = 333 (333.15 K, 60 min)–3240 (313.15 K, 10 min). η (US) = 206 (333.15 K, 60 min)–3080 (313.15 K, 10 min). η vs. T (Arrhenius)—Ea (HT): 64; (US): 59. HT/US, 60 min—η: 1494/833 (313.5 K); 726/290 (323.5 K); 333/206 (333.5 K). At a same temperature and after a certain period of time, η of US samples are lower; honey can be liquefied by US, without the need to increase temperature up to 323.15 K or higher temperatures. | [13] |
| Spain: “Miel de Galicia” | Rotational viscometer CC | Preheating: 55 °C; kept 30 °C. SSF : 0.3–2 s−1 (up- and downward) T: 298.15 K T: 280.15–328.15 K : 1.4 s−1 | η, σ | σ vs. (P-L): K = 7.887 × 10−3– 14.279 × 10−3; n = 0.933–0.969. Shear-thinning behaviour (at low values). η vs. T (Arrhenius; the best regression): Ea: 83.880–96.631. η vs. T (WLF); C1 [-] 54.4–32.2), C2 73.1–194.0; ηg: 1.1 × 106—1.2 × 109 η vs. T (VTF), r2 = 0.996); B: 875.85–992.09. η vs. T (P-L); K: 4.96 × 1016–1.83 × 1018 -; m [-]: 9.25–8.57. Temperature effect more relevant in the low range of temperature. | [2,58] |
| Tunisia: eucalyptus (EU), orange (OB), rosemary (ROM), thyme (TH), mint (MI), horehound (HH) | Rheometer CP, (ϕ 35 mm; gap 0.14 mm) | SSF : 0.01–500 s−1 T: 293.15 K DS Frequency sweep: 0.1–100 rad s−1, σ 0.001 Pa T: 293.15–323.15 K | η, σ G′, G′′, η* | σ vs. (HB, r2 ≥ 0.99), K: 8.47 (HH)–36.23 (TH); n: 0.68 (TH)–0.86 (HH); σy: 3.72 (HH)–41.18 (TH). Non-Newtonian, shear-thinning behaviour. ηapp vs. T (: 10 s−1, Arrhenius, r2 ≥ 0.97); Ea: 21.23 (HH)–34.91 (TH). σ vs. t (Weltman, r2 ≥ 0.97); B: 8.64 (HH)–21.10 (TH). G′′>G′: viscous nature. G′′ vs. ω (P-L), r2 ≥ 0.96; K′′: 0.65 (HH, 323.15 K)–143.10 (TH, 293.15 K); n′′: 0.79 (TH, 323.15 K)–0.91 (TH, 293.15 K); non-Newtonian behaviour. | [33] |
| Turkey: creamed honey | Rheometer PP, (ϕ 50 mm; gap 0.5 mm) | SSF : 1–70 s−1, T: 283.15 K : 1–100 s−1, T: 298.15–313.15 K; (up- and downward) DS Frequency sweep: 0.1–10 Hz, γ 0.5% (LVR) T: 283.15–313.15 K Temperature sweeps: γ 0.5% (LVR), 1 Hz, T: 278.15–323.15 K Thermal Loop 11 thermal cycles: 278.15–323.15 K, 10 rad s−1, γ 0.5% | ηapp, σ G′, G′′, η* | σ vs. (P-L), r2 ≥ 0.9993; K: 269.7 (283.15 K)–10 (313.15 K); n: 0.7641 (283.15 K)–0.8124 (313.15 K). Hysteresis Area: 51,713 (283.15 K)–1129 (313.15 K). ηapp,50 s−1 vs. T (Arrhenius, r2 ≥ 0.9188); Ea: 36.62. G′′>>G′: viscous nature. G′′ vs. T (Arrhenius, r2 ≥ 0.8565); Ea: 41.71. G′′ vs. t (Weltman), r2≥ 0.9541; [-] B: 298.7 (283.15 K)–17.1 (313.15 K G′′ vs. ω (P-L), r2≥ 0.9926; K′′: 273.4 (283.15 K)–4.0 (313.15 K); n′′: 0.881 (283.15 K)–1.033 (313.15 K). Non-Newtonian shear-thinning thixotropic behaviour. Δmin (G′′): 1.00 (cycle 1)–0.566 (cycle 11). Creamed honey with low thermal stability: great structural change by thermal stress. | [29] |
| Turkey: natural honey adulterated with saccharose (HAS) and fructose (HAF) syrups (0–50%, w/w) | Rheometer PP (ϕ 50 mm; gap 0.5 mm) | SSF : 0.1–100 s−1, T: 298.15 K DS T: 298.15 K Amplitude sweep test, 1 Hz, γ: 0.1–100% Frequency sweep test, 1% (LVR), 0.1–10 Hz Temperature sweep test, 278.15–323.15 K, 1 Hz, 50 s−1 Creep phase: 0–150 s; recovery phase: 150–300 s | η, σ G′, G′′, G* | σ vs. (Newton), r2 ≥ 0.996 (HAS), r2 ≥ 0.997 (HAF): Newtonian behaviour. η = HAS: 6.531 (0%)—2.019 (50%); HAF: 6.531 (0%)–1.085 (50%). G′′ >> G′: viscous nature. G′′ vs. ω (HAS, r2 = 0.999; HAF, r2 ≥ 0.998); Newtonian behaviour K′′ = HAS: 6.367 (0%)–2.234 (50%); HAF: 6.367 (0%)–1.111 (50%); good indicator to detect honey adulteration at levels 10–50%, within a 278.15–323.15 K range. K*: same results as K′′; natural honey with the highest total resistance to deformation. J vs. t (Burgers model: r2 = 0.999 (HAS, HAF); η0 = HAS: 2.0–7.0; HAF: 1.1–7.0. G0, G1, η1: no consistent trend with increasing adulterant level; cannot be used to detect adulteration. η, G′′, η*, η0: potential to be good indicators of adulteration with saccharose and fructose, at specified ratios. 93.879% of the total variance in data set was described by four Principal Components, regarding physicochemical and rheological properties of natural and adulterated honeys. | [56] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faustino, C.; Pinheiro, L. Analytical Rheology of Honey: A State-of-the-Art Review. Foods 2021, 10, 1709. https://doi.org/10.3390/foods10081709
Faustino C, Pinheiro L. Analytical Rheology of Honey: A State-of-the-Art Review. Foods. 2021; 10(8):1709. https://doi.org/10.3390/foods10081709
Chicago/Turabian StyleFaustino, Célia, and Lídia Pinheiro. 2021. "Analytical Rheology of Honey: A State-of-the-Art Review" Foods 10, no. 8: 1709. https://doi.org/10.3390/foods10081709
APA StyleFaustino, C., & Pinheiro, L. (2021). Analytical Rheology of Honey: A State-of-the-Art Review. Foods, 10(8), 1709. https://doi.org/10.3390/foods10081709






