Next Article in Journal
Chiral Self-Sorting in Truxene-Based Metallacages
Next Article in Special Issue
Crystal Structure and Thermal Behavior of SbC2O4OH and SbC2O4OD
Previous Article in Journal
Thiazole- and Thiadiazole-Based Metal–Organic Frameworks and Coordination Polymers for Luminescent Applications
Previous Article in Special Issue
High-Pressure Synthesis, Crystal Structure, and Photoluminescence Properties of β-Y2B4O9:Eu3+
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 7
Issue 12
10.3390/inorganics7120145
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

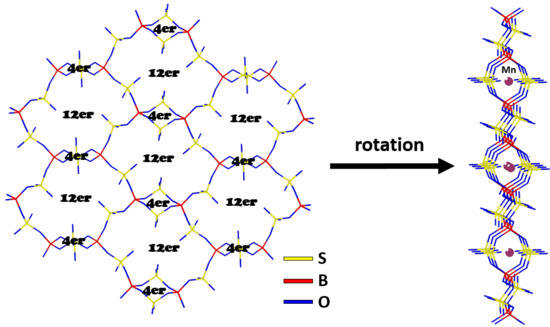
M[B2(SO4)4] (M = Mn, Zn)—Syntheses and Crystal Structures of Two New Phyllosilicate Analogue Borosulfates

by
Leonard C. Pasqualini
1,
Hubert Huppertz
1 and
Jörn Bruns
2,*
1
Institute of General, Inorganic and Theoretical Chemistry, University of Innsbruck, Innrain 80-82, 6020 Innsbruck, Austria
2
Institute of Inorganic Chemistry, University of Cologne, Greinstrasse 6, 50939 Cologne, Germany
*
Author to whom correspondence should be addressed.
Inorganics 2019, 7(12), 145; https://doi.org/10.3390/inorganics7120145
Submission received: 26 November 2019 / Revised: 8 December 2019 / Accepted: 10 December 2019 / Published: 17 December 2019
(This article belongs to the Special Issue Oxido Compounds)
Browse Figures
Versions Notes

Abstract

:
Borosulfates are a rapidly expanding class of silicate analogue materials, where the structural diversity is expected to be at least as large as known for silicates. However, borosulfates with cross-linking of the anionic network into two or even three dimensions are still very rare. Herein, we present two new representatives with phyllosilicate analogue topology. Through solvothermal reactions of ZnO and MnCl2∙4H2O with boric acid in oleum (65% SO3), we obtained single-crystals of Mn[B2(SO4)4] (monoclinic, P21/n, Z = 2, a = 8.0435(4), b = 7.9174(4), c = 9.3082(4) Å, β = 110.94(1)°, V = 553.63(5) Å3) and Zn[B2(SO4)4] (monoclinic, P21/n, Z = 2, a = 7.8338(4), b = 8.0967(4), c = 9.0399(4) Å, β = 111.26(1)°, V = 534.36(5) Å3). The crystal structures reveal layer-like anionic networks with alternating vierer- and zwölfer-rings formed exclusively by corner-linked (SO4)- and (BO4)-tetrahedra.

Graphical Abstract

1. Introduction

The structural chemistry of silicates is dominated by anionic networks of corner-shared (SiO4)-tetrahedra and is still a fascinating field of research for scientists from different disciplines. Friedrich Liebau is one of the pioneers in silicate chemistry and introduced a classification in 1985 [1]. According to this classification, silicates can be assigned to different classes: Nesosilicates reveal exclusively isolated (SiO4)-tetrahedra. Isolated anionic moieties of corner-shared (SiO4)-tetrahedra are predominant in sorosilicates. The anionic substructures of cyclosilicates contain ring-like anionic moieties of corner-shared (SiO4)-tetrahedra with a Si:O ratio of 1:3. Inosilicates are formed by infinite anionic chains or bands. If the anionic network branches in two dimensions phyllosilicates occur, which reveal infinite anionic layers. Last but not least, silicates with 3D network like structures are called tectosilicates. The function of all previously introduced silicates is mostly related to their respective crystal structures, as well as the dimensionality of the anionic substructures [2,3,4,5].
Nowadays, several substitution variants of the aforementioned silicates are known. In these compounds, the central silicon atoms are partially or completely substituted by one or even two different atoms. Thus, the resulting anionic substructures differ by the respective atoms in the tetrahedral centers, which determine the total charge of the anionic network. Especially for alumosilicates, alumophosphates, and borophosphates, where aluminum, phosphorous, and boron atoms reside in the center of the tetrahedra, the correlation between syntheses, structure, and properties are well explored [6,7,8]. Probably, the most prominent examples are microporous alumosilicates, the so-called zeolites. Due to their open network structures, they are used as ion-conducting materials, absorbents, and catalysts [9,10].
A comparably new class of silicate analogue materials are borosulfates, with sulfur and boron occupying the position of silicon. According to Pauling’s rules, networks of corner-shared tetrahedra are stable, if the respective central atoms are able to compensate the occurring charges, either by themselves or by extended crosslinking of the anionic network [11]. To branch networks with sulfur in the center of the tetrahedra into further dimensions, the high charge has to be compensated. Therefore, the combination of (SO4)- and (BO4)-tetrahedra [12,13,14,15,16,17,18,19,20,21,22,23,24,25] or (SO3Cl)- and (BO4)-tetrahedra [26,27,28] is suitable. The structural variety of neat borosulfates covers sorosilicate, inosilicate, phyllosilicate, and tectosilicate analogue materials. Furthermore, borosulfates can overcome Pauling’s rules, which is manifested by the formation of anionic substructures with S–O–S, as well as B–O–B bridges, like in M[B(S2O7)2] (M = Li, Na, K, NH4) [20,21,24], M[B(SO4)(S2O7)] (M = Cs, H) [21] B2S2O9 [22], or M4[B2O(SO4)6] (M = Mn, Co, Ni, Zn) [23], to mention just a few examples.
We assume that the synthesis parameters strongly influence the nature of the tetrahedral linkage. A comparison of the synthesis temperatures of literature known borosulfates gives evidence of this assumption. Accordingly, compounds with S–O–S bridges are realized at low temperatures, whereas B–O–B bridges result from synthesis at high temperatures, most likely under the release of SO3 [20,21,23,24]. However, up to now we have no evidence for the decisive factors leading to the different dimensionalities of the anionic subunits. The most prominent representatives are 0D and 1D compounds like soro- and inosilicate analogues, if we exclude compounds with S–O–S and B–O–B bridges. 2D and 3D materials are only rarely observed. Li[B(SO4)2] [24] is the sole example of a borosulfate with an extended 3D network with exclusively S–O–B bridges, and phyllosilicate analogue substructures are only found for CaB2S4O16 [18] and Mg[B2(SO4)4] [25].
With this publication, we contribute two further representatives, namely Mn[B2(SO4)4] and Zn[B2(SO4)4], with phyllosilicate analogue substructure, charge compensated by divalent subgroup metals, obtained from solvothermal synthesis in SO3-enriched sulfuric acid.

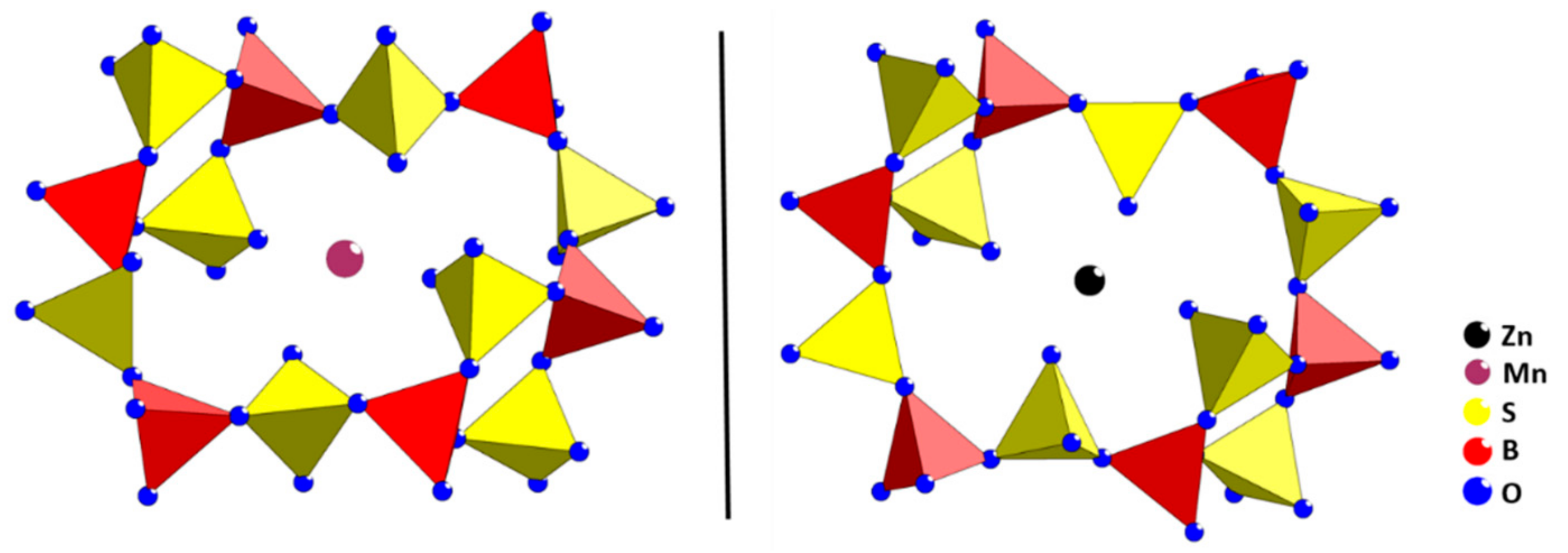
2. Results and Discussion

Both new borosulfates were obtained in form of colorless crystals (see Figures S1 and S2) from a solvothermal reaction with SO3-enriched sulfuric acid in evacuated and torch sealed glass ampoules at elevated temperature (see Materials and Methods). Mn[B2(SO4)4] and Zn[B2(SO4)4] crystallize in the monoclinic space group P21/n with a = 8.0435(4), b = 7.9174(4), c = 9.3082(4) Å, β = 110.94(1)° for Mn[B2(SO4)4] and a = 7.8338(4), b = 8.0967(4), c = 9.0399(4) Å, β = 111.26(1)° for Zn[B2(SO4)4] (see Table 1 and X-ray crystallography for further data and details according the refinement). The crystal structures exhibit layer-like anionic subunits of vertex-shared (BO4)- and (SO4)-tetrahedra (Figure 1) charge compensated by the respective divalent counter cations Mn2+ and Zn2+. Each (BO4)-tetrahedron is coordinated by four different (SO4)-tetrahedra via common corners, whereas for each (SO4)-tetrahedron two oxygen atoms remain terminal. The Niggli formula for the anionic substructure of both borosulfates can be described as B SO 4 4 / 2 − ∞ 2 . The B–O bond lengths range from 1.440(1) to 1.485(1) Å for Mn[B2(SO4)4] and from 1.449(1) to 1.482(1) Å for Zn[B2(SO4)4]. With about 1.52 Å, the S–O bonds within the S–O–B bridges are significantly elongated compared to the terminal or cation coordinating S–O bonds. The latter fall in the region between 1.4125(7) to 1.4427(7) Å for Mn[B2(SO4)4] and 1.4135(7) to 1.442(7) Å for Zn[B2(SO4)4].
In both borosulfates, the O–S–O angles differ significantly from the perfect tetrahedral angle for both crystallographically different (SO4)-tetrahedra. For Mn[B2(SO4)4], the O–S1–O angles range from 96.18(3) to 116.59(5)°, and the O–S2–O angles range from 102.84(3) to 116.23(4)°. The comparable tetrahedra in Zn[B2(SO4)4] reveal angles between 97.64(3) to 116.16(4)° for O–S1–O and 104.18(3) to 115.70(4)° for O–S2–O. The deviations are less drastic for the (BO4)-tetrahedra. These values range from 105.67(6) to 114.05(7)° and from 101.24(6) to 114.58(6)° for Mn[B2(SO4)4] and Zn[B2(SO4)4], respectively (a full list of bond lengths and angles with symmetry operators is given in the Supplementary Materials under Tables S3, S4, S7, and S8).
The layer-like anionic substructures of Mn[B2(SO4)4] and Zn[B2(SO4)4] are very similar. Both reveal twelve-membered (zwölfer) and four-membered (vierer) rings of vertex-shared (BO4)- and (SO4)-tetrahedra (Figure 2, top). Each zwölfer ring is surrounded by six further zwölfer rings. Two of those six are opposite to another and are aligned along the crystallographic b-axis. Each one shares two common (BO4)-tetrahedra with the zwölfer ring. The common (BO4)-tetrahedra are linked via two separate (SO4)-tetrahedra, whereas each is part of one of the two zwölfer rings. As a result, a vierer ring is formed. The other four zwölfer rings share a common (BO4)(SO4)(BO4)-fragment and spread the network along the ac-diagonal, thereby creating a phyllosilicate analogue anionic layer. Each layer is terminated exclusively by (SO4)-tetrahedra (Figure 2, top). However, similarities to the borophosphates also occur. With a B:P ratio <1, compounds with condensed [B(PO4)4]9− anions occur. In this form, highly charged P5+ cations are located within the network as far away from each other as possible [29,30]. In the title compounds, the situation is similar. The highly charged sulfur atoms are in the center of the (SO4)-tetrahedra, coordinated to the low charged boron cations forming repetitive [B(SO4)4] blocks.
Charge compensation of the borosulfates is achieved by Mn2+ and Zn2+ cations. They are packed in a stacked manner parallel to the crystallographic b-axis in the middle of the channels running through the anionic substructures. The cations are exclusively located within the center of the zwölfer rings. They are coordinated by four of their terminal oxygen atoms of (SO4)-tetrahedra and two oxygen atoms of terminal (SO4)-tetrahedra belonging to the anionic layers above and underneath (Figure 3). Besides B2S2O9, a neutral vertex-shared (BO4)-(SO4)-network structure, only two rather similar structures are known, namely CaB2S4O16 and Mg[B2(SO4)4]. Formally, the same sum formula occurs for our new borosulfates and the known compounds. Furthermore, CaB2S4O16 and Mg[B2(SO4)4] also exhibit zwölfer and vierer rings similarly to Mn[B2(SO4)4] and Zn[B2(SO4)4]. However, the positions of the cations with respect to the anionic layers are different. Mn[B2(SO4)4] and Zn[B2(SO4)4] are the first representatives with the charge compensating cations exclusively in the center of the zwölfer rings. In CaB2S4O16 and Mg[B2(SO4)4], the respective cations are located above and underneath the zwölfer rings within the interlayer.
Mn[B2(SO4)4] and Zn[B2(SO4)4] are also not isotypical. Due to the differently rotated tetrahedra within the asymmetric unit, a structural aberration occurs between the anionic substructures of Mn[B2(SO4)4] and Zn[B2(SO4)4] (Figure 4), whereas the octahedral oxygen coordination to the metal cations remains. Focusing on one central zwölfer ring in both borosulfates, the adjoining vierer rings are almost congruent. The main differences occur in the tetrahedra, forming the common (BO4)(SO4)(BO4)-edges to the next zwölfer rings. Especially strong rotated are the (S1O4)-tetrahedra.

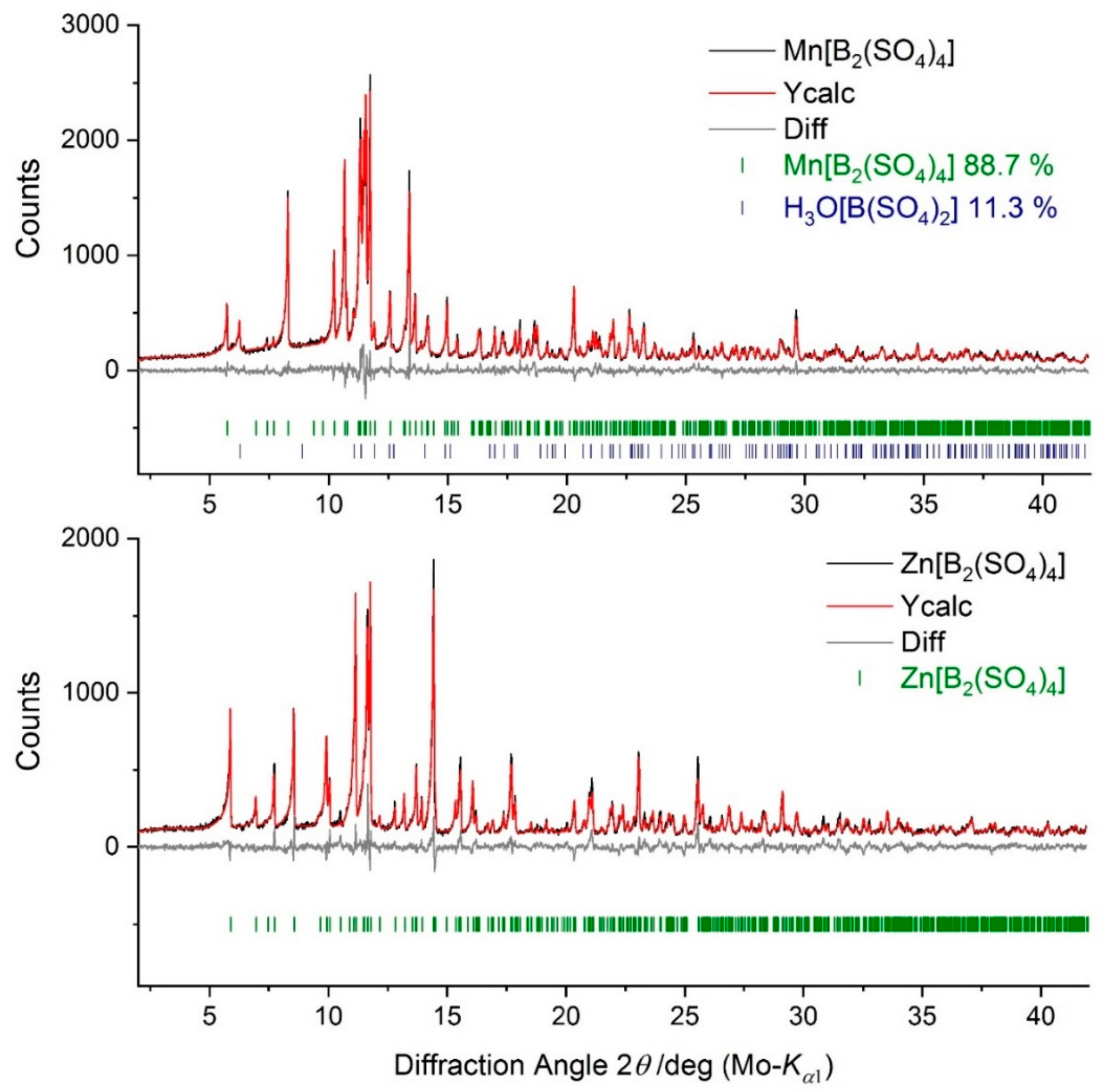
3. Materials and Methods

Synthesis of Mn[B2(SO4)4] and Zn[B2(SO4)4]: MnCl2∙4H2O (133 mg (0.67 mmol), Fluka, Seelze, Germany) or ZnO (55 mg (0.68 mmol), Merck, Darmstadt, Germany) were loaded together with H3BO3 (300 mg (4.85 mmol), Carl Roth, Karlsruhe, Germany), and 1 mL oleum (65% SO3, Merck, Darmstadt, Germany) into a thick-walled glass ampoule (l = 300 mm, ∅ = 16 mm, thickness of the tube wall = 1.8 mm), respectively. The ampoules were torch sealed under reduced pressure (0.01 mbar), and placed into a block-shaped resistance furnace and heated up to 523 K within 150 min. The temperature was maintained for 48 h and finally reduced to 298 K within 96 h. A large number of colorless block-shaped crystals were obtained for both borosulfates (Figures S1 and S2), and the yield was quantitative for ZnO and almost quantitative for MnCl2∙4H2O. The latter suffered from small impurities of (H3O)[B(SO4)2] (see X-ray crystallography). The crystals are very moisture sensitive and decompose immediately after exposure to air. Thus, the products were handled under strictly inert conditions.
Caution: Oleum is a strong oxidizer, which needs careful handling. During and even after the reaction, the ampoules might be under remarkable pressure. It is mandatory to cool down the ampoules using liquid nitrogen prior to opening.
X-ray crystallography: The mother liquor was separated from the crystals via decantation. The acid-containing side of the ampoule was cooled with liquid nitrogen and several crystals were transferred into inert oil directly after opening. The remaining bulk material was transferred to a glovebox for further characterization. Under a polarization microscope, a suitable crystal was prepared, mounted onto a glass needle (∅ = 0.1 mm), and immediately placed into a stream of cold N2 (measurement temperature see Table 1) inside the diffractometer (Bruker D8 Quest κ, Bruker, Karlsruhe, Germany). After unit cell determination, the reflection intensities were collected. Structure solutions and refinements were conducted using the SHELX program package [31].
X-ray powder diffraction was carried out with a Stoe StadiP powder diffractometer (Stoe & Cie GmbH, Darmstadt, Germany) in transmission geometry on a sample washed with CCl4 and dried under reduced pressure before the measurement. To fill a capillary with a solid sample was impossible due to small amounts of adhesive solvent. Finally, a flat sample was irradiated with Ge(111)-monochromatized Mo-Kα1-radiation (λ = 0.7093 Å), which was detected using a Dectris Mythen 1K detector (Dectris AG, Baden-Daettwil, Germany). Due to the fast decomposition of the sample holder matrix, the measurement had to be conducted with a scan range from 2 to 41.9°, with a step size of 2.1° and step time of 11 s. Rietveld refinement was accomplished using TOPAS4.2 [32]. Refined lattice parameters based on powder data: Mn[B2(SO4)4] a = 8.082(4) Å, b =7.942(3) Å, c = 9.288(8) Å, β = 110.84(7)°, V = 557.24(4) Å3; Zn[B2(SO4)4] a = 7.883(5) Å, b = 8.095(3) Å, c = 9.034(2) Å, β = 111.21(9)°, V = 537.45(8) Å3. An amount of 11.3% (H3O)[B(SO4)2] could be detected as a byproduct of Mn[B2(SO4)4] (Figure 5). Differences in the intensities of the experimental and simulated powder patterns might be due to preferred orientations of the crystalline material on the flat sample holder.
Mn[B2(SO4)4] and Zn[B2(SO4)4]: The crystal structures of Mn[B2(SO4)4] and Zn[B2(SO4)4] were solved in the monoclinic space group P21/n. The heavy atom positions were determined by SHELXT-2014/5 [33] using Direct Methods. Further atoms could be successfully located by difference Fourier techniques during refinement with SHELXL-2017/1 [34]. Multi-scan absorption correction was applied to the data using the program SADABS-2014/5 by Bruker [35]. Finally, the structure and model of Mn[B2(SO4)4] were refined to R1 (all data) = 0.0271 and wR2 (all data) = 0.0553 and for Zn[B2(SO4)4] to R1 (all data) = 0.0186 and wR2 (all data) = 0.0468. Selected bond lengths and angles are presented in the Tables S3, S4, S7 and S8.
CSD 1958827 for Mn[B2(SO4)4] and CSD number 1958830 for Zn[B2(SO4)4] contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from FIZ Karlsruhe via www.ccdc.cam.ac.uk/structures.

4. Conclusions

Reactions between oleum enriched with 65% SO3 and boric acid in evacuated torch-sealed glass ampoules seem to be a powerful strategy to synthesize borosulfates with layer-like anionic substructures of divalent metals. As can be seen from this and our previous publications, not only the main group but also subgroup metals can be charge-compensating cations. In comparison to Mg[B2(SO4)4] and CaB2S4O16, Mn[B2(SO4)4] and Zn[B2(SO4)4] are the first representatives of layer-like borosulfates with the cations residing in the plane of the anionic network and the center of zwölfer rings. However, it is still unclear why cations with a comparable atomic radius like Zn2+ and Mg2+ act differently. This problem is currently under investigation using quantum chemical calculations.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/7/12/145/s1, Figures S1 and S2: Crystals of Zn[B2(SO4)4] and Mn[B2(SO4)4] under a polarisation microscope; Table S1: Fractional atomic coordinates (×104) and equivalent isotropic displacement parameters (Å2 × 103) for Mn[B2(SO4)4]; Table S2: Anisotropic displacement parameters (Å2 × 103) for Mn[B2(SO4)4]; Table S3: Bond lengths for Mn[B2(SO4)4]; Table S4: Bond angles for Mn[B2(SO4)4]; Table S5: Fractional atomic coordinates (×104) and equivalent isotropic displacement parameters (Å2 × 103) for Zn[B2(SO4)4]; Table S6: Anisotropic displacement parameters (Å2 × 103) for Zn[B2(SO4)4]; Table S7: Bond lengths for Zn[B2(SO4)4]; Table S8: Bond angles for Zn[B2(SO4)4]; the CIF and the checkCIF output files of Mn[B2(SO4)4] and Zn[B2(SO4)4].

Author Contributions

Synthesis, preparation and characterization of the title compounds were carried out by L.C.P. under the supervision of H.H. and J.B. Supported by L.C.P., the manuscript was written by J.B. and reviewed by H.H.

Funding

L.C.P. is very grateful for the Ph.D. scholarship from the Leopold-Franzens-University Innsbruck. J.B. is thankful for the financial support of the Fonds der Chemischen Industrie (FCI).

Acknowledgment

We thank Klaus Wurst for collecting the single-crystal data and Viktoria Falkowski for the Rietveld refinement.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Liebau, F. Structural Chemistry of Silicates; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
  2. Deer, W.A.; Howie, R.A.; Zussmann, J. An Introduction to Rock-Forming Minerals; Langmanns: London, UK, 1966. [Google Scholar]
  3. Krivovichev, S.V. Minerals as Advanced Materials II; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
  4. Ying, J.Y.; Mehnert, C.P.; Wong, M.S. Synthesis and Applications of Supramolecular-Templated Mesoporous Materials. Angew. Chem. Int. Ed. 1999, 38, 56–77. [Google Scholar] [CrossRef]
  5. Wang, X.; Zhuang, J.; Chen, J.; Zhou, K.; Li, Y. Thermally Stable Silicate Nanotubes. Angew. Chem. Int. Ed. 2004, 43, 2017–2020. [Google Scholar] [CrossRef] [PubMed]
  6. Oliver, S.; Kupermann, A.; Ozin, G.A. A New Model for Aluminophosphate Formation: Transformation of a Linear Chain Aluminophosphate to Chain, Layer, and Framework Structures. Angew. Chem. Int. Ed. 1998, 37, 46–62. [Google Scholar] [CrossRef]
  7. Santilli, D.S.; Zones, S.I. Synthesis of Microporous Materials: Vol. 1: Molecular Sieves; Van Nostrand Reinhold: New York, NY, USA, 1992. [Google Scholar]
  8. Kniep, R.; Gözel, G.; Eisenmann, B.; Röhr, C.; Asbrand, M.; Kizilyalli, M. Borophosphates—A Neglected Class of Compounds: Crystal Structures of MII[BPO5] (MII = Ca, Sr) and Ba3[BP3O12]. Angew. Chem. Int. Ed. 1994, 33, 749–751. [Google Scholar] [CrossRef]
  9. Marakatti, V.S.; Halgeri, A.B. Metal ion-exchanged Zeolites as highly active Solid acid Catalysts for the Green Synthesis of Glycerol Carbonate from Glycerol. RSC Adv. 2015, 5, 14286–14293. [Google Scholar] [CrossRef]
  10. Marakatti, V.; Halgeri, A.B.; Shanbhag, G.V. Metal ion-exchanged Zeolites as Solid acid Catalysts for the Green Synthesis of nopol from Prins reaction. Catal. Sci. Technol. 2014, 4, 4065–4074. [Google Scholar] [CrossRef]
  11. Pauling, L. The Principles determining the structure of complex ionic crystals. J. Am. Chem. Soc. 1929, 51, 1010–1026. [Google Scholar] [CrossRef]
  12. Höppe, H.A.; Kazmierczak, K.; Daub, M.; Förg, K.; Fuchs, F.; Hillebrecht, H. The First Borosulfate K5[B(SO4)4]. Angew. Chem. Int. Ed. 2012, 51, 6255–6257. [Google Scholar] [CrossRef]
  13. Gross, P.; Kirchhain, A.; Höppe, H.A. The Borosulfates K4[BS4O15(OH)], Ba[B2S3O13], and Gd2[B2S6O24]. Angew. Chem. Int. Ed. 2016, 55, 4353–4355. [Google Scholar] [CrossRef]
  14. Bruns, J.; Podewitz, M.; Janka, O.; Pöttgen, R.; Liedl, K.; Huppertz, H. Cu[B2(SO4)4] and Cu[B(SO4)2(HSO4)]—Two silicate analogue borosulfates differing in their dimensionality: A comparative study of stability and acidity. Angew. Chem. Int. Ed. 2018, 130, 9693–9697. [Google Scholar] [CrossRef] [Green Version]
  15. Netzsch, P.; Hämmer, M.; Gross, P.; Bariss, H.; Block, T.; Heletta, L.; Pöttgen, R.; Bruns, J.; Huppertz, H.; Höppe, H.A. RE2[B2(SO4)6] (RE = Y, La–Nd, Sm, Eu, Tb–Lu): A silicate-analogues host structure with weak coordination behaviour. Dalton Trans. 2019, 48, 4387–4397. [Google Scholar] [CrossRef]
  16. Bruns, J.; Podewitz, M.; Schauperl, M.; Liedl, K.; Janka, O.; Pöttgen, R.; Huppertz, H. Ag[B(SO4)2]—Synthesis, crystal structure and characterization of the first precious-metal borosulfate. Eur. J. Inorg. Chem. 2017, 34, 3981–3989. [Google Scholar] [CrossRef]
  17. Schönegger, S.; Bruns, J.; Gartner, B.; Wurst, K.; Liedl, K.; Huppertz, H. Synthesis and characterization of the first lead(II) borosulfate Pb[B2(SO4)4]. Z. Allg. Anorg. Chem. 2018, 644, 1702–1706. [Google Scholar] [CrossRef] [Green Version]
  18. Bruns, J.; Podewitz, M.; Schauperl, M.; Joachim, B.; Liedl, K.; Huppertz, H. CaB2S4O16: A borosulfate exhibiting a new structure type with phyllosilicate topology. Chem. Eur. J. 2017, 23, 16773–16781. [Google Scholar] [CrossRef]
  19. Daub, M.; Hillebrecht, H. Borosulfates Cs2B2S3O13, Rb4B2S4O17, and A3HB4S2O14 (A= Rb, Cs)—Crystalline Approximants for Vitreous B2O3? Eur. J. Inorg. Chem. 2015, 2015, 4176–4181. [Google Scholar] [CrossRef]
  20. Daub, M.; Höppe, H.A.; Hillebrecht, H. Further New Borosulfates: Synthesis, crystal Structure, and vibrational spectra of A[B(SO4)2] (A = Na, K, NH4) and the crystal structures of Li5[B(SO4)4] and NH4[B(S2O7)2]. Z. Anorg. Allg. Chem. 2014, 640, 2914–2921. [Google Scholar] [CrossRef]
  21. Daub, M.; Kazmierczak, K.; Höppe, H.A.; Hillebrecht, H. The borosulfate story goes on-From alkali and oxonium salts to polyacids. Chem. Eur. J. 2013, 19, 16954–16962. [Google Scholar] [CrossRef] [PubMed]
  22. Logemann, C.; Wickleder, M.S. B2S2O9—A boron sulfate with phyllosilicate topology. Angew. Chem. Int. Ed. 2013, 52, 14229–14232. [Google Scholar] [CrossRef]
  23. Netzsch, P.; Gross, P.; Takahashi, H.; Höppe, H.A. Synthesis and characterization of the first borosulfates of magnesium, manganese, cobat nickel, and zinc. Inorg. Chem. 2018, 57, 8530–8539. [Google Scholar] [CrossRef]
  24. Daub, M.; Kazmierczak, K.; Gross, P.; Höppe, H.A.; Hillebrecht, H. Exploring a New Structure Family: Alkali Borosulfates Na5[B(SO4)4], A3[B(SO4)3] (A = K, Rb), Li[B(SO4)2], and Li[B(S2O7)2]. Inorg. Chem. 2013, 52, 6011–6020. [Google Scholar] [CrossRef]
  25. CSD-434487. Available online: www.ccdc.cam.ac.uk/structures (accessed on 11 December 2019).
  26. Mairesse, G.; Drache, M. The Crystal Structure of Potassium Tetraehlorosulfatoborate, K[B(SO3Cl)4]. Acta Cryst. 1978, 34, 1771–1776. [Google Scholar] [CrossRef]
  27. Marsch, R.E. Potassium tetrachlorosulfatoborate: Change in space group. Acta Cryst. 1980, 36, 219–220. [Google Scholar] [CrossRef]
  28. Mairesse, G.; Drache, M. Lithium Tetrakis(chlorosulfato)borate. Acta Cryst. 1980, 36, 2767–2768. [Google Scholar] [CrossRef]
  29. Ruchkina, E.A.; Belokoneva, E.L. Structural Features of Pb, Fe, and Alkali Metal Borophosphates as analysed in terms of topologically similar structural blocks. Russ. J. Inorg. Chem. 2003, 48, 1812–1821. [Google Scholar]
  30. Kniep, R.; Schäfer, G.; Engelhardt, G.; Boy, I. K[ZnBP2O8] and A[ZnBP2O8] (A = NH4+, Rb+, Cs+): Zincoborophosphates as a New Class of Compounds with Tetrahedral Framework Structures. Angew. Chem. Int. Ed. 1999, 38, 3642–3644. [Google Scholar] [CrossRef]
  31. Sheldrick, G.M. A short history of SHELX. Acta Cryst. 2008, 64, 112–122. [Google Scholar] [CrossRef] [Green Version]
  32. TOPAS4.2; Bruker: Karlsruhe, Germany, 2009.
  33. Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Cryst. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef] [Green Version]
  34. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
  35. Sheldrick, G.M. SADABS 2014/5; University of Göttingen: Gottingen, Germany, 1996. [Google Scholar]
Inorganics 07 00145 g001 550
Figure 1. Left: Asymmetric unit of Mn[B2(SO4)4]. The thermal ellipsoids are set on a 90% probability level. Selected bond lengths [Å]: S1–O11 1.4427(7), S1–O12 1.4125(7), S1–O111 1.5263(6), S1–O112 1.5229(6), S2–O21 1.4333(6), S2–O22 1.4298(6), S2–O121 1.5240(6), S2–O122 1.5218(6), B1–O111 1.443(1), B1–O112 1.440(1), B1–121 1.483(1), B1–O122 1.485(1) (Symmetry operators 11−x,−y,1−z; 21/2+x,1/2−y,1/2+z; 31/2−x,−1/2+y,1/2−z; 43/2−x,1/2+y,1/2−z; 51−x,1−y,1−Z); Right: Asymmetric unit of Zn[B2(SO4)4]. The thermal ellipsoids are set on a 90% probability level. Selected bond lengths [Å]: S1–O11 1.4442(7), S1–O12 1.4135(7), S1–O111 1.5247(6), S1–O112 1.5315(6), S2–O21 1.4329(6), S2–O22 1.4277(6), S2–O211 1.5116(6), S2–O212 1.5116(6), B1–O111 1.458(1), B1–O112 1.449(1), B1–O211 1.477(1), B1–O212 1.482(1) (Symmetry operators 11−x,−y,1−z; 2−1/2+x,1/2−y,−1/2+z; 33/2−x,−1/2+y,3/2−z; 43/2−x,1/2+y,1/2−z; 51−x,1−y,1−z).
Figure 1. Left: Asymmetric unit of Mn[B2(SO4)4]. The thermal ellipsoids are set on a 90% probability level. Selected bond lengths [Å]: S1–O11 1.4427(7), S1–O12 1.4125(7), S1–O111 1.5263(6), S1–O112 1.5229(6), S2–O21 1.4333(6), S2–O22 1.4298(6), S2–O121 1.5240(6), S2–O122 1.5218(6), B1–O111 1.443(1), B1–O112 1.440(1), B1–121 1.483(1), B1–O122 1.485(1) (Symmetry operators 11−x,−y,1−z; 21/2+x,1/2−y,1/2+z; 31/2−x,−1/2+y,1/2−z; 43/2−x,1/2+y,1/2−z; 51−x,1−y,1−Z); Right: Asymmetric unit of Zn[B2(SO4)4]. The thermal ellipsoids are set on a 90% probability level. Selected bond lengths [Å]: S1–O11 1.4442(7), S1–O12 1.4135(7), S1–O111 1.5247(6), S1–O112 1.5315(6), S2–O21 1.4329(6), S2–O22 1.4277(6), S2–O211 1.5116(6), S2–O212 1.5116(6), B1–O111 1.458(1), B1–O112 1.449(1), B1–O211 1.477(1), B1–O212 1.482(1) (Symmetry operators 11−x,−y,1−z; 2−1/2+x,1/2−y,−1/2+z; 33/2−x,−1/2+y,3/2−z; 43/2−x,1/2+y,1/2−z; 51−x,1−y,1−z).
Inorganics 07 00145 g001
Inorganics 07 00145 g002 550
Figure 2. Top: Top view of the infinite anionic layer of vertex-shared (BO4)- and (SO4)-tetrahedra in the structure of Mn[B2(SO4)4]. The layers are constructed of zwölfer and vierer rings. Each zwölfer ring is coordinated to four vierer rings and six zwölfer rings. The layers are terminated exclusively by (SO4)-tetrahedra; Bottom: Side view of an infinite anionic layer. The charge compensating Mn2+-cations reside within the zwölfer rings. The interspace between the different anionic layers is free of cations or intercalating molecules.
Figure 2. Top: Top view of the infinite anionic layer of vertex-shared (BO4)- and (SO4)-tetrahedra in the structure of Mn[B2(SO4)4]. The layers are constructed of zwölfer and vierer rings. Each zwölfer ring is coordinated to four vierer rings and six zwölfer rings. The layers are terminated exclusively by (SO4)-tetrahedra; Bottom: Side view of an infinite anionic layer. The charge compensating Mn2+-cations reside within the zwölfer rings. The interspace between the different anionic layers is free of cations or intercalating molecules.
Inorganics 07 00145 g002
Inorganics 07 00145 g003 550
Figure 3. The Mn2+ cations are coordinated octahedrally by three crystallographically different oxygen atoms. Four of the six coordinating oxygen atoms belong to the terminal (SO4)-tetrahedra of the equatorially surrounding layer, two originate from the terminal (SO4)-tetrahedra above and underneath. Bond lengths [Å]: Mn1–O111 2.1388(7), Mn1–O211 2.2276(6), Mn1–O222 2.1400(6) (Symmetry operators 11−x,−y,1−z; 21/2+x,1/2−y,1/2+z).
Figure 3. The Mn2+ cations are coordinated octahedrally by three crystallographically different oxygen atoms. Four of the six coordinating oxygen atoms belong to the terminal (SO4)-tetrahedra of the equatorially surrounding layer, two originate from the terminal (SO4)-tetrahedra above and underneath. Bond lengths [Å]: Mn1–O111 2.1388(7), Mn1–O211 2.2276(6), Mn1–O222 2.1400(6) (Symmetry operators 11−x,−y,1−z; 21/2+x,1/2−y,1/2+z).
Inorganics 07 00145 g003
Inorganics 07 00145 g004 550
Figure 4. Differently rotated zwölfer rings around Zn2+ and Mn2+ in the structures of M[B2(SO4)4] (M = Mn, Zn).
Figure 4. Differently rotated zwölfer rings around Zn2+ and Mn2+ in the structures of M[B2(SO4)4] (M = Mn, Zn).
Inorganics 07 00145 g004
Inorganics 07 00145 g005 550
Figure 5. Rietveld refinement plot for experimental and calculated data of M[B2(SO4)4] (M = Mn, Zn). In the case of Mn[B2(SO4)4], about 11.3% of (H3O)[B(SO4)2] can be refined as a byproduct. Different intensities of experimental and calculated plots might result from the preferred orientation of the crystallites on the flat sample holder. Refined lattice parameters: Mn[B2(SO4)4] a = 8.082(4) Å, b = 7.942(3) Å, c = 9.288(8) Å, β = 110.84(7)°, V = 557.24(4) Å3; Zn[B2(SO4)4] a = 7.883(5) Å, b = 8.095(3) Å, c = 9.034(2) Å, β = 111.21(9)°, V = 537.45(8) Å3.
Figure 5. Rietveld refinement plot for experimental and calculated data of M[B2(SO4)4] (M = Mn, Zn). In the case of Mn[B2(SO4)4], about 11.3% of (H3O)[B(SO4)2] can be refined as a byproduct. Different intensities of experimental and calculated plots might result from the preferred orientation of the crystallites on the flat sample holder. Refined lattice parameters: Mn[B2(SO4)4] a = 8.082(4) Å, b = 7.942(3) Å, c = 9.288(8) Å, β = 110.84(7)°, V = 557.24(4) Å3; Zn[B2(SO4)4] a = 7.883(5) Å, b = 8.095(3) Å, c = 9.034(2) Å, β = 111.21(9)°, V = 537.45(8) Å3.
Inorganics 07 00145 g005
Table
Table 1. Crystal data and structure refinement for Mn[B2(SO4)4] and Zn[B2(SO4)4].
Table 1. Crystal data and structure refinement for Mn[B2(SO4)4] and Zn[B2(SO4)4].
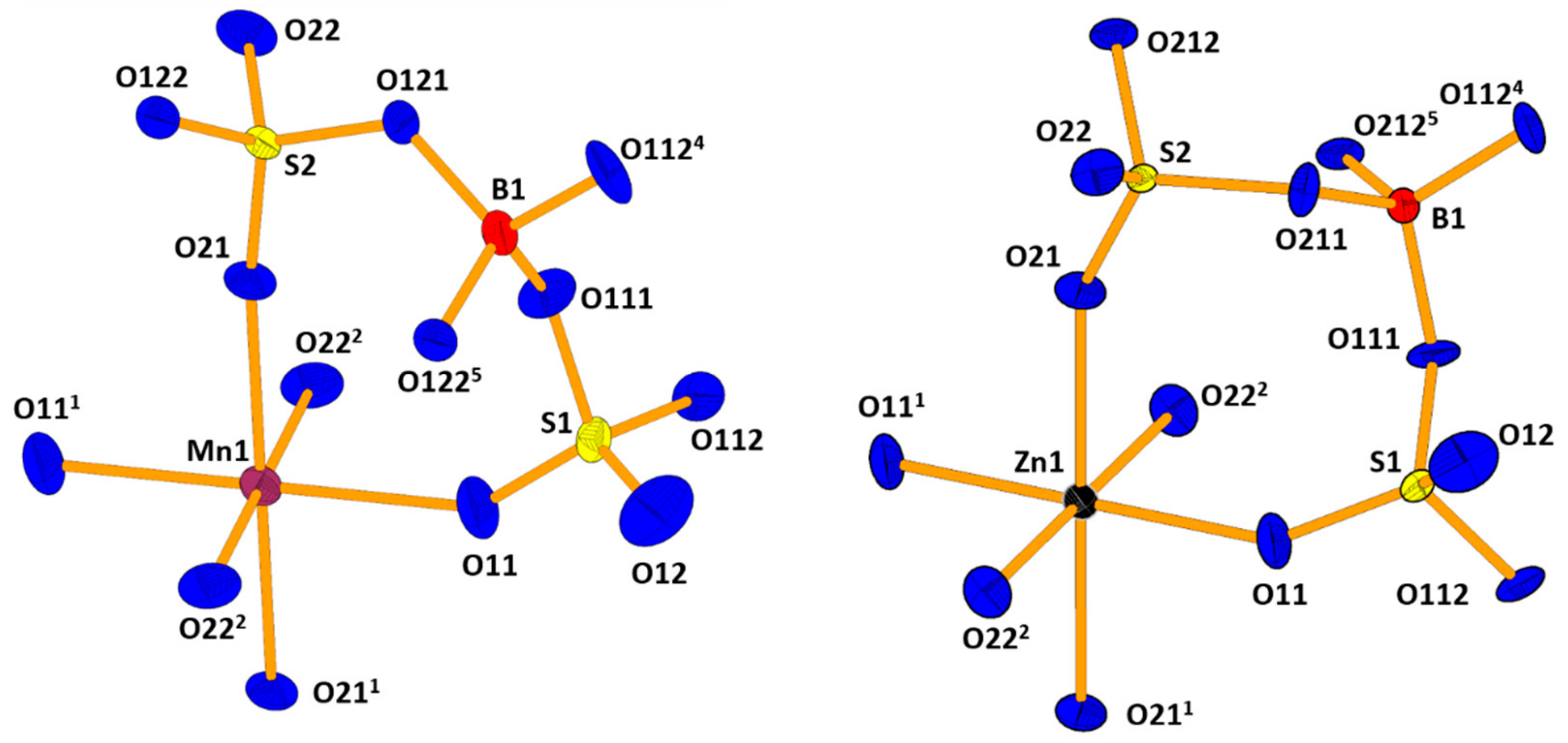
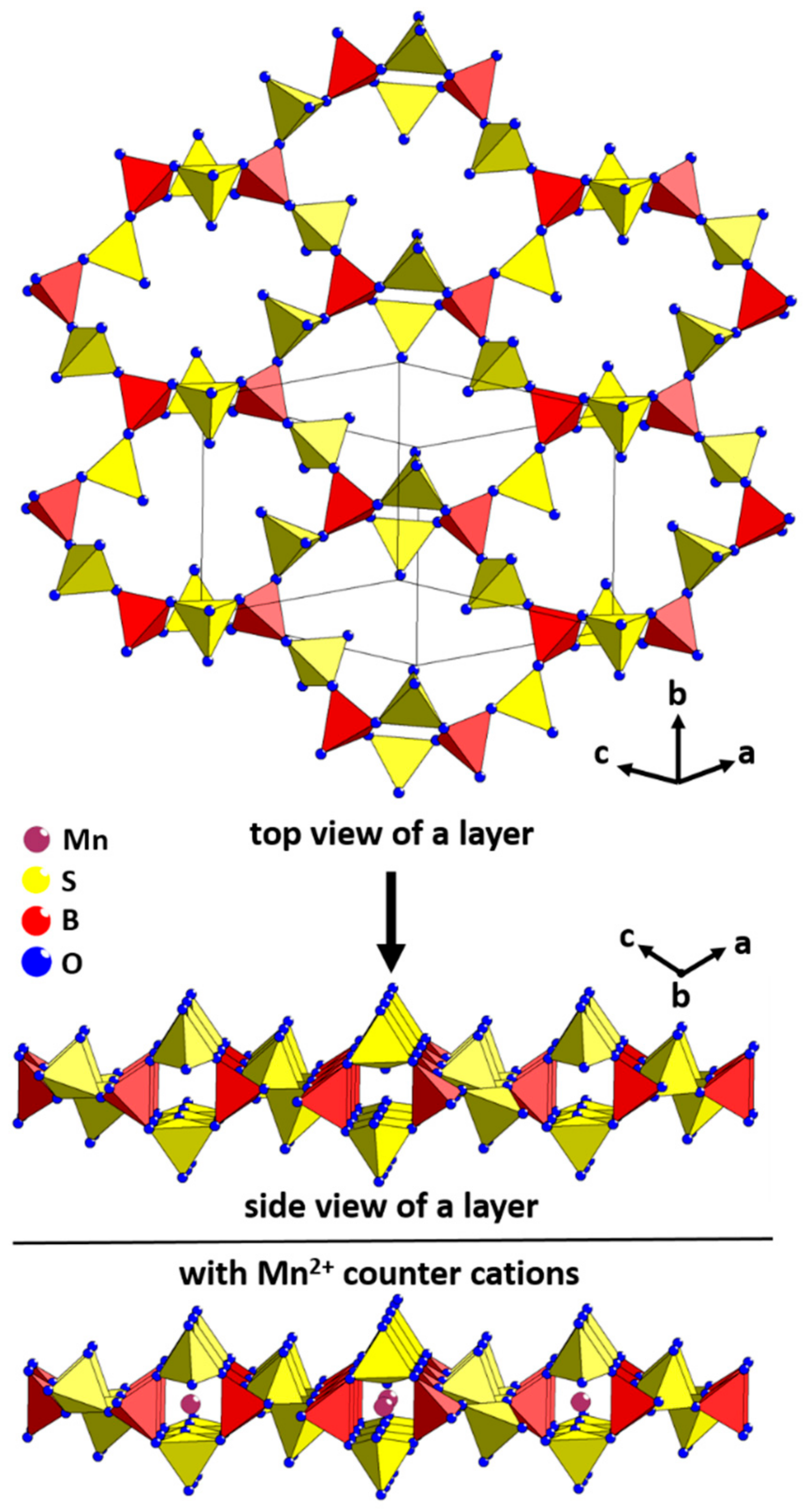
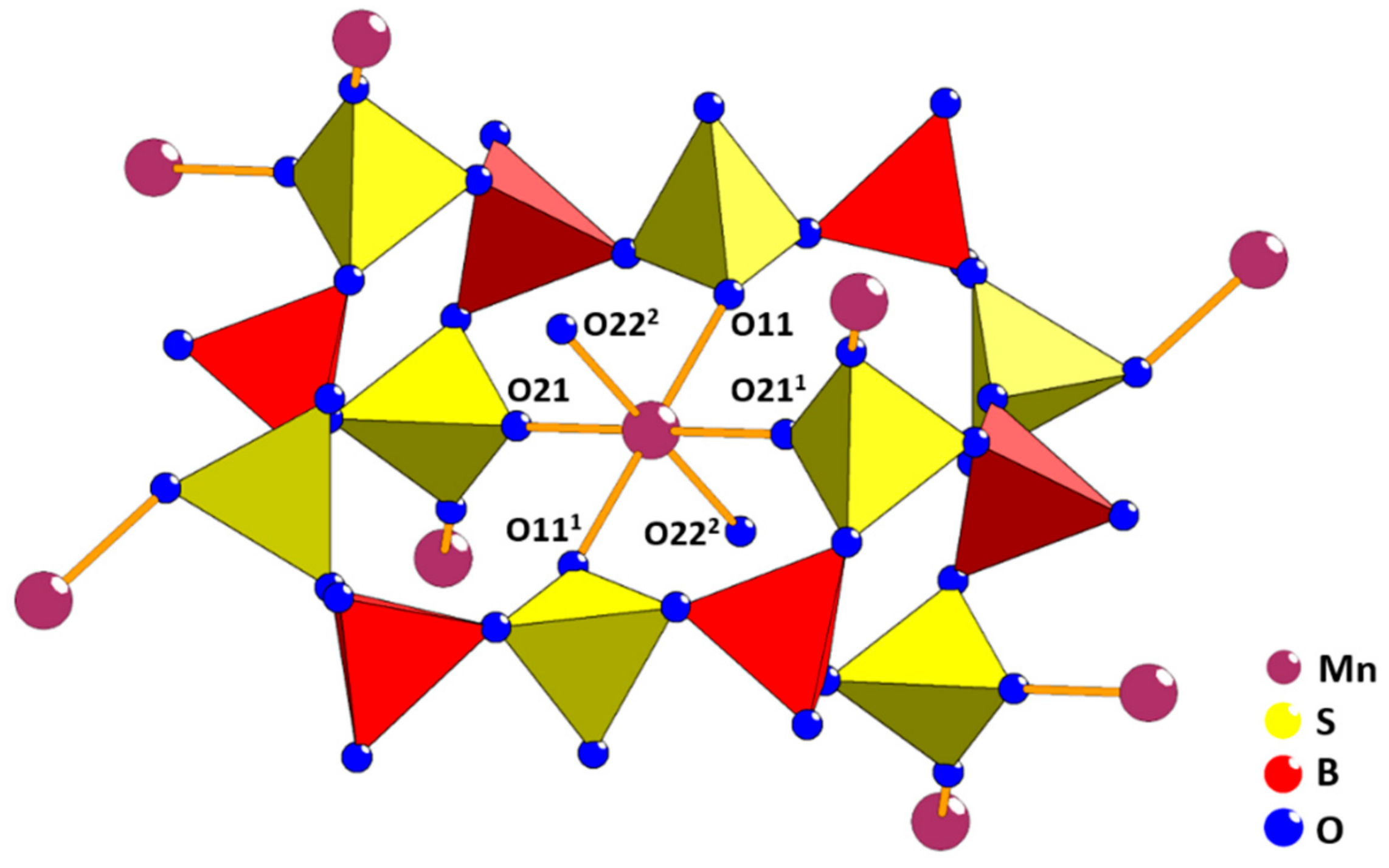
Sum formulaMn[B2(SO4)4]Zn[B2(SO4)4]
Formula weight460.80471.23
Temperature/K173(2)183(2)
Crystal systemmonoclinicmonoclinic
Space groupP21/nP21/n
a/Å8.0435(4)7.8338(4)
b/Å7.9174(4)8.0967(4)
c/Å9.3082(4)9.0399(4)
β/°110.94(1)111.26(1)
Volume/Å3553.63(5)534.36(5)
Z22
ρcalc/g/cm32.7642.929
μ/mm−12.0523.189
F(000)454464
Crystal size/mm30.07 × 0.055 × 0.030.5 × 0.3 × 0.11
RadiationMo-Kα1 (λ = 0.71073)Mo-Kα1 (λ = 0.71073)
2Θ range for data collection/°5.76 to 82.545.91 to 78.95
Index ranges−14 ≤ h ≤ 14, −14 ≤ k ≤ 14, −17 ≤ l ≤ 17−14 ≤ h ≤ 13, −14 ≤ k ≤ 14, −16 ≤ l ≤ 16
Reflections collected5853126941
Independent reflections3710 [Rint = 0.0417, Rsigma = 0.0169]3202 [Rint = 0.0278, Rsigma = 0.0151]
Data/restraints/parameters3710/0/1063202/0/107
Goodness-of-fit on F21.0781.110
Final R indexes [I ≥ 2σ(Io)]R1 = 0.0209, wR2 = 0.0534R1 = 0.0168, wR2 = 0.0460
Final R indexes [all data]R1 = 0.0271, wR2 = 0.0553R1 = 0.0186, wR2 = 0.0468
Largest diff. peak/hole/eÅ−30.48/−0.610.64/−0.46

Share and Cite

MDPI and ACS Style

Pasqualini, L.C.; Huppertz, H.; Bruns, J. M[B2(SO4)4] (M = Mn, Zn)—Syntheses and Crystal Structures of Two New Phyllosilicate Analogue Borosulfates. Inorganics 2019, 7, 145. https://doi.org/10.3390/inorganics7120145

AMA Style

Pasqualini LC, Huppertz H, Bruns J. M[B2(SO4)4] (M = Mn, Zn)—Syntheses and Crystal Structures of Two New Phyllosilicate Analogue Borosulfates. Inorganics. 2019; 7(12):145. https://doi.org/10.3390/inorganics7120145

Chicago/Turabian Style

Pasqualini, Leonard C., Hubert Huppertz, and Jörn Bruns. 2019. "M[B2(SO4)4] (M = Mn, Zn)—Syntheses and Crystal Structures of Two New Phyllosilicate Analogue Borosulfates" Inorganics 7, no. 12: 145. https://doi.org/10.3390/inorganics7120145

APA Style

Pasqualini, L. C., Huppertz, H., & Bruns, J. (2019). M[B2(SO4)4] (M = Mn, Zn)—Syntheses and Crystal Structures of Two New Phyllosilicate Analogue Borosulfates. Inorganics, 7(12), 145. https://doi.org/10.3390/inorganics7120145

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop