Implementation of a Particle Swarm Optimization Algorithm with a Hooke’s Potential, to Obtain Cluster Structures of Carbon Atoms, and of Tungsten and Oxygen in the Ground State

Abstract

Particle Swarm Optimization (PSO) is a metaheuristic optimization technique based on population behavior, inspired by the movement of a flock of birds or a school of fish. In this method, particles move in a search space to find the global minimum of an objective function. In this work, a modified PSO algorithm written in Fortran 90 is proposed. The optimized structures obtained with this algorithm are compared with those obtained using the basin-hopping (BH) method written in Python (3.10), and complemented with density functional theory (DFT) calculations using the Gaussian 09 software. Additionally, the results are compared with the structural parameters reported from single crystal X-ray diffraction data for carbon clusters ${\mathrm{C}}_n$(n = 3–5), and tungsten–oxygen clusters, ${\mathrm{WO}}_n^{m-}$(n = 4–6, $m=2,4,6$). The PSO algorithm performs the search for the minimum energy of a harmonic potential function in a hyperdimensional space $\in {\mathbb{R}}^{3N}$ (where N is the number of atoms in the system), updating the global best position ( $g_{best}$) and local best position ( $p_{best}$), as well as the velocity and position vectors for each swarm cluster. A good approximation of the optimized structures and energies of these clusters was obtained, compared to the geometric optimization and single-point electronic energies calculated with the BH and DFT methods in the Gaussian 09 software. These results suggest that the PSO method, due to its low computational cost, could be useful for approximating a molecular structure associated with the global minimum of potential energy, accelerating the prediction of the most stable configuration or conformation, prior to ab initio electronic structure calculation.

1. Introduction

In science, understanding the physical and chemical properties of materials is of great significance, as these properties depend primarily on their molecular structure. Predicting the atomic structure of a molecule using computational methods, starting from an arbitrary initial position of its atoms, is a complex task, since the system may include a large number of local minima on the potential energy surface (PES) [1,2]. In recent decades, several methods have been developed to optimize molecular structures, such as minimum jumping [3,4], simulated annealing [5,6], the random sampling method [7,8], basin-hopping (BH) [9,10], and metadynamics [10,11].

As the system to be studied increases in size with the number of atoms, the problem becomes more complex, increasing the computational cost. An important aspect of the research on structural configurations of clusters is the determination of their lowest potential energy. This step is essential for the study of the properties of the clusters since the structure with the lowest potential energy corresponds to the most stable configuration [12]. This problem is known as global optimization (GO) since it involves the determination of the lowest minimum value of the energy based on the atomic coordinates of the clusters in the PES. Due to the inherent complexity of the problem, it is impossible to solve it using analytical calculation methods. In practice, the problem can only be addressed through numerical techniques. Furthermore, any algorithm that searches for a global minimum must broadly explore the energy landscape, going deep into its most relevant regions, and thus perform a more efficient exploration [13].

GO is an arduous task due to the enormous number of local equilibrium configurations (local energy minima) of the cluster structures in the PES, which increase exponentially with the number of atoms N in the system [2,14,15,16,17,18,19]. These local minima correspond to different geometric structures, which may present different properties. Thus, the further the optimized structural parameters are separated from those reported experimentally by X-ray diffraction, the less accurate the properties of the modeled structure will be.

Advances in energy landscape theory have helped narrow the search space for the diversity of more stable cluster structures in the PES [20,21,22]. Some studies reported in the literature implement approximations with harmonic or Hookeian potentials to estimate the structure of some clusters [23,24]. A simple harmonic oscillator is a model used to study a wide range of phenomena, such as pendulum oscillations [25], sound waves [26], and bonds between atoms [27]. The latter considers the mass of the atom as a particle oscillating around an equilibrium point under the action of a restoring force, which is proportional to the distance from the equilibrium point, like the mass-spring system in Hooke’s Law, from which the oscillations or vibrations of the bonds are obtained, showing the existence of a vibrational spectrum in the infrared region [18].

One of the methods that is receiving the most attention in the optimization of molecular structures is the Particle Swarm Optimization (PSO) [28]. The algorithm is based on circumstances similar to the movement of a school of fish, a swarm of bees, or a flock of birds in motion by adjusting their positions and velocities. In general, a colony of animals, apparently without a leader, will change their speeds randomly in search of food, following the group member closest to the food source (possible solution). The group of animals optimizes its positions by following the members that have already reached a better orientation. This exploration process is repeated until the best position within the group is obtained, which is considered to be the position vector in the search space, and the velocity vector regulates the subsequent distribution or movement of the particles. The PSO method adjusts or updates the position and velocity of each particle at each step until achieving the best position experienced by the collective or swarm [29,30].

Another alternative is the basin-hopping (BH) method, which is a metaheuristic global optimization method combining local searches with stochastic jumps between different regions of the [9] space. This method involves two-step loops, a perturbation with good candidate solutions, and the application of the local search to the perturbed solution, transforming the complex energy landscape into a collection of basins that are explored by jumps. Monte Carlo random moves and the Metropolis criterion’s acceptance or rejection of the solutions perform these jumps. Alternatively, this method is beneficial for solving problems with multiple local minima, such as particle cluster optimization [9,31].

In the present work, we are interested in optimizing two types of clusters: carbon and those formed by oxygen atoms and transition metals. The first group is important for organic, inorganic, and physical chemistry [32]. Furthermore, these molecules are also of great importance in astrophysics, especially regarding the chemistry of carbon stars [33], comets [34], and interstellar molecular clouds [35]. On the other hand, carbon atom clusters are vital elements in hydrocarbon flames [36], and play a crucial role in gas-phase carbon chemistry, acting as precursors in the production of fullerenes, carbon nanotubes, diamond films, and silicon carbides [37,38,39]. Studying and synthesizing these molecules in the laboratory is challenging due to their high reactivity [40], underscoring the interest in studying the structural information of carbon clusters in theoretical research [41,42,43]. On the other hand, clusters consisting of oxygen atoms and transition metals with a high oxidation state ( ${\mathrm{W}}^{6+}$, ${\mathrm{V}}^{5+}$, or ${\mathrm{Mo}}^{6+}$) have an electronic structure that allows them to act as oxidizing agents, making them good candidates for obtaining new materials. These clusters are precursors of polyoxometalate compounds (POM), which are formed from condensation reactions through the self-assembly of some oxometalates, such as ${\mathrm{WO}}_4^{2-}$, ${\mathrm{MoO}}_4^{2-}$, ${\mathrm{VO}}_3^{-}$, ${\mathrm{WO}}_5^{4-}$, or ${\mathrm{WO}}_6^{6-}$ [44,45].

The optimization was carried out using a PSO algorithm written in Fortran 90 to locate global minimum energy structures. We have used the algorithm on clusters consisting of carbon atoms ${\mathrm{C}}_n$ (n = 3–5) and tungsten–oxygen atoms ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$), where n is the number of mol of atoms of the element in the cluster, and m is the charge of the anion. In this model, the atoms have been considered rigid spheres joined by a spring (link) with a harmonic potential, where the restoring force (Hooke’s Law) is proportional to the displacement from the equilibrium length. The algorithm was based on the search for the global minimum of the potential energy function of the aforementioned clusters in a multidimensional hyperspace $\in {\mathbb{R}}^{3N}$ (where N is the number of atoms in the system). The motions of the conformers of the clusters are guided by their own most favorable known atomic positions as well as by the best-known position of the entire swarm in the search space ${\mathbb{R}}^{3N}$. We have implemented a basin-hopping (BH) method and performed the DFT calculations through the Gaussian 09 software to validate our results. Furthermore, for the case of carbon clusters, we have compared with the results obtained by Jana and collaborators [46] who used a PSO algorithm written in Python, which combines an evolutionary subroutine with a variational optimization technique through an interface of the PSO algorithm with the Gaussian 09 software.

The article is divided into the following sections: Section 2, Discussion and Results, presents the results and compares them with the literature; Section 3, Methodology, presents the details of the algorithm; and Section 4, Conclusions, outlines the main results.

2. Discussion and Results

Tables S1–S4 of the supplementary material present the initial structures of the conformers of 10 clusters (swarms) of three-, four-, and five-carbon atoms, from which Jana et al. initiated their study of the PSO algorithm [46]. Using structures optimized with the commercial software Gaussian 09 as a reference, we observed that our results with PSO and BH showed good agreement with the conformations of the optimized structures reported by Jana et al. [46], for carbon clusters of 3–5 atoms ( ${\mathrm{C}}_3$–$C_5$; see

Table 1. Representation of optimized geometric structures of ${\mathrm{C}}_3$–${\mathrm{C}}_5$ carbon clusters using the BH and PSO algorithms, and Gaussian 09 software.

Cluster	BH	PSO		Gaussian 09
		Jana et al. [46]	In This Work
${\mathrm{C}}_3$
${\mathrm{C}}_4$
${\mathrm{C}}_5$

).

The Python-based PSO algorithm by Jana et al. [46], implemented with a swarm of 10 clusters, operates in synergy with the Gaussian software (version 09). This commercial software optimizes cluster structures at each iteration through the gradient method; however, the article by Jana [46] does not specify whether these optimizations are sequential or parallel. At every step:

• Gaussian software provides optimized atomic coordinates for each cluster to the PSO algorithm.
• The PSO modifies these coordinates through displacements in the hyperspace ${\mathbb{R}}^{3N}$.
• The new coordinates are fed back to Gaussian for the subsequent iteration.
• Gaussian optimizes cluster structures in Hilbert space $\mathcal{H}$, using the Schlegel algorithm [47], which begins by minimizing the electronic energy density functional using the conjugate gradient method at each step. The optimized cluster structure is obtained by minimizing the gradient of the electronic energy concerning the nuclear coordinates, through a series of single-point calculations in the PES, applying the Hellmann–Feynman theorem [48].
• The new atomic positions found by the Gaussian software are used by the PSO algorithm to locate the optimal nuclear coordinates, for each cluster (both $p_{best}$ and $g_{best}$), based on the electronic energy system.
• The cycle repeats during each optimization step performed by the Gaussian software until the electronic energy of the clusters converges.

The critical dependence lies in the fact that the PSO algorithm by Jana [46] lacks an intrinsic objective function. It exclusively utilizes the electronic energy computed by Gaussian software as a reference to guide atomic displacements in the hyperspace ${\mathbb{R}}^{3N}$. This dependence implies two fundamental limitations:

•

If the electronic energy of the system converges to a local minimum on the PES through Gaussian software, the PSO algorithm is hopelessly trapped in this minimum.

•

The absence of an intrinsic model to determine the energy of the system in the hyperspace ${\mathbb{R}}^{3N}$ restricts the PSO to functioning as an atomic configuration generator, without independent evaluation capability during the structural optimization process.

In essence, the algorithm by Jana et al. [46] acts as a conformational exploration mechanism whose efficacy is contingent upon external quantum chemical computations from Gaussian software.

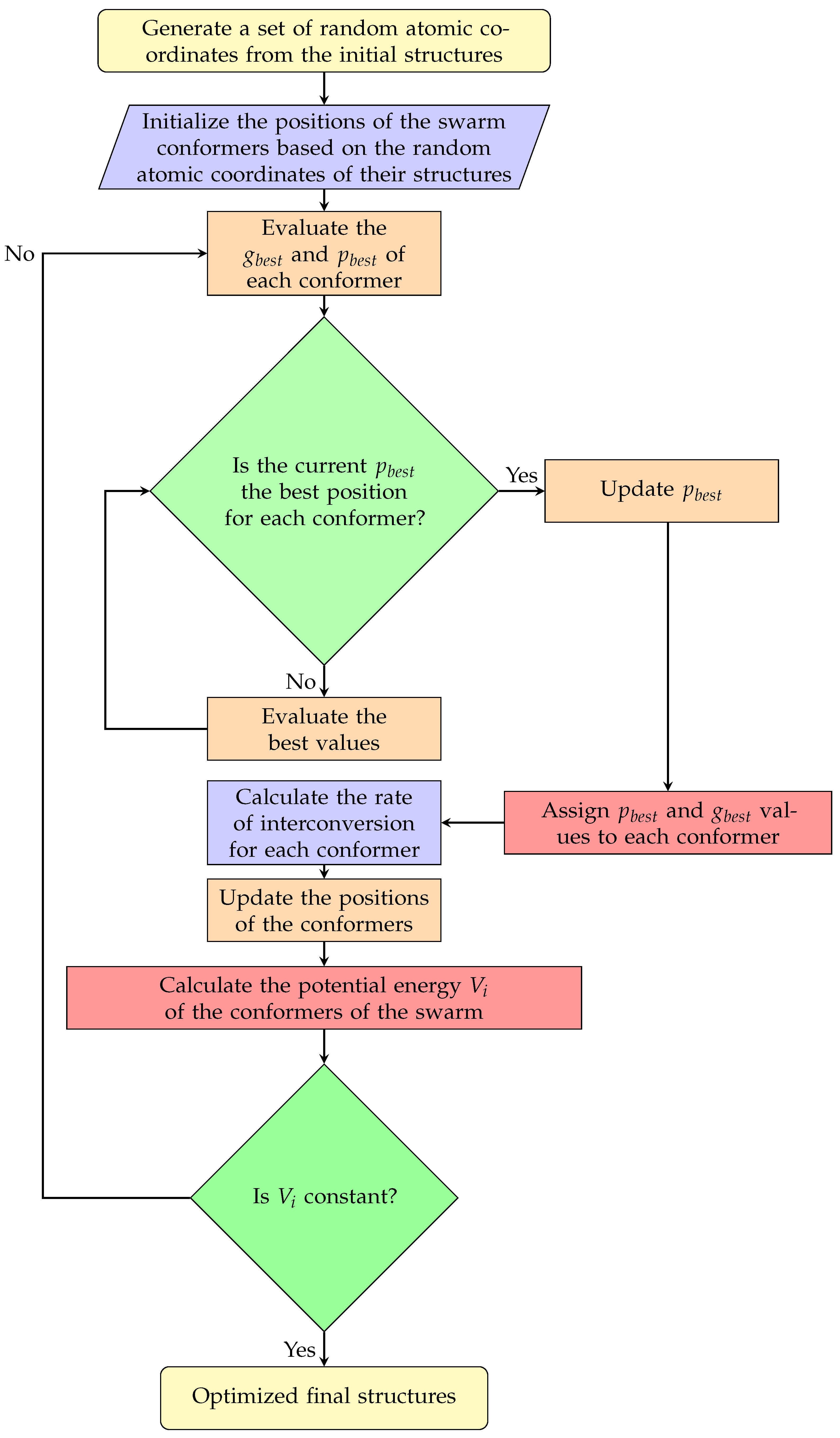
However, in this work, the PSO algorithm independently optimizes the structures of 10 cluster conformers simultaneously, without executing the Gaussian software. The algorithm models atoms as rigid spheres connected by springs and minimizes the potential energy (Equation (5)) for each conformer to determine its optimal positions in the search space ${\mathbb{R}}^{3N}$. At each step t, the algorithm updates the best positions $p_{best}$ and $g_{best}$ until the potential energy of each conformer converges. This convergence is achieved when the velocity and positions vectors satisfy ${\overrightarrow{v}}_{i,j}^{t+1}\to 0$ and ${\overrightarrow{x}}_{i,j}^{t+1}\to {\overrightarrow{x}}_0$, respectively (Equations (3) and (4)). During PES exploration, each cluster individually stores its atomic positions from iteration $t=1$ to $t=n-1$; this enables each cluster to retain its exploration history of the hyperspace ${\mathbb{R}}^{3N}$, providing a global perspective of the energy landscape. Consequently, the possibility of cluster swarm trapping in local minima during geometric optimization is significantly reduced.

The BH algorithm is a global optimization method designed to find the global minimum energy in systems with multiple local minima. This approach combines local optimization with random jumps to explore the configuration space of molecular structures associated with local minima. The algorithm starts by assigning trial positions to each atom, and the structure is defined using the Atomic Simulation Environment (ASE) library. An energy calculator, such as the effective medium theory (EMT) model, is then used to compute the total energy of the configuration. Restrictions based on Hooke’s Law were applied between specific pairs of atoms, imposing a restoring force proportional to the deviation from a target distance, to maintain physically reasonable structures during the optimization process. The algorithm initiates local optimization from the trial structure configuration using the Limited-Memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm [49]. This step searches for the local energy minimum near the current configuration. Once a local minimum is found, the algorithm makes a random jump in the configuration space. This jump allows the exploration of new configurations that may have lower energies. The energy of the new configuration is evaluated, and if it is lower than that of the previous configuration, it is accepted as the new current configuration. The new configuration remains acceptable under specific conditions, determined by the system temperature, which enables the algorithm to escape deep local minima when the energy is higher.

Tables S5–S7 in the supplementary material present the initial structures of the 10 conformers of the tungsten–oxygen clusters ${\mathrm{WO}}_4^{2-}$, ${\mathrm{WO}}_5^{4-}$, and ${\mathrm{WO}}_6^{6-}$ used for geometry optimization.

Table 2. Representation of the optimized geometric structures of tungsten and oxygen clusters ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$), obtained using the BH and PSO (this work) algorithms, the Gaussian 09 commercial software, and those reported experimentally via single-crystal X-ray diffraction.

Cluster	BH	PSO	Gaussian 09	X-Ray [50,51,52]
${\mathrm{WO}}_4^{2-}$
${\mathrm{WO}}_5^{4-}$
${\mathrm{WO}}_6^{6-}$

displays the optimized structures obtained with the BH and PSO algorithms (this work), the commercial Gaussian 09 software, and the experimentally reported structures from single-crystal X-ray diffraction [50,51,52]. The structural conformations of the tungsten–oxygen clusters ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$) indicate that the PSO and BH algorithms provide a close approximation to both the commercial Gaussian 09 software results and the experimentally reported structures from single-crystal X-ray diffraction (see Table 2).

The system energy was computed using a Hookeian potential (Equation (5)), with explicit omission of the electrostatic interaction term. This approach is justified because electrostatic contributions are implicitly incorporated in the force parameters (bond constants $K_r$ and $K_a$ in Equation (5)), which were adjusted using experimental Differential Scanning Calorimetry (DSC) data [53,54,55,56]. Consequently, the force constants inherently account for electrostatic effects associated with interatomic bond energies.

The structural parameters obtained with the PSO algorithm, shown in

Table 3. Average bond lengths (r) and angles ($ang$) of (${\mathrm{C}}_3$–${\mathrm{C}}_5$) carbon clusters, optimized using the BH and PSO algorithms (Jana et al. [46] and this work), and the Gaussian 09 commercial software.

Reference	Cluster	r a	$\mathit{ang}$ b
BH	${\mathrm{C}}_3$	$1.58$	$180.00$
Jana et al. [46] c		$1.29$	$179.89$
In this work c		$1.29$	$179.98$
Gaussian 09		$1.29$	$180.00$
BH	$C_4$ (acyclic)	$1.60$	$179.99$
Jana et al. [46] c		$1.32$	$132.73$
In this work c		$1.35$	$178.74$
Gaussian 09		$1.30$	$179.94$
BH	$C_4$ (cyclic)	$1.58$	$90.00$
Jana et al. [46] c		$1.49$	$88.31$
In this work c		$1.37$	$90.00$
Gaussian 09		$1.45$	$90.00$
BH	${\mathrm{C}}_5$	$1.52$	$179.60$
Jana et al. [46] c		$1.29$	$156.56$
In this work c		$1.29$	$180.00$
Gaussian 09		$1.29$	$179.97$

^a  $r=$ Length (Å); ^b  $ang=$ Angle (°); ^c PSO.

for the ${\mathrm{C}}_3$–${\mathrm{C}}_5$ carbon clusters, are comparable to those derived from the BH algorithm and the Gaussian 09 software. The optimization of the three-carbon cluster showed the highest accuracy in its average bond lengths and angles, except for the C–C single bond length predicted by the BH algorithm, which was slightly elongated compared to those from the PSO algorithms (Jana et al. [46] and the one in this work) and the commercial software Gaussian 09. The average bond lengths for both cyclic and acyclic four-carbon cluster structures showed good agreement, with deviations of 0.02–0.30 Å relative to the Gaussian 09 results. However, a discrepancy of ${47}^{\circ }$ was observed in the angle of the acyclic $C_4$ cluster structures optimized using the PSO algorithm from Jana et al. [46]. For the ${\mathrm{C}}_5$ cluster, the average bond angles (∼${180.00}^{\circ }$) obtained with our PSO algorithm demonstrated higher accuracy than those from the algorithm reported by Jana et al. [46], aligning closely with the structural parameters derived from Gaussian 09 optimizations.

Table 4. Average bond lengths (r) and angles ($an{g}_s$) of tungsten–oxygen clusters ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$), obtained through structure optimizations using the BH and PSO algorithms, the commercial software Gaussian 09, and single-crystal X-ray diffraction [50,51,52].

Reference	Cluster	r a	${\mathit{ang}}_1$ b	${\mathit{ang}}_2$ b	${\mathit{ang}}_3$ b
BH	${\mathrm{WO}}_4^{2-}$	$1.96$	$109.47$	−	−
PSO (in this work)		$1.73$	$109.53$	−	−
Gaussian 09		$1.80$	$109.47$	−	−
X-ray [50,51,52]		$1.79$	$110.26$	−	−
BH	${\mathrm{WO}}_5^{4-}$	$1.97$	$90.00$	$120.00$	$180.00$
PSO (in this work)		$1.92$	$90.00$	$120.00$	$179.88$
Gaussian 09		$1.93$	$90.00$	$120.00$	$179.95$
X-ray [50,51,52]		$1.86$	$93.52$	$120.00$	$158.22$
BH	${\mathrm{WO}}_6^{6-}$	$1.97$	$90.00$	$180.00$	−
PSO (in this work)		$2.24$	$91.10$	$175.24$	−
Gaussian 09		$1.99$	$90.00$	$180.00$	−
X-ray [50,51,52]		$1.95$	$92.64$	$174.87$	−

^a  $r=$ Length (Å); ^b  $an{g}_s=$ Angle (°).

presents the average bond lengths and angles of tungsten–oxygen clusters ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$), optimized using BH and our PSO algorithms, Gaussian 09 software, and the values reported from single-crystal X-ray diffraction studies [50,51,52]. The results show that the structural parameters of the ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$) tungsten–oxygen clusters obtained via the BH and PSO methods are highly consistent with those obtained with Gaussian 09. Furthermore, the calculated average bond lengths and angles closely match the experimental XRD data [50,51,52]. Notably, only the optimized angle $an{g}_3$ of the ${\mathrm{WO}}_5^{4-}$ cluster exhibited a deviation ${20.00}^{\circ }$ compared to the XRD result, likely due to intermolecular interactions associated with crystal lattice packing [51,52].

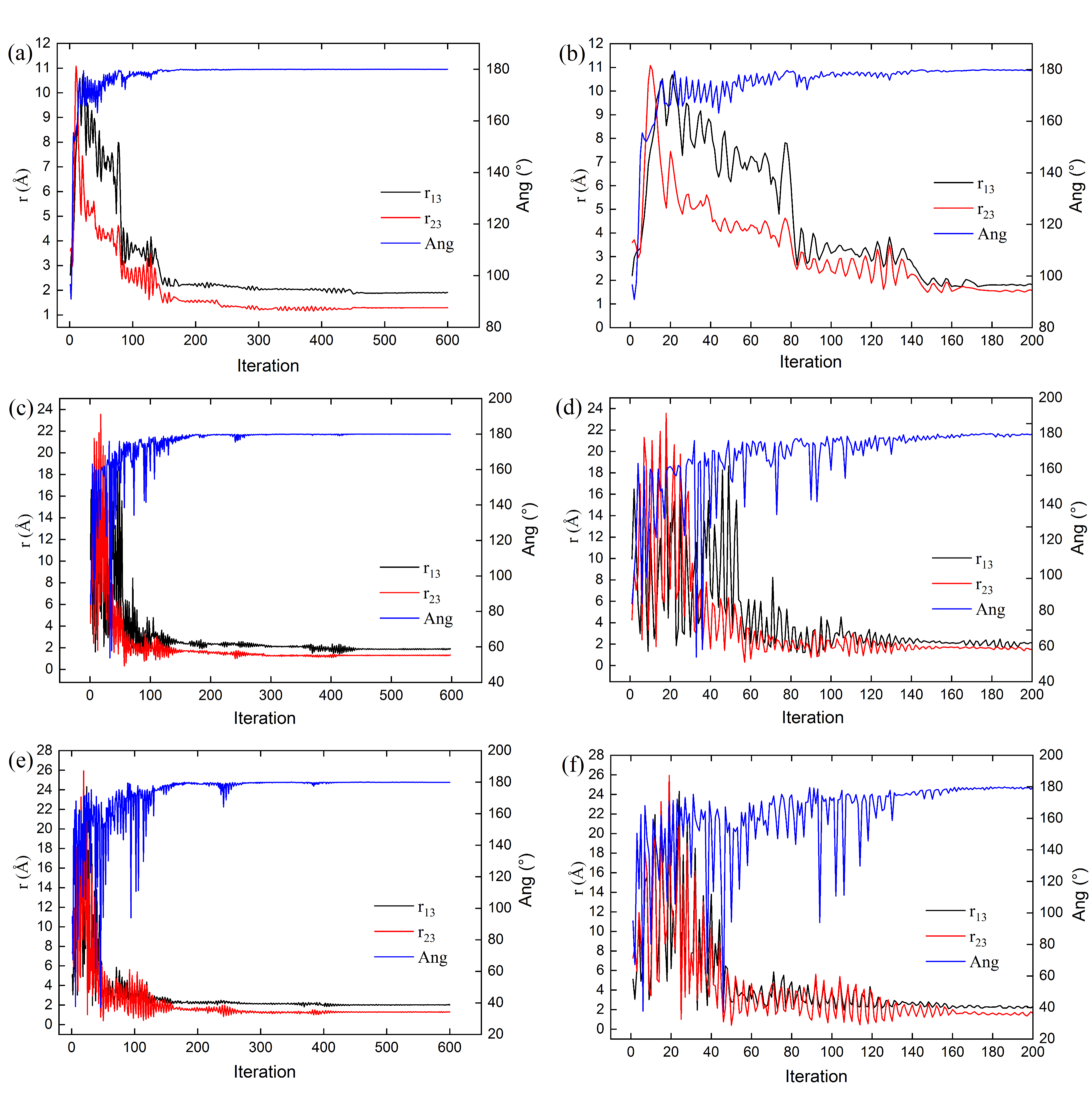
The evolution of the geometric structure optimization for cluster $n^{\circ }$ 1 (composed of three carbon atoms, ${\mathrm{C}}_3$) is illustrated in Figure 1, which displays snapshots of the process across iterations. The cluster bonds ($r_{13}$ and $r_{23}$) are initially elongated during the first 20 iterations (Figure 2b), after they gradually decrease to reach a minimum value of 1.29 Å (Figure 2a and

Table 5. Bond lengths (r), bond angles ($ang$), and potential energies (V) of ${\mathrm{C}}_3$ clusters ${\mathrm{n}}^{\circ }$ 1, 8, and 10, optimized using the PSO algorithm.

Cluster	${\mathit{r}}_{13}$ (Å)	${\mathit{r}}_{23}$ (Å)	${\mathit{ang}}_1$ (°)	V (Ha)  $\times {10}^{-5}$
1	$1.29149$	$1.29341$	$179.80617$	$4.48600$
8	$1.29336$	$1.29080$	$179.71400$	$7.62570$
10	$1.30979$	$1.26546$	$178.49936$	$4.46674$

). Concurrently, the angle formed by the three carbon atoms undergoes minor variations, increasing from $110.00$ to ${179.98}^{\circ }$ as the iterations progress. This angle stabilizes near ${180.00}^{\circ }$ when the potential energy is minimized (Figure 2a,b and Table 5). Similar harmonic motion trends—though with higher frequency—are observed in the C–C bond lengths and the angle increase (denoted as Ang) for clusters $n^{\circ }$ 8 and 10 (Figure 2c–f and Table 5). Notably, within the swarm of 10 clusters, each conformation exhibits distinct dynamics, geometric configurations, and energy profiles during optimization via the PSO algorithm (see Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 and Table 5).

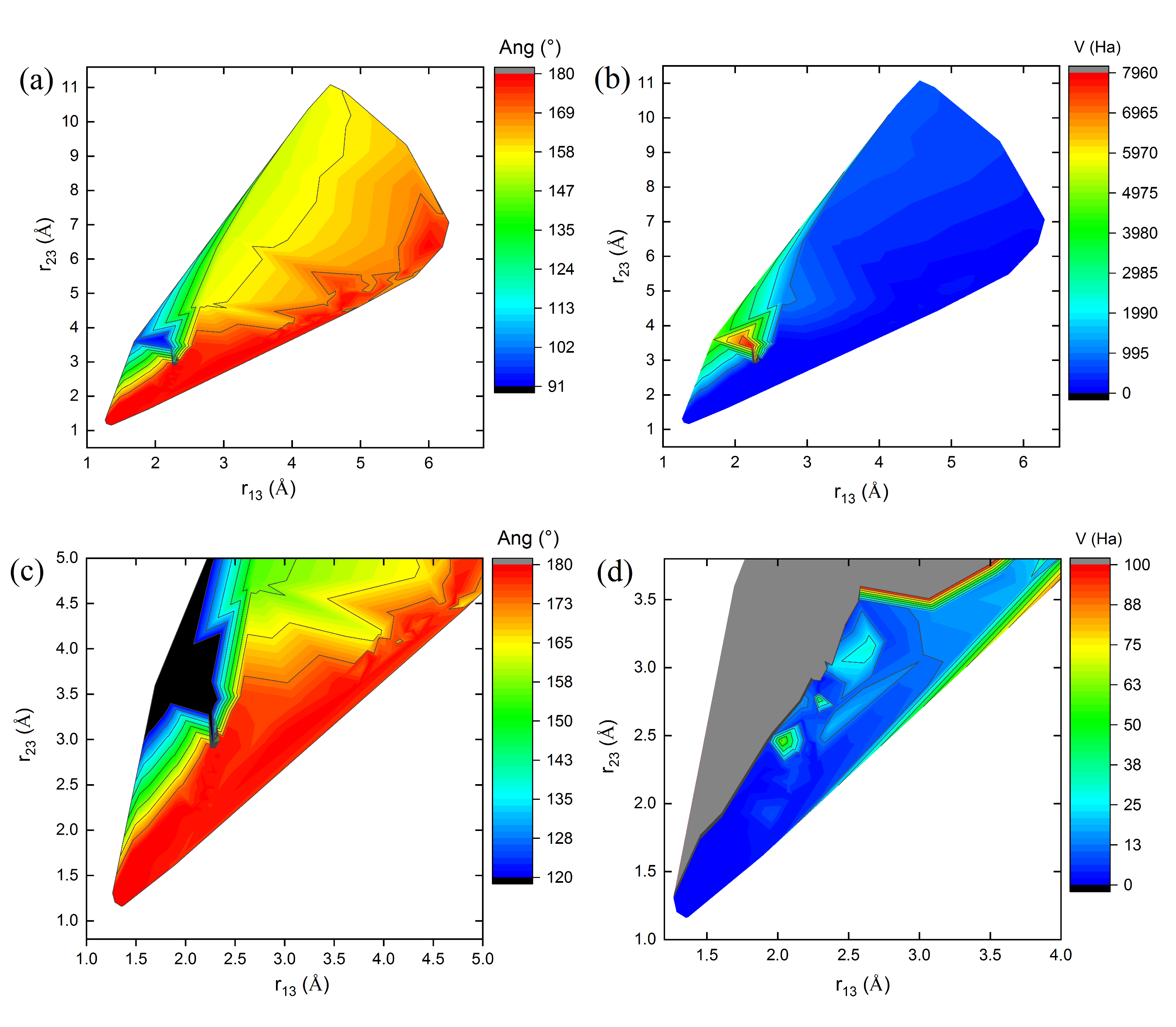
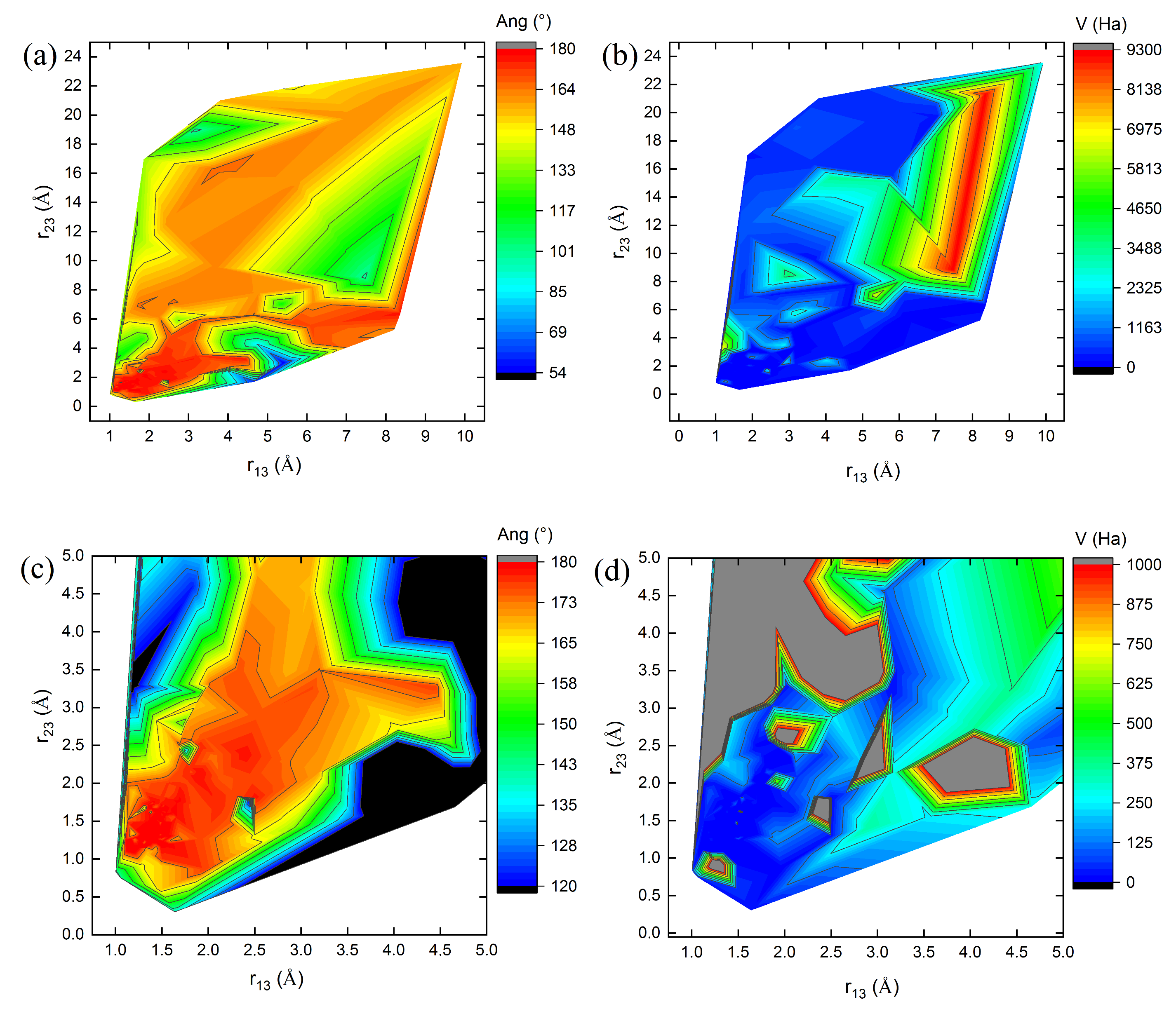
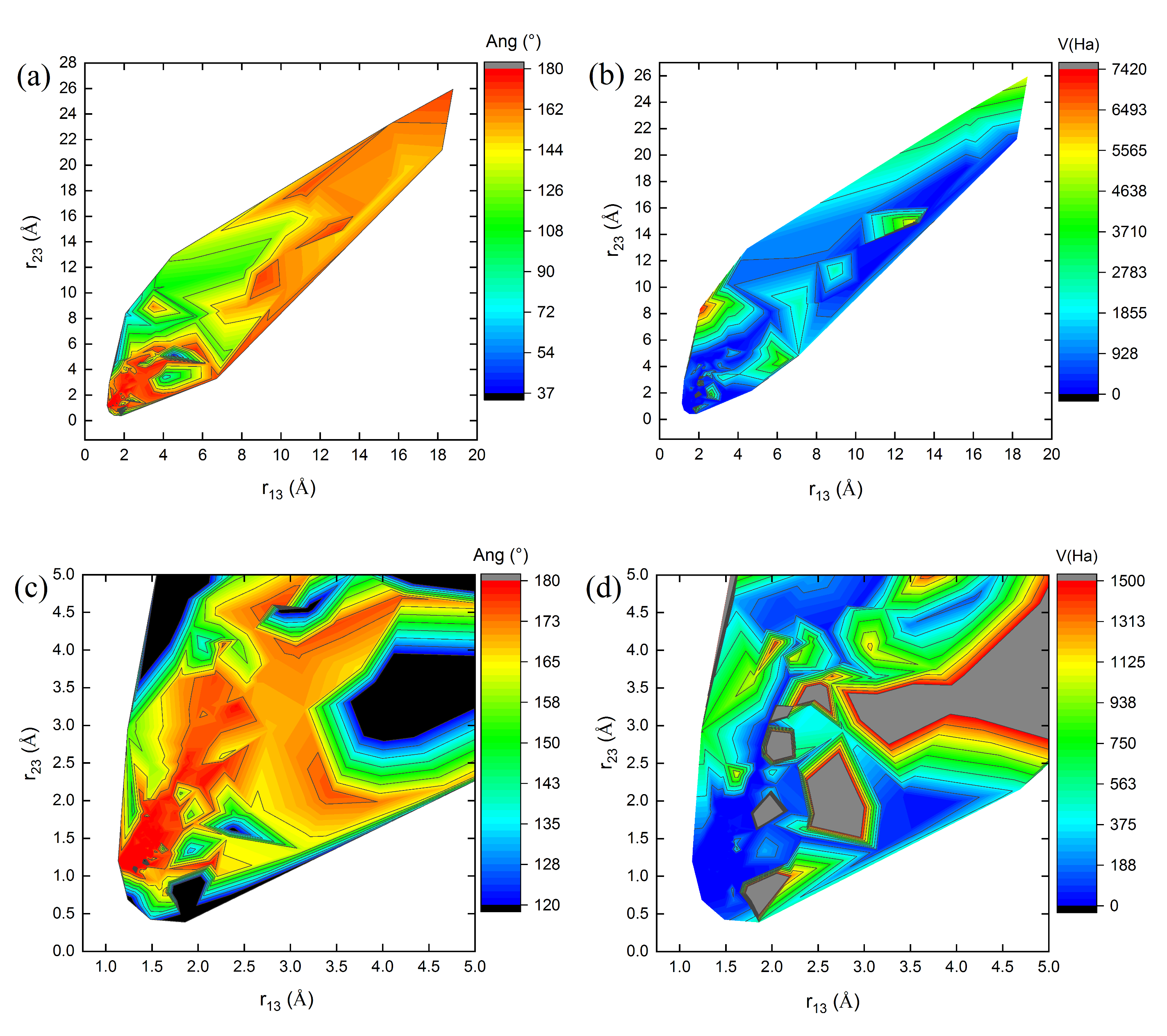
Figure 3, Figure 4 and Figure 5 show 3D relief maps of the angle Ang (a) and the potential energy V (b), with their respective magnifications (c,d), as functions of the lengths $r_{13}$ and $r_{23}$, for the ${\mathrm{C}}_3$ clusters ${\mathrm{n}}^{\circ }$ 1, 8, and 10, over 600 iterations. Each ${\mathrm{C}}_3$ conformer within the swarm exhibits distinct energy landscapes. However, all converge to the same minimum potential energy value, $V_0$, as a function of the positional changes of the clusters during the dynamics of the swarm in the 3N-dimensional hyperspace ${\mathbb{R}}^{3N}$. The blank spaces correspond to regions where bond lengths, angles, and energies of the ${\mathrm{C}}_3$ cluster conformations are undefined in the energy landscape during geometry optimization. The highest Ang values are located at the peaks (red values near ${180.00}^{\circ }$ in parts (a,c) of Figure 3, Figure 4 and Figure 5), protruding from the paper plane. In contrast, the lowest values are found in the valleys (dark blue and black regions near ${100.00}^{\circ }$ in the same figures), oriented towards the paper plane. These features occur when the C–C bond lengths, $r_{13}$ and $r_{23}$, approach 1.29 Å (see Table 5 and Figure 3, Figure 4 and Figure 5).

Similarly, the highest potential energy values V are observed at the peaks (red regions in parts (b) of Figure 3, Figure 4 and Figure 5). Additional intermediate values lie on the slopes (gray regions in the magnified parts (d) of Figure 3, Figure 4 and Figure 5), extending outward from the paper plane. The lowest energy values, however, are concentrated in the valleys of the energy landscape (dark blue regions in parts (b,d) of Figure 3, Figure 4 and Figure 5), oriented toward the paper plane. These observations correspond to the geometry optimization process of the ${\mathrm{C}}_3$ cluster structures.

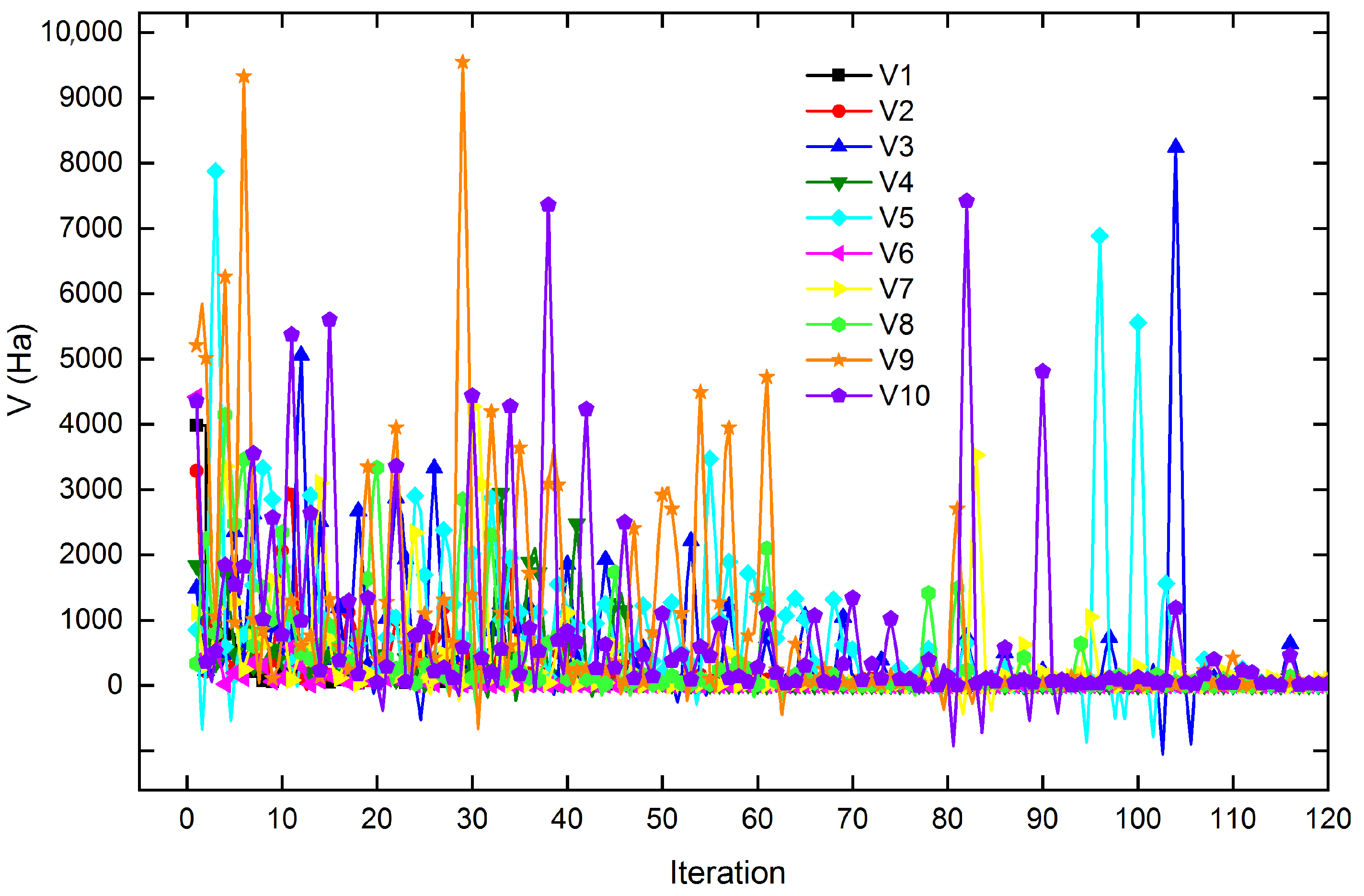
Figure 6 shows the potential energy behavior of the swarm of 10 three-carbon-atom clusters over the first 120 iterations. The cluster $n^{\circ }$ 8 exhibits an intermediate potential energy during the first 60 iterations, subsequently reaching one of the lowest potential energy values in the swarm as its trajectory progresses. However, clusters 4, 5, 9, and 10 exhibit conformations with alternating high potential energy values. At the same time, the remaining conformers maintain a potential energy close to the average for the swarm during the energy minimization of each conformer.

The potential energy behavior of the clusters, as their atoms undergo positional changes, illustrates the various conformations adopted during the search for the global potential energy minimum, a process often characterized by cooperative swarm dynamics. Conformers with higher potential energy require larger displacements within the ${\mathbb{R}}^{3N}$ hyperspace (relative to the average position of the swarm) to contribute to the energy minimization potential [Equation (5)]; this accounts for the bond elongation observed in the three-carbon-atom cluster $n^{\circ }1$ during early iterations. Only by iteration 22 (Figure 1 and Figure 2) do these bond lengths begin to shorten, demonstrating the integration of the cluster $n^{\circ }1$ conformer into the swarm collective, where it assumes positions similar to the other swarm conformers, thereby reducing its potential energy as the system progresses toward convergence.

Table 6. Single-point relative electronic energies (Ha) obtained with Gaussian 09 for carbon, tungsten, and oxygen atom clusters, based on structures optimized using the BH, PSO, and DFT methods.

Cluster		BH a	PSO (In This Work) b	PSO (Jana et al.) b [46]	Gaussian 09 c
${\mathrm{C}}_3$		$1.64\times {10}^{-1}$	$1.20\times {10}^{-5}$	$0.00$	$0.00$
${\mathrm{C}}_4$	acyclic	$3.02\times {10}^{-1}$	$5.79\times {10}^{-2}$	$2.66\times {10}^{-2}$	$0.00$
	cyclic	$2.69\times {10}^{-1}$	$2.26\times {10}^{-1}$	$1.57\times {10}^{-2}$	$0.00$
${\mathrm{C}}_5$		$3.54\times {10}^{-1}$	$5.85\times {10}^{-4}$	$0.00$	$0.00$
${\mathrm{WO}}_4$		$6.41\times {10}^{-2}$	$1.05\times {10}^{-1}$	−	$0.00$
${\mathrm{WO}}_5$		$1.01\times {10}^{-2}$	$9.16\times {10}^{-3}$	−	$0.00$
${\mathrm{WO}}_6$		$7.60\times {10}^{-5}$	$1.29\times {10}^{-2}$	−	$0.00$

^a Relative electronic energy calculated using Gaussian 09 at a single point, based on its BH-optimized structure. ^b Relative electronic energy calculated using Gaussian 09 at a single point, based on its PSO-optimized structure. ^c Relative electronic energies of the optimized structures, calculated using DFT with Gaussian 09.

presents the calculated relative electronic energy values for carbon, tungsten, and oxygen cluster structures studied in this work. To evaluate the precision of the electronic energies for the structures optimized with the PSO and BH methods, we used the absolute electronic energy obtained from Gaussian as a reference (Table 6). Table 6 shows the difference between the electronic energy calculated by Gaussian in a single-point calculation for a optimized structure obtained with PSO/BH, and the corresponding electronic energy obtained directly from Gaussian. In this way, values closest to zero indicate higher precision in the respective optimization method. The small relative electronic energy differences (∼${10}^{-5}$– ${10}^{-1}$ Ha) between BH/PSO-optimized and DFT-optimized structures suggest that both BH and PSO exhibit high accuracy in predicting the electronic energies of these molecular structures, carbon, tungsten and oxygen clusters systems. However, PSO demonstrated slightly higher accuracy compared to BH, particularly for carbon clusters ${\mathrm{C}}_n$ (n = 3–5) and the tungsten–oxygen clusters ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$), where lower relative energy electronic values were observed.

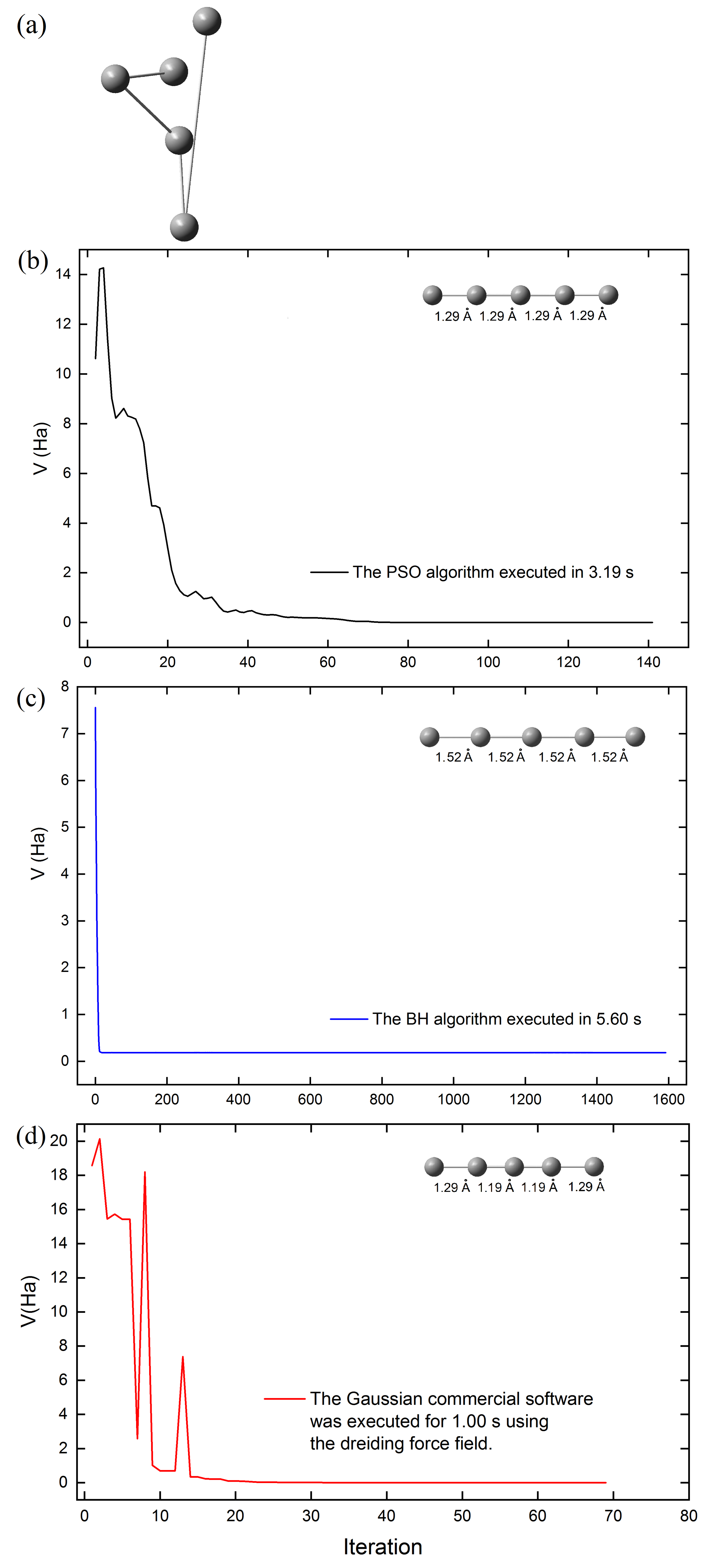
The computational cost of the PSO, BH, and molecular mechanics (using the Dreiding force field in Gaussian), was assessed by tracking the energy minimization of cluster ${\mathrm{C}}_5$ during geometric optimization as a function of optimization steps (Figure 7b,d), starting from the initial structure of cluster ${\mathrm{C}}_5$ (Figure 7a). Figure 7 highlights that the structural optimization of the ${\mathrm{C}}_5$ cluster required the least time with the Gaussian software (69 steps), followed by the PSO algorithm (141 steps), and the BH algorithm (1592 steps). All calculations employed the same initial structure of the ${\mathrm{C}}_5$ cluster. Although Gaussian software optimizes the ${\mathrm{C}}_5$ cluster structure more quickly, it predicts triple bond lengths (1.19 Å) for the carbon atoms inside the cluster. This value differs slightly from the results obtained (1.29 Å in Table 3) when the same structure is optimized at the DFT level of theory using the same software. However, our PSO algorithm predicts double bonds (1.29 Å) in the optimized structure of the ${\mathrm{C}}_5$ cluster (see Figure 7b). Additionally, the structure of the ${\mathrm{C}}_5$ cluster was optimized using the UFF (Unified Force Field) in Gaussian software, but an unexpected cyclic structure was obtained.

Contrarily, it is important to note that the PSO algorithm implemented by Jana et al. [46] uses Gaussian 09 software to calculate the atomic positions at each step of the geometric optimization of cluster structures via DFT. In contrast, our PSO algorithm does not depend on any external software to determine atomic positions during the simultaneous optimization of ten conformer structures. Instead, it relies solely on Equations (1)–(4) to locate each atom of each cluster within the ${\mathbb{R}}^{3N}$ search hyperspace at each iteration and uses the potential energy of each cluster [Equation (5)] as the objective function to be minimized.

A precise understanding of the structures of these clusters is crucial, particularly for compounds of tungsten and oxygen atoms, as they serve as fundamental building blocks for the growth of larger metal oxide arrangements. Through self-assembly, larger compounds, such as polyoxometalates, are formed, which have numerous applications due to their electronic and magnetic properties, which in turn depend on their structural arrangement [57,58].

3. Methodology

3.1. Algorithm and Computational Details

The PSO is an algorithm that explores a set of randomly generated solutions, where each structural conformer learns from its own experience and that of other conformers through their movements during optimization [59]. All conformer structures are located within a hyperspace $\in {\mathbb{R}}^{3N}$ [60], where N is the number of atoms in the cluster, i is the cluster index ( $i=1,\dots ,M$), and j ( $j=1,\dots ,3N$) is the number of dimensions of the hyperspace ${\mathbb{R}}^{3N}$ (Figure 8). Figure 8 shows the equivalence between the coordinates $x_{1,1}^t,\dots ,x_{1,9}^t\in {\mathbb{R}}^{3N}$ and $x_1,y_1,z_1,\dots ,x_3,y_3,z_3\in {\mathbb{R}}^3$ of the position vector ${\overrightarrow{x}}_{1,1}^t$ for the conformer of the cluster $n^{\circ }$ 1 (with three carbon atoms) in the swarm. From Equations (1)–(4), the velocities and positions of the conformers of each cluster in the hyperspace are defined, and Equation (5) represents the potential energy.

$$\begin{array}{cc}\hfill {\overrightarrow{x}}_{i,j}^t& =x_{i,j}^t,\dots ,x_{M,3N}^t\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\overrightarrow{v}}_{i,j}^t& =v_{i,j}^t,\dots ,v_{M,3N}^t\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\overrightarrow{v}}_{i,j}^{t+1}& =w·{\overrightarrow{v}}_{i,j}^t+d_1·{\epsilon }_1(p_{best}-{\overrightarrow{x}}_{i,j}^t)+d_2·{\epsilon }_2(g_{best}-{\overrightarrow{x}}_{i,j}^t)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\overrightarrow{x}}_{i,j}^{t+1}& ={\overrightarrow{x}}_{i,j}^t+{\overrightarrow{v}}_{i,j}^{t+1}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill V_i^t(x_{i,j}^t,\dots ,x_{M,3N}^t)& ={\displaystyle \frac{1}{2}}\left[\sum _{k=1}^p{K}_r{(r_k-l_k)}^2+\sum _{s=1}^q{K}_a{(an{g}_s-{\theta }_s)}^2\right]\hfill \end{array}$$

(5)

where ${\overrightarrow{x}}_{i,j}^t$ and ${\overrightarrow{x}}_{i,j}^{t+1}$ are the positions of the cluster i in iterations t and $t+1$ (Equations (1) and (4)), and ${\overrightarrow{v}}_{i,j}^t$ and ${\overrightarrow{v}}_{i,j}^{t+1}$ are the velocities of the cluster i in iterations t and $t+1$ (Equations (2) and (3)), respectively. The coefficients ${\epsilon }_1$ and ${\epsilon }_2$ in Equation (3) are randomly selected within the interval [0, 1]. The inertia coefficient w governs the tendency of the conformer to remain in its current position, while $d_1$ and $d_2$ (adjustable if necessary) correspond to the individual and global acceleration coefficients, respectively. These coefficients guide the positions of the clusters in the hyperspace ${\mathbb{R}}^{3N}$ to ensure convergence, allowing all candidate solutions to reach the global minimum of the potential energy $V_0$ efficiently.

Table 7. PSO parameters.

Parameters	Value
Number of particles or clusters, i	$10.00$
Inertia coefficient, w	$0.90$
Individual coefficient of acceleration, $d_1$	1.00–1.50
Global coefficient of acceleration, $d_2$	1.00–1.50
Random coefficients ( ${\epsilon }_1$ and ${\epsilon }_2$)	0.00–1.00

shows the allowed values for these parameters, which fall within the optimization ranges reported in previous studies [46,61,62,63]. In these studies, the parameters have demonstrated stability during the process and ensured energy convergence of the cluster structures. The variables $g_{best}$ and $p_{best}$ are the best positions of the swarm and each cluster, respectively, in each iteration t (Equation (3)).

Equation (5) shows that $r_k$ represents the k bonds and $an{g}_s$ are the s bond angles in the cluster, where $r_k$ and $an{g}_s$ are correlated through their components $x_{i,j}^t,\dots ,x_{M,3N}^t$. In this equation, $K_r$ (9.53 mdyn/Å for C=C bonds and 9.73 mdyn/Å for W−O bonds) and $K_a$ (0.372 mdyn/degree) denote the force constants of the k bonds and the angles s in the studied systems. The values $l_k$ and ${\theta }_s$ correspond to the lengths and angles of the experimental bonds, respectively, for each cluster [64,65].

Table 8. ${\theta }_s$ values for the clusters of three and four carbon atoms ( $l_k=1.29$ Å).

Number of Atoms	Structure	${\mathit{\theta }}_{\mathit{s}}{(}^{\circ })$
3		180.00
		60.00
4		180.00
		90.00

shows the values of ${\theta }_s$ when $l_k=1.29$ Å for clusters of three and four atoms.

The learning acquired by the conformers is referred to as collective learning, while that acquired by an individual conformer is termed cognitive learning. Starting from the initial structures, a set of random atomic coordinates was considered, where each conformer was assigned its position ${\overrightarrow{x}}_i^t$ and trial velocity ${\overrightarrow{v}}_i^t$. During optimization, the position ${\overrightarrow{x}}_i^t$ and velocity ${\overrightarrow{v}}_i^t$ vectors are updated using the Equations (3) and (4) at each iteration t, to locate the global minimum energy configuration. As a result of collective learning, each conformer stores in its memory the best position obtained by itself or any other conformer in the swarm during iteration t, denoted as $g_{best}$ (see Equation (3)). The $g_{best}$ is selected by comparing the components $x_{i,j}^t$ of the vector ${\overrightarrow{x}}_{i,j}^t$ for each conformer in the swarm (10 conformers, where $i=1,\dots ,10$) at each iteration t. Throughout the process, each conformer stores in its memory the best position obtained up to iterations $n-1$, denoted as $p_{best}$ [30]. The $p_{best}$ values are selected by each conformer i in the swarm by comparing its components $x_{i,j}^t$ (from vector ${\overrightarrow{x}}_{i,j}^t$) across iterations $t=1,\dots ,n-1$ stored in its memory.

The change in direction of any conformer is determined by its velocity, which represents the rate of change of its position concerning iteration t. In a $3N$-dimensional search space, the position of the i-th conformer in the swarm at iteration t is represented by the vector ${\overrightarrow{x}}_i^t=(x_{i,1}^t,x_{i,2}^t,\dots ,x_{M,3N}^t)$, and its velocity by the vector ${\overrightarrow{v}}_i^t=(v_{i,1}^t,v_{i,2}^t,\dots ,v_{M,3N}^t)$ [30]. The potential energy function of the system $V_i^t$ follows Hooke’s Law [Equation (5)], where atoms are considered rigid spheres connected by a spring. The positions $p_{best}$ and $g_{best}$ in Equation (3) correspond to the minimum value of the objective potential function $V_0\left(x_{i,j}^t\right)=min{V}_i^t(x_{i,j}^t,\dots ,x_{M,3N}^t)$ [Equation (5)] calculated iteratively from $t=1$ to n. At each iteration t, the updated components ( $x_{i,j}^{t+1}$ and $v_{i,j}^{t+1}$) of the atoms in the conformers are obtained utilizing Equations (3) and (4). Vectors ${\overrightarrow{x}}_i^t$ and ${\overrightarrow{v}}_i^t$ are updated in each iteration t until their components $x_{i,j}^t$ and $v_{i,j}^t$ converge ( ${\overrightarrow{x}}_{i,j}^t\to {\overrightarrow{x}}_0$ and ${\overrightarrow{v}}_{i,j}^t\to 0$) during the search for the global minimum of the objective function (potential energy, $V_0$) for each conformer.

3.2. Software

This work used the initial positions of carbon atoms ${\mathrm{C}}_n$ (n = 3–5) in the cluster structures described by Jana et al. [46]. However, the initial positions of the tungsten and oxygen atoms in ${\mathrm{WO}}_n^{m-}$ (n = 4–6, $m=2,4,6$) were randomly generated. The PSO algorithm written in Fortran 90, the commercial software Gaussian 09, and the Atomic (ASE) BH simulation environment in Python 3.10 were used to optimize the structures of the carbon, tungsten and oxygen atom clusters. In the PSO algorithm, a Hooke potential was utilized, while in the ASE-Python algorithm, the basin-hopping (BH) global optimization method was applied using an effective medium theory (EMT) potential to model the interaction between atoms. The force constants used were K = 9.53 mdyn/Å for C=C bonds and 9.73 mdyn/Å for W–O bonds. These parameters enabled comparative analysis of the optimized structures.

In the Gaussian 09 software, the 6-311+G** basis set was used for carbon (C) and oxygen (O) atoms [66,67], along with the B3LYP exchange-correlation functional. The Los Alamos Effective Core Potential (ECP) combined with the LANL2DZ double zeta basis set [68,69] and its corresponding pseudopotential was used to approximate the electron of the tungsten (W) atom. Subsequently, single-point electronic energy calculations were carried out on the optimized cluster structures (obtained via PSO, BH, and DFT methods) using DFT as implemented in Gaussian 09 software [70].

The PSO and BH algorithms do not rely on the Gaussian 09 software to perform geometric optimization of the studied clusters’ structures. These algorithms were compiled and executed on a high-performance computing node equipped with two Intel Xeon E5-2660 v2 processors (Intel Corporation, Santa Clara, CA, USA), each with 10 cores operating at 2.20 GHz, and 48 GB of RAM.

Figure 9 shows the general flowchart of the PSO algorithm.

3.3. PSO Algorithm

The following steps describe the cluster structure prediction algorithm using the PSO technique:

• An initial set of cluster structures with random atomic coordinates is generated without any symmetry restrictions.
• An improved set of atomic coordinates for the conformers is sought in hyperspace ${\mathbb{R}}^{3N}$.
• At each step or iteration t, the potential energy $V_i^t(x_{i,j}^t,\dots ,x_{M,3N}^t)$ is calculated for each conformer in the swarm of M clusters.
• The convergence criteria are verified under the condition $V_i^t=$ constant.
• The velocity vectors ( ${\overrightarrow{v}}_i^t$) and position vectors ( ${\overrightarrow{x}}_i^t$) of each conformer in the swarm are updated in hyperspace ${\mathbb{R}}^{3N}$.
• The best global position ( $g_{best}$) is obtained by comparing and selecting the conformer with the lowest potential energy $V_i^t$ in the swarm at each iteration t.
• Each conformer i in the swarm stores its best individual position ( $p_{best}$) by comparing its lowest potential energy, $V_i^t$, obtained iteratively from $t=1$ to $n-1$.
• The output structures generate a new set of initial structures for the subsequent iteration t, continuing until the lowest potential energy $V_i^t$ for each structural conformer converges to a constant value.

4. Conclusions

Good approximations of the molecular structures of carbon atom clusters ${\mathrm{C}}_n$ (n = 3–5) and tungsten oxide clusters, ${\mathrm{WO}}_n^{m-}$ ( $n=4–6,m=2,4,6$), were obtained through geometric optimization using the PSO method with Hooke’s potential. These structures were compared with those optimized using the BH method and DFT implemented in the Gaussian 09 software, as well as with structures reported in X-ray diffraction studies. The algorithm, written in Fortran 90, was based on a metaheuristic model designed to find the minimum potential energy of a system of ten conformers simultaneously in a hyperdimensional space ${\mathbb{R}}^{3N}$. This optimization was performed concerning to the positions of the atoms (connected by spring), to determine the molecular structure of the cluster in its ground state within the three-dimensional space ${\mathbb{R}}^3$. The implementation of the PSO algorithm represents a non-assumptions option, avoiding constraints such as cluster symmetry and external factors imposed by pressure or temperature. This method operates effectively, converging toward geometric configurations presumed to correspond to the global energy minimum or very close to it. The algorithm could serve as an alternative to gradient descent, conjugate gradient, or Newton methods, which are commonly employed in molecular structure optimization but occasionally fail to converge at specific steps or iterations. Additionally, it offers a computational low-cost option for obtaining molecular structures prior to performing ab initio electronic structure calculations.