Exploring Layered Ruddlesden-Popper Structures for High-Performance Energy Devices
Abstract
1. Introduction
2. Methodology
3. Results and Discussions
3.1. Structural Properties
3.2. Electronic Properties
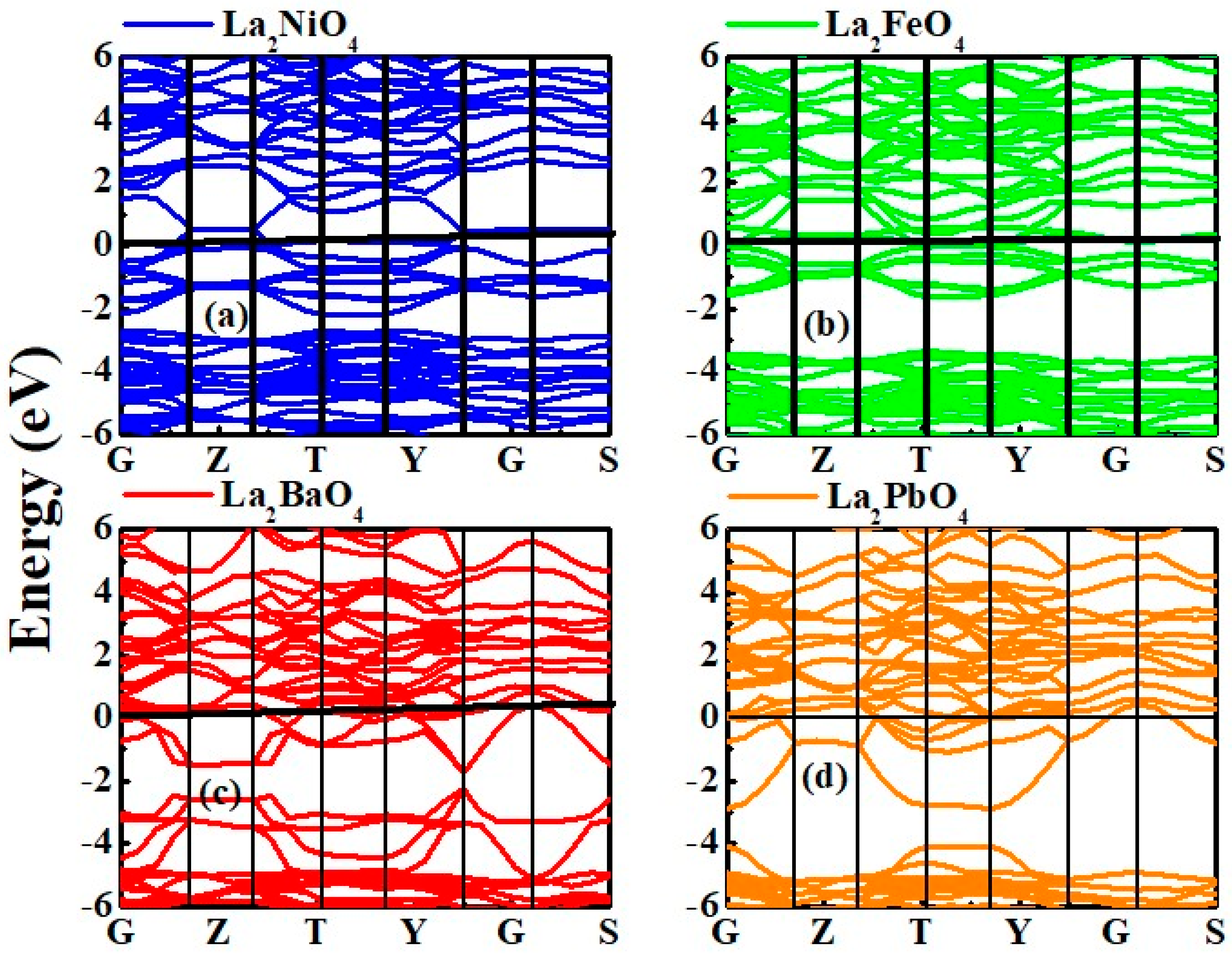
3.2.1. Band Structure
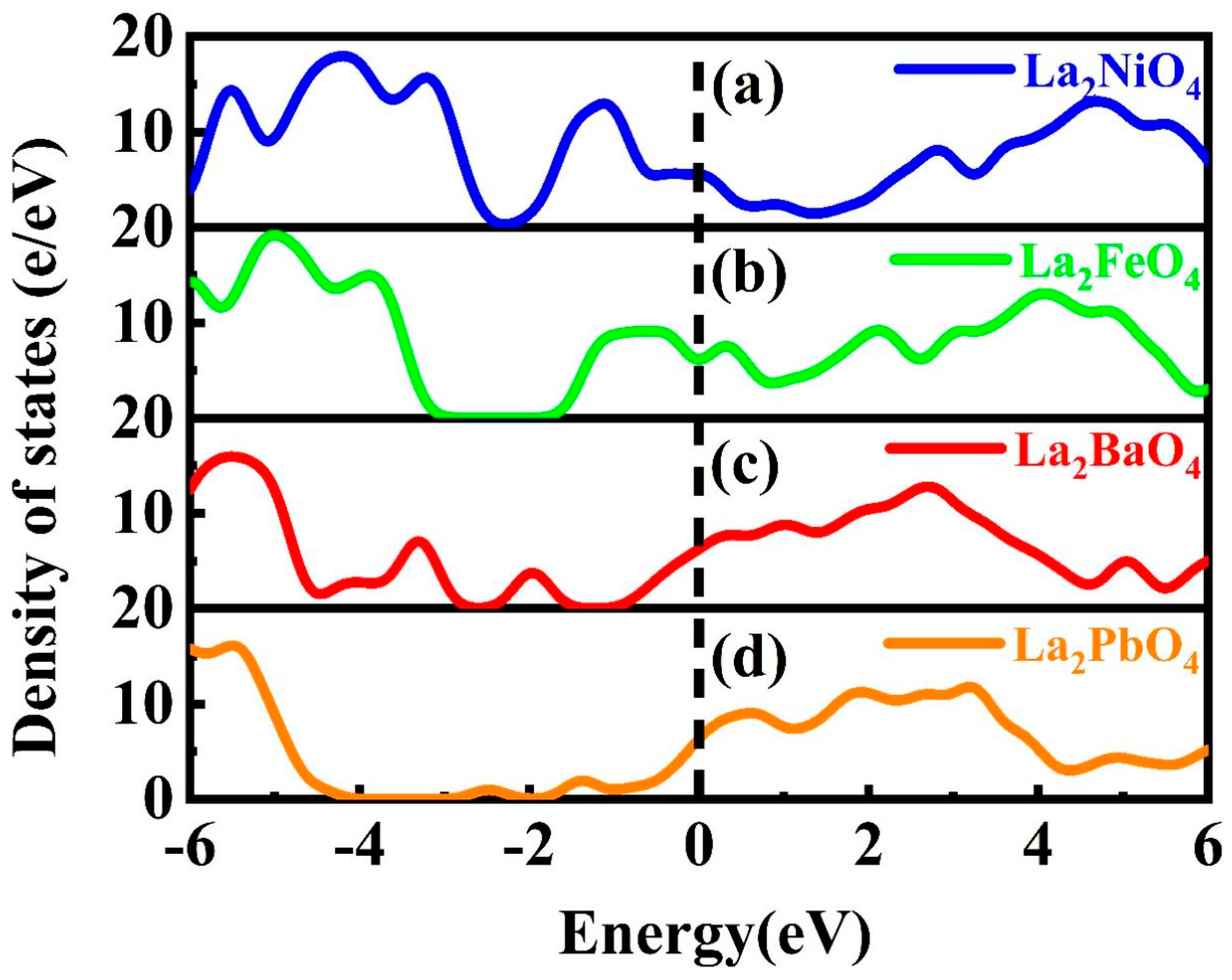
3.2.2. Density of States
La2NiO4
La2FeO4
La2BaO4
La2PbO4
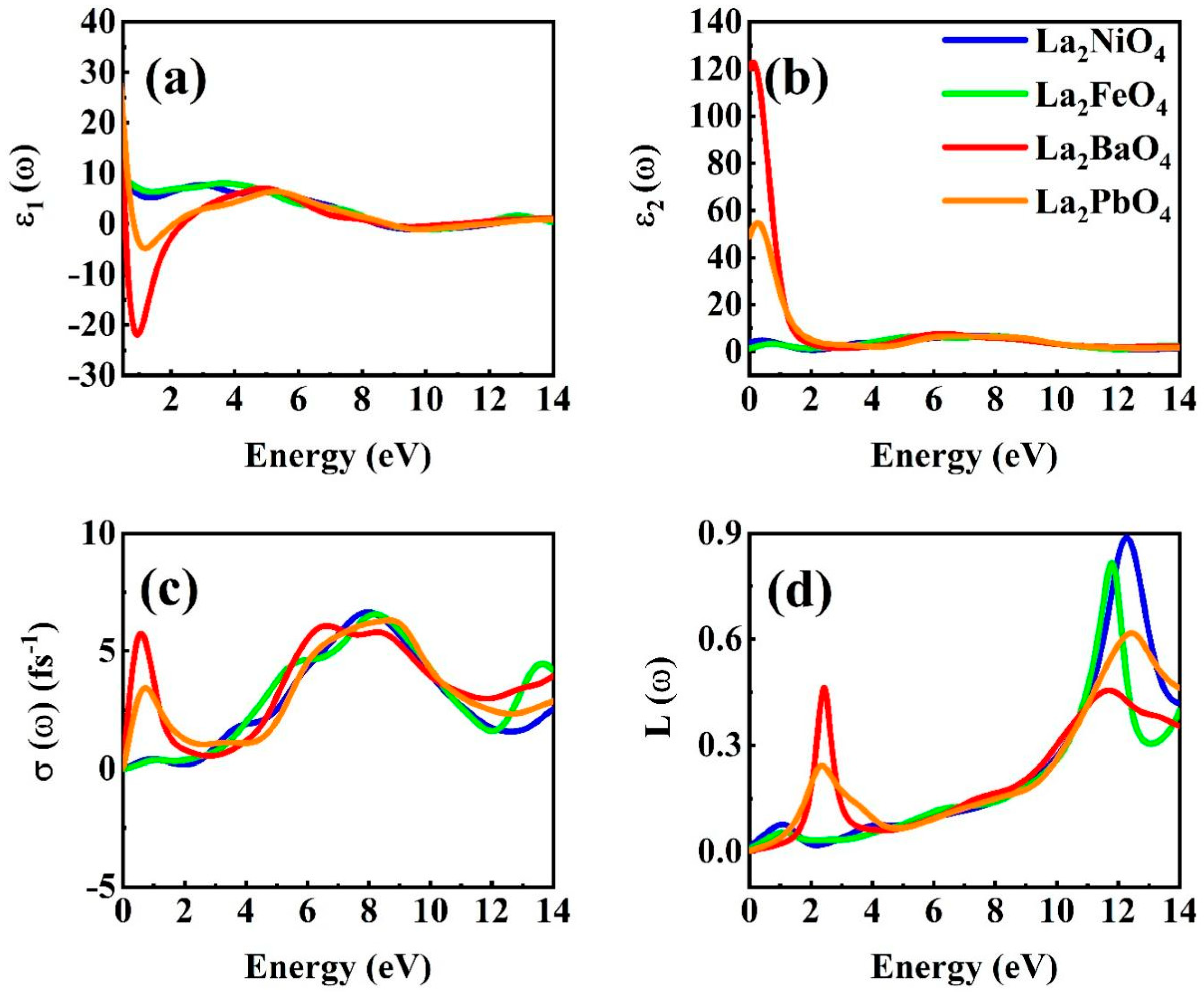
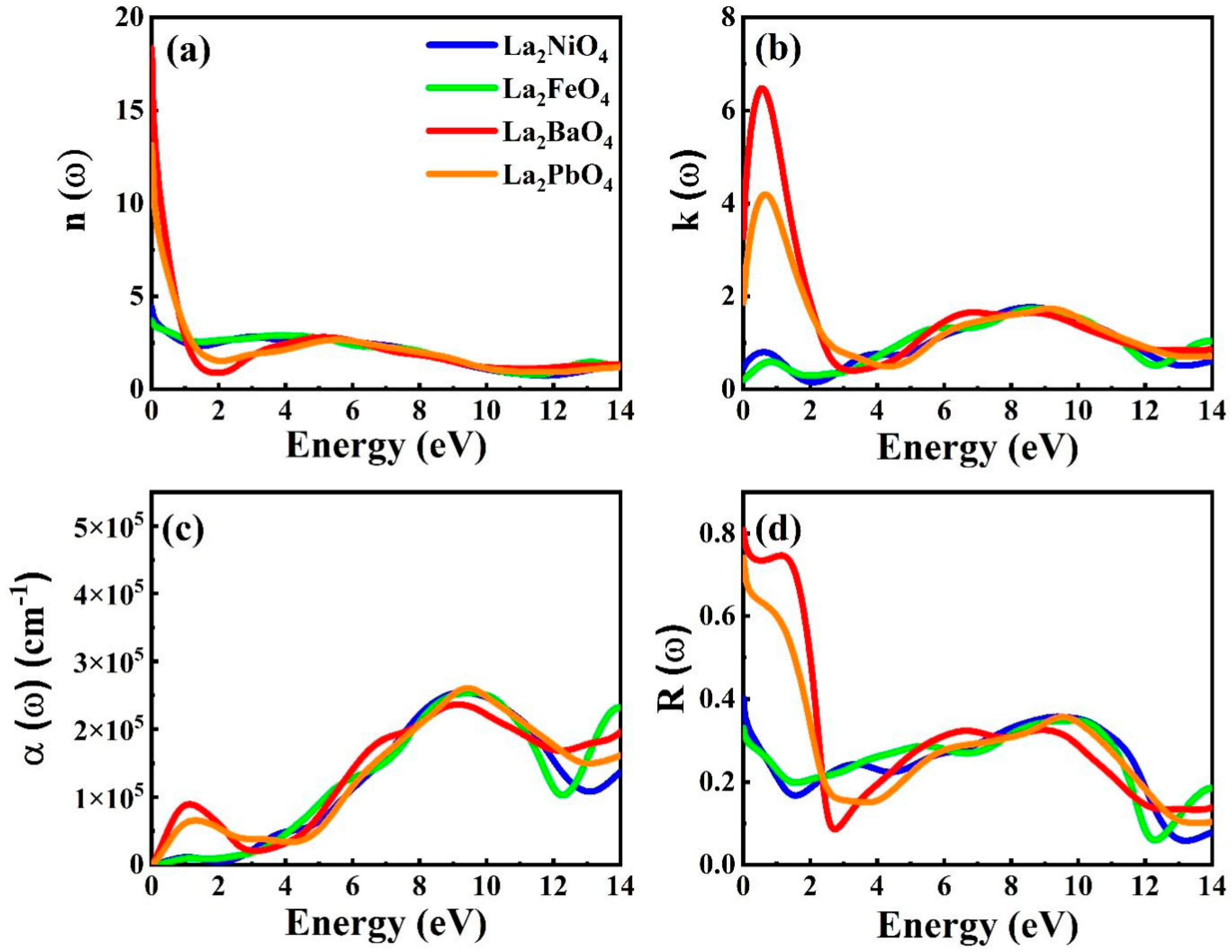
3.3. Optical Properties
3.4. Mechanical Stability
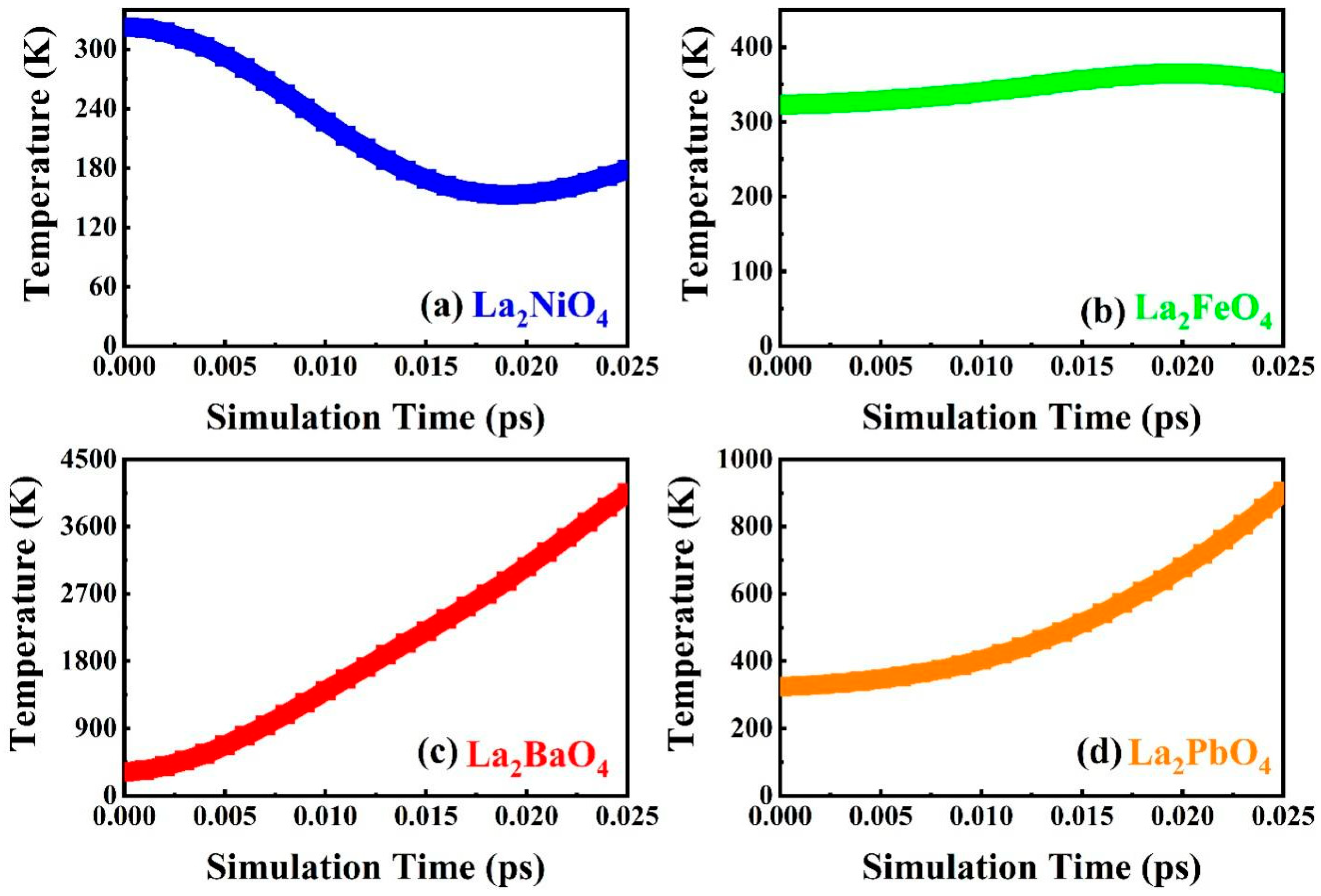
3.5. Time Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, B.A.; Allam, N.K. A first-principles roadmap and limits to design efficient supercapacitor electrode materials. Phys. Chem. Chem. Phys. 2019, 21, 17494–17511. [Google Scholar] [CrossRef] [PubMed]
- Jabeen, N.; Hussain, A.; Shahid, F.; Hessien, M.M. Enhanced performance of Na4Ti5O12 nanowall arrays for next-generation pseudocapacitors through sodiation treatment. FlatChem 2024, 47, 100715. [Google Scholar] [CrossRef]
- Pathak, M.; Jose, J.R.; Chakraborty, B.; Rout, C.S. High performance supercapacitor electrodes based on spinel NiCo2O4@ MWCNT composite with insights from density functional theory simulations. J. Chem. Phys. 2020, 152, 064706. [Google Scholar] [CrossRef] [PubMed]
- Jabeen, N.; Hussain, A.; Ullah, Z.; ul Haq, T.; Elsharkawy, E.R.; El-Bahy, Z.M.; Hessien, M.M. Design and performance evaluation of hierarchical ZnCo2S4@ PANI core-shell nanorod arrays for high-efficiency supercapacitor applications. Mater. Chem. Phys. 2024, 320, 129462. [Google Scholar] [CrossRef]
- Zhan, C.; Lian, C.; Zhang, Y.; Thompson, M.W.; Xie, Y.; Wu, J.; Kent, P.R.C.; Cummings, P.T.; Jiang, D.; Wesolowski, D.J. Computational insights into materials and interfaces for capacitive energy storage. Adv. Sci. 2017, 4, 1700059. [Google Scholar] [CrossRef]
- Jabeen, N.; Zafar, S.; Hussain, A.; Abdullah, A.I.; Kumar, A.; Ahmad, H. A DFT Analysis on the Electronic, Mechanical, Optical, Elastic, Structural and Thermodynamic Properties of XBiNb2O7 (X = Cs, Rb, K and Na) for Photovoltaic Applications. Comput. Condens. Matter 2025, 44, e01063. [Google Scholar] [CrossRef]
- Paek, E.; Pak, A.J.; Hwang, G.S. A computational study of the interfacial structure and capacitance of graphene in [BMIM][PF6] ionic liquid. J. Electrochem. Soc. 2012, 160, A1. [Google Scholar] [CrossRef]
- Hu, R.; Shang, J. Quantum capacitance of transition metal and nitrogen co-doped graphenes as supercapacitors electrodes: A DFT study. Appl. Surf. Sci. 2019, 496, 143659. [Google Scholar] [CrossRef]
- Bissett, M.A.; Kinloch, I.A.; Dryfe, R.A. Characterization of MoS2–graphene composites for high-performance coin cell supercapacitors. ACS Appl. Mater. Interfaces 2015, 7, 17388–17398. [Google Scholar] [CrossRef]
- Chakraborty, B.; Nair, H.T. Theoretical insight for supercapacitors based on 2D materials from DFT simulations. In Fundamentals and Supercapacitor Applications of 2D Materials; Elsevier: Amsterdam, The Netherlands, 2021; pp. 105–128. [Google Scholar]
- Karmakar, S.; Mistari, C.D.; Vaidyanathan, A.; More, M.A.; Chakraborty, B.; Behera, D. Comparison of electrochemical response and electric field emission characteristics of pristine La2NiO4 and La2NiO4/CNT composites: Origin of multi-functionality with theoretical penetration by density functional theory. Electrochim. Acta 2021, 369, 137676. [Google Scholar] [CrossRef]
- Jabeen, N.; Dahshan, A.; Hegazy, H.H.; Hussain, A.; ul Hassan, N. Hierarchical high K content birnessite MnO2 nanosheet arrays as high capacity cathode for asymmetric supercapacitor with broaden potential window of 2.6 V. Electrochim. Acta 2024, 478, 143874. [Google Scholar] [CrossRef]
- Yaqoob, A.; Jabeen, N.; Hamza, A.; Haider, I.; Kainat, F.; Hussain, A. A Theoretical Study for Investigation of Structural, Optical, Electronic, and Mechanical Properties of Double Perovskites Halide for Solar Cell Application. Conclus. Eng. 2025, 72–81. [Google Scholar] [CrossRef]
- Koc, H.; Palaz, S.; Ugur, G.; Mamedov, A.M.; Ozbay, E. Electronic, mechanical, and optical properties of Ruddlesden-Popper perovskite sulfides: First principle calculation. Ferroelectrics 2018, 535, 142–151. [Google Scholar] [CrossRef]
- Li, J.; Yu, Q.; He, Y.; Stoumpos, C.C.; Niu, G.; Trimarchi, G.G.; Guo, H.; Dong, G.; Wang, D.; Wang, L.; et al. Cs2PbI2Cl2, all-inorganic two-dimensional Ruddlesden–Popper mixed halide perovskite with optoelectronic response. J. Am. Chem. Soc. 2018, 140, 11085–11090. [Google Scholar] [CrossRef]
- Hussain, A.; Jabeen, N.; Zafar, S.; Taleb, M.F.A.; Ibrahim, M.M. Theoretical investigation of Ruddlesden Popper phase La2XO4 (X = Zn, Ca, Mg, and Be) compounds with multifunctional properties for flexible photovoltaic applications. J. Electroceramics 2025, 1–14. [Google Scholar] [CrossRef]
- Khalil, R.A.; Hussain, M.I.; Karim, B.; Albalawi, H.; Hussein, K.I.; Hussain, F. DFT-based systematic study on the structural, optoelectronic, thermodynamic, vibrational, and mechanical behavior of Ruddlesden Popper perovskites Sr2XO4 (X = Zr, Hf) for optoelectronic applications. Int. J. Quantum Chem. 2023, 123, e27216. [Google Scholar] [CrossRef]
- Jalem, R.; Tateyama, Y.; Takada, K.; Nakayama, M. First-principles DFT study on inverse Ruddlesden–Popper tetragonal compounds as solid electrolytes for all-solid-state Li+-ion batteries. Chem. Mater. 2021, 33, 5859–5871. [Google Scholar] [CrossRef]
- Glasser, L. Systematic thermodynamics of layered perovskites: Ruddlesden–Popper phases. Inorg. Chem. 2017, 56, 8920–8925. [Google Scholar] [CrossRef]
- Allam, O.; Holmes, C.; Greenberg, Z.; Kim, K.C.; Jang, S.S. Density Functional Theory–Machine Learning Approach to Analyze the Bandgap of Elemental Halide Perovskites and Ruddlesden-Popper Phases. ChemPhysChem 2018, 19, 2559–2565. [Google Scholar] [CrossRef]
- Yan, L.; Niu, L.; Shen, C.; Zhang, Z.; Lin, J.; Shen, F.; Gong, Y.; Li, C.; Liu, X.; Xu, S. Modulating the electronic structure and pseudocapacitance of δ-MnO2 through transitional metal M (M = Fe, Co and Ni) doping. Electrochim. Acta 2019, 306, 529–540. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Liu, N.; Yu, C.; Lee, S.-J.; Zhou, S.; Fu, R.; Yang, J.; Guo, W.; Huang, H.; et al. Operando revealing dynamic reconstruction of NiCo carbonate hydroxide for high-rate energy storage. Joule 2020, 4, 673–687. [Google Scholar] [CrossRef]
- Vigneshwaran, J.; Jose, J.; Thomas, S.; Gagliardi, A.; Narayan, R.L.; Jose, S.P. PPy-PdO modified MXene for flexible binder-free electrodes for asymmetric supercapacitors: Insights from experimental and DFT investigations. Chem. Eng. J. 2024, 487, 150555. [Google Scholar] [CrossRef]
- Radhakrishnan, S.; Selvaraj, S.C.; Kim, B.S. Morphology engineering of Co-MOF nanostructures to tune their electrochemical performances for electrocatalyst and energy-storage applications supported by DFT studies. Appl. Surf. Sci. 2022, 605, 154691. [Google Scholar] [CrossRef]
- Yesuraj, J.; Ramesh, M.; Kim, K.; Biswas, K. Fundamental aspects of perovskite oxides as an emerging material for supercapacitor applications and its anion intercalation mechanism-Review. J. Energy Storage 2024, 78, 109968. [Google Scholar]
- Hussain, A.; Kainat, F.; Hamza, A.; Naz, A.; Jabeen, N.; Munawar, T.; Qaiser, M.A. A DFT Study on the Structural, Electronic, Optical, and Elastic Properties of BLSFs XTi4Bi4O15 (X = Sr, Ba, Be, Mg) for Solar Energy Applications. Ceramics 2024, 7, 1727–1741. [Google Scholar] [CrossRef]
- Berri, S.; Bouarissa, N.; Attallah, M. First-principles predictions on half-metallic results of RBaMn2O6-δ (R = Nd, Pr, La and δ = 0, 1) double Perovskite compounds. J. Supercond. Nov. Magn. 2020, 33, 1737–1746. [Google Scholar] [CrossRef]
- Berri, S. First-principles study on half-metallic properties of the Sr2GdReO6 double perovskite. J. Magn. Magn. Mater. 2015, 385, 124–128. [Google Scholar] [CrossRef]
- Berri, S. First-principles search for half-metallic ferromagnetism in double perovskite X2MnUO6 (X = Sr or Ba) compounds. Acta Phys. Pol. A 2020, 6, 138. [Google Scholar] [CrossRef]
- Wei, M.; Che, W.; Li, H.; Wang, Z.; Yan, F.; Liu, Y.; Liu, J. Ruddlesden-Popper type La2NiO4+δ oxide coated by Ag nanoparticles as an outstanding anion intercalation cathode for hybrid supercapacitors. Appl. Surf. Sci. 2019, 484, 551–559. [Google Scholar] [CrossRef]
- Sang, Z.; Che, W.; Yang, S.; Liu, Y. Ruddlesden-Popper type La2NiO4+δ oxide as a pseudocapacitor electrode. Mater. Lett. 2018, 217, 23–26. [Google Scholar] [CrossRef]
- Berri, S. Half-metallic and thermoelectric properties of Sr2EuReO6. Comput. Condens. Matter 2021, 28, e00586. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Abubakr, M.; Fatima, K.; Abbas, Z.; Hussain, A.; Jabeen, N.; Raza, H.H.; Chaib, Y.; Muhammad, S.; Siddeeg, S.M.; Gorczyca, I. Effect of S, Se and Te replacement on structural, optoelectronic and transport properties of SrXO4 (X = S, Se, Te) for energy applications: A first principles study. J. Solid State Chem. 2022, 305, 122689. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Kainat, F.; Jabeen, N.; Yaqoob, A.; Hassan, N.U.; Hussain, A.; Khalifa, M.E. Effect of Ca, Ba, Be, Mg, and Sr Substitution on Electronic and Optical Properties of XNb2Bi2O9 for Energy Conversion Application Using Generalized Gradient Approximation–Perdew–Burke–Ernzerhof. Crystals 2024, 14, 710. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, A.J. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Wang, Y.; Gould, T.; Dobson, J.F.; Zhang, H.; Yang, H.; Yao, X.; Zhao, H. Density functional theory analysis of structural and electronic properties of orthorhombic perovskite CH3NH3PbI 3. Phys. Chem. Chem. Phys. 2014, 16, 1424–1429. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef]
- Dassault Systèmes. Biovia Materials Studio; Dassault Systèmes: San Diego, CA, USA, 2019. [Google Scholar]
- Hussain, A.; Kainat, F.; Jabeen, N.; Yaqoob, A.; Abbas, T.; Khan, M.U.; Qaiser, M.A.; Mahmoud, M.H.H. First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X = Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications. Crystals 2024, 14, 870. [Google Scholar] [CrossRef]
- Sabir, B.; Murtaza, G.; Khalil, R.A. Ab-initio prediction of structure stability, electromagnetic, optical and thermoelectric behavior of orthorhombic LaXO3 (X = Cr, Mn, Fe): For device application. J. Mol. Graph. Model. 2020, 94, 107482. [Google Scholar] [CrossRef]
- Connétable, D.; Thomas, O. First-principles study of the structural, electronic, vibrational, and elastic properties of orthorhombic NiSi. Phys. Rev. B—Condens. Matter Mater. Phys. 2009, 79, 094101. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Electronic structure of superoxygenated La2NiO4 domains with ordered oxygen interstitials. J. Supercond. Nov. Magn. 2016, 29, 615–621. [Google Scholar] [CrossRef]
- Huda, M.N.; Yan, Y.; Moon, C.Y.; Wei, S.H.; Al-Jassim, M.M. Density-functional theory study of the effects of atomic impurity on the band edges of monoclinic WO 3. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 77, 195102. [Google Scholar] [CrossRef]
- Wafula, J.W.; Manyali, G.S.; Makokha, J.W.; Madallah, Y.; Bouhmaidi, S.; Setti, L. DFT+ U investigation of electronic, optical, and thermoelectric properties of YAuX (X = Si or Ge or Sn) half-Heusler alloys. Results Phys. 2024, 61, 107747. [Google Scholar] [CrossRef]
- Dar, S.A.; Sharma, R.; Srivastava, V.; Sakalle, U.K. Investigation on the electronic structure, optical, elastic, mechanical, thermodynamic and thermoelectric properties of wide band gap semiconductor double perovskite Ba2InTaO6. RSC Adv. 2019, 9, 9522–9532. [Google Scholar] [CrossRef] [PubMed]
- Burhonzoda, A. DFT Study on the Electronic Structure and Optical Properties of Orthorhombic Perovskite CsPbBr3 Doped with I and Cl. Biointerface Res. Appl. Chem. 2023, 13, 516. [Google Scholar]
- Ghaithan, H.M.; Alahmed, Z.A.; Qaid, S.M.; Hezam, M.; Aldwayyan, A.S. Density functional study of cubic, tetragonal, and orthorhombic CsPbBr3 perovskite. ACS Omega 2020, 5, 7468–7480. [Google Scholar] [CrossRef]
- Irfan, M.; Shaheen, N.; Solre, G.F.B.; Alabbad, E.A.; Saleh, E.A.M.; Moharam, M.M.; El-Zahhar, A.A.; Asif, S.U.; Eldin, S.M.; Tahir, M.H.; et al. Fe and Rh doping nanoarchitectonics on properties of Sr2YGaX2O7 pyrochlore oxides with a DFT-based spin-polarized calculation for optoelectronic and thermoelectric applications. J. Inorg. Organomet. Polym. Mater. 2024, 34, 952–968. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, D.; Liu, Z. Structural and elastic DFT study of four structures for Cu2ZnSnS4 under high pressure. J. Alloys Compd. 2017, 696, 86–95. [Google Scholar] [CrossRef]
- Khanzadeh, M.; Alahyarizadeh, G. A DFT study on pressure dependency of TiC and ZrC properties: Interconnecting elastic constants, thermodynamic, and mechanical properties. Ceram. Int. 2021, 47, 9990–10005. [Google Scholar] [CrossRef]
- Hashemkhani Shahnazari, G.; Darvish Ganji, M. Understanding structural and molecular properties of complexes of nucleobases and Au13 golden nanocluster by DFT calculations and DFT-MD simulation. Sci. Rep. 2021, 11, 435. [Google Scholar] [CrossRef] [PubMed]
- Zubair, M.; Azzouz-Rached, A.; Rahman, N.; Tirth, V.; Husain, M.; Uzair, M.; Asif, M.; Alotaibi, A.M. Insight into the structural, elastic, optoelectronic, magnetic and thermodynamic properties of Sr2TbXO6 (X = Bi, Sb) double perovskites employing DFT approach. Opt. Quantum Electron. 2025, 57, 237. [Google Scholar] [CrossRef]
- Rai, D.P.; Sandeep, S.; Shankar, A.; Ghimire, M.P.; Khenata, R.; Thapa, R.K. Half-metallic behavior in non-transition metal based binary compounds XC (X = Be, Mg, Ca, Sr, Ba, and Ra): A first principles study. Chem. Met. Alloys 2014, 7, 160–168. [Google Scholar] [CrossRef]
- Wang, X.; Khachai, H.; Khenata, R.; Yuan, H.; Wang, L.; Wang, W.; Bouhemadou, A.; Hao, L.; Dai, X.; Guo, R.; et al. Structural, electronic, magnetic, half-metallic, mechanical, and thermodynamic properties of the quaternary Heusler compound FeCrRuSi: A first-principles study. Sci. Rep. 2017, 7, 16183. [Google Scholar] [CrossRef]
- Abdullah, D.; Gupta, D.C. Exploring the half-metallic ferromagnetism, dynamical and mechanical stability, optoelectronic and thermoelectric properties of K2NaMI6 (M = Mn, Co, Ni) for spintronic applications. Sci. Rep. 2023, 13, 12795. [Google Scholar] [CrossRef]
- Ali, M.A.; Murtaza, G.; Laref, A. Exploring ferromagnetic half-metallic nature of Cs2NpBr6 via spin polarized density functional theory. Chin. Phys. B 2020, 29, 066102. [Google Scholar]
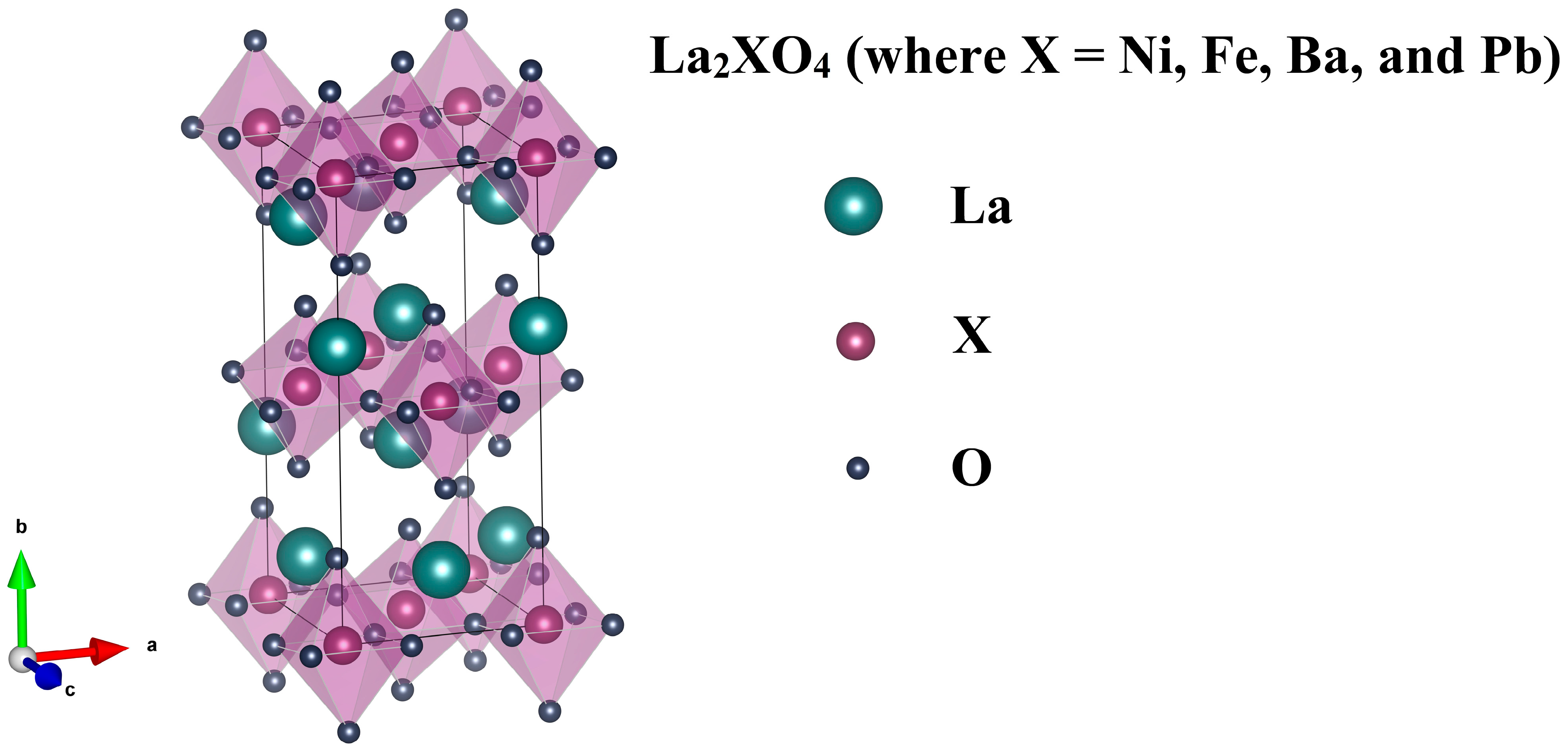


| Compound | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Volume (Å3) | Space Group |
|---|---|---|---|---|---|---|---|---|
| La2NiO4 | 5.5117 | 12.4381 | 5.6765 | 90 | 90 | 90 | 389.15 | Cmce (No. 64) |
| La2FeO4 | 5.4821 | 12.5427 | 5.6081 | 90 | 90 | 90 | 385.61 | Cmce (No. 64) |
| La2BaO4 | 6.9688 | 13.8669 | 6.5513 | 90 | 90 | 90 | 633.09 | Cmce (No. 64) |
| La2PbO4 | 6.6865 | 13.4659 | 6.3709 | 90 | 90 | 90 | 573.64 | Cmce (No. 64) |
| NAME | La2NiO4 | La2FeO4 | La2BaO4 | La2PbO4 |
|---|---|---|---|---|
| C11 | 59.76 | 60.44 | 114.42 | 242.34 |
| C12 | 33.43 | 33.94 | 76.67 | 149.38 |
| C22 | 44.54 | 43.83 | 148.67 | 230.89 |
| C33 | 37.26 | 36.02 | 130.47 | 180.91 |
| C44 | 8.23 | 8.29 | 45.46 | 39.51 |
| C55 | 16.78 | 16.83 | 20.46 | −1.83 |
| C66 | 17.37 | 17.82 | 17.84 | 23.56 |
| B | 36.02 | 36.61 | 95.78 | 179.27 |
| G | 10.16 | 9.30 | 13.55 | 36.66 |
| E | 27.85 | 25.73 | 38.81 | 102.96 |
| B/G | 3.55 | 3.94 | 7.07 | 4.89 |
| G/B | 0.28 | 0.25 | 0.14 | 0.20 |
| ν | 0.37 | 0.38 | 0.43 | 0.40 |
| Materials | Functional | Key Findings | References |
|---|---|---|---|
| La2XO4 (X = Ni, Fe, Ba, Pb) | DFT (CASTEP, PBE-GGA) | Metallic nature, ideal for SC applications, high optical conductivity, mechanical stability confirmed by Born criteria | This study |
| RBaMn2O6 (R = Nd, Pr, La) | FP-LAPW, PBE-GGA | Half-metallic ferromagnets, high magnetic moments (7–10 μB), potential for spintronics | [27] |
| Sr2GdReO6 | FP-LAPW, Spin-DFT | Half-metallic nature (HM), ferromagnetic stability, magnetic moment = 9 μB | [54] |
| X2MnUO6 (X = Sr, Ba) | DFT | Half-metallic ferromagnetism, Mn 3d–O 2p–U 5f hybridization, potential for spintronics | [55] |
| FeCrRuSi | DFT | Half-metallic material with a total magnetic moment of 2.0 μB | [56] |
| K2NaMI6 (M = Mn, Co, Ni) | GGA-PBE | Half-metallic ferromagnetism, magnetic moment = 4 μB, thermoelectric | [57] |
| Cs2NpBr6 | GGA-PBE, GGA+U | Half-metallic ferromagnetic, magnetic moment is 3 μB via spin polarization | [58] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Zafar, S.; Jabeen, N.; Khan, M.U.; Khan, I.A.; Hessien, M.M. Exploring Layered Ruddlesden-Popper Structures for High-Performance Energy Devices. Inorganics 2025, 13, 203. https://doi.org/10.3390/inorganics13060203
Hussain A, Zafar S, Jabeen N, Khan MU, Khan IA, Hessien MM. Exploring Layered Ruddlesden-Popper Structures for High-Performance Energy Devices. Inorganics. 2025; 13(6):203. https://doi.org/10.3390/inorganics13060203
Chicago/Turabian StyleHussain, Ahmad, Sumaira Zafar, Nawishta Jabeen, Muhammad Usman Khan, Imtiaz Ahmad Khan, and Mahmoud M. Hessien. 2025. "Exploring Layered Ruddlesden-Popper Structures for High-Performance Energy Devices" Inorganics 13, no. 6: 203. https://doi.org/10.3390/inorganics13060203
APA StyleHussain, A., Zafar, S., Jabeen, N., Khan, M. U., Khan, I. A., & Hessien, M. M. (2025). Exploring Layered Ruddlesden-Popper Structures for High-Performance Energy Devices. Inorganics, 13(6), 203. https://doi.org/10.3390/inorganics13060203









