Accessing the Magnetic Morphology of Ferromagnetic Molecular-Based Nanoparticles from Polarized Small-Angle Neutron Scattering

Abstract

Polarized Small-Angle Neutron Scattering is a versatile low-energy neutron scattering technique that allows for the access of magnetic information on nanosize objects of size 2–100 nm, from individual properties like the magnetization distribution inside the object to the collective behaviors, e.g., spin-glass effects or long-range magnetic ordering. The multi-scale possibilities of this technique is particularly relevant to encompass simultaneously the individual and collective many-body phenomena. In this article, we report the direct measurement of the magnetic form factor of “Prussian Blue Analog” molecular-based Ferromagnetic nanoparticles ${\mathrm{Cs}}_{\mathrm{x}}^{\mathrm{I}}{\mathrm{Ni}}^{\mathrm{II}}\left[{\mathrm{Cr}}^{\mathrm{III}}{\left(\mathrm{CN}\right)}_6\right]$ embedded in a polymer matrix with use of Polarized Small-Angle Neutron Scattering. We show that PSANS is particularly adapted to evaluate the internal magnetization distribution in nanoparticles and determine their magnetic morphology.

1. Introduction

Nanoparticles are the subject of intense research activities both for the peculiar properties offered by the size-controlled properties and for their applicative potential in a range of fields such as biology, medicine, optics, or even catalysis [1]. Magnetic Nanoparticles (MNPs) are considered potential candidates for high-density magnetic information storage or for magnetic microelectronic devices. Research has made significant progress on the synthesis side, and large efforts are being made to address the precise control of size/shape/composition of MNPs [2,3,4]. One known limitation to the use of MNPs is the “superparamagnetic” regime when decreasing the MNP size below some critical value. In such regime, MNPs are usually “single-domain”—meaning that the magnetization cannot form domain walls for instance—and thermal fluctuations are strong enough to restore spontaneous and collective reversal of the magnetization above the so-called blocking temperature $T_B$. Below $T_B$, the magnetization is blocked (usually ferromagnetically), but some subtlety may appear depending on structural and chemical parameters (size, shape, atomic magnetization, magneto-crystalline, and shape anisotropy). The collective behavior of an assembly of interacting MNPs is also a crucial point as the ability to control one single MNP in an assembly can be critical for potential applications. Inter-particle interactions, such as long-range dipolar interactions, should thus be considered as it can induce collective behavior (“super-ferromagnetism”, spin-glass phases) [5]. For this purpose, key parameters are usually the MNP spin-density, surface effects, and the media used to disperse the MNP. As a starting material for novel synthetic strategies to create original MNPs, the well-known family of Prussian Blue Analog (PBA) compounds has focused attention due to their wide-ranging intrinsic properties. These molecular-based compounds can be grown to MNPs in crystalline form of general formula ${\mathrm{A}}^{\mathrm{I}}{\mathrm{M}}^{\prime \mathrm{II}}\left[{\mathrm{M}}^{\mathrm{III}}{\left(\mathrm{CN}\right)}_6\right]$ (where A is an alkali atom, and M and M’ are two metallic centers) [6]. As shown extensively, they exhibit a wide range of chemical, optical, or magnetic properties by changing the two metallic ions [7]. Amongst those compositions, the compound ${\mathrm{Cs}}_{\mathrm{x}}{\mathrm{Ni}}^{\mathrm{II}}\left[{\mathrm{Cr}}^{\mathrm{III}}{\left(\mathrm{CN}\right)}_6\right]$ is a prototypical paramagnetic example of this family (denominated $\mathrm{CsNiCr}$ in the following) [8,9]. The bulk compound is ferromagnetic ($T_C=90$ K) [10] and the ordering temperature decreases in MNPs with decreasing particle size. The use of SANS to study the magnetic and structural properties of $\mathrm{CsNiCr}$ MNP [11] has exposed the specific influence of the MNP density in an electrically neutral polymer media (PVP in the present case). At low concentration, the single-MNP regime is observed while, at higher concentration, inter-particle (dipole) interactions play a key role in the collective organization of the particles in PVP. On the contrary, in a charged media (CTA+), electrostatic interactions between the media and the MNP induce a higher concentration of CTA on their surface. The crossover between individual and collective magnetic behavior in an assembly of $\mathrm{CsNiCr}$ superparamagnetic MNPs as a function of their size has been addressed using SANS [12].

All these issues related to the magnetic properties (individual as well as collective) can be addressed with Small-Angle Neutron Scattering (SANS) techniques, in particular when neutrons can be polarized as it allows for a more insightful investigation of the magnetic properties [13,14,15,16,17,18,19]. SANS is therefore a perfectly adapted tool to study structural and magnetic information in these systems. However, the direct access to the nuclear (structural) and magnetic form factors of the MNP can only be obtained when using polarized neutron SANS (PSANS). This technique is extremely powerful and insightful, as shown in a large range of magnetic systems [17,20]. As developed in this article, the use of Polarized SANS brings additional information and means of discrimination between nuclear and magnetic contributions to the SANS signal. It is an extra factor that eases the possibility to extract the magnetic information as compared to non-polarized SANS. The present article aims at exposing the experimental capabilities PSANS has to obtain direct access to the magnetic form factor of individual molecular-based PBA MNP. In this contribution, we show that the magnetic form factor in such molecular-based MNPs can be investigated using PSANS as the main experimental tool providing a ground for further studies in magnetic systems presenting intrinsically relatively low spin density.

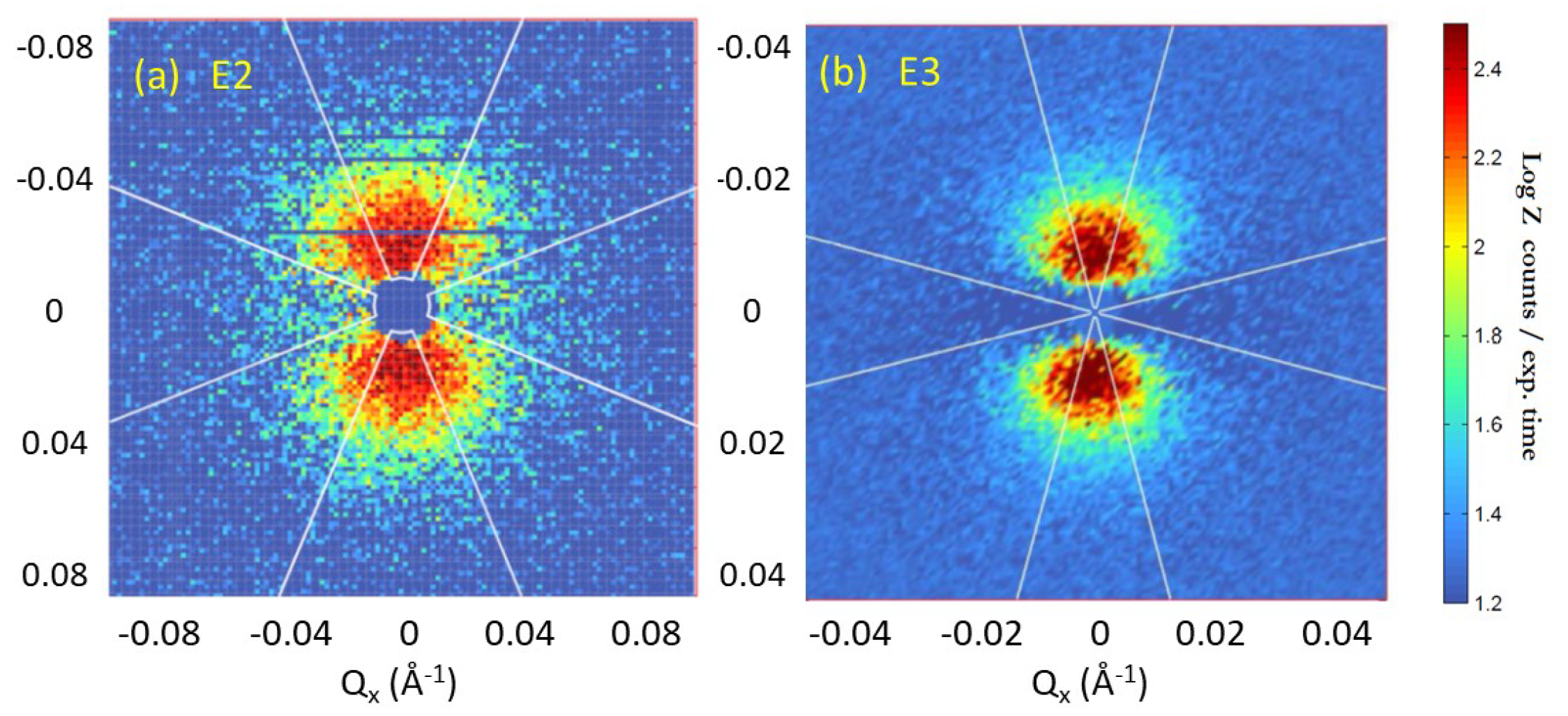
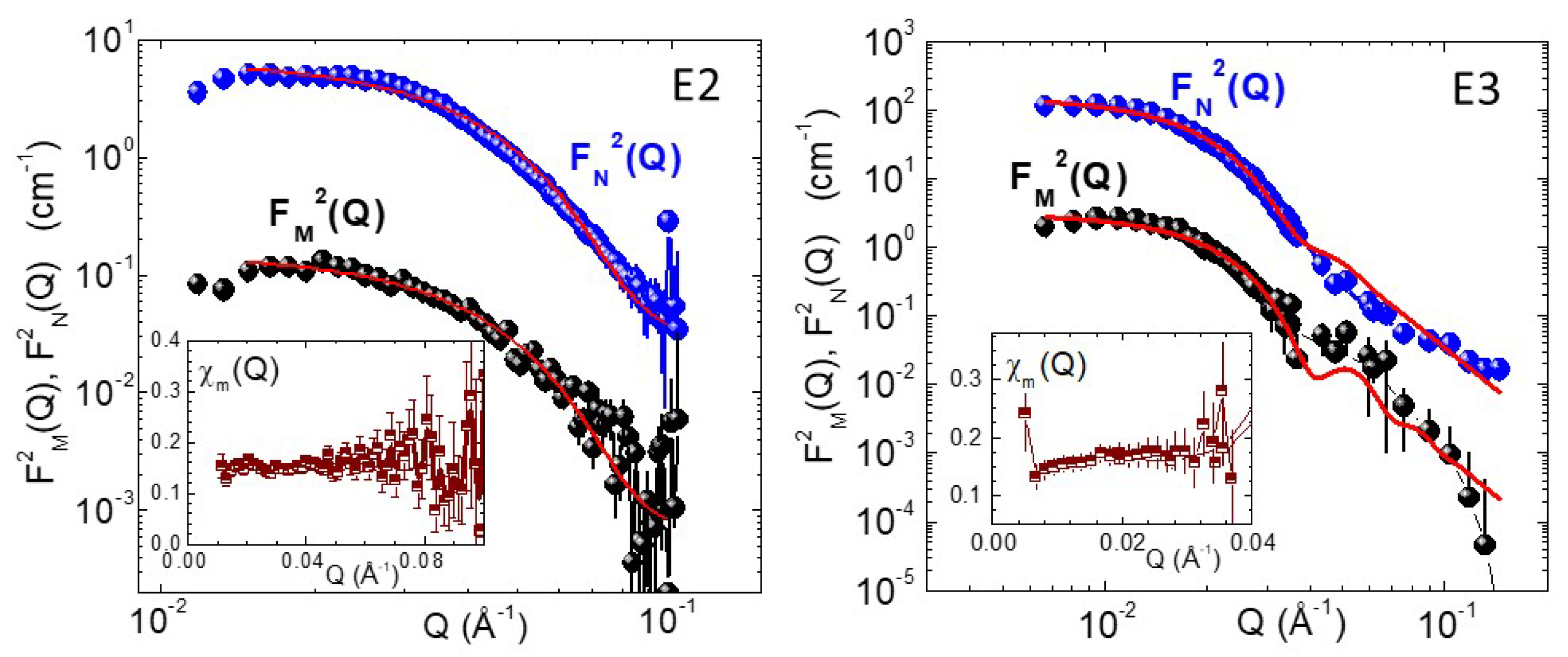
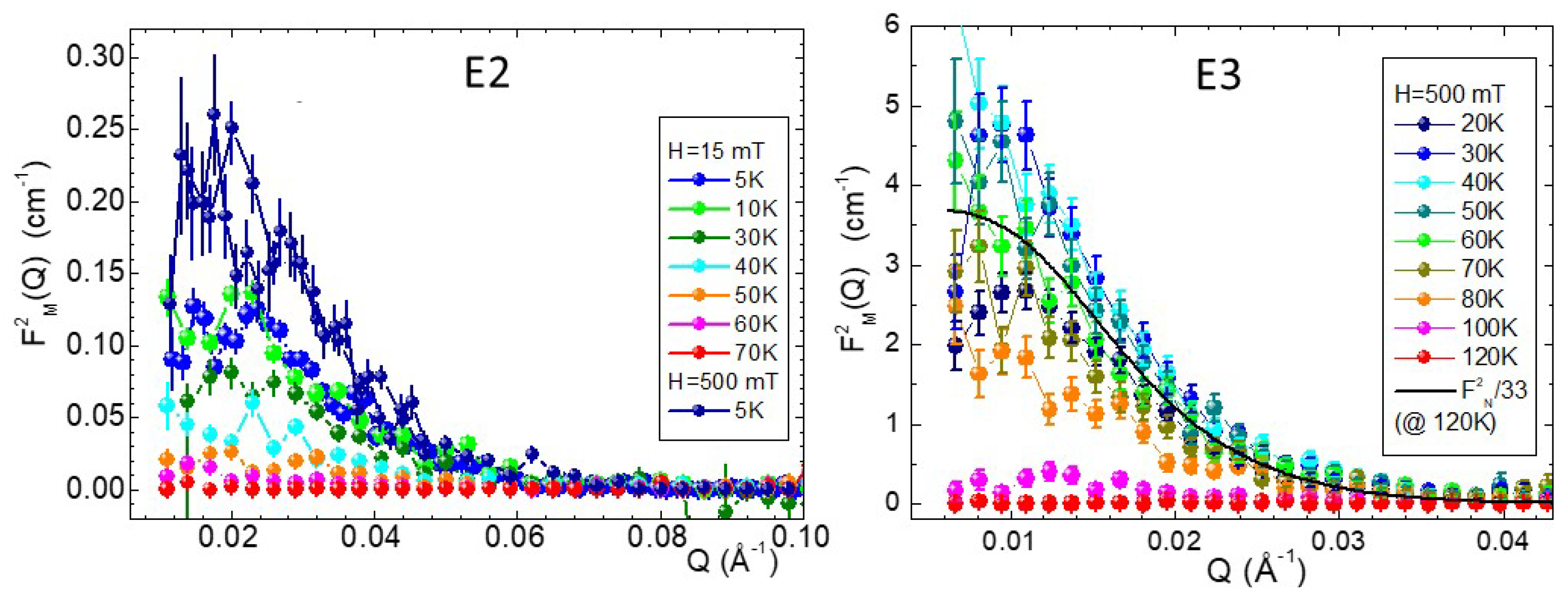
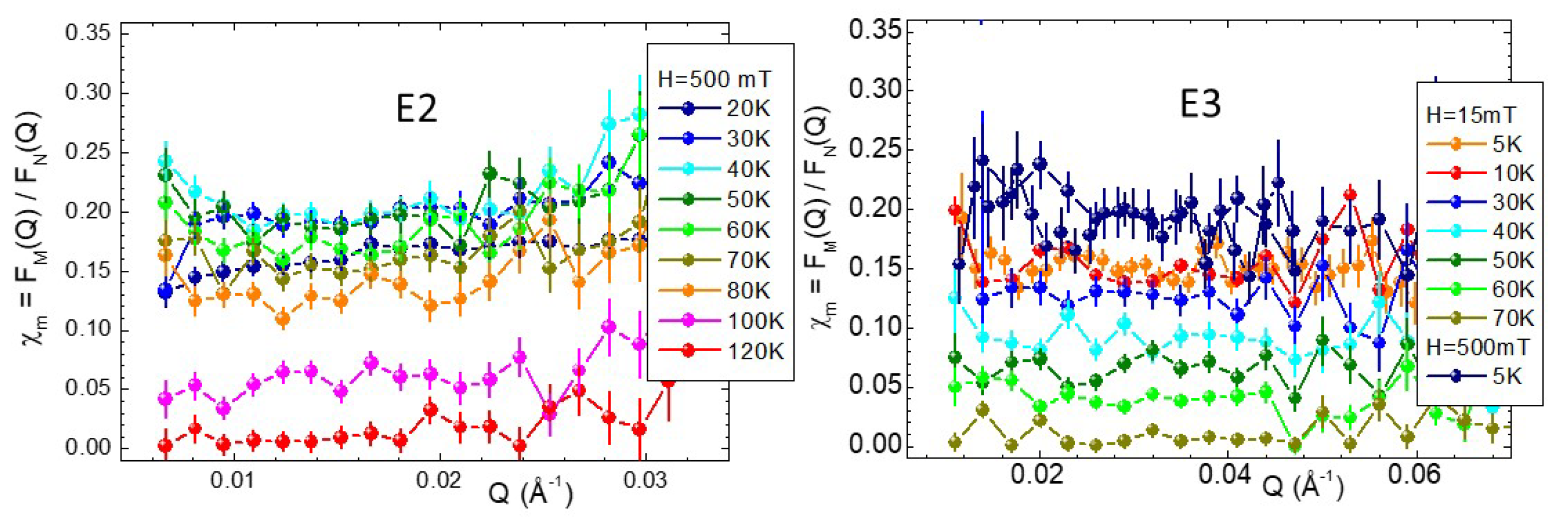
2. Results and Discussion

While the general SANS expressions for nuclear and magnetic scattering are summarized in Appendix A.1 and Appendix A.2, respectively, the specific case of magnetic scattering by magnetic nanoparticles is described in Appendix A.3, treating non-polarized and polarized SANS situations. The magnetic contribution to SANS from MNPs (like also for bulk systems) can be more easily and straightforwardly extracted when using PSANS. The ability to separate the nuclear and magnetic contributions (with some limitation due to the non-perfect polarizer system) by differentiating the signals of opposite polarizations is a key asset of PSANS. Indeed, the PSANS measurements were done with successive neutron polarization UP(+) and DOWN(−), as explained in the experimental description above and the difference between the two PSANS signals. $I^{-}\left(Q\right)$ and $I^{+}\left(Q\right)$ is considered in the following. The expressions $I^{\pm }\left(Q\right)$, for an assembly of non-interacting, or weakly interacting, particles are fully detailed in Appendix A.3.

As given in more detail in Appendix A.3 (see Equation (A23)), in the case of a non-perfect alignment of the particle magnetic moments along the magnetic field, we have

$$I^{\pm }\left(Q\right)={\tilde{F}}_N^2+\left({\tilde{F}}_M^2\mp 2P{\tilde{F}}_N{\tilde{F}}_M\mathcal{L}\left(x\right)\right){sin}^2\alpha +{\tilde{F}}_M^2\left(2\mathcal{L}\left(x\right)/x-\mathcal{Y}\left(x\right){sin}^2\alpha \right),$$

(1)

where ${\tilde{F}}_N^2$ and ${\tilde{F}}_M^2$ are the nuclear and magnetic form factors, respectively.

In this expression, $\alpha$ is the angle between the magnetization direction $\overrightarrow{\mu }$ and the scattering wave-vector $\overrightarrow{Q}$, and $\mathcal{L}\left(x\right)=coth\left(x\right)-(1/x)$ is the Langevin function with argument $x={\mu }_{mS}{H}_{tot}/k_{B}T$. Note that $\mathcal{Y}\left(x\right)={\mathcal{L}}^2\left(x\right)-1+3\mathcal{L}\left(x\right)/x$ is a term that vanishes when the magnetic moments align perfectly along the magnetic field. In this particular case, and taking into account the experimental setup parameters P and $ϵ$ (see Appendix A.3, as well as Equations (A21) and (A24)), the difference $\Delta I\left(Q\right)$ thus becomes

$$\Delta I\left(Q\right)=I^{-}\left(Q\right)-I^{+}\left(Q\right)=2P(1+ϵ){\tilde{F}}_N{\tilde{F}}_M\mathcal{L}\left(x\right){sin}^2\alpha .$$

(2)

Hence, by differentiating the SANS signals from the two neutron polarization states, one can extract information on the magnetic form factor. By considering vertical direction ($\alpha =\pi /2$) and horizontal direction ($\alpha =0$), the nuclear and magnetic contributions can be separated with minimum assumption.

Figure 1 (left) shows 2D PSANS difference $\Delta I\left(Q\right)=I^{-}\left(Q\right)-I^{+}\left(Q\right)$ obtained at 5 K and 15 mT for Sample E2. The coercive magnetic field of these MNPs is about 7–10 mT as shown by previous magnetization curves [2,9,12] so that, at 15 mT, the magnetization is sizeable at low temperature. Figure 1 (right) shows 2D PSANS difference $\Delta I\left(Q\right)$ obtained at 10 K and 500 mT for Sample E3. At 500 mT, the low-T magnetization is essentially maximum [2,9,12]. The flipper “OFF” corresponds to $I^{+}\left(Q\right)$, while the flipper “ON” stands for $I^{-}\left(Q\right)$. In both samples, the typical asymmetry pattern (“butterfly” shape) is visible, as this signal is entirely magnetic a soon as the system acquires some static magnetization, as it originates from the $sin\alpha$ dependence of the interference term (see Equation (A24) in Appendix A.3). Sectorial cuts (horizontal [$\langle \alpha \rangle =0$] and vertical [$\langle \alpha \rangle =\pi /2$] cuts, with angular spread $\pm {15}^{\circ }$, are represented as solid white lines) are used in the following to extract the nuclear and magnetic form factors (cf Appendix A.3).

Figure 2 shows several 2D PSANS differences $\Delta I\left(Q\right)=I^{-}\left(Q\right)-I^{+}\left(Q\right)$ obtained under 15 mT at different temperatures between 10 and 60 K for Sample E2. As the temperature increases, the magnetic scattering contribution decreases and becomes immeasurable, within our background levels, above 70–80 K in agreement with magnetization data [2]. This is a signature of the relation between the temperature dependence of the magnetic form factor $\Delta I\left(Q\right)\sim {\tilde{F}}_M\mathcal{L}\left(x\right)$ and the superparamagnetic behavior of the MNPs as described in Appendix A.3.

Figure 3 (left) shows the extracted nuclear and magnetic form factors, $F_N^2\left(Q\right)$ and $F_M^2\left(Q\right)$, respectively, obtained from the PSANS data at 5 K and 15 mT for the E2 MNP. Taking the plateau-like shape of the form factor at about $Q\simeq 0.02$ Å⁻¹, it is apparent that $F_M\left(Q\right)\simeq 0.15F_N\left(Q\right)$ for the E2 MNP.

The magnetic and nuclear form factors have been fitted using a spherical model with size-dispersion (see Appendix A.4 and [21]). The result indicates a MNP radius $R=4.5\pm 0.1$ nm for both $F_M\left(Q\right)$ and $F_N\left(Q\right)$ with an intensity factor of 0.279 and 1.756, respectively, hence a ratio of 0.159. The size-dispersion is about 25%, a strong indication of significant size distribution. The inset of Figure 3 shows ${\chi }_M=F_M\left(Q\right)/F_N\left(Q\right)$. At low Q, the ratio ${\chi }_M$ is indeed close to 0.15; however, very importantly, there is no significant deviation at higher Q values, at least up to $Q=0.08$ Å⁻¹. Above this value, the signal becomes noisier and less reliable. This means that, for the E2 MNP, the internal magnetization is a homogeneous function of the nuclear structure of the MNP. There is no measurable internal structure of the magnetization profile. As detailed in Appendix A.3, under some assumptions, ${\chi }_M\left(Q\right)$ relates to the physical parameters of interest (${\mu }_S$, $V_p$, and $\Delta {\rho }_p$):

$${\chi }_M\left(Q\right)={\displaystyle \frac{p({\mu }_S/{\mu }_B)}{V_p|\Delta {\rho }_p|}}\approx 0.15.$$

(3)

with this experimental value of ${\chi }_M\left(Q\right)$, $V_p=330$ nm³ and $|\Delta {\rho }_p|=2.30\times {10}^{10}$ cm⁻², one obtains ${\mu }_S\approx 4225{\mu }_B$ for $H=15$ mT. This experimental value is lower than the expected value for a fully magnetized MNP containing 4 Ni and 3.8 Cr ions per unit cell ($M_S=1.69\times {10}^{22}{\mu }_B/$cm³): ${\mu }_{S,theo}=5550{\mu }_B$. Application of Equation (A15) leads to ${\rho }_{m,S}=0.345\times {10}^{10}$ cm⁻² with $V_m\equiv V_p$.

Figure 3 (right) shows similarly $F_N^2\left(Q\right)$ and $F_M^2\left(Q\right)$, obtained from the PSANS data at 20 K and 0.5 T for the E3 MNP. Again, taking the plateau-like shape of the form factor at about $Q\simeq 0.01$ Å⁻¹, we have $F_M\left(Q\right)\simeq 0.17F_N\left(Q\right)$ for the E3 MNP.

The magnetic and nuclear form factors are fitted using a spherical model with size-dispersion (see Appendix A.4 and [21]). The result indicates a MNP radius $R=10.5\pm 0.5$ nm for both $F_M\left(Q\right)$ and $F_N\left(Q\right)$ with an intensity factor of 1.605 and 9.396, respectively, hence a ratio of 0.171. The size-dispersion is about 11%. The inset of Figure 3 shows a direct representation of ${\chi }_M\left(Q\right)$. Throughout the Q-range, the ratio ${\chi }_M$ is close to 0.15–0.18, but we can observe a slight decrease of ${\chi }_M$ at lower Q values: for $Q\ge 0.02$ Å⁻¹, we have ${\chi }_M\simeq 0.17$, while for $Q\simeq 0.01$ Å⁻¹, we have ${\chi }_M\simeq 0.14$. With the experimental value ${\chi }_M\approx 0.17$, $V_p=2700$ nm³ and $|\Delta {\rho }_p|=2.30 \times {10}^{10}$ cm⁻², one obtains ${\mu }_S\approx \mathrm{43,590}{\mu }_B$ for $H=0.5$ T which is very close to the expected value for a fully magnetized MNP (${\mu }_{S,theo}=\mathrm{45,630}{\mu }_B$). Application of Equation (A15) leads to ${\rho }_{m,S}=0.436\times {10}^{10}$ cm⁻² with $V_m\equiv V_p$.

Even if the effect is small, and could be impaired by the extraction procedure of the magnetic form factors, the low-Q decrease of ${\chi }_M$ may be indicative that the magnetization of E3 MNP, as an ensemble of particles, is lower on average than the expected single-MNP magnetization. There could thus be some collective and/or surface effects that intervene to decrease the total magnetization of the system. This was shown to be the case in relatively large particles due to dipolar interactions [22] or Néel surface anisotropy [23]. This means that, for the E3 MNP, the internal magnetization is probably a homogeneous function of the nuclear structure of the MNP, but there are measurable effects acting upon the system to lower the total magnetization.

Figure 4 (left) shows the magnetic form factors, $F_M^2\left(Q\right)$, obtained from the PSANS data at various temperatures between 5 and 70 K, and magnetic fields (at the saturation field) for the E2 MNP. The temperature dependence clearly shows the vanishing intensity with increasing temperature. Above 60 K, there is essentially no magnetic signal left, in accordance with the magnetization data [2].

Similarly, Figure 4 (right) shows $F_M^2\left(Q\right)$ obtained from the PSANS data at various temperature between 20 and 120 K at 0.5 T (the saturation field) for the E3 MNP. As in the case of E2 MNP, the intensity is vanishing with increasing temperature, and above 100 K, there is essentially no magnetic signal anymore, again in agreement with DC magnetization measurements.

Figure 5 shows the temperature evolution of the ratio ${\chi }_M=F_M\left(Q\right)/F_N\left(Q\right)$ for the E2 and E3 MNPs (left and right panel, respectively). The temperature dependence clearly shows the vanishing intensity with increasing temperature. For the E2 MNP, the ratio is about ${\chi }_M\equiv 0.15$ at 5 K/15 mT and progressively decreases with increasing temperatures: ${\chi }_M\equiv 0.13$ at 30 K, ${\chi }_M\equiv 0.07$ at 50 K, and ${\chi }_M\equiv 0.04$ at 60 K. At T = 70 K, the magnetic form factor is essentially gone. At the largest field (500 mT), ${\chi }_M$ is about 0.2, which corresponds to ${\mu }_S\approx 5630{\mu }_B$, in total agreement with the theoretical saturated magnetization of ${\mu }_{S,theo}=5550{\mu }_B$. For the E3 MNP, a similar trend is observed with ${\chi }_M\equiv$ 0.15–0.2 at temperatures up to 70 L, and a sharp decrease is then observed above 80 K down to zero at the transition. In both MNPs, within the accuracy of the measurement, the ratio ${\chi }_M$ mostly flat, showing no identifiable sign of Q-dependence in the relevant Q-range. It is worth noting that ${\chi }_M\left(Q\right)$ remain mostly flat across the temperature range, even close to the magnetic transition temperature, which indicates that the magnetization decrease upon warming occurs most likely in a homogeneous way with the particle volume.

3. Materials and Methods

3.1. Samples

The $\mathrm{CsNiCr}$ MNP embedded in PVP (in concentration of 100 monomers of PVP per Ni ion) have been synthesized according to the method quoted in [11]. From structural analysis and diffraction data, the average radius size of the MNP are E2 (≈$4.3\left(1\right)$ nm) and E3 ($R\approx 8.6\left(2\right)$ nm) [11]. The samples used in the PSANS experiments consist in thin compacted dry powder lodged into an aluminum case and surrounded by a cadmium hollow ring with an inner diameter of 10 mm. Cadmium is a very strong neutron absorber that guarantees that all detected neutrons went through the samples. The samples thicknesses were 1 mm with weights ranging from 38 to 48 mg.

3.2. SANS Experimental Details

SANS experiments under magnetic field ($\overrightarrow{H}$ applied horizontally and perpendicular to the neutron beam direction $\overrightarrow{H}\perp \overrightarrow{k_i}$) were performed on the PA20 SANS beam line at LLB (Saclay) [24,25] with varied neutron wavelength $\lambda$ (5 Å and 7 Å) and Sample-to-Detector distance $d_{S-D}\approx 2.2$–$16.2$ m. The ³He neutron detector is a $64\times 64$ cm² 2D grid with 5 mm pixel size ($128\times 128$ pixels). The direct beam position at the detector (central position) is absorbed by a Cd beam stopper. The wavelength spread of the monochromator (Astrium velocity selector type) is about 10%, which, added to the finite-size pixel resolution of the detector and the natural divergence of the incoming neutron beam, will contribute to the total resolution. A 7 mm slit collimation at the end of the collimator line is used to prevent high background arising from the cryomagnet. The samples were placed perpendicular to the incoming beam, and the data are represented as a function of the projection $Q\approx Q_{\perp }=(2\pi /\lambda )sin\left(\theta \right)$ onto the detector plane of the scattering wave-vector $\overrightarrow{Q}={\overrightarrow{k}}_F-{\overrightarrow{k}}_i$ of norm $\left|Q\right|=(4\pi /\lambda )sin(\theta /2)$. The accessible dynamical Q-range on PA20 is large, typically 0.001–1 Å⁻¹, when combining and varying different neutron wavelengths $\lambda$ and sample-to-detector distances $d_{S-D}$. After corrections for beam transmission and detector efficiency, the different $I\left(Q\right)$ curves from the various settings are grouped together to form a single $I\left(Q\right)$ curve for each set. The corrected data are also normalized from a 1 mm thick plate of plexiglas serving as the incoherent scattering standard for hydrogen. The data are represented as a function of the scattering wave-vector $\overrightarrow{Q}$. The polarization of the neutrons (spin-1/2 “up” or “down”) is ensured by a transmission double V-shape polarizer (Swiss Neutronics) made of a 0.9 m long Si substrate, coated with a polarizing super-mirror Fe/Si (m = 4) under a 45 mT static magnetic field. At $\lambda$ = 5–7 Å, the nominal neutron polarization is about $P\approx 0.94$. The polarization of the neutron beam can be reversed using a radio-frequency solenoid-type spin flipper (Mirrotron) working in the 130–150 kHz range. The spin flipper efficiency, $ϵ\approx 0.99$, has been inferred from neutron reflectivity measurements on a fully polarized ferromagnetic thin layer standard. The measured intensity is thus a function of the incoming beam $I_0$, the polarization rate P, and the flipper efficiency $ϵ$. We note $I^{\pm }$ the measured intensity for the UP (+) and DOWN (−) polarization states, flippers OFF or ON, respectively. The SANS data were reduced, analyzed, and presented in the figures using the GRASP software package developed at the ILL [26]. The instrumental resolution, including incident neutron wavelength spread, detector pixel size, and beam divergence, has been evaluated and is taken into account in the fits described in the present article. The errors bars shown in the figures are the result of the data treatment using GRASP.

4. Conclusions

In conclusion, a PSANS study of $\mathrm{CsNiCr}$ Ferromagnetic Molecular-based Nanoparticles (size 10–20 nm) is reported. It is shown that this technique constitutes a unique tool to probe the spatial magnetization inside nanoparticles of molecular origin. In the present case, the magnetization mapping is found relatively homogeneous, as no dead magnetic layer or significant decrease of the magnetization can be measured. The data analysis developed in the paper permits a straightforward way to derive the nuclear and magnetic form factors of molecular-based nanoparticles from the analysis of the PSANS data. This approach can be utilized for many types of molecular-based MNP, possessing intrinsically a low density of magnetic ions, thanks to the unique and capabilities of PSANS.