Ex-Post Evaluation of Computational Forecast Accuracy: The Potassium Ion Coordination in a Catecholic Compound
Abstract
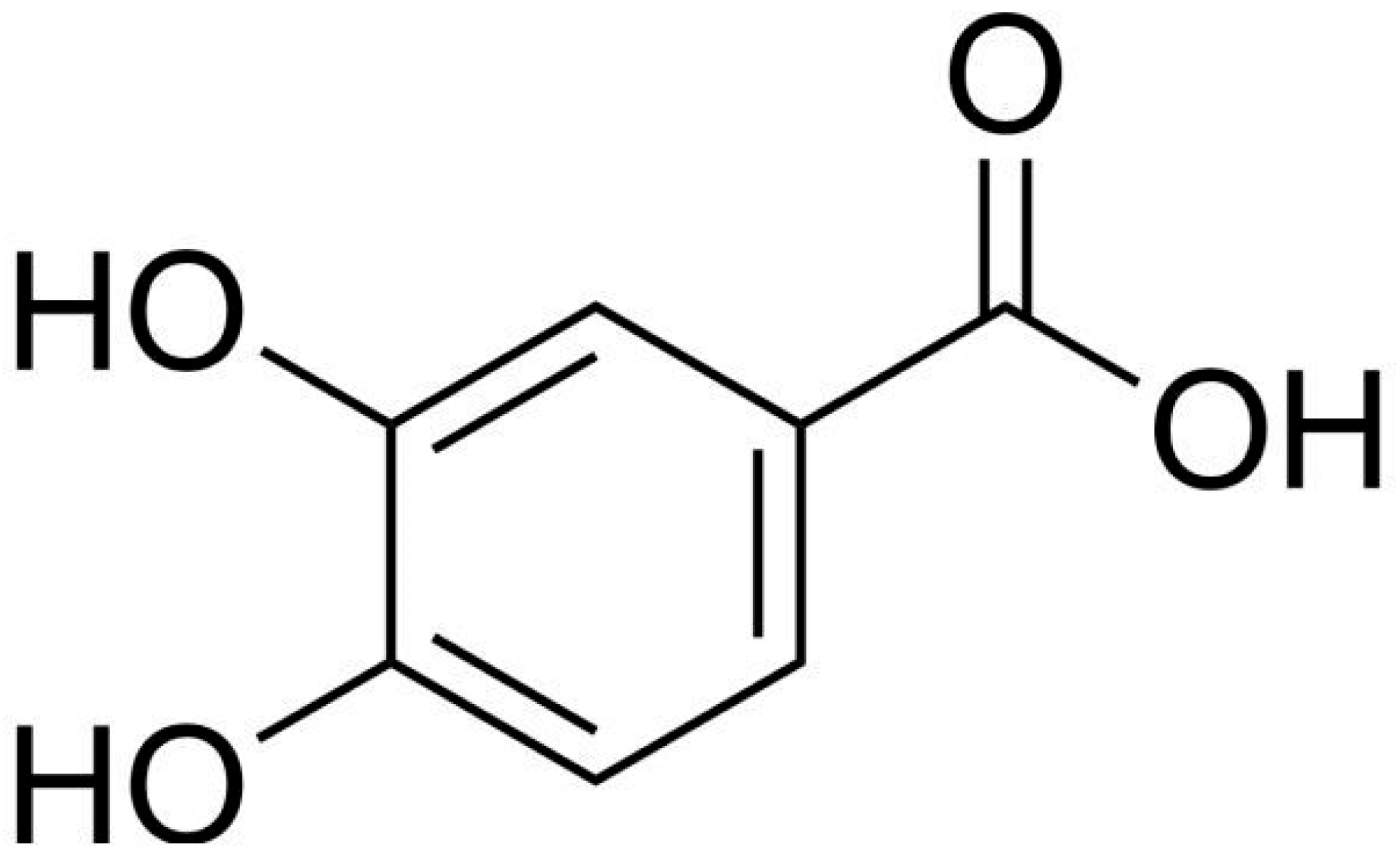
1. Introduction
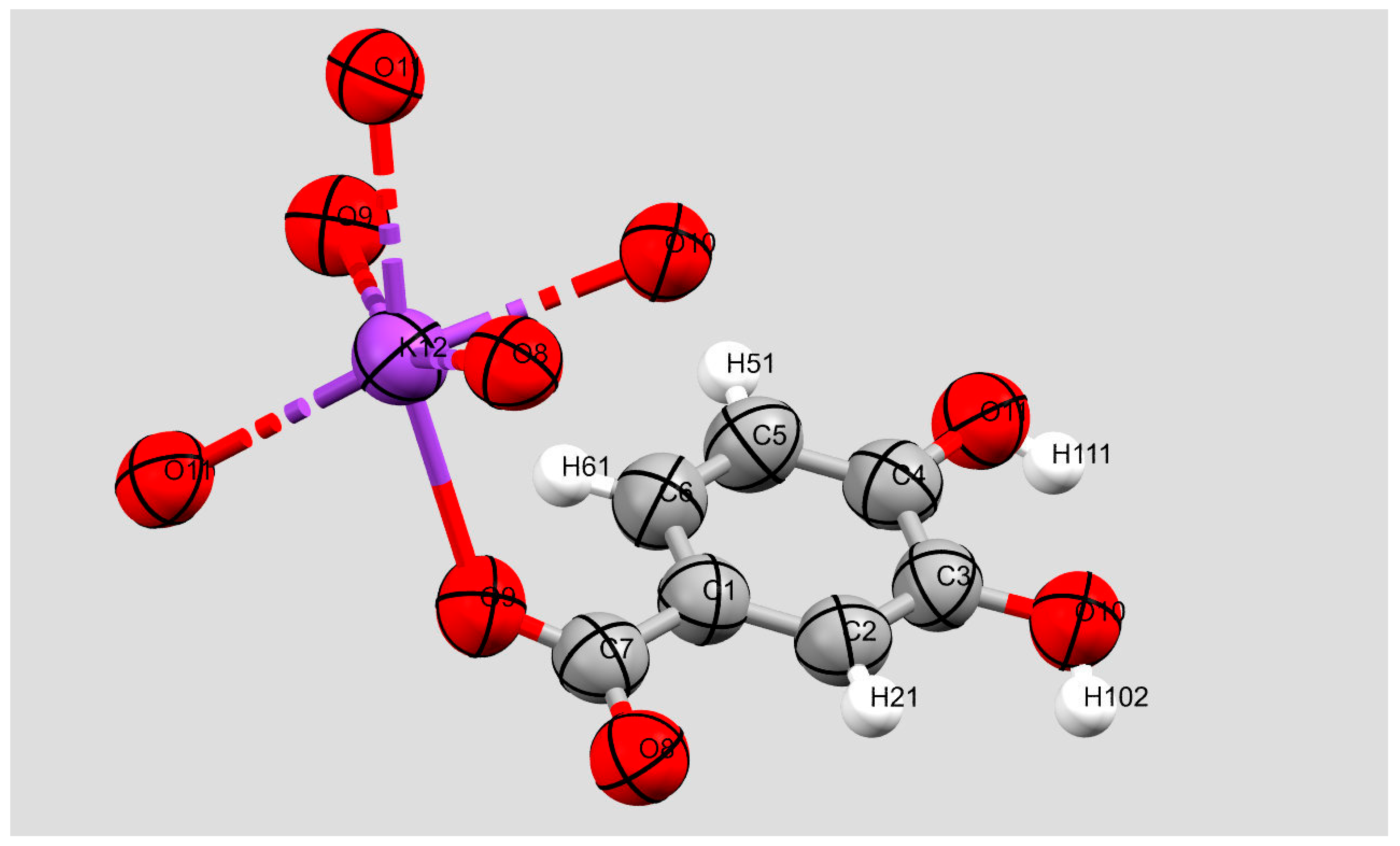
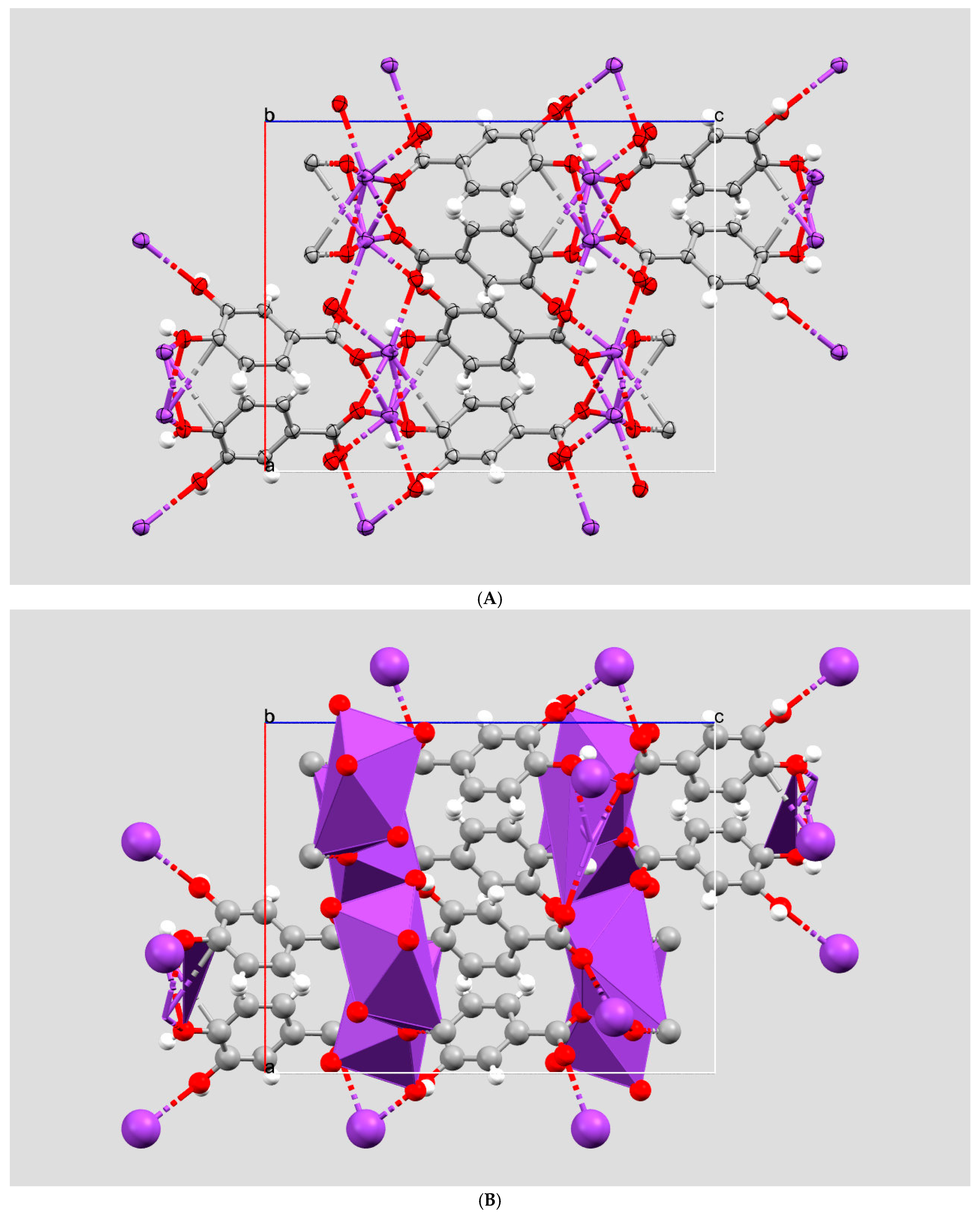
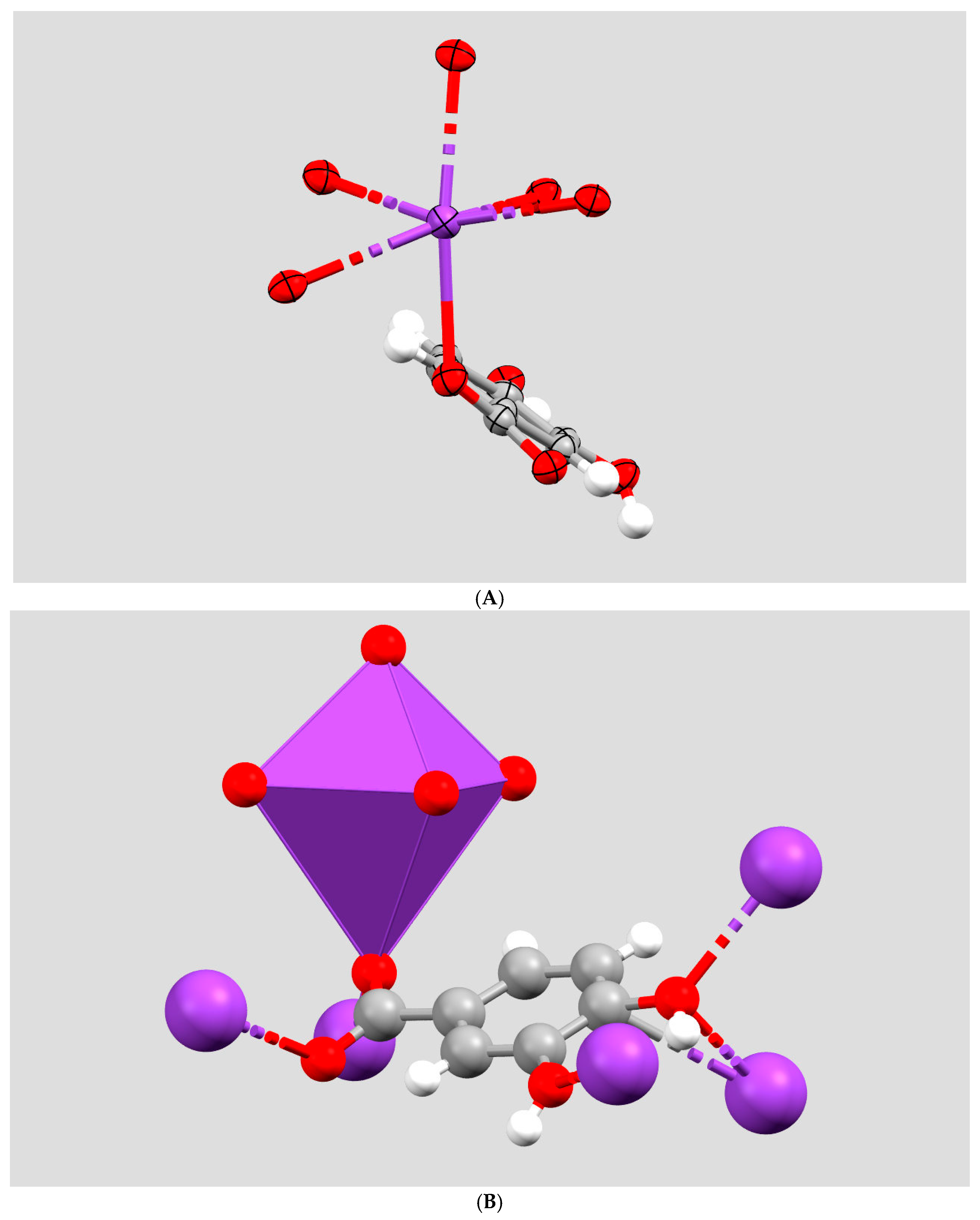
2. Results and Discussion
3. Materials and Methods
3.1. X-Ray Crystallography
3.2. Computational Details
3.2.1. Modelling
3.2.2. Force Field Settings
3.2.3. Charges
3.2.4. Protocols
3.2.5. Quantum Mechanical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stevenson, F. Humus Chemistry: Genesis, Composition, Reactions. Humus Chem. 1994, 72, 512. [Google Scholar]
- Tipping, E. Humic Substances in Soil, Sediment and Water: Geochemistry, Isolation and Characterization Edited by G. R. Aiken, D.M. McKnight, R.L. Wershaw and P. MacCarthy, Wiley, 1985. No. of Pages: 692. Price: £61.35 (Hardback). Geol. J. 1986, 21, 213–214. [Google Scholar] [CrossRef]
- Stevenson, F.J. Humic Substances in the Environment. Soil. Sci. Soc. Am. J. 1975, 39, vii+327. [Google Scholar] [CrossRef]
- Schnitzer, M.; Khan, S.U. Humic Substances in the Environment; References-Scientific Research Publishing; Marcel Dekker, Inc.: New York, NY, USA, 1972; Available online: https://www.scirp.org/reference/referencespapers?referenceid=1371146 (accessed on 7 October 2025).
- Vermeer, A.W.P.; McCulloch, J.K.; Van Riemsdijk, W.H.; Koopal, L.K. Metal Ion Adsorption to Complexes of Humic Acid and Metal Oxides: Deviations from the Additivity Rule. Environ. Sci. Technol. 1999, 33, 3892–3897. [Google Scholar] [CrossRef]
- Lubal, P.; Široký, D.; Fetsch, D.; Havel, J. The Acidobasic and Complexation Properties of Humic Acids: Study of Complexation of Czech Humic Acids with Metal Ions. Talanta 1998, 47, 401–412. [Google Scholar] [CrossRef]
- Tipping, E. Cation Binding by Humic Substances; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Abrahams, B.F.; Commons, C.J.; Hudson, T.A.; Arlt, R.S.; White, K.F.; Chang, M.; Jackowski, J.J.; Lee, M.; Lee, S.X.; Liu, H.D.; et al. Alkali Metal Salts of 4-Hydroxybenzoic Acid: A Structural and Educational Study. Acta Crystallogr. C Struct. Chem. 2021, 77, 340–353. [Google Scholar] [CrossRef] [PubMed]
- Abrahams, B.F.; Commons, C.J.; Hudson, T.A.; Arlt, R.S.; Ahl, R.; Carajias, E.D.; Chan, J.W.K.; Guo, Z.; Hill, R.E.; Mcginty, A.; et al. Complexes of 2,4,6-Trihydroxybenzoic Acid: Effects of Intramolecular Hydrogen Bonding on Ligand Geometry and Metal Binding Modes. Cryst. Struct. Commun. 2022, 78, 653–670. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, G.M.; Portalone, G.; Colapietro, M.; Rescifina, A.; Punzo, F. From the X-Rays to a Reliable “Low Cost” Computational Structure of Caffeic Acid: DFT, MP2, HF and Integrated Molecular Dynamics–X-Ray Diffraction Approach to Condensed Phases. J. Mol. Struct. 2011, 994, 87–96. [Google Scholar] [CrossRef]
- Lombardo, G.M.; Rescifina, A.; Punzo, F. Functional Hybrid Co-Crystals of Humic Substances: A Growth Forecast. CrystEngComm 2014, 16, 5917–5923. [Google Scholar] [CrossRef]
- Lombardo, G.M.; Portalone, G.; Chiacchio, U.; Rescifina, A.; Punzo, F. Potassium Caffeate/Caffeic Acid Co-Crystal: The Rat Race between the Catecholic and Carboxylic Moieties in an Atypical Co-Crystal. Dalton Trans. 2012, 41, 14337–14344. [Google Scholar] [CrossRef]
- Dunitz, J.D. Crystal and Co-Crystal: A Second Opinion. CrystEngComm 2003, 5, 506. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A Generic Force Field for Molecular Simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Grassi, A.; Lombardo, G.M.; Punzo, F. Wrapping and Unwrapping an Indicaxanthin Molecule: A Computational Approach. Comput. Theor. Chem. 2020, 1191, 113028. [Google Scholar] [CrossRef]
- Valkonen, A.; Lombardo, G.M.; Rissanen, K.; Punzo, F.; Cametti, M. X-Ray Crystallographic and Computational Study on Uranyl-Salophen Complexes Bearing Nitro Groups. Dalton Trans. 2017, 46, 5240–5249. [Google Scholar] [CrossRef] [PubMed]
- Fraga, A.R.L.; Ferreira, F.F.; Lombardo, G.M.; Punzo, F. Experimental and Theoretical Characterization of N-(Diethylcarbamothioyl) Benzamide Triclinic Polymorph. J. Mol. Struct. 2013, 1047, 1–8. [Google Scholar] [CrossRef]
- Pistarà, V.; Lombardo, G.M.; Rescifina, A.; Bacchi, A.; D’Andrea, F.; Punzo, F. Experimental and in Silico Characterization of a Biologically Active Inosose. Struct. Chem. 2013, 24, 955–965. [Google Scholar] [CrossRef]
- Álvarez, J.L.G.; Amato, M.E.; Lombardo, G.M.; Carriedo, G.A.; Punzo, F. Self-Organization by Chiral Recognition Based on Ad Hoc Chiral Pockets in Cyclotriphosphazenes with Binaphthoxy and Biphenoxy Substituents: An X-Ray, NMR and Computational Study. Eur. J. Inorg. Chem. 2010, 2010, 4483–4491. [Google Scholar] [CrossRef]
- Lombardo, G.M.; Thompson, A.L.; Ballistreri, F.P.; Pappalardo, A.; Sfrazzetto, G.T.; Tomaselli, G.A.; Toscano, R.M.; Punzo, F. An Integrated X-Ray and Molecular Dynamics Study of Uranyl-Salen Structures and Properties. Dalton Trans. 2012, 41, 1951–1960. [Google Scholar] [CrossRef]
- Bastos, I.T.S.; Costa, F.N.; Silva, T.F.; Barreiro, E.J.; Lima, L.M.; Braz, D.; Lombardo, G.M.; Punzo, F.; Ferreira, F.F.; Barroso, R.C. A Combined Experimental and in Silico Characterization to Highlight Additional Structural Features and Properties of a Potentially New Drug. J. Mol. Struct. 2017, 1146, 735–743. [Google Scholar] [CrossRef]
- Kitaigorodsky, A. Molecular Crystals and Molecules, 1st ed.; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Thorat, A.; Chauhan, R.; Sartape, R.; Singh, M.R.; Shah, J.K. Effect of K+ Force Fields on Ionic Conductivity and Charge Dynamics of KOH in Ethylene Glycol. J. Phys. Chem. B 2024, 128, 3707–3719. [Google Scholar] [CrossRef]
- Robinson, K.; Gibbs, G.V.; Ribbe, P.H. Quadratic Elongation: A Quantitative Measure of Distortion in Coordination Polyhedra. Science (1979) 1971, 172, 567–570. [Google Scholar] [CrossRef]
- Jeffrey, G.A.; Maluszynska, H.; Mitra, J. Hydrogen Bonding in Nucleosides and Nucleotides. Int. J. Biol. Macromol. 1985, 7, 336–348. [Google Scholar] [CrossRef]
- Schlenker, M.; Guigay, J.P. Differences between Neutron and X-Ray Scattering. Int. Tables Crystallogr. 2006, B, 557–569. [Google Scholar] [CrossRef]
- Majumdar, A.; Müller, M.; Busch, S. Computation of X-Ray and Neutron Scattering Patterns to Benchmark Atomistic Simulations against Experiments. Int. J. Mol. Sci. 2024, 25, 1547. [Google Scholar] [CrossRef]
- Reich, V.; Majumdar, A.; Müller, M.; Busch, S. Comparison of Molecular Dynamics Simulations of Water with Neutron and X-Ray Scattering Experiments. EPJ Web Conf. 2022, 272, 01015. [Google Scholar] [CrossRef]
- Fabiola Sanjuan-Szklarz, W.; Woińska, M.; Domagala, S.; Dominiak, P.M.; Grabowsky, S.; Jayatilaka, D.; Gutmann, M.; Woźniak, K. On the Accuracy and Precision of X-Ray and Neutron Diffraction Results as a Function of Resolution and the Electron Density Model. IUCrJ 2020, 7, 920–933. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Do Special Noncovalent π–π Stacking Interactions Really Exist? Angew. Chem. Int. Ed. 2008, 47, 3430–3434. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, U.; Sundholm, D.; Johansson, M.P. The Effect of Hydrogen Bonding on the π Depletion and the π–π Stacking Interaction. Phys. Chem. Chem. Phys. 2024, 26, 27431–27438. [Google Scholar] [CrossRef]
- Martinez, C.R.; Iverson, B.L. Rethinking the Term “Pi-Stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
- Carter-Fenk, K.; Herbert, J.M. Reinterpreting π-Stacking. Phys. Chem. Chem. Phys. 2020, 22, 24870–24886. [Google Scholar] [CrossRef]
- Gao, X.C.; Hao, Q.; Wang, C.S. Improved Polarizable Dipole-Dipole Interaction Model for Hydrogen Bonding, Stacking, T-Shaped, and X-H···φ Interactions. J. Chem. Theory Comput. 2017, 13, 2730–2741. [Google Scholar] [CrossRef]
- Lessa, M.D.; Stoyanov, S.R.; de Carneiro, J.W.M.; da Costa, L.M. Density Functional Theory Investigation of the Contributions of π-π Stacking and Hydrogen Bonding with Water to the Supramolecular Aggregation Interactions of Model Asphaltene Heterocyclic Compounds. J. Mol. Model. 2024, 30, 145. [Google Scholar] [CrossRef]
- Han, T.; Pan, X.; Wang, Y.; Du, Y.; Xue, J. Hydrogen-Bond Stabilized π-π Stacking in the Solvent-Induced Dimerization of 4-Nitro-1-Naphthol: A Spectroscopic and Computational Investigation. J. Mol. Struct. 2024, 1312, 138505. [Google Scholar] [CrossRef]
- Palatinus, L.; Chapuis, G. SUPERFLIP-A Computer Program for the Solution of Crystal Structures by Charge Flipping in Arbitrary Dimensions. J. Appl. Crystallogr. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- MacRae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From Visualization to Analysis, Design and Prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
- Lombardo, G.M.; Punzo, F. False Asymmetry, Pseudosymmetry, Disorder, Polymorphism and Atomic Displacement Parameters. J. Mol. Struct. 2014, 1078, 158–164. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Rappé, A.K.; Goddard, W.A. Charge Equilibration for Molecular Dynamics Simulations. J. Phys. Chem. 1991, 95, 3358–3363. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Strain Fluctuations and Elastic Constants. J. Chem. Phys. 1982, 76, 2662–2666. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Noorizadeh, E.; Theil, F. A Gentle Stochastic Thermostat for Molecular Dynamics. J. Stat. Phys. 2009, 135, 261–277. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
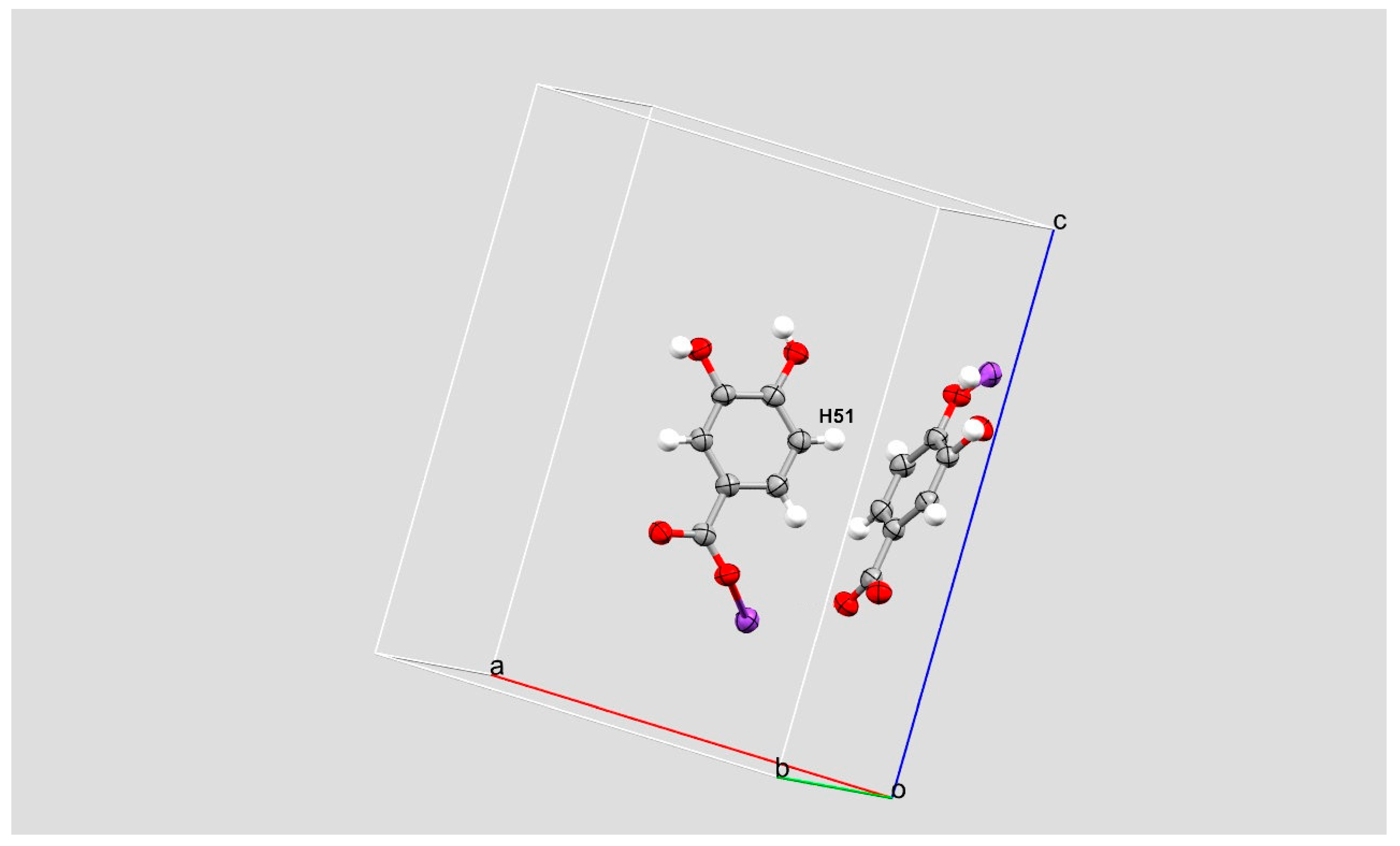
| X-Ray | Castep | Universal | Universal * | Dreiding ** | Dreiding * | |
|---|---|---|---|---|---|---|
| a | 12.1515(8) | 12.3385 | 11.9416 | 11.4487 | 12.0772 | 11.4048 |
| b | 7.4636(5) | 7.3520 | 7.4964 | 7.5250 | 7.5655 | 7.5047 |
| c | 15.6079(10) | 16.0242 | 16.9376 | 16.6679 | 16.2590 | 16.2707 |
| α | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 |
| β | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 |
| γ | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 |
| Bond Type | D—H..A | D–H | H…A | D…A |
|---|---|---|---|---|
| Inter- | O10—H102..O8 a | 0.84 | 1.85 | 2.6594(2) |
| Intra- | O11—H111..O10 | 0.81 | 2.41 | 2.7618(2) |
| Inter- | * O11—H111..O8 b | 0.81 | 1.94 | 2.6946(2) |
| Inter- | * O11—H111..O9 b | 0.81 | 2.54 | 3.0567(2) |
| Intra- | C2—H21..O8 | 0.94 | 2.53 | 2.8405(2) |
| π-Stacking Interactions and T-Shaped Interactions | ||||
| Ring-Ring | Distance (Å) | Angle Between Planes (°) | Slippage (Å) | Crystallogr. Directions |
| Cg1–Cg1 | 3.4928(2) | 0 | 0.855 | 1 − X, 1 − Y, 1 − Z |
| Cg1–Cg1 | 4.9373(3) | 81 | n.a. | ½ − X, 1/2 + Y, Z |
| X-H…Cg(π-Ring) Interactions (Details of the T-Shaped Ones) | ||||
| X—H → Cg(J) | Distance (Å) | Angle of the Bond with the π Plane (°) | Crystallogr. Directions | X—H → Cg(J) |
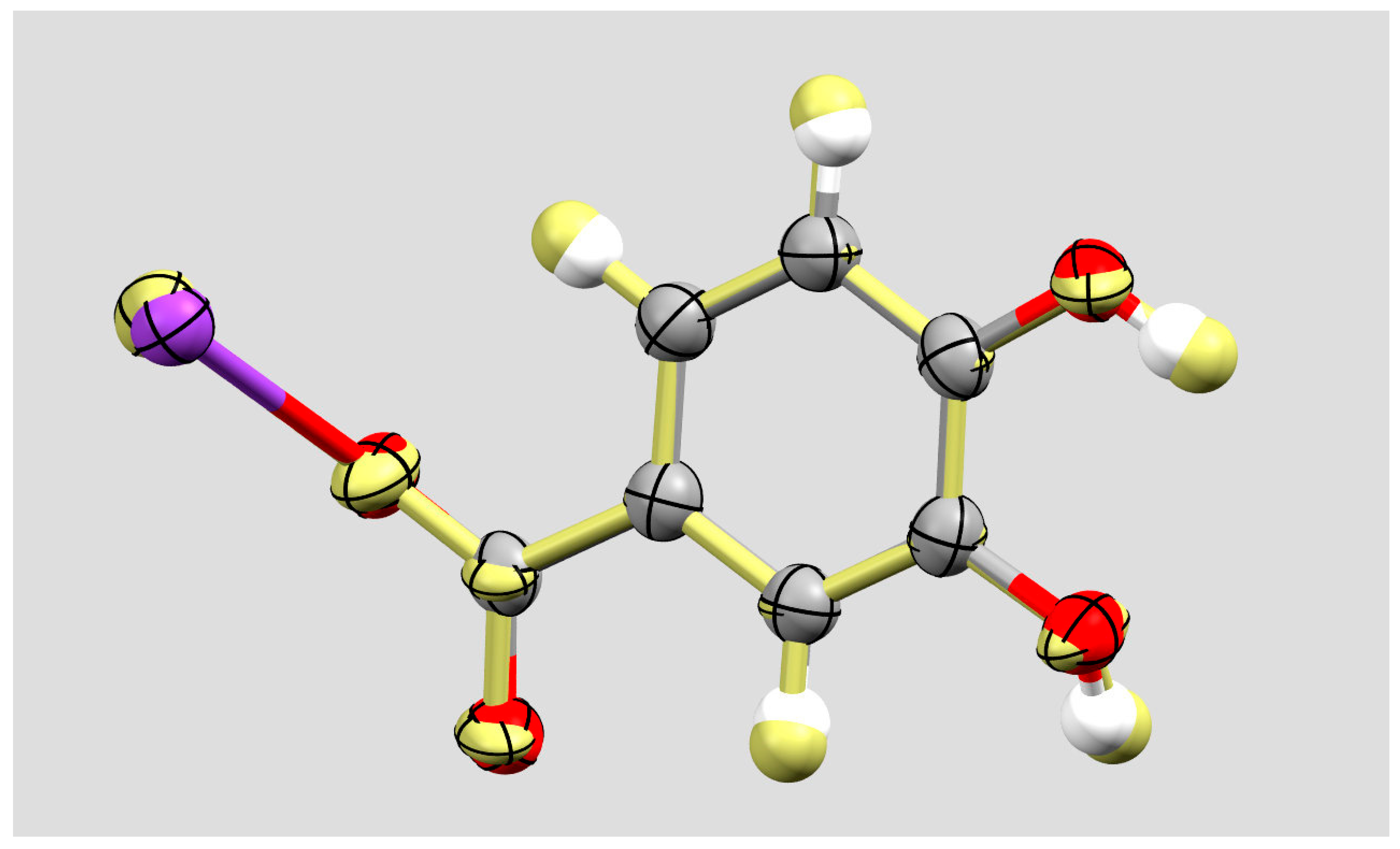
| C5—H51 → Cg1 | 2.71 | 57 | 1/2 − x, −1/2 + y, z | C5—H51 → Cg1 |
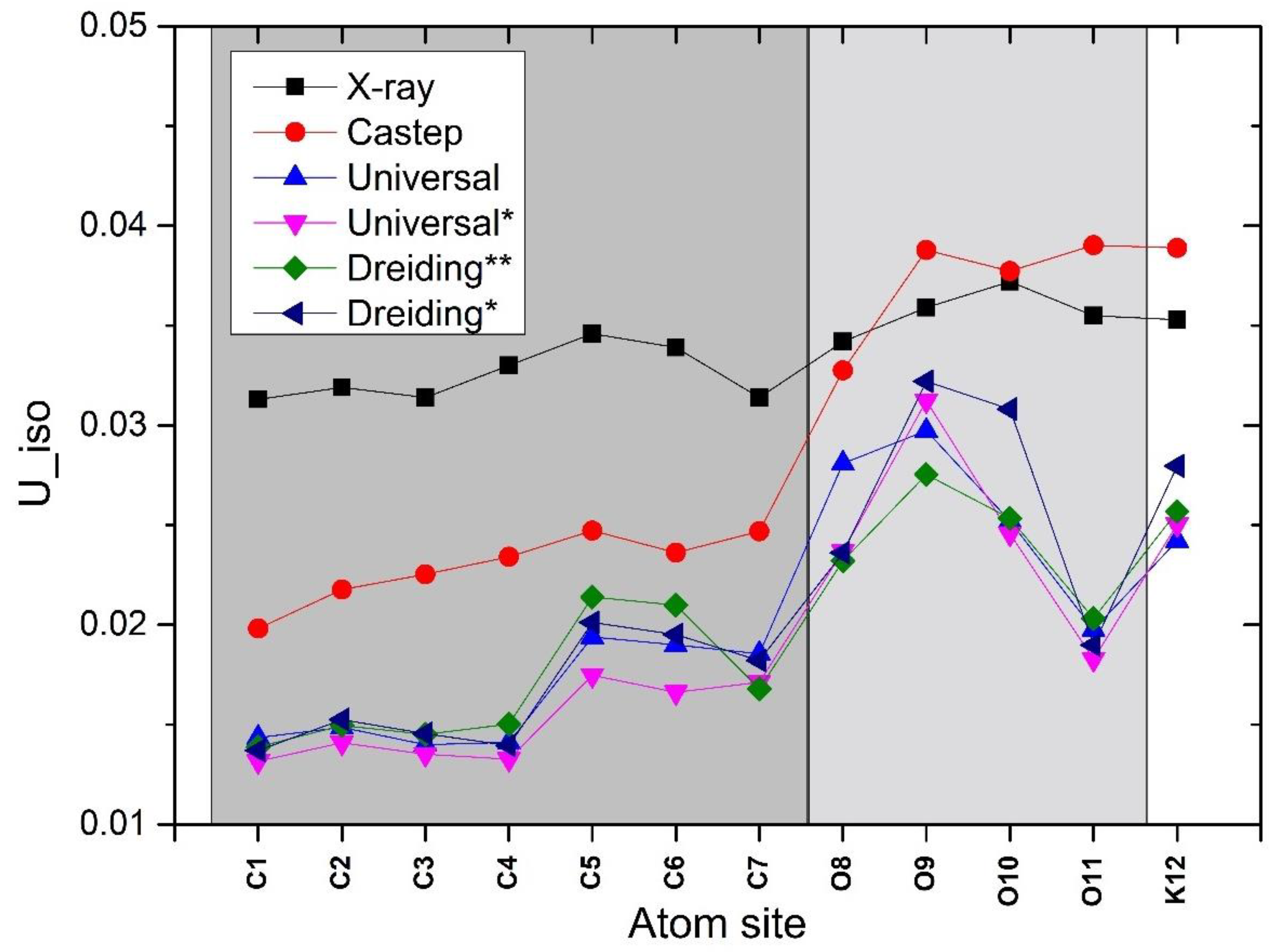
| Uiso | ||||||
|---|---|---|---|---|---|---|
| X-Ray | Castep | Universal | Universal * | Dreiding ** | Dreiding * | |
| C1 | 0.0313 | 0.01981 | 0.01434 | 0.01316 | 0.01387 | 0.01370 |
| C2 | 0.0319 | 0.02176 | 0.01486 | 0.01409 | 0.01495 | 0.01525 |
| C3 | 0.0314 | 0.02253 | 0.01399 | 0.01351 | 0.01451 | 0.01454 |
| C4 | 0.0330 | 0.02340 | 0.01411 | 0.01327 | 0.01502 | 0.01394 |
| C5 | 0.0346 | 0.02472 | 0.01939 | 0.01747 | 0.02139 | 0.02011 |
| C6 | 0.0339 | 0.02362 | 0.01899 | 0.01661 | 0.02098 | 0.01951 |
| C7 | 0.0314 | 0.02468 | 0.01854 | 0.01712 | 0.01679 | 0.01821 |
| 08 | 0.0342 | 0.03276 | 0.02810 | 0.02367 | 0.02321 | 0.02360 |
| 09 | 0.0359 | 0.03878 | 0.02974 | 0.03124 | 0.02754 | 0.03221 |
| 010 | 0.0372 | 0.03773 | 0.02520 | 0.02456 | 0.02533 | 0.03081 |
| 011 | 0.0355 | 0.03903 | 0.01976 | 0.01828 | 0.02031 | 0.01898 |
| K12 | 0.0353 | 0.03889 | 0.02421 | 0.02503 | 0.02567 | 0.02797 |
| H21 | 0.0377 | 0.03500 | 0.02644 | 0.02502 | 0.02514 | 0.02675 |
| H51 | 0.0379 | 0.04273 | 0.03422 | 0.03090 | 0.03790 | 0.03643 |
| H61 | 0.0404 | 0.04232 | 0.03191 | 0.02842 | 0.03743 | 0.03417 |
| H111 | 0.0533 | 0.04216 | 0.02945 | 0.02649 | 0.02556 | 0.02592 |
| H102 | 0.0563 | 0.03017 | 0.04682 | 0.05208 | 0.03896 | 0.07369 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lombardo, G.M.; Punzo, F. Ex-Post Evaluation of Computational Forecast Accuracy: The Potassium Ion Coordination in a Catecholic Compound. Inorganics 2025, 13, 385. https://doi.org/10.3390/inorganics13120385
Lombardo GM, Punzo F. Ex-Post Evaluation of Computational Forecast Accuracy: The Potassium Ion Coordination in a Catecholic Compound. Inorganics. 2025; 13(12):385. https://doi.org/10.3390/inorganics13120385
Chicago/Turabian StyleLombardo, Giuseppe M., and Francesco Punzo. 2025. "Ex-Post Evaluation of Computational Forecast Accuracy: The Potassium Ion Coordination in a Catecholic Compound" Inorganics 13, no. 12: 385. https://doi.org/10.3390/inorganics13120385
APA StyleLombardo, G. M., & Punzo, F. (2025). Ex-Post Evaluation of Computational Forecast Accuracy: The Potassium Ion Coordination in a Catecholic Compound. Inorganics, 13(12), 385. https://doi.org/10.3390/inorganics13120385









