Computational Insights into Iron Coordination Disruption in the Human Transferrin–Neisseria meningitidis Bacterial Protein Complex
Abstract
1. Introduction
2. Materials and Methods
2.1. MD Simulations
2.2. QM/MM Calculations
2.3. Natural Bond Orbital Analysis
3. Results and Discussions
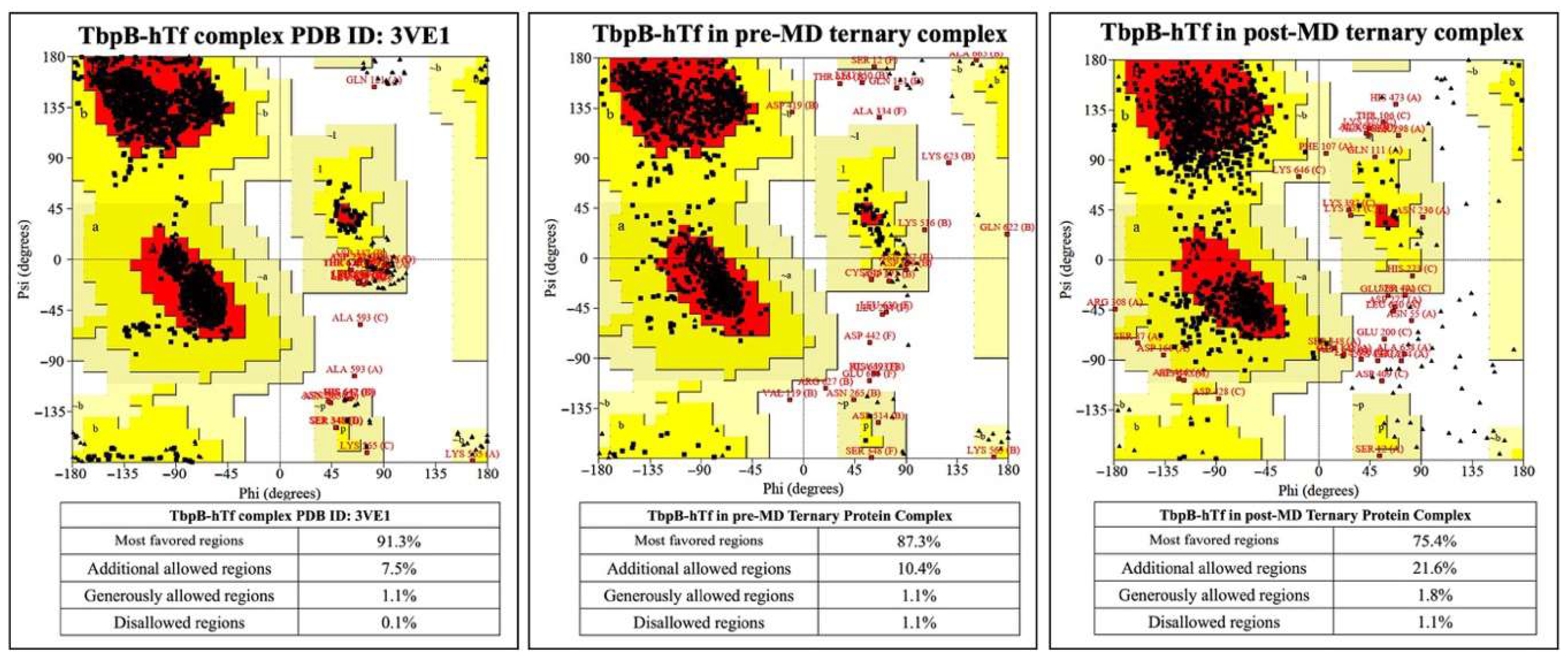
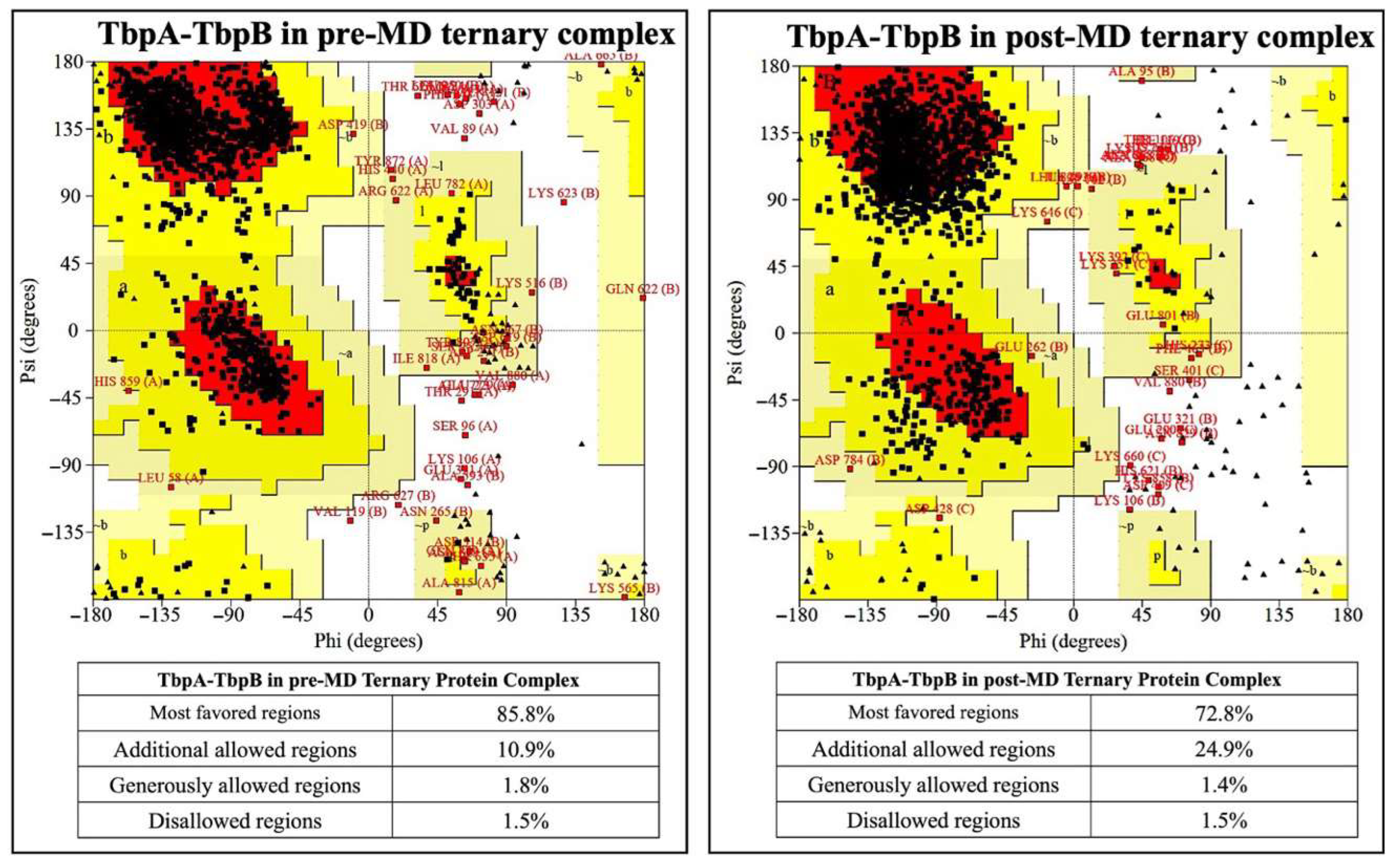
3.1. Results from MD Simulations
3.2. Results from QM/MM Calculations
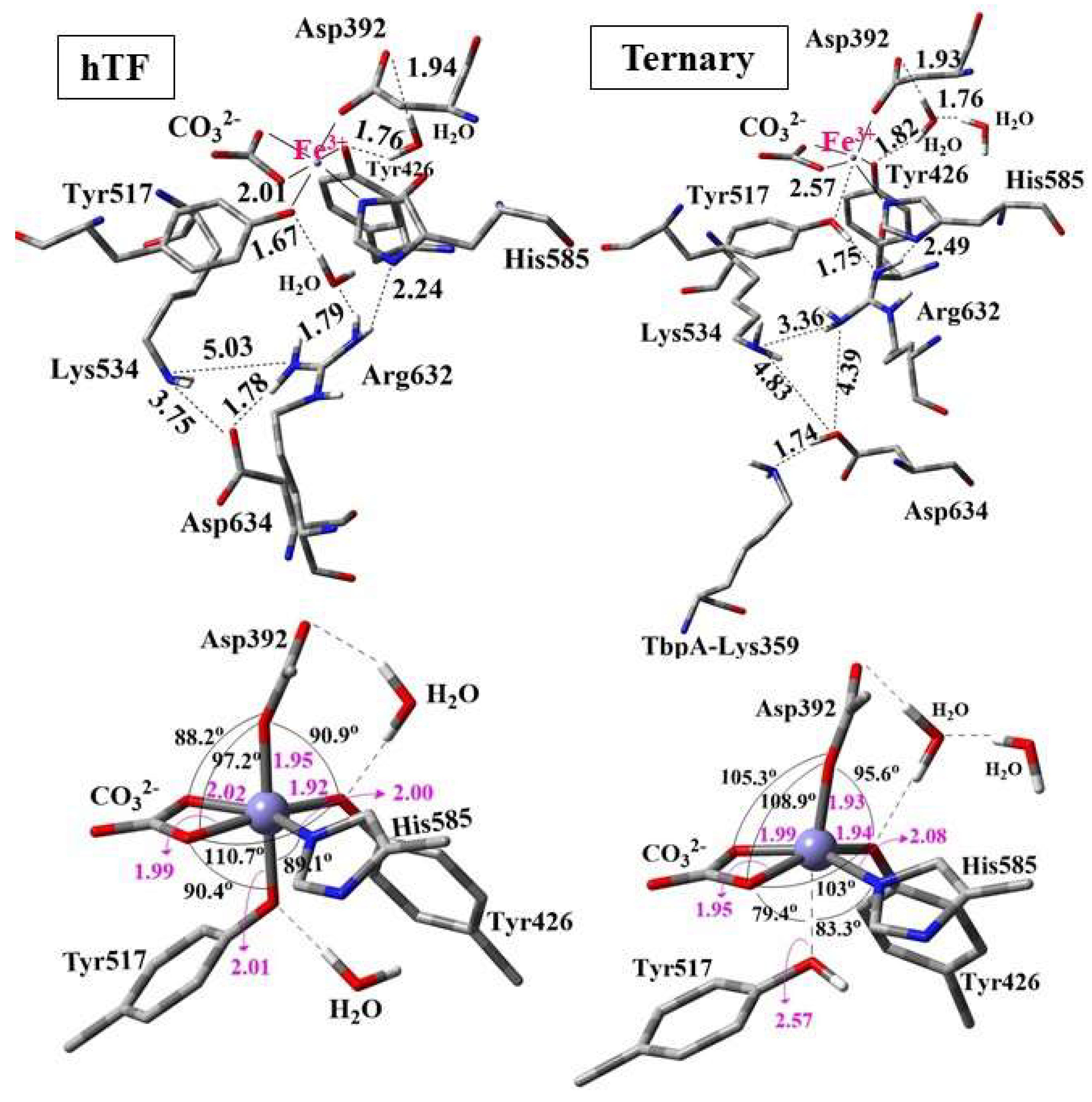
3.2.1. QM/MM Calculations for hTf and TbpA-TbpB-hTf Protein Complex
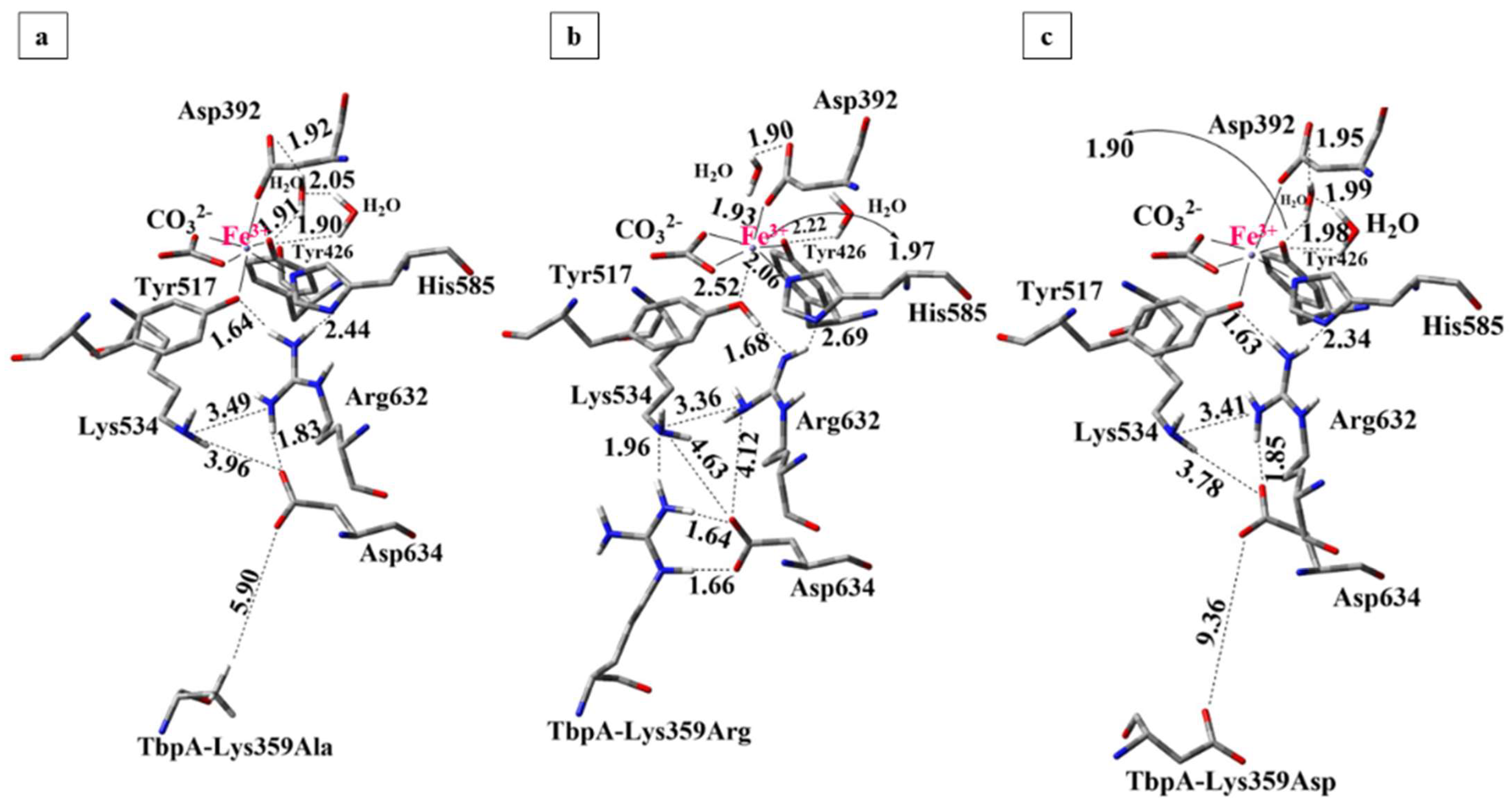
3.2.2. QM/MM Calculations for the Lys359 Mutants of TbpA-TbpB-hTf Protein Complex
3.3. Natural Bond Orbital Stabilization Energies
4. Conclusions
- (1)
- Point mutations Lys359Ala and Lys359Asp, which increase the local electron density by introducing neutral or negative charge in the QM region, significantly enhance Fe3+ binding affinity. In contrast, the positively charged Lys359Arg mutation reduces electron density, weakening Fe3+ coordination. These findings suggest that increased electron density near the Fe3+ center stabilizes its binding, whereas the introduction of positive charge (as in wild-type Lys359 or Lys359Arg mutant) perturbs the electrostatic environment of highly cationic Fe3+, lowering the binding affinity and facilitating Fe3+ release.
- (2)
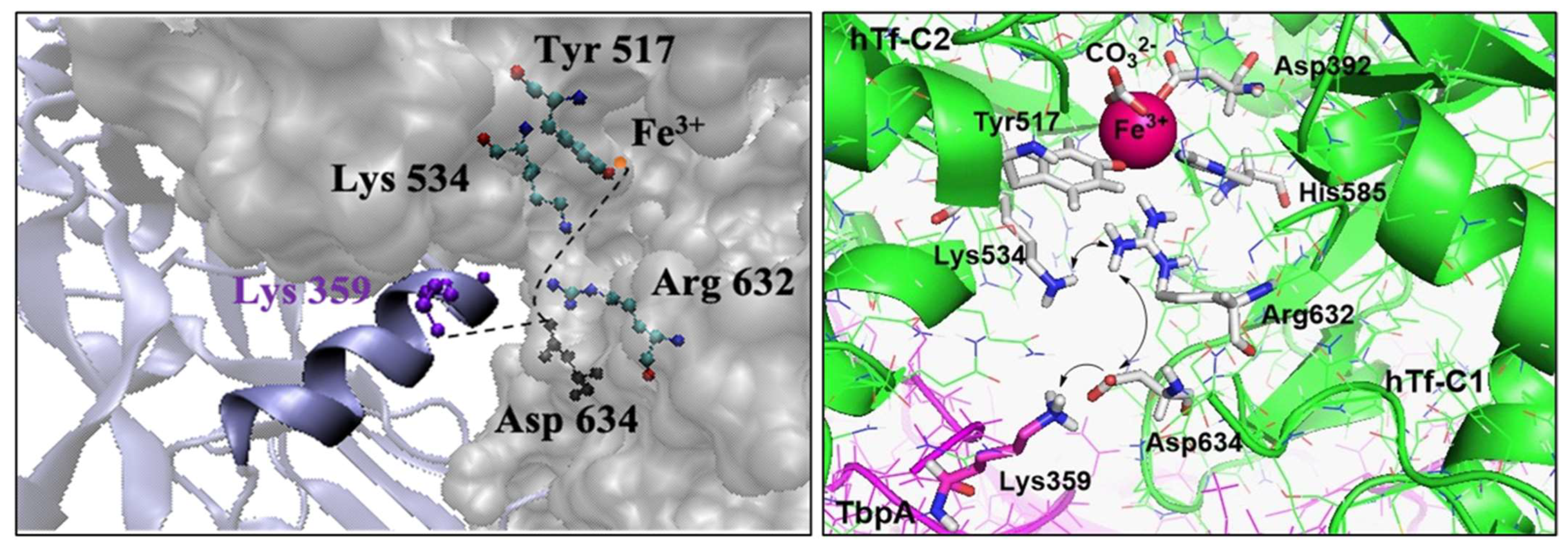
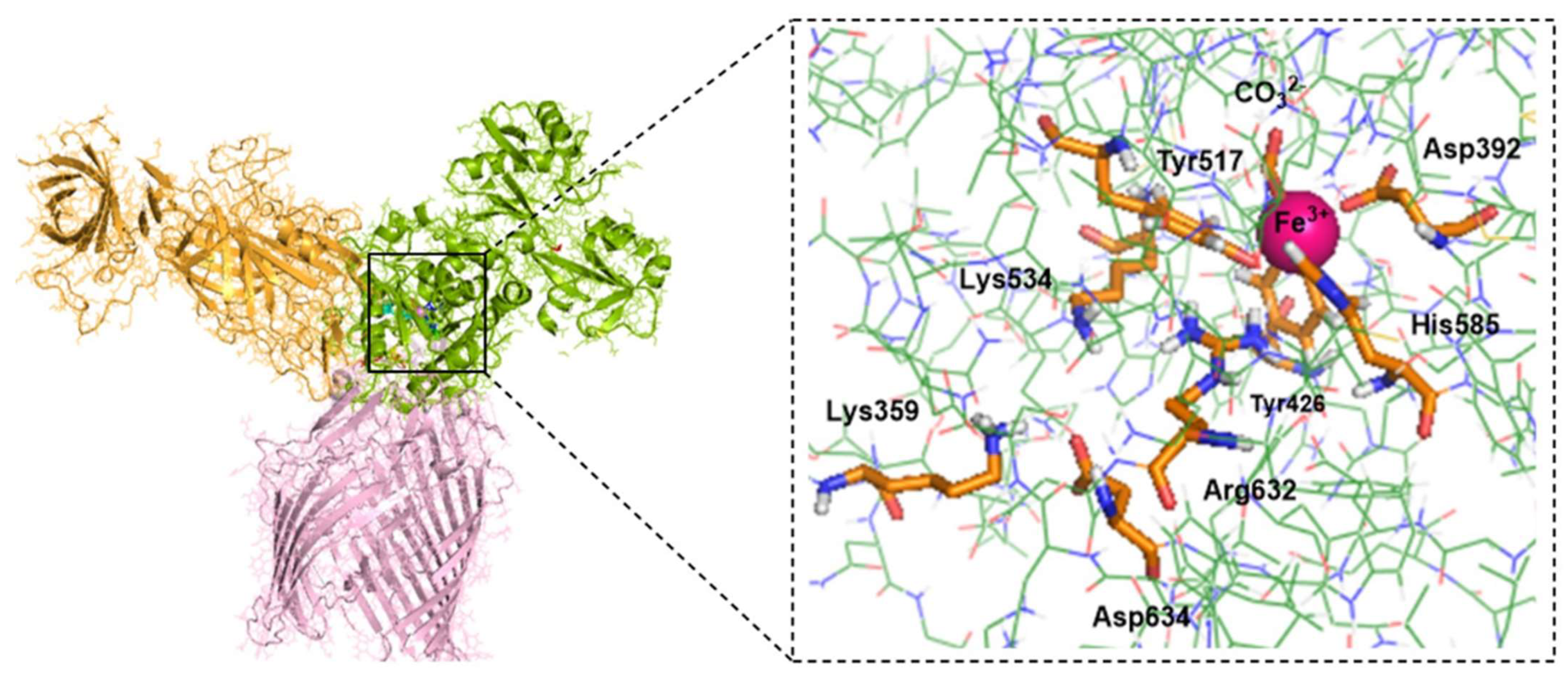
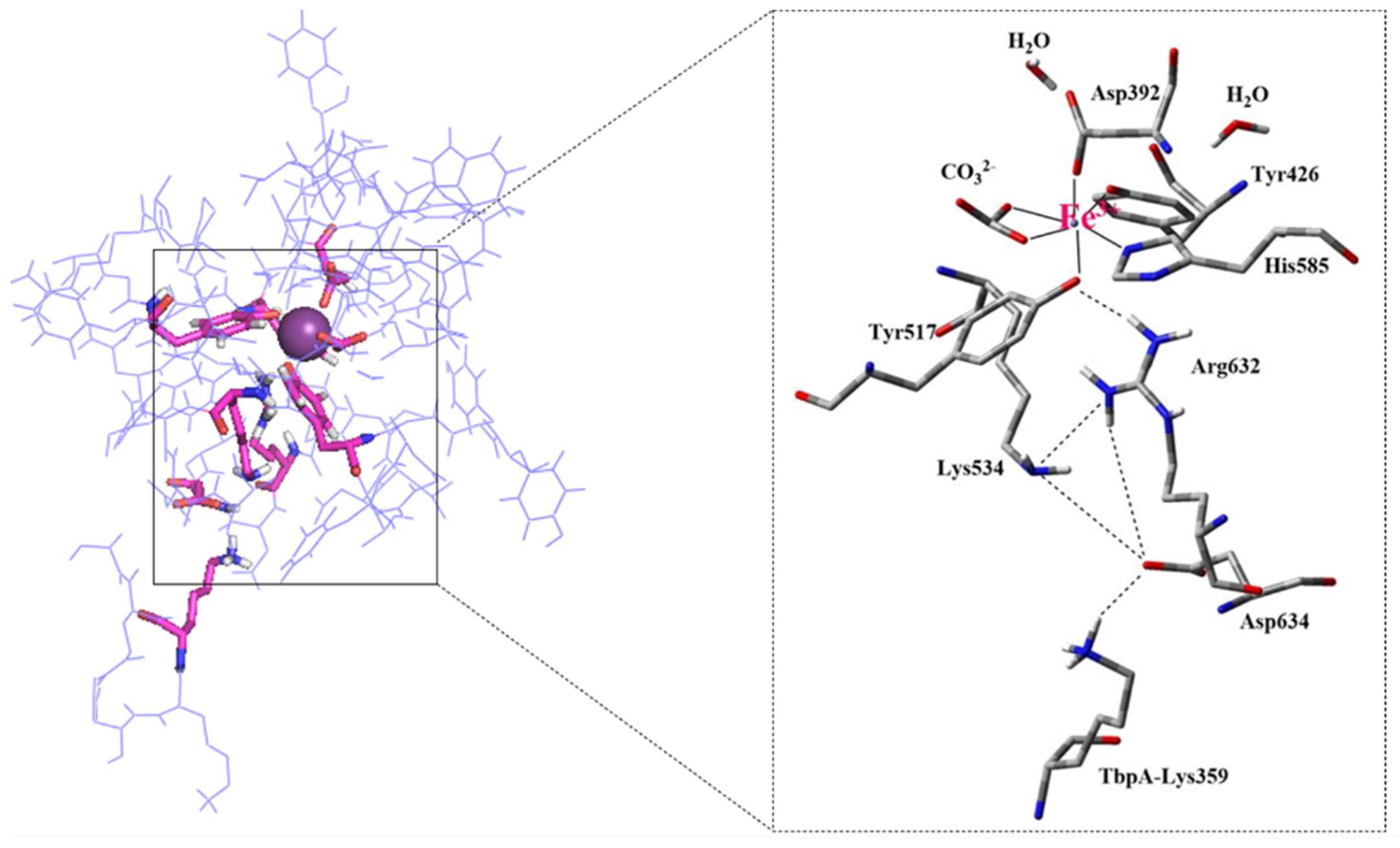
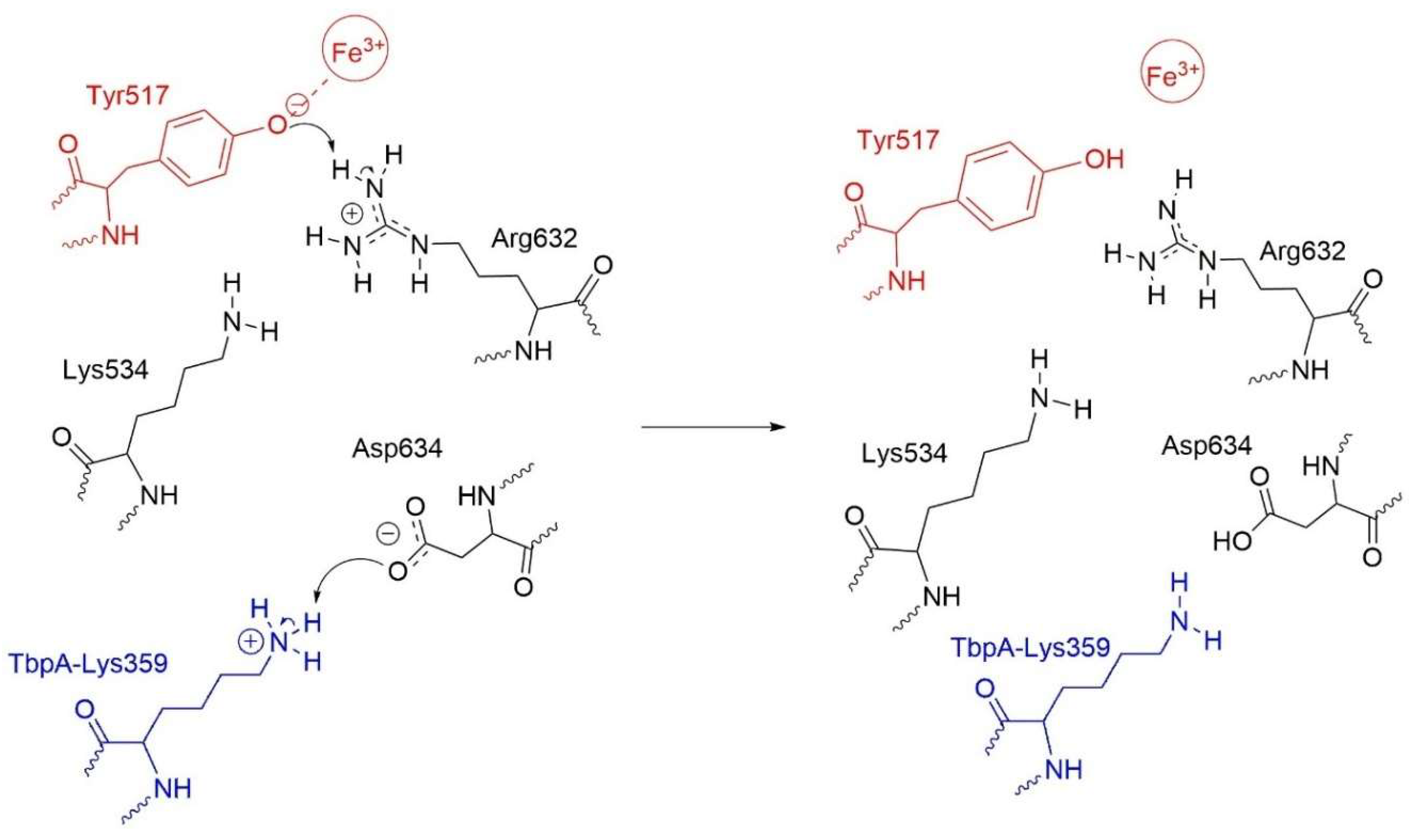
- Consistent with energetic results, structural analyses emphasize the importance of maintaining charge balance within the Asp634–Arg632–Lys534 triad for stable Fe3+ coordination. In protein models exhibiting stronger Fe3+ binding (e.g., hTf, Lys359Ala, Lys359Asp), Asp634 forms a stabilizing H-bond with Arg632 and is positioned proximally to both Arg632 and Lys534 (Figure 10 and Figure 11). In contrast, in weaker-binding systems (wild-type and Lys359Arg), the positively charged Lys359 or Arg359 interacts electrostatically with Asp634, displacing it from Arg632. This displacement disrupts local charge neutrality, leaving Arg632 insufficiently balanced near the Fe3+ center, thereby inducing electrostatic repulsion and destabilizing Fe3+ binding.
- (3)
- Although both the wild-type and Lys359Arg mutant reduce Fe3+ binding relative to neutral or negatively charged mutants, their mechanisms differ slightly. In the wild type, proton transfer from Lys359 to Asp634 enables charge neutralization, which slightly lowers Fe3+ binding energy but triggers a second, spontaneous proton transfer from Arg632 to Tyr517, weakening the Tyr517–Fe3+ bond. In contrast, no proton transfer from Arg359 occurs in the Lys359Arg mutant due to the lower acidity of Arg, resulting in incomplete charge neutralization and a higher binding energy. These findings suggest that Fe3+ release requires both a destabilizing positive charge and an acidic proton to disrupt coordination.
- (4)
- NBO donor–acceptor stabilization energies revealed that reduced Fe3+ binding in the wild-type and Lys359Arg complexes primarily stems from a significant decrease in LP(Tyr517–O)→LP(Fe3+) interactions. Across all models, LP(His585–N)→LP*(Fe3+) and LP(Tyr517–O)→LP*(Fe3+) consistently exhibited the lowest stabilization energies, identifying Tyr517 and His585 as the most labile coordination sites.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peters, K.; Staehlke, S.; Rebl, H.; Jonitz-Heincke, A.; Hahn, O. Impact of Metal Ions on Cellular Functions: A Focus on Mesenchymal Stem/Stromal Cell Differentiation. Int. J. Mol. Sci. 2024, 25, 10127. [Google Scholar] [CrossRef]
- Majorek, K.A.; Gucwa, M.; Murzyn, K.; Minor, W. Metal Ions in Biomedically Relevant Macromolecular Structures. Front. Chem. 2024, 12, 1426211. [Google Scholar] [CrossRef]
- Zhong, M.; Wang, Y.; Min, J.; Wang, F. Iron Metabolism and Ferroptosis in Human Health and Disease. BMC Biol. 2025, 23, 263. [Google Scholar] [CrossRef] [PubMed]
- SantaMaria, A.M.; Rouault, T.A. Regulatory and Sensing Iron–Sulfur Clusters: New Insights and Unanswered Questions. Inorganics 2024, 12, 101. [Google Scholar] [CrossRef]
- Perkins-Balding, D.; Ratliff-Griffin, M.; Stojiljkovic, I. Iron Transport Systems in Neisseria Meningitidis. Microbiol. Mol. Biol. Rev. 2004, 68, 154–171. [Google Scholar] [CrossRef]
- Noinaj, N.; Buchanan, S.K.; Cornelissen, C.N. The Transferrin-Iron Import System from Pathogenic Neisseria Species. Mol. Microbiol. 2012, 86, 246–257. [Google Scholar] [CrossRef]
- Irwin, S.W.; Averil, N.; Cheng, C.Y.; Schryvers, A.B. Preparation and Analysis of Isogenic Mutants in the Transferrin Receptor Protein Genes, TbpA and TbpB, from Neisseria Meningitidis. Mol. Microbiol. 1993, 8, 1125–1133. [Google Scholar] [CrossRef]
- Anderson, J.E.; Sparling, P.F.; Cornelissen, C.N. Gonococcal Transferrin-Binding Protein 2 Facilitates but Is Not Essential for Transferrin Utilization. J. Bacteriol. 1994, 176, 3162–3170. [Google Scholar] [CrossRef] [PubMed]
- Noinaj, N.; Easley, N.C.; Oke, M.; Mizuno, N.; Gumbart, J.; Boura, E.; Steere, A.N.; Zak, O.; Aisen, P.; Tajkhorshid, E. Structural Basis for Iron Piracy by Pathogenic Neisseria. Nature 2012, 483, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Schryvers, A.B.; Gonzalez, G.C. Receptors for Transferrin in Pathogenic Bacteria Are Specific for the Host’s Protein. Can. J. Microbiol. 1990, 36, 145–147. [Google Scholar] [CrossRef]
- McCammon, J.A.; Gelin, B.R.; Karplus, M. Dynamics of Folded Proteins. Nature 1977, 267, 585–590. [Google Scholar] [CrossRef]
- van Gunsteren, W.F.; Berendsen, H.J.C. Algorithms for Macromolecular Dynamics and Constraint Dynamics. Mol. Phys. 1977, 34, 1311–1327. [Google Scholar] [CrossRef]
- Voth, G.A. Computational Approaches for Studying Enzyme Mechanism; Methods in Enzymology; Academic Press/Elsevier: Cambridge, MA, USA, 2016; Volume 577–578, ISBN 9780128053478. [Google Scholar]
- Akyüz, M.A.; Erdem, S.S.; Edmondson, D.E. The Aromatic Cage in the Active Site of Monoamine Oxidase B: Effect on the Structural and Electronic Properties of Bound Benzylamine and p-Nitrobenzylamine. J. Neural Transm. 2007, 114, 693–698. [Google Scholar] [CrossRef]
- Lovell, T.; Himo, F.; Han, W.G.; Noodleman, L. Density Functional Methods Applied to Metalloenzymes. Coord. Chem. Rev. 2003, 238–239, 211–232. [Google Scholar] [CrossRef]
- Akyüz, M.A.; Erdem, S.S. Computational Modeling of the Direct Hydride Transfer Mechanism for the MAO Catalyzed Oxidation of Phenethylamine and Benzylamine: ONIOM (QM/QM) Calculations. J. Neural Transm. 2013, 120, 937–945. [Google Scholar] [CrossRef]
- Cakir, K.; Erdem, S.S.; Atalay, V.E. ONIOM Calculations on Serotonin Degradation by Monoamine Oxidase B: Insight into the Oxidation Mechanism and Covalent Reversible Inhibition. Org. Biomol. Chem. 2016, 14, 9239–9252. [Google Scholar] [CrossRef] [PubMed]
- Fındık, V.; Varınca Gerçik, B.T.; Sinek, Ö.; Erdem, S.S.; Ruiz-López, M.F. Mechanistic Investigation of Lysine-Targeted Covalent Inhibition of PI3Kδvia ONIOM QM:QM Computations. J. Chem. Inf. Model. 2022, 62, 6775–6787. [Google Scholar] [CrossRef]
- Sheng, X.; Himo, F. The Quantum Chemical Cluster Approach in Biocatalysis. Acc. Chem. Res. 2023, 56, 938–947. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M.; Chen, S.; Liao, R. Theoretical Studies of Nickel-Dependent Enzymes. Inorganics 2019, 7, 95. [Google Scholar] [CrossRef]
- Lonsdale, R.; Harvey, J.N.; Mulholland, A.J. A Practical Guide to Modelling Enzyme-Catalysed Reactions. Chem. Soc. Rev. 2012, 41, 3025–3038. [Google Scholar] [CrossRef]
- Vreven, T.; Byun, K.S.; Komáromi, I.; Dapprich, S.; Montgomery, J.A.; Morokuma, K.; Frisch, M.J. Combining Quantum Mechanics Methods with Molecular Mechanics Methods in ONIOM. J. Chem. Theory Comput. 2006, 2, 815–826. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhang, Q.; Chen, K.; Zhu, W. Probing Origin of Binding Difference of Inhibitors to MDM2 and MDMX by Polarizable Molecular Dynamics Simulation and QM/MM-GBSA Calculation. Sci. Rep. 2015, 5, 17421. [Google Scholar] [CrossRef]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef] [PubMed]
- Morokuma, K.L.M. Multi-Scale Quantum Models for Biocatalysis; York, D.M., Lee, T.-S., Eds.; Challenges and Advances in Computational Chemistry and Physics; Springer: Dordrecht, The Netherlands, 2009; Volume 7, ISBN 978-1-4020-9955-7. [Google Scholar]
- Mihaljević-Jurič, P.; Sousa, S.F. A QM/MM Evaluation of the Missing Step in the Reduction Mechanism of HMG-CoA by Human HMG-CoA Reductase. Processes 2021, 9, 1085. [Google Scholar] [CrossRef]
- Yildiz, I.; Yildiz, B.S.; Kirmizialtin, S. Comparative Computational Approach to Study Enzyme Reactions Using QM and QM-MM Methods. ACS Omega 2018, 3, 14689–14703. [Google Scholar] [CrossRef] [PubMed]
- Dautry-Varsat, A.; Ciechanover, A.; Lodish, H.F. Cell Biology PH and the Recycling of Transferrin during Receptor-Mediated Endocytosis (Endocytic Vesicle/Apotransferrin/Transferrin Receptor). Proc. Natl Acad. Sci. USA 1983, 80, 2258–2262. [Google Scholar] [CrossRef] [PubMed]
- Benjamín-Rivera, J.A.; Cardona-Rivera, A.E.; Vazquez-Maldonado, A.L.; Dones-Lassalle, C.Y.; Pabon-Colon, H.L.; Rodriguez-Rivera, H.M.; Rodriguez, I.; Gonzalez-Espiet, J.C.; Pazol, J.; Perez-Rios, J.D. Exploring Serum Transferrin Regulation of Nonferric Metal Therapeutic Function and Toxicity. Inorganics 2020, 8, 48. [Google Scholar] [CrossRef]
- Halbrooks, P.J.; He, Q.Y.; Briggs, S.K.; Everse, S.J.; Smith, V.C.; MacGillivray, R.T.A.; Mason, A.B. Investigation of the Mechanism of Iron Release from the C-Lobe of Human Serum Transferrin: Mutational Analysis of the Role of a PH Sensitive Triad. Biochemistry 2003, 42, 3701–3707. [Google Scholar] [CrossRef]
- Mason, A.B.; Halbrooks, P.J.; James, N.G.; Connolly, S.A.; Larouche, J.R.; Smith, V.C.; MacGillivray, R.T.A.; Chasteen, N.D. Mutational Analysis of C-Lobe Ligands of Human Serum Transferrin: Insights into the Mechanism of Iron Release. Biochemistry 2005, 44, 8013–8021. [Google Scholar] [CrossRef]
- Baldwin, D.A. The Kinetics of Iron Release from Human Transferrin by EDTA. Effect of Salts and Detergents. BBA Protein Struct. 1980, 623, 183–198. [Google Scholar] [CrossRef]
- Zak, O.; Aisen, P. Iron Release from Transferrin, Its C-Lobe, and Their Complexes with Transferrin Receptor: Presence of N-Lobe Accelerates Release from C-Lobe at Endosomal PH. Biochemistry 2003, 42, 12330–12334. [Google Scholar] [CrossRef]
- Steere, A.N.; Byrne, S.L.; Chasteen, N.D.; Mason, A.B. Kinetics of Iron Release from Transferrin Bound to the Transferrin Receptor at Endosomal PH. Biochim. Biophys. Acta Gen. Subj. 2012, 1820, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Koca Fındık, B.; Cilesiz, U.; Bali, S.K.; Atilgan, C.; Aviyente, V.; Dedeoglu, B. Investigation of Iron Release from the N- and C-Lobes of Human Serum Transferrin by Quantum Chemical Calculations. Org. Biomol. Chem. 2022, 20, 8766–8774. [Google Scholar] [CrossRef] [PubMed]
- Mujika, J.I.; Escribano, B.; Akhmatskaya, E.; Ugalde, J.M.; Lopez, X. Molecular Dynamics Simulations of Iron- and Aluminum-Loaded Serum Transferrin: Protonation of Tyr188 Is Necessary to Prompt Metal Release. Biochemistry 2012, 51, 7017–7027. [Google Scholar] [CrossRef] [PubMed]
- Rinaldo, D.; Field, M.J. A Computational Study of the Open and Closed Forms of the N-Lobe Human Serum Transferrin Apoprotein. Biophys. J. 2003, 85, 3485–3501. [Google Scholar] [CrossRef]
- Baker, H.M.; Nurizzo, D.; Mason, A.B.; Baker, E.N. Structures of Two Mutants That Probe the Role in Iron Release of the Dilysine Pair in the N-Lobe of Human Transferrin. Acta Crystallogr. Sect. D Biol. Crystallogr. 2007, 63, 408–414. [Google Scholar] [CrossRef]
- Dewan, J.C.; Mikami, B.; Sacchettini, J.C.; Hirose, M. Structural Evidence for a PH-Sensitive Dilysine Trigger in the Hen Ovotransferrin N-Lobe: Implications for Transferrin Iron Release. Biochemistry 1993, 32, 11963–11968. [Google Scholar] [CrossRef]
- Reilley, D.J.; Fuller, J.T.; Nechay, M.R.; Victor, M.; Li, W.; Ruberry, J.D.; Mujika, J.I.; Lopez, X.; Alexandrova, A.N. Toxic and Physiological Metal Uptake and Release by Human Serum Transferrin. Biophys. J. 2020, 118, 2979–2988. [Google Scholar] [CrossRef]
- Sakajiri, T.; Yajima, H.; Yamamura, T. Density Functional Theory Study on Metal-Binding Energies for Human Serum Transferrin-Metal Complexes. ISRN Biophys. 2012, 2012, 124803. [Google Scholar] [CrossRef]
- Mujika, J.I.; Lopez, X.; Rezabal, E.; Castillo, R.; Marti, S.; Moliner, V.; Ugalde, J.M. A QM/MM Study of the Complexes Formed by Aluminum and Iron with Serum Transferrin at Neutral and Acidic PH. J. Inorg. Biochem. 2011, 105, 1446–1456. [Google Scholar] [CrossRef]
- Mishra, L.; Sundararajan, M. Quantum Chemical Studies of Structures and Spin Hamiltonian Parameters of Iron Transferrin Using Isolated and Embedded Clusters Models. J. Chem. Sci. 2019, 131, 15. [Google Scholar] [CrossRef]
- Sundararajan, M.; Mishra, L.; Bharti, N.K.; Mantry, S.P. Proton-Coupled Electron Transfer Modulates the Metal Release of Blood Serum Iron Transferrin. Dalt. Trans. 2025, 54, 14677–14686. [Google Scholar] [CrossRef]
- Abdizadeh, H.; Atilgan, C. Predicting Long Term Cooperativity and Specific Modulators of Receptor Interactions in Human Transferrin from Dynamics within a Single Microstate. Phys. Chem. Chem. Phys. 2016, 18, 7916–7926. [Google Scholar] [CrossRef]
- Abdizadeh, H.; Atilgan, A.R.; Atilgan, C. Detailed Molecular Dynamics Simulations of Human Transferrin Provide Insights into Iron Release Dynamics at Serum and Endosomal PH. JBIC J. Biol. Inorg. Chem. 2015, 20, 705–718. [Google Scholar] [CrossRef] [PubMed]
- Abdizadeh, H.; Atilgan, A.R.; Atilgan, C.; Dedeoglu, B. Computational Approaches for Deciphering the Equilibrium and Kinetic Properties of Iron Transport Proteins. Metallomics 2017, 9, 1513–1533. [Google Scholar] [CrossRef] [PubMed]
- Abdizadeh, H.; Atilgan, A.R.; Atilgan, C. Mechanisms by Which Salt Concentration Moderates the Dynamics of Human Serum Transferrin. J. Phys. Chem. B 2017, 121, 4778–4789. [Google Scholar] [CrossRef] [PubMed]
- Noinaj, N.; Guillier, M.; Barnard, T.J.; Buchanan, S.K. TonB-Dependent Transporters: Regulation, Structure, and Function. Annu. Rev. Microbiol. 2010, 64, 43–60. [Google Scholar] [CrossRef]
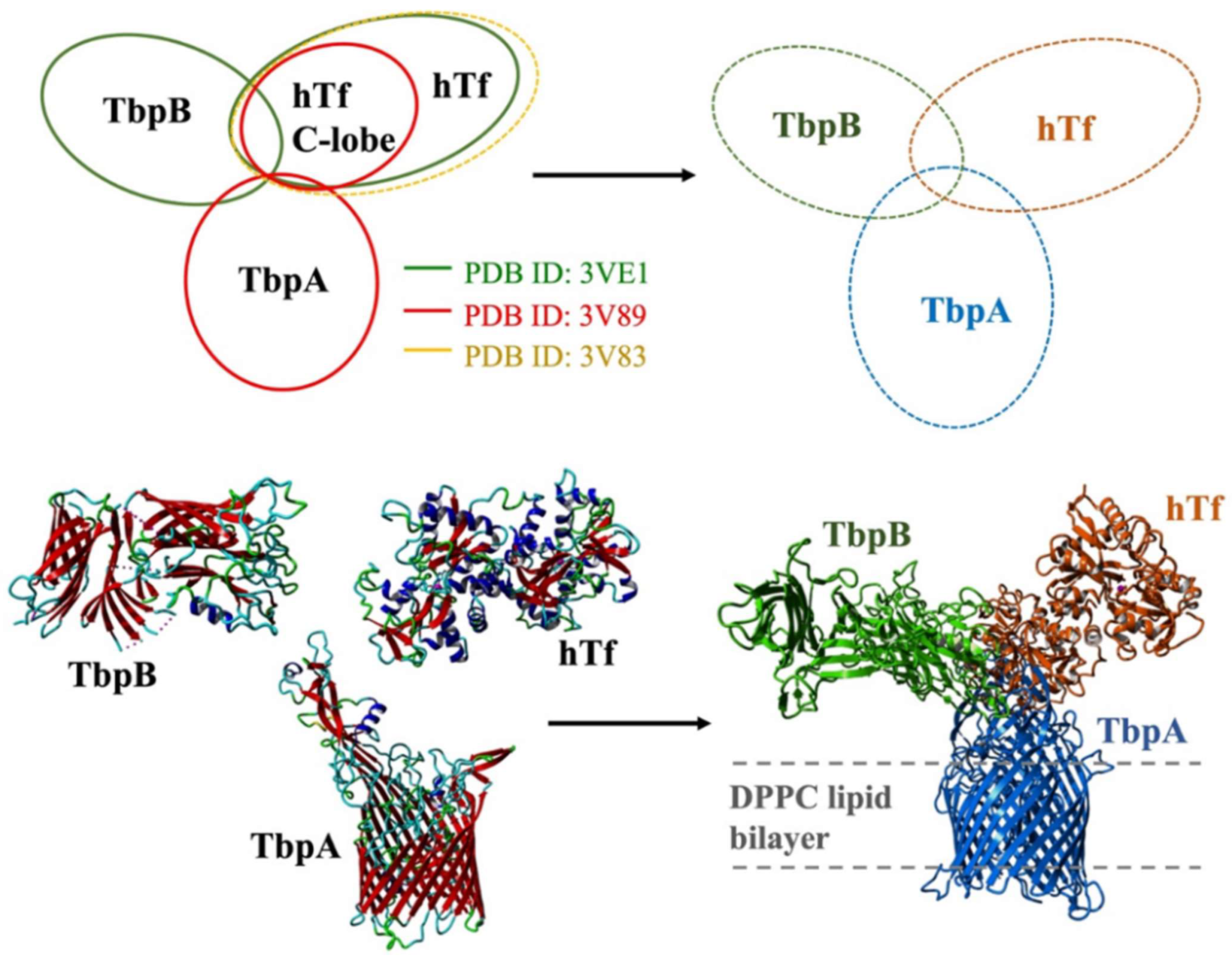
- Duran, G.N.; Ozbil, M. Structural Rearrangement of Neisseria Meningitidis Transferrin Binding Protein A (TbpA) Prior to Human Transferrin Protein (HTf) Binding. Turkish J. Chem. 2021, 45, 1146–1154. [Google Scholar] [CrossRef]
- Laskowski, R.A.; MacArthur, M.W.; Moss, D.S.; Thornton, J.M. PROCHECK: A Program to Check the Stereochemical Quality of Protein Structures. Appl. Crystallogr. 1993, 26, 283–291. [Google Scholar] [CrossRef]
- Laskowski, R.A.; Rullmann, J.A.C.; MacArthur, M.W.; Kaptein, R.; Thornton, J.M. AQUA and PROCHECK-NMR: Programs for Checking the Quality of Protein Structures Solved by NMR. J. Biomol. NMR 1996, 8, 477–486. [Google Scholar] [CrossRef]
- Wiederstein, M.; Sippl, M.J. ProSA-Web: Interactive Web Service for the Recognition of Errors in Three-Dimensional Structures of Proteins. Nucleic Acids Res. 2007, 35, W407–W410. [Google Scholar] [CrossRef]
- Sippl, M.J. Recognition of Errors in Three-dimensional Structures of Proteins. Proteins Struct. Funct. Bioinform. 1993, 17, 355–362. [Google Scholar] [CrossRef]
- Lomize, M.A.; Pogozheva, I.D.; Joo, H.; Mosberg, H.I.; Lomize, A.L. OPM Database and PPM Web Server: Resources for Positioning of Proteins in Membranes. Nucleic Acids Res. 2012, 40, D370–D376. [Google Scholar] [CrossRef] [PubMed]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-Field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Dolinsky, T.J.; Nielsen, J.E.; McCammon, J.A.; Baker, N.A. PDB2PQR: An Automated Pipeline for the Setup of Poisson–Boltzmann Electrostatics Calculations. Nucleic Acids Res. 2004, 32, W665–W667. [Google Scholar] [CrossRef]
- Nagle, J.F. Area/Lipid of Bilayers from NMR. Biophys. J. 1993, 64, 1476–1481. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Krieger, E.; Vriend, G. Models@Home: Distributed Computing in Bioinformatics Using a Screensaver Based Approach. Bioinformatics 2002, 18, 315–318. [Google Scholar] [CrossRef]
- Krieger, E.; Elmar, G.V. YASARA—Yet Another Scientific Artificial Reality Application. YASARA.Org. 2013. Available online: http://www.yasara.org (accessed on 19 November 2025).
- Schüttelkopf, A.W.; Van Aalten, D.M.F. PRODRG: A Tool for High-Throughput Crystallography of Protein-Ligand Complexes. Acta Crystallogr. Sect. D Biol. Crystallogr. 2004, 60, 1355–1363. [Google Scholar] [CrossRef]
- Li, P.; Song, L.F.; Merz, K.M. Parameterization of Highly Charged Metal Ions Using the 12-6-4 LJ-Type Nonbonded Model in Explicit Water. J. Phys. Chem. B 2015, 119, 883–895. [Google Scholar] [CrossRef]
- Benett, W.F.D.; MacCallum, J.L.; Tieleman, D.P. Thermodynamic Analysis of the Effect of Cholesterol on Dipalmitoylphosphatidylcholine Lipid Membranes. J. Am. Chem. Soc. 2009, 131, 1972–1978. [Google Scholar]
- Tieleman, D.P.; Berendsen, H.J.C. Molecular Dynamics Simulations of a Fully Hydrated Dipalmitoylphosphatidylcholine Bilayer with Different Macroscopic Boundary Conditions and Parameters. J. Chem. Phys. 1996, 105, 4871–4880. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Hirao, H.; Thellamurege, N.; Zhang, X. Applications of Density Functional Theory to Iron-Containing Molecules of Bioinorganic Interest. Front. Chem. 2014, 2, 14. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Flynn, C.M. Hydrolysis of Inorganic Iron (III) Salts. Chem. Rev. 1984, 84, 31–41. [Google Scholar] [CrossRef]
- De Abreu, H.A.; Guimaraes, L.; Duarte, H.A. Density-Functional Theory Study of Iron (III) Hydrolysis in Aqueous Solution. J. Phys. Chem. A 2006, 110, 7713–7718. [Google Scholar] [CrossRef]
- Rinaldo, D.; Field, M.J. A Density Functional Theory Study of the Iron-Binding Site of Human Serum Transferrin. Aust. J. Chem. 2004, 57, 1219–1222. [Google Scholar] [CrossRef]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins Struct. Funct. Bioinform. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, I. Computational Analysis of Hydride and Proton Transfer Steps in L-Lactate Oxidase Based on QM and QM–MM Methods. J. Mol. Struct. 2024, 1295, 136706. [Google Scholar] [CrossRef]
- Yildiz, I. Computational Insights on the Hydride and Proton Transfer Mechanisms of L-Proline Dehydrogenase. PLoS ONE 2023, 18, e0290901. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
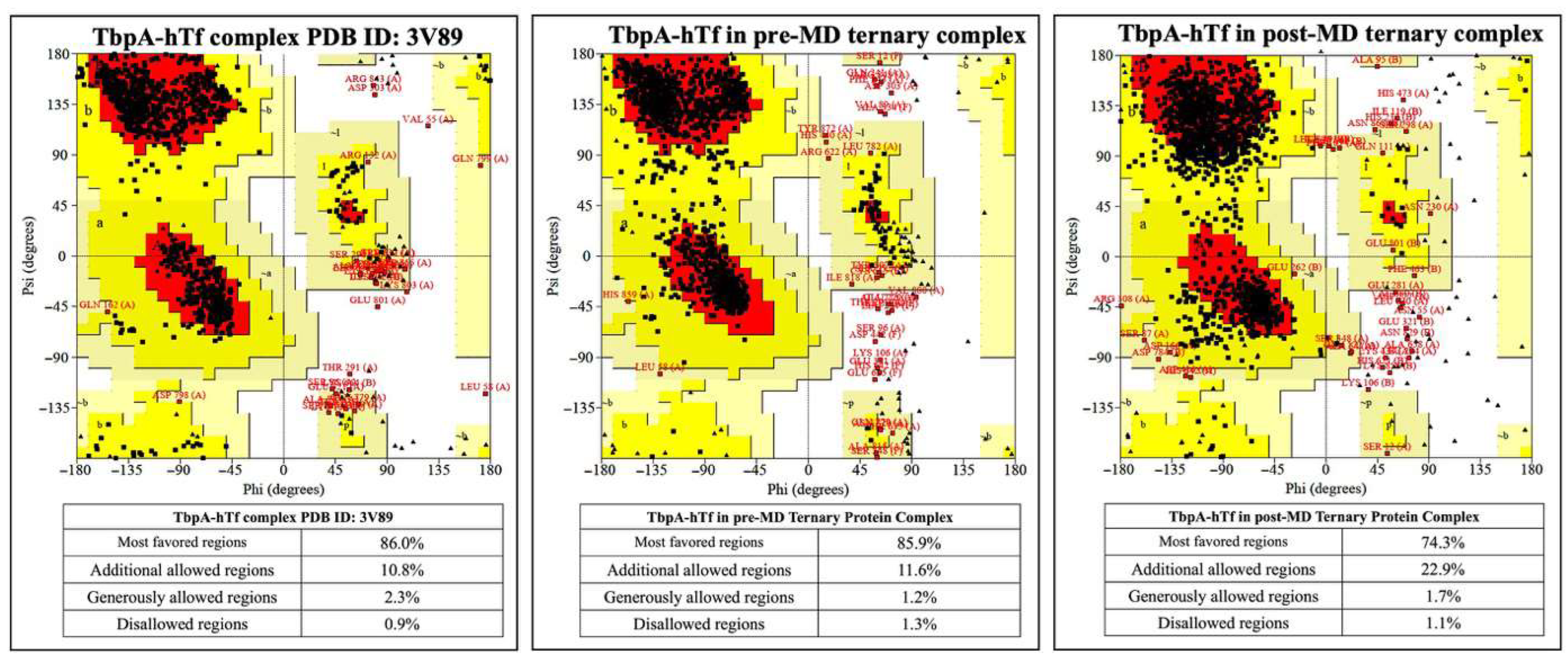
- Park, S.W.; Lee, B.H.; Song, S.H.; Kim, M.K. Revisiting the Ramachandran plot based on statistical analysis of static and dynamic characteristics of protein structures. J. Struct. Biol. 2023, 215, 107939. [Google Scholar]
- Tina, K.G.; Bhadra, R.; Srinivasan, N. PIC: Protein Interactions Calculator. Nucleic Acids Res. 2007, 35, W473–W476. [Google Scholar] [CrossRef]
- Aisen, P.; Leibman, A.; Zweier, J. Stoichiometric and Site Characteristics of the Binding of Iron to Human Transferrin. J. Biol. Chem. 1978, 253, 1930–1937. [Google Scholar] [CrossRef]
- Sun, H.; Li, H.; Sadler, P.J. Transferrin as a Metal Ion Mediator. Chem. Rev. 1999, 99, 2817–2842. [Google Scholar] [CrossRef]
- Schmidt, C.L.A.; Kirk, P.L.; Appleman, W.K. The Apparent Dissociation Constants of Arginine and of Lysine and the Apparent Heats of Ionization of Certain Amino Acids. J. Biol. Chem. 1930, 88, 285–293. [Google Scholar] [CrossRef]
- Findik, V.; Ruiz-López, M.F.; Erdem, S.S. Mechanistic Insights into Lysine-Targeting Covalent Inhibition through a Theoretical Study of Ester Aminolysis. Org. Biomol. Chem. 2021, 19, 9996–10004. [Google Scholar] [CrossRef]

| Protein Complexes | E Holo Form (au) | E Apo Form (au) | ΔE (kcal/mol) | ΔΔE (kcal/mol) |
|---|---|---|---|---|
| hTf | −5086.08907265 | −3821.63039623 | −847 | −171 |
| TbpA-TbpB-hTf | −5508.10670216 | −4243.92058120 | −676 | 0 |
| Lys359Ala Mutant | −5334.28966013 | −4069.95055417 | −772 | −96 |
| Lys359Arg Mutant | −5617.57403448 | −4353.43533450 | −646 | 30 |
| Lys359Asp Mutant | −5522.08640848 | −4257.68692916 | −810 | −134 |
| Donor → Acceptor | hTF | TbpA-TbpB-hTf | Lys359Ala | Lys359Arg | Lys359Asp |
|---|---|---|---|---|---|
| LP (Asp392-O)→LP*Fe | 48.23 | 46.22 | 46.10 | 42.34 | 46.45 |
| LP (Tyr426-O)→LP*Fe | 49.93 | 45.94 | 39.90 | 44.48 | 40.41 |
| LP (Tyr517-O)→LP*Fe | 44.55 | 12.45 | 39.22 | 13.52 | 39.85 |
| LP (His585-N)→LP*Fe | 41.32 | 37.10 | 32.64 | 39.73 | 33.59 |
| LP (CO32−-O1)→LP*Fe | 47.04 | 44.31 | 44.45 | 43.61 | 43.89 |
| LP (CO32−-O2)→LP*Fe | 44.92 | 48.07 | 45.66 | 44.07 | 46.87 |
| total E(2) | 275.99 | 234.09 | 247.97 | 227.75 | 251.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dervişoğlu Özdemir, C.; Duran, G.N.; Fındık, V.; Özbil, M.; Sağ Erdem, S. Computational Insights into Iron Coordination Disruption in the Human Transferrin–Neisseria meningitidis Bacterial Protein Complex. Inorganics 2025, 13, 384. https://doi.org/10.3390/inorganics13120384
Dervişoğlu Özdemir C, Duran GN, Fındık V, Özbil M, Sağ Erdem S. Computational Insights into Iron Coordination Disruption in the Human Transferrin–Neisseria meningitidis Bacterial Protein Complex. Inorganics. 2025; 13(12):384. https://doi.org/10.3390/inorganics13120384
Chicago/Turabian StyleDervişoğlu Özdemir, Celile, Gizem Nur Duran, Volkan Fındık, Mehmet Özbil, and Safiye Sağ Erdem. 2025. "Computational Insights into Iron Coordination Disruption in the Human Transferrin–Neisseria meningitidis Bacterial Protein Complex" Inorganics 13, no. 12: 384. https://doi.org/10.3390/inorganics13120384
APA StyleDervişoğlu Özdemir, C., Duran, G. N., Fındık, V., Özbil, M., & Sağ Erdem, S. (2025). Computational Insights into Iron Coordination Disruption in the Human Transferrin–Neisseria meningitidis Bacterial Protein Complex. Inorganics, 13(12), 384. https://doi.org/10.3390/inorganics13120384







