Accessible Thermoelectric Characterization: Development and Validation of Two Modular Room Temperature Measurement Instruments
Abstract
1. Introduction
2. Materials and Methods
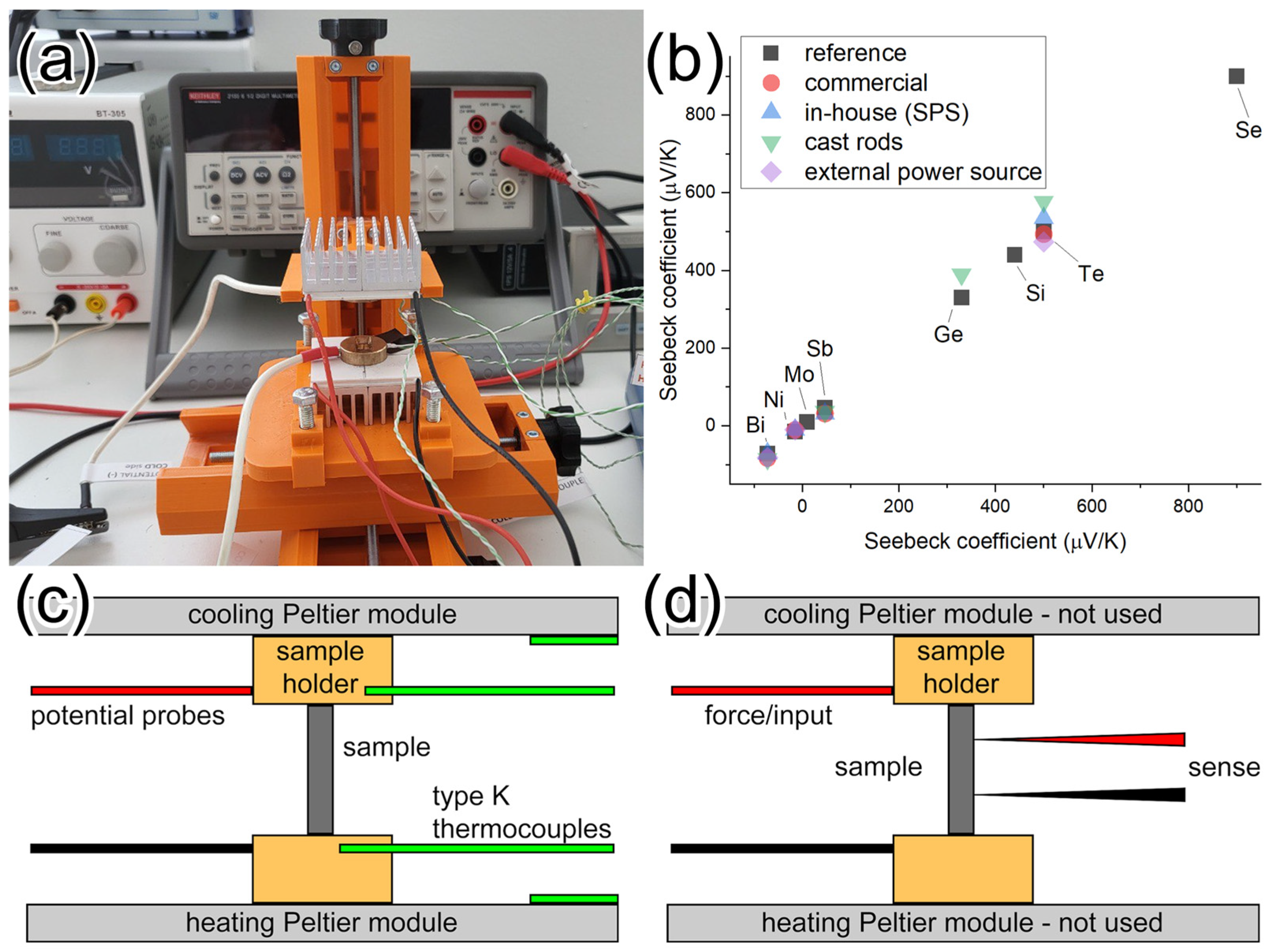
2.1. Instrument THEMA
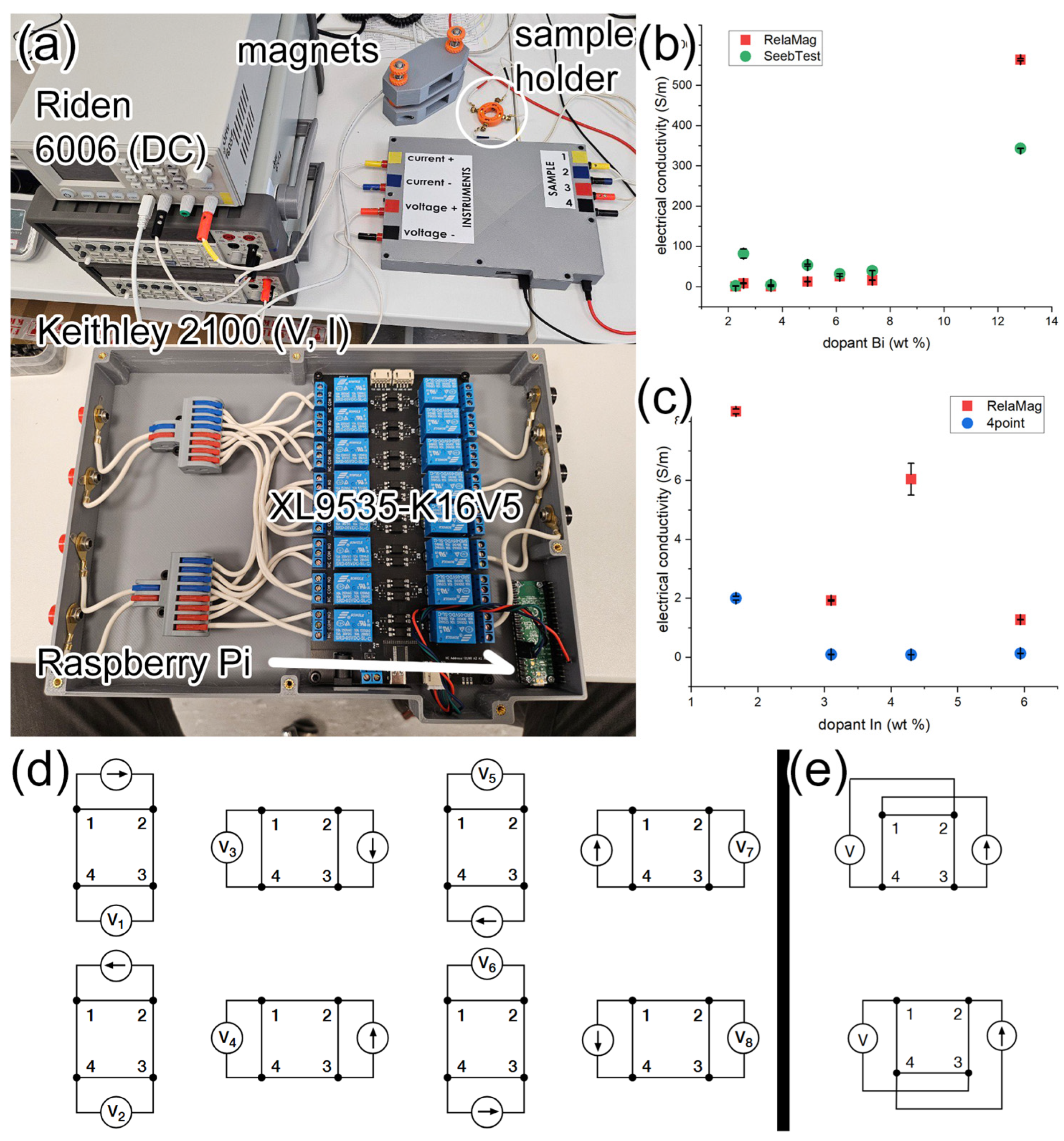
2.2. Instrument RelaMag
3. Results and Discussion
3.1. Instrument for Seebeck Coefficient THEMA
3.2. Instrument for Electrical Conductivity RelaMag
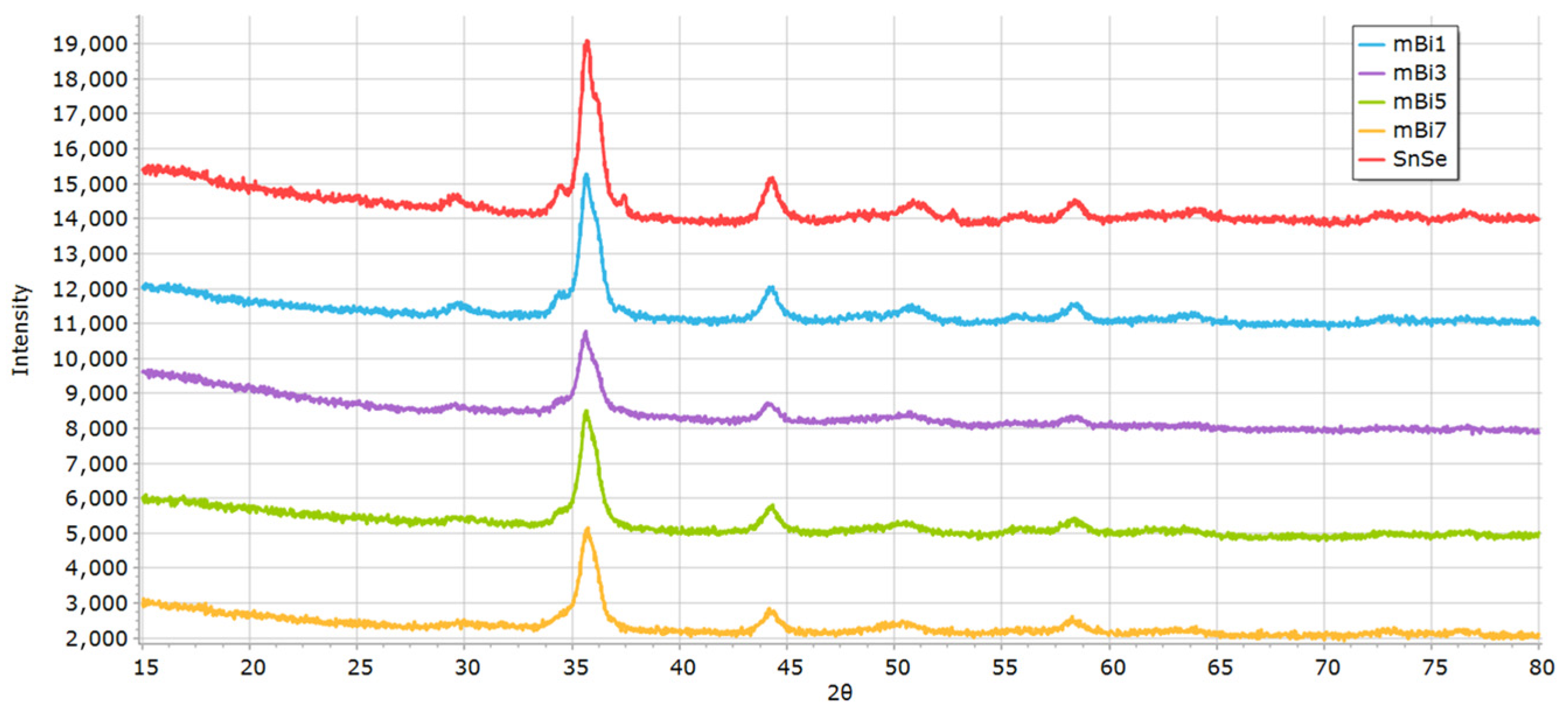
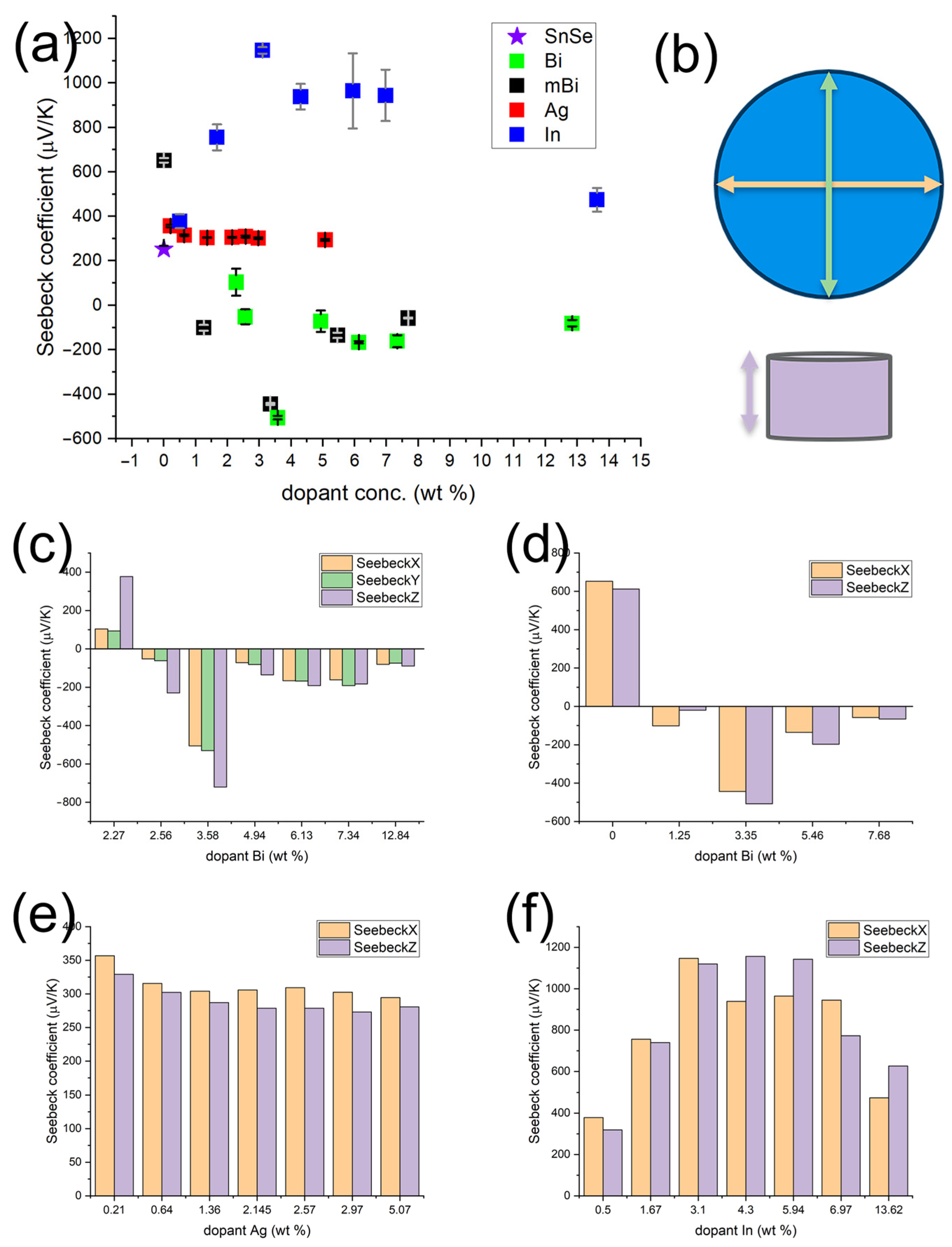
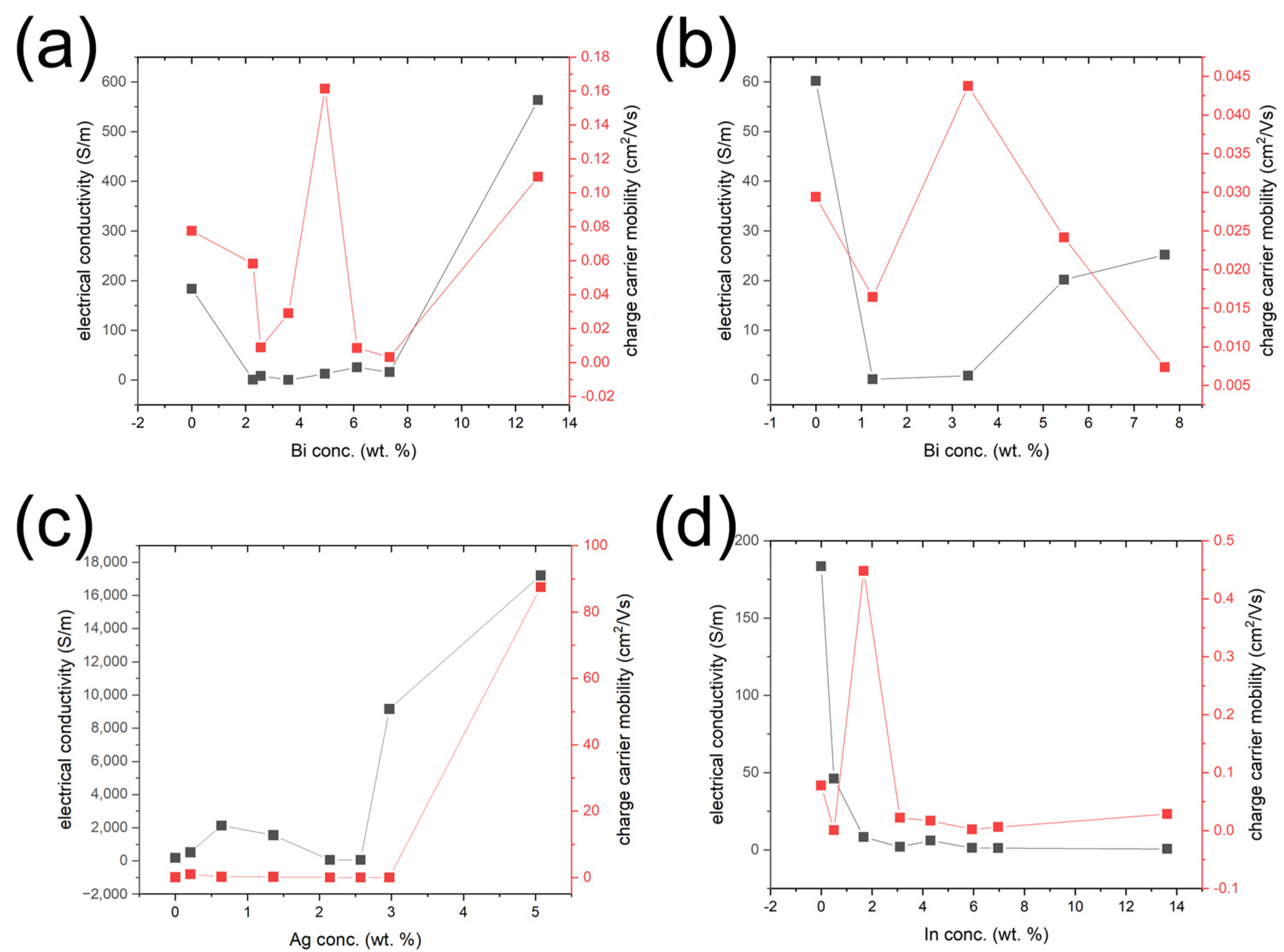
3.3. Polycrystalline-Doped SnSe Thermoelectric Properties at Room Temperature
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Narjis, A.; Elyaagoubi, M.; Outzourhit, A.; Nkhaili, L. Design of a Simple Apparatus for the Measurement of the Seebeck Coefficient. Measurement 2019, 133, 433–438. [Google Scholar] [CrossRef]
- Xiong, R.; Masoumi, S.; Pakdel, A. An Automatic Apparatus for Simultaneous Measurement of Seebeck Coefficient and Electrical Resistivity. Energies 2023, 16, 6319. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, D.; Li, L.; Li, F.; Li, J.-F. Fast Seebeck Coefficient Measurement Based on Dynamic Method. Rev. Sci. Instrum. 2014, 85, 054904. [Google Scholar] [CrossRef]
- Haupt, S.; Edler, F.; Bartel, M.; Pernau, H.-F. Van Der Pauw Device Used to Investigate the Thermoelectric Power Factor. Rev. Sci. Instrum. 2020, 91, 115102. [Google Scholar] [CrossRef]
- Candolfi, C.; El Oualid, S.; Lenoir, B.; Caillat, T. Progress and Perspectives in Thermoelectric Generators for Waste-Heat Recovery and Space Applications. J. Appl. Phys. 2023, 134, 100901. [Google Scholar] [CrossRef]
- Von Lukowicz, M.; Abbe, E.; Schmiel, T.; Tajmar, M. Thermoelectric Generators on Satellites—An Approach for Waste Heat Recovery in Space. Energies 2016, 9, 541. [Google Scholar] [CrossRef]
- Ganesan, P.; Gantepogu, C.S.; Duraisamy, S.; Meledath Valiyaveettil, S.; Tsai, W.-H.; Hsing, C.-R.; Lin, K.-H.; Chen, K.-H.; Chen, Y.-Y.; Wu, M.-K. Carrier Optimization and Reduced Thermal Conductivity Leading to Enhanced Thermoelectric Performance in (Mg, S) Co-Doped AgSbTe2. Mater. Today Phys. 2024, 42, 101358. [Google Scholar] [CrossRef]
- He, Q.; Yang, D.; Xia, S.; Song, H. Ultra-Low Thermal Conductivity and Improved Thermoelectric Performance in La2O3-Dispersed Bi2Sr2Co2Oy Ceramics. Mater. Sci. Eng. B 2024, 299, 116976. [Google Scholar] [CrossRef]
- Cai, Z.; Zheng, K.; Ma, C.; Fang, Y.; Ma, Y.; Deng, Q.; Li, H. Ultra-Low Thermal Conductivity and Improved Thermoelectric Performance in Tungsten-Doped GeTe. Nanomaterials 2024, 14, 722. [Google Scholar] [CrossRef]
- Chatterjee, A.; El Sachat, A.; Banik, A.; Biswas, K.; Castro-Alvarez, A.; Sotomayor Torres, C.M.; Santiso, J.; Chávez-Ángel, E. Improved High Temperature Thermoelectric Properties in Misfit Ca3Co4O9 by Thermal Annealing. Energies 2023, 16, 5162. [Google Scholar] [CrossRef]
- Parzer, M.; Kositz, A.; Süß, J.; Garmroudi, F.; Mori, T.; Bauer, E. Enhanced Thermopower by Double-Site Substitution of Ti in Fe2(VAl)1-xTi2x. Mater. Today Phys. 2025, 54, 101712. [Google Scholar] [CrossRef]
- Mulla, R.; Rabinal, M.K. A Low-Cost Apparatus to Measure the Seebeck Coefficient. Phys. Educ. 2021, 56, 015006. [Google Scholar] [CrossRef]
- Mishra, A.; Bhattacharjee, S.; Anwar, S. Simple Apparatus to Measure Seebeck Coefficient up to 900K. Measurement 2015, 68, 295–301. [Google Scholar] [CrossRef]
- Karpov, A.V.; Sytschev, A.E.; Sivakova, A.O. Device for Measurement the Seebeck Coefficient of Thermoelectric Materials in the Temperature Range 300–800 K. Meas. Tech. 2023, 66, 628–635. [Google Scholar] [CrossRef]
- Tarachand; Saxena, M.; Mukherjee, B.; Okram, G.S. A Load-Based Thermopower Measurement Setup in the Temperature Range of 5–330 K. Rev. Sci. Instrum. 2019, 90, 063904. [Google Scholar] [CrossRef]
- de Boor, J.; Zabrocki, K.; Frohring, J.; Müller, E. Electrical Conductivity Measurements on Disk-Shaped Samples. Rev. Sci. Instrum. 2014, 85, 075104. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, F.S.; Cipriano, R.B.; Da Silva, F.T.; Romão, E.C.; Dos Santos, C.A.M. Simple Analytical Method for Determining Electrical Resistivity and Sheet Resistance Using the van Der Pauw Procedure. Sci. Rep. 2020, 10, 16379. [Google Scholar] [CrossRef]
- Pandey, S.K.; Manivannan, A. A Fully Automated Temperature-Dependent Resistance Measurement Setup Using van Der Pauw Method. Rev. Sci. Instrum. 2018, 89, 033906. [Google Scholar] [CrossRef]
- Rietveld, G.; Koijmans, C.V.; Henderson, L.C.A.; Hall, M.J.; Harmon, S.; Warnecke, P.; Schumacher, B. DC Conductivity Measurements in the van Der Pauw Geometry. IEEE Trans. Instrum. Meas. 2003, 52, 449–453. [Google Scholar] [CrossRef]
- Melios, C.; Huang, N.; Callegaro, L.; Centeno, A.; Cultrera, A.; Cordon, A.; Panchal, V.; Arnedo, I.; Redo-Sanchez, A.; Etayo, D.; et al. Towards Standardisation of Contact and Contactless Electrical Measurements of CVD Graphene at the Macro-, Micro- and Nano-Scale. Sci. Rep. 2020, 10, 3223. [Google Scholar] [CrossRef]
- Mihok, F.; Hricková, G.; Puchý, V.; Szabó, J.; Ballóková, B.; Džunda, R.; Saksl, K. Effect of Multiple Doping Elements on Polarity Switching of Polycrystalline SnSe Semiconductor. Inorganics 2024, 12, 103. [Google Scholar] [CrossRef]
- Snyder, G.J. Complex Thermoelectric Materials. In Proceedings of the 40th International Conference on Thermoelectrics, Krakow, Poland, 30 June–4 July 2024; Available online: https://thermoelectrics.matsci.northwestern.edu/publications/ICTComplexTE-2024.pdf (accessed on 1 October 2025).
- Lindemuth, J. Hall Effect Measurement Handbook: A Fundamental Tool for Semiconductor Material Characterization; Lake Shore Cryotronics, Inc.: Westerville, OH, USA, 2020; ISBN 978-1-7347078-0-9. [Google Scholar]
- Tektronix, Van Der Pauw and Hall Voltage Measurements with the 4200A-SCS Parameter Analyzer. Available online: https://download.tek.com/document/1KW-60641-0_vanderPauw_4200A-SCS_AN.pdf (accessed on 1 October 2025).
- Yamamoto, C.; He, X.; Katase, T.; Ide, K.; Goto, Y.; Mizuguchi, Y.; Samizo, A.; Minohara, M.; Ueda, S.; Hiramatsu, H.; et al. Double Charge Polarity Switching in Sb-Doped SnSe with Switchable Substitution Sites. Adv. Funct. Mater. 2021, 31, 2008092. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihok, F.; Gáborová, K.; Puchý, V.; Saksl, K. Accessible Thermoelectric Characterization: Development and Validation of Two Modular Room Temperature Measurement Instruments. Inorganics 2025, 13, 333. https://doi.org/10.3390/inorganics13100333
Mihok F, Gáborová K, Puchý V, Saksl K. Accessible Thermoelectric Characterization: Development and Validation of Two Modular Room Temperature Measurement Instruments. Inorganics. 2025; 13(10):333. https://doi.org/10.3390/inorganics13100333
Chicago/Turabian StyleMihok, František, Katarína Gáborová, Viktor Puchý, and Karel Saksl. 2025. "Accessible Thermoelectric Characterization: Development and Validation of Two Modular Room Temperature Measurement Instruments" Inorganics 13, no. 10: 333. https://doi.org/10.3390/inorganics13100333
APA StyleMihok, F., Gáborová, K., Puchý, V., & Saksl, K. (2025). Accessible Thermoelectric Characterization: Development and Validation of Two Modular Room Temperature Measurement Instruments. Inorganics, 13(10), 333. https://doi.org/10.3390/inorganics13100333





