Thermoelectric Materials for Spintronics: From Physical Principles to Innovative Half Metallic Ferromagnets, Devices, and Future Perspectives

Abstract

Over the last century, improvements in computational power resulting from the exponential growth of microelectronics have been the driving force of outstanding global economic growth as well as of deep changes in society and ethical values. Manufacturing of silicon-based memory cells has, as a matter of fact, become an industry of strategic importance also from a geopolitical perspective. Despite such advancements, a lot of concern has recently aroused as physical limitations such as tunnel-effect phenomena, current leakage, and high power consumption are increasingly hindering further improvements in dynamic random-access memory. Spintronic technologies are promising alternatives to overcome such issues, being considered no longer merely an academic subject of interest, but increasingly becoming an industrial reality. In this review work, the history and the physical principles of spintronic devices are presented, focussing on new, groundbreaking materials. Concepts are exposed step by step and in an easy-to-understand manner, allowing even researchers who are not specialized in the fields of spintronics, microelectronics, and hardware engineering to understand the fundamentals and gain initial insight into the topic. Special attention is paid to half-metallic ferromagnets and Heusler alloys, which are considered among the most promising materials for the future of spintronics.

1. Introduction

Numerous epistemologists, philosophers of science, and historians acknowledge that the pace of scientific and technological advancement over the past 150 years has exceeded that of all prior human history [1,2,3,4,5].

Advancements in aeronautics are frequently cited to contextualize the statement. Following the construction of the first airplane in 1903, it required only 58 years to achieve the first human spaceflight and merely 66 years to accomplish the first successful lunar landing. Atomic energy provides another illustrative example: while Rutherford and Bohr proposed the first quantitatively reliable atomic model in 1913, the first nuclear reactor was realized just 29 years later, in 1942. Today, fourth-generation nuclear reactors are projected to enter commercial operation as early as 2030. Perhaps the most striking case of exponential technological development in the last century, however, is represented by progress in electronics and computer science. Although it has limitations, Moore’s law—stating that the number of transistors within integrated circuits doubles approximately every two years—is widely used as a straightforward reference for the extraordinary growth of microelectronics since the 1970s.

The exponential increase in computational capability has not only powered exceptional global economic expansion throughout the twentieth century but has also driven profound societal and ethical transformations. Industry has been reshaped by this surge in computing power: automation and production efficiency have risen sharply, enabling manufacturing at unprecedented rates. Computers, once cumbersome and prohibitively expensive machines accessible to only a few, have become essential personal tools worldwide. Smartphones, as the evolutionary successors of early mobile phones, now function as powerful pocket-sized computers that deliver unparalleled access to information, services, and entertainment. Parallel to hardware development, the Internet has revolutionized communication, work, and leisure, connecting the world more tightly than ever before.

At present, silicon-based logic devices constitute a strategically vital industry from a geopolitical standpoint, making continued transistor-based integrated circuit improvements fundamental to both economic and political stability. Nevertheless, growing concerns have emerged as physical constraints—including tunnelling effects, current leakage, and overheating—are increasingly obstructing further transistor miniaturization. In particular, the challenge of controlling current flow near the gate electrode intensifies at the nanoscale. Multi-gate MOSFET architectures, such as FinFETs and GAAFETs, have alleviated some of these difficulties; however, issues such as significant source-to-drain leakage currents and restrictions in gate metals and channel materials persist as device dimensions shrink further. Indeed, microprocessor designers have reported a slowdown in semiconductor scaling since around 2010, reducing the cadence of predicted improvements from two years to approximately two and a half. Intel Corporation, one of the world’s leading semiconductor manufacturers by revenue, publicly stated in 2016 that performance gains in MOSFET devices had begun to decelerate with the introduction of the 22 nm technology node [6]. It should be emphasized that, since 1997, process node designations have been driven primarily by marketing considerations rather than by actual physical dimensions such as gate length, gate pitch, or metal pitch. In reality, according to the IRDS (International Roadmap for Devices and Systems), the contacted gate pitch for 5 nm generation chips—commercially introduced in 2020—measures 51 nm. For the 3 nm technology, first released in 2022, a typical gate pitch of 48 nm is reported, while the forthcoming 2.1 nm generation, expected to enter production between 2024 and 2025, is projected to feature a gate pitch of 45 nm [7].

At the current pace of advancement, the scaling of integrated circuits is expected to reach its endpoint within approximately a decade, as transistor metal pitches will by then approach the resolution threshold of extreme-ultraviolet lithography (EUVL). In 2020, Dr. Paolo Gargini—chairman of the IRDS and former leader of Intel’s first submicron process development team in 1985—projected that lithographic limits would be attained by 2029, indicating that beyond this point, the only viable strategy to further increase transistor density would involve node stacking [8]. To address these limitations, intensive research on novel materials has taken centre stage. Alternative semiconductors such as InGaAs are considered highly promising candidates to replace doped silicon in high-speed, low-power logic devices. Quantum well and tunnel field-effect transistors based on III–V compound semiconductors are likewise attracting significant attention as substitutes for conventional MOSFETs. Graphene, particularly in the form of nanoribbons, has also been investigated, although its application remains largely prospective. More ambitious directions focus on approaches that do not rely solely on physical downscaling or material substitution. Among these, spin-based logic and memory technologies have been extensively explored at the laboratory level and, more recently, have begun to emerge as industrially viable solutions.

This review is structured as follows: Section 2 outlines the fundamentals of random-access memory, clarifying its function, purpose, and historical development. Section 3 examines these concepts within the context of magnetic random-access memory, detailing its various architectures and operating principles. Section 4 provides an overview of state-of-the-art and emerging materials for spintronic applications. Section 5 focusses on Heusler alloys, highlighting their unique properties and their potential for integration into next-generation, high-performance spintronic devices. Finally, Section 6 presents concluding remarks and future perspectives.

2. Random-Access Memory

The earliest form of electronic random-access memory (RAM) was introduced in 1947 with the development of the Williams–Kilburn tube [9]. The operating principle of the Williams–Kilburn tube was relatively straightforward. A grid of luminous spots was displayed on a cathode-ray tube, leading to the accumulation of electric charge at each position. A thin metallic plate placed in front of the screen enabled the reading of this information, allowing the system to determine whether a binary ‘0’ or ‘1’ was stored at each location. Because the luminescence of the spots decayed over time, periodic refreshing of the grid was required. This refresh was carried out by external circuitry using essentially the same procedure as the initial writing process. The introduction of this device marked a turning point in computing, as the speed of electronic memory finally matched that of the electronic components within calculators, greatly surpassing the performance of earlier mechanical or acoustic-based storage technologies. The Williams–Kilburn tube remained an essential component of calculators until the mid-1960s, when it was replaced by more advanced magnetic-core memory devices.

Although now obsolete, the operating mechanisms of the Williams–Kilburn tube share remarkable similarities with those of modern semiconductor-based DRAMs and can be used to illustrate the fundamental principles of random-access memory. By contrast, direct-access memory devices, such as magnetic tapes, hard disks, CD-RWs, and DVD-RWs, rely on sequential reading or writing, where access time strongly depends on the physical location of the data within the medium and is limited by mechanical constraints such as rotation speed or arm movement. In random-access memory, however, any storage location can be read or written in essentially the same time, independent of its position within the device. In the Williams–Kilburn tube, for instance, all spots on the fluorescent screen could be accessed simultaneously, as electron beams from the cathode collided with the screen uniformly.

Despite both serving as data storage, direct-access memory and RAM fulfil different roles in computing. Direct-access devices are typically used for long-term information storage, whereas RAM functions as temporary memory, providing working space for operating systems and applications. Program data are loaded into RAM for execution by the CPU and deleted after use unless explicitly saved to a long-term storage device.

Modern RAM is built upon memory cells, the fundamental storage units of computer memory. Each cell stores a single bit of binary information: a logic ‘1’ corresponds to a high-voltage state, while a logic ‘0’ corresponds to a low-voltage state. Dynamic RAM (DRAM) architectures commonly employ memory cells composed of a single transistor and one capacitor where charge is stored. Because this charge gradually dissipates, the cells require periodic refresh cycles through current injection. While different RAM architectures exist, each with specific advantages and drawbacks, DRAM remains the most widely used due to its high storage density and relatively low cost per unit, despite its higher power consumption. Memory cells are typically organized in arrays, accessible via address lines and supported by multiplexing/demultiplexing circuits, enabling the storage and retrieval of multiple bits through parallel data lines. This architecture gives rise to designations such as “8-bit” or “16-bit” RAM.

For memory cells to function effectively, they must reliably perform several basic operations:

• Writing: This involves setting or modifying the value (1 or 0) stored in a cell. In Williams–Kilburn tubes, this was achieved by altering the direction of electron beams within the cathode-ray tube. In modern DRAM cells, writing is performed by manipulating the transistor integrated into the cell.
• Reading: This operation determines the value of a cell without modifying it. In DRAMs, reading is inherently destructive, as it removes the charge from all memory cells in the addressed row. To address this, specialized circuits called sense amplifiers—one per memory column—temporarily store the read data and immediately rewrite it back into the cells.
• Refreshing: This process periodically reads and rewrites the stored information in the same location to maintain data integrity. Because the charge in DRAM capacitors gradually leaks over time, refreshing is necessary to prevent data loss.

While writing and reading are essential for all computer memory devices, refreshing is specific to dynamic (volatile) memory such as DRAM. These memory devices require a constant power supply to retain information, which is lost when power is removed. In contrast, static (non-volatile) RAM (SRAM) architectures do not require periodic refreshing and can retain data for extended periods. Historically, SRAMs were prevalent between the mid-1960s and mid-1980s, even though today they are more commonly associated with certain direct-access storage technologies such as hard disks, flash drives, and magnetic tapes. SRAM cells, typically composed of six transistors, consume less power since no refresh is needed; however, their architecture is more complex and less scalable than DRAM cells. Additionally, elevated temperatures exacerbate current leakage in SRAMs, contributing to the adoption of DRAM as the industrial standard in computing from the mid-1980s onward.

3. Working Principles of MRAMs

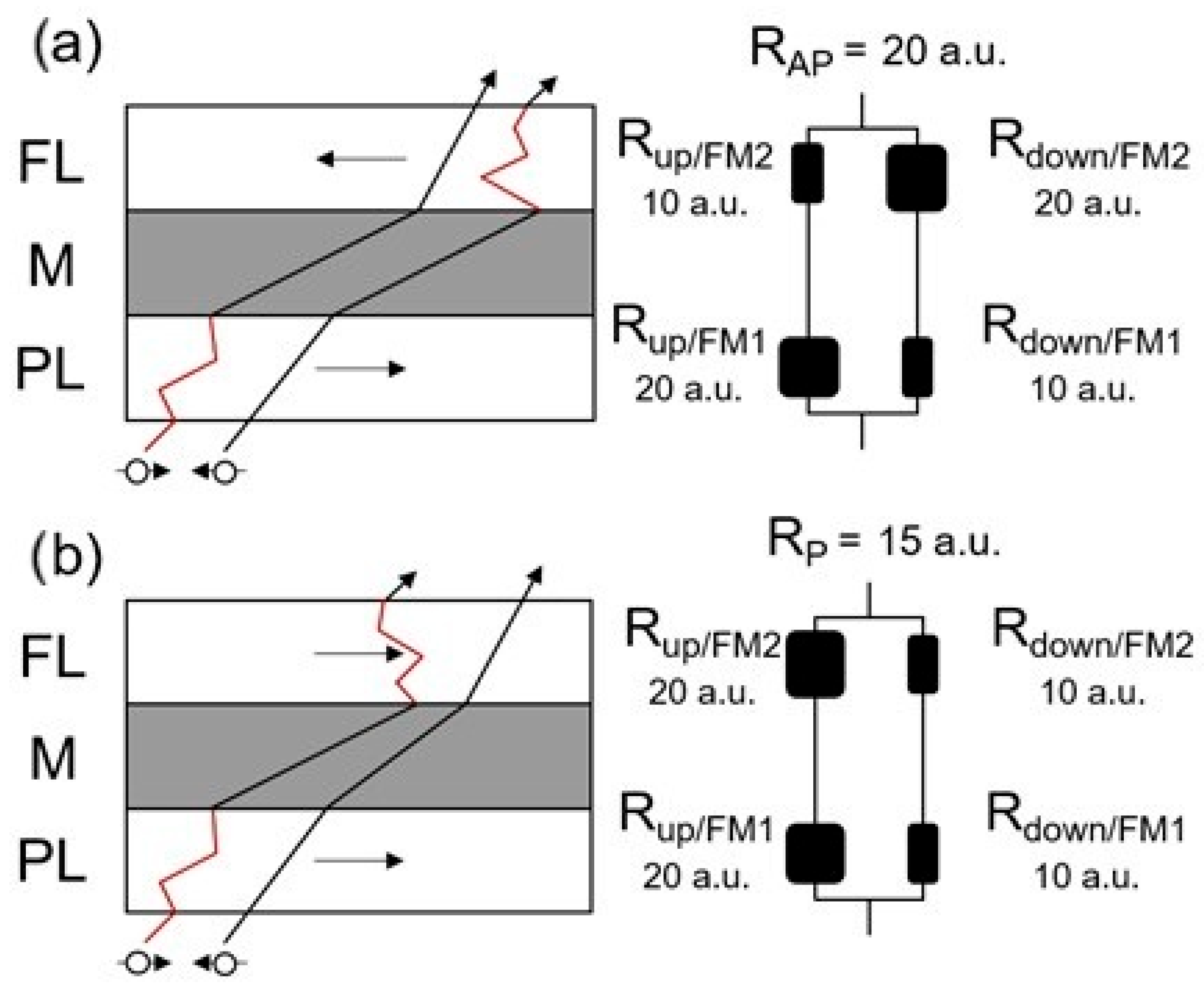
The typical configuration of an MRAM memory cell consists of a transistor and a magnetoresistive element, quite similar to a DRAM cell, which contains a transistor and a capacitor. A transistor is needed in the MRAM cell to provide the current needed for the writing operation and to amplify the voltage difference between the 1 and 0 state. If, in a classic DRAM cell, the information is stored as electric charge inside the capacitor, in an MRAM it is the resulting resistance of the magnetoresistive element which determines the value of the cell [10]. The first example of a magnetoresistive element, which is the component that fundamentally stores binary digits, typically consisted of a spin-valve [11]. This is a layered structure which relies on the physical phenomenon of giant magnetoresistance to store the information, as shown in Figure 1.

Giant magnetoresistance (GMR) occurs in systems composed of two ferromagnetic layers separated by a non-magnetic metal. When an electrical current flows across such a structure, the total resistance depends on the mutual magnetization orientation of the two ferromagnetic elements: this will be lower if the two magnetic moments are parallel or higher if they are antiparallel. This happens because the two different spin states of electrons (up and down) are scattered differently when they flow inside ferromagnets, as the density of states of such materials is non-identical for their majority- and minority-spin sub-bands. The resistance difference at the end of the junction makes the reading process possible in spin-valves, as a binary 1 (low resistance, hence high voltage) is associated with the parallel, and a binary 0 (high resistance, hence low voltage) with the antiparallel configurations, respectively. A similar effect, namely, tunnel magnetoresistance (TMR), occurs when an insulator is used as a separation film instead of a conductive metal. Early models of magnetic memory cells based on the GMR effect were rapidly abandoned in favour of TMR-based devices, or magnetic-tunnel junctions (MTJs), as they were affected by poor reading signal. Representative orders of magnitude of MTJs are of a few nanometres, as a thicker insulator layer would make the tunnelling of electrons between the two ferromagnets impossible. Contrary to spin-valves, resistance differences typical of MTJs are sufficient to produce the voltage swing required for applications in integrated circuits, thus, their widespread use to the detriment of GMR-based cells [11].

As already discussed previously, a memory device should be able to perform three main operations: reading, writing, and storing binary digits. In MRAMs, these tasks are fulfilled as follows:

• The reading operation is performed by sensing the resistance of the MTJ. This is accomplished by flowing an electric current through the layered system and evaluating the final voltage at the end of the circuit to distinguish between 0 and 1 states.
• The writing operation is carried out by changing the orientation of one layer of the junction (called the free layer). This has been historically performed in various ways; however, current state-of-the-art MRAMs’ writing operations are based on the spin-torque transfer effect.
• The storage of information relies on the magnetic anisotropy of the free layer which retains the “written” magnetization over time. In MTJs, the magnetization of the pinned layer (PL) is fixed, while that of the free layer (FL) can vary to store binary 0 and 1 digits. To switch the orientation of magnetization, an energy barrier must be overcome. Since the magnetization of the PL must never be changed, materials with intrinsically high magnetization-switch activation energy are used, whereas, for the FL, materials with non-negligible magnetic anisotropy are selected. Magnetic anisotropy should be sufficiently high to store the value of the memory cell, typically for 10 years. The energy barrier (E_B) for the switching of the free layer is proportional to K_uV (with K_u the magnetic anisotropy constant and V the volume of FL). Thus, K_u must be tuned to be sufficiently higher than the thermal energy k_BT (60 times is considered the standard to achieve an information retention of approximately 10 years) and sufficiently small to allow the writing process to occur without errors. From an engineering point of view, MTJs are classified based on the storage mechanism: junctions in which the magnetization of the ferromagnetic layers is parallel to the film plane are called in-plane MTJs, while perpendicular MTJs have the magnetization perpendicular to the film surface [11].

3.1. Reading Mechanisms: GMR and TMR

From an engineering perspective, a minimum voltage difference of 0.2 V between the low- and high-resistance states is required to read the value of a memory cell correctly and reliably. As already mentioned, in MRAMs, magnetoresistance (MR) is responsible for such difference, thus being the physical principle of their reading mechanism.

The MR effect was first discovered in 1856 by Thomson [12] when the electrical resistance of various metals was measured to be different depending on the orientation of a magnetic field. This was later found to be caused by spin-orbit effects; in fact, the scattering of electrons travelling along the lattice is different as the medium electronic density is slightly deformed by the change in magnetization orientation. Because this effect is intrinsically anisotropic (as are most of the crystalline structure-dependent properties), it was called anisotropic magnetoresistance (AMR). Compounds showing high AMR effects, like NiFe Permalloy, were used in earlier generations of hard disks [13].

In the late 1980s, surprisingly high values of magnetoresistance were independently measured by Fert and Grünberg in layered systems. The discovery of this giant-magnetoresistance effect won them the Nobel prize in physics in 2007, as the application of GMR in digital memory devices revolutionized hard disks and data-storage technologies [14]. 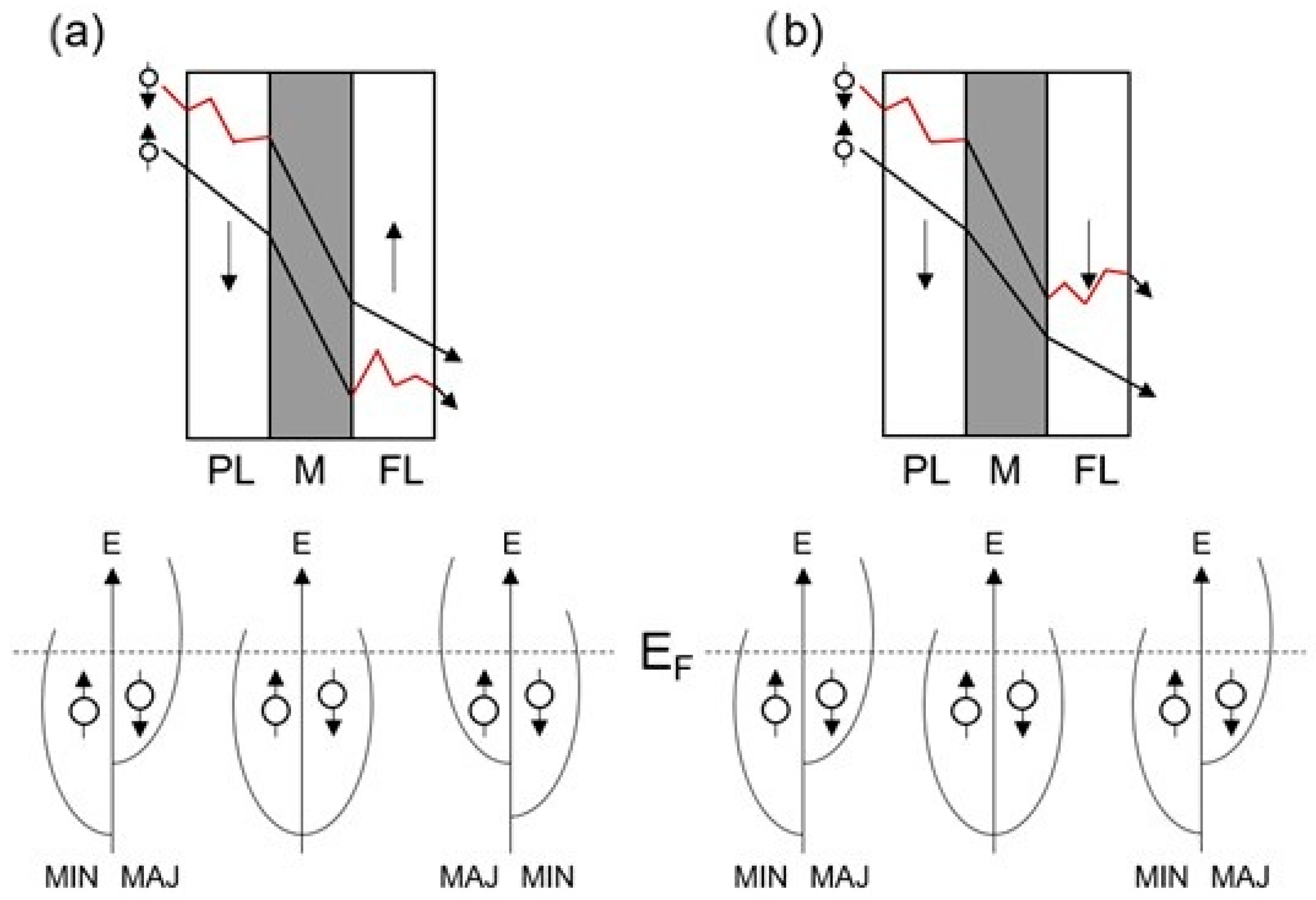The GMR effect is ultimately the result of spin-dependent electron scattering phenomena inside ferromagnetic materials, as schematically depicted in Figure 2.

In ferromagnetic materials, the total magnetic moment is antiparallel to the direction of total spin at the Fermi level (E_F), and the magnitude of electron scattering depends on the filling of the band responsible for the magnetic moment. In non-magnetic materials (NM in Figure 2), both the minority- and majority-spin sub-bands of the density of states are shaped and filled equally, meaning that +1/2 and −1/2 electrons will be evenly scattered. Contrariwise, in FM mediums, the DOS is different for the two spin states. Since the majority spin is conducted in the majority sub-band and minority spin in the minority sub-bands, they will undergo different amounts of scattering. In particular, majority spin electrons will come across a larger magnitude, as the majority sub-band is more filled than the minority. Considering the structure of a spin-valve in Figure 1, when the magnetization of the two films is parallel, one spin state will be the minority for both the layers, experiencing low scattering in both. When magnetization is antiparallel, each spin state will be the majority for one of the two layers, implying large scattering along the route [15]. Representing the scattering magnitude like electrical resistors as in Figure 1, it is straightforward to note that the parallel configuration determines the least total resistance, while the antiparallel is the one that hinders electron conduction the most. GMR-based layered devices, called spin-valves, were able to generate magnetoresistances up to 10–20%, which were insufficient to generate the voltage drop required for a reliable reading process.

In 1995, tunnel magnetoresistance (TMR) was first reported at room temperature [16], dramatically changing the research on MRAMs. From early magnetoresistances values of 15–16%, TMRs of more than 600% were demonstrated at the laboratory scale, while the current industrial standard is around 100–200%, providing sufficient voltage difference for reliable reading of memory cells [11]. Unlike GMR, where the resistance difference was driven by spin-dependent scattering in ferromagnets, in TMR, this is based on spin-dependent tunnelling. In fact, when two FM layers are separated by a thin enough insulator film, the number of electrons tunnelling from one FM to the other is higher when their mutual magnetizations are parallel and lower when antiparallel [15].

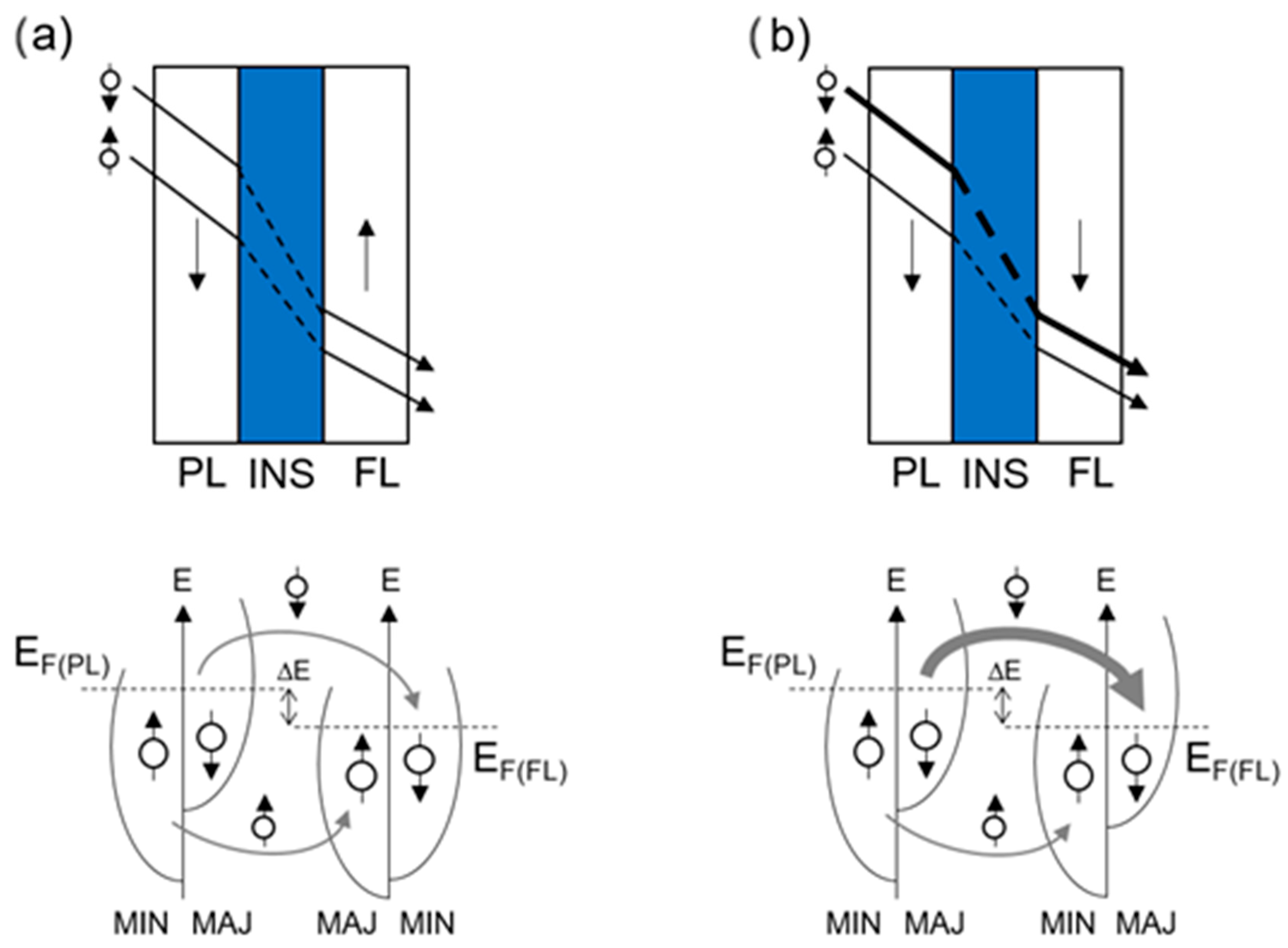
A schematic representation of an MTJ is depicted in Figure 3. Considering the parallel state, both majority- and minority-spin electrons are “free” to tunnel from FM1 to FM2 through the insulator (INS) owing to the strong matching of the density of states sub-bands. On the contrary, in the antiparallel state, the larger mismatch between ferromagnets DOS (which sub-bands now strongly differ in shape and filling) hinders the tunnelling of majority-spin electrons, effectively reducing electric conduction. Since the parallel configuration implies lower resistance than the antiparallel, exactly like in spin-valves, the storage of binary digits is possible [15]. The magnitude of such effect is given by the TMR ratio figure of merit [11]:

$$TMR={\displaystyle \frac{R_{AP}-R_P}{R_P}}$$

(1)

A model proposed by Julliere [17] is also frequently used to express the TMR ratio in terms of the spin polarization of the two ferromagnetic materials. Spin polarization (P) is expressed as a function of the spin-dependent densities of states at the Fermi level (D):

$$P={\displaystyle \frac{D_{+1/2}-D_{-1/2}}{D_{+1/2}+D_{-1/2}}}$$

(2)

where +1/2 electrons are considered those with spin parallel to the magnetic field and −1/2 those antiparallel. With P defined as such, the TMR ratio can be rewritten as follows:

$$TMR={\displaystyle \frac{{2P}_1{P}_2}{1-P_1{P}_2}}$$

(3)

with P₁ and P₂ the spin polarization of the two ferromagnets. When no voltage is applied to the MTJ, electrons can tunnel in both directions at an equal rate; however, if a potential is present, electrons will now tunnel preferentially towards the positive electrode. Assuming that spin is conserved during tunnelling, the current is therefore described as split in two independent components, one for each spin state.

The TMR ratio, and thus reading speed and efficiency, can be enhanced acting on numerous factors, such as FM/INS band matching, layers’ crystalline compatibility, film thickness, stack architecture, etc.; however, increasing the ferromagnets’ spin polarization is perhaps the most straightforward. If both P₁ and P₂ are 1, meaning that both FM layers have 100% spin polarization, TMR becomes infinite. In this condition, the MTJ becomes a switch able to shift between a state of low resistance and one of infinite resistance. Such 100% spin polarization is peculiar to half-metallic ferromagnets, in which conduction of electrons is fully spin polarized [11]. Examples of such materials are CrO₂ and various Co-based Heusler alloys, whose properties are of high interest in spintronics [18]. Experimental proof of half-metallicity and close to 100% conducted electrons spin polarization was found, for example, at the La_0.7Sr_0.3MnO_3/SrTiO₃ interface by Bowen et al. [19], in which spin polarizations up to 99.6% were reported. Later, a P value of 93% was reported for the Co₂MnSi Heusler alloy by Jourdan et al. [20] at the interface with MgO. For Co₂MnSi, TMR ratios of 1995% and 354% were measured at 4.2 and 300 K, respectively [21], allowing their practical implementation in MTJs. Values between 50% and 90% were also observed for the CoFeCrAl Heusler-ordered alloy [22]. Furthermore, half-metallicity was predicted and indirectly observed for numerous other compounds [23]. The research on materials able to show such properties is a hot topic in spintronics and MRAM technology.

As far as the insulator is concerned, layers of amorphous materials like AlO_x led to maximum TMR ratios of 70% [24]. On the other hand, crystalline materials like MgO proved to be extremely effective, as figures of merit up to 1000% were reached at the laboratory scale for the CoFeB/MgO/CoFeB junction [25]. From a metallurgical point of view, an orientation along the (001) direction is considered essential for MgO, as both the surfaces of the film must be textured along that crystallographic direction in order to maximize band matching with ferromagnetic materials. At the current state of MRAM technology, the CoFeB/MgO/CoFeB magnetic tunnel junction is considered the benchmark for industrial applications [11,25].

3.2. Writing Mechanisms: Field-Assisted and Spin-Transfer Torque

The writing process is the operation of changing the value of a memory cell from 0 to 1 and vice versa. In spin-valves and MTJs, this is achieved by switching the magnetization of the free layer. Historically, this has been achieved in various ways, the oldest of which was to apply an external magnetic field in proximity to FL.

External field writing-driven MRAMs were the first to be developed. They consisted of a rather complicated architecture, since a sufficiently high magnetic field had to be applied only in correspondence to the selected cells to be written. In such systems, the magnetic field is brought directly to the specific memory cell, powering two separate lines to half of the required intensity, similarly to what was already achieved for earlier magnetic-core memory [26,27]. As the field that must be applied to obtain a successful switch is inversely proportional to the area of the storing element, down-scalability was found to be problematic. From a practical point of view, field-assisted MRAMs with dimensions smaller than 90 nm were found to be infeasible due to the large current requirements (up to 10 mA for cell sizes of approximately 100 nm) [11,28].

The idea of using spin-transfer torque as the principle for writing magnetic memory cells nevertheless revived the research and commercial interest for MRAM technology [26]. The magnetization switching is here obtained by flowing a spin-polarized current (SPC) through the free layer. When an SPC is injected into a thin enough ferromagnetic film, the angular momentum carried by electrons can be transferred into the layer, flipping the orientation of its magnetization as a result of ferromagnetic resonance. This effect is highly observable at a nanometric scale, whereas at higher scales, phenomena like spin scattering and spin mixing hinder the transport and the injection of SPCs. The intensity of the switching current linearly scales with the size of the film, meaning that as the dimensions of the cell shrink, the required current diminishes as well. As this method finally ensured convenient scalability towards smaller dimensions and simpler cell architecture, STT-MRAMs rapidly become the state of the art for commercially marketed MRAMs [11,15,26]. Currents down to approximately 1 μA were found to be sufficient to write a junction of around 10 nm in size [25].

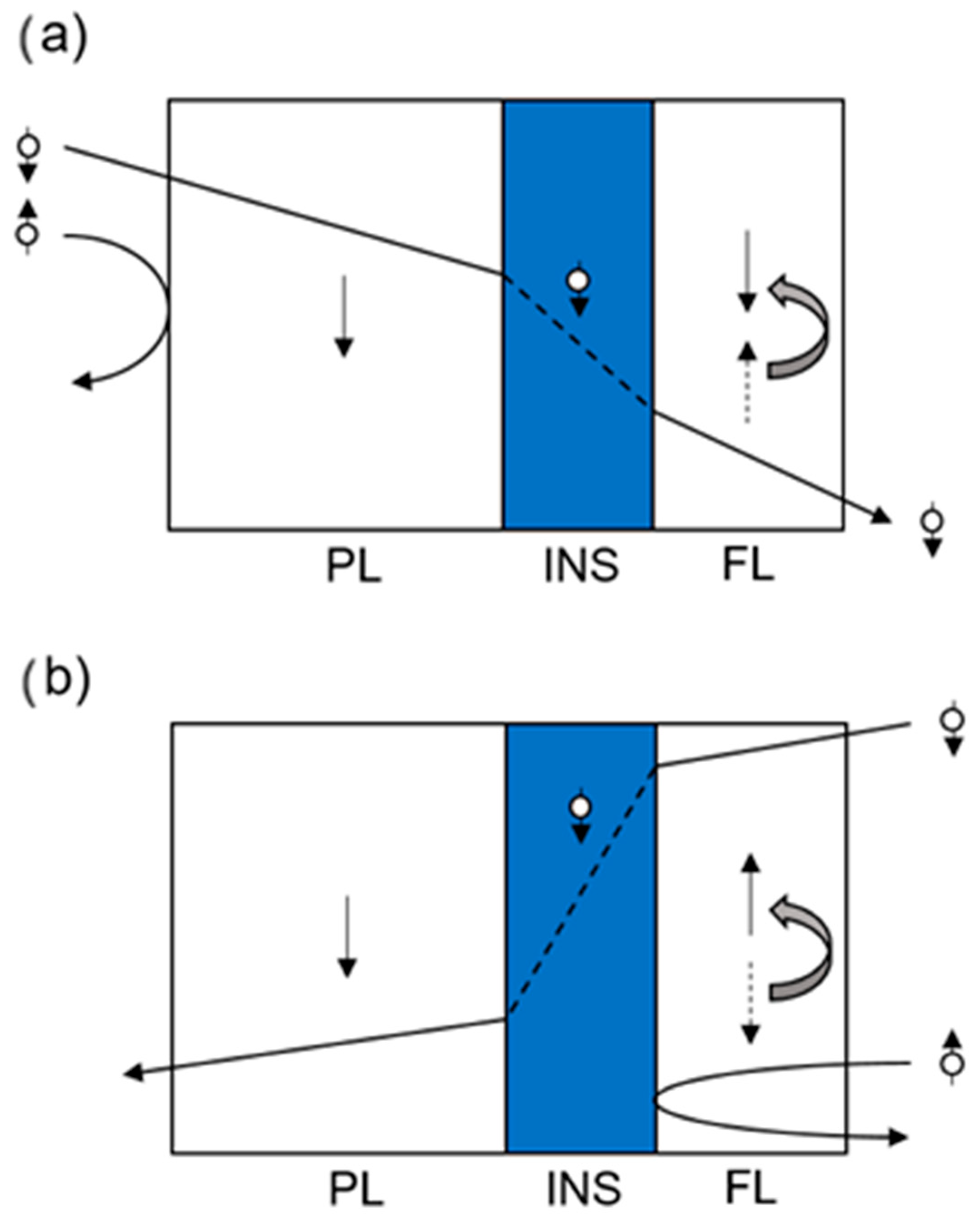
As illustrated in Figure 4, in STT-MRAMs, the writing process is different depending on the final state to be obtained. If the cell must be switched from the antiparallel to the parallel configuration (Figure 4a), a current is sent from PL to FL. When the electrons flow through the pinned layer, the ones having minority spin are scattered, while the majority electrons tunnel towards the free layer. PL acts in this case as a spin filter, allowing only majority electrons to be directed into FL. This selection process is called polarization (or spin filtering) and occurs efficiently only when the filtering layer is thick enough. As spin-polarized electrons reach FL, their spin angular momentum exerts a torque on FL magnetization. If the intensity of the spin-polarized current is high enough, the exerted torque is sufficient to ultimately flip the magnetization, allowing the system to reach the parallel state. However, if the cell must be written from the parallel to the antiparallel configuration (Figure 4b), the current is directed from FL to PL. As the free layer is not thick enough to act as a polarizer, the current reaches the pinned layer in an unpolarized state. Here, only the majority-spin electrons are allowed to tunnel and flow into the PL, while those having minority spin are scattered back. The reflected current being spin polarized, a spin torque is applied on FL, causing its magnetization to switch [11].

The optimization of the current required for the writing process is a key factor in MRAM engineering. In fact, this must be strong enough to ensure irreversible magnetization switch but low enough to avoid excessive power consumption. The critical current J_W is given by [27]

$$J_W=\left({\displaystyle \frac{\alpha }{\eta }}\right)\left({\displaystyle \frac{2e}{\hslash }}\right)M_{s}t{H}_K+2\pi M_s$$

(4)

with Ms the saturation magnetization, H_K the anisotropy field, t the film thickness, and α the Gilbert damping constant, which measures the magnetization relaxing rate. η is the STT efficiency parameter, which is proportional to the spin polarization of the injected current.

3.3. Storage Methods: In-Plane and Perpendicular MRAMs

MRAMs can be classified in two main categories based on the architecture of the MTJ component, namely, in-plane and perpendicular MRAMs. In the first class, magnetizations of PL and FL are parallel to the film plane, whereas in the second class, the magnetization is perpendicular.

In-plane MRAMs were the first to be developed, as they are the easiest to manufacture. Additionally, with the switching field in early field-assisted MRAMs in plane with respect to the MTJ layers, in-plane magnetic fields were easier to be switched by such a writing method. Nevertheless, the main drawback of such architecture is poor down-scalability due to the increase in magnetostatic fields with the shrinking of cell size. In fact, significant magnetization curling at the edge of the films was found to occur when dimensions were scaled down, leading to the formation of undesirable magnetic vortexes [29]. One way to minimize the presence of such vortexes is fixing the aspect ratio (length/width) of the layers to be equal to or more than two, implying the use of elliptically shaped junctions instead of cylindrical. However, MTJs with elliptic shapes are not optimal, as they require a larger space than cylindrical, decreasing information density [30]. Furthermore, magnetization curling is also known to cause anomalous switching related to thermal stability issues. For these reasons, dimensions of in-plane MRAMs cannot be scaled down enough to guarantee sufficient cell density [29].

As already mentioned, the thermal stability factor Δ must be larger than 60 to ensure a data retention goal of at least 10 years. In the case of uniform rotation of magnetization, as in MTJs, Δ can be expressed as follows [16]:

$$∆ ={\displaystyle \frac{H_K{M}_{s}V}{2k_{B}T}}$$

(5)

with V the volume and T the temperature. Considering the properties of the state-of-the-art CoFeB/MgO-based MTJs, values of Δ > 60 result for cell dimensions not inferior to 60 nm, limiting the miniaturization of in-plane cells to such ultimate size.

The fabrication of films with perpendicular magnetic anisotropy (PMA) allows a significant reduction in magnetostatic fields in MTJs, as magnetization can be stabilized perpendicularly to the film plane [11]. The first alloys used in these applications were well-established PMA materials such as GdFe/CoFe and other transition metal alloys such as TbFeCo and GdFeCo. Nevertheless, all of these were affected by nearly unavoidable oxidation issues [31]. Surprisingly, the solution for this material problem came again from CoFeB, which was already predominantly used in in-plane MRAMs. In fact, CoFeB was found to show significant perpendicular magnetic anisotropy for film thicknesses smaller than 1.5 nm [32]. CoFeB/MgO-based perpendicular magnetic tunnel junctions (pMTJs) were observed to show TMR ratios higher than 100% as well as good thermal stability and low J_W [33].

3.4. Main Issues and Solutions

Although the introduction of STT-MRAMs solved a large quantity of issues related to reliability and cost-effectiveness, important challenges are still present as a result of a relatively young technology compared with that of silicon-based industry. Failure issues can be divided into correctable (fixable) and non-correctable (non-fixable).

Fixable errors are caused by the properties of FL and can be solved by sending a new signal to the cell (namely, by attempting to reread or rewrite). These issues are frequently caused by thermal fluctuations, which can cause reversals of magnetization orientations. Possible solutions would be to increase the intensity of the writing current or increase the time of the current pulse during the reading process; however, breakdowns in the insulator layer were found to occur when the current flux was too high [32,34]. Non-fixable errors are usually caused by issues with the insulator layer. The breakdown of the oxide film leads to irreversible degradation of the MTJ. During the reading process, a significant resistance difference has to occur between the 0 and 1 states; therefore, thin oxide barriers must be used in order to avoid disturbances during the reading operation [34]. Furthermore, since the reading and writing operations in STT-MRAMs share the same access path through the junction (see Figure 3 and Figure 4), the value of the memory cell can be switched mistakenly during the reading process if the current flux is too high.

To solve such problems, two main paths can be followed. On the one hand, the research on the current state-of-the-art (mainly CoFeB and MgO) and new, innovative materials is crucial. On the other hand, developing new solutions for the architecture and engineering of memory cells plays a key role as well. As the perspectives on new materials in spintronics are discussed in detail in the next section, this part focusses on the latter topic.

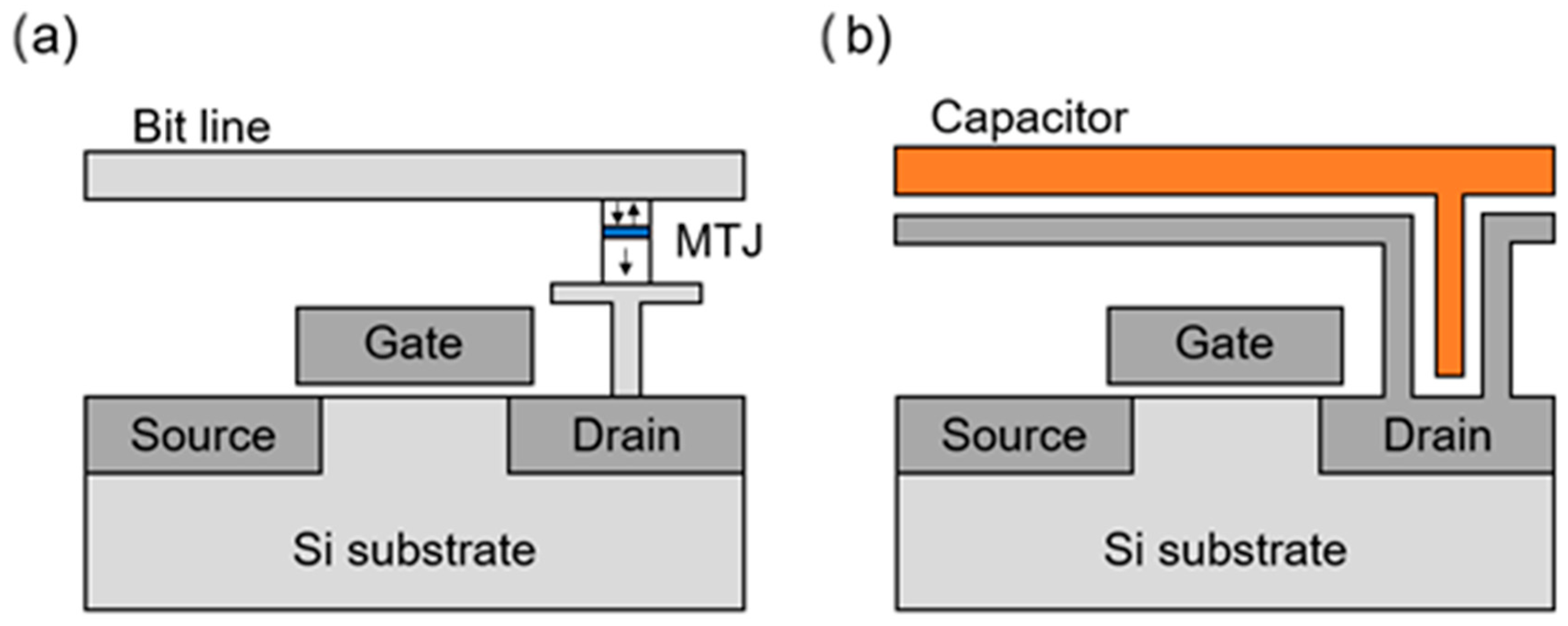
The basic architecture of an STT-MRAM memory cell is shown in Figure 5. As already mentioned, an STT-MRAM cell differs from a common DRAM cell fundamentally because of the resistive element: an MTJ for the former (Figure 5a) and a capacitor, which can be built in various forms, for the latter (Figure 5b). A transistor is present on both, as it provides the necessary current to perform the reading and writing operations. In comparison with resistive RAMs, STT-MRAMs achieve up to 100 times faster switching speeds [11]. Switching speed was found to be directly proportional to the applied writing current and inversely proportional to the resistance-area product of the MTJ [11]. Increasing the current and reducing the thickness of the insulator barrier are the most straightforward methods to achieve faster writing; however, a careful optimization has to be carried out to avoid breakdowns of the insulator barrier [13]. Other methods involve the tilting of FL with respect to PL in pMTJs. It was reported that a 5° tilt angle led to an improvement of 30% of the switching speed, while simultaneously reducing the current by 36% [35]. In orthogonal spin-transfer MRAMs, a spin-polarization layer is magnetized perpendicularly to FL, leading to a large STT effect and fast writing speed. With such systems, reliable writing has been achieved with current pulses of approximately 550 ps, leading to a speed in the range of 2 GHz [36]. Increasing the spin-transfer torque efficiency (η) is also beneficial for writing efficiency, as J_W is inversely proportional to η (see Equation (4)). The use of dual MTJs, which are composed of two PLs and one FL, was found to double the STT efficiency compared with an MTJ having the same resistance-area product [37].

Improvements that involve more drastic changes in memory cells’ architecture are also under investigation. Alternative spin-based memory devices such as spin-Hall effect (SHE)-based MRAMs are receiving attention due to potential lower thermal stability-induced retention failure rate and lower writing delay. In such devices, spin-polarized currents are produced inside FL using the spin-Hall conduction properties of certain metals, such as Pt and β-Ta, which are deposited as thin films adjacently to the MTJ ferromagnetic layer. In fact, SHE is a phenomenon in which spin-orbit coupling causes the deflection of electrons of different spins in different directions, ultimately generating spin-polarized currents. Such SPCs are produced transversally to the applied charge current [38]. Spin-orbit interaction was also found to generate a torque on magnetization similarly to what was already observed for the spin-transfer torque effect. In spin-orbit torque MRAMs (SOT-MRAMs), a current flows through an electrode, the write line, adjacent to FL. The direction of magnetization of the free layer is decided by the verse of the current. Although in such architectures, the reading and writing paths are separated, implying a higher degree of reliability, SOT-MRAM memory cells are more complex, as they consist of a two-transistor circuit with an additional line for writing. Although the spin-orbit effect is quite efficient for magnetization switching, the physical principle causing such a phenomenon is not yet fully understood, requiring more fundamental research before large-scale commercial use [39]. Other practical improvements on the STT-MRAM cell include the application of a voltage to the FL/insulator interface to reduce the magnetic anisotropy of the free layer, enabling the writing process to be performed at lower currents [40]. The voltage control of magnetic anisotropy (VCMA) is based on the fact that electric fields were observed to change the occupancy of atomic orbitals at the interface. This effect, coupled with spin-orbit interactions, leads to a change in anisotropy. Also in this case, no clear physical explanation has yet been provided, as only a qualitative description based on the Rashba effect has been proposed [41]. Other devices like domain-wall memory and skyrmion-racetrack memory are currently under intensive study; however, due to the complicated nature of the physical principles on which they are based, more extensive research is still required [11].

4. Materials in Spintronics

As already mentioned, the current state of the art for MTJs built inside commercially available STT-MRAMs is the CoFeB/MgO/CoFeB junction. Faster and more reliable MRAMs are those which boost the efficiency of the reading and writing processes and can also store data for a sufficient amount of time. In addition to the already discussed engineering improvements, in order to enhance the reading efficiency, it is necessary to increase the TMR ratio, while to boost the writability one has to lower the critical writing current J_w. Ultimately, this leads to the need to maximize Equations (1)–(3) and minimize Equation (4). Also, to keep the data safely stored for a time of more than 10 years, the result of Equation (5) should be at least higher than 60.

Considering Equations (3) and (4), it can be noted how the spin polarization, P, is present in both. In Equation (3), P is an explicit term and leads to a TMR ratio that tends to infinite when its value is 1. In Equation (4), P is not explicit; however, the STT efficiency parameter η directly depends on spin polarization, meaning that high values of P minimize J_W. It is easy to understand that the research on materials exhibiting high spin polarization (possibly even above room temperature) is of major importance in spintronics, as such a parameter is simultaneously beneficial for both the reading and writing of MRAMs [11].

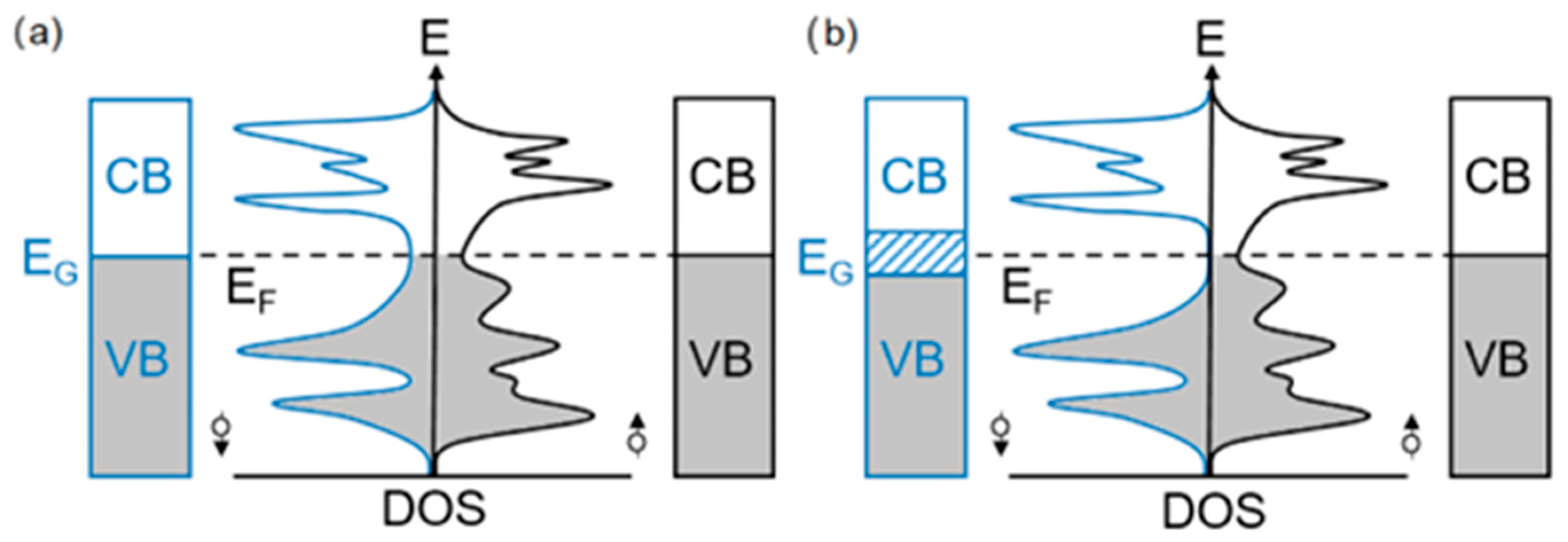
Half-metallic ferromagnets (HMFs) are materials which recently have attracted extensive interest due to their ability to potentially achieve 100% spin polarization. Such a property arises from the peculiar DOS of these compounds, schematically shown in Figure 6. In ferromagnetic materials, the imbalance of electrons having spin 1/2 and −1/2 can be described with two separate sub-bands of the DOS diagram. Here, despite the presence of a majority-spin channel (black) and a minority-spin channel (cyan), the density of states at the Fermi level is not zero for both. In a half-metallic ferromagnet, a band gap is present in correspondence of E_F in the minority-spin sub-band, leading to a conductor-like majority band and a semiconductor-like minority channel. This peculiar electronic structure is responsible for several interesting properties which are of high interest in spintronic applications, the most important probably being their ability to achieve theoretical 100% P. In fact, when a current is directed through an HMF, electrons having majority spin are free to flow across the material, as they travel following the conductive channel. Nevertheless, electrons having minority spin cannot be conducted, as the access to CB in the minority-spin sub-band is hindered by the presence of the band gap [21,42].

Co-based Heusler alloys, which are ternary compounds of X₂YZ stoichiometry (where X, Y are transition metals, and Y is a p-group element) and L2₁ crystal structure, have been reported to show half-metallic properties. Direct proof of half metallicity was found, for example, for Co₂MnSi [20], Co₂FeAl [43], and Co₂FeAl_0.5Si₀₅ [44]. Spin polarizations up to 93%, leading to TMR ratios of 354% at room temperature, were measured for Co₂MnSi [20]. Evidence of half metallicity was found for a large number of other Co-based Heusler compounds, such as Co₂FeSi [45], Co₂V(Al,Ga) [46], Co₂Ti(Si,Ge,Sn) [47], Co₂ZrSn [48,49], and Co₂HfSn [50,51], as well as others [52].

Concerning the transport properties of HMF materials, in 2014 Boona et al. [53] described the spin-dependent Seebeck effect as the result of the spin dependence of the electronic density of states in ferromagnetic materials, where each spin component (up and down) gives rise to a separate thermopower contribution (S_up and S_down). According to the Stoner model, the two spin populations being mutually independent, each population will have independent internal conductance and will form separate conduction channels (G_up and G_down). If a thermal gradient ΔT is imposed, the total thermopower of the material, SΔT (S is the Seebeck coefficient), is obtained by considering the two spin channels as two voltage generators connected in parallel. Therefore, the total current density j created by the thermal voltage inside the material will be equal to $j=\left(G_{up}+G_{down}\right)S∆T$. This is ultimately the sum of two different terms, j_up and j_down, which are describable as follows:

$$j_{up}=G_{up}S∆T; j_{down}=G_{down}S∆T$$

(6)

At this point, if zero-current density conditions are imposed (j = 0), the resulting spin accumulation that will occur at the edges of the material (and that will decay over the spin-scattering diffusion length) is the spin-dependent Seebeck effect. This is the result of the imbalance between the number of spin-up and -down electrons displaced from their equilibrium state when a temperature gradient is imposed and represents the spin accumulation density caused by such gradient. The spin-injection process occurs when a non-magnetic (NM) layer is positioned in contact with the HMF spin-voltage generator. In this configuration, the NM material will act as a spin sink, and the accumulated spin voltage will result in a polarized spin current (inside the limits of the spin diffusion length of the material). Although the presence of an HMF/NM interface is not a necessary condition for the occurrence of a spin-dependent Seebeck effect, it is within this layered configuration that thermal spin injection found the majority of interest in spintronics, as the spin-Seebeck effect was found to be an effective way to generate and transport SPCs even over relatively long distances. A more extensive discussion of the properties of Co-based Heusler alloys is performed in the next section; nevertheless, it is already possible to state that, since Heusler compounds are known to be among the most promising thermoelectric materials, the study of their spin-Seebeck effect is well embedded in a solid and established research and competence framework. Moreover, their potential as spin injectors makes them suitable for other spintronic applications in addition to those in MTJs, such as in spin lasers, sensors, and actuators [18].

Concerning thermoelectric materials, machine learning (ML) has been recently evaluated as an effective tool to understand and optimize synthesis and processing paths for the optimization of the figure of merit zT (zT = S²σT/k, with σ the electrical conductivity and k the thermal conductivity) [54]. In 2020, Tang et al. successfully used ML for guiding the synthesis of MoS₂ by chemical vapour deposition as well as the hydrothermal synthesis of carbon nanostructures [55]. In 2023, Mitra et al. [56] used the random forest regression ML model to predict lattice constants, magnetic moments, and formation energies of several Heusler alloys, with suggested high accuracy of the predicted properties when compared with DFT calculations. This approach was used for the optimization of spintronic properties as well. Magnetoresistance ratios of Co-based Heusler alloys were investigated with the use of ML by Kurniawan et al. [57], who focussed on the effect of alloy mixing to tune the position of the Fermi level and achieve high spin polarizations. High-throughput DFT databases were used as training data by Hu et al. [58] in a deep neural network to identify six new potential half-metallic Heusler alloys with high spin polarization. The use of ML models is, hence, gaining significant momentum in the literature as a new tool for the identification of new materials and optimization of processing routes in both the thermoelectric and spintronic fields [59].

Ferromagnetic oxide thin films have been also extensively studied due to their various and highly tuneable electronic properties. Fe₂O₃, which shows a spinel ferrite structure, is one of the most studied. Showing a magnetic moment of 4.1 μ_B and a high Curie point at 850 K, it has been predicted to be half metallic. Subsequent spin-resolved photoemission measurements reported spin polarizations up to approximately 80% [18]. The substitution of one Fe ion with divalent metal ions such as Mn, Co, and Ni was found to possibly increase the half-metallic properties. Despite the promising perspectives, their half-metallic behaviour was found to be extremely sensible to film imperfections such as antiphase boundaries and atomic-site disorder and dislocations. High quality of films is indeed crucial for achieving satisfactory half metallicity and spin filtering [18]. CrO₂, which has a rutile structure, has been proved to be half metallic at low temperatures. Point-contact Andreev reflection (PCAR) measurements indicated spin polarization of 90% at low temperatures; however, half metallicity at room temperature has not yet been demonstrated [60]. A phase transformation is known to occur above 391 K, which is a major cause of the reduction in half-metallic properties [61]. Double perovskites such as Sr₂FeMoO₆ (SFMO) also achieved high P at low T (approximately 80%) and a T_C of 420 K. Their high reactivity with water and the loss of half metallicity as a result of site disordering are the main obstacles to overcome [62].

Magnetically doped semiconductors such as (Cd,Mn)Te, (In,Mn)As, and (Ga,Mn)As are versatile materials, as the carrier density of the semiconductor is tailored via doping with ferromagnetic elements. In fact, their magnetic properties can be tuned by increasing the carrier density by applying an electric field, photoexcitation, or heating [63]. The main issue with such materials is the low Curie point, as the perspective for a reliable ferromagnetic semiconductor at room T remains elusive. Dilute magnetic semiconductors (DMSs) like (In,Mn)As and (Ga,Mn)As are considered promising; however, the upper achieved T_C is around 330 K [64,65]. Recently discovered (Ba,K)(Zn,Mn)₂As₂ DMS compounds are considered more promising even if their T_C remains around 230 K [66].

Two-dimensional (2D) materials are also regarded as a major possible breakthrough in spintronics. Their unique physical properties such as spin-orbit and spin-valley coupling and their extreme thickness dimension make them suitable for nanoelectronics applications [67]. Graphene was taken in consideration as a material for spintronics due to the high carrier mobility and low spin-orbit coupling (SOC), leading to a high retention of spin coherence over long distances. In fact, in 2016 Drögeler et al. reported the transportation of a spin signal in graphene over 30.5 μm (90 μm when carrier drift was used) [68]. Because of this property, graphene was found useful for solving one important problem in spintronic devices, namely, the fundamental conductivity mismatch between the FM material and the semiconductive layer, which makes spin injection difficult. The use of graphene as spin-transport channel has thus been taken into consideration as a viable route for emerging spintronic logic devices [69]. The insertion of thin-tunnel barriers (mainly TiO₂ and MgO) between the FM and graphene layers has been found to improve the spin-injection efficiency significantly [67]. Significant effort was also put into inducing a magnetic moment in graphene, which is intrinsically a strong diamagnetic material due to the lack of d or f electrons. The insertion of extrinsic defects, most prominently H and F atoms, has been the most popular [70,71]. Magnetic moments in graphene were thus experimentally measured via superconducting quantum interference devices (SQUIDs) and other techniques; however, in addition to the localized magnetic moments which arise from the local presence of extrinsic defects, the induction of permanent magnetic moments in graphene remains a challenge [67]. Somewhat more successful has been the research into graphene as a tunnel barrier material (INS) between the FM layers in MTJs. TMRs were, however, limited to approximately 5% [72].

Transition metals dichalcogenides (TMDs) were found to be remarkable 2D materials, with compounds such as WSe₂ and MoS₂ emerging as strong candidates to overcome the limitations of Si [73]. The application of 2D TMDs is related to a proposed class of spintronic devices called spin transistors. Spintronic devices are usually passive, meaning that they are not capable of amplifying electric signals. In spin transistors, the spin injected from the source FM contact travels towards the drain FM contact via Larmor precession due to the generation of a magnetic field generated by the application of an electric field at the gate electrode (Rashba spin-orbit interaction) [67]. In its normal state, the spin transistor is typically in depletion mode, as the absence of precession in proximity to the gate electrode leads to a spin direction parallel to the drain. The application of a voltage at the gate alters the precession angle and results in a modulation of the current between the source and drain [67,74]. The suitable properties of bidimensional TMDs as spin-transport materials are ideal for such applications, which have the potential for higher speed and energy efficiency than Si-based transistors. Van der Waals TMD/graphene heterostructures aim to combine the long-distance spin-transport capabilities of graphene (low SOC) with the TMDs’ potential of efficiently manipulating the spin (high SOC, which means high capability to exert a torque on spin-exhibiting particles) [75]. The occurrence of charge-to-spin conversion in graphene/TMD heterostructures was demonstrated in graphene/WS₂ via Rashba–Edelstein effect [76,77]. Such SOC-induced spin current is of great interest for the development of advanced SOC-based MRAMs and spin-Hall oscillators [67]. Electrons in bidimensional honeycomb crystal structures, such as MoS₂, were also found to possess an additional valley degree of freedom in addition to charge and spin, originating the whole new research field of valleytronics [78].

5. Heusler Alloys

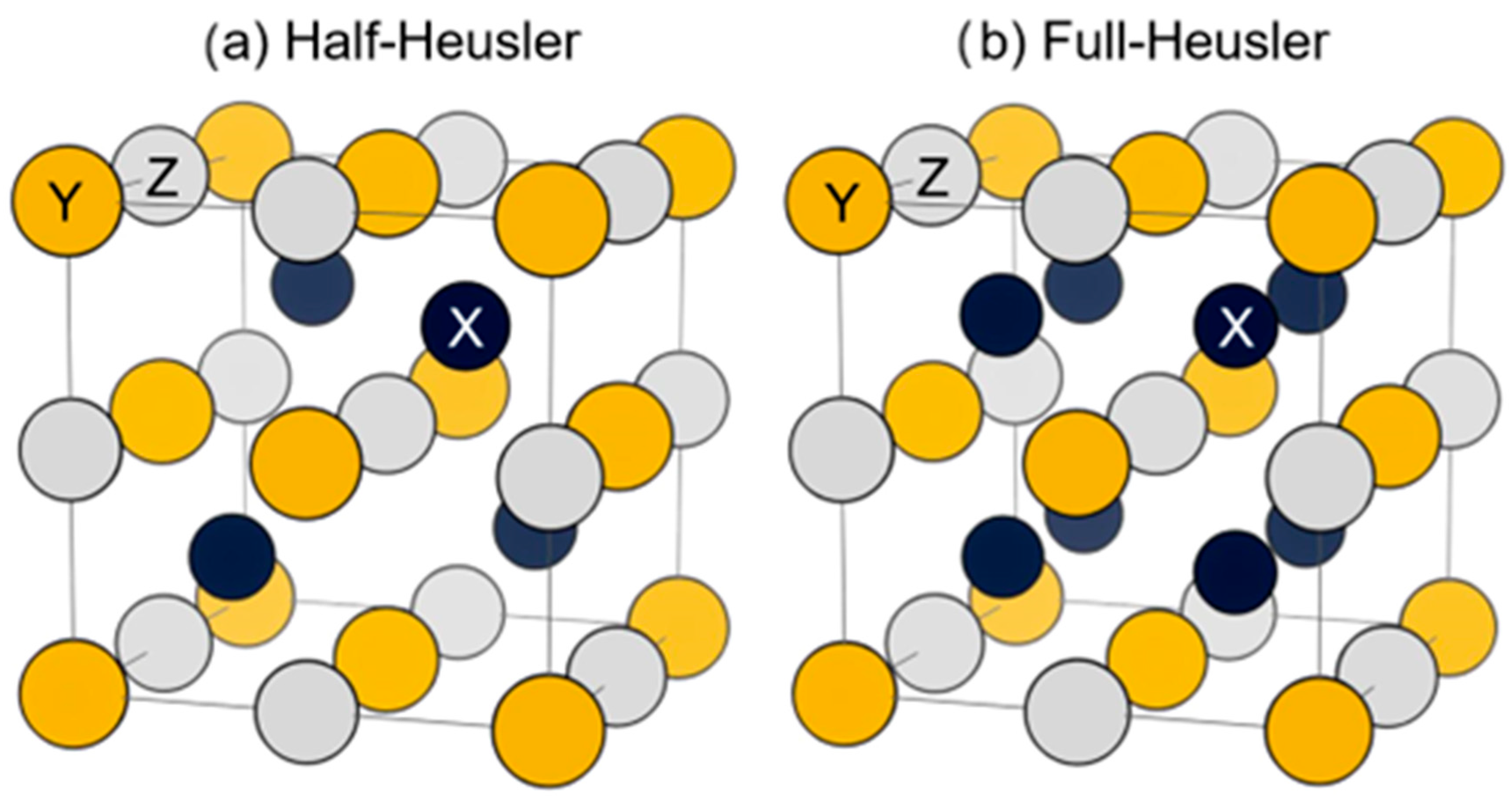
Heusler alloys are a family of highly ordered ternary intermetallic compounds, usually divided in two sub-categories: half-Heusler alloys with XYZ stoichiometry (X, Y are transition or alkaline metals; Z is a p-block element) and C1_b structure, and full-Heusler (referred here simply as Heusler, or FH) with X₂YZ stoichiometry and L2₁ structure. Both categories attracted a lot of attention in spintronics; they are currently, in fact, the most studied materials for such applications.

Concerning half-Heuslers (Figure 7a), the most well-known compound is NiMnSb [79], as in 1983 de Groot at al. [80] predicted by ab initio calculations its half metallicity with a 100% spin polarization at the Fermi level. Its half-metallic behaviour was later experimentally verified in single crystals by multiple techniques such as infrared absorption [81] and spin-polarized positron annihilation [82,83]. Interestingly, in thin films, half metallicity was found to be hindered by Sb and Mn segregations at the surface, leading to a maximum 58% spin polarization [84]. Despite the well-known half metallicity of NiMnSb [85], a large number of half-Heusler compounds are semiconductors, like TiNiSn, or conductors which exhibit a high Seebeck coefficient (S) and thermoelectric figure of merit (zT) [86].

Considering full-Heusler compounds (Figure 7b), they were the first to be discovered in 1903 by Franz Heusler after the synthesis of Cu₂MnAl. This alloy was found to be ferromagnetic even if none of its constituent elements are magnetic by themselves [87]. This evidence immediately highlighted the non-trivial nature of the electronic structure of such compounds, actively stimulating further research. The mechanisms behind the stabilization of the ferro- or antiferromagnetism of Heusler alloys was studied in a seminal work by Kübler et al. in 1983 [88]. The prediction of half metallicity of several full-Heuslers was performed with ab initio calculations by several Japanese research groups, such as Ishida et al. for Co₂MnZ (Z = Si, Ge) [89] and Fuji et al. for Fe₂MnZ (Z = Si, Ge) [90]. Subsequently, the half metallicity of Co₂MnAl and Co₂MnSn was experimentally investigated by Brown et al. [91], leading to further studies as thin films grown on MgO substrates [92]. Finally, in 2004, MTJs based on Co₂MnSi [93] and Co₂Cr_0.6Fe_0.4Al [94] were first assembled, paving the way for all the subsequent Heusler alloys’ applications in spintronics. Currently, Co-based Heusler compounds are the most promising candidates to achieve half metallicity at RT, as they are characterized by Curie points well above room temperature, good lattice matching with major substrates, large magnetic moments, and high compositional versatility [18]. As already mentioned, the main obstacle to this objective is represented by atomic disorder, symmetry break in proximity to the film surface, misfit dislocations, and other symmetry-breaking structural perturbations. More in general, the properties of many Heusler alloys can be predicted by a simple account of their valence electrons [95]. For instance, closed-shell compounds like Fe₂VAl are semiconductors which have found applications in energy-harvesting technologies. On the contrary, non-magnetic Heuslers with approximately 27 valence electrons display superconductive behaviour [95]. Magnetic Heusler materials have found applications in a wide range of fields owing to their multifunctional properties, such as magneto-optical [96], magnetocaloric [97], magneto-electric (half-metallic ferromagnetism), and magneto-structural features [98]. Other peculiar properties include shape-memory effects, topological insulators, Kondo systems, and compounds displaying heavy-Fermion behaviour.

5.1. Electronic Properties

In the L2₁ structure, all X atoms are chemically equivalent, as both their sub-lattices are surrounded by the same environment. Although they are located on second-neighbour positions, the mutual interaction of X atoms is crucial to explain the electronic and magnetic properties. It must be also remarked that in Heusler compounds, even in the presence of atoms with a large atomic number, orbital magnetism and spin-orbit interactions can usually be neglected, as they were found to play a minor role [99].

Because Co₂MnAl is one of the most studied half-metallic Heusler alloys in spintronics, in this section, this compound is taken as a case study for the description of the electronic structure of half-metallic FH compounds. Here, the Co moment is large, positive, and is originated by two unoccupied bands in the minority-spin conduction band, as better explained in Figure 8. If all their majority states are occupied, Co atoms have, together, a total moment of approximately 2 μ_B. The Z atoms have, instead, a small and negative magnetic moment, which is about an order of magnitude lower than that of Co. Co₂MnAl and Co₂MnGa have 28 valence electrons, presenting both an experimental and calculated total magnetic moment of 4 μ_B. Considering the similarities of Co₂MnSi and Co₂MnGa, they have 29 valence electrons, showing magnetic moments of 5 μ_B [100,101].

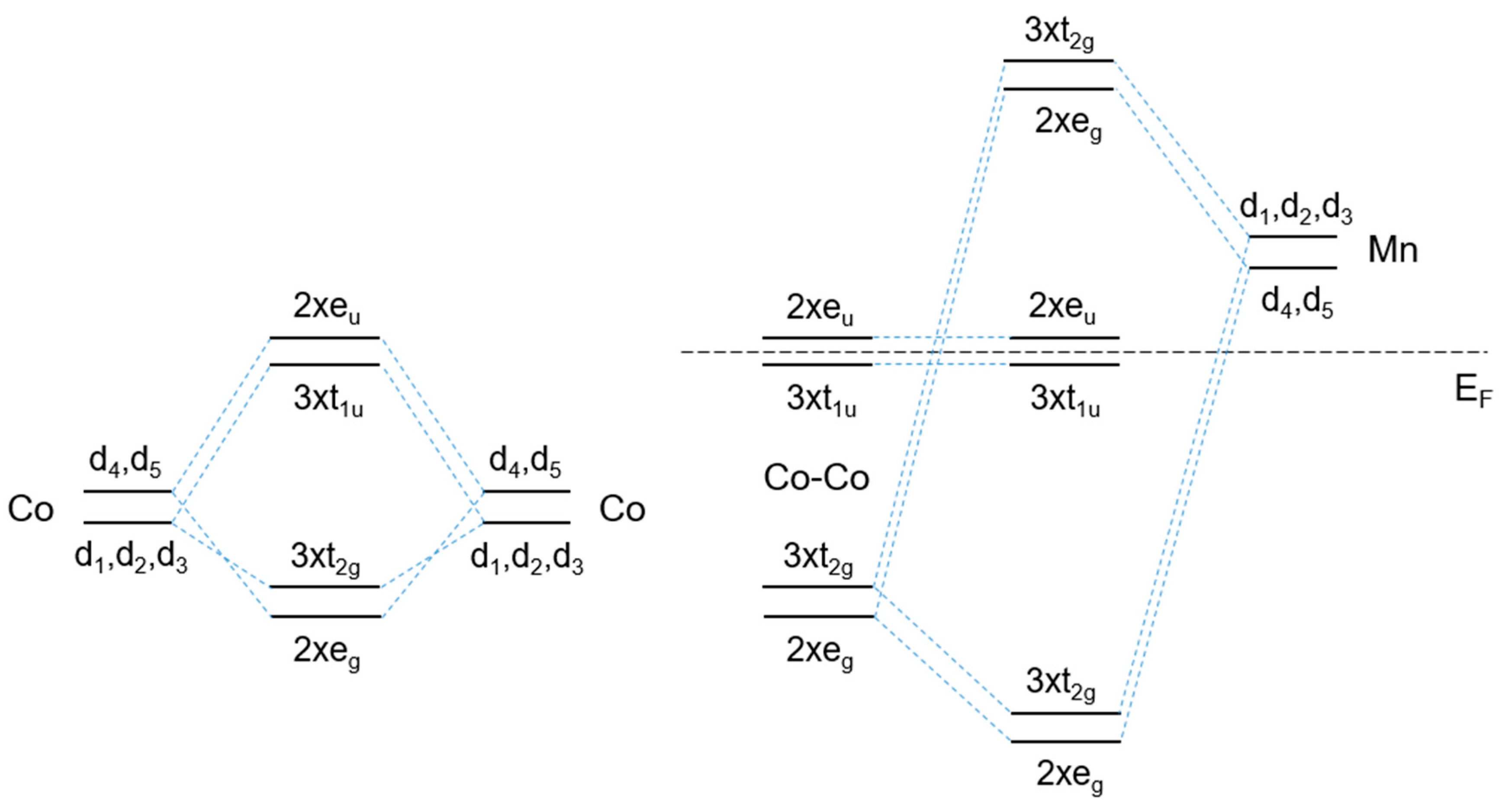
Co atoms’ hybridization is crucial in determining Co₂MnAl’s magnetic and electronic properties [102]. Since the 4 sp-bands of the Z element, as well as the sp-bands of Co and Mn, are located far below the Fermi level, only the hybridization of the 15 d states of Co and Mn are important in determining the electronic structure near E_F. As represented in Figure 8, the 5 d orbitals of Co are divided into twofold degenerate d₄,d₅ (d_r^2, d_x^2-y^2, respectively) and threefold degenerate d₁, d₂, d₃ (d_xy, d_yx, d_zx, respectively) orbitals. Since the e_g can couple with e_g orbitals only, and since the same is valid for t_2g, the hybridization of two Co atoms forms two sets of bonding (e_g and t_2g) and two set of antibonding (e_u and t_1u) orbitals, which correspondent degeneracy is indicated by the respective coefficient. Considering the hybridization of the Co-Co and Mn d orbitals, the double-degenerated e_g hybridize with d₄, d₅, forming a bonding e_g state, which is very low in energy, and an unoccupied antibonding well above the Fermi level.

Similarly, the t_2g states couple with d₁, d₂, d₃, creating six new orbitals, three of which are bonding and occupied while the other three are anti-bonding and above E_F. The e_u and t_1u orbitals of Co cannot couple with any of the d orbitals of Mn, since none of these are compatible with the u symmetry representation, being orthogonal to the e_1u and t_1u states. This is the reason behind the fact that, as predicted by ab initio calculations, in half-metallic Co-based Heusler alloys, the DOS at the Fermi level is usually almost exclusively determined by the bands of Co atoms. The t_1u states, which lie below E_F, are therefore occupied, while the e_1u states are located just above E_F. In total, accounting for the degeneracy of each orbital, eight minority d-bands are filled, and seven are empty. This means that all five Co-Mn bonding bands are occupied, and all five Co-Mn antibonding bands are empty, while the Fermi energy lies between the five non-bonding Co bands. Since the minority band contains 12 electrons per unit cell (4 occupying the low-lying s- and p-bands of the Z element, and 8 the Co-like minority d-bands, namely 2xe_g, 3xt_2g, and 3xt_1u), and since 7 minority bands are unoccupied (2xe_u, 2xe_g, 3xt_2g), the largest possible magnetic moment for an FH compound is 7 μ_B, and it occurs when all majority d states are occupied. Considering the total number of electrons in the system, both majority and minority, it is possible to conclude that the magnetic moment of a Heusler compound can be predicted by a simple account of valence electrons (Z_t) according to the following equation, which took the name of the Slater–Pauling (SP) rule:

$$\mu =Z_t-24.$$

(7)

Because of the strong hybridization, no evidence is present of FH compounds having a moment of 7 μ_B. Systems with 30 valence electrons should have μ of 6 μ_B; however, none of them reach this exact value; Co₂MnAl is the closest, with 5.8 μ_B [102]. This happens because while the two Co atoms have no problem contributing with a total of 2 μ_B to the total moment because of the empty e_u states, the Mn-related moment is limited by its hybridization, with an upper limit of approximately 3 μ_B. Having 24 valence electrons, Fe₂VAl is non-magnetic, while Co₂VAl, which has 2 more electrons, accordingly has a moment of 2 μ_B. Compounds with less than 24 Z_t, like Mn₂Val and Mn₂VGe, are predicted to follow the SP rule showing negative moment. A negative total spin moment would mean that the minority band (which exhibits the half-metallic gap) is more occupied than the majority sub-band.

The SP rule refers to pristine, defectless compounds. The occurrence of defects or distortions in the Heusler lattice can dramatically lower the magnetic moment, introducing states in the half-metallic gap. The occurrence of Co antisites in Co₂MnAl and Co₂MnSi was found to destroy the half metallicity, while the disorder of the Y and Z atoms left the half-metallic properties unaltered. Interestingly, in Co₂MnSi, a small stoichiometric surplus of Mn replacing Si was observed not to have an effect on the minority spin band gap, while in Co₂MnAl, the same situation involving Mn and Al led to a complete loss of half metallicity [103]. Vacancies are also extremely common defects occurring during film growth or bulk sample solidification. In Co₂CrZ and Co₂MnZ alloys, vacancies occurring at the Co site completely disrupt the half-metallic properties, whereas vacancies involving the Y and Z elements leave the gap unaltered.

In Co₂CrAl, the formation of Co-Cr antisite defects leads to significant deviation from the SP rule according to the measured magnetic moment (1.42 μ_B/f.u. instead of 3 μ_B/f.u.) and loss of half metallicity on the basis of ab initio calculations [104]. In this case, the formation of the detrimental Co-Cr antisite defect can be suppressed by partially substituting Co with Mn or Fe and forming quaternary CoMnCrAl and CoFeCrAl Heusler alloys. In these quaternary alloys, the main defects are the antisites Cr-Al, Mn-Cr, and Fe-Cr that have little effect on the semiconducting sub-band since no Co atoms are involved. As a consequence, the measured magnetic moment values (1.96 μ_B/f.u. and 0.92 μ_B/f.u. for CoFeCrAl and CoMnCrAl, respectively) are in agreement with those predicted by the SP rule (i.e., 2 μ_B/f.u. and 0.92 μ_B/f.u. for CoFeCrAl and CoMnCrAl, respectively). The concurrent relatively low magnetic moment, high Curie temperature (above room temperature), and defect-tolerant half metallicity suggest that these quaternary Heusler alloys are suitable for STT-based MTJ devices.

Thermal and excitation effects were also found to introduce levels or progressively smear out the minority spin gap. Spin-orbit interactions can theoretically cause a coupling of the two spin sub-bands, leading to the introduction of states; nevertheless, this effect is weak in FH alloys, leaving spin polarization in most cases as high as approximately 99% [105]. Excitation effects, which can potentially lead to the introduction of levels in the gap, can be described in the adiabatic approximation of static spin waves, which are accounted as superpositions of spin-up and spin-down states. At higher temperatures, magnons (or spin waves) progressively smear out the gap, driving the system to the paramagnetic state above T_C [106]. At low temperatures, the magnon–electron interactions cause non-quasiparticle excitations in the minority gap above E_F [107]. This was also described as the only form of spin-scattering mechanism possible to occur at low T in half-metallic ferromagnets [108]. It is to be added that in the first case, spin-wave excitations introduce new states both above and below the Fermi level, whereas in the latter case, the non-quasiparticle excitations introduce additional bands only at and above E_F [102].

5.2. Electron Scattering and Transport Properties

For transition metals, phonon-related electrical resistivity is modelled by the Bloch–Grüneisen equation (Equation (8)), which takes into account the scattering of electrons with acoustic phonons [109]:

$$R\left(T\right)=A{\left({\displaystyle \frac{T}{{\Theta }_R}}\right)}^{\beta }{\int }_0^{{\Theta }_R/T}{\displaystyle \frac{t^{\beta }}{(e^t-1)(1-e^{-t})}}dt$$

(8)

with R the resistivity, T the temperature, and Θ_R the Bloch–Grüneisen temperature, which usually matches the Debye temperature. Under Θ_R, electrons are assumed to deviate by only a small angle after the interaction with phonons, while above such limit, electrons will be scattered by a large angle because of the higher energy of phonons as T increases. The resistivity over temperature predicted by the Bloch–Grüneisen law can be separated in different regimes, as shown in Figure 9a. At sufficiently high temperatures, resistivity linearly depends on T (β = 1 in Equation (8)). In such a range, electron–phonon scattering quantitatively dominates on grain boundary-related and impurity-induced scattering, as phonons have sufficient frequency to intensively perturb the electron density. Approaching a certain crossover temperature, the resistivity starts to fall less drastically, as a $R\propto T^{\beta }$ with $3<\beta <5$ regime is reached. This occurs in proximity to the Bloch–Grüneisen temperature, which is usually equivalent to the Debye temperature. Here, the lower frequency of phonons reduces the angle with which electrons are scattered, thus causing the slower decrease of R. The exact value of β depends on the nature of conduction electrons and on the shape of the Fermi surface. For T approaching absolute zero, R scales with T⁰, meaning that phonon-induced resistivity becomes negligible. This happens as, in such conditions, phonon frequency is so small as to have no effect on electron density.

In ferromagnetic and nearly ferromagnetic materials, the contribution of magnons (or spin waves) has also to be taken into account. Magnons are defined as quasiparticles or collective excitations of the electronic spin structure in a crystal lattice. Considering electrons in their wave form, an equivalent quantum-mechanical picture is to describe such excitations as quantized spin waves. At low T, only long wavelengths are excited, implying only weak relative deviations of first-neighbour spin. In this case, electrons keep locally their spin orientation, including those responsible for current conduction. As prescribed by the Goldstone rule [94], in the absence of anisotropy, magnetization can rotate without an energy barrier. The spin of current carriers will follow the rotation accordingly, preserving the polarization at the Fermi level. Quantitatively, the contribution of spin waves to electrical resistivity has been modelled by several authors; nevertheless, a nearly complete description was provided in 1975 by Ueda et al. [110]. Here, the resistivity is described in Equation (9):

$$R={\displaystyle \frac{m}{n{e}^2}}{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\epsilon }_F}{\hslash }}{\left({\displaystyle \frac{G}{2V}}\right)}^2{\rho }_s{\rho }_d{\left({\displaystyle \frac{k_F^{*}}{k_F}}\right)}^4\left({\displaystyle \frac{{\epsilon }_F^{*}}{{\epsilon }_F}}\right)\overline{R}\left(T\right)$$

(9)

$$\overline{R}\left(T\right)=T^{-1}{\int }_0^{2k_F/k_F^{*}}{q}^3 dq{\int }_{-\infty }^{\infty }\omega n\left(\omega \right)\left[n\left(\omega \right)+1\right]F\left(q,\omega \right)d\omega$$

(10)

$$F\left(q,\omega \right)={\displaystyle \frac{1}{3{\rho }_d}}Im[2{\chi }_{ZZ}\left(q,\omega \right)+{\chi }_{\mp }\left(q,\omega \right)+{\chi }_{\pm }(q,\omega )$$

(11)

Here, m and n are the effective mass and the density number of s-electrons, respectively; ε_F the Fermi energy of the s- and d-bands measured from the bottom of the band; G the coupling constant; ρ_s and ρ_d the density of states of the s- and d-bands at the Fermi level, respectively; k_F and k_F* the Fermi wave vectors of the s- and d-bands, respectively; n(ω) the Bose function; and χ_zz, ${\chi }_{\mp }$, ${\chi }_{\pm }$ the dynamical susceptibilities of the d-band electrons at their equilibrium. $\overline{R}$(T) is a dimensionless quantity which express the temperature dependence of R as described in Equation (10). Here, the reduced units q/kF* → q, ℏω/εF* → ω, and kBT/εF* → T are used. F(q,ω) is the form factor, as written in Equation (11).

By considering only the spin wave (or magnon) contribution, this is given by

$${\displaystyle \frac{3}{2}}{\left[\overline{R}\left(T\right)\right]}_{sw}={\displaystyle \frac{\pi f_{\zeta }\left(\mathrm{0,0}\right)}{\alpha }}{\displaystyle \frac{1}{T}}{\int }_0^{q_c}{q}^3{\displaystyle \frac{{\omega }_{q}n\left({\omega }_q\right)\left[n\right({\omega }_q)+1]}{\left|\partial f{\zeta }^{\text{'}}(q,{\omega }_q)/\partial {\omega }_q\right|}}dq$$

(12)

where ω_q is the spin wave (magnon) frequency, q_c the cutoff wave vector of the spin wave, and f_ζ(q,ω) the reduced transversal dynamical susceptibility of the non-interacting electron system under a given magnetization. Considering this last parameter as in an electron gas, Equation (12) can be solved analytically, giving two results in the following limits (with Z(n) defined as in Equation (15)):

$${\displaystyle \frac{3}{2}}{\left[\overline{R}\left(T\right)\right]}_{sw}={\displaystyle \frac{\pi f_{\zeta }\left(\mathrm{0,0}\right)}{\alpha }}{\displaystyle \frac{3{∆}^2}{8\zeta D^2}}Z\left(2\right)T^2 (T\to 0)$$

(13)

$${\displaystyle \frac{3}{2}}{\left[\overline{R}\left(T\right)\right]}_{sw}={\displaystyle \frac{\pi f_{\zeta }\left(\mathrm{0,0}\right)}{\alpha }}{\displaystyle \frac{3{∆}^3{q}_c^2}{8\zeta D}}T (T\to T_C)$$

(14)

$$Z\left(n\right)=\Gamma (n+1)\zeta \left(n\right)$$

(15)

with Γ(n) the gamma function and ζ(n) the Riemann’s zeta function. From Equations (13) and (14), the most important aspect to note is that for temperatures approaching absolute zero, magnon-related resistivity follows a T² law, while approaching T_C, it is linearly dependent on the temperature.

In the specific case of ferromagnetic materials, electrical resistivity can be described as the sum of a spin-wave (magnon) contribution and temperature-induced spin fluctuations (spin flip). Depending on the temperature of the system, the following equations were obtained:

$$3{\left[\overline{R}\left(T\right)\right]}_z={\displaystyle \frac{\pi \left(1+{\delta }_{\zeta }\right)C}{2\alpha A^{3/2}}}Z\left(2\right){\displaystyle \frac{T^2}{{\delta }_{\zeta }^{1/2}}} (T\ll T_C)$$

(16)

$$3{\left[\overline{R}\left(T\right)\right]}_z={\displaystyle \frac{2\pi \left(1+{\delta }_{\zeta }\right)C^{2/3}}{3\alpha A^{5/3}}}Z\left(5/3\right)T^{5/3} (T\lesssim T_C)$$

(17)

$$\left[\overline{R}\left(T\right)\right]={\displaystyle \frac{2\pi \left(1+\delta \right)C^{2/3}}{3\alpha A^{5/3}}}Z\left(5/3\right)T^{5/3} (T\gtrsim T_C)$$

(18)

$$\left[\overline{R}\left(T\right)\right]={\displaystyle \frac{\pi (1+\delta )}{\alpha }}\left[{\displaystyle \frac{2r^2}{A}}-{\displaystyle \frac{\delta }{2A^2}}\ln {\displaystyle \frac{\delta +4A{r}^2}{\delta }}\right]T (T\gg T_C)$$

(19)

For temperatures sufficiently lower than T_C, the resistivity is mainly induced by spin waves and is indeed proportional to T² (Equation (16)). Approaching T_C, a T^5/3 trend is followed, with Equations (17) and (18) being identical at the Curie point. After T_C, spin fluctuations contribute linearly to determining the total electrical resistivity of a ferromagnetic material. For nearly ferromagnetic materials, equations determined by Ueda et al. [110] are qualitatively the same as those above.

As already mentioned, the behaviour of ferromagnetic materials, as well as that of HMFs, is described in the assumption of two separate sub-bands for majority and minority spin. Accordingly, electronic scattering can be seen as a sum of $R_{\uparrow }$, $R_{\downarrow }$, and $R_{\uparrow \downarrow }$ contributions (up electrons are assumed as the majority). In half-metallic ferromagnets, $R_{\downarrow }$ corresponds to the resistivity induced by the existence of a semiconductive-like band gap in the minority sub-band. On the other hand, $R_{\uparrow }$ is the resistivity strictly related to majority electrons such as low-T spin waves, which, according to the Goldstone rule, do not imply spin mixing. Finally, $R_{\uparrow \downarrow }$ is caused by temperature-induced inelastic transitions across the gap. These should appear only when kT is comparable to the band-gap energy, E_G.

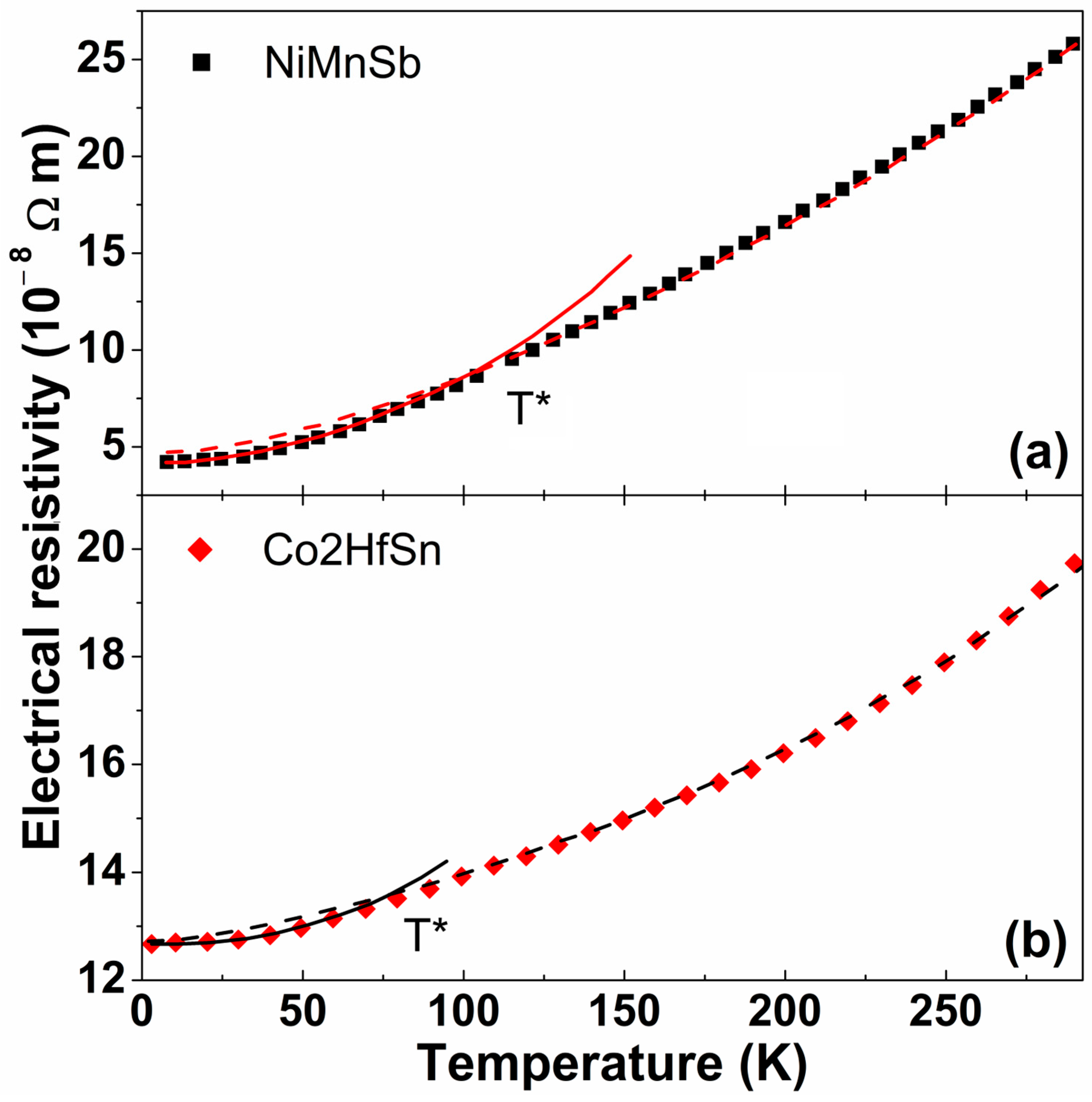
In half-metallic ferromagnets, the measurement of electrical resistivity was found to give peculiar results, which were interpreted as evidence of the presence of an actual band gap on the minority spin sub-band [85,108]. Two examples are reported in Figure 9, related to the half-Heusler NiMnSb [85] and the full-Heusler Co₂HfSn compounds [50].

A crossover temperature was reported by several studies around 80–100 K. Above such limit, resistivity was found to scale with T^α (α = 1.35–1.55, depending on the study [85,108]). In such temperature range, phonon-related resistivity should give a linear contribution with T, as prescribed by the Bloch–Grüneisen model. Also, spin diffusion would be accounted for with a T^5/3 contribution, as predicted by Ueda and Moriya (Equation (14)). Spin waves would also contribute with a linear T term, as in Equation (11). Thus, the total exponent of temperature should be a combination of those of the various contributions, which range between 1 and 5/3. Accordingly, an experimental exponent of 1.35 [108] was observed. Below 80–100 K, resistivity starts to decrease slower, as the trend was experimentally found to be proportional to T². This coincides with an electron scattering essentially caused predominantly by spin waves, as demonstrated by Ueda and Moriya (Equations (13) and (16)). As at such temperatures, the phonon contribution is negligible, the trend of resistivity ultimately can be caused by spin waves and spin-flip scattering ($R_{\uparrow \downarrow }$). Since in NiMnSb, the presence of a half-metallic band gap hinders spin-flip phenomena, the T² dependency is coherently related only to electron–magnon interactions. Such behaviour was also found for other half-metallic ferromagnets, being thus considered typical of such class of materials [111].

5.3. Spintronic Applications

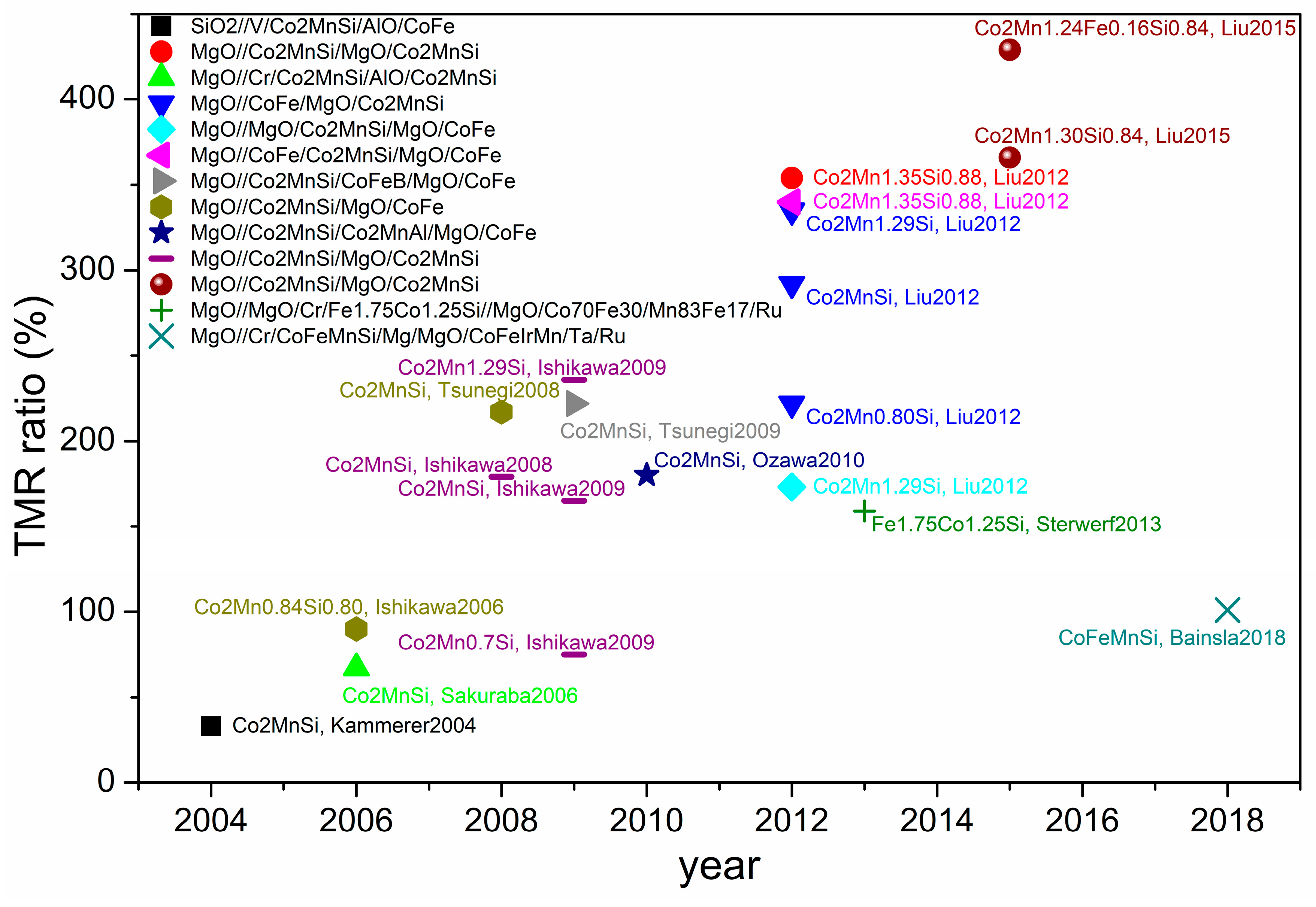
Figure 10 shows the performance evolution over the years for different MTJs (mainly based on Co₂MnSi full-Heusler compounds) in terms of the TMR ratio at room temperature (300 K ± 10 K) [93,112,113,114,115,116,117,118,119,120,121]. The performance improvement can be explained by two main factors: the MTJs’ construction and the accurate control of the alloy stoichiometry. If the same type of MTJ is considered (e.g., see the pentagon, down triangle, and sphere symbols in Figure 10, the TMR ratio increases when the amount of Mn (α) in Co₂Mn_αSi_β is increased. The observed behaviour can be explained by the detrimental effect of Co_Mn antisite defects on the spin polarization due to the insertion of gap states near E_F. Such defects have a low formation energy for Mn-poor (α < 1) and stoichiometric (α = 1) compounds and are intrinsically stable. Conversely, for Mn-rich (α > 1) compounds, Mn_Co and Mn_Si antisite defects show the lowest formation energy, suppressing the formation of the harmful Co_Mn antisite defects. It should be noted that the presence of Mn_Co and Mn_Si antisite defects does not alter the DOS around E_F, preserving the half-metallic nature of the compound and the high spin polarization [119]. Further improvement of the TMR ratio was obtained by Fe doping; also in this case, the authors claimed the suppression of the Co_Mn/Fe antisite defects due to the Mn/Fe excess [115]. Since Co is a critical raw material, it would be ideal to substitute it partially or completely. However, the attempts at substituting Co with Fe led to lower performance, as reported by Sterwerf et al. [116] and Bainsla et al. [113].

Concerning the MTJs’ construction, Liu et al. [21] explained the improved performance of the Co₂Mn_1.29Si-based junctions in terms of high-quality interfaces, showing a decreased misfit dislocation density and leading to an enhanced coherent tunnelling contribution. For the Co₂MnSi (3)/MgO (2.5)/Co₂MnSi (3) (thickness in nm) MTJ, TMR ratios of 1910% and 354% were measured at 4 K and RT, respectively [122]. A steep reduction in the TMR ratio was reported when the temperature was increased above 100 K, which was attributed to spin fluctuations at the interface with MgO. This may be caused possibly by the formation of small fractions of atomically disordered phases in proximity to the MgO barrier [52]. The Co₂FeAl (5)/MgAl₂O₄ (1.2)/Co₂FeAl (5) MTJ achieved a TMR ratio of 342% at RT [43]. The MgAl₂O₄ barrier was used instead of MgO to improve the lattice matching while maintaining coherent tunnelling. The synthesis of highly ordered Co₂FeAl_0.5Si_0.5 films in the Co2FeAl_0.5Si_0.5 (30)/MgO (1.8)/Co₂FeAl_0.5Si_0.5 (5) MTJ led to ratios of 386% at RT and 832% at 9 K [44]. Sputtered polycrystalline films have been used in a Co₂FeAl (2)/MgO (1.95)/Co_0.75Fe_0.25 (5) MTJ, achieving 175% ratio at RT [123]. The rather small figure of merit is mainly due to the film interfacial smoothness. Such value is, however, still comparable with the state-of-the-art perpendicular CoFeB/MgO/CoFeB junction, which at RT achieved 124% TMR ratio [32].

Perpendicular Heusler-based MTJs have also been characterized. Although the cubic L2₁ crystalline structure is not suited to strong magnetic orientations, perpendicular anisotropy can be induced by introducing tetragonal D0₂₂ distortion or by interfacial coupling: a Co₂FeAl (1)/MgO (1.8)/Co_0.2Fe_0.6B_0.2 (1.4) junction with a TMR ratio of 53% at RT [124]. Here, the perpendicular magnetization was introduced by interface coupling with MgO. The insertion of a 0.1 nm thick CoFe layer between MgO and Co_0.2Fe_0.6B_0.2 was found to enhance the ratio up to 91%. The magnetoresistance ratio improved up to 132% after further refinement [125].

Having mentioned such successes in practical applications, the discovery of new half-metallic Heusler alloys is crucial, as they will open more possibilities for crystal matching with insulator barriers and tailoring of magnetic properties. Co₂VAl and Co₂VGa were reported to be half metallic with 100% spin polarization by several ab initio calculations [126,127]. Single-phase bulk samples were successfully synthesized, showing lattice parameters of 5.7798 Å and 5.7920 Å, respectively [46]. Neutron diffraction measurements assessed that the L2₁ crystalline ordering of Co₂VGa is almost perfect [128], making the alloy quite suitable for in-device applications. Both magnetic and electrical conductivity characterizations suggested the existence of a half-metallic band gap in this compound [129]; however, a direct measurement of its degree of spin polarization is still lacking. On the other hand, combined pressure-dependent magnetization measurements and ab initio simulations indicated a non-perfect half metallicity for Co₂VAl, probably caused by a phase separation between the ordered L2₁ and a disordered BCC phase [46]. The series of Co₂TiSi, Co₂TiGe, and Co₂TiSn compounds was also extensively studied. The suggested half metallicity and high T_C combined with constant Seebeck coefficient was found to be of important interest for spin-caloric applications. The measurement of electric transport and magnetic properties overall suggested the occurrence of half metallicity for all three alloys. The comparison between the calculated density of states, which presents a band gap in the minority spin sub-band, and the curves obtained by hard X-ray photoelectron spectroscopy (HAXPES) were found to be rather similar, indicating that the electronic structure of the experimental samples might be similar [47].

Concerning Co₂ZrSn and Co₂HfSn, they are predicted to be half-metallic ferromagnets by ab initio calculations [130,131]. The first experimental measurements of magnetic properties from the early 1970s already reported magnetic moments of 1.51 and 1.55 μ_B, respectively. Such values are associated with lattice parameters of 6.082 Å and 6.218 Å, respectively, obtained by neutron diffraction [132]. Since the Slater–Pauling rule of thumb for ferromagnetic compounds would suggest a magnetic moment of 2.0 μ_B, assuming a perfect half metallicity [23], considerable interest has been attracted by such alloys, as their HMF behaviour is an object of debate. Another open point of discussion is the rather remarkable scattering of data in the literature concerning structural and magnetic properties. In fact, on the one hand, almost every first-principles calculation agrees on the existence of a half-metallic density of states at absolute zero and on a consequent theoretical magnetic moment of 2.0 μ_B [48,50,51,130,133]. On the other hand, experimental measurements range from 1.34 to 2.00 μ_B and from 1.50 to 2.00 μ_B for Co₂ZrSn [96,132,133,134,135,136,137] and Co₂HfSn [51,96,132,134,135,138], respectively. Such data are associated with equally scattered values of the lattice parameter of 6.226–6.251 Å for Co₂ZrSn and of 6.218–6.236 Å for Co₂HfSn (see same Ref. as above). Interestingly, in 1973, Ziebeck et al. measured a magnetization of 1.51 μ_B for Co₂ZrSn having a lattice parameter of 6.249 Å (measured by neutron diffraction) [132], whereas in 2006, Zhang et al. obtained an extremely similar magnetization value of 1.56 μ_B for a sample having an extremely different lattice parameter of 6.226 Å [137]. Such specimens were nevertheless synthesized following two extremely different routes: arc melting followed by annealing in the first case and melt spinning in the second. This difference, as well as the great dispersion of the literature data, can, with all probability, be attributed to dissimilar processing routes which ultimately lead to extremely non-reproducible samples. An explanation was proposed in 2017 by Kushwaha et al. [139], who synthesized Co₂ZrSn in different stoichiometry in the form of both single crystals and polycrystalline bulk specimens, later confirmed by Difalco et al. [49,140]. The structural and magnetic properties of Co₂ZrSn in its various compositional range were measured, eventually finding a linear dependency of magnetization and lattice parameter on the concentration of Co. The degree of disorder in the lattice was also estimated by XRD diffraction, finding that the reduction in magnetization was linearly proportional to the occupancy factor of the Co site. Such a result, which is straightforwardly linked to Co vacancy defects, was also linked to a linear shrinking of the lattice parameter as the occupancy decreased inside the samples. According to experiments and first-principles calculations, half metallicity is not affected by the presence of vacancies, underlining the robustness of this ground state. However, a shrinking of the minority-spin band gap is predicted ab initio as the vacancy concentration increases [49]. Concerning Co₂HfSn, similar explanations have been provided; nevertheless, samples with high degrees of crystalline ordering have recently been obtained more easily, making the investigation of its half-metallic properties simpler [50,51].

As far as the transport properties are concerned, the literature data are generally extremely scarce. This is disappointing, since the generation of spin-polarized currents via spin-Seebeck effect can play a major role in spintronic and spin-caloric devices [52].

6. Summary

Recently, spintronic devices have been greatly sought as a potential way to solve DRAM related issues such as high power consumption. This has become especially true recently, considering the huge power consumption of artificial intelligence facilities, making the research towards the minimization of energy consumption of microelectronic devices more important than ever.

Historically, advancements in spintronics proceeded in leaps and bounds accordingly with the discovery of new, innovative ways to enhance the signal-to-noise ratio during the reading and writing processes. The use of STT to switch the magnetization of the free layer paved the way for a first wave of renewed interest. Secondly, the ability to synthesize films with stable perpendicular magnetic anisotropy greatly improved the reliability of reading and data storage. Last, the research into innovative materials such as highly engineered CoFeB films and half-metallic Heusler alloys was also responsible for a renewed interest from the academic community and from the industry. In particular, the search for materials with high spin polarization greatly improved TMR ratios and critical writing currents, J_W, leading to important enhancements of the efficiency of MRAMs.

From the materials point of view, one key aspect in addition to obtaining the highest possible spin polarization is the electronic matching between the magnetic and the spacer layers. The discovery of MgO as the most efficient insulating barrier in MTJs can be regarded as one of the most important in spintronics; however, the formation of defects as a result of film deposition still crucially hinders optimal DOS matching. For this reason, the study of crystalline disorder, point defects, and lattice mismatches of spintronic materials has become more relevant than ever, particularly concerning half-metallic Heusler alloys. Concerning the construction of devices, CoFeB-based STT-MRAMs have become the benchmark for next-generation high-performance memory. Spin-orbit-based and voltage-controlled anisotropic (VCMA) MTJs proved to be promising candidates for future implementations; however, the physical background of their functioning is still, in most cases, not yet fully understood, requiring further research before an industrial application.

Despite such significant improvements, major challenges remain. Limited spin-injection efficiency from the ferromagnetic material to the semiconductive layer still represents a major obstacle to the advancement of devices such as spin transistors. The control at an atomic level of Heusler films represents a major problem, as does the optimization of the Gilbert damping constant to achieve faster magnetization switching. Also, a further increase in T_C is to be pursued for diluted magnetic semiconductors. Furthermore, recent advancements in the characterization and fabrication of nanoscale frameworks paved the way for the investigation of films down to the 2D limit. With the advancements in large-scale 2D growth techniques (i.e., chemical vapour deposition), two-dimensional spintronic logic devices are seen by many as a new frontier for next-generation materials [141].

Overall, the compatibility between spintronic MTJs and already existing Si-based frameworks, and the promising perspectives of MRAMs to solve the intrinsic issues of capacitor-based DRAMs (high power consumption, charge leakage, etc.), are the driving force that justify the scientific effort towards the development of more reliable and powerful spintronic memory, increasingly making such devices objects not only of limited academic interest, but of large-scale consumer-goods products.