A Self-Consistent Exact Diagonalization Approach to the Ground State Magnetic Properties of the Meridional [V(ddpd)2]3+ Complex
Abstract
1. Introduction
2. Theoretical Background
2.1. General Considerations
2.2. The Hamiltonian
2.3. Computational Details
- A module for defining and accessing basis functions under SymPy. Using the tesseral spherical harmonics for the representation of single-electron 3d orbitals, we constructed all antisymmetric two-electron basis states relevant to the considered system (see Supplementary Material, Equation (S1)) to be accessed when computing the corresponding energy spectrum.
- A kernel module for computing the matrix elements , with the Hamiltonian presented in Equation (1) and state functions given in the Supplementary Material Equation (S1). Each matrix element was computed along with the appropriate parameterization (see Table 1).
- An analysis module, which was used to substitute numerical values for the parameters of the model, perform direct diagonalization, and make predictions, such as the energy eigenstates and the corresponding 3d orbital configurations.
- A master module, which was used to control and schedule the execution of all previously-mentioned modules.
2.4. The Effective Zero-Field Single-Ion Spin Hamiltonian
3. Magnetic Properties
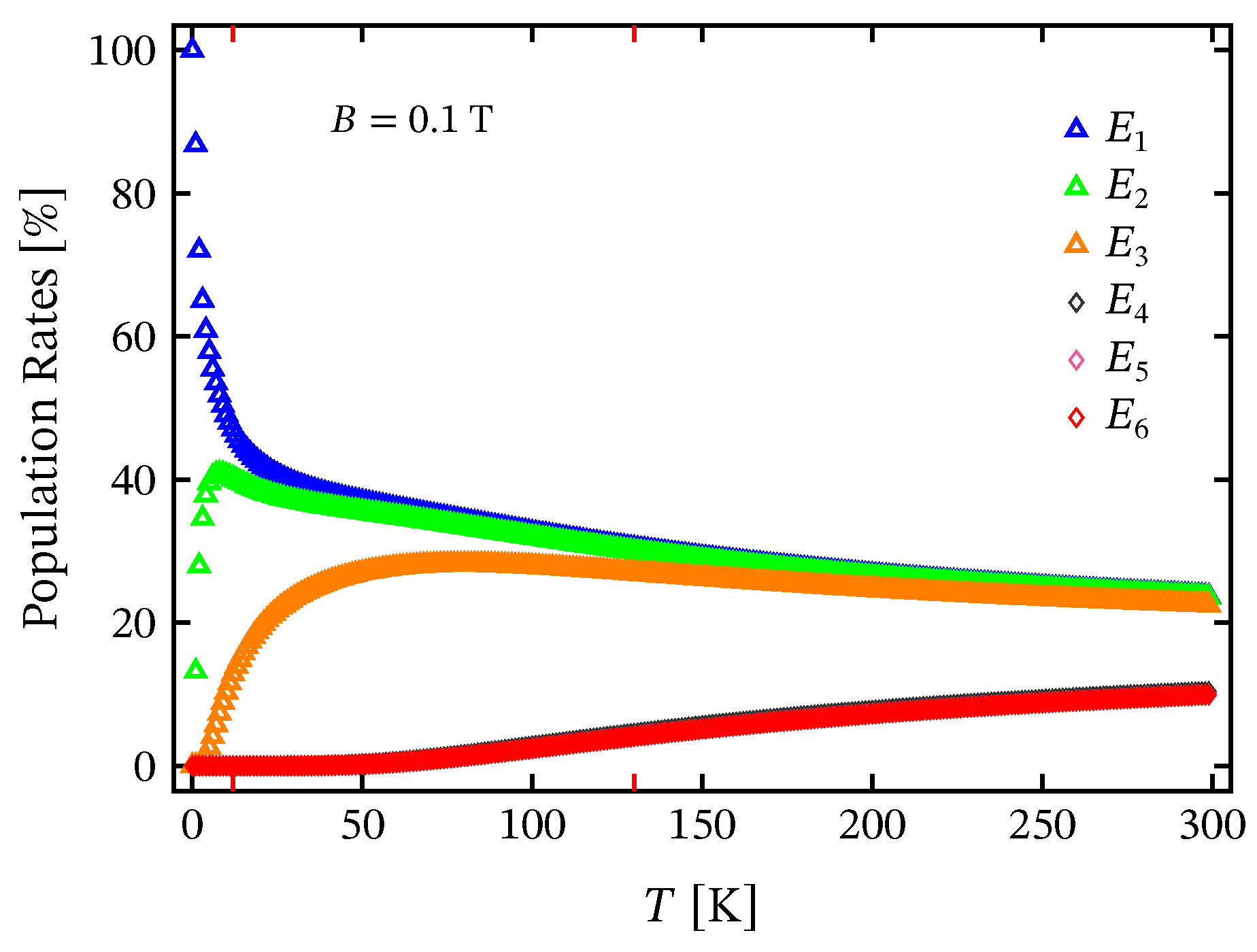
3.1. Zero-Field Properties
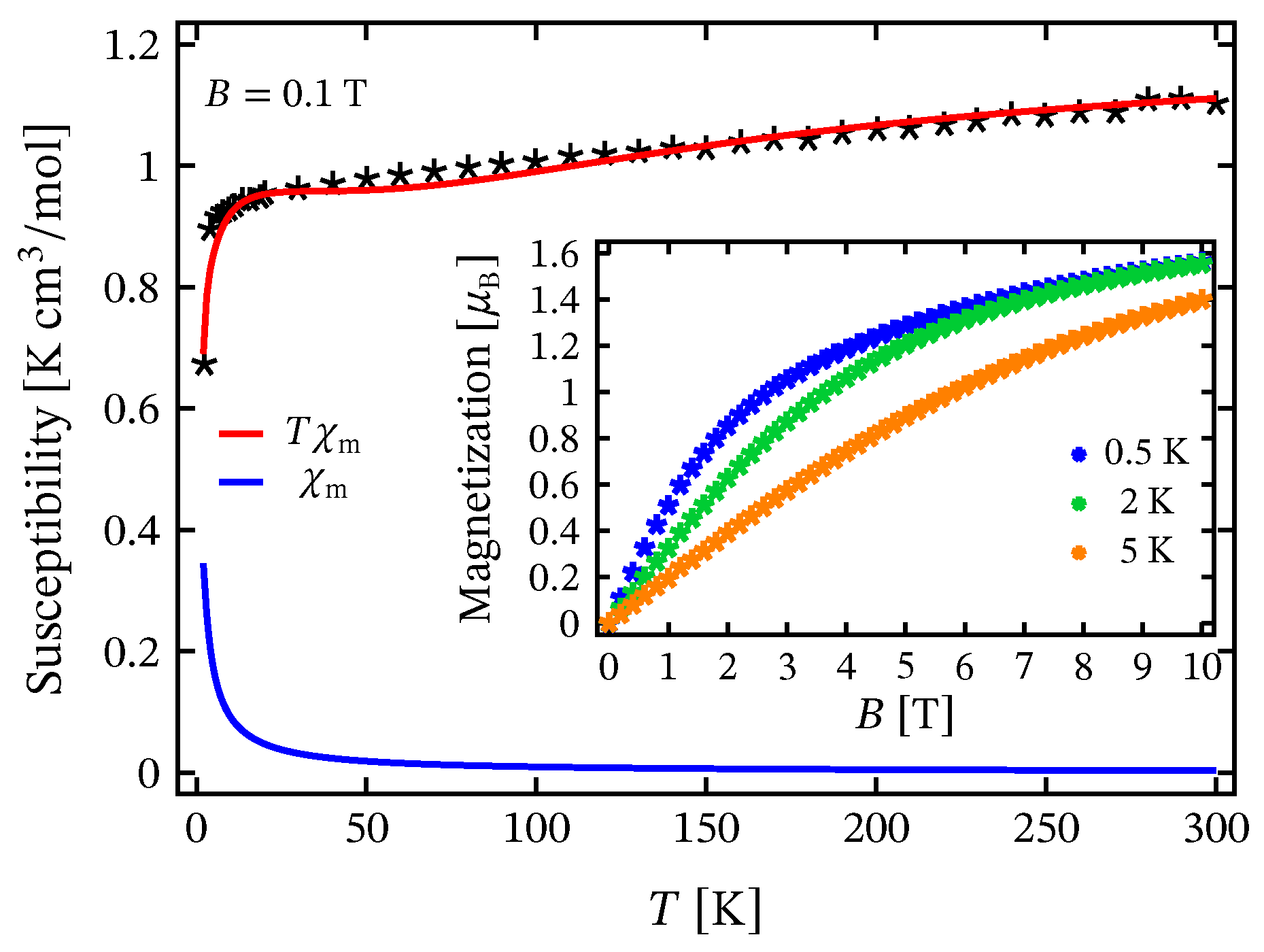
3.2. Susceptibility and Magnetization
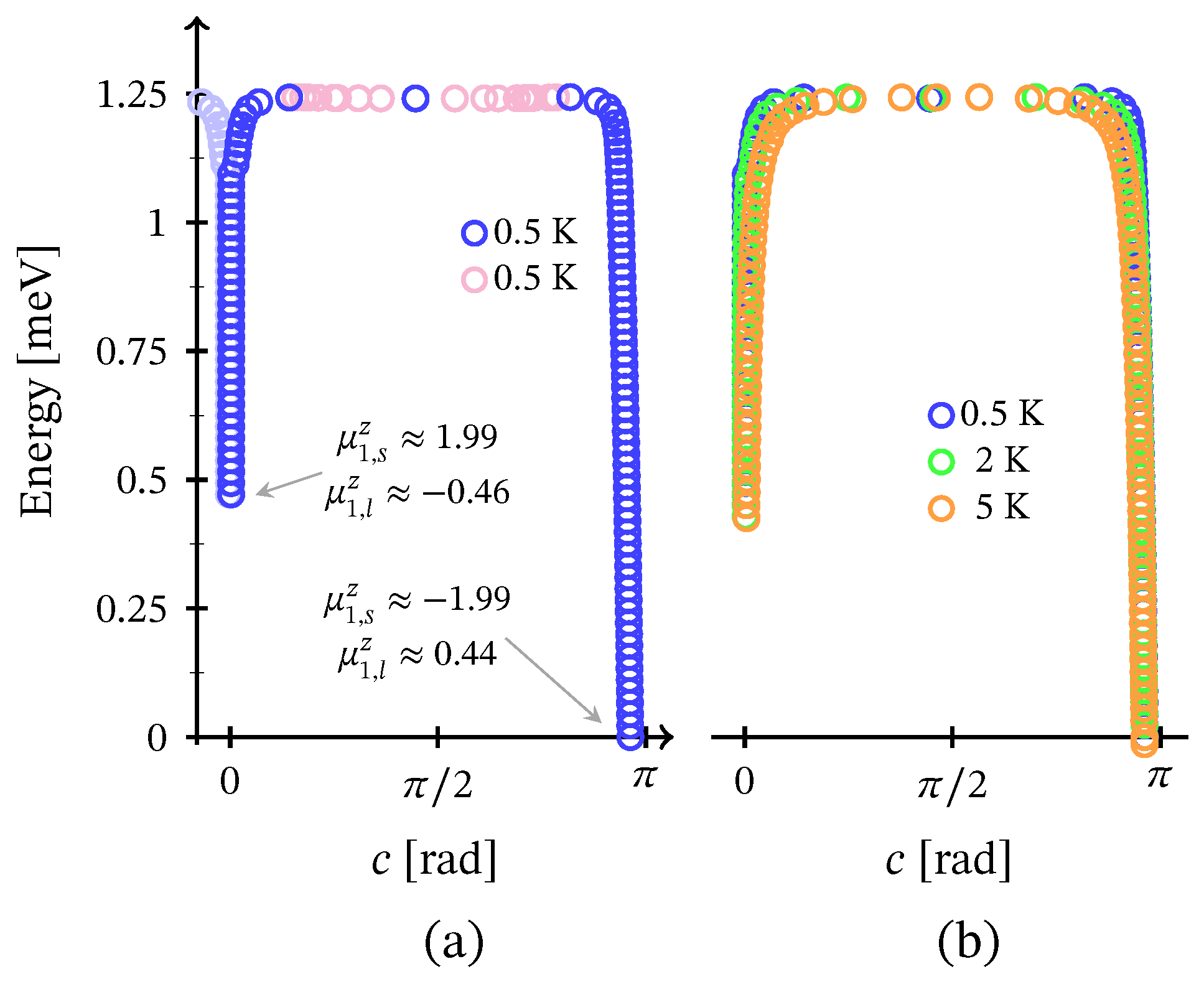
3.3. Magnetization Reversal
4. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boča, R. Theoretical Foundations of Molecular Magnetism; Elsevier: Burlington, MA, USA, 1999. [Google Scholar]
- Kahn, O. Molecular Magnetism, 4th ed.; Wiley-VCH: New York, NY, USA, 2001. [Google Scholar]
- Linert, W.; Verdaguer, M. (Eds.) Molecular Magnets Recent Highlights; Springer: Vienna, Austria, 2003. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Coulon, C.; Miyasaka, H.; Clérac, R. Single-Chain Magnets: Theoretical Approach and Experimental Systems. In Single-Molecule Magnets and Related Phenomena; Winpenny, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 122, pp. 163–206. [Google Scholar] [CrossRef]
- Winpenny, R. Molecular Cluster Magnets; World Scientific Series in Nanoscience and Nanotechnology; World Scientific: Singapore, 2011; Volume 3. [Google Scholar] [CrossRef]
- Bartolomé, J.; Luis, F.; Fernández, J.F. (Eds.) Molecular Magnets: Physics and Applications; NanoScience and Technology; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Sessoli, R. Magnetic molecules back in the race. Nature 2017, 548, 400–401. [Google Scholar] [CrossRef] [PubMed]
- Sieklucka, B.; Pinkowicz, D. (Eds.) Molecular Magnetic Materials: Concepts and Applications; Wiley: Weinheim, Germany, 2017. [Google Scholar]
- Hołyńska, M. Single-Molecule Magnets: Molecular Architectures and Building Blocks for Spintronics; Wiley: Weinheim, Germany, 2019. [Google Scholar]
- Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. [Google Scholar] [CrossRef]
- Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow Magnetic Relaxation in a High-Spin Iron(II) Complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef] [PubMed]
- Harman, W.H.; Harris, T.D.; Freedman, D.E.; Fong, H.; Chang, A.; Rinehart, J.D.; Ozarowski, A.; Sougrati, M.T.; Grandjean, F.; Long, G.J.; et al. Slow Magnetic Relaxation in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes. J. Am. Chem. Soc. 2010, 132, 18115–18126. [Google Scholar] [CrossRef] [PubMed]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Marriott, K.E.R.; Bhaskaran, L.; Wilson, C.; Medarde, M.; Ochsenbein, S.T.; Hill, S.; Murrie, M. Pushing the limits of magnetic anisotropy in trigonal bipyramidal Ni(II). Chem. Sci. 2015, 6, 6823–6828. [Google Scholar] [CrossRef]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef]
- Feng, M.; Tong, M.L. Single Ion Magnets from 3d to 5f: Developments and Strategies. Chem. Eur. J. 2018, 24, 7574–7594. [Google Scholar] [CrossRef]
- Shao, D.; Wang, X. Development of Single-Molecule Magnets. Chin. J. Chem. 2020, 38, 1005–1018. [Google Scholar] [CrossRef]
- Perlepe, P.S.; Maniaki, D.; Pilichos, E.; Katsoulakou, E.; Perlepes, S.P. Smart Ligands for Efficient 3d-, 4d- and 5d-Metal Single-Molecule Magnets and Single-Ion Magnets. Inorganics 2020, 8, 39. [Google Scholar] [CrossRef]
- Zhuo, Z.; Li, G.; Huang, Y. Understanding Magneto-Structural Correlations Toward Design of Molecular Magnets. In Advanced Structural Chemistry; Cao, R., Ed.; Wiley: Weinheim, Germany, 2021; pp. 777–832. [Google Scholar] [CrossRef]
- Landart-Gereka, A.; Quesada-Moreno, M.M.; Díaz-Ortega, I.F.; Nojiri, H.; Ozerov, M.; Krzystek, J.; Palacios, M.A.; Colacio, E. Large easy-axis magnetic anisotropy in a series of trigonal prismatic mononuclear cobalt(II) complexes with zero-field hidden single-molecule magnet behaviour: The important role of the distortion of the coordination sphere and intermolecular interactions in the slow relaxation. Inorg. Chem. Front. 2022, 9, 2810–2831. [Google Scholar] [CrossRef]
- Krzystek, J.; Ozarowski, A.; Telser, J.; Crans, D.C. High-frequency and -field electron paramagnetic resonance of vanadium(IV, III, and II) complexes. Coord. Chem. Rev. 2015, 301–302, 123–133. [Google Scholar] [CrossRef]
- Wegeberg, C.; Wenger, O.S. Luminescent First-Row Transition Metal Complexes. JACS Au 2021, 1, 1860–1876. [Google Scholar] [CrossRef]
- Beaulac, R.; Tregenna-Piggott, P.L.W.; Barra, A.L.; Weihe, H.; Luneau, D.; Reber, C. The Electronic Ground State of [V(urea)6]3+ Probed by NIR Luminescence, Electronic Raman, and High-Field EPR Spectroscopies. Inorg. Chem. 2006, 45, 3399–3407. [Google Scholar] [CrossRef]
- Tregenna-Piggott, P.L.W.; Spichiger, D.; Carver, G.; Frey, B.; Meier, R.; Weihe, H.; Cowan, J.A.; McIntyre, G.J.; Zahn, G.; Barra, A.L. Structure and Bonding of the Vanadium(III) Hexa-Aqua Cation. 1. Experimental Characterization and Ligand-Field Analysis. Inorg. Chem. 2004, 43, 8049–8060. [Google Scholar] [CrossRef]
- Bowman, A.C.; Sproules, S.; Wieghardt, K. Electronic Structures of the [V(tbpy)3]z (z = 3+, 2+, 0, 1−) Electron Transfer Series. Inorg. Chem. 2012, 51, 3707–3717. [Google Scholar] [CrossRef]
- Van Stappen, C.; Maganas, D.; DeBeer, S.; Bill, E.; Neese, F. Investigations of the Magnetic and Spectroscopic Properties of V(III) and V(IV) Complexes. Inorg. Chem. 2018, 57, 6421–6438. [Google Scholar] [CrossRef]
- Dorn, M.; Kalmbach, J.; Boden, P.; Kruse, A.; Dab, C.; Reber, C.; Niedner-Schatteburg, G.; Lochbrunner, S.; Gerhards, M.; Seitz, M.; et al. Ultrafast and long-time excited state kinetics of an NIR-emissive vanadium(III) complex I: Synthesis, spectroscopy and static quantum chemistry. Chem. Sci. 2021, 12, 10780–10790. [Google Scholar] [CrossRef]
- Fataftah, M.S.; Bayliss, S.L.; Laorenza, D.W.; Wang, X.; Phelan, B.T.; Wilson, C.B.; Mintun, P.J.; Kovos, B.D.; Wasielewski, M.R.; Han, S.; et al. Trigonal Bipyramidal V3+ Complex as an Optically Addressable Molecular Qubit Candidate. J. Am. Chem. Soc. 2020, 142, 20400–20408. [Google Scholar] [CrossRef]
- Georgiev, M.; Chamati, H. Magnetostructural Dependencies in 3d2 Systems: The Trigonal Bipyramidal V3+ Complex. Phys. Status Solidi B 2022, 2100645. [Google Scholar] [CrossRef]
- Goh, T.; Pandharkar, R.; Gagliardi, L. Multireference Study of Optically Addressable Vanadium-Based Molecular Qubit Candidates. J. Phys. Chem. A 2022, 126, 6329–6335. [Google Scholar] [CrossRef] [PubMed]
- Dorn, M.; Hunger, D.; Förster, C.; Naumann, R.; Van Slageren, J.; Heinze, K. Towards Luminescent Vanadium(II) Complexes with Slow Magnetic Relaxation and Quantum Coherence. Chem. A Eur. J. 2023, 29, e202202898. [Google Scholar] [CrossRef] [PubMed]
- Dorn, M.; Kalmbach, J.; Boden, P.; Päpcke, A.; Gómez, S.; Förster, C.; Kuczelinis, F.; Carrella, L.M.; Büldt, L.A.; Bings, N.H.; et al. A Vanadium(III) Complex with Blue and NIR-II Spin-Flip Luminescence in Solution. J. Am. Chem. Soc. 2020, 142, 7947–7955. [Google Scholar] [CrossRef] [PubMed]
- Yosida, K. Theory of Magnetism; Springer Series in Solid-State Sciences; Springer: Berlin, Germany; New York, NY, USA, 1996. [Google Scholar]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Oxford Classic Texts in the Physical Sciences; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Rudowicz, C.; Karbowiak, M. Disentangling intricate web of interrelated notions at the interface between the physical (crystal field) Hamiltonians and the effective (spin) Hamiltonians. Coord. Chem. Rev. 2015, 287, 28–63. [Google Scholar] [CrossRef]
- Maurice, R.; Broer, R.; Guihéry, N.; de Graaf, C. Zero-Field Splitting in Transition Metal Complexes: Ab Initio Calculations, Effective Hamiltonians, Model Hamiltonians, and Crystal-Field Models. In Handbook of Relativistic Quantum Chemistry; Liu, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 765–796. [Google Scholar] [CrossRef]
- Rudowicz, C. Concept of Spin Hamiltonian, Forms of Zero Field Splitting and Electronic Zeeman Hamiltonians and Relations between Parameters Used in EPR: A Critical Review. Mag. Res. Rev. 1987, 13, 1–89, Erratum in Mag. Res. Rev. 1988, 13, 335. [Google Scholar] [CrossRef]
- Joyce, J.P.; Portillo, R.I.; Rappé, A.K.; Shores, M.P. Doublet Ground State in a Vanadium(II) Complex: Redox and Coordinative Noninnocence of Tripodal Ligand Architecture. Inorg. Chem. 2022, 61, 6376–6391. [Google Scholar] [CrossRef]
- Bazhenova, T.A.; Zorina, L.V.; Simonov, S.V.; Mironov, V.S.; Maximova, O.V.; Spillecke, L.; Koo, C.; Klingeler, R.; Manakin, Y.V.; Vasiliev, A.N.; et al. The first pentagonal-bipyramidal vanadium(III) complexes with a Schiff-base N3O2 pentadentate ligand: Synthesis, structure and magnetic properties. Dalton Trans. 2020, 49, 15287–15298. [Google Scholar] [CrossRef]
- Georgiev, M.; Chamati, H. Fine Structure and the Huge Zero-Field Splitting in Ni2+ Complexes. Molecules 2022, 27, 8887. [Google Scholar] [CrossRef]
- Newman, D.J.; Ng, B. The superposition model of crystal fields. Rep. Prog. Phys. 1989, 52, 699–762. [Google Scholar] [CrossRef]
- Meurer, A.; Smith, C.P.; Paprocki, M.; Čertík, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S.; et al. SymPy: Symbolic computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]
- Georgiev, M.; Chamati, H. Single-Ion Magnets with Giant Magnetic Anisotropy and Zero-Field Splitting. ACS Omega 2022, 7, 42664–42673. [Google Scholar] [CrossRef]
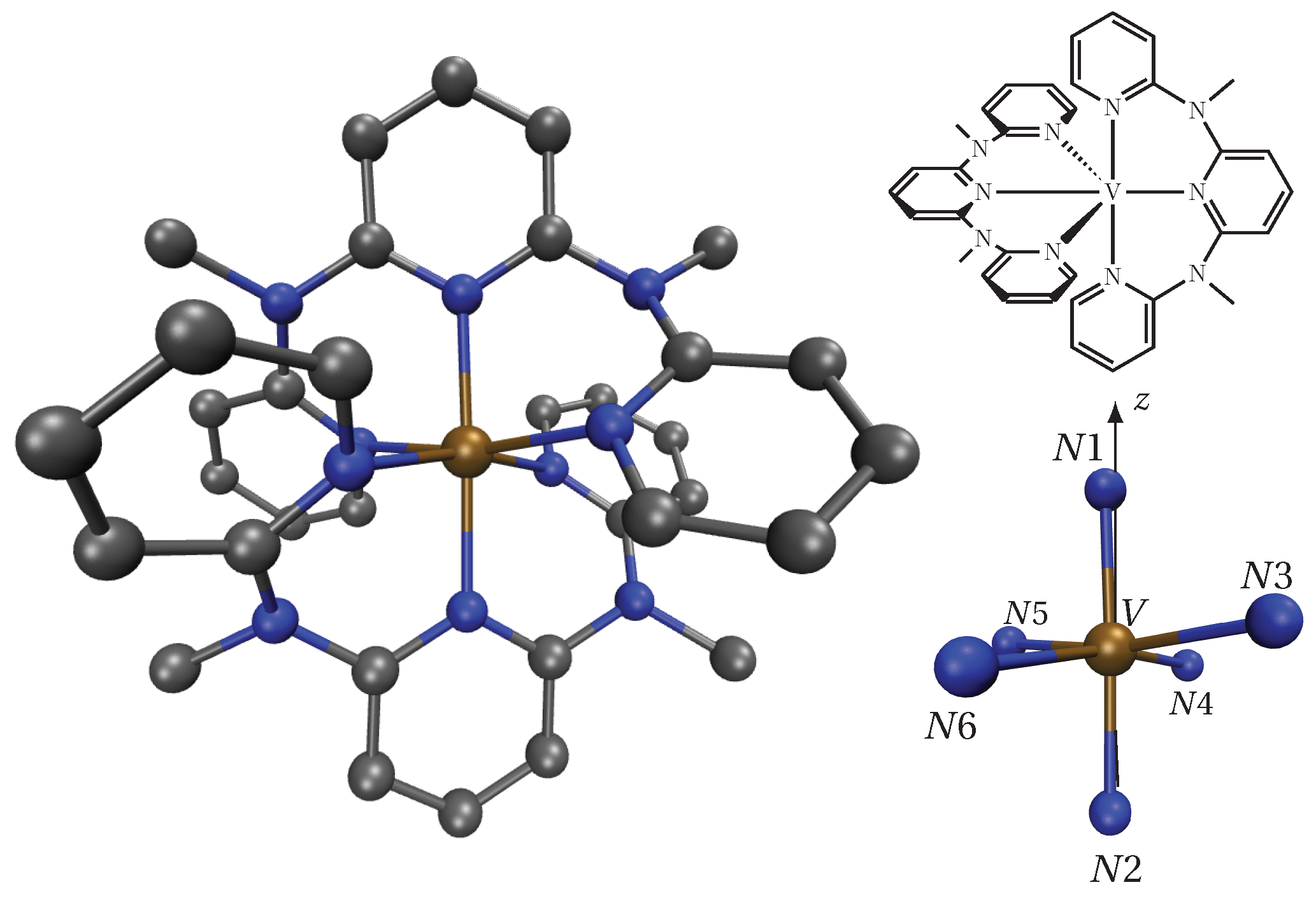
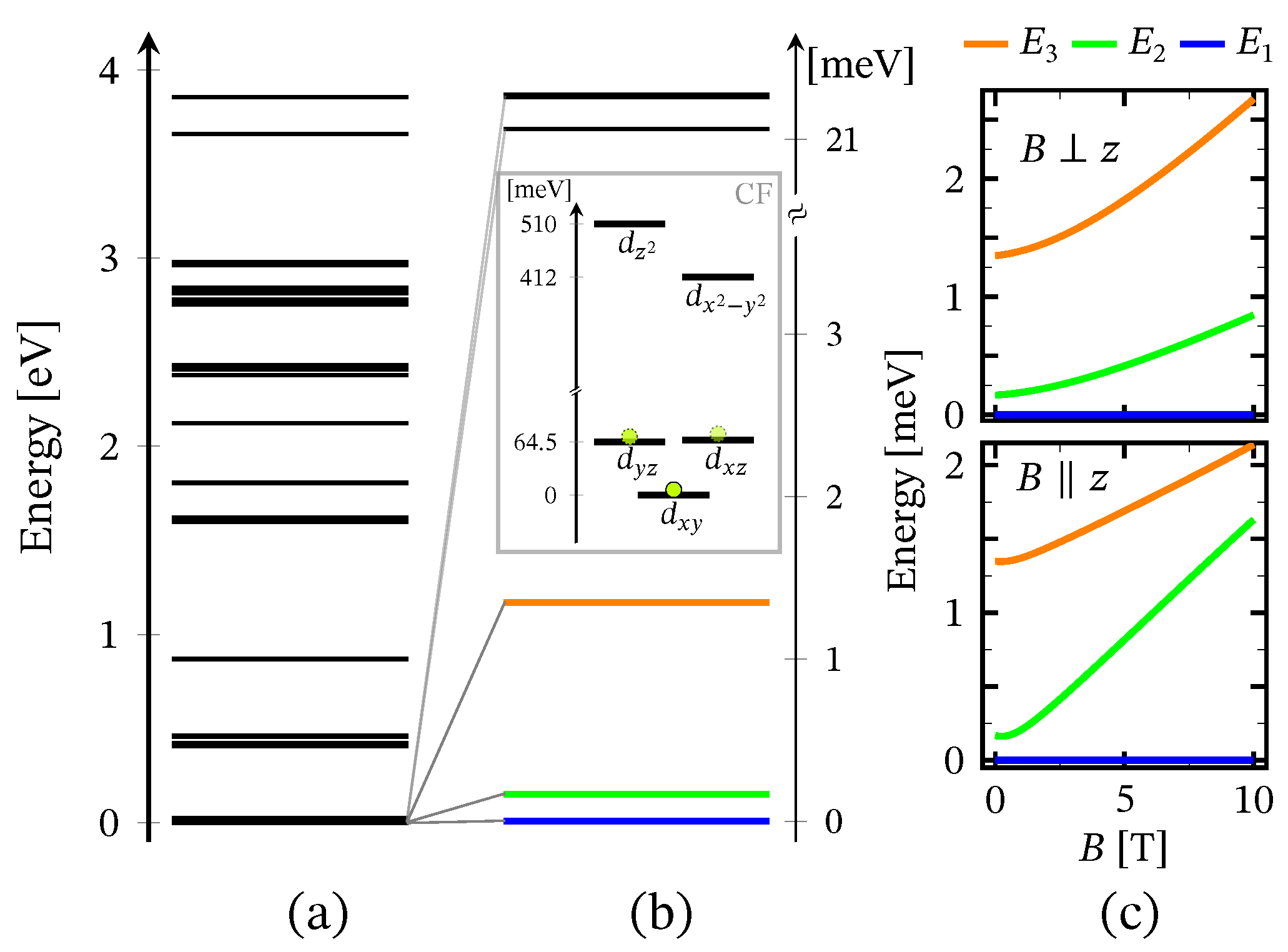
| N1 | N2 | N3 | N4 | N5 | N6 | V | |
|---|---|---|---|---|---|---|---|
| [deg] | 270 | 270 | 270 | – | |||
| [deg] | 179 | – | |||||
| [Å] | – | ||||||
| Z | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, M.; Baronian, T.; Chamati, H. A Self-Consistent Exact Diagonalization Approach to the Ground State Magnetic Properties of the Meridional [V(ddpd)2]3+ Complex. Inorganics 2023, 11, 268. https://doi.org/10.3390/inorganics11070268
Georgiev M, Baronian T, Chamati H. A Self-Consistent Exact Diagonalization Approach to the Ground State Magnetic Properties of the Meridional [V(ddpd)2]3+ Complex. Inorganics. 2023; 11(7):268. https://doi.org/10.3390/inorganics11070268
Chicago/Turabian StyleGeorgiev, Miroslav, Takvor Baronian, and Hassan Chamati. 2023. "A Self-Consistent Exact Diagonalization Approach to the Ground State Magnetic Properties of the Meridional [V(ddpd)2]3+ Complex" Inorganics 11, no. 7: 268. https://doi.org/10.3390/inorganics11070268
APA StyleGeorgiev, M., Baronian, T., & Chamati, H. (2023). A Self-Consistent Exact Diagonalization Approach to the Ground State Magnetic Properties of the Meridional [V(ddpd)2]3+ Complex. Inorganics, 11(7), 268. https://doi.org/10.3390/inorganics11070268






