Electrolytes in Multiple-Phase Hydrogen Storage Reactions

Abstract

Multiple-phase hydrogen storage materials such as metal alanates and borohydrides, and destabilized systems offer the possibility of high hydrogen storage capacity with favorable thermodynamics. However, the multiphase nature of these materials intrinsically limits the kinetics due to the required transport of species between phases, which are typically in dry powder form. To address this limitation, the influence of added electrolytes is explored. This approach is motivated by analogy with similar multiphase battery reactions that show reduced kinetic limitations while necessarily containing electrolytes. Previous experimental results showing improved kinetics for MgH₂/Sn (using a LiBH₄/KBH₄ eutectic electrolyte) and NaAlH₄ (using a diglyme electrolyte) are further analyzed in terms of this analogy. The results show that the analogy is useful and rate constants are increased. Importantly, the inclusion of an electrolyte also appears to alleviate the continuously decreasing rates with the extent of reaction, which is characteristic of many multiphase hydrides. Instead, reaction rates are approximately constant until near completion. Together, these effects can lead to >10× shorter overall reaction times. In addition, new results are presented for the hydrogenation of MgB₂ using Li/K/CsI and Li/K/CsCl eutectic electrolytes, where >60% conversion to Mg(BH₄)₂ was demonstrated at 350 bar.

1. Introduction

Many candidate hydrogen storage materials with high capacities and thermodynamics appropriate for proton exchange membrane (PEM) fuel cells used in transportation applications contain multiple solid phases that must nucleate, grow, and be consumed as hydrogen is released and stored. The presence of multiple solid phases in these materials hinders the kinetics of the solid phase transformations that occur as hydrogen is exchanged because solid–solid reactions can only occur where particles of different phases are in physical contact at the atomic scale. This contact is difficult given the typical mixed powder form of these materials and the irregular shape of powder particles at the atomic scale. Overall, this limits the rate at which hydrogen can be released and stored. As a result, most multiple solid-phase hydrogen storage materials are not practical for commercial use.

In our previous work, an investigation of electrolyte-assisted hydrogen storage reactions in destabilized hydrides (MgH₂/Sn) and complex hydrides (LiAlH₄, NaAlH₄, Mg(BH₄)₂) revealed significantly reduced reaction times for hydrogen desorption and uptake in the presence of an electrolyte [1,2]. In this work, we provide motivation and background for the use of electrolytes by describing the kinetic limitations in terms of subjective kinetic temperatures and excess free energies. Using these descriptors, we compare multiphase hydrogen storage reactions with analogous multiphase battery reactions, in which electrolytes are necessarily always present due to the electrochemical form of the reactions [3]. Within this context, we summarize the influence of electrolytes on MgH₂/Sn (using a LiBH₄/KBH₄ eutectic electrolyte), NaAlH₄ (using a diglyme electrolyte) and also give further results for the hydrogenation of MgB₂ (using Li/K/CsI and Li/K/CsCl eutectic electrolytes). We found that, in addition to the expected increase in reaction rates, electrolytes enable reactions to proceed at a constant rate, independent of the extent of the reaction.

2. Motivation and Background

To describe the kinetic limitations for thermochemical reactions (in dry powder form) and compare them with those for electrochemical reactions (containing liquid electrolytes) we first discuss the MgH₂/Si destabilized hydride reaction and then the Mg/Sn battery reaction.

2.1. Kinetic Limitations and Excess Free Energy

The MgH₂/Si system is based on MgH₂, which has a high gravimetric hydrogen capacity of 7.6 wt% but is thermodynamically too stable for practical use. Specifically, the enthalpy (∆H) for dehydrogenation is 74.5 kJ/mol-H₂ and the entropy (∆S) is 135 J/K-mol-H₂ [4] (thermodynamic values for the reactions discussed in this work are compiled in

Table 1. Thermodynamic values for various hydrogen storage and battery reactions.

Reaction	ΔG0 (kJ/mol-H2 or Mg)	ΔH (kJ/mol-H2)	ΔS (J/K-mol-H2)	T1bar (°C)
MgH2	37.0	74.5	135	280
MgH2/Si	0.7	36.8	128	15
MgH2/Sn	2.3	39.0	125	39
Mg/Si	−37.5
Mg/Sn	−34.7
LiBH4/MgH2	15.4	45.8	104	170
Mg(BH4)2 (1st step)		39.2	99.8	20
NaAlH4 (1st step)		39.1	127	33

). These values give a temperature for an equilibrium hydrogen pressure of 1 bar (T_1bar) of 280 °C, using T_1bar = ∆H/∆S, which is too high for transportation applications. However, the thermodynamic properties of MgH₂ can be tuned by using silicon as a destabilizing additive [5,6]. MgH₂ and Si react according to the reaction 2 MgH₂ + Si → Mg₂Si + 2 H₂, which contains 5.0 wt% hydrogen and has a much lower T_1bar of ~15 °C (Table 1), due to the stability of Mg₂Si relative to pure Mg. For this reaction to proceed, MgH₂ in a single-step reaction, or Mg metal in a two-step reaction, must react with Si to form Mg₂Si. This requires atomic scale contact between the MgH₂ and Si solid phases, which is difficult to achieve. As a result, effectively no reaction occurs between MgH₂ and Si at 15 °C. As shown in Figure 1a for a typical formulation of a mechanically milled mixture of 2 MgH₂ + Si undergoing a constant heating ramp (2 °C/min), the onset of the desorption reaction occurs at ~270 °C. Following Ref. [7] (p. 4554), we define this temperature as the kinetic temperature, T_K = 270 °C. This temperature is a subjective assessment of where a reaction begins to occur at a practical rate. For this system, the rate at 270 °C is 0.28 wt%-H₂/h. The difference between T_1bar and T_K illustrates the kinetic limitation, i.e., T_K = ~270 °C >> T_1bar = ~15 °C.

Using T_K, we can further define the kinetic limitation in terms of an excess kinetic free energy (∆G_K) using the expression ∆G_K = (T_K − T_1bar)•∆S. We note that ∆G_K is not a true thermodynamic quantity; rather it is subjective based on T_K chosen at a practical rate of dehydrogenation. Although reactions are thermodynamically spontaneous for ∆G < 0, we express ∆G_K as a positive quantity to represent the free energy required to drive a kinetically hindered reaction that is in excess of the thermodynamic driving force. The values above give ∆G_K = 34 kJ/mol-H₂ for the MgH₂/Si system (values for ∆G_K are tabulated in Table 2). Considerable effort has been devoted to improving (i.e., lowering) T_K and ∆G_K. Using catalysts and nanoscale particles to increase interfacial area, T_K = 200 °C with ∆G_K = 24 kJ/mol-H₂ has been achieved [8]. Although improved, these values are still too high for practical use.

Other hydrogen storage materials display similar excess kinetic free energies. For example, the hydrogen storage reaction 2 LiBH₄ + MgH₂ → 2 LiH + MgB₂ + 2 H₂ contains 11.4 wt% hydrogen with T_1bar = 170 °C (Table 1), while experimentally, T_K = 380 °C [7]. Thus, ∆G_K = 22 kJ/mol-H₂. Another example is Mg(BH₄)₂, which has 14.8 wt% hydrogen and dehydrogenates according to the overall reaction Mg(BH₄)₂ → MgB₂ + 4 H₂. In detail, this reaction actually occurs in 3 or 4 steps beginning with the formation of MgB₁₂H₁₂ at T_K = 250 °C [7,9,10]. The enthalpies and entropies for these reactions have not been determined experimentally, although density functional theory calculations give T_1bar = 20 °C (Table 1) for the 1st step [11]. This gives, ∆G_K = 23 kJ/mol-H₂. These examples are further evidence that dehydrogenation reactions across solid/solid interfaces are kinetically limited and typically require ≥20 kJ/mol-H₂ of excess kinetic free energy to initiate the reaction.

2.2. Analogy with Multiphase Electrochemical Battery Reactions

In contrast to the extremely poor kinetics of the multiphase hydrogen storage reactions, similar multiphase battery reactions (known as “alloy” and “conversion” reactions in the battery research community) can operate at or near room temperature [12]. Examples include Li/SnO₂ [13], which forms Li₂O irreversibly and Li_nSn alloys reversibly, Li/FeF₂ [14], which forms LiF + Fe reversibly, and Mg/Sn [15], which forms Mg₂Sn reversibly.

To illustrate quantitatively the difference between a battery reaction and an analogous hydrogen storage reaction, we consider here the free energy driving forces (ΔG) for the Mg/Sn alloying battery reaction and then relate these to the MgH₂/Si hydrogen storage reaction. Discharge of a Mg/Sn battery, given by the reaction Mg + 0.5 Sn → 0.5 Mg₂Sn, is exothermic with a calculated free energy ΔG = −34.7 kJ/mol-Mg, which for this electrochemical reaction corresponds to a reversible potential E_rev = 0.18 V (using ΔG = −n•F•E with n = 2 and F = 96,485 C/mol). As shown in Figure 1b, a complete reaction between Mg and Sn has been observed at room temperature in a battery with an electrolyte appropriate for Mg²⁺ [15]. The discharge reaction occurs at 0.16 V (ΔG = −30.9 kJ/mol-Mg), which is lower than E_rev indicating some kinetic limitation. This is typically called an overpotential. However, to make a connection to hydrogen storage reactions, we use free energy. From the differences in free energy with −34.7 kJ/mol-Mg possible but only −30.9 kJ/mol-Mg obtained, the excess free energy is (as above, expressed as a positive quantity) ∆G_K = 3.8 kJ/mol-Mg. For an electrochemical reaction in general, the excess kinetic free energy can be given by ∆G_K = |−n•F•(E_dis/recharge − E_rev)|, where E_dis/recharge is the actual measured potential for discharge or recharge and the absolute value is use to express ∆G_K as a positive quantity. More importantly, the reverse recharging reaction which is endothermic (ΔG = +34.7 kJ/mol-Mg) was also observed at room temperature by applying a voltage of 0.21 V (−40.5 kJ/mol-Mg), giving ∆G_K = 5.8 kJ/mol-Mg. Thus, in the battery environment, this multiphase alloying reaction was reversibly driven electrochemically at room temperature at practical rates with an excess kinetic free energy ∆G_K ~ 5 kJ/mol.

Figure 1. The analogy between thermochemical hydrogen storage reactions and electrochemical battery reactions. (a) MgH₂/Si destabilized the hydride system. Following the convention used for batteries, the extent of the hydrogen desorption reaction (during heating ramp of 2 °C/min) is shown on the x-axis (given by the amount of desorbed hydrogen in wt%) with the driving force for the reaction (given by the temperature) on the left y-axis. Although the equilibrium temperature at 1 bar is calculated to be 15 °C, no significant hydrogen desorption occurs until the temperature is increased to 270 °C. The corresponding excess kinetic free energy is given on the right y-axis. (b) Mg/Sn battery reaction (based on data obtained from Ref. [15]). A conventional depiction is shown with the extent of reaction (given by the specific capacity in mAh/g) on the x-axis and the driving force (given for an electrochemical reaction by the potential in V) on the left y-axis. The capacity is shown as increasing during the discharge reaction (forming Mg₂Sn) and decreasing during the recharge reaction (reforming Mg + Sn). The calculated reversible, i.e., equilibrium, potential is 0.18 V. Discharge is seen to occur at a lower potential of 0.16 V while the recharge occurs at a higher potential of 0.21 V. The corresponding excess kinetic free energy is given on the right y-axis with positive values below 0.18 V pertaining to the discharge reaction and positive values above 0.18 V pertaining to the recharge reaction.

Figure 1. The analogy between thermochemical hydrogen storage reactions and electrochemical battery reactions. (a) MgH₂/Si destabilized the hydride system. Following the convention used for batteries, the extent of the hydrogen desorption reaction (during heating ramp of 2 °C/min) is shown on the x-axis (given by the amount of desorbed hydrogen in wt%) with the driving force for the reaction (given by the temperature) on the left y-axis. Although the equilibrium temperature at 1 bar is calculated to be 15 °C, no significant hydrogen desorption occurs until the temperature is increased to 270 °C. The corresponding excess kinetic free energy is given on the right y-axis. (b) Mg/Sn battery reaction (based on data obtained from Ref. [15]). A conventional depiction is shown with the extent of reaction (given by the specific capacity in mAh/g) on the x-axis and the driving force (given for an electrochemical reaction by the potential in V) on the left y-axis. The capacity is shown as increasing during the discharge reaction (forming Mg₂Sn) and decreasing during the recharge reaction (reforming Mg + Sn). The calculated reversible, i.e., equilibrium, potential is 0.18 V. Discharge is seen to occur at a lower potential of 0.16 V while the recharge occurs at a higher potential of 0.21 V. The corresponding excess kinetic free energy is given on the right y-axis with positive values below 0.18 V pertaining to the discharge reaction and positive values above 0.18 V pertaining to the recharge reaction.

The chemistry of Mg reacting (alloying) with Sn and Si is similar. For example, with Si the battery reaction Mg + 0.5 Si → 0.5 Mg₂Si has ΔG = −37.5 kJ/mol-Mg (versus −34.7 kJ/mol-Mg for Sn). However, the reaction rates are much different for the analogous MgH₂/Si hydrogen storage reaction where endothermic dehydrogenation is not observed until ≥200 °C [8], at which temperature the excess free energy is 24 kJ/mol-H₂. A comparison of these analogous reactions reveals that a ΔG_K = 5 kJ is sufficient to drive the battery reaction (electrochemically), while ΔG_K = 24 kJ is needed to drive a similar hydrogen storage reaction (thermochemically). Furthermore, despite being exothermic, the reverse hydrogenation reaction of Mg₂Si has not been observed even under 1850 bar H₂ [16], which is equivalent to an excess free energy of ~20 kJ at room temperature.

We contend that the lower excess free energy required to drive reactions electrochemically (as opposed to thermochemically) is due to the presence of an electrolyte [17]. In batteries, the ion transport species from one electrode is necessarily solubilized in a liquid solvent as an ion (e.g., the cation Mg²⁺ for the Mg/Sn example) because the electrons travel through an external circuit providing the electrical work of the battery [3]. Solubilization in a liquid solvent facilitates transport between different electrodes and enables the direct, atomic scale contact between reacting species over the full electrolyte-wetted surface area of the Sn electrode. Once transported to the Sn electrode, the electrons and Mg²⁺ ions must still react in a solid/solid reaction, with Mg and Sn inter-diffusing and alloying to form Mg₂Sn. However, now the reaction is occurring within a single particle. Given that the relatively low ΔG_K ~ 5 kJ in the battery reaction reflects the overall reaction, including both transport through the electrolyte and interdiffusion within the Sn electrode, the much higher ΔG_K ~ >20 kJ in hydrogen storage reactions indicate additional limitations in the transport between particles. This suggests that the excess free energy required to drive multiphase hydrogen storage reactions may be significantly reduced (i.e., lowering the reaction temperature) with appropriate electrolytes to improve the transport rates of the various species involved in the reaction.

Even with an electrolyte, a hydrogen storage reaction would still be thermochemical, with the term “electrolyte” here meaning a liquid phase containing or consisting of dissociated mobile cations and anions. The addition of an electrolyte would be equivalent to chemically short-circuiting a battery by mixing both electrode materials together. In this case, as solubilized ions form (e.g., Mg²⁺) and enter the electrolyte, the electrons must still travel through atomic scale contacts between different powder particle phases. However, due to its lighter mass and therefore more delocalized quantum mechanical nature, electron transport is typically much faster than ion transport.

Table 2. Excess kinetic free energies for various hydrogen storage reactions and for the Mg/Sn battery reaction.

Reaction	Conditions	ΔGK (kJ/mol-H2 or Mg)
MgH2/Si	No electrolyte	34
MgH2/Si [8]	Nanoscale/catalyzed/no electrolyte	24
MgH2/Sn	No electrolyte	22
MgH2/Sn	With LiBH4/KBH4 eutectic	20
Mg/Sn discharge [15]	With battery electrolyte	3.8
Mg/Sn charge [15]	With battery electrolyte	5.8
LiBH4/MgH2	Catalyzed/no electrolyte	22
Mg(BH4)2 (1st step) [7]	No electrolyte	23
NaAlH4 (1st step)	No electrolyte	19
NaAlH4 + TiCl3 (1st step)	Catalyzed/no electrolyte	4.7
NaAlH4 + TiCl3 (1st step)	Catalyzed/with glyme electrolyte	2.8

Table 2. Excess kinetic free energies for various hydrogen storage reactions and for the Mg/Sn battery reaction.

Reaction	Conditions	ΔGK (kJ/mol-H2 or Mg)
MgH2/Si	No electrolyte	34
MgH2/Si [8]	Nanoscale/catalyzed/no electrolyte	24
MgH2/Sn	No electrolyte	22
MgH2/Sn	With LiBH4/KBH4 eutectic	20
Mg/Sn discharge [15]	With battery electrolyte	3.8
Mg/Sn charge [15]	With battery electrolyte	5.8
LiBH4/MgH2	Catalyzed/no electrolyte	22
Mg(BH4)2 (1st step) [7]	No electrolyte	23
NaAlH4 (1st step)	No electrolyte	19
NaAlH4 + TiCl3 (1st step)	Catalyzed/no electrolyte	4.7
NaAlH4 + TiCl3 (1st step)	Catalyzed/with glyme electrolyte	2.8

3. Results and Discussion

Based on a comparison of thermochemical and electrochemical multiphase reactions, we have investigated the use of liquid electrolytes in the form of eutectics, ionic liquids, or solvents containing dissolved salts, to facilitate the transport of atoms such as Li, Mg, B, and Al, between phases and thereby increase reaction rates (or reduce desorption temperatures and hydrogenation pressures) in complex and destabilized hydride materials. Here we further analyze previous results for MgH₂/Sn and NaAlH₄ and then present new results for the hydrogenation of MgB₂.

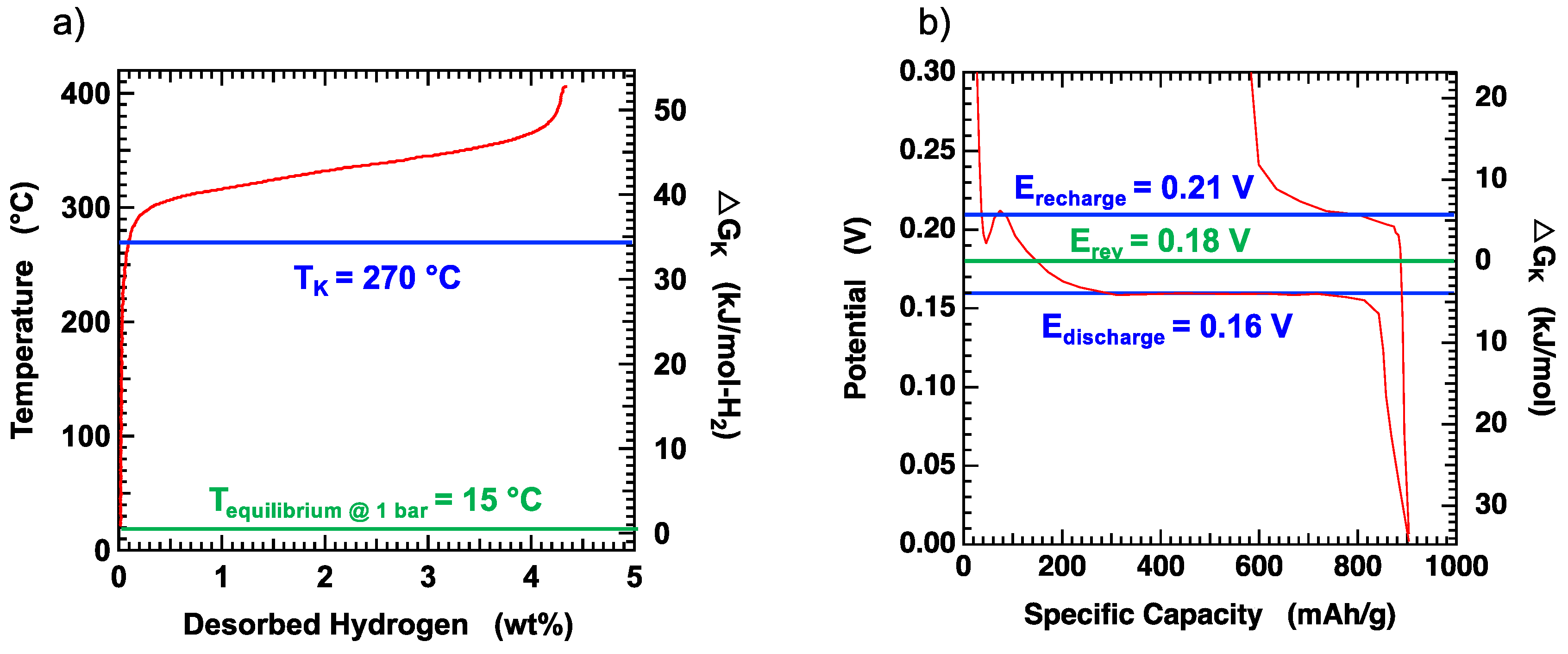
3.1. Analysis of the Electrolyte-Assisted MgH₂/Sn Hydrogen Storage Reaction Using ∆G_K

The MgH₂/Sn destabilized hydride system was studied using a eutectic electrolyte with a composition of 0.725 LiBH₄/0.275 KBH₄ [1]. This composition was chosen to have a melting point (~110 °C) [18] well below the melting point of Sn (232 °C). Straightforward measurement of T_K during a heating ramp (as shown in Figure 1a for MgH₂/Si) was not observed due to the extremely slow reaction rates even with the eutectic. Instead, rates were measured over extended times at fixed temperatures of 150 °C, 175 °C, and 200 °C. Although slow, the rate of dehydrogenation at 150 °C increased 12× from 0.0008 wt%-H₂/h without eutectic to 0.01 wt%-H₂/h with the eutectic. At 200 °C, the rate with eutectic is 0.23 wt%-H₂/h, which is similar to the rate described above for MgH₂/Si (without electrolyte). Thus, we chose T_K = 200 °C, which gives ΔG_K = 20 kJ/mol-H₂ (based on data in Table 1). By using the measured rates and extrapolating, we estimate that the same rate (0.23 wt%-H₂/h) would occur without the eutectic at 215 °C. This gives ΔG_K = 22 kJ/mol-H₂, so there is a modest reduction of 2 kJ/mol-H₂ upon the addition of the eutectic electrolyte.

In addition to improving dehydrogenation, the 0.725 LiBH₄/0.275 KBH₄ electrolyte also enabled full (re)hydrogenation of Mg₂Sn back to MgH₂/Sn using 1000 bar H₂ at 215 °C−175 °C [1]. Without the eutectic, essentially no hydrogenation was observed. This was the first time that significant hydrogenation was observed in the Mg₂Si or Mg₂Sn systems. A similar attempt using an eutectic electrolyte was made with Mg₂Si but no hydrogenation was seen. The thermodynamics of the two systems are similar. The difference may have been a more inert oxide layer on the Mg₂Si and/or more mobility in the Sn-based system due to the relatively low melting points for Sn (232 °C) and Mg₂Sn (778 °C) compared to Si (1400 °C) and Mg₂Si (1100 °C).

3.2. Analysis of Electrolyte-Assisted NaAlH₄ Dehydrogenation Using the Avrami-Erofe’ev Model

The influence of electrolytes was also explored for the dehydrogenation of LiAlH₄ and NaAlH₄ [2]. These hydrides dehydrogenate in two steps beginning from a single phase. Thus, the multiphase reaction transport limitations between reacting phases described for MgH₂ + Si or Sn might be considered to not apply. However, there are three solid phase products when MAlH₄ dehydrogenates, M₃AlH₆ + Al for the 1st step and MH + Al for the 2nd step. These products must form at 3-phase boundaries that could present transport limitations. Indeed, pure NaAlH₄ does not decompose until it melts at ~180 °C, despite a thermodynamic T_1bar = 33 °C (Table 1) for the 1st step. This gives ΔG_K = 19 kJ/mol-H₂, which is somewhat lower than other hydrogen storage reactions but still much higher than the Mg/Sn battery reaction.

For NaAlH₄ catalyzed with 3 mol% TiCl₃, dehydrogenation was compared without an electrolyte and with 50 wt% diglyme [2]. No additional electrolyte salt was included with the diglyme. Rather, the solubility of NaAlH₄ or NaCl (formed during milling with TiCl₃) was relied upon to possibly provide mobile [AlH₄]⁻ or Na⁺ ions. The results are shown in Figure 2 following the format in Figure 1. The two dehydrogenation steps are clearly seen. Without electrolyte, the T_K for the 1st step is 70 °C, giving ΔG_K = 4.7 kJ/mol-H₂. This is a significant decrease from pure NaAlH₄ and similar to that for the Mg/Sn battery reaction. Thus, as is well known, catalyzed NaAlH₄ dehydrogenates with rates that are, or are close to, practical. Including diglyme further decreases T_K by 15 °C to 55 °C, ΔG_K = 2.8 kJ/mol-H₂, a decrease of ~2 kJ/mol-H₂. However, perhaps more significantly, is how the electrolyte influences the rates as the reactions proceed. For the 1st step, the rates at a given wt% with and without electrolytes are similar, except that the reaction occurs ~15 °C lower with electrolytes. A more distinct difference is seen in the 2nd step where the dependence of the rate on the extent of reaction is very different. Specifically, with diglyme the rate increased reaching ~3.5 wt%-H₂/h at 4 wt% desorbed hydrogen while without electrolyte the rate simply decreases starting from ~0.5 wt%-H₂/h at 3 wt%.

To understand this further, a full kinetic analysis was performed using the Avrami-Erofe’ev (A-E) model:

α = 1 − exp(−(kt)ⁿ),

(1)

which is typical for systems with rates driven by nucleation and growth, where α is the extent of reaction, k is a temperature-dependent rate constant, and n is a growth parameter (with typical values between ~1 and 4) that is related to nucleation and growth of the product phases [19]. A series of A-E calculations were performed at a fixed rate constant to illustrate how the growth parameter (n) affects the shape of the desorption curve (Figure 3). Simulated curves are shown in Figure 3a at various values of n (all other parameters were fixed). Similarly, Figure 3b,c show the same data plotted as the rate vs. time and rate vs. fractional decomposition, respectively. At n = 1, the A-E equation is equivalent to a traditional first-order (homogeneous) rate equation where the reaction starts at the highest rate and decays as the reaction proceeds. For systems with 2 ≤ n ≤ 4 the fractional decomposition curve takes on a sigmoidal shape with an initial induction period (nucleation), followed by an acceleratory period (growth of nuclei), and finally, a deceleration period (growth with overlap). For these systems, the n value determines the growth geometry and the maximum rate (during the acceleratory period) increases with n.

Using data from Figure 2, the rate of dehydrogenation from the 2nd step (Na₃AlH₆ + Al → 3 NaH + Al + 3/2 H₂) with and without the electrolyte is shown in Figure 3d where the fractional decomposition (extent of reaction) is plotted on the x-axis and the temperature is constant (150 °C). As previously mentioned, the first step (not shown) is first order (with n ~ 1) with and without electrolytes. The 2nd desorption step without the electrolyte is clearly characteristic of a first-order reaction (n ~ 1) with a continuously decreasing rate with the extent of the reaction (open circles in Figure 3d). A very different shape is observed with the sample containing an electrolyte, where the rate increases initially, plateaus (constant rate), and then decreases at the very end of the reaction (filled circles). This behavior is consistent with A-E with n = 3.5. The increase in the growth parameter from n ~ 1 to n = 3.5 coupled with a ~5× increase in the rate constant leads to the observed ~10× decrease in overall reaction time.

The unusual kinetic behavior observed in the 2nd desorption step of NaAlH₄ was also seen with an electrolyte in MgH₂/Sn [1] and LiAlH₄ 2nd step [2]. In multiphase hydrogen storage reactions (and more generally, solid-state reactions) without an electrolyte, the majority of the reaction can be treated as the first order, where the rate continuously decreases or the temperature must be continuously increased to maintain a constant rate. The difference with an electrolyte suggests that in addition to improving interparticle transport, the electrolyte also enables intraparticle transport, presumably over the particle surface (assuming the electrolyte does not penetrate or break up a multiphase particle). For a solid-state reaction that generates two new solid phases (such as dehydrogenation of M₃AlH₆ to MH + Al), a reaction occurs along a triple-phase boundary (assuming the product phases are not continuously nucleated). These boundaries are spatially very confined; locally, they are one-dimensional. This confinement will favor possible alternative transport pathways such as surface transport linking the different phases. This transport could be facilitated by an electrolyte, which effectively increases the velocity of the advancing reactant-product interface, and decreases the activation energy. The concept of expanding the growth geometry (in addition to the rate constants) is supported by the kinetic analysis which shows an increase in the growth parameters from n = 1 with no electrolyte to n = 3 with electrolyte.

3.3. Influence of Electrolytes on MgB₂ Hydrogenation

The hydrogenation of MgB₂ was also studied [1]. Similar to the dehydrogenation of LiAlH₄ and NaAlH₄, an influence of an electrolyte might not be expected for MgB₂ because hydrogenation begins from a single phase (and for MgB₂ also ends in a single phase, Mg(BH₄)₂). However, it is thought that there are multiple intermediate phases including MgH₂, Mg, and MgB₁₂H₁₂ [7] that perhaps could be contained within a single particle. As described above, the reaction at the confined multiphase boundaries could be improved by providing surface transport through an electrolyte.

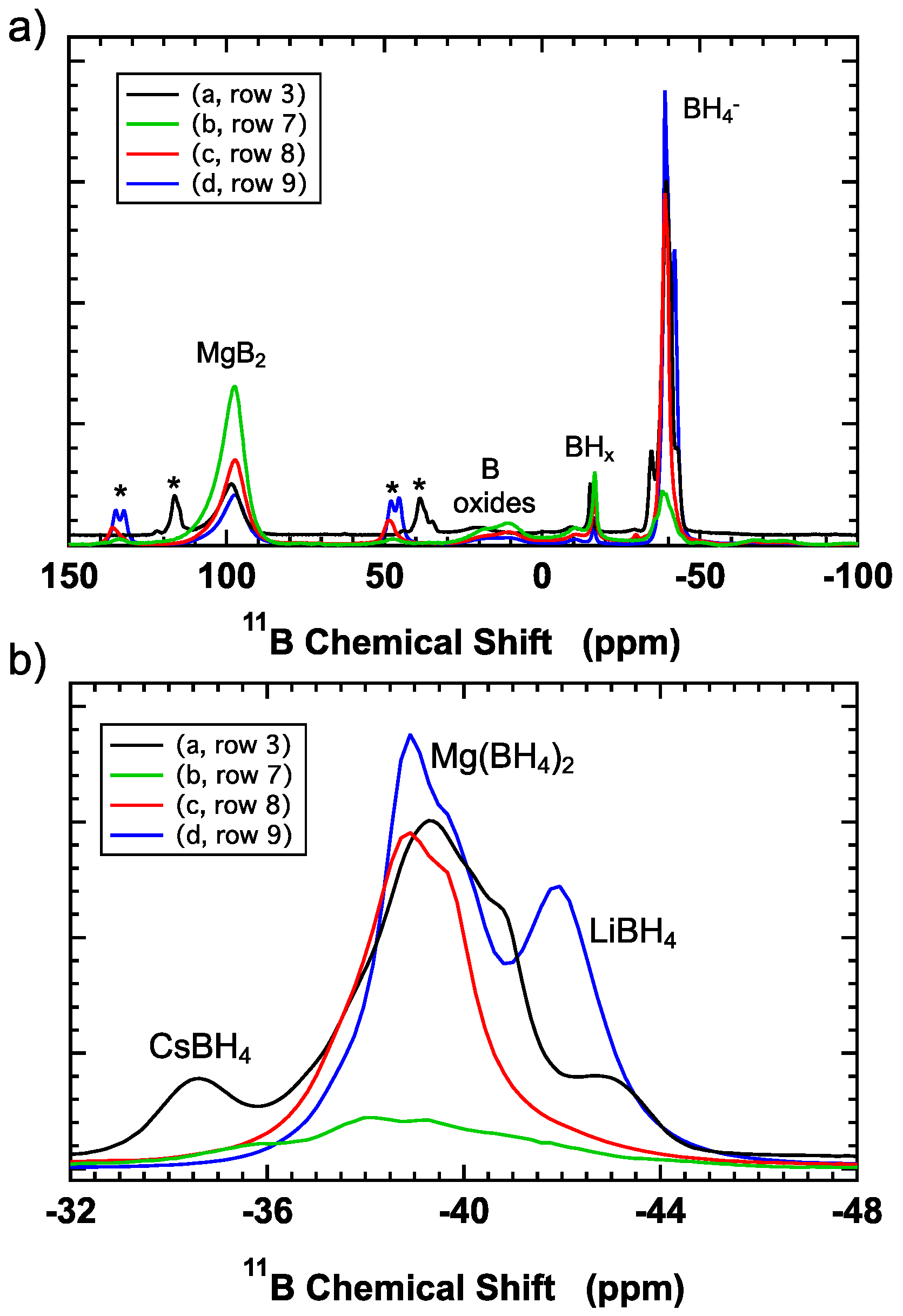
Significant hydrogenation of MgB₂ was shown using a 0.33 LiI/0.33 KI/0.33 CsI eutectic electrolyte at 53 wt% with hydrogen treatment at 1000 bar and 320 °C for 50 h. [1]. As shown in

Table 3. ¹¹B NMR analysis of hydrogenated MgB₂ formulations.

	Composition	Eutectic	Hydrogenation Conditions (50 h)	MgB2	B-O	BHx	[BH4]−
1	MgB2	Li/K/CsI 53 wt%	No treatment	0.96	0.04	0	0
2	MgB2	none	1000 bar 320 °C	0.93	0.04	0	0.03
3	MgB2	Li/K/CsI 53 wt%	1000 bar 320 °C	0.21	0.04	0.04	0.72
4	MgB2	Li/K/CsI 50 wt%	700 bar 300 °C	0.79	0.04	0.04	0.13
5	MgB2 + 3 at% TiF3	Li/K/CsI 50 wt%	700 bar 300 °C	0.61	0.04	0.09	0.26
6	MgB2 + 3 at% TiF3	Li/K/CsI 50 wt%	350 bar 320 °C	0.68	0.05	0.11	0.16
7	MgB2 + 3 at% TiCl3	Li/K/CsI 50 wt%	350 bar 310 °C	0.65	0.07	0.13	0.14
8	MgB2 + 3 at% TiCl3	Li/K/CsCl 50 wt%	350 bar 310 °C	0.35	0.05	0.11	0.49
9	MgB2 + 0.2 LiH + 3 at% TiCl3	Li/K/CsCl 50 wt%	350 bar 310 °C	0.21	0.03	0.03	0.73

, from a starting boron-based composition of 96% B in MgB₂ and 4% B in (impurity) boron oxides (Table 3, row 1) using ¹¹B nuclear magnetic resonance (NMR), the hydrogen treatment with eutectic resulted in a final composition with 72% of the boron as [BH₄]⁻ (Table 3, row 3). In contrast, without the eutectic, only 3% of the B was hydrogenated to [BH₄]⁻ (Table 3, row 2). The portion of the ¹¹B NMR spectrum focused on the borohydride region is shown in Figure 4. Comparison with literature spectra indicates the formation of Mg(BH₄)₂ together with CsBH₄ and LiBH₄. Although the ¹¹B chemical shift can be influenced by the local environment and mixed cation solid solution phases are possible, an approximate composition (based on areas between the minima between the peaks) is 12%BH₄ in CsBH₄; 74%BH₄ in Mg(BH₄)₂; 14%BH₄ in LiBH₄. The extremely high pressure used (1000 bar) clearly resulted in some hydrogenation of the eutectic.

In this work, we present new results where lower pressures were explored. Reducing the pressure to 700 bar and (unintentionally) the temperature to 300 °C (Table 3, row 4) reduced the [BH₄]⁻ fraction drastically, from 72% to 13%. The inclusion of 3 at% TiF₃ as a catalyst (by milling) increased the [BH₄]⁻ fraction to 26% but also increased the fraction of non-[BH₄]⁻ boron hydride species (BH_x) from 4% to 9% (Table 3, row 5). These results indicate that well-known catalysts for complex hydrides (such as TiF₃) can still operate in an electrolyte environment. This is not surprising if we consider that the catalyst facilitates reaction on the surface of and within individual powder particles, while the eutectic facilitates transport between particles.

Further reducing the pressure to 350 bar (at 320 °C) reduced the [BH₄]⁻ fraction to 16% but actually increased the BH_x fraction to 11% (Table 3, row 6). Switching the catalyst from TiF₃ to TiCl₃ (and using a different high-pressure hydrogenation apparatus, at 310 °C) gave similar results with 14% [BH₄]⁻ and 13% BH_x (Table 3, row 7). The increased BH_x fraction at lower pressure suggests that these species are intermediates on the way to formation of the fully hydrogenated [BH₄]⁻ anions and that lower pressure favors these partially hydrogenated species. While the yields are much greater than the yields possible without a eutectic, the total yield of hydrogenated MgB₂ was only ~30% with only ~50% of that yield being [BH₄]⁻. Although the yield is low, the hydrogenation appears to give predominately Mg(BH₄)₂ as shown in Figure 4, curve b.

Next, to try and improve the yields, the electrolyte was switched from the Li/K/Cs iodide-based eutectic to a Li/K/Cs chloride-based eutectic, with the specific composition of 0.575 LiCl/0.165 KCl/0.26 CsCl [20,21]. Significant improvement was seen with the [BH₄]⁻ fraction increasing from 0.14 (with the iodide) to 0.49 (with the chloride), while the BH_x fraction actually decreased slightly (Table 3, row 8). The NMR spectrum (Figure 4, curve c) suggests the formation of relatively pure Mg(BH₄)₂. Compared with the sample hydrogenated at 1000 bar, the peaks associated with CsBH₄ and LiBH₄ are not clearly visible.

The chloride eutectic has a melting point of ~266 °C (higher than the iodide, ~210 °C) but still below the temperature for these hydrogenations, >300 °C. During hydrogenation, the higher melting point may lead to greater viscosity and therefore reduced transport properties. However, counteracting the viscosity and perhaps more important, the molar mass of the chloride eutectic is lower; 80.4 g/mol-Cl compared to 186.5 g/mol-I. This difference means that at 50 wt%, the eutectic: MgB₂ molar ratio increases from 0.25:1 for the iodide eutectic to 0.57:1 for the chloride eutectic, a factor of ~2.3×. Thus, during hydrogenation, there are 2.3× more liquid-state anions (Cl⁻) and total cations (individually 4 × Li⁺, 1.15 × K⁺, and 1.8 × Cs⁺) to possibly (depending on solubility) facilitate the transport of Mg²⁺ cations and [BH₄]⁻ or other intermediate anions within the reacting mixture. Testing other eutectic compositions with suitable melting temperatures may reveal the relative importance of the Cl⁻ anions compared to the different cations in facilitating hydrogenation.

A final variation involved the addition of 0.2 LiH per mole of MgB₂. The 2 LiH + MgB₂ system is a well-known destabilized hydride system, which can be nearly completely hydrogenated to 2 LiBH₄ + MgH₂ at ~100 bar [7]. Thus at 350 bar, the addition of 0.2 LiH should result in the facile formation of 0.2 LiBH₄, reacting 10% of the MgB₂ and leaving the remaining 90% for possible hydrogenation to Mg(BH₄)₂. As shown in Table 3 (row 9), hydrogenation at 350 bar of a MgB₂ + 0.2 LiH + 3 at% TiCl₃ mixture with 50 wt% LiKCsCl eutectic resulted in 73% of the boron as [BH₄]⁻ with only 3% as BH_x. From the NMR spectrum (Figure 4, curve d), the [BH₄]⁻ is a mixture of Mg(BH₄)₂ and LiBH₄. Using the area of the spectrum (divided using the minimum between the peaks) indicates that ~25% of the [BH₄]⁻ is present as LiBH₄. This is more than the expected amount of ~14%, assuming 10% of the [BH₄]⁻ boron was LiBH₄ and the remaining 63% was in Mg(BH₄)₂. The origin is this difference is not understood. One possibility is that the simple area estimate is inaccurate. Another possibility is that some of the Li from the chloride eutectic is forming LiBH₄ although, there was no clear indication of LiBH₄ in the sample without added LiH. Despite clearly being a mixture, the utility of this formulation lies in the dehydrogenation behavior, i.e., if it cycles hydrogen well with high capacity, it is not particularly important whether pure Mg(BH₄)₂ or a mixture with LiBH₄ is formed. Thus far, the dehydrogenation has not been tested. Overall, the total amount of hydrogenation (73% [BH₄]⁻) in the MgB₂ + 0.2 LiH sample hydrogenated at 350 bar is comparable to that originally achieved at 1000 bar. Including the complete formulation with the 50 wt% electrolytes, the uptake is 5.6 wt% hydrogen. If similar uptake could be achieved with an electrolyte at 28 wt% (or 10.5 wt%), the uptake would be 8 (or 10) wt% hydrogen.

4. Materials and Methods

The materials and methods including the Sieverts apparatus, the 1000 bar hydrogenation system, and the ¹¹B NMR setup (Bruker, Billerica, MA, USA) used for the MgH₂/Sn, MgB₂, LiAlH₄, and NaAlH₄ experiments have been described completely in Refs. [1,2]. For the additional MgB₂ hydrogenation experiments, a custom high-pressure manifold was constructed using a 25 mL Series 4740 pressure vessel from Parr Instruments (Moline, IL, USA) with valves and fittings from High-Pressure Equipment (Erie, PA, USA). The pressure was limited to ~400 bar using burst disks. To reach 350 bar from a standard hydrogen tank and regulator, the manifold contained a coiled ¼ inch diameter tubing volume that could be immersed in liquid nitrogen. Based on the manifold volume including the Parr vessel, the volume of the coil was chosen so that when the system was pressurized to 50 bar with the coil in liquid nitrogen, the pressure increased to 175 bar when the coil was warmed to room temperature (with the H₂ tank sealed off). Finally, heating the Parr vessel to 310 °C further increased the pressure to 350 bar.

5. Conclusions

The use of electrolytes to improve the kinetics of thermochemical multiphase hydrogen storage reactions has been explored based on an analogy with electrochemical multiphase battery reactions. A subjective excess free energy, based on a subjective practical reaction temperature, was used to relate the hydrogen storage and battery reactions. The difference between electrolyte-based and solid-state diffusion-based interparticle atomic transport between the reacting phases was discussed. Using this analogy, the hydrogen storage reaction kinetics with and without added electrolytes for Mg₂/Sn, NaAlH₄, and MgB₂ were analyzed. While the hypothesized increases in reaction rates were observed, the kinetics displayed more complex behavior. Perhaps more important than a simple reduction in reaction temperature and contrary to most multiphase solid-state reactions, the kinetics showed reaction rates that were often independent of the extent of the reaction. The behavior suggests that electrolytes also improve intraparticle transport, likely over the surface of a particle. This transport alleviates the spatial restrictions of multiple phase boundaries inherent in solid-state reactions.

The practical aspects of using electrolytes for hydrogen storage reactions were not discussed in detail here. For most of the reactions studied here, compositions containing ~50 wt% electrolytes were used. To be practical, likely <~25 wt% is needed. However, by a final analogy with batteries, where electrolyte loadings are typical ~15 wt%, we feel that optimized commercially viable compositions are feasible.

6. Patents

U.S. Patent with the number US-11050075-B1 resulted from this work.