Abstract
Thiocarbohydrazone-based catalysts feature ligands that are potentially electrochemically active. From the synthesis point of view, these ligands can be easily tailored, opening multiple strategies for optimization, such as using different substituent groups or metal substitution. In this work, we show the possibility of a new strategy, involving the nuclearity of the system, meaning the number of metal centers. We report the synthesis and characterization of a trinuclear nickel-thiocarbohydrazone complex displaying an improved turnover rate compared with its mononuclear counterpart. We use DFT calculations to show that the mechanism involved is metal-centered, unlike the metal-assisted ligand-centered mechanism found in the mononuclear complex. Finally, we show that two possible mechanisms can be assigned to this catalyst, both involving an initial double reduction of the system.
1. Introduction
Hydrogen has been widely sought out as an alternative energy source [1,2,3], giving rise to a quest for its cost-effective industrial scale production. The search for obtaining optimal homogeneous green catalysts to perform hydrogen evolution reactions (HER) has taken inspiration from understanding how hydrogenases work. The inorganic cofactors of these enzymes are able to mediate the reversible conversion of protons and electrons into hydrogen [4,5,6]. This family of enzymes is very attractive for HER due to their low overpotential requirement, high turnover rates, and use of earth-abundant metals [7,8]. Conventional strategies have explored copying the structural and mechanistic features of hydrogenase active sites, attempting to mimic the same kind of chemistry found in those enzymes. This resulted in the emergence of a large number of biomimetic and bio-inspired catalysts in the past few years [9,10,11]. The best-performing catalysts able to generate molecular hydrogen in organic and aqueous media are usually cobalt- and nickel-based complexes with various ligand skeletons [12,13,14,15]. In the past few decades, a new class of complexes has been developed, where the once metal-centered reactivity was shifted toward a ligand-centered one [16,17]. Prominent examples have been found with complexes based on thiosemicarbazone ligands [18,19,20,21,22,23,24].
Thiosemicarbazone-based complexes are characterized by the redox non-innocent character of the ligand that displays several N- and S-atoms as potential proton relays, a key feature to enhance and promote catalytic activity [25,26]. Such complexes have been found to possess a rather low overpotential requirement, with the ligand playing an active role in HER, and being highly customizable [16,27]. Recently, we have characterized and studied a set of mononuclear nickel-thiosemicarbazone (NiL) complexes, with chemically tuned para substituents in phenyl groups present in the ligand [24,28]. To lower the potential of the redox-active ligand, we attempted to increase the delocalization of the electronic density. The idea was that delocalization would lead to lower overpotential requirements. The use of electron-withdrawing phenyl substituents did not give us the optimal approach we looked for, as some impact was found on the kinetic rates of H2 formation [29]. Thus, other approaches in catalyst design need to be envisioned.
In this work, we show a new possibility of modifying thiosemicarbazone-based complexes, based on nuclearity. Herein, we introduce an original trinuclear nickel-thiocarbohydrazone Ni3L2 complex, being equivalent to the previously reported NiL complexes [18,24]. Compared to its mononuclear counterpart, this multiple metal centre complex displays larger turnover frequency (TOF) values, whilst utilizing higher overpotential requirements for HER. Experimental and theoretical investigations show that the trinuclear equivalent of the mononuclear NiL complex has a purely metal-centred reactivity, involving exclusively the central Ni atom, in contrast with the metal-assisted ligand-centred reactivity identified in its mononuclear form, which uses the nitrogen atoms close to the metal centre. Such change in reactivity likely explains the moderate performance of the new catalyst with respect to the key parameters for catalyst evaluation: the overpotential () and the rate of catalysis (TOF).
2. Results and Discussions
2.1. Synthesis and Single-Crystal X-ray Diffraction Analysis
The ligand was prepared using a one-step procedure (Figure S1). The reaction involves the addition of two equivalents of 1-isothiocyanato-4-methoxy-benzene to one equivalent of thiocarbohydrazide. The reaction was performed in ethanol at reflux for two hours. The products precipitate from ethanolic solution with a 95% yield for the ligand, corresponding to 1,5-Bis(p-methoxyphenylthiocarbamoyl)thiocarbonohydrazi-de (H6L) and did not require any additional purification. The nickel complex was obtained in a 70% yield by reacting three equivalents of Ni(NO3)2 with two equivalents of H6L ligand in a DMSO/MeOH mixture in the presence of two equivalents of NaSH. The crude compound precipitated as a brown microcrystalline powder and did not require any purification, except washing with methanol (Figure 1 and Figure S2). Both ligand and complex were characterized by elemental analysis, ESI-MS, and NMR spectroscopy (Figures S3–S6). These data are consistent with the indicated trinuclear structure that is the only one found in solution. They also show that the complex is diamagnetic, having a singlet S = 0 ground spin state (see the Section 3). DOSY NMR experiments provided a unique diffusion coefficient of 1.10 × 10−10 m2·s−1 which supports the presence of a single species in solution (Figure S7).
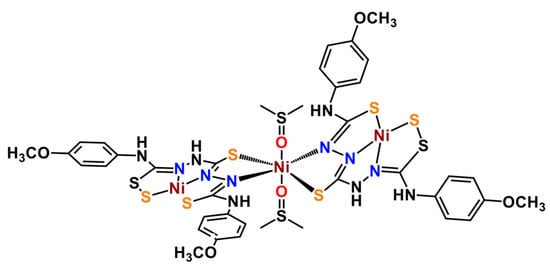
Figure 1.
Structure of the trinuclear nickel thiocarbohydrazone complex, [Ni3(SH3L)2(DMSO)2], (Ni3L2) presented in this work.
Crystals suitable for X-ray diffraction analysis were obtained from DMSO solution by slow evaporation of the solvent. Details of data collection and structure refinement parameters for the nickel complex are shown in the Supplementary Material (Tables S1 and S2). The single-crystal X-ray diffraction study revealed the compound to be crystallized in the C2/c space group of the monoclinic system. The asymmetric part of the unit cell comprises 1.5 [Ni3(SH3L)2(DMSO)2] (Ni3L2) molecular complexes and one and 2.5 co-crystallized H2O and DMSO molecules, respectively. The two trinuclear complexes are crystallographically independent, but chemically identical, while in one of them the central metal atom, Ni5, occupies a special position on a two-fold rotational axis. Thus, according to X-ray crystallography, the chemical composition of the compound is in accordance with the following formula: [Ni3(SH3L)2(DMSO)2] 1.67DMSO 0.67H2O, where each SL3- anion acts as a bridging hexadentate ligand. The symmetry equivalent Ni4 and Ni4i atoms are tetracoordinated in N2S2 square-planar geometry, while the central Ni5 metal atom exhibits a slightly distorted N2O2S2 coordination environment. It is worth noting the presence of intramolecular hydrogen bonds that are formed between the N13-H group (donor) and the O9 atom from the coordinated DMSO molecule (acceptor), which consolidate the trinuclear structure (Figure 2).
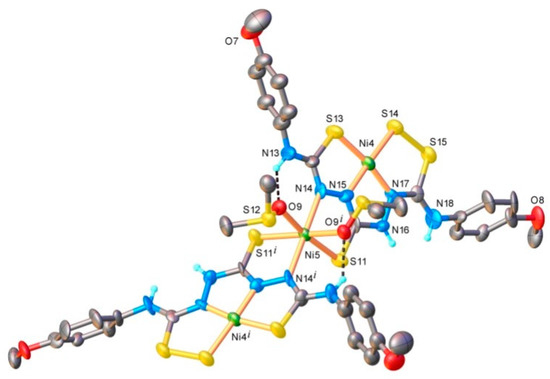
Figure 2.
X-ray molecular structure of Ni3L2 with selected atom labelling and thermal ellipsoids at 40% level. Non-relevant H-atoms are omitted for clarity. Symmetry code: I) 1)2 − x, y, 1.5 − z. Selected bonds (Å) and angles (°): Ni4-S13 2.133(3), Ni4-S14 2.145(3), Ni4-N15 1.843(8), Ni4-N17 1.786(9), Ni5-S11 2.392(3), Ni5-O9 2.131(6), Ni5-N14 2.137(9), N15-Ni4-S13 85.7(3), N17-Ni4-S14 92.8(3), N15-Ni4-S14 176.5(4), N17-Ni4-S13 1···69.7(3), N14-Ni5-S11 85.2(3), N14-Ni5-O9 90.4(3), O91-Ni5-O9 85.0(4), O9-Ni5-S11 172.1(2). H bond parameters: N13-H···O9 [N13-H 0.86 Å, H···O9 2.02 Å, N13···O9 2.73(1) Å, ∠N13HO9 138.7°.
2.2. Magnetic Studies
Figure 3 shows the dependence of the magnetic susceptibility on the temperature, χT, at 0.1, 1, and 4 T. At room temperature, χT is 1.254 emu·K·mol−1 and does not show any significant temperature dependence while cooling down to about 10 K. Then, it decreases at high fields due to the thermal saturation of the ground state. The dashed line is the best fit for a paramagnetic centre of spin S = 1 and giso = 2, in agreement with only one magnetic NiII ion (S = 1) being present in the complex. This is expected, as the latter displays an octahedral coordination sphere while the other two external NiII ions are square planar compatible with a low-spin configuration (S = 0). Therefore, the magnetic behaviour of Ni3L2 is ascribed to the central high-spin NiII ion in an octahedral environment. The possible inter-trimer interactions are weak and mostly hidden by the static field effect.
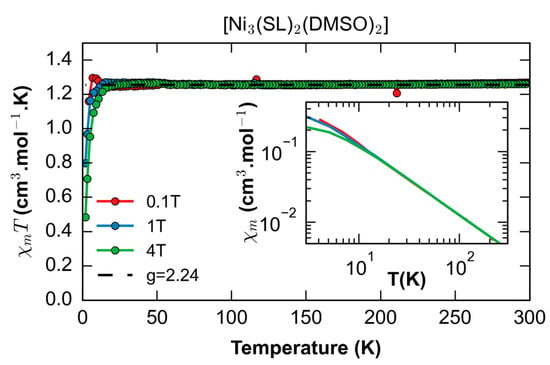
Figure 3.
Temperature dependence of the magnetic susceptibility for Ni3L2. The inset is the temperature dependence of the susceptibility in log scale showing the expected Curie behaviour for any field at T > 10 K.
2.3. UV-Vis Spectroscopy
The optical properties of the ligand and the nickel complex were followed by UV/Vis spectroscopy in DMF (Figure 4). The evolution of the spectra upon ligand metalation allowed us to confirm the nickel binding to the ligand and the stability of the complex in solution. The H6L ligand displays two main absorption bands centered at 270 and 325 nm while the Ni3L2 complex displays two main electronic transitions at 268 and 363 nm and two weaker broad bands around 518 and 895 nm (Table S3). The absorption bands present at high energy have been previously attributed to metal–ligand-to-metal–ligand transitions [18,24], while the low-energy features are compatible with d-d transitions.
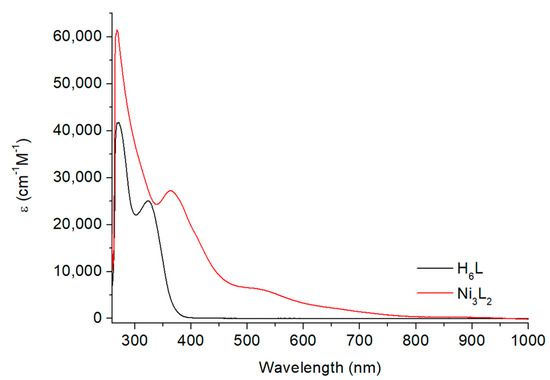
Figure 4.
Electronic absorption spectra for the H6L ligand and the Ni3L2 complex, concentration of 0.05 mM in DMF.
These results were further supported by TD-DFT calculations performed on a neutral, closed-shell singlet Ni3L2 considering no bound DMSO molecules. Indeed, the predicted spectroscopic data provide a calculated spectrum that compares reasonably well with the experimental observations (Figure S10). The low-intensity features around 575 nm are due to excitations from the outer Ni ions and ligands to the central Ni ion. At higher energies, additional excitations on the outer Ni ions are found (Table S4 and Figure S11). The computed UV-vis spectrum thus supports the dissociation of the solvent molecules from the complex once solubilized, with preference for a singlet state in solution (see details in the electronic structure section).
2.4. Electrochemistry
We investigated the redox behaviour of H6L and Ni3L2 by cyclic voltammetry (CV) at room temperature using a glassy carbon electrode in anhydrous DMF with 0.1 M TBAPF6 as the supporting electrolyte. The electrochemical responses were investigated in the potential range between 0 and −2.5 V vs. Fc+/0 (Figure 5). The cyclic voltammogram of H6L was recorded in the absence and in the presence of 100 mM of trifluoroacetic acid (TFA, Figure S12). A scan in the negative direction without TFA reveals one irreversible wave, while in its presence, no catalytic wave was detected. These data confirm that the ligand itself cannot mediate catalytic proton reduction, which is consistent with our previous observations on related thiosemicarbazone ligands [18,24].
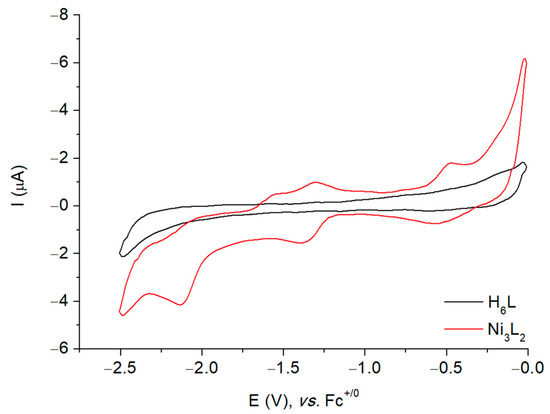
Figure 5.
Cyclic voltammogram of a 1 mM solution of H6L and Ni3L2 in DMF at stationary glassy carbon electrode in DMF at 500 mV s−1. Potentials are referenced to the Fc+/0 electrode.
In the cathodic region, the cyclic voltammogram of Ni3L2 displays two redox systems: one quasi-reversible at −1.35 V and another irreversible at −2.10 V vs. Fc+/0 (Figure S13). The plot of the peak currents versus the square root of the scan rates for the quasi-reversible cathodic wave was found to be linear, indicating that this is a diffusion-controlled process (Figure S14). The redox behaviour of Ni3L2 in the cathodic region is reminiscent of the one obtained with another trinuclear nickel complex previously reported by our group [30] for which the reduction events were ascribed as successive metal-based processes. Such a rationale has been further investigated using both chronoamperometry and EPR spectroscopy.
To determine the numbers of electrons involved in each electrochemical event, chronoamperometric experiments on Ni3L2 were performed at −1.50 and −2.25 V vs. Fc+/0 (Figures S15 and S16). The first chronoamperogram can be fitted considering one electron being passed in the system, while at the most negative applied potential, the current response is compatible with a two-electron transfer. EPR spectroscopy was used to further characterize the one-electron reduced species of Ni3L2. Using the sample generated upon chronoamperometry at −1.50 V vs. Fc+/0, we recorded the EPR spectrum on a continuous wave (cw) spectrometer, which resulted in an axial signal (Figure S17). Simulation of the spectrum provided a set of of g-values of 2.012, 2.010 and 2.114, which was found to be compatible with the presence of a single paramagnetic center that was tentatively ascribed to a NiI center. These data were then confronted with DFT calculations performed on the one-electron reduced form of Ni3L2 considering a doublet state (S = 1/2) and no bound DMSO molecules. The predicted g-values of 2.052, 2.055 and 2.113 were found to be in fair agreement with the experimental ones. The electronic structure of the computed one-electron reduced species shows that the Singly Occupied Molecular Orbital (SOMO) is centered on the central nickel with the spin density being mainly distributed on the same site (see details in the electronic structure section). These data thus support the first reduction of the complex being a metal-based process with the central nickel center going from NiII to NiI, possibly due to stereochemical reasons.
2.5. Electrocatalytic Production of H2
To explore the activity of Ni3L2 for catalytic proton reduction, we investigated its electrochemical response recorded at a glassy carbon electrode in DMF under argon in the presence of TFA as the proton source (pKa = 6.00 ± 0.3 in DMF) [31,32]. The addition of increasing amounts of acid triggered the appearance of two peak-shaped waves with potentials starting at about −1.10 V vs. Fc+/0, suggesting potential-dependent mechanisms. The current response of the two waves is proportional to the concentration of protons in the electrolyte solution (Figure S18). While the peak potential of the more negative process is shifted from −1.99 V to −2.47 V vs. Fc+/0, the potential of the first process remains unaffected (Figure 6). We only investigated the process occurring at the more positive potential with a midwave potential of −1.52 V versus Fc+/0. In this case, the peak current increases with the acid concentration, and plateaus for concentration and scan rates higher than 100 mM and 2 V·s−1, respectively (Figure S19).
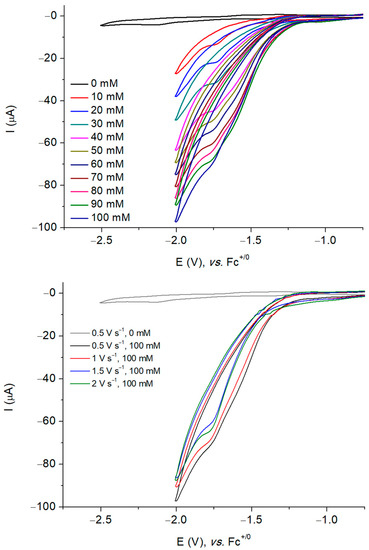
Figure 6.
Successive cyclic voltammograms of a 1 mM solution of Ni3L2 in DMF (0.1 M NBu4PF6) recorded at a glassy carbon electrode with increasing amounts of TFA at 500 mV s−1 (top) and with 100 mM TFA at five different scan rates (bottom). Potentials are referenced to the Fc+/0 electrode.
Control experiments were performed in the absence of the complex and the resulting CV clearly indicates the role played by the nickel complex in the observed current enhancement (Figure 6 and Figure S18). We verified that the observed catalytic response can be attributed to the complex in solution and not due to adsorbed species on the surface electrode. To do so, dip and rinse tests were performed. After each electrocatalytic measurement, the glassy carbon electrode was removed from the solution and immersed into a fresh DMF solution, followed by the addition of 100 mM TFA. The electrochemical response recorded upon sweeping the potential in the cathodic region only showed a residual background current, and upon the addition of TFA, only the acid blank was observed (Figure S20). These results thus confirm that no active adsorbed species is formed during electrocatalysis and indicate that the catalytic activity is due to the dissolved complex Ni3L2.
To confirm that the current response in the presence of acid does correspond to the catalytic reduction of protons into H2, we performed a bulk electrolysis experiment on a 100 mM solution of TFA in 8 mL of DMF at a constant potential in the presence of Ni3L2 (1 mM). Gas products were monitored by continuous in-line GC analysis. A potential of −1.70 V versus Fc+/0 was applied to the mercury-pool working electrode, resulting in the immediate formation of hydrogen. These experiments confirm that catalysis is homogeneous in nature, as the use of the mercury-pool electrode allowed us to rule out the possibility that proton reduction occurs due to the formation of nickel nanoparticles since the latter would amalgamate on the electrode surface. During a 4 h experiment, Ni3L2 mediated hydrogen evolution with an 82% faradaic efficiency and a turnover number of 31 was reached (Figure S21). In similar conditions, our reference catalyst NiL produced hydrogen during 16 h with 80% faradaic efficiency and a turnover number of 21. These data first indicate that the trinuclear catalyst Ni3L2 is probably less stable than the parent catalyst and likely points to degradation of the complex during turnover (Figures S8 and S22). Nevertheless, the trinuclear complex is able to produce more hydrogen on a shorter timescale when compared with its mononuclear counterpart NiL, which would support that nuclearity is playing a role in partially enhancing the catalytic activity of nickel thiosemicarbazone complexes. This is further investigated in terms of mechanistic implications using computations.
2.6. Benchmarking of Performances
A value of 534 mV was calculated for the overpotential requirement, , of Ni3L2 for proton reduction in the presence of TFA in DMF (see details in the Supplementary Material) [31]. The rates and the performance of the catalyst during the hydrogen evolution reaction were quantified. The TOF value of Ni3L2 was evaluated using the catalytic cyclic voltammograms recorded in DMF at different scan rates ( = 0.5, 1, 1.5, and 2 V·s−1) for various amounts of TFA (10 to 100 mM). The TOF value can be calculated from the ratio between the peak current of the catalyst in the absence () and presence of substrate () as given by Equation (1) [33]:
In the case of Ni3L2, the ratio varies linearly with the inverse of the square root of scan rate (), which confirms the validity of the above equation (see details in the Supplementary Material and Figure S23). Using this approach, and considering a first order reaction in acid and in catalyst (Figures S24 and S25), a maximum TOF value of 2072 s−1 was obtained in the presence of 100 mM TFA.
Based on this latter value, a mid-wave potential of −1.52 V versus Fc+/0, and an apparent equilibrium potential of the H+/H2 couple (−1.01 V vs. Fc+/Fc) [32] at 1 M TFA concentration, we could derive catalytic Tafel plots correlating the turnover frequency (TOF) to the driving force of the reaction, the overpotential (), that is related to H2 evolution under the conditions used [34]. Focusing on Ni3L2 (purple trace, Figure 7), we observe that this catalyst displays a significant catalytic activity (log(TOF) > 2) for moderate overpotential values. While it does not surpass benchmark molecular catalysts such as cobaloxime (blue trace, Figure 7) [14], tetraphenylporphyrin iron [35] or nickel bisdiphosphine (orange trace, Figure 7) [36,37,38], it performs better than the parent thiosemicarbazone complex NiL (green trace, Figure 7) as far as the turnover frequency is concerned.
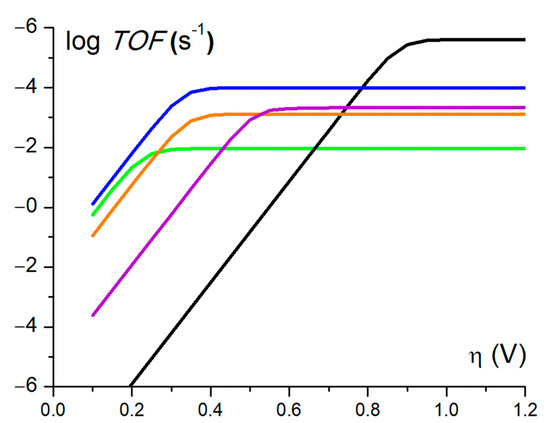
Figure 7.
Catalytic Tafel plots: comparison of performances for HER catalysed by Ni3L2 in DMF in the presence of 1M TFA (purple line) and NiL in DMF in the presence of 1M TFA (green line) [18,24] with other catalysts reported in the literature. Black: FeIITPP, DMF, Et3NH+ [34,35]; blue: [CoII(dmgH)2py], DMF, Et3NH+ [25,34]; orange: [NiII(P2PhN2C6H4X)2 ]2+, X = CH2P(O)(OEt)2, MeCN, DMFH [34,36].
When compared to each other, Ni3L2 and NiL feature quite different catalytic performances. For instance, while their faradaic yields appear comparable with a value around 80% for both catalysts, Ni3L2 displays a higher TON value (31 vs. 21) and thus produces more H2 on a shorter timescale [18]. These data suggest that Ni3L2 is a faster catalyst (TOF = 2072 s−1) than its mononuclear counterpart (TOF = 90 s−1) [24], but this is highly detrimental to the driving force of the reaction, with increased overpotential values for Ni3L2. Taken together, these results support the fact that changing the nuclearity of the catalyst affects its electronic structure and, as such, its redox behaviour, which influences its catalytic performance.
2.7. Electronic Structure: Solvent Binding and Redox Processes
The electrochemical investigations shown above were performed in DMF. This raises the question as to whether DMSO molecules are stably bound to the central nickel atom, Nic, in DMF, or if they dissociate. To address this issue, we performed DFT calculations to assess the electronic structure of the complex (see the Section 3 for details). All calculations performed here concern Ni3L2 to allow for a more straightforward comparison with the related mononuclear NiL complex we have previously studied [29]. In the solid state, Ni3L2 has an octahedral Nic at the centre, distinct from the two peripheral metal centers, Nis, which are square planar. Such geometry can render it paramagnetic, and we indeed show this is the case upon measuring the magnetic susceptibility of the complex (Figure 3). However, if DMSO dissociation occurs, two cases might arise: a tetrahedral or a square planar geometry for Nic can be formed. The former will keep the Nic paramagnetic, whilst the latter will not carry any magnetic moment. Thus, we need to investigate the energetics of Ni3L2 in two cases: including and excluding the DMSO molecules initially bound. We performed free energy calculations for the complex, considering the initial neutral state as being either triplet (open shell, paramagnetic Nic), or singlet (closed shell diamagnetic Nic, Table S5).
When considering the DMSO molecules initially bound to Nic, geometry optimization shows they remain bound only in the triplet state, whereas they dissociate in the singlet state, leading to a distorted square planar geometry. We compared the free energies for each state, and saw a preference of 3.6 kcal·mol−1 for the singlet over the triplet state. To confirm the preference of singlet over triplet, we performed the same calculations without DMSO molecules. Here, DFT shows a slight preference of 1.8 kcal·mol−1 for the singlet over the triplet state, and geometry optimization again resulted in a distorted square planar geometry around the Nic (Table S5). Thus, our calculations show that upon solvation of the complex, one can expect DMSO dissociation and the formation of a singlet ground spin. These findings are thus in agreement with the NMR data, which showed that the complex is diamagnetic.
We proceeded with DFT calculations to assess the spin states associated at each oxidation state for Ni3L2 upon reduction, as well as the redox potential associated with each process. We investigated the spin states with the lowest energies and used them to compute the free energy differences, which were then converted to redox potentials versus Fc+/0. Our calculations show that, initially, the complex starts at a neutral singlet state, proceeding through a doublet state after the first one-electron reduction (Table S5, first entry), and finishing with a doublet after a second two-electron reduction (Table S5, fifth entry). We obtained reduction potentials of −1.06 V and −1.97 V, which compare fairly well with the two redox systems observed at −1.35 V and −2.10 V in Figure 5 (Table S6). The fair agreement between the experimental and calculated redox potentials allow us to assign each peak in the voltammogram from Figure 5 to successive one- and two-electron reduction processes, which is consistent with the results obtained from chronoamperometry (Figures S15 and S16). It is worth noting that we have also considered the possibility of a two-electron reduction process and the calculated potential for this process was found to be −1.47 V (Table S6, fourth entry and Figure S26). Although no clear peak was experimentally observed at this voltage, we will later discuss that such a process can take place during catalysis, when potentials below −1.80 V are applied.
To investigate the nature of these experimentally observed processes, we plotted the spin density distributions and singly occupied molecular orbitals (SOMOs) for each of the oxidation states involved in the redox potential calculations (Figure 8). Our results show that they correspond to successive metal-centred reductions (NiII® NiI), different from the ligand-centred processes established with the mononuclear NiL complex [18,24]. Compared to the computed structure for the first one-electron reduced species, the geometry of the complex upon a subsequent two-electron reduction produced a more distorted Nic center whose coordination geometry was more tetrahedral. Such a rearrangement would explain the irreversibility observed experimentally for the second redox system in Figure 5.
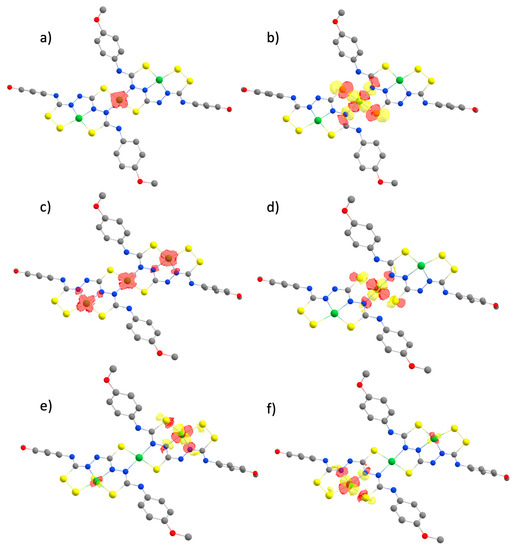
Figure 8.
Spin density plots (a,c) and localized SOMOs (b,d–f) calculated for Ni3L2 after subsequent one- and two-electron reduction reactions. The complex starts in its neutral, singlet state, passing through a doublet monoanionic state (a), and finishing as a trianion in a doublet state (c).
Mulliken spin population analysis shows that Nic holds larger values of spin density than the other Ni sites (Table S7). Besides, as we shall see next, when comparing the energetics of protonating different sites of the system, Nic is indeed the most favourable site for protonation. This points toward a metal-centered reactivity, in contrast to the ligand-centered reactivity seen in the mononuclear NiL complex previously studied [29]. The presence of multiple metal centres could then not only play a role in delocalizing electrons in the complex, but also have a direct impact on catalysis.
2.8. Mechanistic Considerations: Relative pKas and Reaction Pathways
In the context of H2 production, studying a catalytic mechanism implies knowing where protons will bind in the catalyst. Thus, we need to probe the energetics associated with protonating every potential site. Since obtaining absolute values can be very complicated, we calculated relative from free energy differences between protonating different sites for distinct oxidation states. In line with our mononuclear studies [18,29], and taking symmetry into account, we chose nine possible sites: the three Ni centers, the three N atoms adjacent to the Ni centers, and all S atoms. We calculated the relative by performing free energy calculations of the protonated complex at each site, and took the structure with Nic protonated as our reference. Results are shown in Table 1 and Table S8, with large positive values corresponding to the most preferable sites for protonation. UV-Vis experiments in the absence and presence of trifluoroacetic acid displayed almost identical features, indicating that the structure of the complex is unaffected by the addition of the proton source (Figure S9). Since it is a strong acid, our complex will not become protonated spontaneously. Thus, a mechanism starting with a chemical step (CE and CC) is unlikely to occur and we ultimately consider the first step as being an electrochemical one.

Table 1.
Relative pKa values for Ni3L2 after the first and second reduction steps. Values are relative to the free energy of protonating the Nic atom. ‘X’ corresponds to cases where geometry optimization of the protonated complex shows cleavage of the complex. Cleavage cases are not considered, as they will affect the ability to restore the catalyst at the end of the catalytic cycle.
With that in mind, we now had to probe how and where the first protonation step occurs. To investigate the likelihood of the first proton transfer occurring upon successive reductions, we attempted to obtain the energetics associated with the reactant and product states of the proton transfer between Ni3L2 and TFAH. We started by putting TFAH in H-bonding positions with Nic, the preferred protonation in terms of , and we conducted geometry optimization of the system in the product state, i.e., with the proton attached to the complex. When performing such calculations with the complex reduced up to two times, stable product states were found. We then proceeded with the analysis of this first proton transfer. To do so, we performed a potential energy surface (PES) scan where we constrained the distance between the transferred H atom and proton donor O from TFAH. The idea was to obtain an approximation to the transition state, which corresponds to the highest energy point of the scan (Figure S27). From there, we performed harmonic analysis to obtain the free energies at the reactant, transition, and product states of the proton transfer from TFAH to Nic. The transition state had a single negative frequency whose normal mode correspondedto the proton transfer reaction, thus indicating it was a reasonable approximation. We obtained an activation barrier ΔG‡ = 11.5 kcal·mol−1, with a reaction free energy ΔG0 = −0.2 kcal·mol−1 after the first reduction, and ΔG‡= 6.1 kcal·mol−1 and ΔG0 = −0.2 kcal·mol−1 after the second reduction. These energies correspond to rather fast intermolecular proton transfer reactions, meaning that they should not limit the kinetics of H2 formation.
Our previous results show that the first event must be an electron transfer, else proton transfer becomes impractical. We needed to figure out whether the second step was an electron or proton transfer (EE vs. EC). For the former, redox potential calculations were already performed in the previous section: we obtained reduction potentials of −1.06 V and −1.83 V for successive one-electron reduction processes. When inspecting the cyclic voltammogram of the complex in the presence of TFAH (Figure S18), we notice two main features: a shoulder around −1.72 V, and a peak at −1.99 V. Now, for an EC-sequence, we have the same one-electron reduction at −1.06 V. We calculated the redox potential for a second reduction occurring after the first protonation, i.e., ECE-sequence, resulting in −1.19 V. An ECEC-sequence for HER cannot capture the main feature of the CV at −1.52 V. Thus, such a mechanism cannot be described in terms of experimental electrochemical data. Additionally, an ECCE-type mechanism would yield a second redox potential that was even less negative than the −1.19 V observed for the second reduction in the ECEC sequence. Thus, it is not a sequence to be observed under the experimental condition used for H2 production in this work.
To further investigate the likelihood of the first proton transfer occurring between the first and second reduction (EC vs. EEC), we calculated the difference between protonating Ni3L2 at Nic and TFAH, in line with previous works [39,40]. The idea is that a positive means that the complex is thermodynamically more likely to take the proton from TFAH, whereas this is not the case for a negative value. The difference was calculated as . We obtained (EC) = −4.5 and (EEC) = 6.3. Such difference supports the fact that the catalyst should be doublyreduced before performing a proton transfer.
To finalize this study, we needed to investigate the second proton transfer event. In principle, this could occur after the first protonation (EECC), or even after a third reduction (EECEC), depending on the potential requirements for such a process. We calculated the redox potential for this third reduction, obtaining −1.47 V. Unless such a process would have a very large reorganization energy and/or very low electronic coupling with the electrode, it could take place within the experimental conditions applied for H2 production. Since calculating such properties is beyond the scope of this work, we shall consider it as a possibility. For the second proton transfer, we attempted to initially protonate all possible sites, but we found that protonation of Nic resulted in the immediate formation and release of H2. When putting TFAH in close proximity to the protonated Nic, geometry optimizations led to a spontaneous proton transfer to form H2, followed by its release. This occurred for both the EECC and EECEC cases, with a favorable free energy difference (−0.47 and −0.22 eV for EECC and EECEC, respectively). We summarize all the calculated redox potentials, pKa values and free energy differences for proton transfer events in Figure 9. Our results thus support that there are two possible reaction mechanisms to mediate proton reduction into hydrogen when using Ni3L2: (i) either an (EECC) pathway involving two electrochemical and two chemical events, or (ii) an (EECEC) involving three electrochemical and two chemical events. In both cases, the complex displays a metal-centered reactivity to promote HER which differs significantly from the conclusions raised with the parent complex NiL.
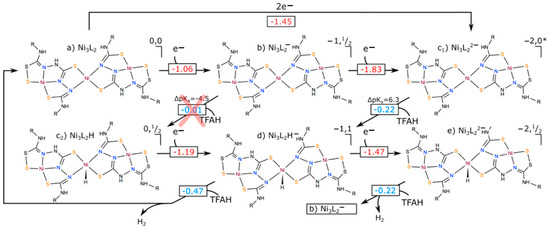
Figure 9.
Different catalytic cycles that could be performed by Ni3L2. Numbers in red correspond to redox potentials (in V), whereas those in blue are free energy differences for proton transfer events, in eV. displayed for the first proton transfer event corresponds to the difference in between Ni3L2H and TFAH. The red cross indicates that the ECEC path is thermodynamically unfavourable due to a higher of TFAH compared to the catalyst. Note that an EECEC mechanism would cycle back to point (b) once H2 is formed, since two electrons and two protons would be gone, leaving one unpaired electron in the complex.
3. Materials and Methods
3.1. Synthesis and Characterization
All solvents and chemicals were purchased from Sigma Aldrich (Merck KGaA, Darmstadt, Germany) and used without further purification. 1H NMR spectra were recorded on Bruker 400 MHz Avance III Nanobay (Bruker, Wissembourg, France). Chemical shifts for 1H and 13C NMR spectra are referred to TMS or the residual protonated solvent. 2D DOSY experiments were acquired on a BRUKER AVANCE III 600 MHz NMR spectrometer with a Double Resonance Broad Band Probe (BBFO, Bruker, Wissembourg, France) at 300 K, using a pulse sequence that incorporated bipolar gradient pulses and a longitudinal eddy current delay (LED). A total of 32 gradient values were lineary sampled from 6% to 95%. A total of 32 scans were acquired with 32k data points, for a total acquisition time of ca. 60 min. The gradient pulse duration (∂/2) and the diffusion time (∆) were set to 1.8 ms and 150 ms, respectively, with a gradient recovery delay of 0.1 ms and a LED of 5 ms. The DOSY spectra were simply obtained by using the single-exponential fitting routine of the EDDOSY feature of the TopSpin software from Bruker. Elemental analysis was performed on a Thermo Finnigan EA 1112 instrument. The results were validated by at least two measurements. ESI-MS analyses were performed using a SYNAPT G2 HDMS (Waters) spectrometer equipped with a pneumatically assisted atmospheric pressure ionization (API) source. Samples were ionized by negative electrospray mode as follows: ion-spray voltage: −2.27 kV; sampling cone: 20 V; nitrogen flux (nebulization): 100 L·h−1. High resolution mass spectra (HRMS) were performed on a QStar Elite (Applied Biosystems SCIEX) spectrometer equipped with a pneumatically assisted atmospheric pression ionization source (API). The samples were dissolved in DMF (300 μL) and placed in a methanol/3 mM ammonium acetate solution. The results were validated by three measurements. UV/Vis spectra were recorded on a Varian Cary 50 spectrophotometer. Continuous-wave EPR measurements were performed using a conventional Bruker EMX spectrometer operating in the X-band with microwave frequencies of about 9.624 GHz. This spectrometer is equipped with a He-flow cryostat (ESR900) and a cryogen-free cooler (Bruker Stinger). The measurements were performed at 50 K, a microwave power of 20 mW, and modulation amplitude of 6.7G. Particular attention was given to avoiding the saturation of the signal while keeping a good signal-to-noise ratio. The EPR spectrum simulations were performed using the Matlab program package Easyspin [41].
3.2. Synthesis of H6L
The thiocarbohydrazide (2.5 mmol 0.265 g) was dissolved in 20 mL of ethanol, and 10 mL of 1-isothiocyanato-4-methoxy-benzene (5 mmol, 0.825 g) solution in 10 mL ethanol was added dropwise. The mixture was refluxed for 2 h. After the reaction mixture was cooled to room temperature, the white product was filtered and washed twice with ethanol. The crude product was used in the next step without further purification. Yield 95%. 1H NMR (400 MHz, DMSO-d6, 298K, TMS), δ: 10.36–9.17 (m, 6H, NH), 7.33 (d, 2J = 8.5 Hz, 4H, o-CH), 6.9 (d, 2J = 9 Hz, 4H, p-CH), 3.75 ppm (s, 6H, O-CH3). 13C NMR (75 MHz, DMSO-d6, 298K, TMS), δ = 55.2, 113.4, 126.8, 131.7, 156.80, 183.9 ppm. Elemental analysis for C17H20N6O2S3: Calcd (%): C 46.77, H 4.62, N 19.25, S 22.03; found: C 45.71, H 4.54, N 20.29, S 22.05. HR ESI-MS [M-H]- for C17H20N6O2S3: Calcd: 435.0737; found: 435.0741.
3.3. Synthesis of [Ni3(SH3L)2(DMSO)2] (Ni3L2)
To the suspension of H6L (0.225 mmol, 0.1 g) in 5 mL of methanol was added solid sodium hydrosulfide (0.112 mmol, 0.0062 g). The Ni(NO3)2 (0.337 mmol, 0.098 g) dissolved in 5 mL of methanol was added dropwise to this solution. DMSO was added to fully dissolve the suspension. The solution was stirred at reflux for 2 h. Slow evaporation from this solution gave single crystals suitable for crystallographic analysis with a 70% yield. 1H NMR (600 MHz, DMSO-d6, 298K, TMS), δ: 8.75 (s broad, 6H, NH), 7.07–6.83 (s, 16H, Ph-H), 3.85 (s, 6H, -OCH3) 3.70 ppm (s, 6H, -OCH3). 13C NMR (150 MHz, DMSO-d6, 298K, TMS), δ = 55.1, 114.2, 116.1, 116.5, 125.4, 132.2, 153.8, 157.4 ppm. Elemental analysis for C42H58N12O8S12Ni3: Calcd (%): C 35.49, H 4.08, N 11.83, S 27.04; found: C 35.56, H 4.10, N 11.24, S 27.11. HR ESI-MS [M-H]- for C34H34N12O4S8Ni3: Calcd: 1104.8542; found: 1104.8548.
3.4. X-ray Crystallography
X-ray diffraction measurements were carried out with a Rigaku Oxford-Diffraction XCALIBUR E CCD diffractometer equipped with graphite-monochromated MoKα radiation. The unit cell determination and data integration were carried out using the CrysAlis package of Oxford Diffraction [42]. The structures were solved by Intrinsic Phasing using Olex2 [43] software with the SHELXT [44] structure solution program and refined by full-matrix least-squares on F2 with SHELXL-2015 [45] using an anisotropic model for non-hydrogen non-disordered atoms. All H atoms were introduced in idealized positions with dCH = 0.96 Å. The positional parameters of the disordered atoms were refined using available tools (PART, DFIX, and SADI) of SHELXL. The molecular plots were obtained using the Olex2 program. The crystallographic data and refinement details, as well as bond lengths and angles, are presented in the Supplementary Material.
3.5. SQUID Magnetometry
Magnetic characterization has been performed using a conventional SQUID magnetometer MPMS-XL from Quantum Design working at a magnetic field up to 5 T and temperature down to 2 K. The samples (powder) are filled in polypropylene sleeves, then sealed in order to remove the maximum dioxygen, which gives a signal around 50 K (antiferromagnetic transition). The diamagnetic contribution of the sample holder was removed as well as the diamagnetism of Ni3L2. To avoid field-dependent effects (such as ferromagnetic impurities), the temperature dependence of the susceptibility was recorded for three magnetic fields: 0.1, 1, and 4T. Considering non-interacting inter-trimer paramagnetic centres, we fitted χT by 1/8.S(S + 1).giso2 in CGS units.
3.6. Electrochemistry
Cyclic voltammetry experiments were performed using a BioLogic SP300 potentiostat and a three-electrode setup consisting of a glassy carbon working electrode, a platinum wire counter electrode, and a leakless (Ag/AgCl) reference electrode. Ferrocene was used as an internal standard with E0(Fc+/0) = 0.53 V versus Ag/AgCl. Chronoamperometric experiments were conducted with another three-electrode setup composed of a 1 mm glassy carbon electrode as the working electrode, a platinum wire as the counter electrode, and a leakless Ag/AgCl reference electrode. All studies were performed in deoxygenated DMF containing NBu4PF6 (0.1 M) as the supporting electrolyte. Controlled potential electrolysis experiments were carried out in a two-compartment cell. The volume of solution (DMF, 0.1 M NBu4PF6) used in the working compartment of the cell was 8 mL. The working electrode used was a pool of mercury, separated from the coiled platinum wire counter electrode by a porous frit. Bulk electrolysis solutions were purged with N2 gas for at least 20 min prior to electrolysis and stirred throughout the bulk electrolysis experiment. During the experiment, the cell was continuously purged with nitrogen (5 mL·min−1) and the output gas was analyzed at two-minute intervals in a Perkin–Elmer Clarus 500 gas chromatographer using a previously described setup [46]. Dip and rinse tests were performed after electrocatalytic measurements. The glassy carbon working electrode was removed from the solution and immersed into a fresh DMF solution followed by the addition of 100 mM of acid. The electrochemical response was then recorded upon sweeping the potential in the cathodic region.
3.7. DFT Calculations
The methodology is essentially the same used in our previous work with NiL [29]. We used ORCA 4.2.1 [47,48], with BP86 as our functional of choice [49,50], and def2-TZVP(-f) as our basis set [51]. Full geometry optimizations were undertaken by taking advantage of the resolution of the identity (RI) approximation in the Split-RI-J variant [52] with the appropriate Coulomb fitting sets [53]. Increased integration grids (Grid4 in ORCA convention) and tight SCF convergence criteria were used. According to the experimental conditions, these calculations were performed in DMF solvent by invoking the Control of the Conductor-like Polarizable Continuum Model (CPCM) [54]. We considered various possible spin configurations, including open-shell singlets. For the latter, we performed broken-symmetry DFT calculations, using the “FlipSpin” feature of ORCA [55,56,57]. Free energy differences were extracted from the Gibbs free energies obtained from numerical frequencies calculations. Electronic structures were obtained from single-point DFT calculations using the hybrid functional B3LYP [58,59] together with the def2-TZVP(-f) basis set [51]. TD-DFT calculations [60,61,62] used the Tamm-Dancoff approximation [63,64] and included triplet excitations. A total of 100 roots were calculated with the B3LYP [58,65] density functional under the RIJCOSX approximation with the def2-TZVP(-f) [51] and def2/J basis sets and the CPCM solvent model. [54] The grid sizes were increased to Grid7 and GridX9 in ORCA nomenclature. While other density functionals including PBE0 [66] and TPSSh [67] were tested, B3LYP gave the most favorable agreement with experiment. All the calculated reduction potentials (E) were relative to Fc+/0. The calculated Gibbs free energy difference using the BP86 functional to account for ferrocene in DMF was ∆G = 4.87 eV. The relative acidities were computed with respect to TFAH in DMF. Spin density plots, molecular orbitals, and difference density plots for each transition were generated using the orca plot utility program and were visualized with the Chemcraft program [68].
4. Conclusions
This work reports on an original trinuclear nickel complex, [Ni3(SH3L)2(DMSO2)], (Ni3L2) that was experimentally characterized and evaluated as a potential electrocatalyst for hydrogen evolution. Ni3L2 exhibited enhanced catalytic performances for the electrochemical reduction of protons into hydrogen. Interestingly, when compared to its mononuclear analogue NiL, the trinuclear complex features a comparable faradaic yield but displays higher TON and TOF values, and is able to produce more hydrogen on a shorter timescale. Ni3L2 is a faster catalyst but it comes with the cost of requiring a larger overpotential, the drawback to these improved performances lying thus in the driving force of the reaction. These results support the fact that the nuclearity of the catalyst affects its electronic and redox properties, which influences its catalytic performances.
The theoretical investigations showed that the reactivity of the trinuclear complex shifted with respect to that of the mononuclear catalyst. While the NiL exhibited a metal-assisted ligand-centred reactivity making use of the N-atoms close to the metal centre [29], only the central nickel ion is involved in the case of Ni3L2. Such change in reactivity might explain the improved efficiency of the complex. On the other hand, the increase in potential requirements of Ni3L2 is probably associated with the electronic density being strictly localized at the metal centre, losing the benefit from delocalization onto the ligand, as observed with the mononuclear NiL catalyst.
Replacement of the two catalytically-inactive peripheral nickel centres of Ni3L2 with more electron-rich and redox-innocent metals such as zinc might improve the catalytic performance of the system by diminishing the overpotential requirements. Another important question to address is whether a metal-centred reactivity is indeed responsible for better turnover rates. For comparison, the Co-based thiosemicarbazone complex has been shown to be an efficient HER catalyst requiring smaller overpotentials than its Ni counterpart [22]. Synthetizing a trinuclear Co complex could further probe how focusing density at the metal centre actually impacts the electrochemical properties of the system and assists in the catalytic turnover rates.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics11040149/s1, Figure S1: Synthetic protocol used for H6L.; Figure S2: Synthetic protocol used for Ni3L2; Figure S3: 1H NMR spectrum and partial assignment for H6L in DMSO at 298 K; Figure S4: 13C NMR spectrum and partial assignment for H6L in DMSO at 298 K; Figure S5: 1H NMR spectrum and partial assignment for Ni3L2 in DMSO at 298 K; Figure S6: 13C NMR spectrum and partial assignment for Ni3L2 in DMSO at 298 K; Figure S7: 2D DOSY spectrum for Ni3L2 in DMF at 298 K processed using DOSY Toolbox (GNU General Public License) with 512 points for the self-diffusion axis; Figure S8: Electronic absorption spectra for the Ni3L2 complex (black line), and upon chronoamperometry (−1.7 V vs. Fc+/0 with 100 mM of TFA, blue line); Figure S9: Electronic absorption spectra of 0.5 mM solutions of Ni3L2 in DMF in the absence (black line) or in the presence (red, blue green, pink and khaki lines) of TFA; Figure S10: Comparison between experimental and calculated UV-Vis spectra for Ni3L2 in DMF. Calculations performed on the neutral complex in a closed-shell singlet state (B3LYP/def2-TZVP(-f), see Electronic structure section in the main text); Figure S11: Difference densities of the most important transitions of Ni3L2 predicted with TDDFT (B3LYP/def2-TZVP(-f); yellow: density loss, red: density gain) listed in Table S4; Figure S12: Cyclic voltammogram of a 1 mM solution of H6L (black line) in DMF recorded at a stationary glassy carbon with 0.1 M NBu4PF6 as supporting electrolyte. The cyclic voltammograms of a 100 mM of TFA solution in the absence (blue line) and in the presence (red line) of 1 mM H6L are also shown. Scan rate: 500 mV s−1. Potentials are referenced to the Fc+/0 electrode; Figure S13: Successive cyclic voltammograms of a 1 mM solution of Ni3L2 in DMF at a stationary glassy carbon electrode at different scan rates (v) in DMF with 0.1 M NBu4PF6 as supporting electrolyte. Potentials are referenced to the Fc+/0 electrode; Figure S14: Linear plot of ip versus the square root of the scan rate v1/2 for anodic and cathodic waves of the quasi-reversible redox process of Ni3L2; Figure S15: Chronoamperogram of a 1 mM solution of Ni3L2 in DMF recorded at −1.50 V vs. Fc+/0 at 1 mm glassy carbon electrode; Figure S16: Chronoamperogram of a 1 mM solution of Ni3L2 in DMF recorded at −2.25 V vs. Fc+/0 at 1 mm glassy carbon electrode; Figure S17: Simulated (blue line) and experimental (dotted line) cw X-band EPR spectrum of a 1 mM solution of Ni3L2 in DMF at T = 50 K recorded upon chronoamperometry at −1.50 V vs. Fc+/0 at 1 mm glassy carbon electrode; Figure S18: Successive cyclic voltammograms of a 1 mM solution of Ni3L2 in DMF (0.1 M NBu4PF6) recorded at a glassy carbon electrode with increasing amounts of TFA at 500 mV s−1. Potentials are referenced to the Fc+/0 electrode; Figure S19: Plot of icat of Ni3L2 for increasing concentrations of TFA at different scan rates; Figure S20: Cyclic voltammograms recorded after electrocatalysis of Ni3L2 upon washing the working electrode and immersion into a fresh solution of dry DMF (0.1M NBu4PF6, black dashed line) and in the presence of 100 mM of TFA (blue line). Scan rate 500 mV s−1; Figure S21: Electrocatalytic hydrogen production vs. time, by applying −1.70 V vs. Fc+/0 to a pool mercury working electrode in 0.1 M NBu4PF6 solution of DMF containing 100 mM TFA in the absence (red line) and presence of 1 mM of Ni3L2 (black line); Figure S22: Coulometry during bulk electrolysis experiment at −1.70 V vs. versus Fc+/0 using a pool mercury working electrode. The electrolytic solution contains 0.1 M NBu4PF6 in DMF, 100 mM TFA and 1 mM of Ni3L2; Figure S23: Plot of versus inverse of the square root of the scan rate () for Ni3L2 in DMF in the presence of different amounts of TFA. The plots were derived from the voltammograms recorded at different scan rates in the absence and presence of proton source; Figure S24: Plot of versus the square root of the acid concentration ( for Ni3L2 in DMF at different scan rates. The plots were derived from the voltammograms recorded at different scan rates in the absence and presence of proton source; Figure S25: Plot of versus the [Ni3L2] concentration in DMF in the presence of 100 mM TFA at 500 mV s−1; Figure S26: Spin density plot (a) and localized Singly Occupied Molecular Orbital (SOMO, b) for Ni3L2 after two subsequent one-electron reduction reactions. The complex is in a triplet dianionic state; Figure S27: Potential energy surface scans for the proton transfer between TFAH and Ni3L2 after the first (left) and second (right) reductions (top), free energy diagrams of the proton transfer, where the transition state was taken as the highest point in the PES scan (middle) and transition state geometries, with Ni-H and OTFA-H distances displayed in Å (bottom). Their cartesian coordinates are provided in Tables S14 and S15; Table S1: Crystal data and details of data collection for Ni3L2; Table S2: Bond distances (Å) and angles (°) for Ni3L2; Table S3: Selected features of the electronic absorption spectra of H6L and Ni3L2 in DMF; Table S4: Selected intense transitions in the calculated UV-vis spectra of Ni3L2 and their assignment with difference densities (yellow: density loss, red: density gain; CT: charge transfer, MMCT: metal-to-metal CT, LMCT: ligand-to-metal CT, MLCT: metal-to-ligand CT; d → d: local excitation on the metals, L → L: local excitation on the ligands, see Figure S11 for depictions); Table S5: Comparison of free energies for each oxidation state of Ni3L2 for up to three reduction events (top) and comparison of free energies for the neutral state of Ni3L2 including 2 bound DMSO molecules (bottom); Table S6: Redox potentials of Ni3L2, considering three successive one-electron as well as two-electron reduction events for the deprotonated complex, and redox processes including protonation of the complex. We are considering Nic as our protonation site (see Mechanistic considerations section in the main text). All results are reported vs. Fc+/0 electrode, where the reference was calculated to be −4.87 V using the same level of theory (BP86/def2-TZVP(-f), CPCM(DMF)); Table S7: Mulliken spin densities of the Ni centers (central, c and side, s and s’) in the one-, two-, and three-electron reduced complex Ni3L2; Table S8: Relative pKa values for Ni3L2 before reduction steps. Values are relative to the free energy of protonating the Nic atom. ‘X’ corresponds to cases where geometry optimization of the protonated complex showed cleavage of the complex. Cleavage cases are not considered, as they will affect the ability to restore the catalyst at the end of the catalytic cycle; Table S9: Cartesian coordinates of Ni3L2 used as the reference for the study including 2 DMSO; Table S10: Cartesian coordinates of Ni3L2 in its neutral form (Q = 0, S = 0); Table S11: Cartesian coordinates of Ni3L2 in its monoanionic form (Q = (−1), S = 1/2), Table S12: Cartesian coordinates of Ni3L2 in its dianionic form (Q = (−2), S = 1), Table S13: Cartesian coordinates of Ni3L2 in its trianionic form (Q = (−3), S = 1/2) Table S14: Cartesian coordinates of TS for the proton transfer between Ni3L2 and TFAH after the first reduction (Q = (−1), S = 1/2); Table S15: Cartesian coordinates of TS for the proton transfer between Ni3L2 and TFAH after the second reduction (Q = (−2), S = 1).
Author Contributions
Conceptualization, M.O.; methodology, M.O.; validation: R.H. and M.O.; formal analysis, S.S., V.K., S.B., A.B. and M.O.; investigation, M.P, L.D., T.S. and A.B.; writing—original draft preparation, M.P, T.S., A.B. and M.O.; writing—review and editing, M.P., A.B. and M.O.; visualization: M.P., T.S., A.B. and M.O.; supervision, M.R., R.H. and M.O.; project administration, M.O.; funding acquisition, M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Agence Nationale de la Recherche, grant number ANR-19-CE05_0030_01.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors gratefully acknowledge financial support of this work by the ANR, the CNRS, and the Academy of Sciences of Moldova. The authors thank Jennifer Fize for conducting the bulk electrolysis experiments, Roselyne Rosas for her help in performing NMR measurements, and Mehdi Yemoul for assisting in the analysis of the DOSY data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Turner, J.A. Sustainable Hydrogen Production. Science 2004, 305, 972–974. [Google Scholar] [CrossRef]
- Edwards, P.P.; Kuznetsov, V.L.; David, W.I.F.; Brandon, N.P. Hydrogen and Fuel Cells: Towards a Sustainable Energy Future. Energy Policy 2008, 36, 4356–4362. [Google Scholar] [CrossRef]
- Kumar, S.S.; Himabintu, V. Hydrogen production by PEM water electrolysis—A review. Mater. Sci. Energy Technol. 2019, 2, 442–454. [Google Scholar] [CrossRef]
- Volbeda, A.; Charon, M.-H.; Piras, C.; Hatchikian, E.C.; Frey, M.; Fontecilla-Camps, J.C. Crystal Structure of the Nickel–Iron Hydrogenase from Desulfovibrio Gigas. Nature 1995, 373, 580–587. [Google Scholar] [CrossRef]
- Fontecilla-Camps, J.C.; Volbeda, A.; Cavazza, C.; Nicolet, Y. Structure/Function Relationships of [NiFe]- and [FeFe]-Hydrogenases. Chem. Rev. 2007, 107, 4273–4303. [Google Scholar] [CrossRef] [PubMed]
- Volbeda, A.; Garcin, E.; Piras, C.; de Lacey, A.L.; Fernandez, V.M.; Hatchikian, E.C.; Frey, M.; Fontecilla-Camps, J.C. Structure of the [NiFe] Hydrogenase Active Site: Evidence for Biologically Uncommon Fe Ligands. J. Am. Chem. Soc. 1996, 118, 12989–12996. [Google Scholar] [CrossRef]
- Lubitz, W.; Ogata, H.; Rüdiger, O.; Reijerse, E. Hydrogenases. Chem. Rev. 2014, 114, 4081–4148. [Google Scholar] [CrossRef] [PubMed]
- Vincent, K.A.; Parkin, A.; Armstrong, F.A. Investigating and Exploiting the Electrocatalytic Properties of Hydrogenases. Chem. Rev. 2007, 107, 4366–4413. [Google Scholar] [CrossRef]
- McKone, J.R.; Marinescu, S.C.; Brunschwig, B.S.; Winkler, J.R.; Gray, H.B. Earth-Abundant Hydrogen Evolution Electrocatalysts. Chem. Sci. 2014, 5, 865–878. [Google Scholar] [CrossRef]
- Dalle, K.E.; Warnan, J.; Leung, J.J.; Reuillard, B.; Karmel, I.S.; Reisner, E. Electro- and Solar-Driven Fuel Synthesis with First Row Transition Metal Complexes. Chem. Rev. 2019, 119, 2752–2875. [Google Scholar] [CrossRef]
- Orio, M.; Pantazis, D.A. Successes, Challenges, and Opportunities for Quantum Chemistry in Understanding Metalloenzymes for Solar Fuels Research. Chem. Commun. 2021, 57, 3952–3974. [Google Scholar] [CrossRef] [PubMed]
- Helm, M.L.; Stewart, M.P.; Bullock, R.M.; DuBois, M.R.; DuBois, D.L. A Synthetic Nickel Electrocatalyst with a Turnover Frequency Above 100,000 s −1 for H2 Production. Science 2011, 333, 863–866. [Google Scholar] [CrossRef] [PubMed]
- DuBois, M.R.; DuBois, D.L. The Roles of the First and Second Coordination Spheres in the Design of Molecular Catalysts for H2 Production and Oxidation. Chem. Soc. Rev. 2009, 38, 62–72. [Google Scholar] [CrossRef]
- Razavet, M.; Artero, V.; Fontecave, M. Proton Electroreduction Catalyzed by Cobaloximes: Functional Models for Hydrogenases. Inorg. Chem. 2005, 44, 4786–4795. [Google Scholar] [CrossRef] [PubMed]
- Kaeffer, N.; Chavarot-Kerlidou, M.; Artero, V. Hydrogen Evolution Catalyzed by Cobalt Diimine–Dioxime Complexes. Acc. Chem. Res. 2015, 48, 1286–1295. [Google Scholar] [CrossRef]
- Drosou, M.; Kamatsos, F.; Mitsopoulou, C.A. Recent Advances in the Mechanisms of the Hydrogen Evolution Reaction by Non-Innocent Sulfur-Coordinating Metal Complexes. Inorg. Chem. Front. 2020, 7, 37–71. [Google Scholar] [CrossRef]
- Lyaskovskyy, V.; de Bruin, B. Redox Non-Innocent Ligands: Versatile New Tools to Control Catalytic Reactions. ACS Catal. 2012, 2, 270–279. [Google Scholar] [CrossRef]
- Straistari, T.; Fize, J.; Shova, S.; Réglier, M.; Artero, V.; Orio, M. A Thiosemicarbazone-Nickel(II) Complex as Efficient Electrocatalyst for Hydrogen Evolution. ChemCatChem 2017, 9, 2262–2268. [Google Scholar] [CrossRef]
- Haddad, A.Z.; Garabato, B.D.; Kozlowski, P.M.; Buchanan, R.M.; Grapperhaus, C.A. Beyond Metal-Hydrides: Non-Transition-Metal and Metal-Free Ligand-Centered Electrocatalytic Hydrogen Evolution and Hydrogen Oxidation. J. Am. Chem. Soc. 2016, 138, 7844–7847. [Google Scholar] [CrossRef] [PubMed]
- Straistari, T.; Hardré, R.; Massin, J.; Attolini, M.; Faure, B.; Giorgi, M.; Réglier, M.; Orio, M. Influence of the Metal Ion on the Electrocatalytic Hydrogen Production by a Thiosemicarbazone Palladium Complex. Eur. J. Inorg. Chem. 2018, 2018, 2259–2266. [Google Scholar] [CrossRef]
- Jain, R.; Mamun, A.A.; Buchanan, R.M.; Kozlowski, P.M.; Grapperhaus, C.A. Ligand-Assisted Metal-Centered Electrocatalytic Hydrogen Evolution upon Reduction of a Bis(Thiosemicarbazonato)Ni(II) Complex. Inorg. Chem. 2018, 57, 13486–13493. [Google Scholar] [CrossRef]
- Straistari, T.; Hardré, R.; Fize, J.; Shova, S.; Giorgi, M.; Réglier, M.; Artero, V.; Orio, M. Hydrogen Evolution Reactions Catalyzed by a Bis(Thiosemicarbazone) Cobalt Complex: An Experimental and Theoretical Study. Chem. Eur. J. 2018, 24, 8779–8786. [Google Scholar] [CrossRef] [PubMed]
- Cronin, S.P.; Mamun, A.A.; Toda, M.J.; Mashuta, M.S.; Losovyj, Y.; Kozlowski, P.M.; Buchanan, R.M.; Grapperhaus, C.A. Utilizing Charge Effects and Minimizing Intramolecular Proton Rearrangement to Improve the Overpotential of a Thiosemicarbazonato Zinc HER Catalyst. Inorg. Chem. 2019, 58, 12986–12997. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, M.; Barrozo, A.; Straistari, T.; Queyriaux, N.; Putri, A.; Fize, J.; Giorgi, M.; Réglier, M.; Massin, J.; Hardré, R.; et al. Ligand-Based Electronic Effects on the Electrocatalytic Hydrogen Production by Thiosemicarbazone Nickel Complexes. Dalton Trans. 2020, 49, 5064–5073. [Google Scholar] [CrossRef]
- Coutard, N.; Kaeffer, N.; Artero, V. Molecular Engineered Nanomaterials for Catalytic Hydrogen Evolution and Oxidation. Chem. Commun. 2016, 52, 13728–13748. [Google Scholar] [CrossRef]
- DuBois, D.L. Development of Molecular Electrocatalysts for Energy Storage. Inorg. Chem. 2014, 53, 3935–3960. [Google Scholar] [CrossRef]
- Das, A.; Hessin, C.; Ren, Y.; Desage-El Murr, M. Biological Concepts for Catalysis and Reactivity: Empowering Bioinspiration. Chem. Soc. Rev. 2020, 49, 8840–8867. [Google Scholar] [CrossRef]
- Ladomenou, K.; Papadakis, M.; Landrou, G.; Giorgi, M.; Drivas, C.; Kennou, S.; Hardré, R.; Massin, J.; Coutsolelos, A.G.; Orio, M. Nickel Complexes and Carbon Dots for Efficient Light-Driven Hydrogen Production. Eur. J. Inorg. Chem. 2021, 2021, 3097–3103. [Google Scholar] [CrossRef]
- Barrozo, A.; Orio, M. Unraveling the Catalytic Mechanisms of H2 Production with Thiosemicarbazone Nickel Complexes. RSC Adv. 2021, 11, 5232–5238. [Google Scholar] [CrossRef]
- Pieri, C.; Bhattacharjee, A.; Barrozo, A.; Faure, B.; Giorgi, M.; Fize, J.; Réglier, M.; Field, M.; Orio, M.; Artero, V.; et al. Hydrogen evolution reaction mediated by an all-sulfur trinuclear nickel complex. Chem. Commun. 2020, 56, 11106–11109. [Google Scholar] [CrossRef]
- Fourmond, V.; Canaguier, S.; Golly, B.; Field, M.J.; Fontecave, M.; Artero, V. A Nickel–Manganese Catalyst as a Biomimic of the Active Site of NiFe Hydrogenases: A Combined Electrocatalytical and DFT Mechanistic Study. Energy Environ. Sci. 2011, 4, 2417–2427. [Google Scholar] [CrossRef]
- Fourmond, V.; Jacques, P.-A.; Fontecave, M.; Artero, V. H2 Evolution and Molecular Electrocatalysts: Determination of Overpotentials and Effect of Homoconjugation. Inorg. Chem. 2010, 49, 10338–10347. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Sharma, B.; Pécaut, J.; Simon, P.; Fontecave, M.; Tran, P.D.; Derat, E.; Artero, V. Molecular Cobalt Complexes with Pendant Amines for Selective Electrocatalytic Reduction of Carbon Dioxide to Formic Acid. J. Am. Chem. Soc. 2017, 139, 3685–3696. [Google Scholar] [CrossRef]
- Artero, V.; Saveant, J.-M. Toward the Rational Benchmarking of Homogeneous H2-Evolving Catalysts. Energy Environ. Sci. 2014, 7, 3808–3814. [Google Scholar] [CrossRef]
- Bhugun, I.; Lexa, D.; Savéant, J.-M. Homogeneous Catalysis of Electrochemical Hydrogen Evolution by Iron(0) Porphyrins. J. Am. Chem. Soc. 1996, 118, 3982–3983. [Google Scholar] [CrossRef]
- Galan, B.R.; Schöffel, J.; Linehan, J.C.; Seu, C.; Appel, A.M.; Roberts, J.A.S.; Helm, M.L.; Kilgore, U.J.; Yang, J.Y.; DuBois, D.L.; et al. Electrocatalytic Oxidation of Formate by [Ni(PR2NR′2)2(CH3CN)]2+ Complexes. J. Am. Chem. Soc. 2011, 133, 12767–12779. [Google Scholar] [CrossRef]
- Wilson, A.D.; Newell, R.H.; McNevin, M.J.; Muckerman, J.T.; Rakowski DuBois, M.; DuBois, D.L. Hydrogen Oxidation and Production Using Nickel-Based Molecular Catalysts with Positioned Proton Relays. J. Am. Chem. Soc. 2006, 128, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Wiedner, E.S.; Appel, A.M.; DuBois, D.L.; Bullock, R.M. Thermochemical and Mechanistic Studies of Electrocatalytic Hydrogen Production by Cobalt Complexes Containing Pendant Amines. Inorg. Chem. 2013, 52, 14391–14403. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.; Ghosh, P.; Lunsford, A.M.; Wang, N.; Bhuvanesh, N.; Hall, M.B.; Darensbourg, M.Y. Hemilabile Bridging Thiolates as Proton Shuttles in Bioinspired H2 Production Electrocatalysts. J. Am. Chem. Soc. 2016, 138, 12920–12927. [Google Scholar] [CrossRef]
- Tang, H.; Hall, M.B. Biomimetics of [NiFe]-Hydrogenase: Nickel- or Iron-Centered Proton Reduction Catalysis? J. Am. Chem. Soc. 2017, 139, 18065–18070. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
- CrysAlis Pro. Available online: https://www.rigaku.com/products/crystallography/crysalis (accessed on 1 March 2023).
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT—Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Cobo, S.; Heidkamp, J.; Jacques, P.-A.; Fize, J.; Fourmond, V.; Guetaz, L.; Jousselme, B.; Ivanova, V.; Dau, H.; Palacin, S.; et al. A Janus Cobalt-Based Catalytic Material for Electro-Splitting of Water. Nat. Mater. 2012, 11, 802–807. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, Version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824, Erratum in Phys. Rev. B 1986, 34, 7406–7406. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Neese, F. An Improvement of the Resolution of the Identity Approximation for the Formation of the Coulomb Matrix. J. Comput. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Noodleman, L. Valence Bond Description of Antiferromagnetic Coupling in Transition Metal Dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Noodleman, L.; Case, D.A. Density-Functional Theory of Spin Polarization and Spin Coupling in Iron—Sulfur Clusters. In Advances in Inorganic Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 38, pp. 423–470. [Google Scholar]
- Noodleman, L.; Davidson, E.R. Ligand Spin Polarization and Antiferromagnetic Coupling in Transition Metal Dimers. Chem. Phys. 1986, 109, 131–143. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree–Fock and Local Density-functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Lester, W.A. Recent Advances in Quantum Monte Carlo Methods; Recent Advances in Computational Chemistry; World Scientific: Singapore, 1997; Volume 2, ISBN 978-981-02-3009-8. [Google Scholar]
- Stratmann, R.E.; Scuseria, G.E.; Frisch, M.J. An Efficient Implementation of Time-Dependent Density-Functional Theory for the Calculation of Excitation Energies of Large Molecules. J. Chem. Phys. 1998, 109, 8218–8224. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of Electronic Excitations within the Adiabatic Approximation of Time Dependent Density Functional Theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Hirata, S.; Head-Gordon, M. Time-Dependent Density Functional Theory within the Tamm–Dancoff Approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
- Hirata, S.; Head-Gordon, M. Time-Dependent Density Functional Theory for Radicals An Improved Description of Excited States with Substantial Double Excitation Character. Chem. Phys. Lett. 1999, 302, 375–382. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Chemcraft. Available online: https://www.chemcraftprog.com (accessed on 1 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).