Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates
Abstract
:1. Introduction
2. Theoretical Analysis
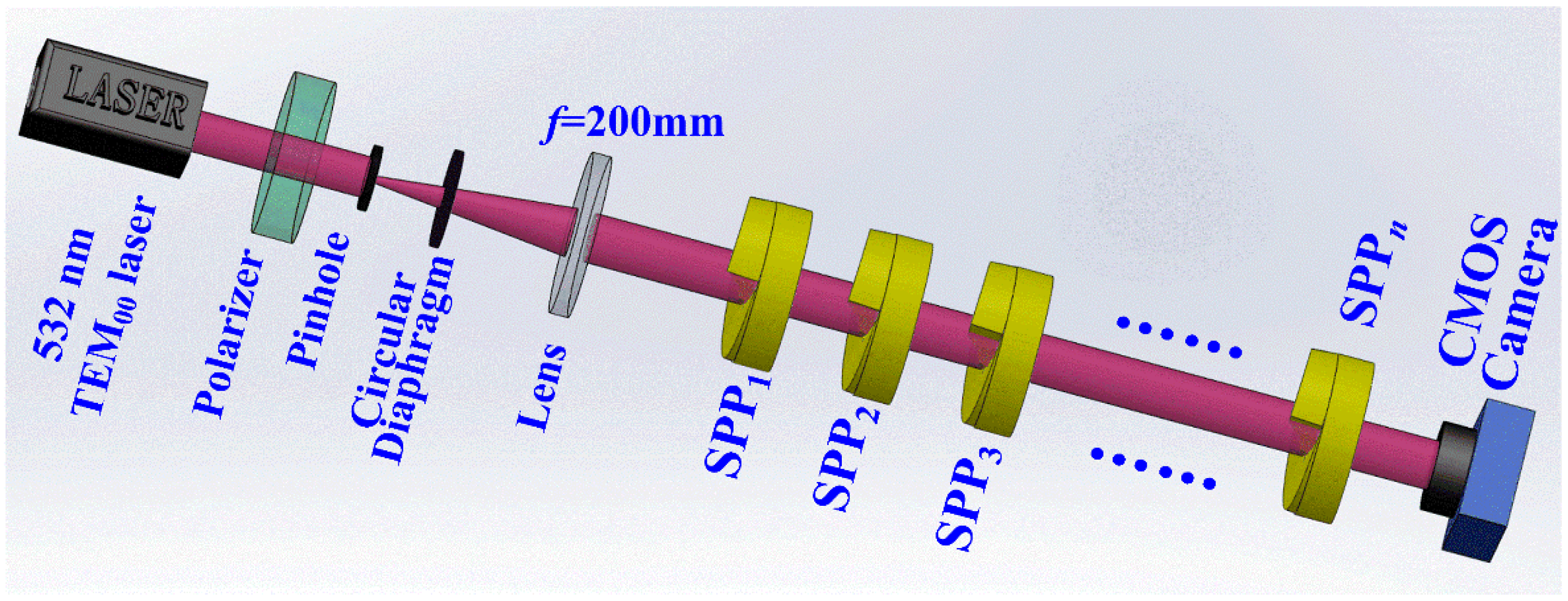
3. Experimental Setup
4. Results and Discussion
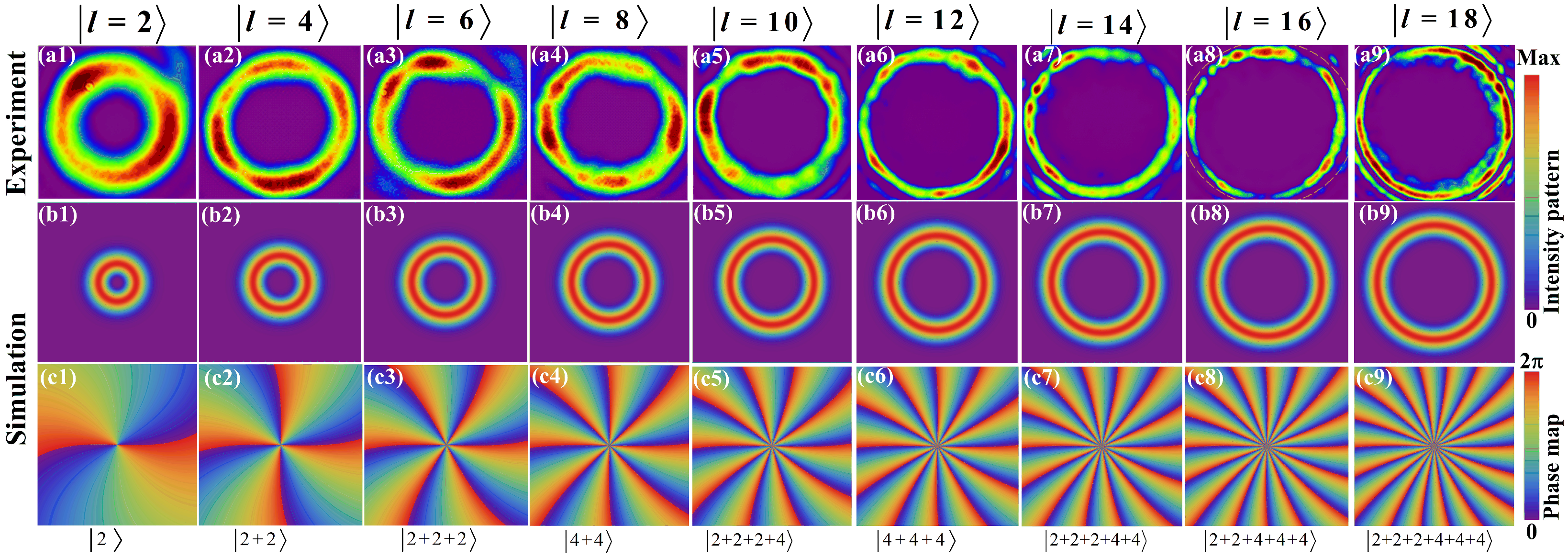
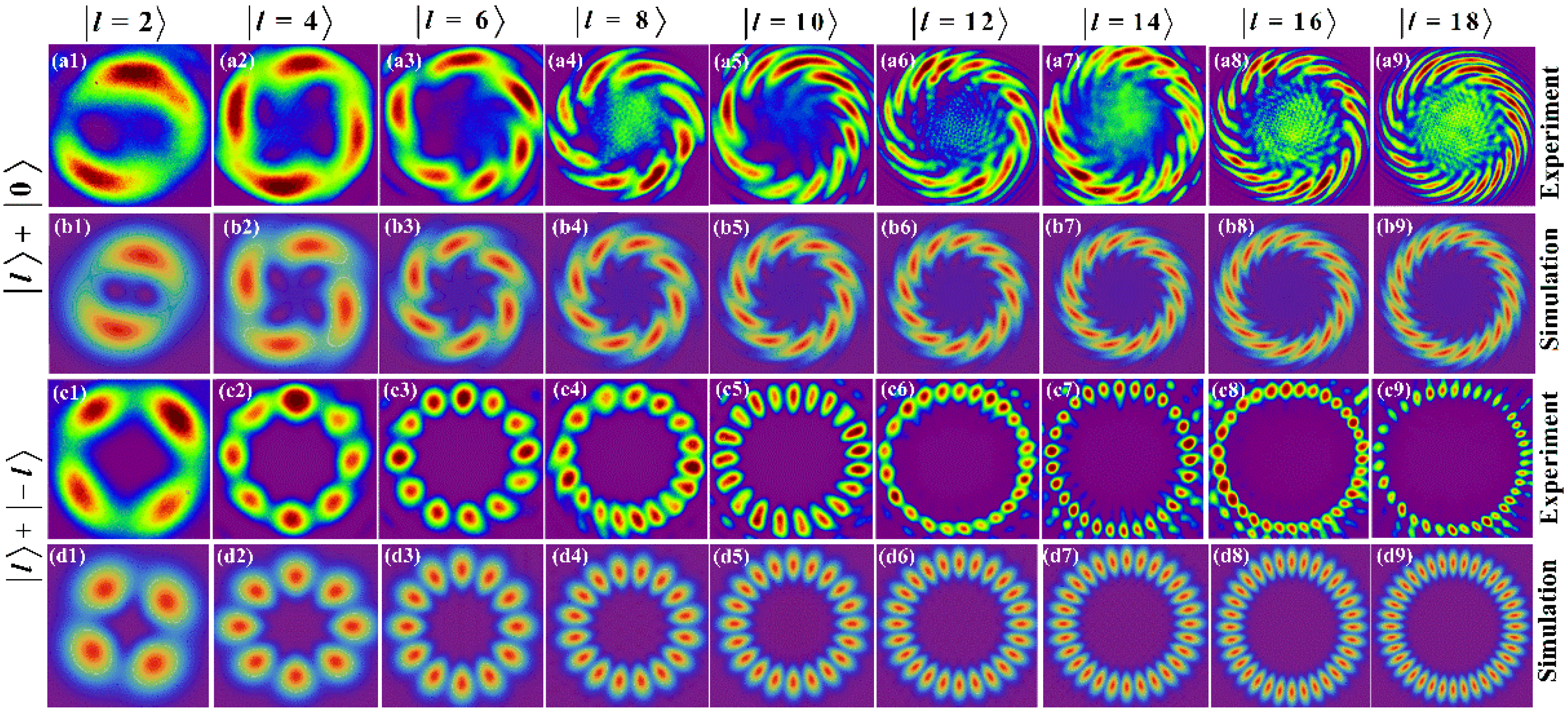
4.1. High Order VB Generated by Multiple Cascaded SPPs
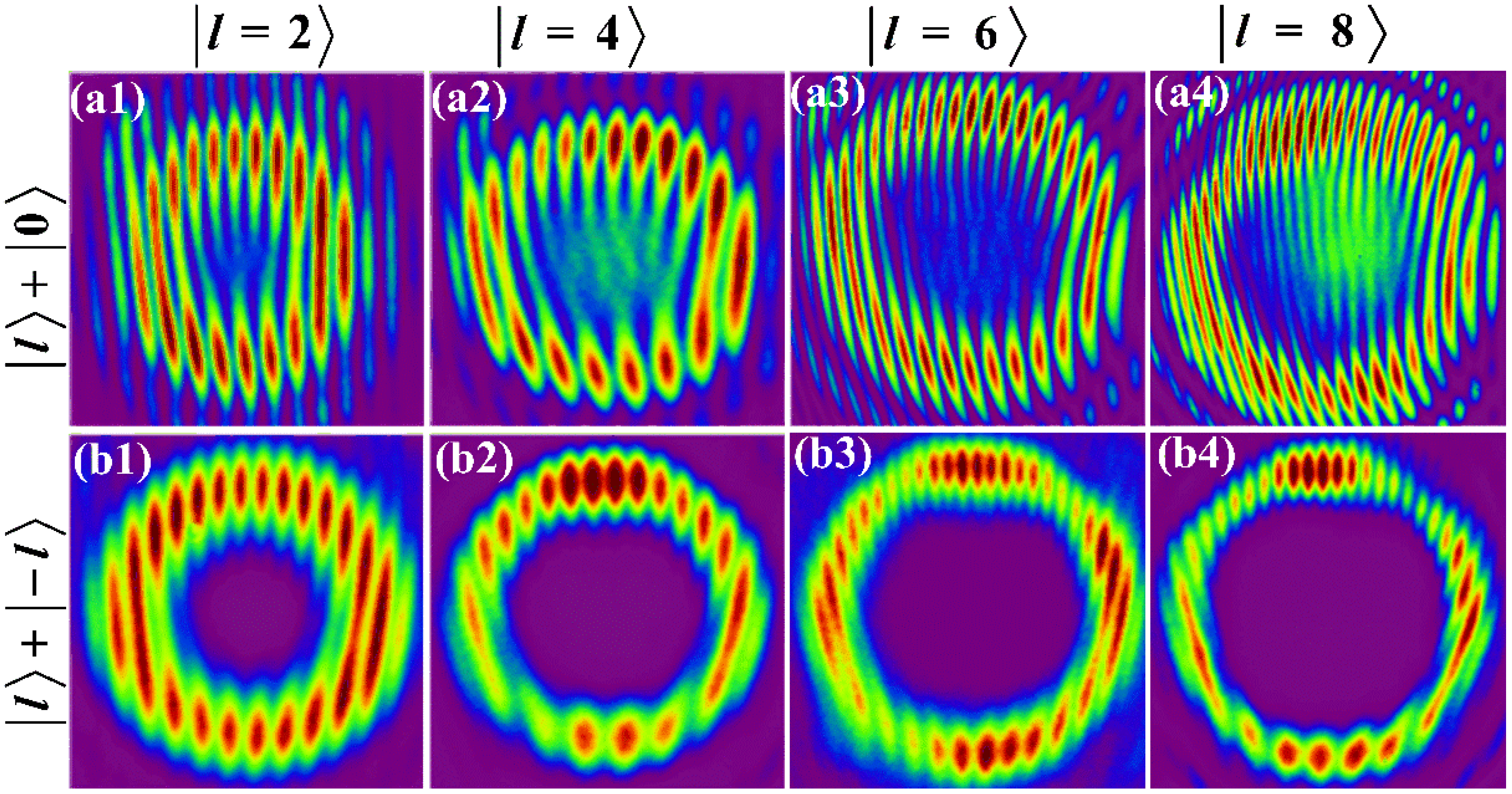
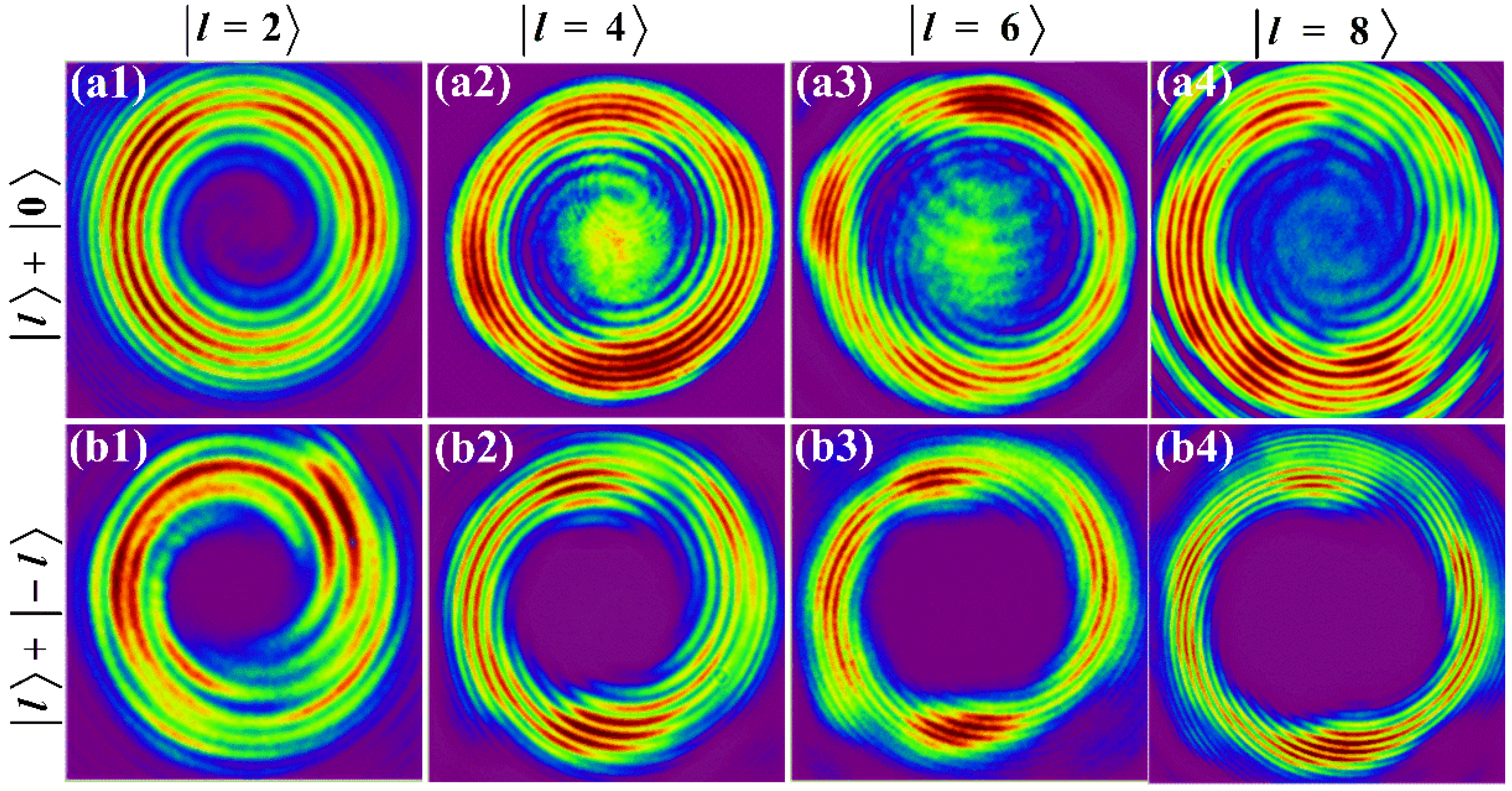
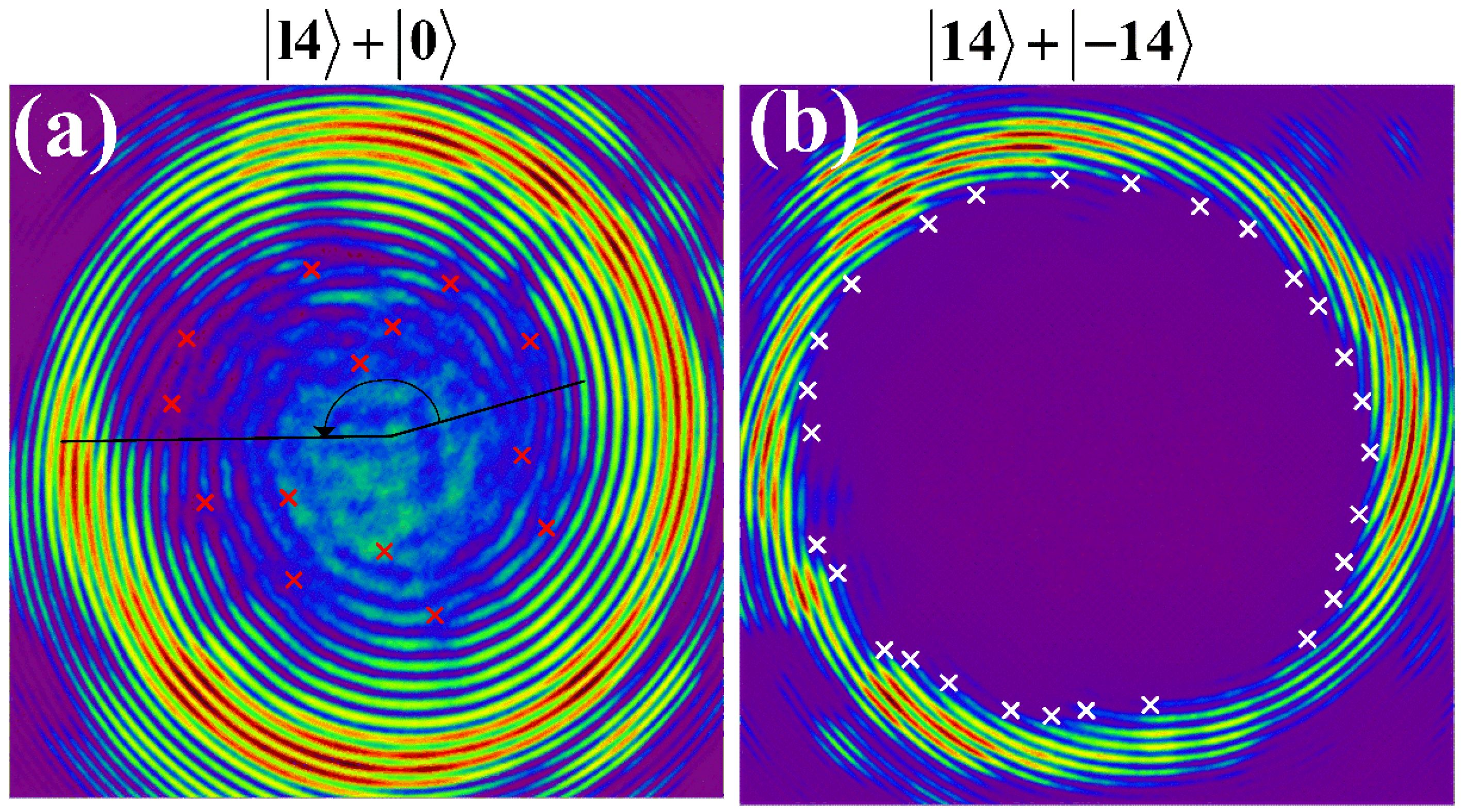
4.2. Interference between a VB and a TEM00 Gaussian Beam (or Its Conjugate One)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plociniczak, L.; Popiolek-Masajada, A.; Szatkowski, M.; Masajada, M. High order vortex in the optical vortex microscope. Proc. SPIE 2015, 9581, 95810N. [Google Scholar]
- Fickler, R.; Lapkiewicz, R.; Plick, W.N.; Krenn, M.; Schaeff, C.; Ramelow, S.; Zeilinger, A. Quantum Entanglement of High Angular Momenta. Science 2012, 338, 640–643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fickle, R.; Campbell, G.; Buchler, B.; Lam, P.K.; Zeilinger, A. Quantum entanglement of angular momentum states with quan-tum numbers up to 10010. Proc. Natl. Acad. Sci. USA 2016, 113, 13642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Z.Y.; Li, Y.; Ding, D.S.; Zhang, W.; Shi, S.; Shi, B.S. Optical vortex beam based optical fan for high-precision optical measurements and optical switching. Opt. Lett. 2014, 39, 5098–5101. [Google Scholar] [CrossRef] [PubMed]
- Emile, O.; Emile, J. Naked eye picometer resolution in a Michelson interferometer using conjugated twisted beams. Opt. Lett. 2017, 42, 354–357. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.X.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488. [Google Scholar] [CrossRef]
- Grier, D.G. A resolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Optical orbital angular momentum: Twisted light and chirality. Opt. Lett. 2018, 43, 435–438. [Google Scholar] [CrossRef]
- Bai, Y.; Lv, H.; Fu, X.; Yang, Y. Vortex beam: Generation and detection of orbital angular momentum [Invited]. Chin. Opt. Lett. 2022, 20, 012601. [Google Scholar] [CrossRef]
- Shen, Y.J.; Wang, X.J.; Xie, Z.W.; Min, C.J.; Fu, X.; Liu, Q.; Gong, M.L.; Yuan, X.C. Optical vortices 30 years on: OAM ma-nipulation from topological charge to multiple singularities. Light Sci. Appl. 2021, 8, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Fang, Z.X.; Ren, Y.X.; Gong, L.; Lu, R.D. Generation and characterization of a perfect vortex beam with a large top-ological charge through a digital micromirror device. Appl. Opt. 2015, 54, 8030–8035. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Liu, H.; Garcia-Vidal, F.J.; Hong, M.H.; Luk’yanchuk, B.; Teng, J.; Qiu, C.W. Ultrahigh-capacity non-periodic photon sieves operating in visible light. Nat. Commun. 2015, 6, 7059. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Zhao, Q.; Liu, L.; Liu, Y.; Rosales-Guzmán, C.; Qiu, C.-W. Manipulation of Orbital-Angular-Momentum Spectrum Using Pinhole Plates. Phys. Rev. Appl. 2019, 12, 064007. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.V.; Shinkaryev, M.V.; Soifer, V.A.; Uspleniev, G.V. The phase rotator filter. J. Mod. Opt. 1992, 39, 1147–1154. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Turnbull, G.A.; Robertson, D.A.; Smith, G.M.; Allen, L.; Padgett, M.J. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phasplate. Opt. Commun. 1996, 127, 183–188. [Google Scholar] [CrossRef]
- Machavariani, G.; Davidson, N.; Hasman, E.; Blit, S.; Ishaaya, A.A.; Friesem, A.A. Efficient conversion of a Gaussian beam to a high purity helical beam. Opt. Commun. 2002, 209, 265–271. [Google Scholar] [CrossRef]
- Peele, A.G.; McMahon, P.J.; Paterson, D.; Tran, C.Q.; Mancuso, A.P.; Nugent, K.A.; Hayes, J.P.; Harvey, E.; Lai, B.; McNulty, I. Observation of an x-ray vortex. Opt. Lett. 2002, 27, 1752–1754. [Google Scholar] [CrossRef]
- Sueda, K.; Miyaji, G.; Miyanaga, N.; Nakatsuka, M. Laguerre-Gaussian beam generated with a multilevel spiral phase plate for high intensity laser pulses. Opt. Express 2004, 12, 3548–3553. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Fujii, M.; Watanabe, Y.; Toyama, N.; Iketaki, Y. Generation of a doughnut-shaped beam using a spiral phase plate. Rev. Sci. Instrum. 2004, 75, 5131–5135. [Google Scholar] [CrossRef]
- Rotschild, C.; Zommer, S.; Moed, S.; Hershcovitz, O.; Lipson, S.G. Adjustable spiral phase plate. Appl. Opt. 2004, 43, 2397–2399. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.M.S.; Yuan, X.-C.; Cheong, W.C. Optical vortex beam shaping by use of highly efficient irregular spiral phase plates for optical micromanipulation. Opt. Lett. 2004, 29, 1796–1798. [Google Scholar] [CrossRef] [PubMed]
- Cheong, W.C.; Lee, W.M.; Yuan, X.-C.; Zhang, L.-S.; Dholakia, K.; Wang, H. Direct electron-beam writing of continuous spiral phase plates in negative resist with high power efficiency for optical manipulation. Appl. Phys. Lett. 2004, 85, 5784–5786. [Google Scholar] [CrossRef] [Green Version]
- Moh, K.J.; Yuan, X.-C.; Cheong, W.C.; Zhang, L.S.; Lin, J.; Ahluwalia, B.P.S.; Wang, H. High-power efficient multiple optical vortices in a single beam generated by a kinoform-type spiral phase plate. Appl. Opt. 2006, 45, 1153–1161. [Google Scholar] [CrossRef]
- Yuan, X.-C.; Lin, J.; Bu, J.; Burge, R.E. Achromatic design for the generation of optical vortices based on radial spiral phase plates. Opt. Express 2008, 16, 13599–13605. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, X.; Shum, P. Generating doughnut-shaped beams with large charge numbers by use of liquid-crystal spiral phase plates. Appl. Opt. 2004, 43, 2292–2297. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, X.W.; Shum, P.; Yin, X.J. Dynamic switching of optical vortices with dynamic gamma-correction liquid crystal spiral phase plate. Opt. Express 2005, 13, 10285–10291. [Google Scholar] [CrossRef]
- Oemrawsingh, S.S.R.; Eliel, E.R.; Woerdman, J.P.; Verstegen, E.J.K.; Kloosterboer, J.G.; Hooft, G.W. Half-integral SPPs for op-tical wavelengths. J. Opt. A Appl. Opt. 2004, 6, S288–S290. [Google Scholar] [CrossRef]
- Oemrawsingh, S.S.R.; van Houwelingen, A.W.; Eliel, E.R.; Woerdman, J.P.; Verstegen, E.J.K.; Kloosterboer, J.G.; ’t Hooft, G.W. Production and characterization of spiral phase plates for optical wavelengths. Appl. Opt. 2004, 43, 688–694. [Google Scholar] [CrossRef] [PubMed]
- Ruffato, G.; Massari, M.; Romanato, F. Generation of high-order Laguerre-Gaussian modes by means of spiral phase plates. Opt. Lett. 2014, 39, 5094–5097. [Google Scholar] [CrossRef] [PubMed]
- Schemmel, P.; Pisano, G.; Maffei, B. A modular spiral phase plate design for orbital angular momentum generation at millimetre wavelengths. Opt. Express 2014, 22, 14712–14726. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Zhang, Z.; Cao, A.; Luo, X.; Deng, Q. One exposure processing to fabricate spiral phase plate with continuous surface. Opt. Express 2015, 23, 8620–8629. [Google Scholar] [CrossRef]
- Massari, M.; Ruffato, G.; Gintoli, M.; Ricci, F.; Romanato, F. Fabrication and characterization of high-quality spiral phase plates for optical applications. Appl. Opt. 2015, 54, 4077–4083. [Google Scholar] [CrossRef]
- Harm, W.; Bernet, S.; Ritsch-Marte, M.; Harder, I.; Lindlein, N. Adjustable diffractive spiral phase plates. Opt. Express 2015, 23, 413–421. [Google Scholar] [CrossRef]
- Wu, W.-B.; Sheng, Z.-Q.; Wu, H.-W. Design and application of flat spiral phase plate. Acta Phys. Sin. 2019, 68, 054102. [Google Scholar] [CrossRef]
- Isakov, D.; Wu, Y.; Allen, B.; Grant, P.S.; Stevens, C.J.; Gibbons, G.J. Evaluation of the Laguerre-Gaussian mode purity pro-duced by three-dimensional-printed microwave spiral phase plates. R. Soc. Open Sci. 2020, 7, 200493. [Google Scholar] [CrossRef]
- Wei, Y. Propagation characteristic analysis of vortex beams produced by spiral phase plate. Laser Infrared 2016, 46, 857–861. [Google Scholar]
- Wang, C.; Liu, T.; Ren, Y.; Shao, Q.; Dong, H. Generating optical vortex with large topological charges by spiral phase plates in cascaded and double-pass configuration. Optik 2018, 171, 404–412. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, C.; Liu, T.; Shao, Q. Method of optical vortex generation by cascaded spiral phase plates. In Proceedings of the Optical Precision Manufacturing, Testing, and Applications, Beijing, China, 12 December 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10847, p. 1084703. [Google Scholar] [CrossRef]
- Wang, C.; Liu, T.; Shao, Q.L.; Ren, Y.; Miao, J.S. Quadrupling topological charges of vortex using multi-passed spiral phase plate. Infrared Laser Eng. 2018, 47, 0918008. [Google Scholar] [CrossRef]
- Ma, J.; Li, P.; Zhou, Z.; Gu, Y. Characteristics of fork-shaped fringes formed by off-axis interference of two vortex beams. J. Opt. Soc. Am. A 2020, 38, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Nishcal, N.K. Modified Mach-Zehnder interferometer for determining the high-order topological charge of La-guerre-Gaussian vortex beam. J. Opt. Soc. Am. A 2019, 36, 1447–1455. [Google Scholar] [CrossRef] [PubMed]
- Bazhenov, V.Y.; Vasnetsov, M.V.; Soskin, M.S. Screw dislocations of wavefront. J. Mod. Opt. 1992, 39, 985–990. [Google Scholar] [CrossRef]
- Wang, J.; Cao, A.; Zhang, M.; Pang, H.; Hu, S.; Fu, Y.; Shi, L.; Deng, Q. Study of Characteristics of Vortex Beam Produced by Fabricated Spiral Phase Plates. IEEE Photonics J. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Ma, J.B.; Li, P.; Gu, Y.Z. Characteristics of spiral patterns formed by coaxial interference between two vortex beams with dif-ferent radii of wavefront curvatures. Photonics 2021, 8, 393. [Google Scholar] [CrossRef]
- Cui, S.; Xu, B.; Luo, S.; Xu, H.; Cai, Z.; Luo, Z.; Pu, J.; Chávez-Cerda, S. Determining topological charge based on an improved Fizeau interferometer. Opt. Express 2019, 27, 12774–12779. [Google Scholar] [CrossRef]
- Pan, S.; Pei, C.; Liu, S.; Wei, J.; Wu, D.; Liu, Z.; Yin, Y.; Xia, Y.; Yin, J. Measuring orbital angular momentums of light based on petal interference patterns. OSA Contin. 2018, 1, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Galvez, E.J.; Smiley, N.; Fernandes, N. Composite optical vortices formed by collinear Laguerre-Gauss beams. In Proceedings of the Nanomanipulation with Light II, San Jose, CA, USA, 9 February 2006; SPIE: Bellingham, WA, USA, 2006; Volume 131, p. 613105. [Google Scholar] [CrossRef]
- Lv, F.; Li, X.; Tai, Y.; Zhang, L.; Nie, Z.; Chen, Q. High-order topological charges measurement of LG vortex beams with a modified Mach–Zehnder interferometer. Optik 2015, 126, 4378–4381. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Zhong, J.; Qi, S.; Guo, X.; Wu, D.; Liu, S.; Zhao, J. Measuring singularities of cylindrically structured light beams using a radial grating. Appl. Phys. Lett. 2018, 113, 221108. [Google Scholar] [CrossRef]
- Zhao, Q.; Dong, M.; Bai, Y.; Yang, Y. Measuring high orbital angular momentum of vortex beams with an improved multipoint interferometer. Photon. Res. 2020, 8, 745. [Google Scholar] [CrossRef]
- Narag, J.P.C.; Hermosa, N. Probing Higher Orbital Angular Momentum of Laguerre-Gaussian Beams via Diffraction through a Translated Single Slit. Phys. Rev. Appl. 2019, 11, 054025. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhao, S. Efficient separating orbital angular momentum mode with radial varying phase. Photon. Res. 2017, 5, 267–270. [Google Scholar] [CrossRef] [Green Version]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhu, J.; Zhang, Y.; Yu, S. Spiral Transformation for High-Resolution and Efficient Sorting of Optical Vortex Modes. Phys. Rev. Lett. 2018, 120, 193904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, J.; Zhang, W.; Chen, L. Experimental detection of high-order or fractional orbital angular momentum of light based on a robust mode converter. Appl. Phys. Lett. 2016, 108, 111108. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Elfstrom, H.; Turunen, J.; Almazov, A.A.; Khonina, S.; Soifer, V. Generation of phase singularity through diffracting a plane or Gaussian beam by a spiral phase plate. J. Opt. Soc. Am. A 2005, 22, 849–861. [Google Scholar] [CrossRef]
- Mawardi, A.; Hild, S.; Widera, A.; Meschede, D. ABCD-treatment of a propagating doughnut beam generated by a spiral phase plate. Opt. Express 2011, 19, 21205–21210. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Soskin, M.S.; Gorshkov, V.N.; Vasnetsov, M.V.; Malos, J.T.; Heckenberg, N.R. Topological charge and angular momentum of light beams carrying optical vortices. Phys. Rev. A 1997, 56, 4064–4075. [Google Scholar] [CrossRef] [Green Version]
- Mao, B.; Liu, Y.; Chang, W.; Chen, L.; Feng, M.; Guo, H.; He, J.; Wang, Z. Singularities splitting phenomenon for the superposition of hybrid orders structured lights and the corresponding interference discrimination method. Nanophotonics 2022, 11, 1413–1426. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Li, P.; Ma, J.; Zhang, S.; Gu, Y. Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates. Photonics 2022, 9, 354. https://doi.org/10.3390/photonics9050354
Zhou Z, Li P, Ma J, Zhang S, Gu Y. Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates. Photonics. 2022; 9(5):354. https://doi.org/10.3390/photonics9050354
Chicago/Turabian StyleZhou, Ziheng, Peng Li, Jingbo Ma, Shirui Zhang, and Yuzong Gu. 2022. "Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates" Photonics 9, no. 5: 354. https://doi.org/10.3390/photonics9050354
APA StyleZhou, Z., Li, P., Ma, J., Zhang, S., & Gu, Y. (2022). Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates. Photonics, 9(5), 354. https://doi.org/10.3390/photonics9050354




