The BER Performance of the LDPC-Coded MPPM over Turbulence UWOC Channels
Abstract
1. Introduction
2. System and Channel Models
3. LLR Calculation
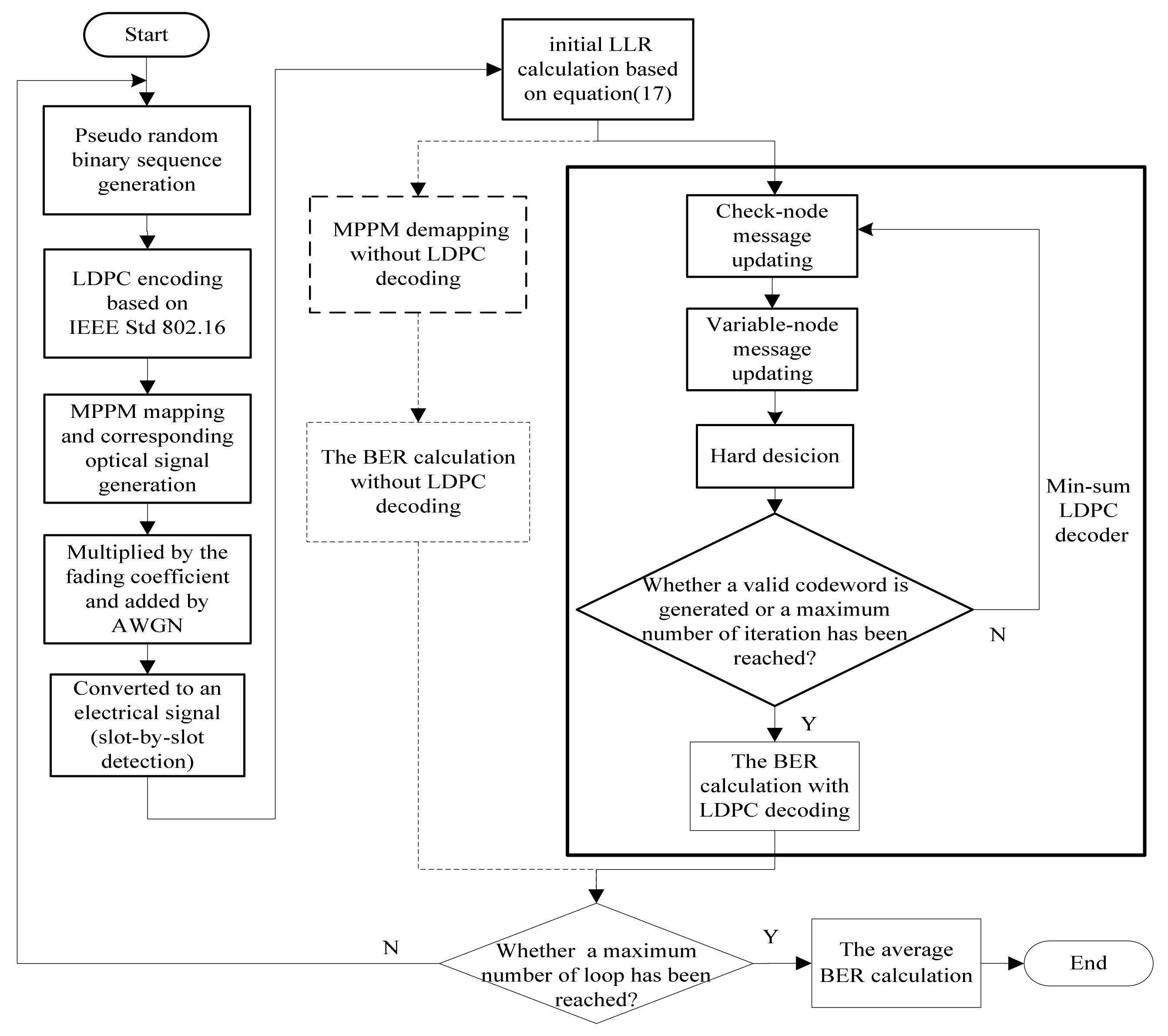
4. BER Performance without the FEC
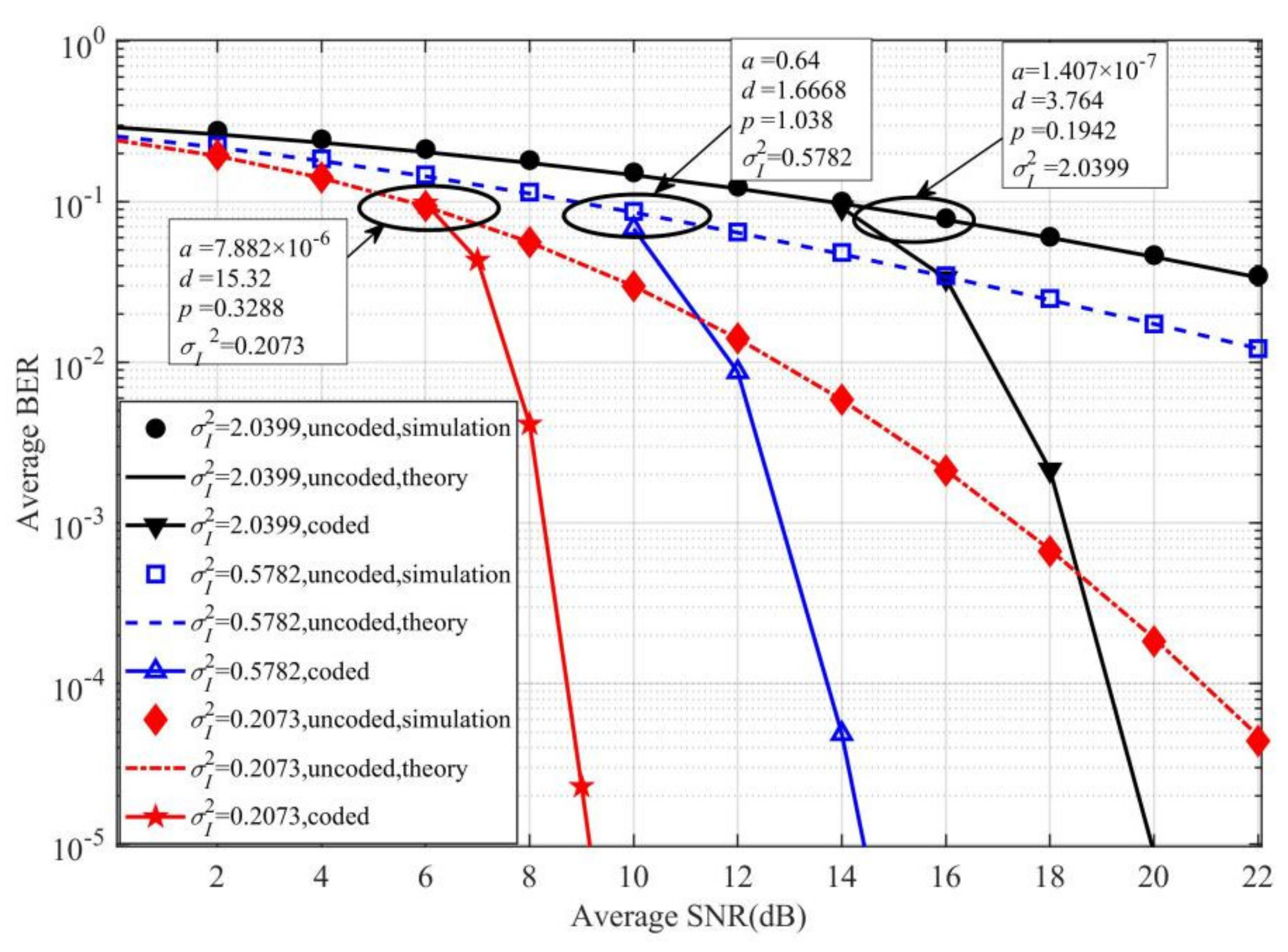
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiang:, R.; Sun, C.; Zhang, L.; Tang, X.; Wang, H.; Zhang, A. Deep Learning Aided Signal Detection for SPAD-Based Underwater Optical Wireless Communications. IEEE Access 2020, 8, 20363–20374. [Google Scholar] [CrossRef]
- Lian, J.; Gao, Y.; Wu, P.; Lian, D. Orthogonal frequency division multiplexing techniques comparison for underwater optical wireless communication systems. Sensors 2019, 19, 160. [Google Scholar] [CrossRef] [PubMed]
- Loisel, H.H.; André, M. Light scattering and chlorophyll concentration in Case 1 waters: A re-examination. Limnol. Oceanogr. 1998, 43, 847–858. [Google Scholar] [CrossRef]
- Tang, S.; Dong, Y.; Zhang, X. Impulse Response Modeling for Underwater Wireless Optical Communication Links. IEEE Trans. Commun. 2013, 62, 226–234. [Google Scholar] [CrossRef]
- Miramirkhani, F.; Uysal, M. Visible Light Communication Channel Modeling for Underwater Environments with Blocking and Shadowing. IEEE Access 2017, 6, 1082–1090. [Google Scholar] [CrossRef]
- Saeed, N.; Celik, A.; Al-Naffouri, T.Y.; Alouini, M.S. Underwater optical wireless communications, networking, and local-ization: A survey. Ad. Hoc. Netw. 2019, 94, 101935. [Google Scholar] [CrossRef]
- Vahid Jamali, M.; Mirani, A.; Parsay, A.; Abolhassani, B.; Nabavi, P.; Chizari, A.; Khorramshahi, P.; Abdollahramezani, S.; Salehi, J.A. Statistical Studies of Fading in Underwater Wireless Optical Channels in the Presence of Air Bubble, Temperature, and Salinity Random Variations (Long Version). IEEE Trans. Commun. 2018, 66, 4706–4723. [Google Scholar]
- Yue, P.; Wu, M.; Yi, X.; Cui, Z.; Luan, X. Underwater optical communication performance under the influence of the eddy diffusivity ratio. J. Opt. Soc. Am. A 2018, 36, 32–37. [Google Scholar] [CrossRef]
- Xu, G.; Lai, J. Average capacity analysis of the underwater optical plane wave over anisotropic moderate-to-strong oceanic turbulence channels with the Málaga fading model. Opt. Express 2020, 28, 24056. [Google Scholar] [CrossRef]
- Ata, Y.; Baykal, Y. Scintillations of optical plane and spherical waves in underwater turbulence. J. Opt. Soc. Am. A 2014, 31, 1552–1556. [Google Scholar] [CrossRef]
- Jamali, M.V.; Khorramshahi, P.; Tashakori, A.; Chizari, A.; Shahsavari, S.; Abdollah Ramezani, S.; Fazelian, M.; Bahrani, S.; Salehi, J.A. Statistical distribution of intensity fluctuations for underwater wireless optical channels in the presence of air bubbles. In Proceedings of the 2016 Iran Workshop on Communication and Information Theory (IWCIT), Tehran, Iran, 3–4 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zedini, E.; Oubei, H.M.; Kammoun, A.; Hamdi, M.; Ooi, B.S.; Alouini, M.-S. A New Simple Model for Underwater Wireless Optical Channels in the Presence of Air Bubbles. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Oubei, H.M.; Zedini, E.; Elafandy, R.T.; Kammoun, A.; Abdallah, M.; Ng, T.K.; Hamdi, M.; Alouini, M.-S.; Ooi, B.S. Simple statistical channel model for weak temperature-induced turbulence in underwater wireless optical communication systems. Opt. Lett. 2017, 42, 2455–2458. [Google Scholar] [CrossRef] [PubMed]
- Geldard, C.T.; Thompson, J.; Popoola, W.O. Empirical Study of the Underwater Turbulence Effect on Non-Coherent Light. IEEE Photon.-Technol. Lett. 2020, 32, 1307–1310. [Google Scholar] [CrossRef]
- Oubei, H.M.; Zedini, E.; ElAfandy, R.T.; Kammoun, A.; Ng, T.K.; Alouini, M.-S.; Ooi, B.S. Efficient Weibull channel model for salinity induced turbulent underwater wireless optical communications. In Proceedings of the 2017 Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 31 July–4 August 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Zedini, E.; Oubei, H.M.; Kammoun, A.; Hamdi, M.; Ooi, B.S.; Alouini, M.-S. Unified Statistical Channel Model for Turbulence-Induced Fading in Underwater Wireless Optical Communication Systems. IEEE Trans. Commun. 2019, 67, 2893–2907. [Google Scholar] [CrossRef]
- Jiang, H.; Qiu, H.; He, N.; Zhao, Z.; Popoola, W.; Ahmad, Z.; Rajbhandari, S. LDPC-coded CAP with spatial diversity for UVLC systems over generalized-gamma fading channel. Sensors 2020, 20, 3378. [Google Scholar] [CrossRef]
- Jamali, M.V.; Akhoundi, F.; Salehi, J.A. Performance characterization of relay-assisted wireless optical CDMA networks in turbulent underwater channel. IEEE Trans. Wirel. Commun. 2016, 15, 4104–4116. [Google Scholar] [CrossRef]
- Gökçe, M.C.; Baykal, Y. Aperture averaging and BER for Gaussian beam in underwater oceanic turbulence. Opt. Commun. 2018, 410, 830–835. [Google Scholar] [CrossRef]
- Jamali, M.V.; Nabavi, P.; Salehi, J.A. MIMO underwater visible light communications: Comprehensive channel study, performance analysis, and multiple-symbol detection. IEEE Trans. Veh. Technol. 2018, 67, 8223–8237. [Google Scholar] [CrossRef]
- Zhu, B.; Cheng, J.; Yan, J.; Wu, L.; Wang, Y.; Wang, J. A New Asymptotic Analysis Technique for Diversity Receptions Over Correlated Lognormal Fading Channels. IEEE Trans. Commun. 2017, 66, 845–861. [Google Scholar] [CrossRef]
- Xu, F.; Khalighi, A.; Caussé, P.; Bourennane, S. Channel coding and time-diversity for optical wireless links. Opt. Express 2009, 17, 872–887. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with MATLAB; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Nistazakis, H.E.; Stassinakis, A.N.; Sinanović, S.; Popoola, W.O.; Tombras, G.S. Performance of quadrature amplitude modulation orthogonal frequency division multiplexing-based free space optical links with non-linear clipping effect over gamma-gamma modelled turbulence channels. Optoelectron. IET 2017, 9, 269–274. [Google Scholar] [CrossRef]
- Jiao, W.; Liu, H.; Yin, J.; Wei, Z.; Luo, A.; Deng, D. Performance of a QAM/FSO communication system employing spatial diversity in weak and saturation turbulence channels. J. Mod. Opt. 2019, 66, 965–975. [Google Scholar] [CrossRef]
- Chatzidiamantis, N.; Lioumpas, A.; Karagiannidis, G.K.; Arnon, S. Adaptive subcarrier PSK intensity modulation in free space optical systems. IEEE Trans. Commun. 2011, 59, 1368–1377. [Google Scholar] [CrossRef]
- Khallaf, H.S.; Shalaby, H.M.H.; Balsells, J.M.G.; Sampei, S. Performance analysis of a hybrid QAM-MPPM technique over turbulence-free and gamma–gamma free-space optical channels. J. Opt. Commun. Netw. 2017, 9, 161–171. [Google Scholar] [CrossRef]
- Yin, C.S.; He, Z.Y.; Deng, S.; Liang, S.; He, N. Investigation on pulse response and the large current optical modulation of high power LEDs. J. Optoelectron. Laser 2015, 26, 1041–1047. [Google Scholar]
- Xu, F.; Khalighi, M.-A.; Bourennane, S. Coded PPM and Multipulse PPM and Iterative Detection for Free-Space Optical Links. J. Opt. Commun. Netw. 2009, 1, 404–415. [Google Scholar] [CrossRef]
- Wang, P.; Yang, B.; Guo, L.; Shang, T. SER performance analysis of MPPM FSO system with three decision thresholds over exponentiated Weibull fading channels. Opt. Commun. 2015, 354, 1–8. [Google Scholar] [CrossRef]
- Zhou, D.; Cao, T.; Yang, Y.; Zhang, J.; Wang, P.; Yang, B. Symbol error rate performance analysis of soft-decision decoded MPPM free space optical system over exponentiated Weibull fading channels. Chin. Opt. Lett. 2017, 15, 50602–50606. [Google Scholar] [CrossRef][Green Version]
- Bykhovsky, D. Symbol error rate of soft-decision multiple pulse position modulation over turbulent channels. Appl. Opt. 2019, 58, 1193–1199. [Google Scholar] [CrossRef]
- Peppas, K.P.; Boucouvalas, A.C.; Ghassemloy, Z. Performance of underwater optical wireless communication with multi-pulse pulse-position modulation receivers and spatial diversity. IET Optoelectron. 2017, 11, 180–185. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Serrato, N.G.; Garrido-Balsells, J.M.; Castillo-Vázquez, M. Error probability analysis of OOK and variable weight MPPM coding schemes for underwater optical communication systems affected by salinity turbulence. OSA Contin. 2018, 1, 1131–1143. [Google Scholar] [CrossRef]
- Hou, J.; Siegel, P.; Milstein, L. Performance analysis and code optimization of low density parity-check codes on Rayleigh fading channels. IEEE J. Sel. Areas Commun. 2001, 19, 924–934. [Google Scholar] [CrossRef]
- Anguita, J.A.; Djordjevic, I.B.; Neifeld, M.A.; Vasic, B.V. Shannon capacities and error-correction codes for optical atmospheric turbulent channels. J. Opt. Netw. 2005, 4, 586–601. [Google Scholar] [CrossRef]
- Djordjevic, I.B.; Vasic, B.; Neifeld, M.A. LDPC coded OFDM over the atmospheric turbulence channel. Opt. Express 2007, 15, 6336–6350. [Google Scholar] [CrossRef] [PubMed]
- IEEE Std 802. 16-2009; IEEE Standard for Local and Metropolitan Area Networks Part 16: Air Interface for Broadband Wireless Access Systems. IEEE: New York, NY, USA, 2009; pp. 1–2080.
- Yuan, J.; Liu, F.; Ye, W.; Huang, S.; Wang, Y. A new coding scheme of QC-LDPC codes for optical transmission systems. Optik 2014, 125, 1016–1019. [Google Scholar] [CrossRef]
- Islam, M.R.; Han, Y.S. Cooperative MIMO communication at wireless sensor network: An error correcting code approach. Sensors 2011, 11, 9887–9903. [Google Scholar] [CrossRef]
- Hamkins, J.; Moision, B. Multipulse Pulse-Position Modulation on Discrete Memoryless Channels. Interplanet. Netw. Prog. Rep. 2005, 42, 1–13. [Google Scholar]
- Du, J.; Zhou, T.; Chen, W.; Hu, F. Performance Analysis of Underwater Optical Communication Based on LDPC and PPM. Laser Optoelectron. Prog. 2016, 53, 120605. [Google Scholar]
- Jurado-Navas, A.; Álvarez-Roa, C.; Álvarez-Roa, M.; Castillo-Vázquez, M. Cooperative Terrestrial-Underwater Wireless Optical Links by Using an Amplify-and-Forward Strategy. Sensors 2022, 22, 2464. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M. Vertical Underwater Visible Light Communication Links: Channel Modeling and Performance Analysis. IEEE Trans. Wirel. Commun. 2020, 19, 6948–6959. [Google Scholar] [CrossRef]
- Popoola, W.O.; Ghassemlooy, Z. BPSK subcarrier intensity modulated free-space optical communications in atmospheric turbulence. J. Light. Technol. 2009, 27, 967–973. [Google Scholar] [CrossRef]




| 0.13779347054049237 | 0.308441 |
| 0.7294545495031706 | 0.40112 |
| 1.8083429017403165 | 0.218068 |
| 3.4014336978549595 | 0.0620875 |
| 5.552496140063418 | 0.00950152 |
| 8.330152746764144 | 0.000753008 |
| 11.843785837899944 | 0.0000282592 |
| 16.279257831377613 | 4.24931 × 10−7 |
| 21.99658581198083 | 1.83956 × 10−9 |
| 29.92069701227372 | 9.91183 × 10−13 |
| Channel Condition | a | d | p | |
|---|---|---|---|---|
| Salinity random variations | 7.882 × 10−6 | 15.32 | 0.3288 | 0.2073 |
| Temperature random variations mixed presence of air bubbles | 0.64 | 1.6668 | 1.038 | 0.5782 |
| Random presence of air bubbles | 1.407 × 10−7 | 3.764 | 0.1942 | 2.0399 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; He, N.; Liao, X.; Popoola, W.; Rajbhandari, S. The BER Performance of the LDPC-Coded MPPM over Turbulence UWOC Channels. Photonics 2022, 9, 349. https://doi.org/10.3390/photonics9050349
Jiang H, He N, Liao X, Popoola W, Rajbhandari S. The BER Performance of the LDPC-Coded MPPM over Turbulence UWOC Channels. Photonics. 2022; 9(5):349. https://doi.org/10.3390/photonics9050349
Chicago/Turabian StyleJiang, Hongyan, Ning He, Xin Liao, Wasiu Popoola, and Sujan Rajbhandari. 2022. "The BER Performance of the LDPC-Coded MPPM over Turbulence UWOC Channels" Photonics 9, no. 5: 349. https://doi.org/10.3390/photonics9050349
APA StyleJiang, H., He, N., Liao, X., Popoola, W., & Rajbhandari, S. (2022). The BER Performance of the LDPC-Coded MPPM over Turbulence UWOC Channels. Photonics, 9(5), 349. https://doi.org/10.3390/photonics9050349







