Near-Field Light-Bending Photonic Switch: Physics of Switching Based on Three-Dimensional Poynting Vector Analysis
Abstract
1. Introduction
2. Results and Discussion
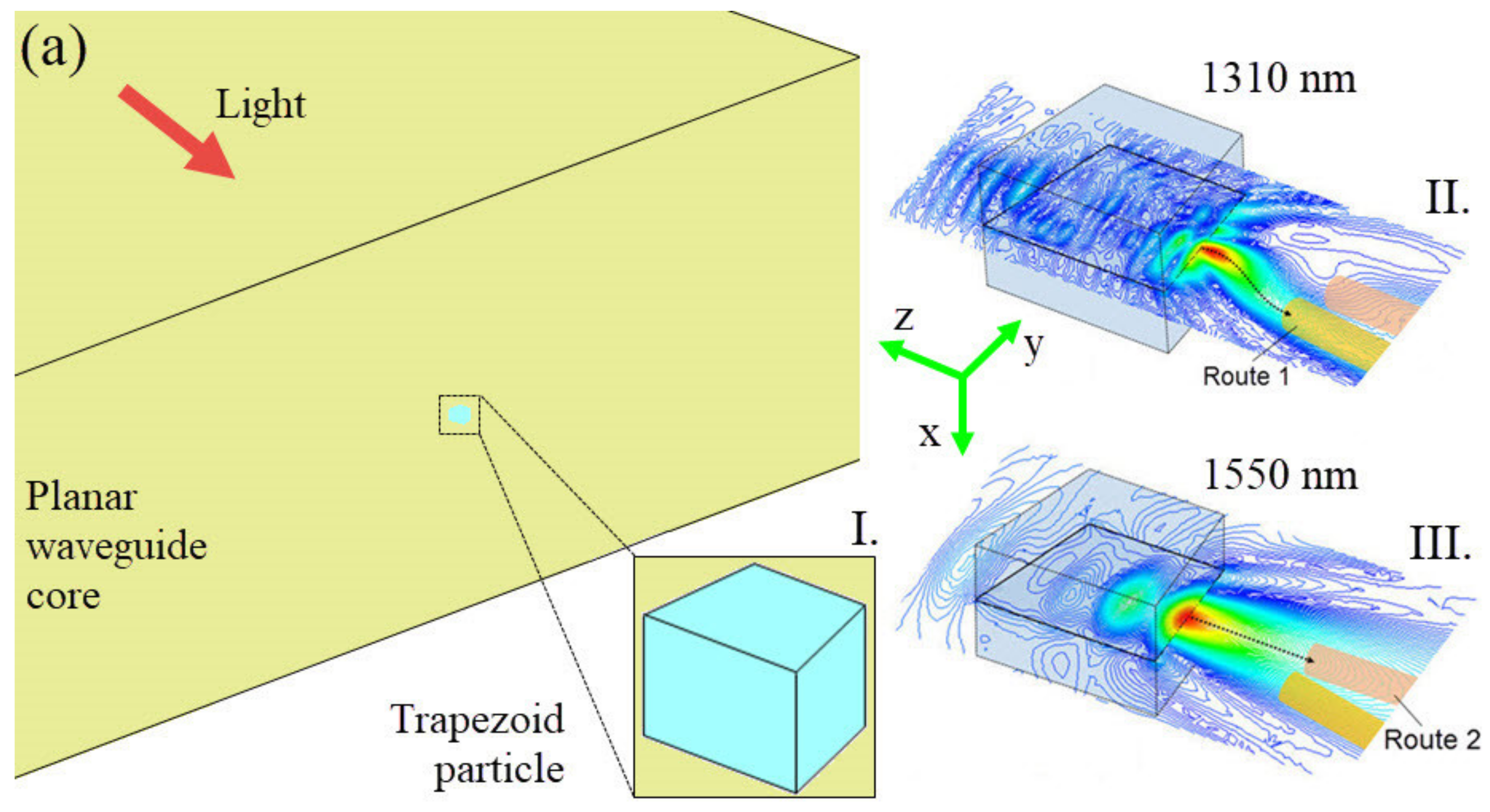
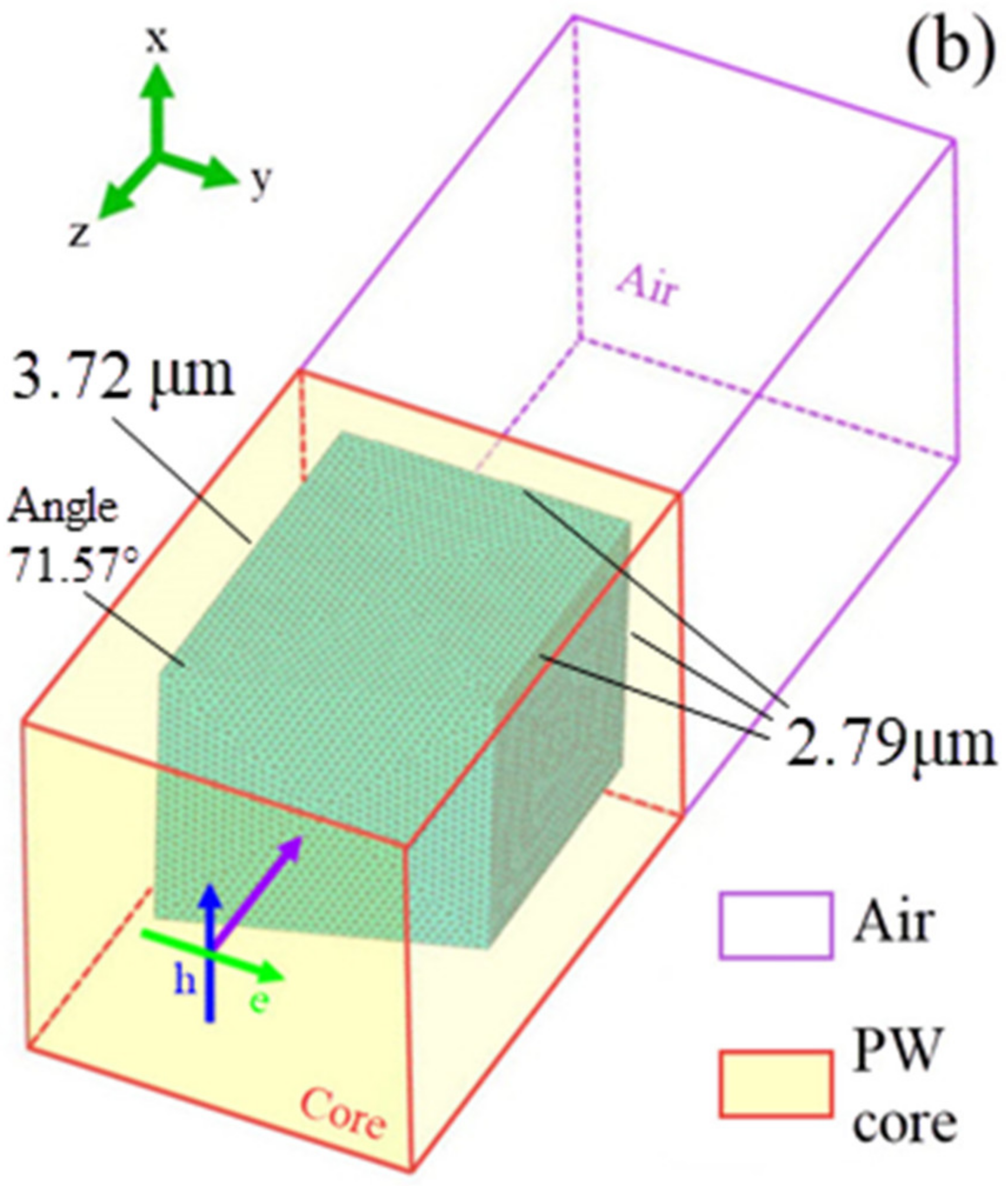
2.1. Concept and Modelling
2.2. Switching and 2D Distributions
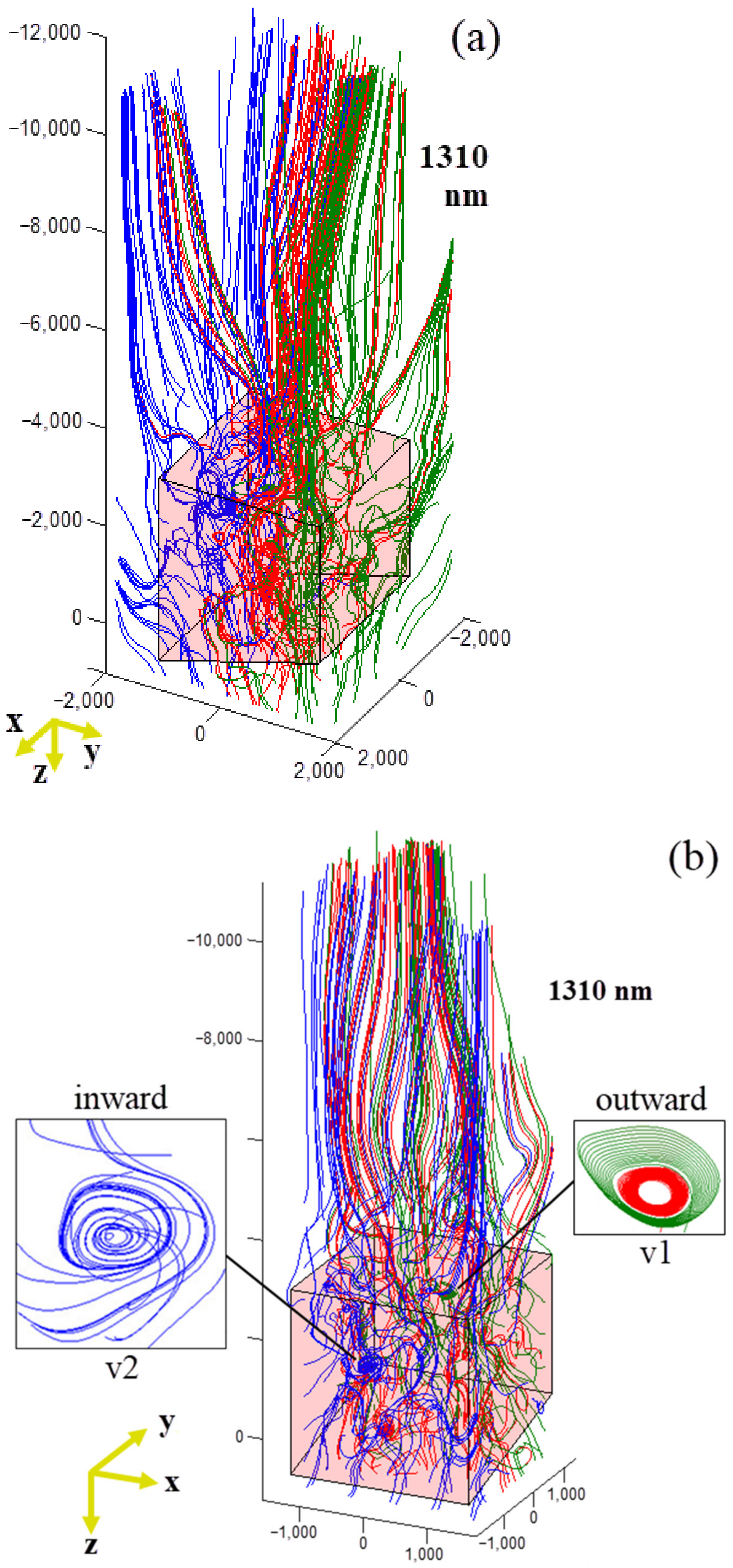
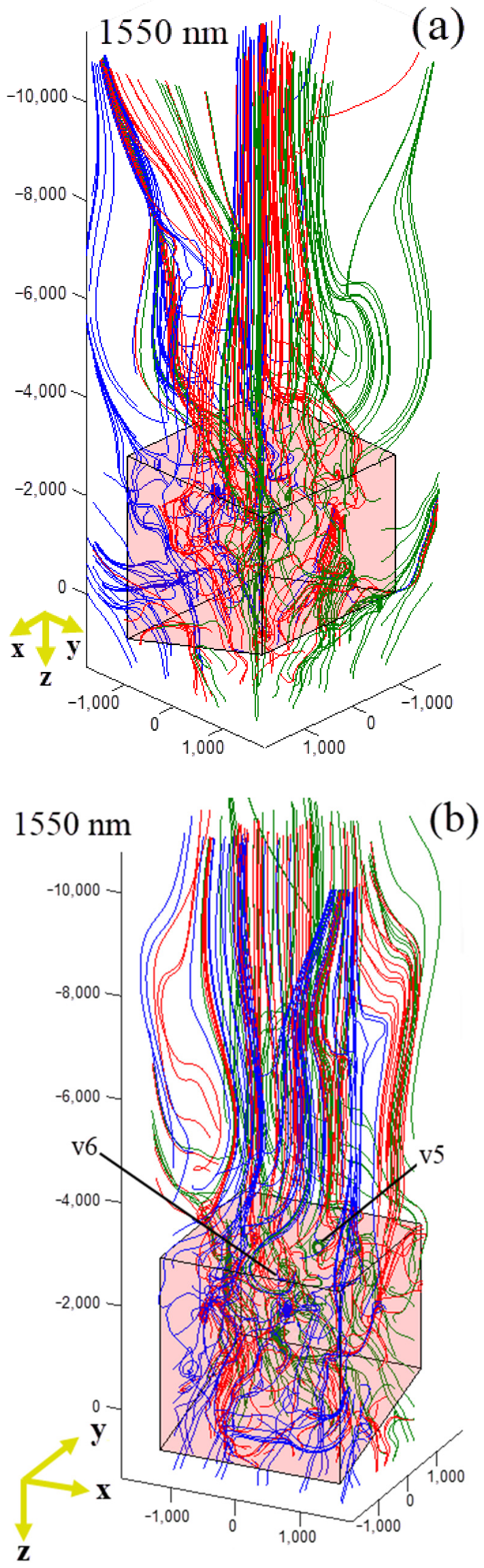
2.3. 3D Poynting Vector Analysis
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaeger, R.C. Microelectronic Circuit Design; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Rao, M.M. Optical Communication; Universities Press: Hyderabad, India, 2001. [Google Scholar]
- Senior, J.M.; Jamro, M.Y. Optical Fiber Communications; Pearson/Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Jin, C.Y.; Wada, O. Photonic switching devices based on semiconductor nano-structures. J. Phys. D Appl. Phys. 2014, 47, 133001. [Google Scholar] [CrossRef]
- Testa, F.; Pavesi, L. Optical Switching in Next Generation Data Centers; Springer: Beilin, Germany, 2017. [Google Scholar]
- Bernstein, G.M.; Lee, Y.; Galver, A.; Martensson, J. Modeling WDM Wavelength Switching Systems for Use in GMPLS and Automated Path Computation. IEEE/OSA J. Opt. Commun. Netw. 2009, 1, 187–195. [Google Scholar] [CrossRef]
- Cancellieri, G. Single-Mode Optical Fibres; Elsevier Science: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Ozcelik, D.; Parks, J.W.; Wall, T.A.; Stott, M.A.; Cai, H.; Parks, J.W.; Hawkins, A.R.; Schmidt, H. Optofluidic wavelength division multiplexing for single-virus detection. Proc. Natl. Acad. Sci. USA 2015, 112, 12933–12937. [Google Scholar] [CrossRef]
- Sadot, D.; Boimovich, E. Tunable optical filters for dense WDM networks. IEEE Commun. Mag. 1998, 36, 50–55. [Google Scholar] [CrossRef]
- Ramo, S.; Whinnery, J.R.; van Duzer, T. Fields and Waves in Communications Electronics; John Wiley and Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Prajzler, V.; Nekvindova, P.; Lyutakov, O. Flexible polymer planar optical waveguides. Radioengineering 2014, 23, 776–782. [Google Scholar]
- Polky, J.N.; Mitchell, G.L. Metal-clad planar dielectric waveguide for integrated optics. J. Opt. Soc. Am. 1974, 64, 274–279. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Diffractive Optics and Nanophotonics: Resolution below the Diffraction Limit; Springer: Berlin, Germany, 2016. [Google Scholar]
- Yue, L.; Minin, O.V.; Wang, Z.; Monks, J.N.; Snalin, A.S.; Minin, I.V. Photonic hook: A new curved light beam. Opt. Lett. 2018, 43, 771–774. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V.; Katyba, G.M.; Chernomyrdin, N.V.; Kurlov, V.N.; Zaytsev, K.I.; Yue, L.; Wang, Z.; Christodoulides, D.N. Experimental observation of a photonic hook. Appl. Phys. Lett. 2019, 114, 031105. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Glinskiy, I.A.; Khalilubin, R.A.; Malureanu, R.; Lavrinenko, A.; Yakubovsky, D.I.; Volcow, V.S.; Ponomarev, D.S. Experimental verification of a plasmonic hook in a dielectric Janus particle. Appl. Phys. Lett. 2021, 118, 131107. [Google Scholar] [CrossRef]
- Geints, Y.E.; Minin, O.V.; Yue, L.; Minin, I.V. Wavelength-Scale Photonic Space Switch Proof-of-Concept Based on Photonic Hook Effect. Ann. Phys. 2021, 553, 2100192. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 2011, 5, 523–530. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.N.; Dhama, R.; Jiang, C.; Minin, O.V.; Minin, I.V.; Wang, Z. Full three-dimensional Poynting vector flow analysis of great field-intensity enhancement in specifically sized spherical-particles. Sci. Rep. 2019, 9, 20224. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Yan, B.; Wang, Z.B. Photonic nanojet of cylindrical metalens assembled by hexagonally arranged nanofibers for breaking the diffraction limit. Opt. Lett. 2016, 41, 1336–1339. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, S.Y.; Jeong, T.Y.; Jung, S.; Yee, K.J. Refractive Index Dispersion of Hexagonal Boron Nitride in the Visible and Near-Infrared. Phys. Status Solidi B 2018, 256, 1800417. [Google Scholar] [CrossRef]
- Tan, C.Z. Determination of refractive index of silica glass for infrared wavelengths by IR spectroscopy. J. Non-Cryst. Solids 1998, 223, 158–163. [Google Scholar] [CrossRef]
- MICROPOSIT® S1800® Photoresist Datasheet. Available online: https://amolf.nl/wp-content/uploads/2016/09/datasheets_S1800.pdf (accessed on 25 January 2022).
- Elson, J.M. Propagation in planar waveguides and the effects of wall roughness. Opt. Express 2001, 9, 461–475. [Google Scholar] [CrossRef]
- Gomez-Correa, J.E.; Balderas-Mata, S.E.; Garza-Rivera, A.; Jaimes-Najera, A.; Trevino, J.P.; Coello, V.; Rogel-Salazar, J.; Chavez-Cerda, S. Mathematical-Physics of propagating modes in planar waveguides. Rev. Mex. F’ısica E 2019, 65, 218–222. [Google Scholar] [CrossRef]
- Yan, B.; Yue, L.; Monks, J.N.; Yang, X.; Xiong, D.; Jiang, C.; Wang, Z. Superlensing plano-convex-microsphere (PCM) lens for direct laser nano-marking and beyond. Opt. Lett. 2020, 45, 1168–1171. [Google Scholar] [CrossRef]
- Dietrich, P.I.; Blaicher, M.; Reuter, I.; Billah, M.; Hoose, T.; Hofmann, A.; Caer, C.; Dangel, R.; Offrein, B.; Troppenz, U.; et al. In situ 3D nanoprinting of free-form coupling elements for hybrid photonic integration. Nat. Photon. 2018, 12, 241–247. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory, 1st ed.; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Wang, Z.B.; Luk’yanchuk, B.S.; Hong, M.H.; Lin, Y.; Chong, T.C. Energy flow around a small particle investigated by classical Mie theory. Phys. Rev. B 2004, 70, 035418. [Google Scholar] [CrossRef]
- Kumar, V.; Viswanathan, N.K. Topological structures in the Poynting vector field: An experimental realization. Opt. Lett. 2013, 38, 3886–3889. [Google Scholar] [CrossRef] [PubMed]
- Minin, O.V.; Minin, I.V. Optical Phenomena in Mesoscale Dielectric Particles. Photonics 2021, 8, 591. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, L.; Wang, Z.; Yan, B.; Xie, Y.; Geints, Y.E.; Minin, O.V.; Minin, I.V. Near-Field Light-Bending Photonic Switch: Physics of Switching Based on Three-Dimensional Poynting Vector Analysis. Photonics 2022, 9, 154. https://doi.org/10.3390/photonics9030154
Yue L, Wang Z, Yan B, Xie Y, Geints YE, Minin OV, Minin IV. Near-Field Light-Bending Photonic Switch: Physics of Switching Based on Three-Dimensional Poynting Vector Analysis. Photonics. 2022; 9(3):154. https://doi.org/10.3390/photonics9030154
Chicago/Turabian StyleYue, Liyang, Zengbo Wang, Bing Yan, Yao Xie, Yuri E. Geints, Oleg V. Minin, and Igor V. Minin. 2022. "Near-Field Light-Bending Photonic Switch: Physics of Switching Based on Three-Dimensional Poynting Vector Analysis" Photonics 9, no. 3: 154. https://doi.org/10.3390/photonics9030154
APA StyleYue, L., Wang, Z., Yan, B., Xie, Y., Geints, Y. E., Minin, O. V., & Minin, I. V. (2022). Near-Field Light-Bending Photonic Switch: Physics of Switching Based on Three-Dimensional Poynting Vector Analysis. Photonics, 9(3), 154. https://doi.org/10.3390/photonics9030154







