Quantitative Photoacoustic Reconstruction of the Optical Properties of Intervertebral Discs Using a Gradient Descent Scheme
Abstract
:1. Introduction
2. Morphology and Composition of the Intervertebral Disc
3. Photoacoustic Synthetic Measurements
4. Building the Numerical Phantom
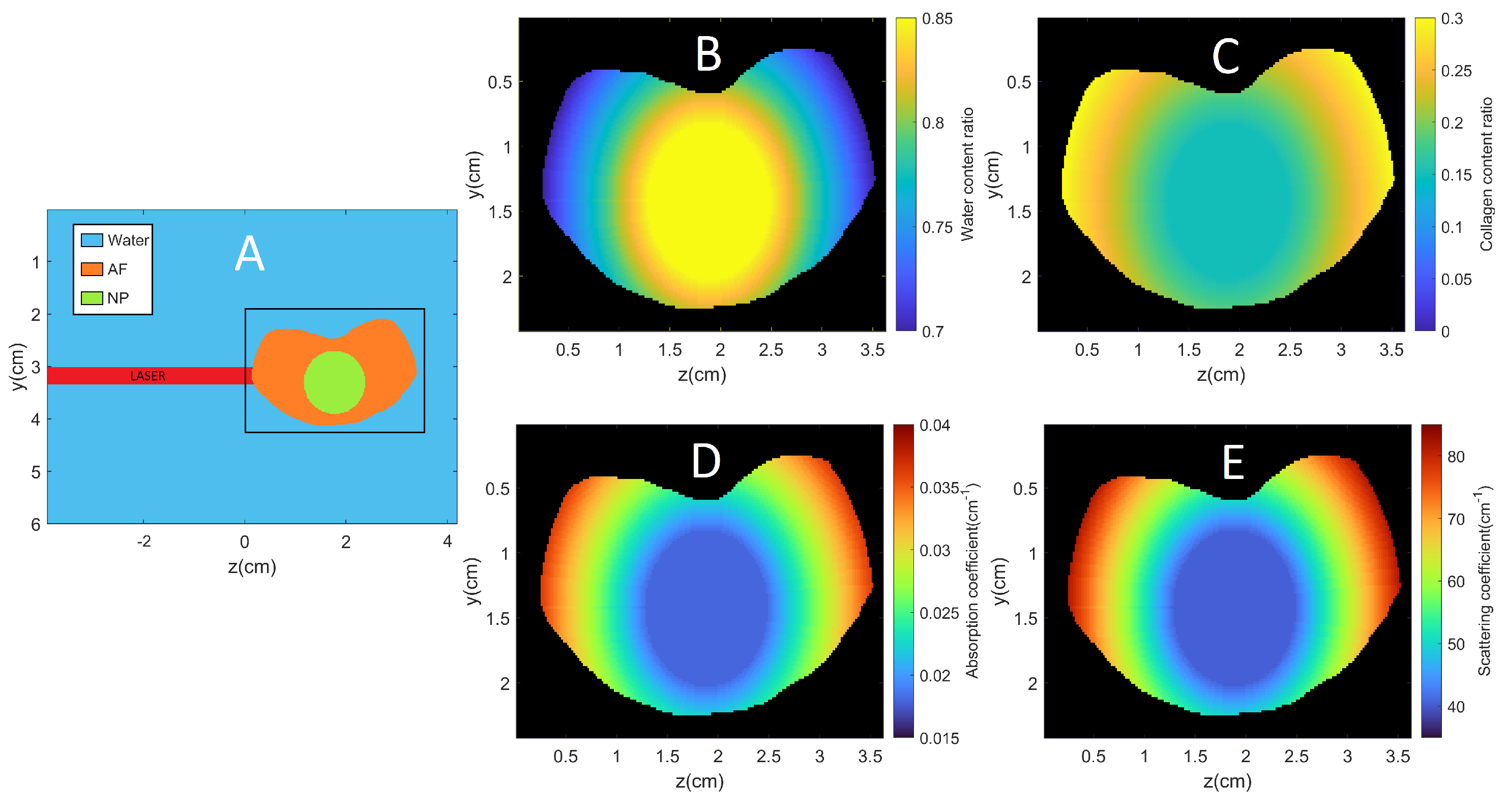
4.1. Defining the Morphology and Optical Properties
4.2. Gradient Descent Scheme
5. Results
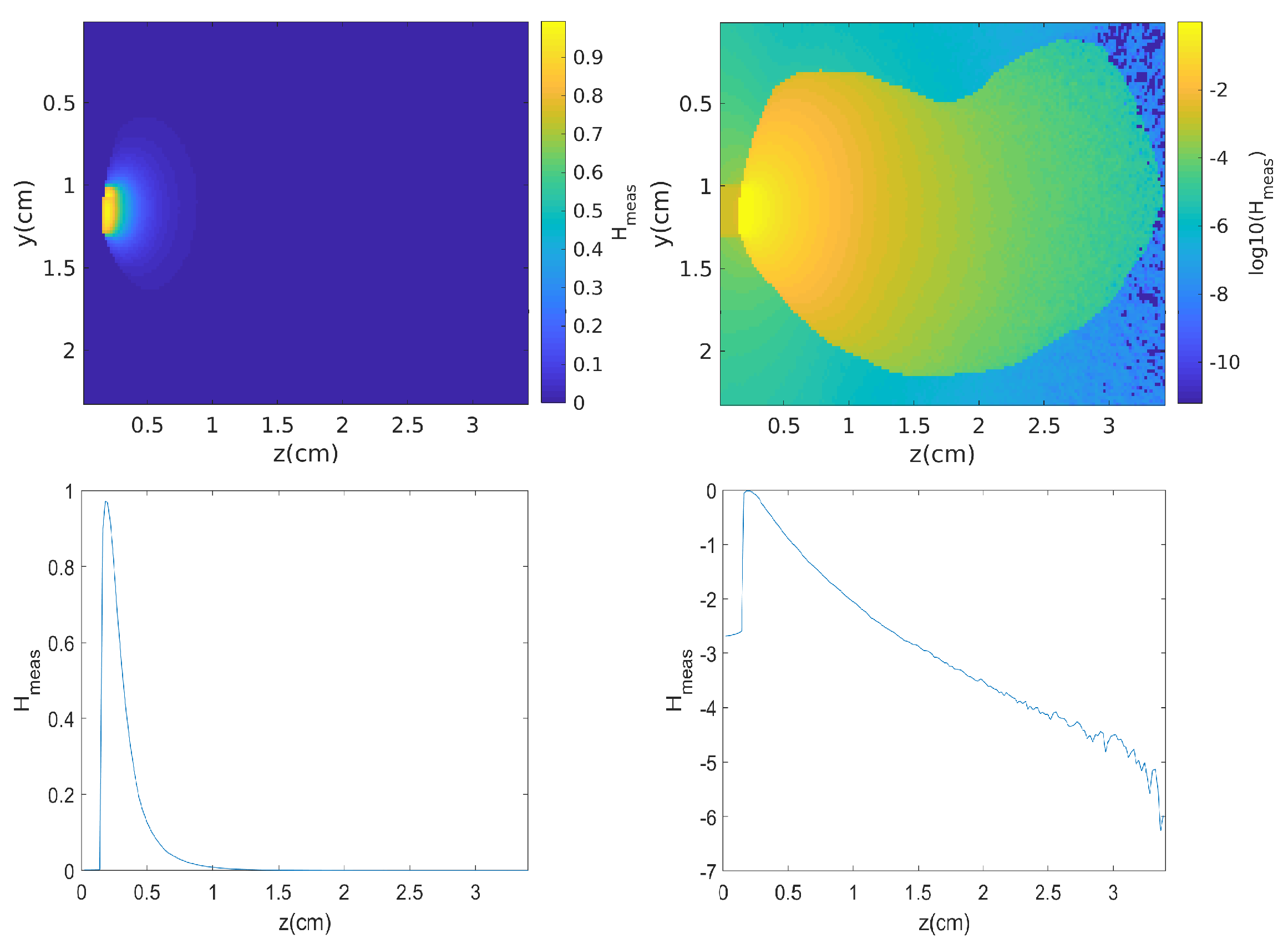
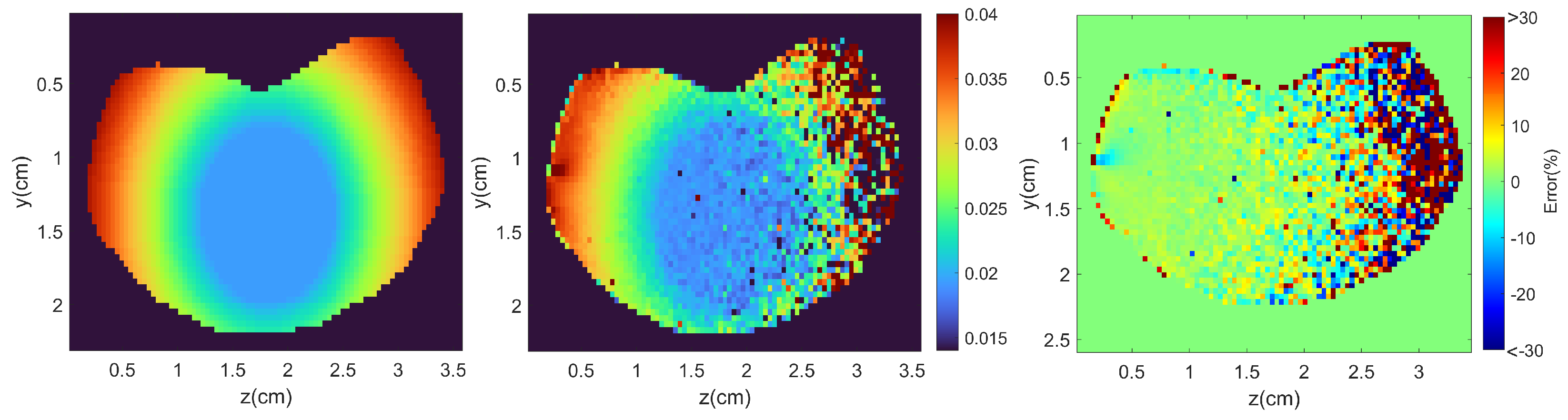
5.1. Noise-Free Reconstruction
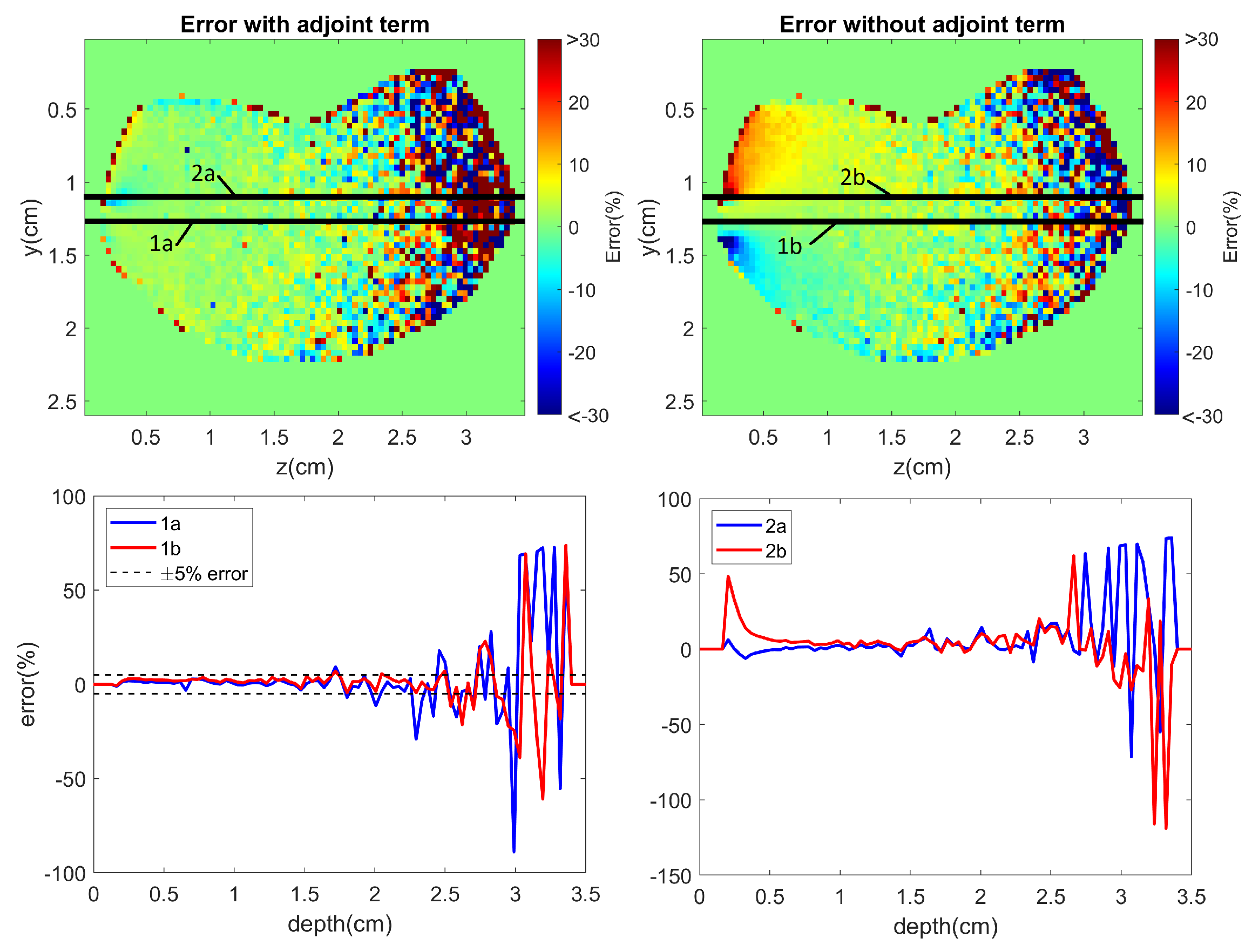
5.2. Reconstruction without the Radiance Term
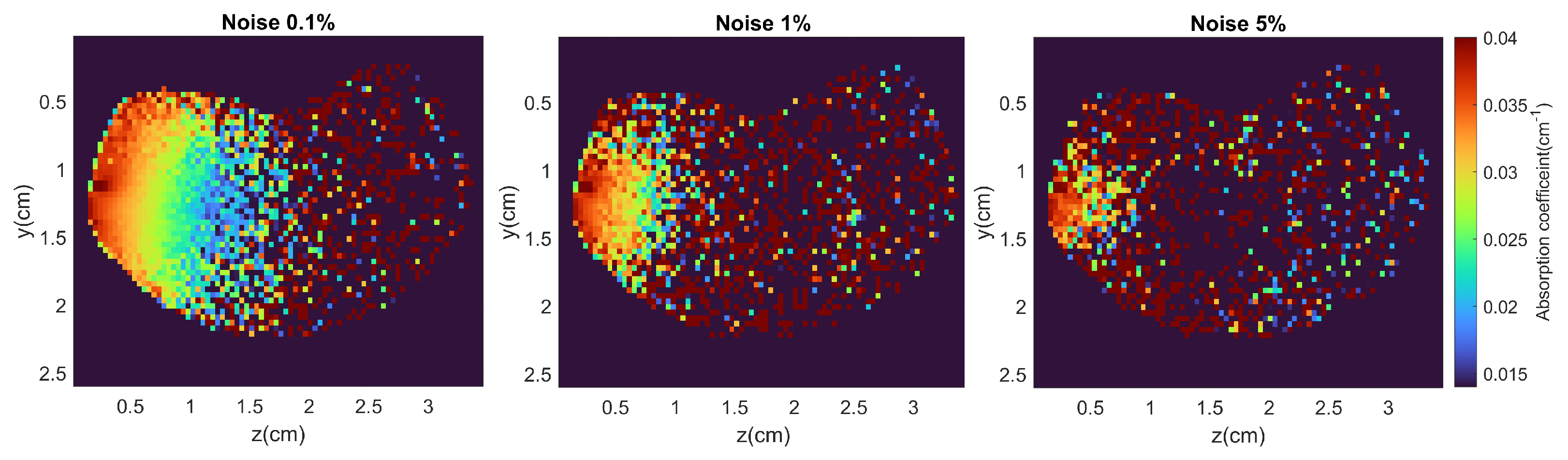
5.3. Reconstruction with Added Noise
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Newell, N.; Little, J.; Christou, A.; Adams, M.; Adam, C.; Masouros, S. Biomechanics of the human intervertebral disc: A review of testing techniques and results. J. Mech. Behav. Biomed. Mater. 2017, 69, 420–434. [Google Scholar] [CrossRef] [PubMed]
- Kos, N.; Gradisnik, L.; Velnar, T. A Brief Review of the Degenerative Intervertebral Disc Disease. Med. Arch. 2019, 73, 421. [Google Scholar] [CrossRef] [PubMed]
- Katz, J.N. Lumbar Disc Disorders and Low-Back Pain: Socioeconomic Factors and Consequences. J. Bone Jt. Surg. 2006, 88, 21–24. [Google Scholar] [CrossRef]
- Lee, C.K. Accelerated Degeneration of the Segment Adjacent to a Lumbar Fusion. Spine 1988, 13, 375–377. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Zhou, B.; Li, F.; Wang, W.; Liu, Y.; Wang, X.; Liu, C.; Ye, X. Advances of Naturally Derived and Synthetic Hydrogels for Intervertebral Disk Regeneration. Front. Bioeng. Biotechnol. 2020, 8, 745. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.P.; Qian, W.W.; Yin, G.Y.; Ren, Y.X.; Hu, Z.Y. MRI Assessment of Lumbar Intervertebral Disc Degeneration with Lumbar Degenerative Disease Using the Pfirrmann Grading Systems. PLoS ONE 2012, 7, e48074. [Google Scholar] [CrossRef] [PubMed]
- Metwally, K.; Boiron, O.; Deplano, V.; Prost, S.; Da Silva, A. Probing intervertebral discs with photoacoustics. In Opto-Acoustic Methods and Applications in Biophotonics IV; Ntziachristos, V., Zemp, R., Eds.; SPIE: Munich, Germany, 2019; p. 61. [Google Scholar] [CrossRef]
- Cox, B.T.; Arridge, S.R.; Beard, P.C. Gradient-based quantitative photoacoustic image reconstruction for molecular imaging. In Photons Plus Ultrasound: Imaging and Sensing 2007: The Eighth Conference on Biomedical Thermoacoustics, Optoacoustics, and Acousto-Optics; Oraevsky, A.A., Wang, L.V., Eds.; International Society for Optics and Photonics, SPIE: Munich, Germany, 2007; Volume 6437, pp. 445–454. [Google Scholar] [CrossRef]
- Hochuli, R.; Powell, S.; Arridge, S.; Cox, B. Quantitative photoacoustic tomography using forward and adjoint Monte Carlo models of radiance. J. Biomed. Opt. 2016, 21, 126004. [Google Scholar] [CrossRef] [PubMed]
- Buchmann, J.; Kaplan, B.A.; Powell, S.; Prohaska, S.; Laufer, J. Three-dimensional quantitative photoacoustic tomography using an adjoint radiance Monte Carlo model and gradient descent. J. Biomed. Opt. 2019, 24, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chetoui, M.A.; Boiron, O.; Ghiss, M.; Dogui, A.; Deplano, V. Assessment of intervertebral disc degeneration-related properties using finite element models based on ρH-weighted MRI data. Biomech. Model. Mechanobiol. 2019, 18, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Ghiss, M.; Giannesini, B.; Tropiano, P.; Tourki, Z.; Boiron, O. Quantitative MRI water content mapping of porcine intervertebral disc during uniaxial compression. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 1079–1088. [Google Scholar] [CrossRef] [PubMed]
- Antoniou, J.; Steffen, T.; Nelson, F.; Winterbottom, N.; Hollander, A.P.; Poole, R.A.; Aebi, M.; Alini, M. The human lumbar intervertebral disc: Evidence for changes in the biosynthesis and denaturation of the extracellular matrix with growth, maturation, ageing, and degeneration. J. Clin. Investig. 1996, 98, 996–1003. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, M.; Ghosh, S. Silk biomaterials for intervertebral disk (IVD) tissue engineering. In Silk Biomaterials for Tissue Engineering and Regenerative Medicine; Elsevier: London, UK, 2014; pp. 377–402. [Google Scholar] [CrossRef]
- Iatridis, J.C.; MacLean, J.J.; O’Brien, M.; Stokes, I.A.F. Measurements of Proteoglycan and Water Content Distribution in Human Lumbar Intervertebral Discs. Spine 2007, 32, 1493–1497. [Google Scholar] [CrossRef] [PubMed]
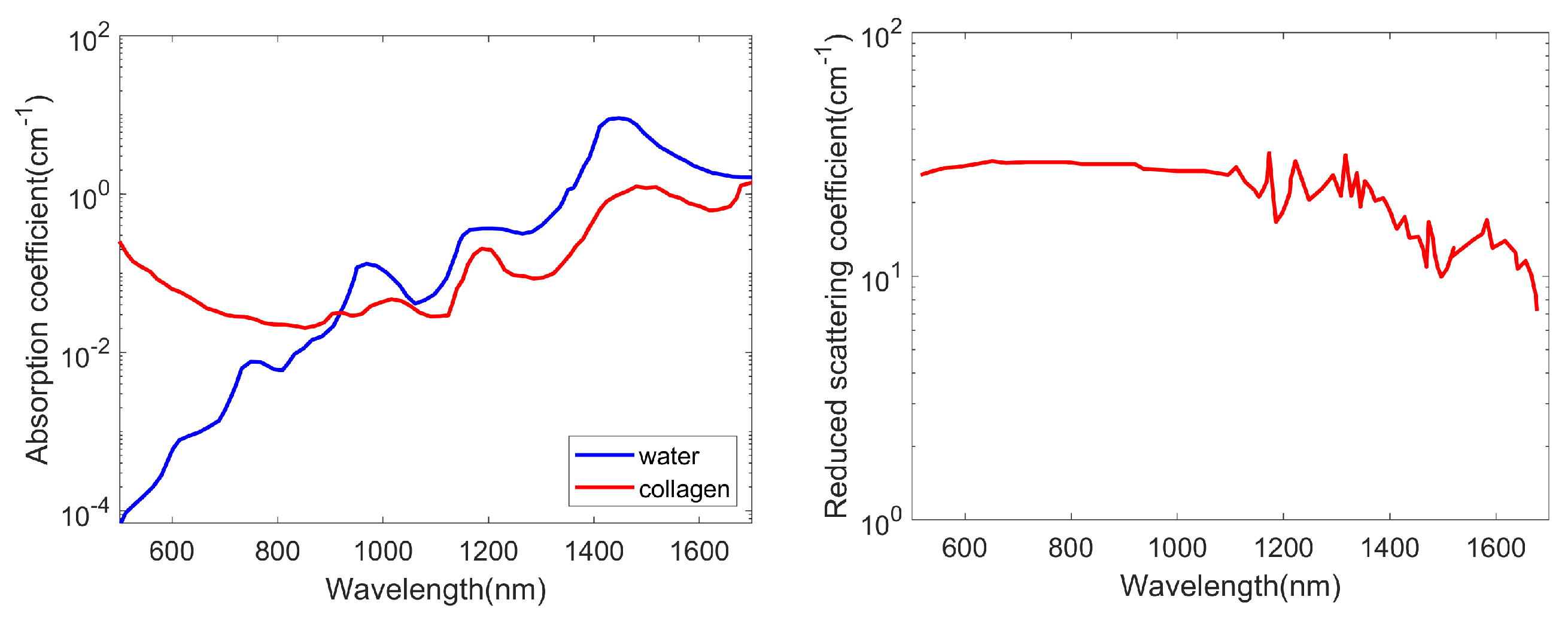
- Sekar, S.K.V.; Bargigia, I.; Mora, A.D.; Taroni, P.; Ruggeri, A.; Tosi, A.; Pifferi, A.; Farina, A. Diffuse optical characterization of collagen absorption from 500 to 1700 nm. J. Biomed. Opt. 2017, 22, 015006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mamonov, A.V.; Ren, K. Quantitative photoacoustic imaging in the radiative transport regime. Commun. Math. Sci. 2014, 12, 201–234. [Google Scholar] [CrossRef]
- Bal, G.; Ren, K. On multi-spectral quantitative photoacoustic tomography in diffusive regime. Inverse Probl. 2012, 28, 025010. [Google Scholar] [CrossRef]
- Marti, D.; Aasbjerg, R.N.; Andersen, P.E.; Hansen, A.K. MCmatlab: An open-source, user-friendly, MATLAB-integrated three-dimensional Monte Carlo light transport solver with heat diffusion and tissue damage. J. Biomed. Opt. 2018, 23, 1. [Google Scholar] [CrossRef] [PubMed]
- Barzilai, J.; Borwein, J.M. Two-Point Step Size Gradient Methods. IMA J. Numer. Anal. 1988, 8, 141–148. [Google Scholar] [CrossRef]
- Tarvainen, T.; Cox, B.T.; Kaipio, J.P.; Arridge, S.R. Reconstructing absorption and scattering distributions in quantitative photoacoustic tomography. Inverse Probl. 2012, 28, 084009. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capart, A.; Wojak, J.; Allais, R.; Ghiss, M.; Boiron, O.; Da Silva, A. Quantitative Photoacoustic Reconstruction of the Optical Properties of Intervertebral Discs Using a Gradient Descent Scheme. Photonics 2022, 9, 116. https://doi.org/10.3390/photonics9020116
Capart A, Wojak J, Allais R, Ghiss M, Boiron O, Da Silva A. Quantitative Photoacoustic Reconstruction of the Optical Properties of Intervertebral Discs Using a Gradient Descent Scheme. Photonics. 2022; 9(2):116. https://doi.org/10.3390/photonics9020116
Chicago/Turabian StyleCapart, Antoine, Julien Wojak, Roman Allais, Moncef Ghiss, Olivier Boiron, and Anabela Da Silva. 2022. "Quantitative Photoacoustic Reconstruction of the Optical Properties of Intervertebral Discs Using a Gradient Descent Scheme" Photonics 9, no. 2: 116. https://doi.org/10.3390/photonics9020116
APA StyleCapart, A., Wojak, J., Allais, R., Ghiss, M., Boiron, O., & Da Silva, A. (2022). Quantitative Photoacoustic Reconstruction of the Optical Properties of Intervertebral Discs Using a Gradient Descent Scheme. Photonics, 9(2), 116. https://doi.org/10.3390/photonics9020116



