Abstract
In this study, we propose a novel design of triangular mesoscale Janus prisms for the generation of the long photonic hook. Numerical simulations based on the finite-difference time-domain method are used to examine the formation mechanism of the photonic hook. The electric intensity distributions near the micro-prisms are calculated for operation at different refractive indices and spaces of the two triangular micro-prisms. The asymmetric vortices of intensity distributions result in a long photonic hook with a large bending angle. The length and the bending angle of the photonic hook are efficiently modulated by changing the space between the two triangular micro-prisms. Moreover, the narrow width of the photonic hook is achieved beyond the diffraction limit. The triangular Janus micro-prisms have high potential for practical applications in optical tweezers, nanoparticle sorting and manipulation and photonic circuits.
1. Introduction
Pyramidal structures, which are drawn from the Greek words Pyro (fire) and Amid (from the centre), are one of the simple geometric shapes widely found in nature. Many molecules and crystals have the shape of a pyramid [1,2,3]. It is known that the space within the pyramids generates or/and enhances energy in the electro-magnetic band [4,5,6]. The pyramidal shapes are used in three-fold rotational symmetry quantum dots [7] to enhance the light-capturing ability in sensors [8], nano- and meso-scale resonators with a high Q-factor [9,10], Si-based photodetectors [11,12] and solar cells [13,14]. They are also used for subwavelength light focusing [15,16], to form Bessel beams [17], to enhance Raman scattering [18] and in food and health technologies [19,20]. Recently, it was shown that the formation of the localized optical field in the form of photonic jets (PJ) [21,22] can be done by the pyramidal structures [22,23,24,25,26]. For example, the micropyramid array enhances the interference effect of incident and scattered lights, and the intensity of the focused field reaches 33.8 times that of the incident light [18]. Photonic hook (PH) is a new type of PJ in which the artificial curved beam is focused by a Janus dielectric particle with a waist less than the half of wavelength [27,28,29,30]. The PH forming mechanism requires asymmetry of illumination wavefront, the dielectric particle in the manner of geometric shape, or the optical properties of particle material [31,32]. Additionally, double PHs can be formed using two coherent illuminations [33], adjacent dielectric cylinders [34], or twin-ellipse mesoscale cylinders [35]. The PH has the potential to revolutionize mesotronics [36] within wide fields of applications, including optical trapping, subwavelength imaging and signal switching. However, despite the abundance of methods to obtain PH, a method based on pyramidal particles has not yet been considered. Obviously, the PH properties of the mesoscale Janus particles based on pyramids are worth further investigation when multi-dielectric structures are considered [37,38]. The main purpose of this article is to identify the key characteristics of the PH based on Janus particles from triangular prisms. The possibility of generating long PHs makes it possible to expand the arsenal of methods for creating structured localized beams of this type and in related applications.
2. Simulation Model
In this study, the physical mechanism of the near-field spatial intensity distributions of optical scattering is considered by triangular Janus micro-prisms. The optical diffraction in the Janus prisms with mesoscale dimensions [22,23,36] is a near-field problem because of the interference by diffracted and scattered lights on an inhomogeneous medium [39]. Since such a light scattering problem has no analytical solution, the only a numerical approach is suitable for this complicated, inhomogeneous material. We demonstrate a proof-of-concept method of controlling the PH curvature by choosing the structure parameters. Figure 1 shows the conception of a curved optical focusing beam by means of an index-contrast triangular Janus micro-prism. The width and height of the triangular micro-prism are w = 6 μm and h. The refractive indices of the two triangular micro-prisms are n1 and n2. The space between the two triangular micro-prisms is d. The triangular Janus micro-prism is surrounded by air (n0 = 1). A laser beam with 671-nm wavelength with linear polarization along the z-axis is introduced into the bottom of the triangular Janus micro-prism along the positive x direction. A photonic hook along the positive x direction is generated by the triangular Janus micro-prism. For characterizing the photonic hook, the focal length between the point of maximum intensity peak and the vertex of the triangular prism along the x direction is f. For evaluating the bending angle θ of the PH, we use the following procedure [30,31]. First, the contour map at 1/e of the maximum intensity peak are rendered based on the 2D intensity-distributions of the PH, and then conditionally divided into two parts representing the left and right arms of the PH with the inflection point having maximal intensity Imax. Next, the start and end points are selected as the extreme points of both the left and right arms, respectively, relative to the point with Imax. To demonstrate the performance of the photonic hook, a two-dimensional finite-difference time-domain computation is implemented with perfectly matched absorbing boundaries [40]. The computational field is in the x-y plane, and the triangular prism along the z direction is regarded to have an infinite length. The triangular grid mesh is used to ensure the accuracy and speed of numerical calculation, which is set as 10 nm in the computational field.
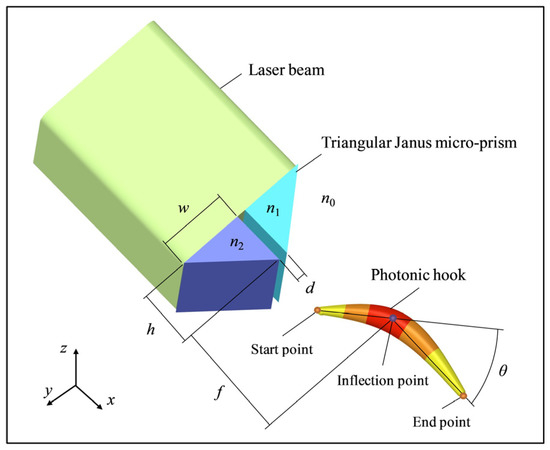
Figure 1.
Schematic stereogram of the triangular Janus micro-prism for photonic hook.
3. Simulations and Results
First, the formations of classical PJ by conventional triangular all dielectric prisms with different heights h are shown in Figure 2. When the height of the micro-prism decreases, the focus point of the electromagnetic field moves away from the micro-prisms and the intensity at the focus point also decreases. The position of the maximum intensity field is crucial to the length of the PJ. A decrease in h as the PJ length increases is caused by the movement of the focus point outside the micro-prisms. The key parameters of the PJ are the maximum intensity enhancement, the full width at half maximum (FWHM) and the focal distance from the shadow surface of Janus particle to the point with maximal field intensity. One can see from Figure 2 that, by increasing the height of a prism, the maximal field intensity on PJ increases, but the length of the PJ, FWHM and the focal distance decreases. In quantitative terms, the corresponding dependencies are shown in Figure 3. Let us note that the waist of the PJ decreases and tends to be smaller than half wavelength when the height h increases. The height h leads to an improvement in the key parameters of the PJ, because the height h increases the field intensity along the beam propagation direction. It should be noted that FWHM of the PJ is always subwavelength and at h > 2.25 it is less than the diffraction limit (λ/2).
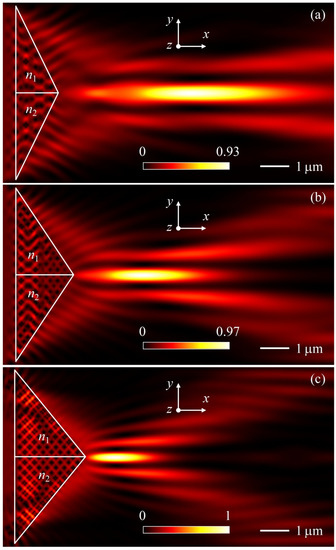
Figure 2.
Normalized intensity distributions of the photonic nanojets formed by conventional triangular micro-prisms at (a) h = 1.5 μm, (b) h = 2 μm, and (c) h = 2.5 μm. The refractive index of triangular micro-prisms is n1 = n2 = 1.5.
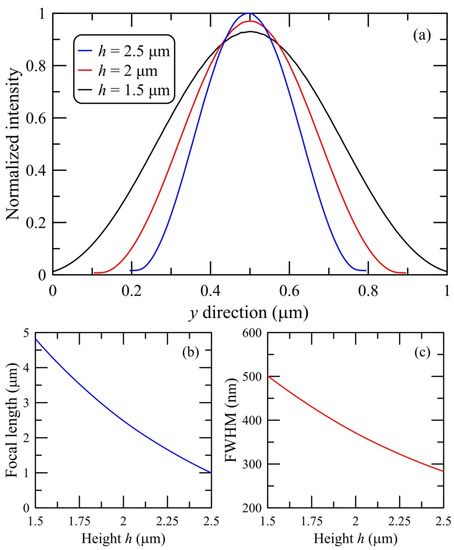
Figure 3.
(a) Normalized intensity profiles of the photonic nanojets along the y direction for conventional triangular micro-prisms. (b) Focal length and (c) FWHM as a function of the height h of the triangular micro-prisms.
In this article, we are interested in the possibility of forming curvilinear localized beams of the PH type. This can be achieved by introducing a refractive index gradient of the micro-prisms. Normalized intensity distributions of the PHs formed by triangular Janus micro-prisms with different refractive index contrasts are shown in Figure 4. The geometrical parameters of micro-prisms are h = 1.5 μm and w = 3 μm. The scattering of electromagnetic waves by the triangular micro-prisms leads to formation of the PH on the shadow side of the micro-prisms. The length of the PH decreases as the refractive index contrast increases. In addition, normalized intensity profiles of the PHs along the y direction for triangular mesoscale Janus prisms at different refractive index n2, focal length, FWHM and bending angle [36] are shown in Figure 5. The dependencies of the key parameters of the PH are presented against the refractive index contrast of the two triangular micro-prisms. It can be clearly seen that an increase in the optical contrast of the materials of the two micro-prisms leads to a decrease in the FWHM and focal length, but to an increase in the curvature (bending angle θ–see Figure 1) of the PH.
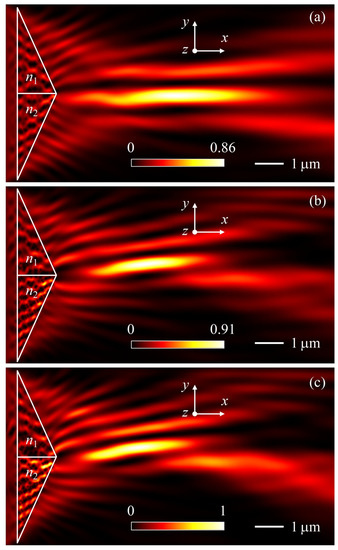
Figure 4.
Normalized intensity distributions of the photonic hooks formed by triangular Janus micro-prisms at n1 = 1.5, (a) n2 = 1.58, (b) n2 = 1.88, and (c) n2 = 1.95. The height and width of triangular Janus micro-prisms are h = 1.5 μm and w = 3 μm.
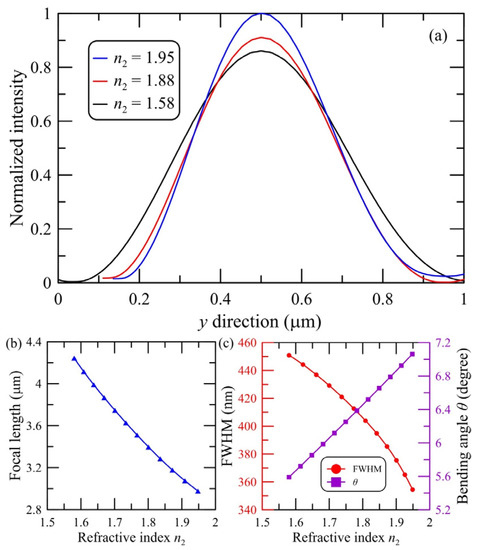
Figure 5.
(a) Normalized intensity profiles of the photonic hooks along the y direction for triangular Janus micro-prisms at different refractive index n2. (b) Focal length, (c) FWHM and bending angle as a function of the refractive index n2 of the triangular micro-prisms.
In the scheme of PH formation under consideration, there is one more additional degree of freedom which makes it possible to control the characteristics of a localized, structured electromagnetic flow. This factor is the space d between two conjugate micro-prisms. We have used this additional parameter to modulate the PH bending angle. Normalized intensity distributions of the PHs formed by triangular Janus prisms at different spaces and corresponding key parameters of the PHs are shown below in Figure 6 and Figure 7. The length of the PH increases as the space d increases. Direct comparison of the results presented in Figure 5 and Figure 7 demonstrates a fundamental difference in the key characteristics of the generated PHs. With an increase in the space between the conjugate micro-prisms with the remaining parameters of the problem, the focal length increases nonlinearly. This is due to the constructive interference of the transmitted, scattered and diffracted waves in the shadow part of the triangular micro-prisms. The same trend is also observed for the minimum beam width in Figure 7c. At the same time, the bending angle decreases as the space between the two micro-prisms increases. Note that the distance d between the prisms in perspective can be used for the flow of environmental material and the analysis of nanoparticles in the region of the PH. These studies are planned to be carried out in future works.
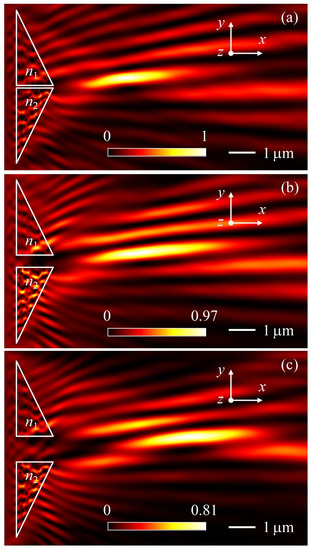
Figure 6.
Normalized intensity distributions of the photonic hooks formed by triangular Janus micro-prisms at (a) d = 100 nm, (b) d = 500 nm, and (c) d = 1000 nm. The refractive indices of triangular Janus micro-prisms are n1 = 1.5 and n2 = 1.88.
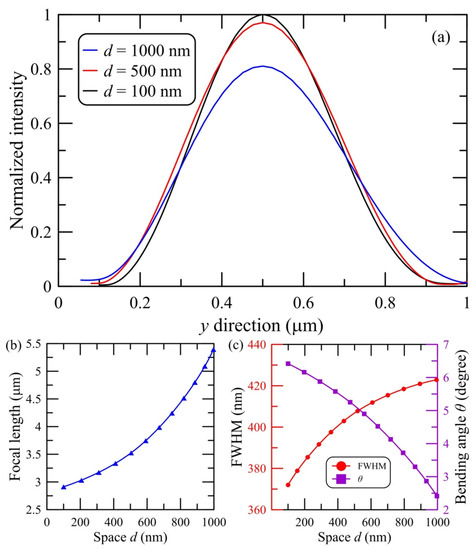
Figure 7.
(a) Normalized intensity profiles of the photonic hooks along the y direction for triangular Janus micro-prisms at different spaces d. (b) Focal length, (c) FWHM and bending angle as a function of the space d of the triangular micro-prisms.
To understand the physical process, Figure 8 shows Poynting vectors and energy flow streamlines for triangular micro-prisms at n1 = n2 = 1.5 (see Figure 2), n1 = 1.5, n2 = 1.88 (see Figure 4) and n1 = 1.5, n2 = 1.88, d = 500 nm (see Figure 6). In the case of the PJ formation, the subwavelength vortices inside the micro-prism are located symmetrically with respect to the axis of symmetry of the Janus particle. The introduction of optical contrast between conjugated prisms leads to a spatial redistribution of vortices. Accordingly, a curvature of the electromagnetic energy flux is generated behind the shadow part of the Janus particle. This is similar to the square Janus particle consisting of two diagonally conjugate micro-prisms [30]. When the micro-prisms are separated by a space d, the energy flux is responsible for the curvature of the localized beam due to the influence of a portion of the energy passing in the space between the two micro-prisms. This leads to a decrease in the bending angle of the beam as a whole. Moreover, an increase in the space d also elongates the length, scatter and direction of the PH over a wider range. The refractive indices in the figures are chosen as an example. The use of the two triangular micro-prisms leads to a dependence of the PH length and PH curvature on the refractive index contrast and the space between the two micro-prisms.
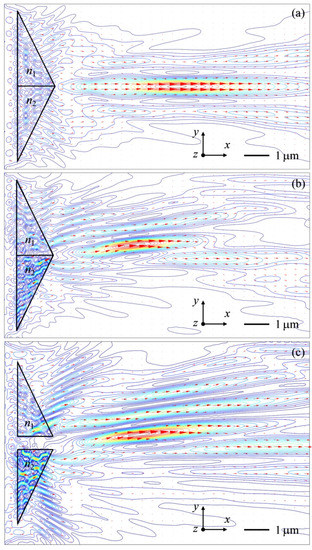
Figure 8.
Poynting vectors and energy flow streamlines for triangular Janus micro-prisms at (a) n1 = n2 = 1.5, (b) n1 = 1.5, n2 = 1.88, and (c) n1 = 1.5, n2 = 1.88, d = 500 nm. The height and width of triangular Janus micro-prisms are h = 1.5 μm and w = 3 μm.
In this paper, the triangle prism is not an axicon-shaped structure. An axicon is a specialized type of lens, which has a conical surface. An axicon transforms a laser beam into a ring-shaped distribution in the far field [41]. In our case, we used wavelength-scaled structure that cannot be described by ray-optics [22,23]. Moreover, the triangle structure under consideration is not a lens, Bessel or Airy-beam structured field. In such mesoscale structures, the geometrical optics approximation is not valid [42]. In the geometric-optical approximation, an axicon with Bessel-like beam forms parallel optical beams crossing the symmetry axis at the same angle [43,44]. In our work, this specific condition of an axicon is not satisfied, and the PJ generation of the triangle structure was experimentally reported in previous study [45].
4. Conclusions
In summary, the scattering of electromagnetic waves by triangular Janus micro-prisms has been studied in order to demonstrate the possibility of long high-intensity PH formation. The relationship of the refractive index contrast and the space between the two micro-prisms is found to form the PH with subwavelength waist and bending angle on the shadow side of the Janus micro-prisms. The space between the two micro-prisms leads to an improvement in the characteristics of the PHs. It was shown that the triangular Janus micro-prisms make it possible to focus optical beam in free space into the PH with waist smaller than the scalar diffraction limit and expands the range of dielectric structures for the formation of structured beams in mesotronics [36,46]. In particular, the triangular Janus micro-prism with n1 = 1.5, n2 = 1.95 forms a PH with a FWHM of 353 nm and a bending angle of 7°. Due to the asymmetric vortexes of intensity distributions, the long PH of 4.36 μm is obtained by the triangular Janus micro-prism at n1 = 1.5, n2 = 1.88, and d = 500 nm. By changing the space between the two micro-prisms, the PH length and the PH bending angle are efficiently modulated. From a practical point of view, a triangular Janus micro-prism can be fabricated by several modern technologies [47,48]. The controlled synthesis of materials with refractive indices is in the range from 1.05 to 2.0. The effects of the asymmetric optical energy flow may be used in many interesting applications such as nanoscopy in cell biology and nanoparticle trapping in light-analyte interaction procedures [49]. Moreover, taking into account the results of previous study [50], the current research may be extended into the 3D case.
Author Contributions
Conceptualization, W.-Y.C., C.-Y.L. and I.V.M.; methodology, O.V.M. and I.V.M.; software, Y.-K.H.; validation, O.V.M., W.-Y.C. and C.-Y.L.; formal analysis, W.-Y.C.; investigation, O.V.M. and I.V.M.; resources, Y.-K.H.; data curation, W.-Y.C. and Y.-K.H.; writing—original draft preparation, C.-Y.L., O.V.M. and I.V.M.; writing—review and editing, W.-Y.C. and C.-Y.L.; visualization, Y.-K.H. and C.-Y.L.; supervision, I.V.M. and O.V.M.; project administration, O.V.M.; funding acquisition, C.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science and Technology Council of Taiwan, grant number NSTC 111-2221-E-A49-102-MY2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
I.V.M. and O.V.M. acknowledge the Tomsk Polytechnic University Development Program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alderman:, P.; Owston, P. The square pyramidal configuration in a five-co-ordinate nitrosyl complex. Nature 1956, 178, 1071–1072. [Google Scholar] [CrossRef]
- Alamer, B.; Bootharaju, M.; Kozlov, S.; Cao, Z.; Shkurenko, A.; Nematulloev, S.; Maity, P.; Mohammed, O.; Eddaoudi, M.; Cavallo, L.; et al. [Ag9(1,2-BDT)6]3–: How square-pyramidal building blocks self-assemble into the smallest silver nanocluster. Inorg. Chem. 2021, 60, 4306–4312. [Google Scholar] [CrossRef] [PubMed]
- Bragg, W.H. The Structure of Magnetite and the Spinels. Nature 1915, 95, 561. [Google Scholar] [CrossRef]
- Natural Pyramids. Sci. Am. 1857, 13, 88. [CrossRef]
- Narimanov, A. Pyramid effect. Science 1999, 5446, 286. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Yue, L. Electromagnetic properties of pyramids from positions of photonics. Russ. Phys. J. 2020, 62, 1763–1769. [Google Scholar] [CrossRef]
- Gershoni, D. Pyramidal quantum dots. Nat. Photon. 2010, 4, 271–272. [Google Scholar] [CrossRef]
- Fallahazad, P.; Naderi, N.; Taherkhani, M.; Bazargan, A. Porous pyramidal silicon structures for improved light sensing performance. Optik 2020, 222, 165433. [Google Scholar] [CrossRef]
- Weber, F.; Karl, M.; Lupaca-Schomber, J.; Löffler, W.; Li, S.; Passow., T. Optical modes in pyramidal GaAs microcavities. Appl. Phys. Lett. 2007, 90, 161104. [Google Scholar] [CrossRef]
- Al-Wahsh, H.; Dobrzyński, L.; Akjouj, A. Long-lived resonances: Photonic triangular pyramid. Photonics Nanostructures Fundam. Appl. 2022, 50, 101022. [Google Scholar] [CrossRef]
- Desiatov, B.; Goykhman, I.; Mazurski, N.; Shappir, J.; Khurgin, J.; Levy, U. Plasmonic enhanced silicon pyramids for internal photoemission Schottky detectors in the near-infrared regime. Optica 2015, 2, 335–338. [Google Scholar] [CrossRef]
- Syu, H.; Chuang, H.; Lin, M.; Cheng, C.; Huang, P.; Lin, C. Ultra-broadband photoresponse of localized surface plasmon resonance from Si-based pyramid structures. Photonics Res. 2019, 7, 1119–1126. [Google Scholar] [CrossRef]
- Fan, Y.; Han, P.; Liang, P.; Xing, Y.; Ye, Z.; Hu, S. Differences in etching characteristics of TMAH and KOH on preparing inverted pyramids for silicon solar cells. Appl. Surf. Sci. 2013, 264, 761–766. [Google Scholar] [CrossRef]
- Almenabawy, S.; Zhang, Y.; Flood, A.; Prinja, R.; Kherani, N. Nanometer-mesa inverted-pyramid photonic crystals for thin silicon solar cells. ACS Appl. Energy Mater. 2022, in press. [Google Scholar] [CrossRef]
- Lindquist, N.; Johnson, T.; Nagpal, P.; Norris, D.; Oh, S. Plasmonic nanofocusing with a metallic pyramid and an integrated C-shaped aperture. Sci. Rep. 2013, 3, 1857. [Google Scholar] [CrossRef]
- Mu, J.; Liu, Z.; Li, J.; Hao, T.; Wang, Y.; Sun, S.; Li, Z.; Li, J.; Li, W.; Gu, C. Direct laser writing of pyramidal plasmonic structures with apertures and asymmetric gratings towards efficient subwavelength light focusing. Opt. Express 2015, 23, 22564–22571. [Google Scholar] [CrossRef]
- Martin, J.; Proust, J.; Gérard, D.; Bijeon, J.; Plain, J. Intense Bessel-like beams arising from pyramid-shaped microtips. Opt. Lett. 2012, 37, 1274–1276. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, S.; Jiang, Z.; Shi, Z.; Wang, J.; Du, L. Highly sensitive and reproducible SERS substrates based on ordered micropyramid array and silver nanoparticles. ACS Appl. Mater. Interfaces 2021, 13, 29222–29229. [Google Scholar] [CrossRef]
- Abdelsamie, M.; Rahman, R.; Mustafa, S. Pyramid shape power as a new halal-compliant food preservation and packaging technique. Procedia Soc. Behav. Sci. 2014, 121, 232–242. [Google Scholar] [CrossRef][Green Version]
- Abdelsamie, M.; Rahman, R.; Mustafa, S.; Hashim, D. Effect of packaging shape and storage on the keeping quality of mineral water and development of a water-treatment device. J. Food Process Technol. 2013, 4, 231. [Google Scholar] [CrossRef]
- Horiuchi, N. Photonic nanojets. Nat. Photonics 2012, 6, 138–139. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Diffractive Optics and Nanophotonics Resolution Below the Diffraction Limit; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Geints, Y. Localized EM and photonic jets from non-spherical and non-symmetrical dielectric mesoscale objects. Ann. Phys. 2015, 527, 491–497. [Google Scholar] [CrossRef]
- Ge, S.; Liu, W.; Zhang, J.; Huang, Y.; Xi, Y.; Yang, P.; Sun, S.; Li, S.; Lin, D.; Zhou, S.; et al. Novel bilayer micropyramid structure photonic nanojet for enhancing a focused optical field. Nanomaterials 2021, 11, 2034. [Google Scholar] [CrossRef] [PubMed]
- Abramov, A.; Yue, Y.; Wang, M.; Wang, Z.; Xu, Y. Numerical modeling of photonic jet behind triangular Prism. Asian J. Res. Rev. Phys. 2021, 4, 1–6. [Google Scholar] [CrossRef]
- Zaitsev, V.; Stafeev, S. The photonic nanojets formation by two-dimensional microprisms. Comput. Opt. 2020, 44, 909–916. [Google Scholar] [CrossRef]
- Dholakia, K.; Bruce, G. Optical hooks. Nat. Photonics 2019, 13, 229–230. [Google Scholar] [CrossRef]
- Gu, G.; Shao, L.; Song, J.; Qu, J.; Zheng, K.; Shen, X.; Peng, Z.; Hu, J.; Chen, X.; Chen, M.; et al. Photonic hooks from Janus microcylinders. Opt. Express 2019, 27, 37771–37780. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Yue, L.; Wang, Z.; Christodoulides, D. Photonic hook —A new type of subwavelength self-bending structured light beams: A tutorial review. arXiv 2019, arXiv:1910.09543. [Google Scholar]
- Minin, O.V.; Minin, I.V. The Photonic Hook: From Optics to Acoustics and Plasmonics; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Liu, C.; Wei, H.; Geints, Y.; Karabchevsky, A. Experimental demonstration of tunable photonic hook by partially illuminated dielectric microcylinder. Opt. Lett. 2020, 45, 4899–4902. [Google Scholar] [CrossRef]
- Liu, C.; Chen, Y.; Li, C.; Chen, W.; Chien, S. Photonic hook generated by the Janus microcylinder under point-source illumination. J. Opt. Soc. Am. B 2021, 38, 2938–2944. [Google Scholar] [CrossRef]
- Zhou, S. Twin photonic hooks generated from two coherent illuminations of a micro-cylinder. J. Opt. 2020, 22, 085602. [Google Scholar] [CrossRef]
- Zhou, S. Twin photonic hooks generated from two adjacent dielectric cylinders. Opt. Quantum Electron. 2020, 52, 389. [Google Scholar] [CrossRef]
- Shen, X.; Gu, G.; Shao, L.; Peng, Z.; Hu, J.; Bandyopadhyay, S.; Liu, Y.; Jiang, J.; Chen, M. Twin photonic hooks generated by twin-ellipse microcylinder. IEEE Photonics J. 2020, 12, 6500609. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Mesotronics: Some new unusual optical effects. Photonics 2022, 9, 762. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, S.; Sun, Y.; Fang, X.; Wu, L. Fabrication, properties and applications of Janus particles. Chem. Soc. Rev. 2012, 41, 4356–4378. [Google Scholar] [CrossRef] [PubMed]
- Poggi, E.; Gohy, J. Janus particles: From synthesis to application. Colloid Polym. Sci. 2017, 295, 2083–2108. [Google Scholar] [CrossRef]
- Pacheco-Peña, V.; Riley, J.; Liu, C.; Minin, O.V.; Minin, I.V. Diffraction limited photonic hook via scattering and diffraction of dual-dielectric structures. Sci. Rep. 2021, 11, 20278. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S. Computational Electrodynamics: The Finite Difference Time Domain Method; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Martirosyan, A.; Altucci, C.; Lisio, C.; Porzio, A.; Solimeno, S.; Tosa, V. Fringe pattern of the field diffracted by axicons. J. Opt. Soc. Am. A 2004, 21, 770–776. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Paniagua-Domínguez, R.; Minin, I.O.; Minin, O.V.; Wang, Z. Refractive index less than two: Photonic nanojets yesterday, today and tomorrow [Invited]. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
- Khonina, S.; Kazanskiy, N.; Khorin, P.; Butt, M. Modern types of axicons: New functions and applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef]
- Khonina, S.; Degtyarev, S.; Savelyev, D.; Ustinov, A. Focused, evanescent, hollow, and collimated beams formed by microaxicons with different conical angles. Opt. Express 2017, 25, 19052–19064. [Google Scholar] [CrossRef]
- Liu, C.; Minin, O.V.; Minin, I.V. First experimental observation of array of photonic jets from saw-tooth phase diffraction grating. EPL 2018, 123, 54003. [Google Scholar] [CrossRef]
- Minin, O.V.; Minin, I.V. Optical Phenomena in Mesoscale Dielectric Particles. Photonics 2021, 8, 591. [Google Scholar] [CrossRef]
- Poco, J.; Hrubesh, L. Method of Producing Optical Quality Glass Having a Selected Refractive Index. U.S. Patent 6,158,244, 2008. [Google Scholar]
- Jiang, S.; Granick, S. Janus Particle Synthesis, Self-Assembly and Applications; The Royal Society of Chemistry: Cambridge, UK, 2012. [Google Scholar]
- Park, E.; Jin, S.; Park, Y.; Guo, S.; Chang, H.; Jung, Y. Trapping analytes into dynamic hot spots using Tyramine-medicated crosslinking chemistry for designing versatile sensor. J. Colloid. Interface Sci. 2022, 607, 782–790. [Google Scholar] [CrossRef] [PubMed]
- Geints, Y.; Minin, O.V.; Minin, I.V. Systematic study and comparison of photonic nanojets produced by dielectric microparticles in 2D- and 3D- spatial configurations. J. Opt. 2018, 20, 065606. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).