Abstract
A novel experimental setup for the generation of arbitrary vector beams is proposed. The system major includes two reflective liquid crystal spatial light modulators (RLC-SLM) and a polarizing beam splitting prism. Moreover, this method is not limited by the wavelength of light wave and the pixel size of SLM. Theoretical analysis shows that when Gaussian beam or a plane beam is illuminated on a computer-generated hologram (CGH) specially designed in this work, the complex amplitudes of the vector field’s two orthogonal polarization components may be changed by modifying the encoding parameters, resulting in a vector beam with arbitrary complex amplitude and polarization in the output field. The experimental results also show that the two independent coding channels of the device have good polarization-selective imaging ability, which greatly improves the flexibility of generating arbitrary vector beams.
1. Introduction
Recently, as one of the important properties of light, polarization has been extensively studied. As an extension of conventional uniformly polarized beams, the study of vector beams is becoming more and more in-depth. The exploration of new effects and new applications of the vector beams has a profound impact on the progress of optical technology. Due to their special polarization characteristics, vector beams have been used in many disciplines and engineering fields such as focus-shaping [1,2,3], particle trapping [4,5], surface plasmon excitation [6], super-resolution imaging [7,8], and laser processing [9,10,11,12].
Most commercial lasers output a single mode of laser beam, but the research of light field application requires a specific polarization state and a vector light field with complex amplitude distribution. Based on the above requirements, researchers are constantly looking for a new method to completely control the shape of light. At present, it is mainly divided into static generation mode and dynamic generation mode. Although these approaches are conducive to generating vector beams, they all share a common disadvantage of being inflexible and dynamic about the configurations and optics they are designed for. Therefore, light field modulation technology came into being, which is based on liquid crystal spatial light modulator (LC-SLM) [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. LC-SLM can control the amplitude and phase in real time, and a new spatially structured light field with arbitrary complex amplitude and polarization distribution can be generated. For instance, Han et al. [16] proposed a method based on SLM polarization selectivity. This method divides the two SLMs into four regions, which enables the generation of arbitrary light fields. Zhou et al. [26] also proposed a method based on SLM polarization selectivity, which combines 96° prism and SLM split screen method to realize a compact and efficient device for generating arbitrary vector vortex beams (VVBs). Similarly, Liu et al. [27] put forward an optical plant, including a single phase-type SLM, which also can generate vector beams. The above methods show that vector beams with arbitrary complex amplitudes can be generated by SLM modulation, but controlling a vector beam often requires modulate two orthogonal polarization states with the complex amplitudes independently, which will increase the complex of the system and thus reduce the stability of the system. The main content of this research is to decrease the complicacy degree of the system by improving an encoding method of computer-generated-hologram (CGH).
In this work, a novel approach is presented. It can generate vector light fields of arbitrary complex amplitudes. The main part of the approach includes two reflective liquid crystal spatial light modulators (RLC-SLM) and a polarizing beam splitting prism. It is well-known that vector beams can be decomposed into two sets of complex amplitudes with orthogonal polarization states. Taking advantage of this feature, two RLC-SLMs were used to modulate the two sets of complex amplitudes, respectively. At the same time, the CGH specially designed is in combination with the modified off-axis interference-type hologram coding method to achieve real-time regulation of the spatial construction in the optical field. The advantage of the structure is that it does not need a complex optical path, and the modulation process is more flexible. By simply changing the parameters of CGH, vector beams can be acquired with arbitrary polarization and plural amplitude distributions. When encoding and calculating holograms, the pixel size of SLM plays a crucial role, SLM for displaying CGH is equivalent to a grating, and pixel size affects the number of raster lines. The number of raster lines and wavelength will have an impact on the diffraction angle, thus affecting the coupling of two beams of light. In this work, two angle-adjustable SLMs are used, and only the tilt angle of the SLM needs to be adjusted to eliminate the influence of different pixel sizes and wavelengths. However, when adjusting the geometric optical path, mechanical errors are difficult to avoid. As a result, there is an angle between the wavefronts of two orthogonally polarized parallel lights, and then interference fringes appear, affecting the final imaging. Therefore, to achieve the accurate coupling of the two beams of light in the phase plane and produce an ideal vector light field, the spatial frequency component representing the tilt factor of the light wave front, was added to the CGH to adjust the wavefront of the two beams of orthogonally polarized light. By adjusting the tilt angle of SLM and the four parameters of the spatial frequency component, the influence of light wavelength and SLM pixel size can be completely eliminated. The specific theoretical analysis and experimental study of this method are introduced in Section 2 and Section 3.
2. Principle and Analysis
Figure 1 shows the principal framework of the experimental setup of generating arbitrary complex amplitude vector beams based on double RLC-SLM system (D-RLC-SLM). In this research, a horizontally polarized He-Ne laser with λ = 632.8 nm is expanded, collimated, and orientated onto the D-RLCSLM system. The two RLC-SLMs with 1024 × 768 pixels and pixel size of 18 μm are adopted. The size of the 90° polarizing splitting prism is 35 mm 35 mm 35 mm, and the extinction ratio is 1000:1. In order to meet the size requirements of matching with CCD, two Fourier lenses with focal lengths of 300 mm and 180 mm were used. The presented approach does not necessitate complicated optical components, as the figure shows. First, a beam of expanding and collimating parallel light passes through the half-wave plate. The half-wave plate’s function is to modify the incident light field’s polarization state so as to achieve the same intensity of the two orthogonal components separated by the polarization beam splitter. Next, it enters the polarization splitting prism and is divided into two beams. Through a quarter-wave plate, two reflected light beams are sent to RLC-SLM1 and RLC-SLM2, respectively (used to adjust the beam irradiated to the liquid crystal spatial light modulator as circularly polarized light). It includes RLC-SLM1 and RLC-SLM2, which are positioned on the Fourier Lens L1′s front focal plane (P1), in order to change the complex amplitude of the beam. The -CGH in Figure 1 is displayed on the corresponding SLM1, and the -CGH is displayed on the corresponding SLM2. Next, the modulated two light fields are output by the splitting prism, and the polarization states of the output two light beams are orthogonal to each other. In case the RLC-SLM is not inclined, the forms of the two beams on the spectral plane of L1 are shown in Figure 1a1,a2, respectively. Figure 1b is the result of the superposition of the two beams on the spectral plane (P2) of L1. In order to couple the first-order diffraction term in the diffracted light and spread along the optical axis, the RLC-SLM should be tilted. Finally, to eliminate further diffraction effects, the filtered aperture (FA) was positioned on the spectral plane of L1 (as shown in Figure 1c), and the vector beam can be obtained in the output optical field of the system. The second Fourier lens is only applied to convert the resulting vector beam into its distribution on the CGH, not the inverse Fourier transform. In many practical applications, the L2 can be removed.
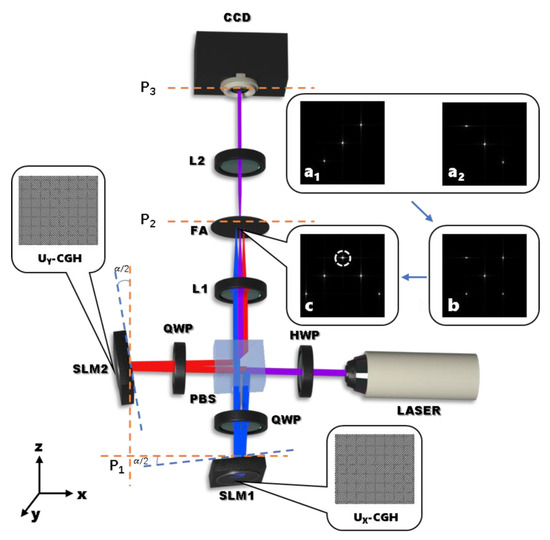
Figure 1.
Architecture of the experiment setup. LASER: He-Ne laser; HWP: half-wave plate; PBS: polarizing beam splitting prism; QWP: quarter-wave plate; SLM1-SLM2: reflective liquid crystal spatial light modulators; L1-L2: the Fourier Lens; FA: the filtered aperture; CCD: charge-coupled device; a1 is the spectral distribution of x-polarized light on the spectral plane of lens 1; a2 is the spectral distribution of y-polarized light on the spectral plane of lens 1; b is the spectral surface when the liquid crystal spatial light modulator is not tilted; c is the spectral surface after the liquid crystal spatial light modulator is tilted.
In the plane of the vertical optical axis, a vector beam can usually be decomposed into two orthogonal polarization constituents. Suppose that the complex amplitude distribution of the proposed vector beam Jones vector or its orthogonal polarization component is and , which can be expressed as:
where (, ) and (, ) are the phase and amplitude distributions of the two polarization components, respectively. Apparently, a vector beam has four degrees of freedom, so a device that can actually generate any vector beam would need to independently control four parameters at each pixel. In this experiment, two RLC-SLMs were used to regulate two components of a vector beam, respectively. Assume that the transmittance function of the SLM is . Taking advantage of the polarization imaging characteristics of the optical path is shown in Figure 1. In order to couple the two components together, the complex amplitudes and of the two orthogonal polarization components of the vector beam to be generated need to be translated appropriately along the x direction. The translation parameter is set as , where d represents the optical path length from RLC-SLM1 to L1 and RLC-SLM2 to L1, and is the angle between the main optical axis and z axis of the reflected light of the RLC-SLM. Therefore, in order to make the coordinate translation of and be and , the RLC-SLM should be tilted by . The spatial frequency component of illumination light along y direction is set as . The , as the illumination wavelength, is encoded into two different diffraction directions of the CGH, and the carrier frequency of appropriate size is set, so that when the CGH is illuminated with appropriate illumination light, its corresponding diffraction reproduction image can just realize polarization superposition on the output plane. Meanwhile, the incident light illuminating CGH is circularly polarized plane light. For example, in the coordinate guideline displayed in Figure 1, and can be encoded in the diffraction direction of +45° and −45° with respect to the X-axis and their carrier frequency components along the X-axis, which are and , respectively. When this method is used to generate an ideal vector beam, it is necessary to encode two CGHs to independently control two beams of orthogonal polarized light. Meanwhile, each CGH will contain two sets of parameters in the x and y directions, and the four parameters of the spatial frequency components are . By adjusting the four parameters of the spatial frequency component, the problem of no coplanar wavefronts of two orthogonal polarized beams can be completely eliminated.
Taking modified off-axis interference-type hologram encoding as an example, the CGH of and in this experiment can be encoded using the following equation:
Equation (2) can be further revised as follows:
According to Equation (3), t0 is a constant greater than 0, is the complex amplitude of the light field, and A is the amplitude of the light field. CGH is encoded in this manner such that when a hologram of this type is placed on the input surface P1 of the light path depicted in Figure 1, the influence of FA and the focal length of the lens are ignored. Meanwhile, the Jones vector form of the output light field at the output surface P3 can be expressed as follows:
In Equation (4), , , is the amplitude of incident light, j is the imaginary symbol; and are two constants less than 1, which are used to characterize the reflection efficiency of CGH to the two orthogonal polarization states, and θ is the angle formed by the incident light’s polarization direction and the Y-axis. For a CGH of isotropy, is usually equal to , in which case the polarization angle of the incident light can be set to 45°. If the CGH is anisotropic (e.g., CGH output with a LC-SLM), is not usually equal to . In this instance, the angle can be adjusted from to . At the same time, Equation (4) can be rewritten as:
In this way, by substituting Equation (3) into Equation (5) and expanding it, the output light field at the system output surface P3 will have the following form:
The second term in Equation (6) is exactly the required vector light field. Although there are some redundant terms in it, they can be eliminated by spatial filtering, because the spatial spectrum of the optical field is shown in Equation (6). In other words, the distribution of the light field on the spatial spectrum surface P2 in the system is directly proportional to the Fourier transform of Equation (6), namely:
After passing through a polarization splitting prism and FA, the diffracted light can just produce the desired vector beam on the output surface P3.
3. Experiments and Discussions
The following experimental process is carried out using the experimental device described in Figure 1.
Firstly, in order to determine the independent imaging capability and system parameters of two orthogonal polarization components, two binary grayscale images with letters X and Y, which are only black and white grayscale (Figure 2a,b), are substituted into Equation (3) as and , respectively. The modified off-axis CGH encoding method was used to design corresponding CGH (as depicted in Figure 2c,d), which was displayed on RLC-SLM1 and RLC-SLM2. The spatial frequency component in the y direction was adjusted to achieve perfect coupling of two beams of light, and the FA placed on the L1 spectrum plane was used to filter out excess terms. Finally, the image sensor that records the output light field’s intensity distribution is placed on the system’s output plane, and the light field with the desired polarization state can be obtained. The distance between RLC-SLM1 or RLC-SLM2 and L1 is approximately equal to one focal length of L1. The intensity distribution pictures of the system’s output plane after the offset detector have been installed are in Figure 2e–h. According to the guided wave effect of the RLC-SLM, the black, gray pixel (corresponding control voltage is zero) will rotate the linearly polarized beam passing through the polarizer P by 90°. However, the beam with linear polarization passing through the white gray pixel (corresponding control voltage is high) will keep the linearly polarized direction unchanged. The aforementioned theory also demonstrates that the experimental findings are accurate.

Figure 2.
(a,b) show two binary grayscale images as functions of and ; (c,d) are their corresponding CGHs designed according to Equation (3); (e–h) are the light intensity distribution of different polarizer orientations. The polarization analyzer’s direction in relation to the image sensor is shown by the arrows in the sub-image’s top right corners.
To further confirm the system’s ability to generate arbitrary complex amplitude vector light fields, we designed a typical vector beam that seems like a Gaussian cylindrically symmetric polarized beam in this work, which can be expressed as:
The additional phase of the two components of the vector field can be expressed in the form of with spiral distribution, in which w spot radius of Gauss beam waist, for the input plane of the polar coordinates. That is to say , integers m for vector beam topology nuclear, n for the vector beam radial index, and for the initial phase, the initial phase difference between the radial and azimuthal vector fields is . In the experiment, and with different parameters are substituted into Equation (3), and some CGHs that generate cylindrical symmetric vector beams are designed and displayed on the SLM. For the purpose of detecting the polarization characteristics of the output vector beam, the analyzer is placed between the lens L2 and CCD.
In Figure 3, without the polarizer, there is no difference in the distribution of intensity of the light field, except that there is a dark point in the center. The dark point is called phase singularity or polarization singularity, which is caused by the phase uncertainty or polarization state uncertainty of the center point. It is also said that the center point has the same polarization, but the phase is opposite, which satisfies the destructive interference condition, and thus forms the destructive interference dark spot.
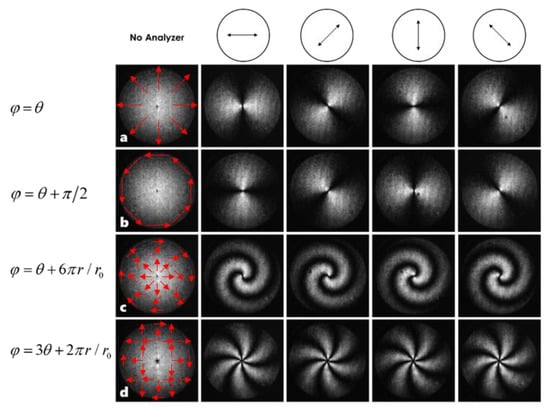
Figure 3.
(a–d) shows the intensity distribution of the optical field under different direction polarizers when is taken as , , and , respectively. The polarization analyzer’s orientation that positions the image sensor’s front is shown by the arrow at the top of the image.
This is followed by a Laguerre–Gaussian (LG) beam with a linearly polarization state. This can be expressed as:
where,
where is the polar coordinate of the input plane, is the normalization constant, is the width of the beam, and is the Laguerre polynomial. In the experiment, a computational hologram designed to generate a LG beam is displayed on the SLM. Using a polarizer placed between L2 and CCD, the polarization characteristics of the output beam is checked. The experimental results are shown in Figure 4.

Figure 4.
(a,b) is the intensity distribution without a polarizer. (c,d) shows the optical field intensity distribution under horizontal polarization. (e,f) is the corresponding phase distribution. (g,h) shows the intensity distribution under vertical polarization conditions. (i,j) is the corresponding phase distribution.
In Figure 4, the parameters are = (equivalent to = 1, = 3) and (equivalent to = 2, = 1); and = (equivalent to = 1, = 4) and (equivalent to = 4, = 1). Figure 4a,b show the total intensity distribution of the output vector beam recorded by the CCD without a polarizer placed. Figure 4c, d, g, and h are the intensity distribution of the output vector beam recorded by the CCD when the detector is placed. Figure 4e,f,i, and j are the phase distribution of the output vector beam. Figure 4c,d shows the optical field intensity distribution under horizontal polarization. Figure 4e,f is the corresponding phase distribution. It can be seen that with the increase of , the radius of the spot ring gradually increases. Figure 4g,h shows the intensity distribution under vertical polarization conditions. Figure 4i,j is the corresponding phase distribution. It can be seen that with the increase of , the number of extinction rings also increases and equals . The experimental results also show that the two independent coding channels of the device have good polarization-selective imaging ability.
4. Conclusions
In conclusion, we described a variable setup for producing vector beams with variable complex amplitude and polarization using two RLC-SLM and a polarization splitting prism. Since the system has two imaging channels and polarization encoding, two independent CGHs can be designed to control two RLC-SLMs, respectively. Finally, the desired light field with arbitrary polarization state can be processed or obtained. This method can greatly improve the flexibility of the original device and the energy utilization efficiency of the light field. Theoretical analysis and practical findings demonstrate that it is possible to regulate the complex amplitude of the two orthogonal polarization components of the beam in order to produce vector beams with arbitrary complex amplitude and polarization. As an example, it was successfully verified that the two imaging channels in this method have independent imaging capability, and the radial vector beam and LG vector beam with inhomogeneous helical phase distribution were successfully generated. This approach offers a convenient way for us to investigate the characteristics of other complicated vector beams in actual experiments.
Author Contributions
Writing—original draft preparation, Z.L. and Y.X.; writing—review and editing, W.Z., Q.F., G.L., B.Z. and S.K.; project administration, funding acquisition—Y.X., F.G., Y.W., X.S., S.K. and B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by National Natural Science Foundation of China (61905103); Natural Science Foundation of Shandong Province (ZR2021QF025); National Natural Science Foundation of China (61905104, 62105134); Natural Science Foundation of Shandong Province (ZR2020QF093).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
S. Kumar acknowledge to Double-Hundred Talent Plan of Shandong Province, China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, F.; Yu, H.; Fang, J.; Zhang, M.; Chen, S.; Wang, J.; He, A.; Chen, J. Efficient generation and tight focusing of radially polarized beam from linearly polarized beam with all-dielectric metasurface. Opt. Express 2016, 24, 6656–6664. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.-F.; Zhou, Y.; Wu, H.-W.; Chen, H.-J.; Sheng, Z.-Q.; Qu, J. Focus shaping of the radially polarized Laguerre-Gaussian-correlated Schell-model vortex beams. Opt. Express 2018, 26, 20076–20088. [Google Scholar] [CrossRef]
- Xu, H.-F.; Zhang, R.; Sheng, Z.-Q.; Qu, J. Shaping the focal intensity distribution using a partially coherent radially polarized beam with multiple off-axis vortices. Opt. Express 2020, 28, 28858–28867. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhang, P.; Zhang, X.; Hu, Y.; Chen, Z.; Xu, J. Selective trapping of chiral nanoparticles via vector Lissajous beams. Opt. Express 2022, 30, 3592–3600. [Google Scholar] [CrossRef]
- Liang, Y.; Su, Y.; Li, J.; Yang, C. Optical trapping of Rayleigh particles based on four-petal Gaussian vortex beams. J. Opt. Soc. Am. A 2022, 39, 1378–1384. [Google Scholar] [CrossRef] [PubMed]
- Shang, W.; Xiao, F.; Zhu, W.; Han, L.; Mei, T.; Zhao, J. Characterizing localized surface plasmon resonances using focused radially polarized beam. Appl. Opt. 2019, 58, 5812–5816. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Ji, Z.; Dong, D.; Yang, X.; Xiao, Y.; Gong, Q.; Xi, P.; Shi, K. Super-resolution deep imaging with hollow Bessel beam STED microscopy. Laser Photonics Rev. 2016, 10, 147–152. [Google Scholar] [CrossRef]
- Cheng, K.; Li, Z.; Wu, J.; Hu, Z.-D.; Wang, J. Super-resolution imaging based on radially polarized beam induced superoscillation using an all-dielectric metasurface. Opt. Express 2022, 30, 2780–2791. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Shvedov, V.; Krolikowski, W.; Rode, A. Revealing Local Field Structure of Focused Ultrashort Pulses. Phys. Rev. Lett. 2011, 106, 123901. [Google Scholar] [CrossRef]
- Drevinskas, R.; Zhang, J.; Beresna, M.; Gecevičius, M.; Kazanskii, A.G.; Svirko, Y.P.; Kazansky, P.G. Laser material processing with tightly focused cylindrical vector beams. Appl. Phys. Lett. 2016, 108, 221107. [Google Scholar] [CrossRef]
- Matsusaka, S.; Kozawa, Y.; Sato, S. Micro-hole drilling by tightly focused vector beams. Opt. Lett. 2018, 43, 1542–1545. [Google Scholar] [CrossRef] [PubMed]
- Ge, W.; Xing, C.; Veiko, V.; Li, Z. All-optical, self-focused laser beam array for parallel laser surface processing. Opt. Express 2019, 27, 29261. [Google Scholar] [CrossRef] [PubMed]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Wang, X.-L.; Ding, J.; Ni, W.-J.; Guo, C.-S.; Wang, H.-T. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement. Opt. Lett. 2007, 32, 3549–3551. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Li, X.; Wang, W.; Wang, X.; Sun, W.; Liao, J. Generation and double-slit interference of higher-order vector beams. Appl. Opt. 2013, 52, 8369–8375. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Yang, Y.; Cheng, W.; Zhan, Q. Vectorial optical field generator for the creation of arbitrarily complex fields. Opt. Express 2013, 21, 20692–20706. [Google Scholar] [CrossRef] [PubMed]
- Maluenda, D.; Juvells, I.; Martínez-Herrero, R.; Carnicer, A. Reconfigurable beams with arbitrary polarization and shape distributions at a given plane. Opt. Express 2013, 21, 5432–5439. [Google Scholar] [CrossRef]
- Otte, E.; Schlickriede, C.; Alpmann, C.; Denz, C. Complex light fields enter a new dimension: Holographic modulation of polarization in addition to amplitude and phase. In Proceedings of the SPIE OPTO, San Francisco, CA, USA, 7–12 February 2015; Volume 9379, p. 937908. [Google Scholar]
- Xie, Y.-Y.; Cheng, Z.-J.; Liu, X.; Wang, B.-Y.; Yue, Q.-Y.; Guo, C.-S. Simple method for generation of vector beams using a small-angle birefringent beam splitter. Opt. Lett. 2015, 40, 5109–5112. [Google Scholar] [CrossRef]
- Davis, J.A.; Moreno, I.; Badham, K.; Sánchez-López, M.M.; Cottrell, D.M. Nondiffracting vector beams where the charge and the polarization state vary with propagation distance. Opt. Lett. 2016, 41, 2270–2273. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Ma, C.; Liu, S.; Cheng, H.; Han, L.; Zhao, J. Efficient generation of vector beams by calibrating the phase response of a spatial light modulator. Appl. Opt. 2017, 56, 4956–4960. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Liu, S.; Cheng, H.; Han, L.; Wu, D.; Zhao, J. Generation and self-healing of vector Bessel-Gauss beams with variant state of polarizations upon propagation. Opt. Express 2017, 25, 5821–5831. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Li, Y.; Jia, W.; Zhou, J.; Zhao, Y.; Fu, Y.; Wang, J. Generation of arbitrary vector vortex beams based on the dual-modulation method. Appl. Opt. 2019, 58, 1508–1513. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Yao, L.; Pang, Y.; Xia, J. Flexible and high-efficiency generation of arbitrary vector vortex beams on hybrid-order Poincaré sphere. Chin. Opt. Lett. 2018, 16, 092601. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, Z.; Ding, J.; Wang, H.-T. Single ultra-high-definition spatial light modulator enabling highly efficient generation of fully structured vector beams. Appl. Opt. 2019, 58, 6591–6596. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Cai, Y.; Zhang, Y.; Yan, S.; Zhou, M.; Li, M.; Yao, B. Compact optical module to generate arbitrary vector vortex beams. Appl. Opt. 2020, 59, 8932–8938. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Qi, S.; Zhang, Y.; Li, P.; Wu, D.; Han, L.; Zhao, J. Highly efficient generation of arbitrary vector beams with tunable polarization, phase, and amplitude. Photonics Res. 2018, 6, 228. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).