Plasmonic Surface Lattice Resonances in Suspended Symmetric Double-Layer Gratings
Abstract
1. Introduction
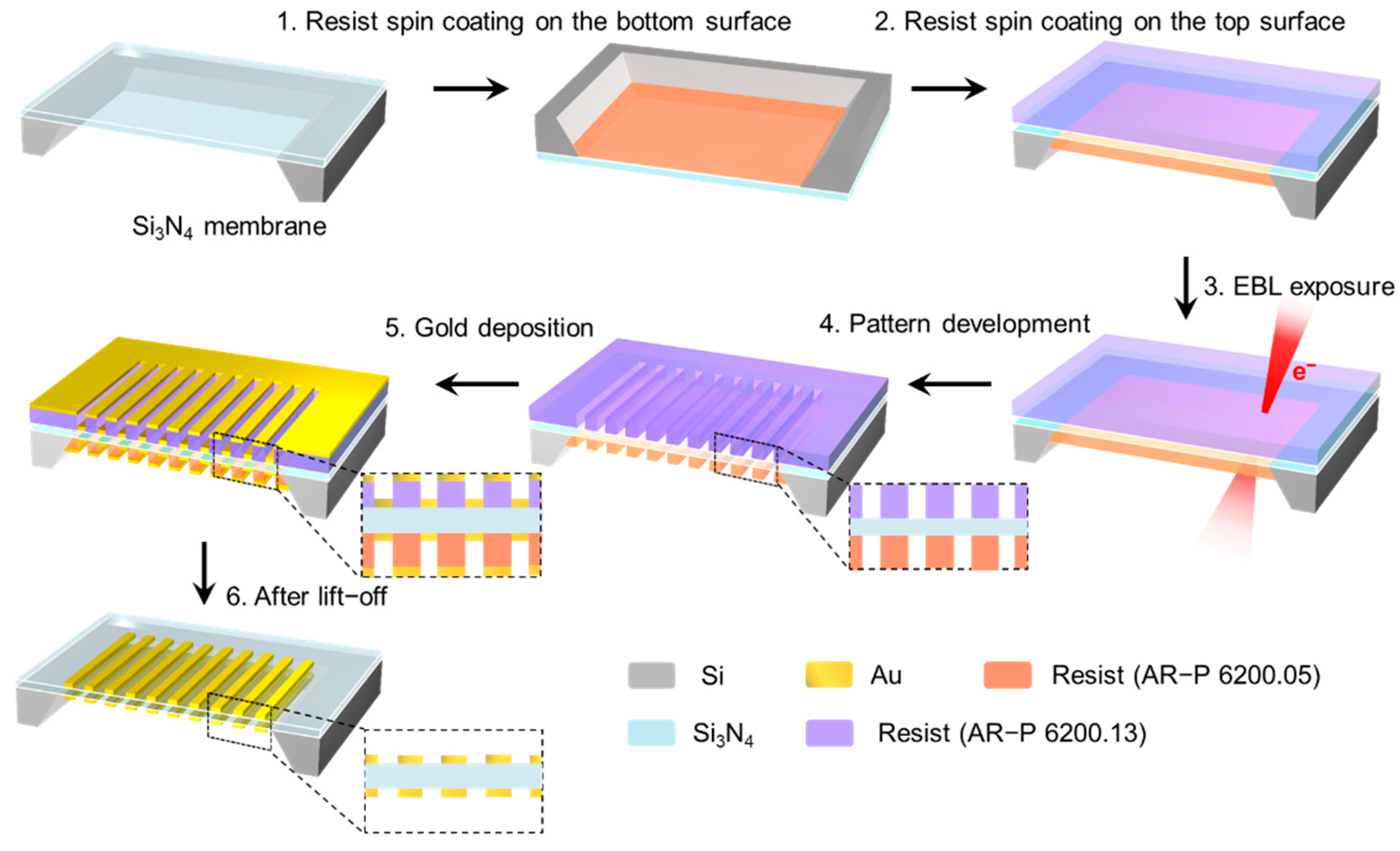
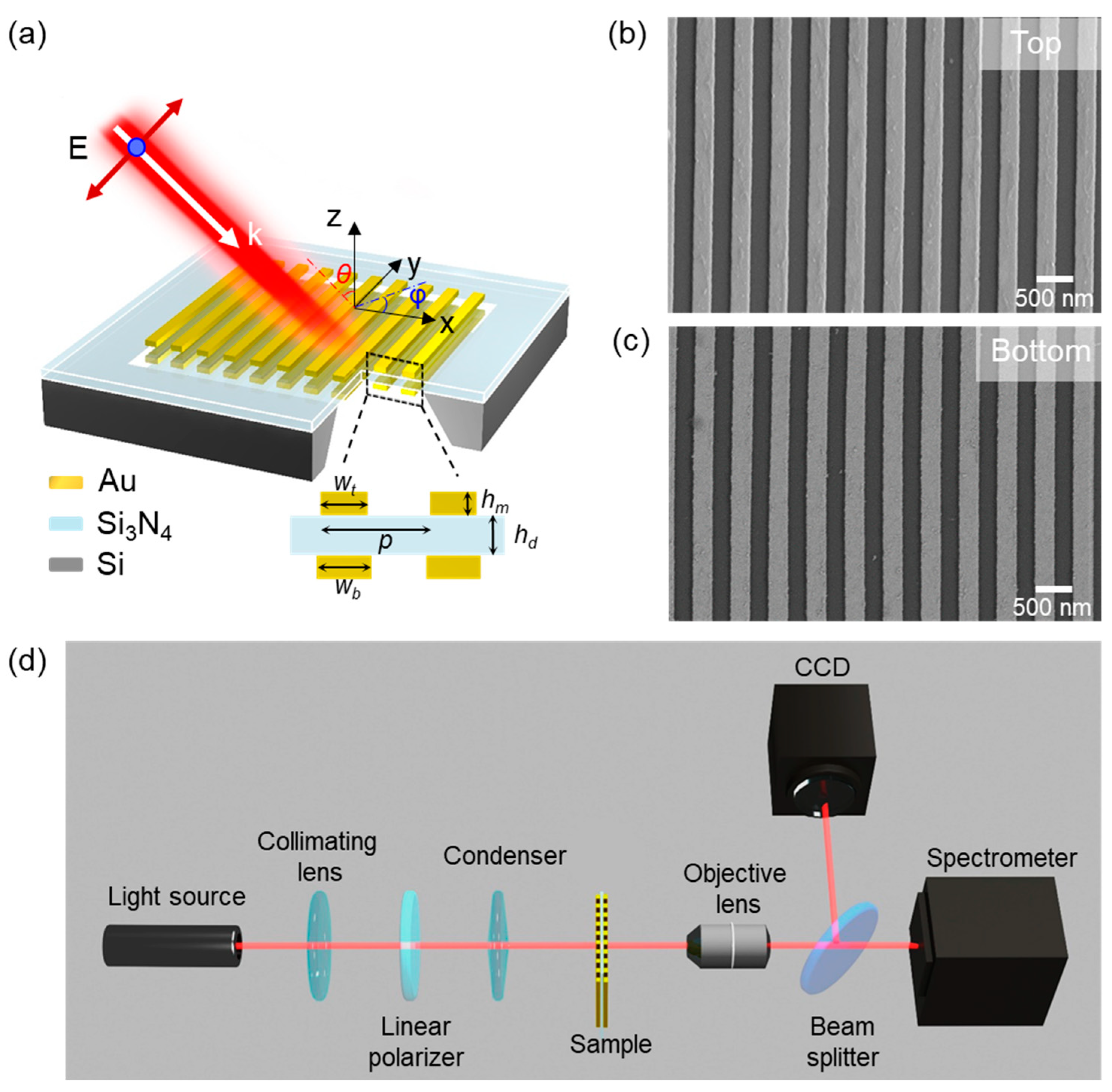
2. Fabrication of Suspended Double-Layer Gratings
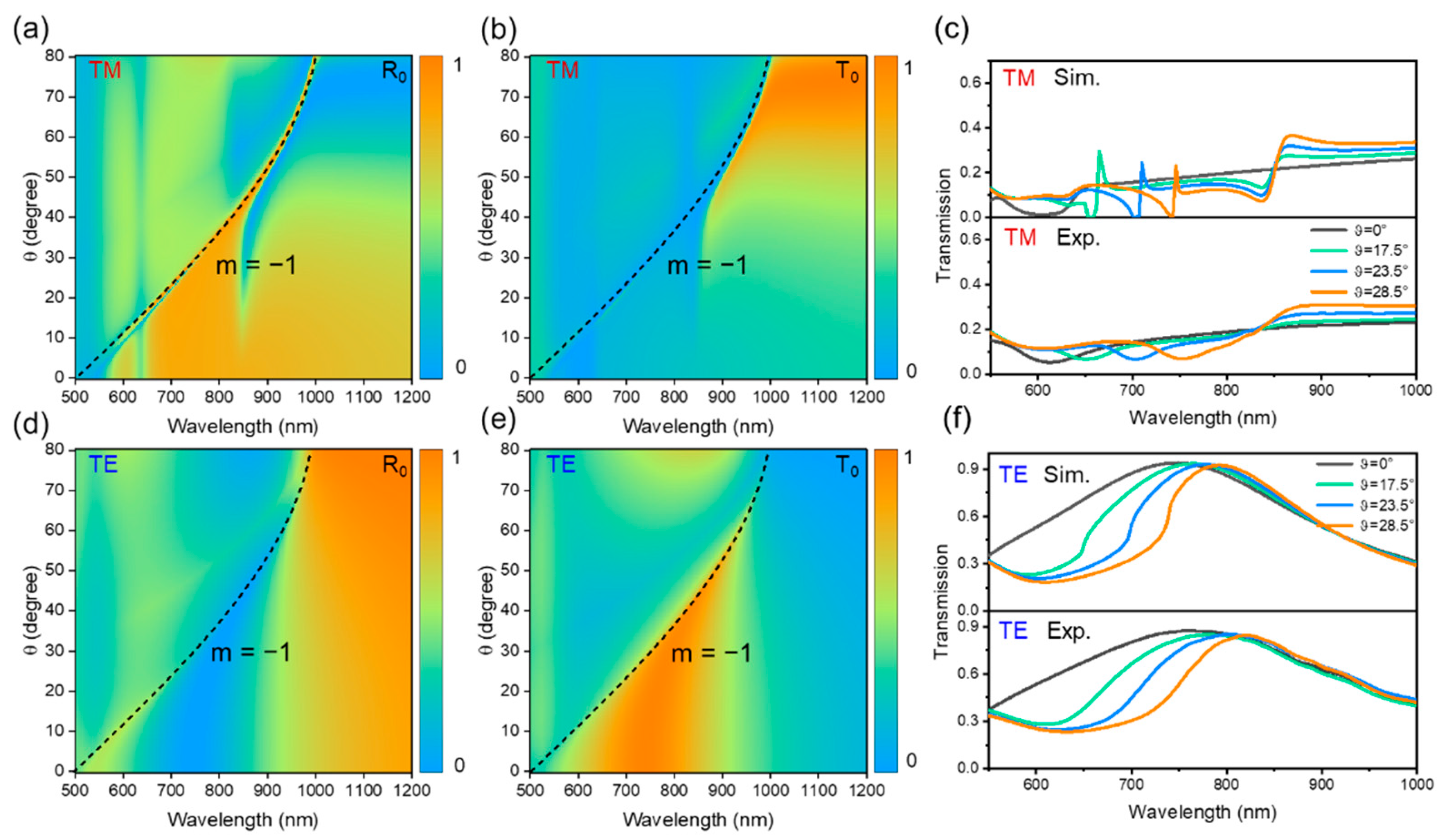
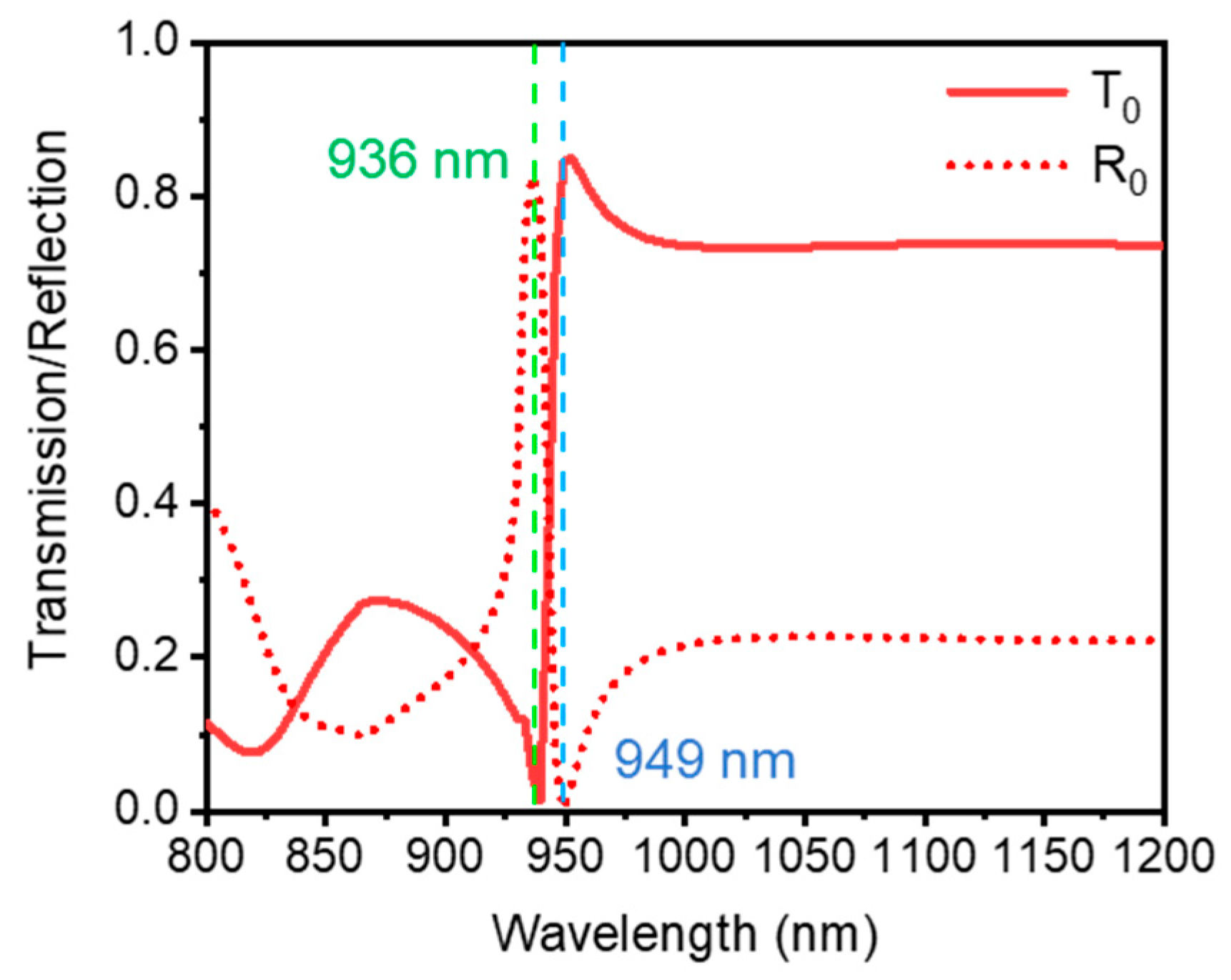
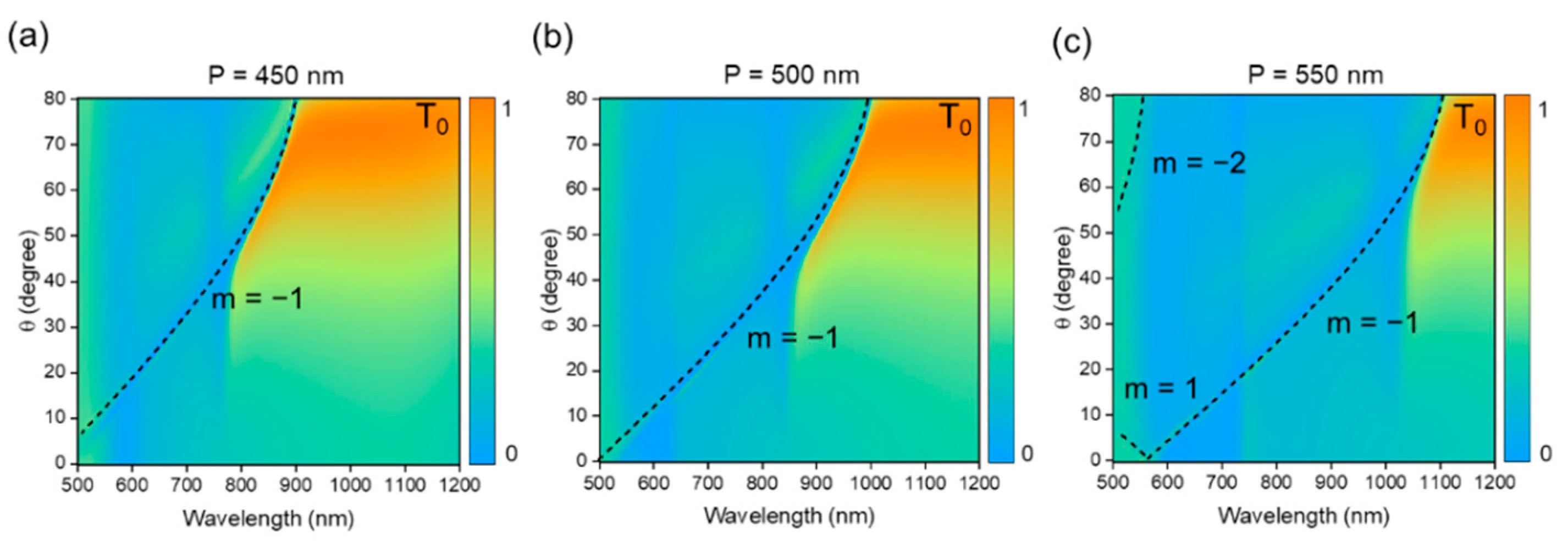
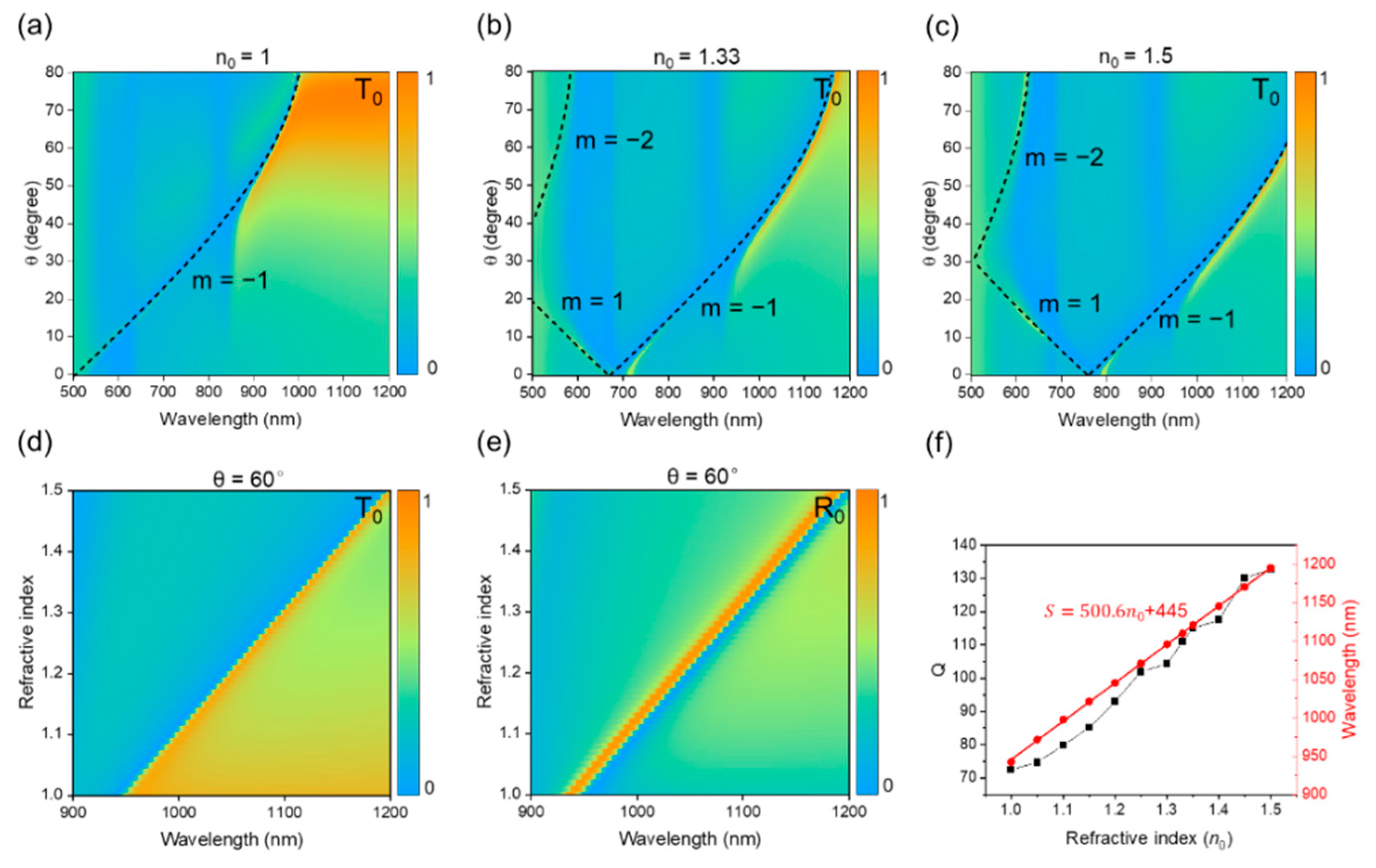
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ramezani, M.; Väkeväinen, A.I.; Törmä, P.; Rivas, J.G.; Odom, T.W. The rich photonic world of plasmonic nanoparticle arrays. Mater. Today 2018, 21, 303–314. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Grigorenko, A.N. Extremely narrow plasmon resonances based on diffraction coupling of localized plasmons in arrays of metallic nanoparticles. Phys. Rev. Lett. 2008, 101, 087403. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; He, H.; Xiao, D.; Yin, S.; Ji, W.; Jiang, S.; Luo, D.; Wang, B.; Liu, Y. Recent advances of plasmonic nanoparticles and their applications. Materials 2018, 11, 1833. [Google Scholar] [CrossRef] [PubMed]
- Goerlitzer, E.S.A.; Mohammadi, R.; Nechayev, S.; Volk, K.; Rey, M.; Banzer, P.; Karg, M.; Vogel, N. Chiral surface lattice resonances. Adv. Mater. 2020, 32, 202001330. [Google Scholar] [CrossRef]
- Auguié, B.; Barnes, W.L. Collective resonances in gold nanoparticle arrays. Phys. Rev. Lett. 2008, 101, 143902. [Google Scholar] [CrossRef] [PubMed]
- Ross, M.B.; Mirkin, C.A.; Schatz, G.C. Optical properties of one-, two-, and three-dimensional arrays of plasmonic nanostructures. J. Phys. Chem. C 2016, 120, 816–830. [Google Scholar] [CrossRef]
- Wang, D.; Guan, J.; Hu, J.; Bourgeois, M.R.; Odom, T.W. Manipulating light-matter interactions in plasmonic nanoparticle lattices. Acc. Chem. Res. 2019, 52, 2997–3007. [Google Scholar] [CrossRef]
- Hakala, T.K.; Rekola, H.T.; Väkeväinen, A.I.; Martikainen, J.P.; Nečada, M.; Moilanen, A.J.; Törmä, P. Lasing in dark and bright modes of a finite-sized plasmonic lattice. Nat. Commun. 2017, 8, 13687. [Google Scholar] [CrossRef]
- Wang, D.; Yang, A.; Wang, W.; Hua, Y.; Schaller, R.D.; Schatz, G.C.; Odom, T.W. Band-edge engineering for controlled multi-modal nanolasing in plasmonic superlattices. Nat. Nanotechnol. 2017, 12, 889–894. [Google Scholar] [CrossRef]
- Chu, A.; He, H.; Yin, Z.; Peng, R.; Yang, H.; Gao, X.; Luo, D.; Chen, R.; Xing, G.; Liu, Y.J. Plasmonically enhanced upconversion luminescence via holographically formed silver nanogratings. ACS Appl. Mater. Interfaces 2020, 12, 1292–1298. [Google Scholar] [CrossRef]
- Czaplicki, R.; Kiviniemi, A.; Laukkanen, J.; Lehtolahti, J.; Kuittinen, M.; Kauranen, M. Surface lattice resonances in second-harmonic generation from metasurfaces. Opt. Lett. 2016, 41, 2684–2687. [Google Scholar] [CrossRef]
- Michaeli, L.; Keren-Zur, S.; Avayu, O.; Suchowski, H.; Ellenbogen, T. Nonlinear surface lattice resonance in plasmonic nanoparticle arrays. Phys. Rev. Lett. 2017, 118, 243904. [Google Scholar] [CrossRef] [PubMed]
- Hooper, D.C.; Kuppe, C.; Wang, D.; Wang, W.; Guan, J.; Odom, T.W.; Valev, V.K. Second harmonic spectroscopy of surface lattice resonances. Nano Lett. 2019, 19, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Gutha, R.R.; Sadeghi, S.M.; Sharp, C.; Wing, W.J. Biological sensing using hybridization phase of plasmonic resonances with photonic lattice modes in arrays of gold nanoantennas. Nanotechnology 2017, 28, 355504. [Google Scholar] [CrossRef]
- Danilov, A.; Tselikov, G.; Wu, F.; Kravets, V.G.; Ozerov, I.; Bedu, F.; Grigorenko, A.N.; Kabashin, A.V. Ultra-narrow surface lattice resonances in plasmonic metamaterial arrays for biosensing applications. Biosens. Bioelectron. 2018, 104, 102–112. [Google Scholar] [CrossRef]
- Gutha, R.R.; Sadeghi, S.M.; Wing, W.J. Ultrahigh refractive index sensitivity and tunable polarization switching via infrared plasmonic lattice modes. Appl. Phys. Lett. 2017, 110, 153103. [Google Scholar] [CrossRef]
- Li, G.; Shen, Y.; Xiao, G.; Jin, C. Double-layered metal grating for high-performance refractive index sensing. Opt. Express 2015, 23, 8995–9003. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Wang, J.; Ma, Z.; Kong, D.; Jiang, S.; Luo, D.; Liu, Y.J. Graphene oxide-coated metal–insulator–metal SERS substrates for trace melamine detection. Nanomaterials 2022, 12, 1202. [Google Scholar] [CrossRef]
- Li, J.; Ma, Y.; Gu, Y.; Khoo, I.C.; Gong, Q. Large spectral tunability of narrow geometric resonances of periodic arrays of metallic nanoparticles in a nematic liquid crystal. Appl. Phys. Lett. 2011, 98, 213101. [Google Scholar] [CrossRef]
- Thackray, B.D.; Thomas, P.A.; Auton, G.H.; Rodriguez, F.J.; Marshall, O.P.; Kravets, V.G.; Grigorenko, A.N. Super-narrow, extremely high quality collective plasmon resonances at telecom wavelengths and their application in a hybrid graphene-plasmonic modulator. Nano Lett. 2015, 15, 3519–3523. [Google Scholar] [CrossRef]
- Lee, U. Spectral Element Method in Structural Dynamics; John Wiley & Sons Asia: Singapore, 2009. [Google Scholar]
- Mahariq, I.; Kurt, H. On- and off-optical-resonance dynamics of dielectric microcylinders under plane wave illumination. J. Opt. Soc. Am. B 2015, 32, 1022–1030. [Google Scholar] [CrossRef]
- Mahariq, I.; Giden, I.H.; Alboon, S.; Aly, W.H.F.; Youssef, A.; Kurt, H. Investigation and analysis of acoustojets by spectral element method. Mathematics 2022, 10, 3145. [Google Scholar] [CrossRef]
- Reshef, O.; Saad-Bin-Alam, M.; Huttunen, M.J.; Carlow, G.; Sullivan, B.T.; Ménard, J.M.; Dolgaleva, K.; Boyd, R.W. Multiresonant high-Q plasmonic metasurfaces. Nano Lett. 2019, 19, 6429–6434. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, S.M.; Wing, W.J.; Campbell, Q. Tunable plasmonic-lattice mode sensors with ultrahigh sensitivities and figure-of-merits. J. Appl. Phys. 2016, 119, 244503. [Google Scholar] [CrossRef]
- Yang, X.; Xiao, G.; Lu, Y.; Li, G. Narrow plasmonic surface lattice resonances with preference to asymmetric dielectric environment. Opt. Express 2019, 27, 25384. [Google Scholar] [CrossRef] [PubMed]
- Khlopin, D.; Laux, F.; Wardley, W.P.; Martin, J.; Wurtz, G.A.; Plain, J.; Bonod, N.; Zayats, A.V.; Dickson, W.; Gérard, D. Lattice modes and plasmonic linewidth engineering in gold and aluminum nanoparticle arrays. J. Opt. Soc. Am. B 2017, 34, 691–700. [Google Scholar] [CrossRef]
- Vecchi, G.; Giannini, V.; Gómez Rivas, J. Surface modes in plasmonic crystals induced by diffractive coupling of nanoantennas. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 80, 201401. [Google Scholar] [CrossRef]
- Li, G.H.Y.; Li, G. Necessary conditions for out-of-plane lattice plasmons in nanoparticle arrays. J. Opt. Soc. Am. B 2019, 36, 805–810. [Google Scholar] [CrossRef]
- Auguié, B.; Barnes, W.L. Diffractive coupling in gold nanoparticle arrays and the effect of disorder. Opt. Lett. 2009, 34, 401–403. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Kabashin, A.V.; Grigorenko, A.N. Sensitivity of collective plasmon modes of gold nanoresonators to local environment. Opt. Lett. 2010, 35, 956–958. [Google Scholar] [CrossRef]
- Si, G.; Zhao, Y.; Lv, J.; Lu, M.; Wang, F.; Liu, H.; Xiang, N.; Huang, T.J.; Danner, A.J.; Teng, J.; et al. Reflective plasmonic color filters based on lithographically patterned silver nanorod arrays. Nanoscale 2013, 5, 6243–6248. [Google Scholar] [CrossRef] [PubMed]
- Leong, E.S.P.; Deng, J.; Khoo, E.H.; Wu, S.; Phua, W.K.; Liu, Y.J. Fabrication of suspended, three-dimensional chiral plasmonic nanostructures with single-step electron-beam lithography. RSC Adv. 2015, 5, 96366–96371. [Google Scholar] [CrossRef]
- Cen, M.; Wang, J.; Liu, J.; He, H.; Li, K.; Cai, W.; Cao, T.; Liu, Y.J. Ultrathin suspended chiral metasurfaces for enantiodiscrimination. Adv. Mater. 2022, 34, 2203956. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Cen, M.; Wang, J.; Xu, Y.; Liu, J.; Cai, W.; Kong, D.; Li, K.; Luo, D.; Cao, T.; et al. Plasmonic chiral metasurface-induced upconverted circularly polarized luminescence from achiral upconversion nanoparticles. ACS Appl. Mater. Interfaces 2022, in press. [Google Scholar] [CrossRef]
- Rodriguez, S.R.K.; Rivas, J.G. Surface lattice resonances strongly coupled to rhodamine 6G excitons: Tuning the plasmon-exciton-polariton mass and composition. Opt. Express 2013, 21, 27411–27421. [Google Scholar] [CrossRef] [PubMed]
- Leong, E.S.P.; Wu, S.; Zhang, N.; Loh, W.W.; Khoo, E.H.; Si, G.Y.; Dai, H.T.; Liu, Y.J. Optical properties of ultrafine line and space polymeric nanogratings coated with metal and metal-dielectric-metal thin films. Nanotechnology 2014, 25, 055203. [Google Scholar] [CrossRef]
- Liu, Y.J.; Si, G.Y.; Leong, E.S.P.; Xiang, N.; Danner, A.J.; Teng, J.H. Light-driven plasmonic color filters by overlaying photoresponsive liquid crystals on gold annular aperture arrays. Adv. Mater. 2012, 24, 131–135. [Google Scholar] [CrossRef]
- Si, G.; Zhao, Y.; Lv, J.; Wang, F.; Liu, H.; Teng, J.; Liu, Y.J. Direct and accurate patterning of plasmonic nanostructures with ultrasmall gaps. Nanoscale 2013, 5, 4309–4313. [Google Scholar] [CrossRef]
- Lv, J.; Khoo, E.H.; Leong, E.S.P.; Hu, L.; Jiang, X.; Li, Y.; Luo, D.; Si, G.; Liu, Y.J. Maskless fabrication of slanted annular aperture arrays. Nanotechnology 2017, 28, 225302. [Google Scholar] [CrossRef]
- Cattoni, A.; Ghenuche, P.; Haghiri-Gosnet, A.M.; Decanini, D.; Chen, J.; Pelouard, J.L.; Collin, S. λ3/1000 plasmonic nanocavities for biosensing fabricated by soft UV nanoimprint lithography. Nano Lett. 2011, 11, 3557–3563. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Evlyukhin, A.B.; Goņalves, M.R.; Reinhardt, C.; Koroleva, A.; Arnedillo, M.L.; Kiyan, R.; Marti, O.; Chichkov, B.N. Laser fabrication of large-scale nanoparticle arrays for sensing applications. ACS Nano 2011, 5, 4843–4849. [Google Scholar] [CrossRef]
- Yin, Z.; Shi, Y.; Cen, M.; Cao, T.; Xu, C.; Luo, D.; Li, G.; Liu, Y.J. Vectorial holography-mediated growth of plasmonic metasurfaces. Sci. Bull. 2021, 66, 1518–1524. [Google Scholar] [CrossRef]
- Auguié, B.; Bendaña, X.M.; Barnes, W.L.; García De Abajo, F.J. Diffractive arrays of gold nanoparticles near an interface: Critical role of the substrate. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 155447. [Google Scholar] [CrossRef]
- Bin-Alam, M.S.; Reshef, O.; Mamchur, Y.; Alam, M.Z.; Carlow, G.; Upham, J.; Sullivan, B.T.; Ménard, J.M.; Huttunen, M.J.; Boyd, R.W.; et al. Ultra-high-Q resonances in plasmonic metasurfaces. Nat. Commun. 2021, 12, 974. [Google Scholar] [CrossRef]
- Humphrey, A.D.; Barnes, W.L. Plasmonic surface lattice resonances on arrays of different lattice symmetry. Phys. Rev. B-Condens. Matter Mater. Phys. 2014, 90, 075404. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constant of the Nobel Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Zheng, F.; Chen, Z.; Zhang, J. A finite-difference time-domain method without the courant stability conditions. IEEE Microw. Guid. Wave Lett. 1999, 9, 441–443. [Google Scholar] [CrossRef]
- Zhou, W.; Odom, T.W. Tunable subradiant lattice plasmons by out-of-plane dipolar interactions. Nat. Nanotechnol. 2011, 6, 423–427. [Google Scholar] [CrossRef] [PubMed]
- Hua, Y.; Fumani, A.K.; Odom, T.W. Tunable lattice plasmon resonances in 1D nanogratings. ACS Photonics 2019, 6, 322–326. [Google Scholar] [CrossRef]
- Fang, X.; Xiong, L.; Shi, J.; Li, G. High-Q quadrupolar plasmonic lattice resonances in horizontal metal–insulator–metal gratings. Opt. Lett. 2021, 46, 1546–1549. [Google Scholar] [CrossRef] [PubMed]
- Sung, J.; Hicks, E.M.; Van Duyne, R.P.; Spears, K. Nanoparticle spectroscopy: Plasmon coupling in finite-sized two-dimensional arrays of cylindrical silver nanoparticles. J. Phys. Chem. C 2008, 112, 4091–4096. [Google Scholar] [CrossRef]
- Nisar, M.S.; Kang, S.; Zhao, X. Photothermal effect in plasmonic nanotip for LSPR sensing. Sensors 2020, 20, 671. [Google Scholar] [CrossRef]
- Baffou, G.; Quidant, R.; García De Abajo, F.J. Nanoscale control of optical heating in complex plasmonic systems. ACS Nano 2010, 4, 709–716. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cen, M.; Wang, J.; Liu, J.; Li, Y.; Cai, W.; Kong, D.; Luo, D.; Cao, T.; Liu, Y.J. Plasmonic Surface Lattice Resonances in Suspended Symmetric Double-Layer Gratings. Photonics 2022, 9, 890. https://doi.org/10.3390/photonics9120890
Cen M, Wang J, Liu J, Li Y, Cai W, Kong D, Luo D, Cao T, Liu YJ. Plasmonic Surface Lattice Resonances in Suspended Symmetric Double-Layer Gratings. Photonics. 2022; 9(12):890. https://doi.org/10.3390/photonics9120890
Chicago/Turabian StyleCen, Mengjia, Jiawei Wang, Jianxun Liu, Ye Li, Wenfeng Cai, Delai Kong, Dan Luo, Tun Cao, and Yan Jun Liu. 2022. "Plasmonic Surface Lattice Resonances in Suspended Symmetric Double-Layer Gratings" Photonics 9, no. 12: 890. https://doi.org/10.3390/photonics9120890
APA StyleCen, M., Wang, J., Liu, J., Li, Y., Cai, W., Kong, D., Luo, D., Cao, T., & Liu, Y. J. (2022). Plasmonic Surface Lattice Resonances in Suspended Symmetric Double-Layer Gratings. Photonics, 9(12), 890. https://doi.org/10.3390/photonics9120890







