The Dynamics of Multi-Peak Pulsed Generation in a Q-Switched Thulium-Doped Fiber Laser

Abstract

We demonstrate a detailed theoretical and experimental study of a thulium-doped fiber laser being Q-switched by means of an acousto-optic modulator. The processes leading to the generation of discontinuous multi-peak pulses with an energy of up to 5 μJ and a nanosecond structure are described. The dynamics of the multi-peak structure’s evolution is demonstrated and a method of switching to a single-pulse mode is proposed.

1. Introduction

Today, fiber lasers and amplifiers are applied in a variety of ways due to their high efficiency, good emission quality and compactness [1,2]. The first thulium-doped (Tm³⁺) silica-based fiber laser with pumping at λ_p = 810 nm and generating in the spectral range of λ_s = 1780–2060 nm was experimentally demonstrated in 1990 [3], and since then, these systems have been continuously improved [4,5,6]. These lasers and amplifiers are used in laser surgery [7,8,9], for pumping holmium active elements [10,11,12], as a part of measuring systems [13] and laser LIDARs [14], in scientific research and in other applications [15,16]. Thulium-doped fibers with another glass matrix or structure [17] can be used to operate in the spectral range over the 2000 nm thereby expanding the application area of these laser systems [18,19,20].

To obtain pulsed generation with high amplitude, the modes of periodic active gain modulation [21] and the Q-switching of cavity [22] are often used. The amplitude depends on the pulse repetition rate, which is set depending on the purpose of the experiment or a particular way of laser application. As a rule, a higher pulse repetition rate contributes tolower amplitude, since during the time between pulses, the medium pumping may not completely restore the inversion. The increasing rate of the light field in the modulated cavity depends on both the properties of the active medium and the switching time of its Q-factor T_q. The lower T_q, the faster the field increases, the higher pulse amplitude becomes, and the energy removal enlarges. Thus, the Q-switching mode parameters affect the laser efficiency.

In fiber lasers, the electro-optic [23] and acousto-optic modulators (AOM) are used to obtain Q-switching. The latter method is very widespread and can handle higher input optical power. Thus, active Q-switching with AOM is used to obtain pulses with durations ranging from a few to tens of ns and repetition rates from 1 to hundreds of kHz in a wide spectral range from 1 to 3 μm [24,25]. Typically, the output power of actively Q-switched fiber lasers is limited by the power density that the optical modulators can handle. The highest peak power and energy of an all-fiber laser of 5 kW and 0.2 mJ with a 20 kHz repetition rate was obtained in a linearly polarized ytterbium-doped fiber laser at a wavelength of 1064 nm [26]. A recent paper [27] presents a broad review and the current state of research on the actively Q-switched all-fiber lasers. Active Q-switching technologies and Q-factor optical modulators were considered in detail.

The best AOMs models allow for turning on the quality factor for the time Tq of 10 ns and below. If the turn-on time T_q is shorter or comparable with the cavity round-trip time 2T_c, a multi-peak pulse structure appearance is possible [28,29]: the output pulse splits into several pulses of different amplitude, separated by an interval close to 2T_c. This structure of the output pulse decreases the peak power, does not meet the requirements of some tasks and is not always acceptable for practical applications. So, in this case the problem of optimizing the operation mode of the modulator arises. The desired pulse shape can be obtained using external modulation with the supply of a given pulse shape. In addition, a single-pulse regime can be obtained using saturable absorbers, but in this case, the pulse repetition rate depends on the pump power.

The dynamics of thulium laser generation, as well as the capabilities of multi-peak structure control can be analyzed using numerical simulation. In most scientific studies, numerical models of the active medium based on velocity equations quite correctly take into account excitation, relaxation, and cross-relaxation processes [4,30,31]. At the same time, to describe the pumping and generation fields, the cited studies use quasi-stationary approximation, in which it is assumed that the field distribution at each time moment corresponds to the distribution of populations. The use of such models is suitable for studying stationary generation modes, but it is impossible to correctly describe the generation dynamics on their basis. For the intensities of the traveling pump waves and the amplified spontaneous emission (ASE), the radiation transfer equations should be used, as in [22,28] for ytterbium-doped fiber lasers and for bismuth-doped fiber lasers in [32,33]. Additionally, the equations for populations should be solved at each point of the medium.

In thulium fiber lasers, which have a typical active medium length of several meters [1,4,32,34], the intermediate case is usually implemented when T_q ~ 2T_c. With such a ratio of the indicated times, it is difficult to predict the temporal structure of the output radiation in the Q-switched mode. The purpose of this work is a more detailed experimental and theoretical study of an active medium and the generation dynamics of the thulium-doped fiber laser. The pattern of the output radiation formation from the ASE and consideration of the conditions for the peak structure appearance are revealed on the basis of an improved numerical model, in which radiation transfer equations are used, and the broadband and narrowband components of the ASE are calculated separately. A good agreement with the experimental data on the intensities and generation pulse shapes indicates the correctness of the obtained simulation results. The comparison results allow us to recommend a method of obtaining periodic single output pulses of increased amplitude.

2. Experiment

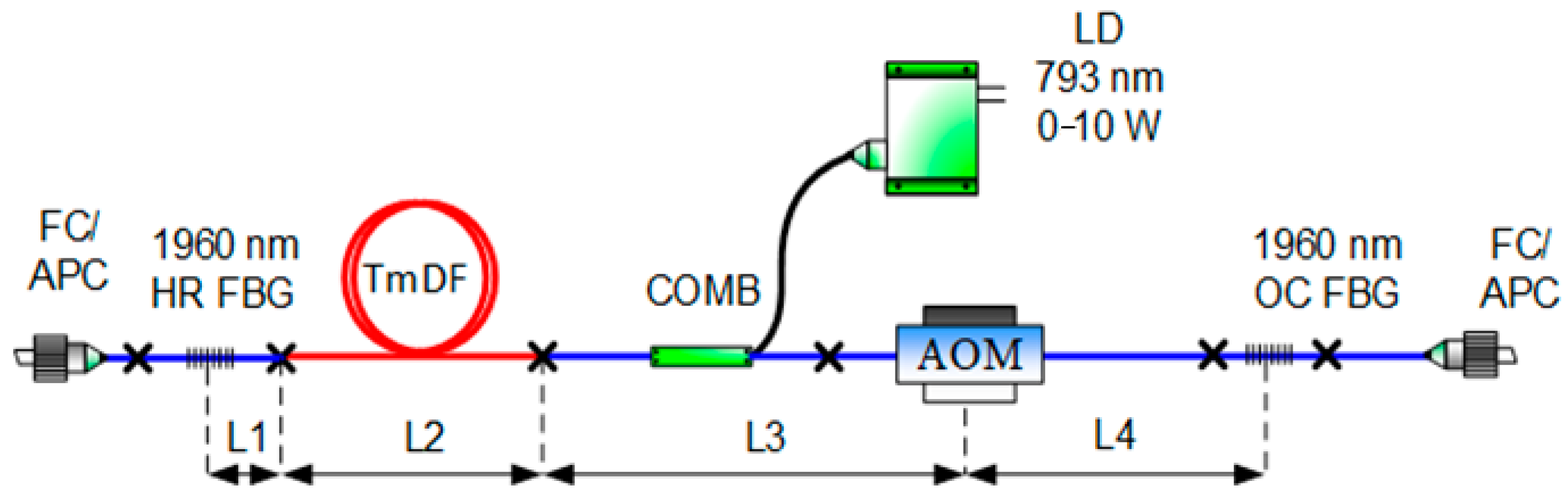
Figure 1 shows the optical scheme of the thulium-doped fiber laser. A multimode laser diode (LD, manufactured by BWT) with a fiber output was used to pump the active fiber. The central wavelength of radiation reached 793 nm, and the maximum output power was up to 10 W. The input of pump radiation was injected into the active fiber using a pump and signal combiner (COMB). The double-clad silica-based fiber doped with thulium ions (TmDF, Tm800-10/125DC) was used as an active medium. The length of Tm-doped fiber was 5 m, core diameter d_core = 10 µm and inner cladding diameter d_clad = 127 µm. Dissipative losses for the pump and signal wavelengths were θ_p = 1.2 × 10⁻⁴ cm⁻¹ and θ_s = 0.23 × 10⁻⁴ cm⁻¹, accordingly at low light intensity. The active ion concentration was calculated from the measured absorption of a weak signal at a wavelength of 793 nm, introduced into the cladding, as in [26]. The resulting concentration was obtained as N = 3 × 10²⁰ cm⁻³.

The laser cavity was formed by two fiber Bragg gratings with a reflection peak at a wavelength of 1960 nm and reflection coefficients R₁ = 96% (HR FBG) and R₂ = 30% (OC FBG), inscribed by femtosecond laser pulses [35]. The cavity includes sections of passive fiber with lengths L₁ = 0.5 m, L₃ = 4 m, L₄ = 1.5 m. Connection losses between active and passive fibers depended on the quality of splices. Splicing losses θ_m were estimated as 0.5–1.5 dB. The acousto-optic modulator (AOM MT80-FIR40-FIO-SM5-J1-A-VSF with driver MODA80-B4-34, manufactured by AA Opto-Electronic) of traveling wave was placed inside the cavity to achieve Q-switching mode. The frequency of the ultrasonic wave was 80 MHz. Electric pulses with an amplitude of 5 V with such a carrier frequency were applied to the modulator and could vary in duration and repetition rate. The minimum light modulation front experimentally measured in this modulator was 40 ns and could be increased by increasing the envelope front of the electrical pulses. The total diffraction, input and output losses at a wavelength of 1960 nm were measured experimentally and amounted to 3.42 dB.

During the experiments, the temporal, spectral and energy parameters of the laser radiation were measured. The spectra were measured using an optical spectrum analyzer Yokogawa AQ6375B with a resolution of 0.1 nm. The time parameters of pulsed radiation were analyzed using an oscilloscope (Tektronix MDO3052 500 MHz) and photodetector (Thorlabs PDA 10D2 900–2600 nm) with a maximum time of 23 ns. A pyroelectric meter (Ophir) operating in the range from 1 µJ to 10 mJ and in the spectral range of 0.15–12 μm was used to measure the pulse energy. The average power was measured with a thermoelectric detector (Ophir).

3. Numerical Model

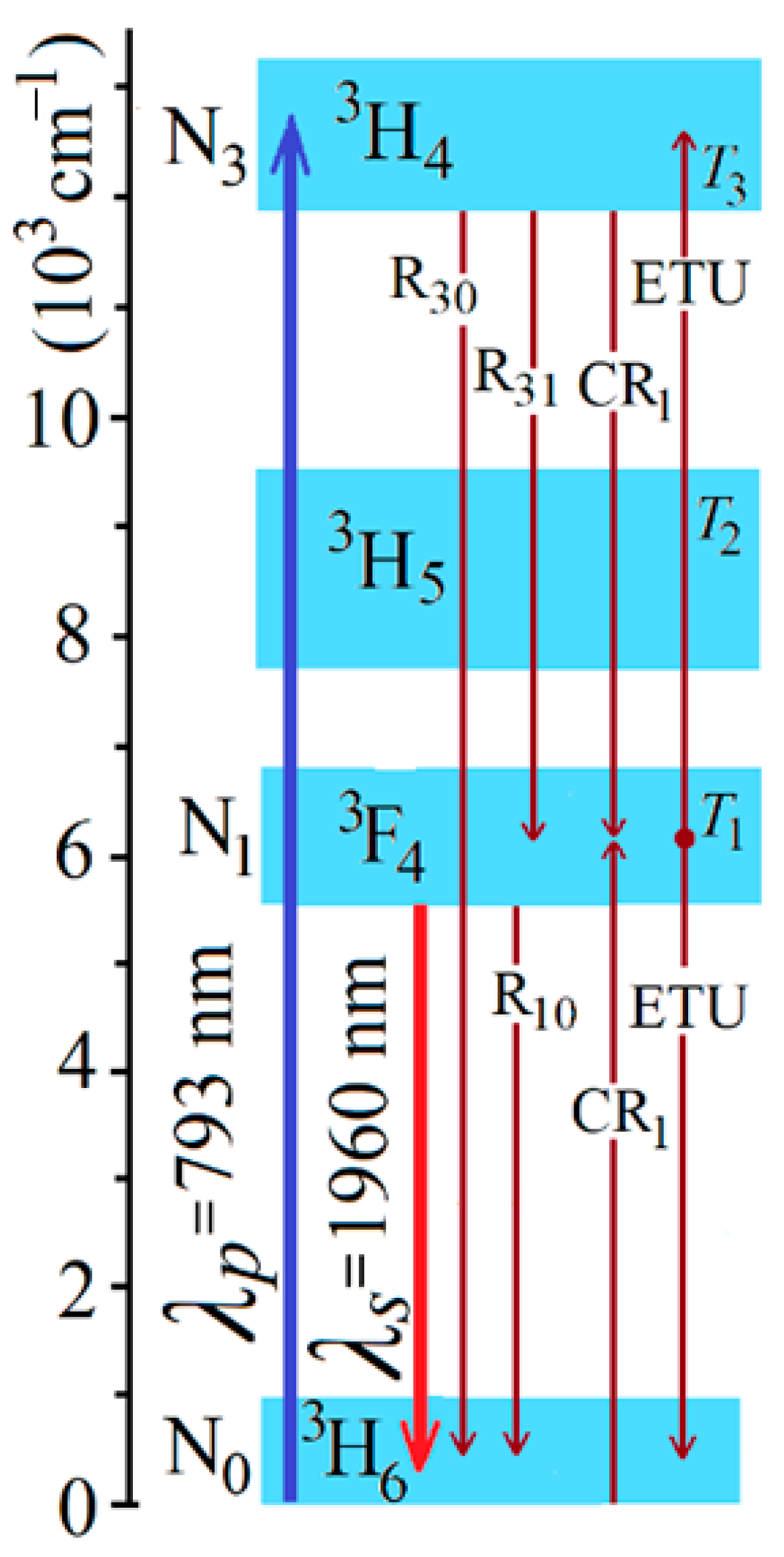
Figure 2 shows a scheme of four lower states of Tm³⁺, consisting of a set of Stark components between which there is a Boltzmann equilibrium. The widths of these states were approximately reconstructed based on the data on absorption cross sections from the ground state and luminescence cross sections shown in [4,30,31]. The relaxation processes R₃₀, R₃₁, R₁₀ and cross-relaxation processes are the basic processes of energy transfer in the active medium. The slowest one is R₁₀. The resonance cross-relaxation process CR₁ has a higher probability than energy transfer upconversion (ETU) [31,36]. Other cross-relaxation processes are less probable. Processes in which the state ³H₅ is involved are not considered separately due to the short lifetime of this state T₂.

In the simplified model of an active medium, only the processes mentioned above are considered, similar to [10,30,31]. Spontaneous emission is conventionally divided into a narrowband component with a spectrum width of reflecting mirrors and a broadband component with a width of the gain band order: Narrowband ASE waves form feedback in the cavity, and broadband waves are not reflected by mirrors. This separation allows us to correctly take into account the effect of the ASE on the inversion at different stages of nonstationary laser operation. In the model, it is assumed that the growth rate of the ASE is determined by the decay rate of the upper laser level and depends on the spatial fraction of the radiation falling into the fiber mode (corresponding coefficient κ_l) and the spectral fraction of the gain band (coefficient κ_s). For the narrowband component, κ_s is approximately calculated as κ_s = Δω_R/Δω_a, where Δω_R is reflection bandwidth of the spectral-selective mirror and Δω_a is the gain bandwidth. For the broadband components, κ_s = 1.

It is appropriate to make the following remark on the numerical model description. In the active fiber of a thulium laser at sufficiently high generation intensity in the Q-switched mode, a nonlinear effect of modulation instability is observed [37]. Two bands, located symmetrically relative to the generation line, appear in the radiation spectrum. Additionally, as the pumping increases, the side band intensity and width increase, but the intensity growth in the lasing line slows down. Experiments [38] have shown that in a fiber with 6 µm core diameter, the impact of this effect on the thulium laser output characteristics becomes noticeable if the pulse peak power exceeds 1 kW. Preliminary experiments showed that in this case, for 10 µm diameter fiber, in the Q-switching mode for a pumping power not exceeding the value of P_p* = 3 W, the peak pulse power should be expected to be about an order of magnitude lower. For this reason, within the framework of the used model, the possibility of the quantitative comparison of simulated and experimental results for the pump power P_p ≤ P_p* should be considered correct ones.

Taking into account the above-mentioned assumptions, the model equations for the level populations and wave intensities in normalized values have the form:

$$\frac{\partial n_1\left(x,\tau \right)}{\partial \tau }=-\frac{n_1\left(x,\tau \right)}{{\tau }_1}+\frac{\beta n_3\left(x,\tau \right)}{{\tau }_3}+2{\kappa }_{3101}·\left[n_3\left(x,\tau \right)n_0\left(x,\tau \right)-{\gamma }_k{n}_1^2\left(x,\tau \right)\left]-{\Gamma }_s{w}_s\left(x,\tau \right)·\right[n_1\left(x,\tau \right)-{\gamma }_s{n}_0\left(x,\tau \right)\right]$$

(1)

$$\frac{\partial n_3\left(x,\tau \right)}{\partial \tau }=-\frac{n_3\left(x,\tau \right)}{{\tau }_3}-{\kappa }_{3101}\cdot \left[n_3\left(x,\tau \right)n_0\left(x,\tau \right)-{\gamma }_k{n}_1^2\left(x,\tau \right)\right]+w_p^{-}\left(x,\tau \right){\gamma }_p{n}_0\left(x,\tau \right)$$

(2)

$$n_0\left(x,\tau \right)=n-n_3\left(x,\tau \right)-n_1\left(x,\tau \right)$$

(3)

$$\frac{\partial w_p^{-}\left(x,\tau \right)}{\partial \tau }-\frac{\partial w_p^{-}\left(x,\tau \right)}{\partial x}=-\left[{\gamma }_p{\Gamma }_p{n}_0\left(x,\tau \right)+L{\theta }_p\right]\cdot w_p^{-}\left(x,\tau \right)$$

(4)

$$\frac{\partial w_s^{+}\left(x,\tau \right)}{\partial \tau }+\frac{\partial w_s^{+}\left(x,\tau \right)}{\partial x}=\left[{\Gamma }_s{n}_1\left(x,\tau \right)-{\Gamma }_s{\gamma }_s{n}_0\left(x,\tau \right)-L{\theta }_s\right]\cdot w_s^{+}\left(x,\tau \right)+\frac{{\kappa }_l{\kappa }_s{n}_1\left(x,\tau \right)}{{\tau }_1}$$

(5)

$$\frac{\partial w_s^{-}\left(x,\tau \right)}{\partial \tau }-\frac{\partial w_s^{-}\left(x,\tau \right)}{\partial x}=\left[{\Gamma }_s{n}_1\left(x,\tau \right)-{\Gamma }_s{\gamma }_s{n}_0\left(x,\tau \right)-L{\theta }_s\right]\cdot w_s^{-}\left(x,\tau \right)+\frac{{\kappa }_l{\kappa }_s{n}_1\left(x,\tau \right)}{{\tau }_1}$$

(6)

$$\frac{\partial {\mathrm{v}}_a^{+}\left(x,\tau \right)}{\partial \tau }+\frac{\partial {\mathrm{v}}_a^{+}\left(x,\tau \right)}{\partial x}=\left[{\Gamma }_s{n}_1\left(x,\tau \right)-{\Gamma }_s{\gamma }_s{n}_0\left(x,\tau \right)-L{\theta }_s\right]\cdot {\mathrm{v}}_a^{+}\left(x,\tau \right)+\frac{{\kappa }_l{n}_1\left(x,\tau \right)}{{\tau }_1}$$

(7)

$$\frac{\partial {\mathrm{v}}_a^{-}\left(x,\tau \right)}{\partial \tau }-\frac{\partial {\mathrm{v}}_a^{-}\left(x,\tau \right)}{\partial x}=\left[{\Gamma }_s{n}_1\left(x,\tau \right)-{\Gamma }_s{\gamma }_s{n}_0\left(x,\tau \right)-L{\theta }_s\right]\cdot {\mathrm{v}}_a^{-}\left(x,\tau \right)+\frac{{\kappa }_l{n}_1\left(x,\tau \right)}{{\tau }_1}$$

(8)

Edge conditions for broadband components ${\mathrm{v}}_a^{-}$(1,τ) = 0, ${\mathrm{v}}_a^{+}$(0,τ) = 0, for narrowband $w_s^{+}$(0,τ) = $R_1{w}_s^{-}\left(0,\tau \right)$, $w_s^{-}$(1,τ) = $R_2{w}_s^{+}\left(1,\tau \right)$. Output intensity $w_{out}=\left(1-R_2\right)w_s^{+}\left(1,\tau \right)$, where R₂(x = 1)—reflection coefficient of the output mirror. The superscript “+” indicates light waves propagating along the positive direction of the X axis (traveling forward), and the superscript “-” indicates the backward light waves propagating.

Table 1. Parameters used in numerical simulation.

Symbol	Parameter
ni (i = 0, 1, 3)	normalized populations
τ1, τ3	characteristic relaxation times of T1 and T3 states
β	parameter determining the fraction of 3H4 level relaxation rate from which the 3F4 level is populated
κ3101	normalized rate constant of CR1 process
${\gamma }_k$	ratio of rate constants of ETU and CR1 processes
Γs	overlap parameter, which reduces the gain in fiber core [26]
${\gamma }_s$	ratio of absorption and emission cross sections at the signal wave-length
${\gamma }_p$	ratio of absorption cross section at the pump wavelength to emission cross section at the signal wavelength
Γp	overlapping factor of the pump
$w_p^{-}$	pump wave
L	total fiber length
θp	dissipative losses at the pump wavelength
θs	dissipative losses at the signal wavelength
$w_s^{\pm }$	narrowband components
$w_s$	sum of narrowband components
${\mathrm{v}}_a^{\pm }$	broadband components
κl	coefficient corresponding to the spatial fraction of the radiation falling into the fiber mode
κs	coefficient corresponding to the spectral fraction of the gain band

provides a description of the parameters used in the equations above. After Table 1, their meanings and methods for determining them are presented.

To determine the above parameters, we used the following expressions and definitions: time τ = t/T_c, where single cavity round trip time is T_c = η_s∙L/c, η_s—refractive index at the signal wavelength, L—total fiber length (fiber segments have the same dimensions as in the experiment); c—speed of light; x = X/L, X—dimensional coordinate along the fiber; τ₁ = T₁/T_c and τ₃ = T₃/T_c—characteristic relaxation times of states; κ₃₁₀₁ = T_c∙k₃₁₀₁/${\sigma }_{es}$·L, k₃₁₀₁—rate constant of the CR₁ process, ${\sigma }_{es}$—emission cross section at the signal wavelength; n_i = N_i·${\sigma }_{es}$∙L (i = 0, 1, 3)—normalized populations, N_i—corresponding dimensional populations; $w_s^{\pm }=P_s^{\pm }·{\sigma }_{es}·T_c/A_{core}$, $P_s^{\pm }$—the power of the corresponding signal waves, A_core—fiber core area; ${\mathrm{v}}_a^{\pm }=P_a^{\pm }·{\sigma }_{es}·T_c/A_{core}$, $P_a^{\pm }$—power of the corresponding broadband ASE waves; $w_p^{-}=P_p^{-}·{\sigma }_{ap}·T_c/A_{clad}$, $P_p^{-}$—pump power, A_clad—fiber cladding area; ${\gamma }_p={\sigma }_{ap}/{\sigma }_{es}$, ${\sigma }_{ap}$—absorption cross section at the pump wavelength; ${\gamma }_s={\sigma }_{as}/{\sigma }_{es}$, ${\sigma }_{as}$—absorption cross section at the signal wavelength, ${\gamma }_k$ = k₁₃₁₀/k₃₁₀₁, k₁₃₁₀—rate constant of the ETU process; β—parameter determining the fraction of ³H₄ level relaxation rate from which the ³F₄ level is populated; Γ_p = A_core/A_clad, Γ_s—overlap parameter, which reduces the gain in fiber core [31]; θ_p and θ_s dissipative losses at the pump and signal wavelengths, respectively.

In simulation, we used characteristics of the single-mode double-clad fiber given in the description of the experimental part. The values of cross sections, characteristic times, constants and fiber parameters with similar characteristics were taken from [4,30,31,34,38]. The values of the absorption and emission cross sections were as follows: ${\sigma }_{ap}$ = 6 × 10⁻²¹ cm², ${\sigma }_{es}$ = 4.2 × 10⁻²¹ cm² and ${\sigma }_{as}$ = 0.1 × 10⁻²¹ cm². Lifetimes of states and cross-relaxation constants: T₃ = 14.2 µs, T₁ = 540 µs, k₃₁₀₁ = 20 × 10⁻¹⁷ cm³/s, k₁₃₁₀ = 2 × 10⁻¹⁷ cm³/s, parameters: β = 0.74, Γ_s = 0.934. The single cavity round trip time was T_c = 53 ns.

4. Features of the Thulium Laser Active Medium

The characteristics of the active medium states, arising both in conditions of the cavity absence or stationary generation, allow for understanding the physical features of the active medium, and as a consequence, evaluating the output laser characteristics and the possibilities for improving them. Thus, by simulation, it is possible to determine how inhomogeneously the main parameters of the medium are distributed along the fiber and to estimate its optimal length. The stationary generation mode provides, for example, data about the total losses in the cavity, individual types of which are not always well known.

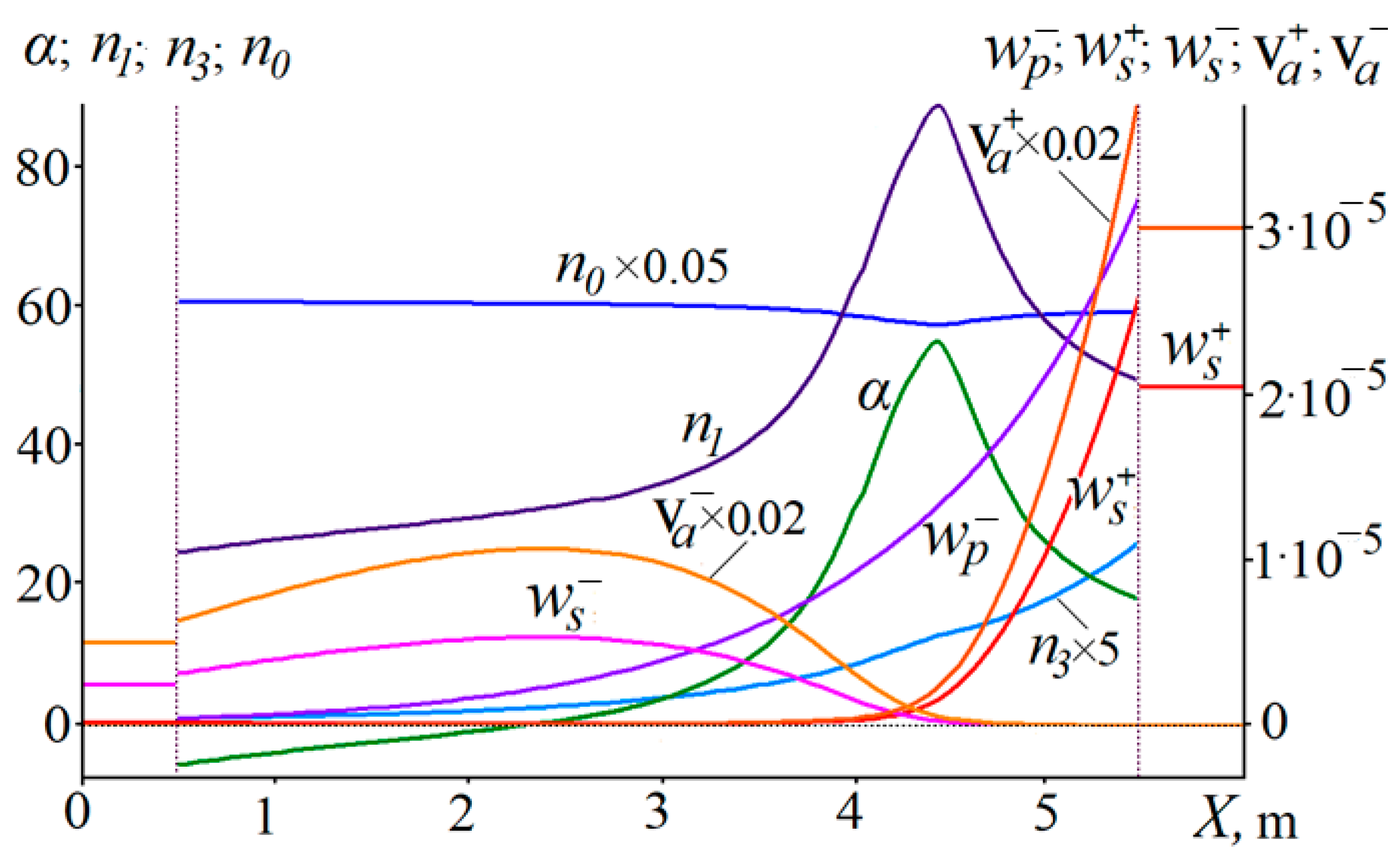
Figure 3 shows the characteristics of the thulium laser active medium (without a cavity) obtained by simulation for pump power $P_p^{-}$ = 5 W. This figure presents the intensities of narrowband $w_s^{+}$, $w_s^{-}$ and broadband ${\mathrm{v}}_a^{+}$, ${\mathrm{v}}_a^{-}$ ASE waves and pump wave $w_p^{-}$ (right scale). There are also the level populations n₀, n₁, n₃ and the gain coefficient α (left scale). Vertical dashed lines at X = 0.5 m and X = 5.5 m show the splice points of active and passive fibers. In these places, due to losses, there are jumps in the intensity of traveling waves. Among all the ASE waves, the highest intensities are observed for ${\mathrm{v}}_a^{+}$ due to the broader spectrum and $w_s^{+}$ due to the reflection of the $w_s^{-}$ wave from the left mirror.

The main feature of the active medium is the extreme gain inhomogeneity α = Γ_s[n₁(x,τ) − γ_sn₀(x,τ)] (at the peak α_max = 55, at the minimum α_min = −6, the average ā = 11.8). During the pump absorption, there is no noticeable medium transparency due to the high relaxation rate of the ³H₄ state. The balance of pumping rates, relaxation processes and ³F₄ level population decrease because the ASE determines the nature of α changes along the fiber. The intensities of the ASE components ${\mathrm{v}}_a^{+}$ and $w_s^{+}$ increase sharply near the right boundary of the active fiber. Therefore, α does not change monotonically along the fiber. The α_max is reached at a distance of about 1.25 m from the pump radiation input.

For the same reasons, even at high pumping level, the population of ³H₄ ground state exceeds the population of ³F₄ state from which the laser transition occurs. A complete inversion between the two groups of Stark component sublevels involved in the generation occurs because the lower state sublevels are located higher than the upper one. In the numerical model, this is represented by the difference in the values of cross sections ${\sigma }_{es}$ and ${\sigma }_{as}$.

It can be seen that for selected parameters, the active fiber length is not optimal. Reducing the length to L₂ = 3 m can lead to an increase in laser efficiency. The simulation shows that for the selected pumping conditions, an increase of L₂ to 8 m leads to such a significant decrease in ā that lasing becomes impossible.

5. Stationary Generation

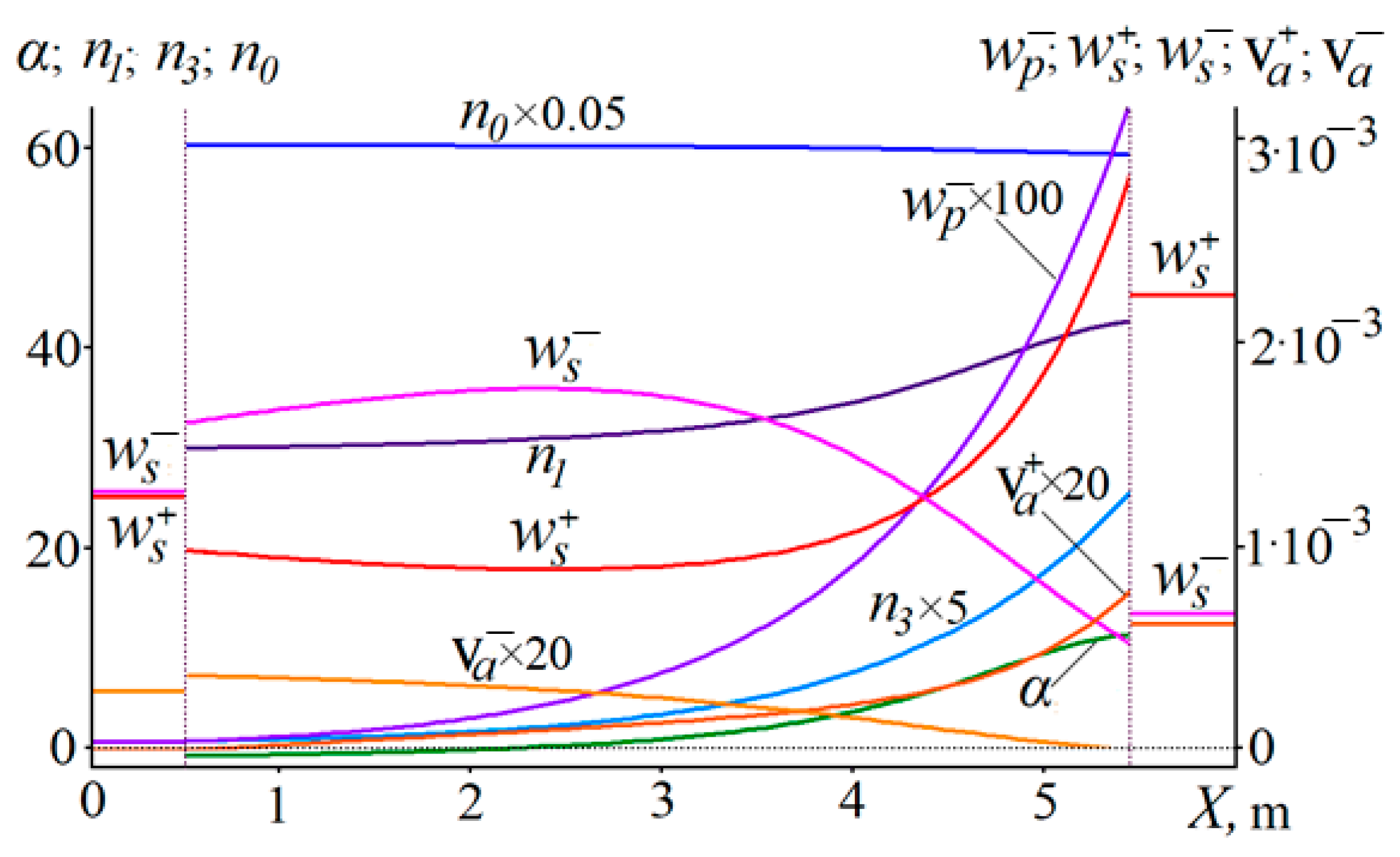
Figure 4 shows the spatial distributions of values for the same pumping and active fiber parameters as in Figure 3 but for a stationary generation of laser. Dissipative losses for pump and radiation wavelengths, output losses introduced by FBG mirrors with R₁ = 0.96 and R₂ = 0.3, as well as losses on fiber splices θ_m were taken into account. The refinement of the latter value was carried out by a quantitative comparison of the experimental and simulated values of the threshold generation power. The comparison results in the obtained value of θ_m = 1.1 dB. Under these conditions, the simulated value of the average gain ā = 2.51 is quite close to the total losses.

The comparison with the data in Figure 3 shows that the intensities of $w_s^{\pm }$ increased by an order of magnitude, but ${\mathrm{v}}_a^{\pm }$, on the contrary, decreased significantly. This is explained by the fact that $w_s^{\pm }$ is growing and repeatedly passes through the active medium, reducing the population n₁ and thereby decreasing ${\mathrm{v}}_a^{\pm }$. The distributions $w_s^{+}$ and $w_s^{-}$ along the active fiber are such that the total intensity remains approximately constant (at the right end of the active medium, it is slightly higher due to the action of high pump intensity $w_p^{-}$).

The output power was measured versus the pumping power. The experimental and simulated data are shown in Figure 5 for two cases: for the cavity without AOM and when the working AOM is placed inside the cavity (in simulations, the losses introduced by the working AOM into the cavity are taken into account in the diffraction coefficient D_m = 0.46). As can be seen, a fairly close agreement of experimental (points) and simulated (lines) results is achieved.

6. Q-Switching

6.1. Formation of Intensity Peaks from ASE When the Quality Factor Is Turned on

The formation of the peak mode for a set of parameters close to the experiment is illustrated in Figure 6. Pump power of 2.9 W is chosen for demonstration. The active medium has an average unsaturated gain of ā = 7. The total loss in the cavity is θ_f = 4.3. For clarity a steep modulation front is considered (≈10 ns). The Q-switching is modeled by increasing the diffraction coefficient D from 0 to D_m. A simplified functional laser scheme is shown in the upper part of Figure 6. The active and passive fiber sections have the same lengths as in the experiment. As for Figure 4, the output mirror has the reflection of R₂ = 0.3. The AOM is located at the point X = 9.5 m.

Figure 6a shows the medium state at the time of τ = τ₀ + 0.1τ, where τ₀ is the moment of turned-on Q-switching. In the model simulations for dimensionless values, dx = dτ was selected, so for the time of 0.1τ, waves pass the way of 0.1 L. The propagation of the narrowband wave $w_s^{+}$ and the broadband ASE wave ${\mathrm{v}}_a^{+}$ is shown by the arrow. Further, wave $w_s^{+}$ creates the first intensity peak at the output. After the partial reflection of the $w_s^{+}$ component from the OC FBG at X = L, the wave $w_s^{-}$ is generated, which, with losses on the AOM and splices, reaches the active medium. Figure 6b presents the amplification of $w_s^{-}$ wave in the active medium. Then it passed the section of the passive fiber, and at the moment of time 0.9τ, the front was in the active medium at a distance of 1.5 m from the left mirror (HR FBG). Wave $w_s^{-}$ has the same front as $w_s^{+}$ in Figure 6a.

Since the intensity $w_s^{+}$ (L) at this time remains unchanged, the output signal will have the step shape. Similar steps will appear during the next passes of the $w_s^{+}$ wave. The step shape will be preserved until each pass causes the medium saturation (for the first passes of the traveling waves saturation is negligible due to the low intensity of the ASE).

For the simulation conditions after 10–12 single passes, the intensities of $w_s^{+}$ and $w_s^{-}$ waves grow to a level where each single pass of the active medium noticeably reduces the average gain. The data in Figure 6c (the moment of time 12.1τ after Q-switching is on) shows that the medium is already highly saturated, and the next output radiation peak has a gentle decline. The intensities of the ${\mathrm{v}}_a^{+}$ and ${\mathrm{v}}_a^{-}$ waves are approximately 5 orders of magnitude lower and are not shown in Figure 6c.

The result of active medium high saturation with several intensity peaks is shown in Figure 6d (τ = τ₀ + 15.5τ). It can be seen that the significant part of the active medium becomes transparent. There are also zones of positive and negative gain. At the next pass of the medium, the peak amplitude decreases after the average gain ā is below the level of cavity losses.

From the data in Figure 6, we can note two general features. Firstly, the more extended in time the Q-switching front τ_q is, the greater the overlap of individual pulses and the lower amplitude of each of them will be. Secondly, these dynamics of generation lead to the fact that ā is lower than θ_f after the peak series are completed. The natural limit for the single peak series energy increasing is to reach the medium state with ā → 0 after the series is completed. The possibilities of approaching this limit [18] are related to the use of AOM, with three radiation input–output ports and a short time of τ_q.

6.2. Comparison with the Experiment

The results of individual pulse shape, amplitude and energy simulations were compared with the experimental data obtained for pulse-periodic generation at pump power of 2.6 W and the modulator switching frequency of 2 kHz with output mirror R₂ = 0.3 (the experiments showedthat this is the upper limit of pulse energy since during the time between AOM switching on, the inversion is completely restored).

Figure 7a shows the simulation results. Despite the close values for the times τ_q = 0.75 (or 40 ns) and τ_c = 1 (or 53 ns), the peak structure of the output radiation is clearly visible. The output pulse energy E_out = 7 μJ is slightly higher than that obtained in the experiment E_out = 5 μJ. This can be explained by uncounted losses, which can occur in the poor-quality splicing of passive fiber sections, or in the AOM operating in the pulse-periodic mode. It is also seen that the active medium saturation comes to a level below the cavity losses (dashed line).

As τ_q increases, the maximum power of the peak structure is reached later by 2τ, since the growth of ASE waves is slower. Energy E_out retains its value. At the same time, a decrease in the irregularity of peak structure reduces its total duration, while a decrease in peak intensity has the opposite effect, so that the total duration is insignificantly changed. In general, it can be noted that the experimental data in Figure 7b,c demonstrate reasonable agreement with the simulation performed for the same conditions (Figure 6). Figure 7d shows the experimentally obtained spectrum with a generation wavelength of 1960 nm, as well as a pulse train with a repetition rate of 2 kHz. The generation wavelength corresponds to reflection of the used FBGs and the pulse repetition rate to the modulator switching frequency.

6.3. The Possibilities of Obtaining Single Pulses of Increased Amplitude

From the data in Figure 6 and Figure 7, it is obvious that an increase in the quality factor over time τ_q ~ τ_c in each period of the pulse-periodic mode of thulium laser with the set of parameters used in the experiment, including the AOM parameters, leads to the appearance of a peak structure of the output pulse. In [32,33], it was proposed to use an AOM with three ports [22] to obtain single pulses with increased amplitude in a bismuth laser. The point of the proposed method is that in each period, the AOM is switched on several times for a short time (for τ_q << τ_c) required to reflect the traveling wave from the output mirror. The switching-on moments and their number are calculated beforehand and achieve the maximum energy removal from the active medium. In a thulium-doped fiber laser with the active medium length of several meters (accordingly, a relatively small value of τ_c), the realization of this method is limited by the extent to which the above inequality is fulfilled and therefore may encounter difficulties. For this reason, in this subsection, we propose another simulation mode of the AOM operation, which is less profitable in terms of energy removal per pulse but much easier in practical implementation.

The used AOM has three ports: the first is for the radiation input, the second is for the output of diffracted radiation, and the third is for the output of radiation that has not been diffracted. A highly reflective mirror (R₂ ≈ 0.99) is placed behind the second port. Figure 8 shows the result of the AOM switching on (T_q = 40 ns, as in the experiment) at the zero time point τ₀ for the set of parameters as in Figure 6. When the AOM is turned on for a long time, the output signal that has passed the highly reflective mirror has a low output power $P_{out}^l$ (at maximum is only about 0.1 W). At the same time, due to the high intensity $w_s=w_s^{+}+w_s^{-}$ inside the high-quality cavity, the active medium remains highly saturated, and the average gain goes below the losses in the cavity (ā(τ) and θ_f in Figure 8).

If the AOM is turned off at one of the time points while the output radiation is still present, a radiation pulse with a duration close to the turn-off time occurs at the output of the third port. The benefit in the output peak power P_out occurs due to the fact that the high-intensity wave $w_s^{+}$ outputs by passing the mirror. The curve $P_{out}^m\left(\tau \right)$ shows the amplitude of a single pulse, which can be obtained when the AOM is turned off at a time moment τ. The inset shows the output pulse that occurs when the AOM is turned off at τ_m = τ₀ + 12.5τ and time dependence of D(τ). It can be seen that maximum P_out ≈ 50 W, which is almost twice as much as in the normal mode (Figure 7).

Obviously, a single pulse, which replaces the generation at some point in time, removes significantly less energy from the active medium than the whole multi-peak structure. For instance, for the pulse shown in the inset of Figure 8, the energy E_out is about 1 µJ. The medium saturation level with a single pulse is also less than for the entire structure. Therefore, in connection with the arising question of the practical application of this modulation method, it should be noted that the low gain saturation depth allows for increasing the repetition rate of single pulses. Thus, at a repetition rate of 6 kHz, the simulation and experiment results show a twofold energy decrease in a multi-peak structure, while the simulation of this method shows that the single pulses energy decreases by no more than 2% even at a repetition rate of 12 kHz. A decrease in τ_q (AOM characteristic) leads to single pulse power increasing.

7. Discussion

As can be seen from the previous sections, we carried out a theoretical and experimental study of a Q-switched thulium fiber laser using an acousto-optic modulator. We considered the processes that lead to the generation of discontinuous multi-peak pulses with an energy of up to 5 μJ and a nanosecond structure. We demonstrated the development dynamics of a multi-peak structure and proposed a method for switching to a single-pulse generation mode.

To understand the physical features of an active medium, as well as to estimate the output characteristics of laser radiation and the possibilities for their improvement, we considered the characteristics of Tm-doped fiber states in the absence of a cavity and under conditions of stationary generation. This allowed us to estimate the gain inhomogeneity and its maximum in the active fiber by simulation, as well as to estimate the optimal fiber length, which leads to an increase in the laser efficiency (L₂ = 3 m). In addition, in the stationary generation mode, the total losses occurring in the cavity were calculated (θ_f = 4.3).

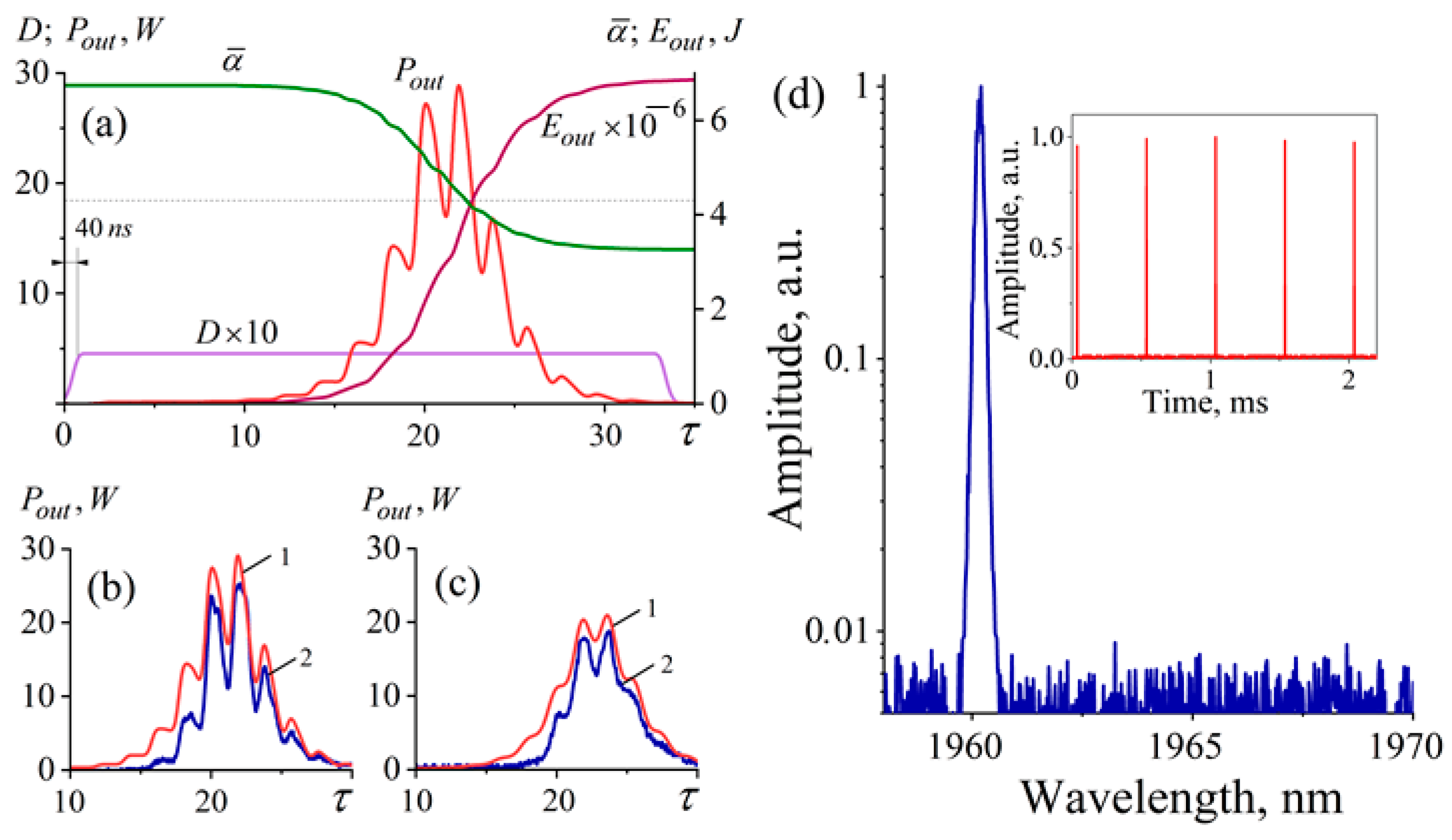
We compared the simulation and experimental results on the formation of intensity peaks at close pump parameters of 2.9 W and 2.6 W, respectively, at a modulator switching frequency of 2 kHz and with an output mirror reflection of R₂ = 0.3 (Figure 6 and Figure 7). The simulation showed that the longer the Q-switching front τ_q is, the stronger the overlap of individual pulses and the lower the amplitude of each. In addition, these generation dynamics lead to a decrease in ā to a level below the losses in the cavity θ_f. To increase the energy of separate peaks series, it is necessary to achieve a state of the medium with ā → 0, which is possible when using an AOM with three radiation input–output ports and a short time τ_q. The experimental data demonstrate reasonable agreement with the simulation. The pulse energy obtained in the experiment was E_out = 5 μJ, and the instantaneous power was slightly more than 20 W. In [39], similar multi-peak pulses were demonstrated. However, energies in that case were higher than in our work 200–220 μJ vs. 5–7 μJ. Nevertheless, in mentioned manuscript the unique water-cooled Tm-Ho-codoped fiber and bulky AOM were used. In [40] all-polarization maintaining Tm-doped fiber laser based on the acousto-optic Q-switching technique was demonstrated. The output power was about 5 mW, and pulse duration with a slightly multi-peak structure was about 67 ns at 20 kHz repetition rate.

To obtain single pulses of increased amplitude, it is proposed to use an AOM with three ports: for the radiation input, for the output of diffracted radiation, and for the output of radiation that has not been diffracted. Behind the second port, there is a highly reflective mirror (R₂ ≈ 0.99). When the AOM is turned off at the moment of time while the output radiation is present, a radiation pulse with a duration close to the turn-off time appears at the output of the third port. Thus, the peak power of the output signal can be almost doubled (P_out ≈ 50 W), due to the fact that the high-intensity wave $w_s^{+}$ outputs by passing the mirror.

The AOM with a typical response time of 10 ns is currently the mainstream modulator used for active Q-switching in all-fiber lasers [27]. For example, in Tm-doped fiber lasers Q-switched by the AOM in configuration with multiple stages of amplification, the maximum output average power over 50 or 100 W can be achieved [41,42]. The pulse width can be tuned from tens to hundreds of nanoseconds by changing the pump power or the modulation repetition rate. Despite this, there is ongoing research and development of new promising materials to create real all-fiber modulators, as well as various methods of Q-switching being investigated. In [43], an actively Q-switched all-fiber thulium laser at a wavelength of 1920 nm was experimentally demonstrated. The Q-switching was realized by polarization modulation through the stress-induced birefringence using a piezoelectric transducer (PZT) as the Q-switcher. Average output powers of 2.23 and 2.74 mW were obtained at the pulse repetition rates of 50 and 100 kHz, respectively. The pulse repetition rate ranged from 25 to 175 kHz, and the pulse duration increases with the repetition rate growing. The shortest pulse duration of about 413 ns was achieved at a pump power of 145 mW and the repetition rate of 25 kHz. Work [44] presents the same type of Q-switching with single-frequency generation at 1950 nm in Tm-doped fiber laser with an average power of several milliwatts. At repetition rates below several tens of kilohertz the pulse durations of about 40 ns or less were measured. At higher repetition rates (e.g., >100 kHz), the longer pulses were observed (100–200 ns). In this type of Q-switching, the bias and amplitude of the PZT need to be carefully adjusted to avoid spurious oscillations while changing the PZT frequency and pump power. Methods of obtaining active Q-switching are not limited to the above. They can be related with optimization or rational applications of already existing standard devices. For example, the use of a dynamic periodic microbend in fiber that is electrically controlled with a piezoelectric actuator as in [45]. The authors demonstrated Q-switched Tm-doped fiber laser with a ring cavity operating in the 2 µm range. When the piezoelectric actuator voltage-off period was set at 20 µs for the pump power of 120 mW, the output pulse power was 420 mW with a pulse width of 1.3 µs.

In addition, there are works on passive Q-switching in Tm-doped fiber lasers. In [46], the authors used nonlinear fiber to achieve up to 50 μJ of pulses energy with a pulse width of about 20 ns, and the pulse repetition rate tuning from several kilohertz to tens of kilohertz by changing the pump power, but the scheme simplicity also led to high pulse energy instability in time and amplitude. Work [47] demonstrates using a heavily holmium-doped fiber for Q-switching a Tm-doped fiber laser with linear cavity. Lasing was obtained at 1.96 μm, with a pulse energy of 3 μJ and pulse duration of 600 ns. The highest pulse repetition rate was 80 kHz.

Taking into account the obtained parameters of laser radiation and their stability, as well as the compactness of the design, it can be said that AOMs still remain more preferable for obtaining Q-switching in fiber lasers. Therefore, in this work we propose a more detailed experimental and theoretical study of an active medium and generation dynamics of the thulium doped fiber laser Q-switched by the AOM. The pattern of the output radiation formation from the ASE and the consideration of the conditions for the peak structure appearance are revealed on the basis of an improved numerical model, in which radiation transfer equations are used, and the broadband and narrowband components of the ASE are calculated separately. We believe that this information will be useful in optimizing and improving of actively Q-switched fiber lasers under development.

8. Conclusions

The numerical simulation of the Tm-doped fiber laser was performed based on the improved model of the active medium and cavity. It demonstrated agreement with the experimental results in stationary and pulsed modes. Particularly, the active medium of thulium laser is characterized by a strong gain inhomogeneity along the fiber. Taking into account the presence of inhomogeneities, it is possible to find the optimal length of an active fiber according to its parameters and the given pump power.

The simulated characteristics of the output radiation demonstrate agreement with the experiment in the stationary state and Q-switching generation mode using AOM, which confirms the relevance of the used model. The found patterns of the output laser radiation formation from the amplified spontaneous emission allow for understanding the influence degree of the Q-switching rate on the output pulse and medium saturation depth characteristics.

We proposed a simple method of periodic single pulses obtaining by Q-switching for a time τ_q ~ τ_c, based on the same fast Q-switching off at the calculated time. This method allows for increasing the output power at a doubled pulse repetition rate, although the energy of each pulse remains below that one corresponding to the multi-peak structure.