Multi-Channel Polarization Manipulation Based on All-Dielectric Metasurface
Abstract
1. Introduction
2. Theoretical Analysis
2.1. General Scheme for Spin Decoupling
2.2. Theory of Different Types of Polarization in Transmission
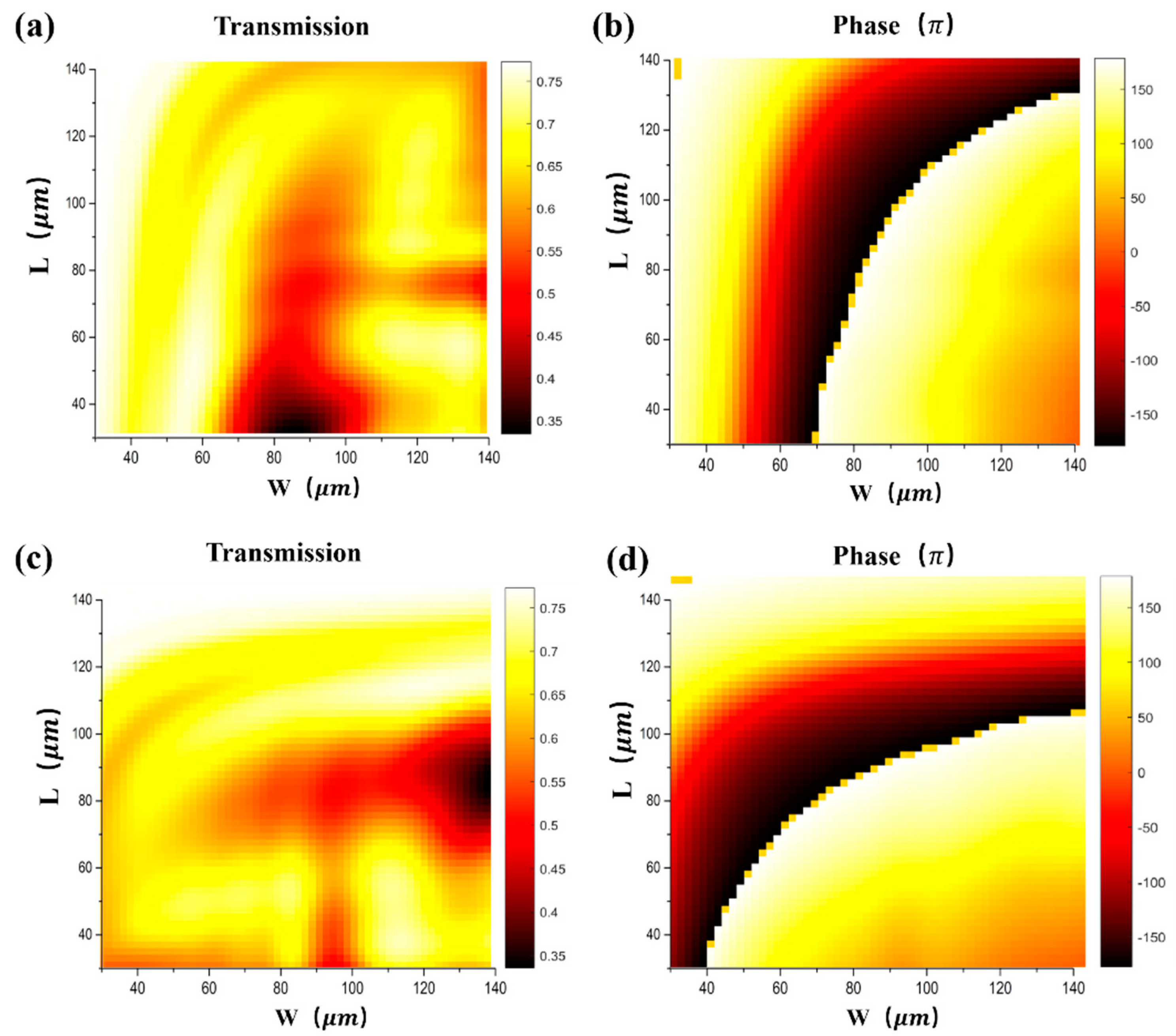
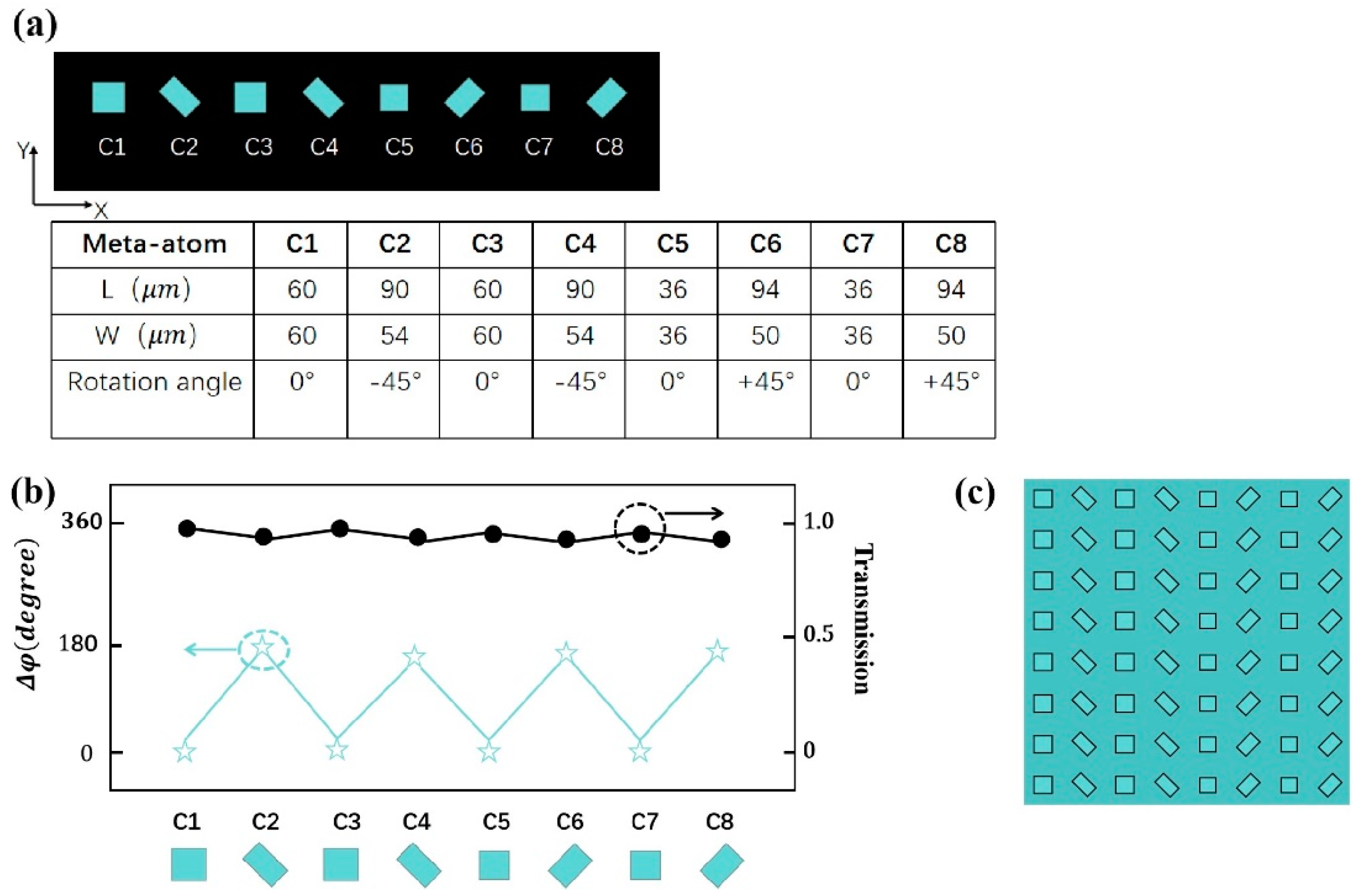
3. Metasurface Design
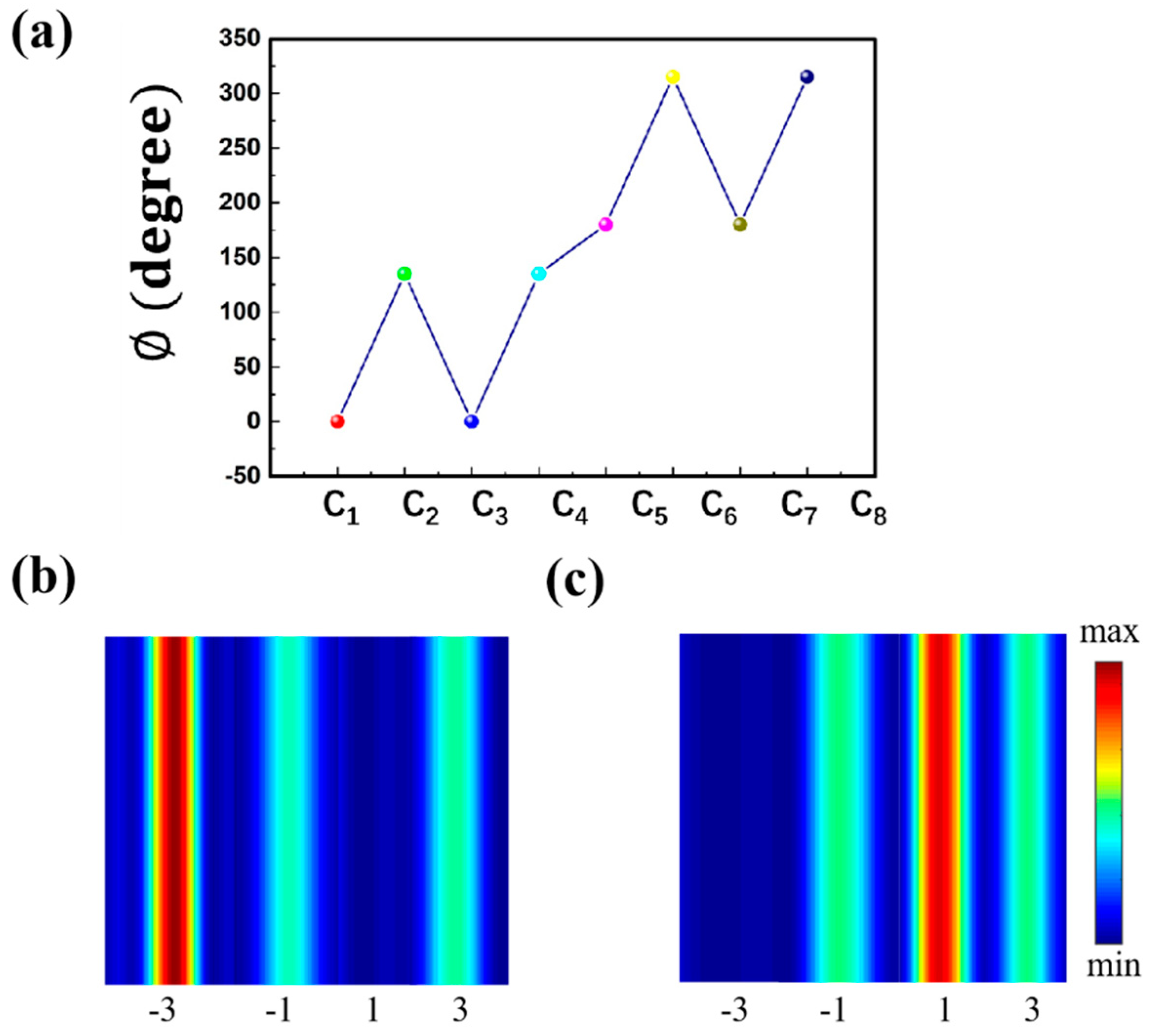
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reineke, B.; Sain, B.; Zhao, R.; Carletti, L.; Liu, B.; Huang, L.; De Angelis, C.; Zentgraf, T. Silicon metasurfaces for third harmonic geometric phase manipulation and multiplexed holography. Nano Lett. 2019, 19, 6585–6591. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Khorasaninejad, M.; Huang, Y.W.; Roques-Carmes, C.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Ding, Z.-W.; Tamagnone, M.; Chaudhary, K.; et al. Single-Layer Metasurface with Controllable Multiwavelength Functions. Nano Lett. 2018, 18, 2420–2427. [Google Scholar] [CrossRef]
- Gong, S.-H.; Alpeggiani, F.; Sciacca, B.; Garnett, E.C.; Kuipers, L. Nanoscale chiral valley-photon interface through optical spin-orbit coupling. Science 2018, 359, 443–447. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-Insensitive Metalenses at Visible Wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Liu, Z.; Li, J.; Cheng, H.; Yu, P.; Liu, W.; Tang, C.; Gu, C.; Li, J.; et al. High-Performance Broadband Circularly Polarized Beam Deflector by Mirror Effect of Multinanorod Metasurfaces. Adv. Funct. Mater. 2015, 25, 5428–5434. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Aieta, F.; Kanhaiya, P.; Kats, M.A.; Genevet, P.; Rousso, D.; Capasso, F. Achromatic Metasurface Lens at Telecommunication Wavelengths. Nano Lett. 2015, 15, 5358–5362. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Kats, M.A.; Genevet, P.; Capasso, F. Multiwavelength Achromatic Metasurfaces by Dispersive Phase Compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef]
- Jiang, S.-C.; Xiong, X.; Hu, Y.-S.; Hu, Y.-H.; Ma, G.-B.; Peng, R.-W.; Sun, C.; Wang, M. Controlling the Polarization State of Light with a Dispersion-Free Metastructure. Phys. Rev. X 2014, 4, 021026. [Google Scholar] [CrossRef]
- Xie, Y.N.; Liu, X.Y.; Cai, Y.J.; Zhu, J.F. Polarization-insensitive dielectric metamaterial absorber for near-unity UV-light trapping in monolayer graphene. Opt. Commun. 2022, 503, 127459. [Google Scholar] [CrossRef]
- Gao, X.; Tang, L.; Wu, X.; Li, S. Broadband and high-efficiency ultrathin Pancharatnam-Berry metasurfaces for generating X-band orbital angular momentum beam. J. Phys. D Appl. Phys. 2021, 54, 075104. [Google Scholar] [CrossRef]
- Ding, G.; Chen, K.; Luo, X.; Zhao, J.; Jiang, T.; Feng, Y. Dual-Helicity Decoupled Coding Metasurface for Independent Spin-to-Orbital Angular Momentum Conversion. Phys. Rev. Appl. 2019, 11, 044043. [Google Scholar] [CrossRef]
- Bouchard, F.; Leon, I.D.; Schulz, S.A.; Upham, J.; Karimi, E.; Boyd, R.W. Optical spin-to-orbital angular momentum conversion in ultra-thin metasurfaces with arbitrary topological charges. Appl. Phys. Lett. 2014, 105, 36–262. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Zhang, X.; Wei, M.; Xu, Q.; Wang, Q.; Zhang, H.; Zhang, W.; Hu, C.; Zhang, Z.; et al. Spin-decoupled multifunctional metasurface for asymmetric polarization generation. ACS Photonics 2019, 6, 2933. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Li, Q.; Zhang, X.; Zhang, W.; Hu, C.; Zhang, X.; Han, J.; Zhang, W. Generation of terahertz vector beams using dielectric metasurfaces via spin-decoupled phase control. Nanophotonics 2020, 9, 3393–3402. [Google Scholar] [CrossRef]
- Meng, C.; Tang, S.; Ding, F.; Bozhevolnyi, S.I. Optical Gap-Surface Plasmon Metasurfaces for Spin-Controlled Surface Plasmon Excitation and Anomalous Beam Steering. ACS Photonics 2020, 7, 1849–1856. [Google Scholar] [CrossRef]
- Mueller, J.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, S.; Chen, Y.; Zhang, K.; Ding, X.; Ratni, B.; Wu, Q.; Burokur, S.N.; Qiu, C.-W. A Fully Phase-Modulated Metasurface as An Energy-Controllable Circular Polarization Router. Adv. Sci. 2020, 7, 2001437. [Google Scholar] [CrossRef]
- Kruk, S.; Hopkins, B.; Kravchenko, I.I.; Miroshnichenko, A.; Neshev, D.N.; Kivshar, Y.S. Broadband highly-efficient dielectric metadevices for polarization control. APL Photonics 2016, 1, 917. [Google Scholar] [CrossRef]
- Yin, Z.; Chen, F.; Zhu, L.; Guo, K.; Shen, F.; Zhou, Q.; Guo, Z. High-efficiency dielectric metasurfaces for simultaneously engineering polarization and wavefront. J. Mater. Chem. C 2018, 6, 6354–6359. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, L.; Shen, F.; Zhou, H.; Gao, R. Dielectric metasurface based high-efficiency polarization splitters. RSC Adv. 2017, 7, 9872. [Google Scholar] [CrossRef]
- Owiti, E.O.; Yang, H.; Ominde, C.F.; Sun, X. Broadband quarter-wave plate based on dielectric-embedded plasmonic metasurface. RSC Adv. 2017, 7, 37495–37501. [Google Scholar] [CrossRef]
- Gao, S.; Park, C.-S.; Lee, S.-S.; Choi, D.-Y. All-Dielectric Metasurface for Simultaneously Realizing Polarization Rotation and Wavefront Shaping for Visible Light. Nanoscale 2019, 11, 4083–4090. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Du, W.; Zhang, D.; Xu, W.; Chen, X.; Zhang, X. Multi-Channel Polarization Manipulation Based on All-Dielectric Metasurface. Photonics 2022, 9, 847. https://doi.org/10.3390/photonics9110847
Hu S, Du W, Zhang D, Xu W, Chen X, Zhang X. Multi-Channel Polarization Manipulation Based on All-Dielectric Metasurface. Photonics. 2022; 9(11):847. https://doi.org/10.3390/photonics9110847
Chicago/Turabian StyleHu, Susu, Wenhan Du, Dawei Zhang, Weilong Xu, Xiaogang Chen, and Xinhua Zhang. 2022. "Multi-Channel Polarization Manipulation Based on All-Dielectric Metasurface" Photonics 9, no. 11: 847. https://doi.org/10.3390/photonics9110847
APA StyleHu, S., Du, W., Zhang, D., Xu, W., Chen, X., & Zhang, X. (2022). Multi-Channel Polarization Manipulation Based on All-Dielectric Metasurface. Photonics, 9(11), 847. https://doi.org/10.3390/photonics9110847



