Abstract
Molecular assembly in a complex cellular environment is vital for understanding underlying biological mechanisms. Biophysical parameters (such as single-molecule cluster density, cluster-area, pairwise distance, and number of molecules per cluster) related to molecular clusters directly associate with the physiological state (healthy/diseased) of a cell. Using super-resolution imaging along with powerful clustering methods (K-means, Gaussian mixture, and point clustering), we estimated these critical biophysical parameters associated with dense and sparse molecular clusters. We investigated Hemaglutinin (HA) molecules in an Influenza type A disease model. Subsequently, clustering parameters were estimated for transfected NIH3T3 cells. Investigations on test sample (randomly generated clusters) and NIH3T3 cells (expressing Dendra2-Hemaglutinin (Dendra2-HA) photoactivable molecules) show a significant disparity among the existing clustering techniques. It is observed that a single method is inadequate for estimating all relevant biophysical parameters accurately. Thus, a multimodel approach is necessary in order to characterize molecular clusters and determine critical parameters. The proposed study involving optical system development, photoactivable sample synthesis, and advanced clustering methods may facilitate a better understanding of single molecular clusters. Potential applications are in the emerging field of cell biology, biophysics, and fluorescence imaging.
1. Introduction
Single-molecule-based live-cell imaging is becoming an essential technique in applied physics, biophysics, and fluorescence microscopy [1,2,3,4,5,6,7,8,9,10,11,12]. Since its first inception, the field has grown by leaps and found new applications in diverse research disciplines ranging from single-molecule physics to cell biophysics [13,14,15,16,17,18,19]. The following years have observed a surge in several important variants of super-resolution imaging such as individual molecule localization–selective plane illumination microscopy (IML-SPIM) [20], ground state depletion microscopy (GSDIM) [21], super-resolution optical fluctuation imaging (SOFI) [22], points accumulation for imaging in nanoscale topography (PAINT) [23,24], simultaneous multiplane imaging-based localization encoded (SMILE) [9,25], MINFLUX [26], Probabilistic Optically Selective Single-molecule Imaging Based Localization Encoded (POSSIBLE) [6], and other techniques [27,28,29,30,31,32,33,34]. Thus, the resultant high-resolution images form the basis for understanding biophysical mechanisms and estimating critical statistical parameters related to single-molecule dynamics. This calls for reliable clustering methods and for accurate parameter estimation. Thus, employing an appropriate clustering method is central for understanding molecule clusters in the complex cellular environment.
In general, super-resolution imaging involves recording single-molecule data and subsequent estimation of key features such as location and number of photons detected per molecule. Physical models are developed to determine the parameter of interest (such as number of molecules/cluster, cluster-density, cluster-area, and pairwise-distance). These parameters form the basis for understanding the underlying biological mechanism at a single molecule in a cellular system. Molecular clustering is a process that represents an accumulation of proteins/single-molecules (here, Hemaglutinin) as determined by local cell physiology. Specifically, single-molecule clusters are known to form during the onset of diseases and viral infection (Influenza A) [4,35]. Hence, it becomes vital to understand clustering and to devise methods to disrupt the process. Hemagglutinin proteins is an antigenic glycoprotein found on the surface of influenza viruses. It is responsible for binding the virus to the cell that is being infected. The protein has the ability to cause cells to clump together in vitro. In our study, we have studied NIH 3T3 cells transfected with Dendra2HA plasmid. Post-transfection (24 h), it was found that hemagglutinin proteins begin to form small clusters, which in turn integrate together to form large clusters [36]. HA clustering has a direct bearing on the infectivity rate.
The basic fact that different physical models employ different assumptions and specific statistical distribution rules out the possibility of a single model to accurately estimate all the relevant parameters. Moreover, a lot depends on the natural biological processes that result in a specific distribution of single-molecules based on local cell physiology. The complex nature of biological processes necessitates multi-model analysis [4,35]. The K-means clustering method is often used for single-molecule analysis [37,38,39]. While K-means is an efficient technique, it has its limitations. Recently, a non-parametric descriptor has been used for quantifying the density of cluster [40]. Traditionally, Ripley’s K-test, histogram analysis, and point clustering methods are used for understanding single-molecule clustering in cellular systems [2,4]. Most of these clustering techniques perform well for determining specific parameters and particularly when data are complete. Investigation shows that none of these techniques are found to be accurate for multi-parameter estimation. Since single-molecule data are known to be incomplete (containing only a subset of observed single-molecules) and have complex distribution, a single model may not adequately estimate all relevant parameters. Moreover, existing clustering methods are not equipped to handle multi-parameter estimation; thus, they are not readily extendable to single-molecule imaging. This is a bottleneck and remains a challenge. Thus, there is a constant need for a reliable clustering method that can be used for characterizing molecular clusters [4,35].
Existing methods used for analysing clustering process in SMLM include Ripley’s K function [41,42] and density-based spatial clustering of applications with noise (DBSCAN) [43]. While Ripley’s function is basically a second moment property that describes the relationship between two or more patters, mathematically, Ripley’s K-function is given by [41], , where is the i-th point, N is the total number of points, and is the number of points per area. On the other hand, DBSCAN is a density-based method that primary uses two parameters, neighbourhood radius (say rmin), and minimum number of points (nmin) for identifying a cluster. The technique looks for the minimum density of molecules within rmin. Although effective, the technique is not robust and are prone to imaging artifacts. Moreover, the subjectivity and ambiguity in selecting algorithm parameters makes it more complex, and this affects its performance. Both techniques are supervised techniques and, thus, can be used in combination with other analysis methods.
In this report, we report the co-development of a single-molecule imaging system and advanced clustering methods to estimate critical biophysical parameters in a cellular system. A multi-modal clustering approach is employed for estimating multiple parameters. This is predominantly due to single-molecule dynamics in a complex cellular system driven by interlinked biophysical processes. Here, we investigate the Influenza A disease model that involves clustering of Hemagglutinin (HA) protein in NIH3T3 cells. Clustering is an important step in the entire cycle of HA entry to its maturation during infection. In short, the viral glycoproteins of hemagglutinin (HA) are used by virus for fusion, viral budding, and infection [44]. Once inside the cell, HA dynamics and its clustering in the plasma membrane are critical for budding and fusion. The biophysical parameters (number of molecules per cluster, density, and cluster size) are critical indicators of HA dynamics and overall infectivity (release of bud-particles from infected cells) [45,46]. Hence, there is an urgent need for cluster analysis techniques and tracking HA dynamics overtime in a cellular system.
2. Results
Figure 1A shows the schematic diagram of the single-molecule imaging system developed for cluster analysis. Two lasers are employed: one for activation and the second for excitation of conjugate photoactivable molecule (Dendra2-HA). The beams are combined using a dichroic mirror (DM 505) and directed towards the high NA objective lens (Olympus UPlanFL N 100X, 1.30 NA, Oil immersion) that focus the combined beam to transfected cells cultured on a coverslip. To understand the dynamics of HA molecules during viral infection, a photoactivable probe (Dendra2) is conjugated with the protein-of-interest Hemaglutinin (HA) to study its dynamics in a cellular environment. This enables both photoactivation and photoexcitation of single-molecules. Upon activation and subsequent excitation, the target molecules (Dendra2-HA) blinks with a duration of ∼30 ms (triplet state lifetime). The fluorescence, thus, emitted during this time window is collected by the same objective and directed towards the EMCCD camera (iXon 897 Ultra). The description of actual optical setup is detailed in Supplementary S1. Images containing single-molecule signatures are recorded at a rate of 33 Hz and a total of 5000 frames were collected with an average of molecules per frame. The images are processed and rendered using developed MATLAB scripts [9,14,25]. Subsequently, super-resolved image is constructed from single-molecule data. The high intensity spots (on the recorded images) representing single-molecule were extracted and approximated by a Gaussian function, , where is the radial distance from the centroid (), is the background pixel value, and is the peak pixel value. Subsequently, the centroid and standard-deviation of single-molecule are extracted to, respectively, determine its location (centroid, ) and localization precision () in the reconstructed super-resolved image. Here, is the diffraction-limited PSF with N as the number of photons detected per molecule. We have neglected background and insignificant pixel-size effect to arrive at the above relation from Thompson’s well-known relation [47].
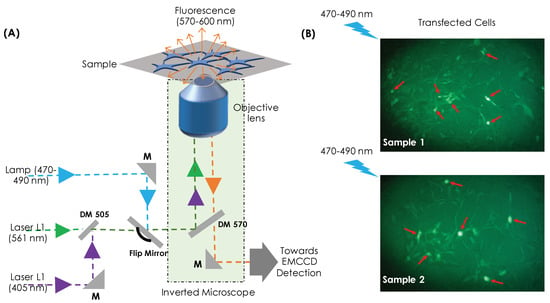
Figure 1.
(A) Schematic diagram of the developed optical super-resolution imaging system for studying molecular clusters, (B) Dendra2-HA transfected cells where strong transfected cells appear bright and are indicated by a red arrow.
NIH3T3 cells were chosen for the present study following similar studies in the literature [2,4]. NIH3T3 cells are a standard fibroblast cells extracted from swiss albino mouse embryo tissue. The cells are well suited for transfection studies using plasmid DNA (Dendra2-HA). As they are receptive to transformations, 3T3 is capable of undergoing spontaneous transformations in culture. The lipid-based transfection reagents used in the present study are specifically optimized for transfection of DNA and RNA into NIH3T3 cells. Altogether, the efficiency of transfection makes 3T3 cell lines suitable for single-molecule studies. For the present study, the cells were thawed and cultured using the standard protocol [9,29]. To ensure healthy growth before carrying out transfection, cells were passaged a few times. Subsequently, the cells were PBS washed and transfected with Dendra2-HA plasmid using standard Lipofectamine 3000 (Thermo Fisher Scientific, L3000001) based protocol. A confluence of was ensured before transfection was carried out. The cells were incubated overnight and fixed using paraformaldehyde after 24 h [6]. Post fixation, widefield-inverted fluorescence microscopy studies were carried out to look for transfected cells and their efficiency. Figure 1B shows a transfection efficiency of about as observed in an inverted fluorescence microscope equipped with 20X objective lens (Meiji 20X, 0.4 NA). Subsequently, single-molecule studies were carried out on the transfected cells, as shown in Figure 1B.
It may be noted that HA is known to exist as a trimer, but here we are dealing with HA monomer. This has been verified, and the details can be found in Refs. [48,49]. The monomers are known to form compact and elongated clusters. Specifically, HA has basic residues and palmitoylation sites in the cytoplasmic tail (CT). It contains at least two highly conserved, positively charged amino acids and three acylation sites per monomer [48]. A detailed description of HA glycoprotein can be found in Ref. [49].
The transmission images of the cells chosen for the study is shown in Figure 2A. We have carefully chosen strongly and weakly transfected cell. These selections helps in determining the tolerance limit of clustering methods and related parameter estimation. The corresponding super-resolution images are shown in Figure 2B for both the cases along with a few enlarged clusters (see green and red boxes). The centroid and localization precision for the detected molecules are determined as shown in Figure 2C. These parameters are estimated by using developed MATLAB scripts [4,9] and subjected to further analysis.
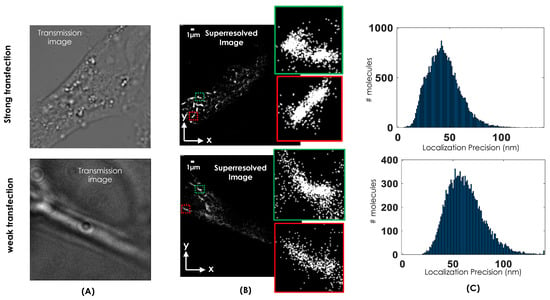
Figure 2.
(A) Transmission image of the transfected cells chosen for study. (B) Reconstructed super-resolved images of a single NIH3T3 cell along with transmission images and enlarged clusters (red and green regions). (C) The localization plot of resolved single molecules for strong and weak transfected cell that show an average localization precision of 45 nm and 55 nm, respectively.
To determine the performance of single-molecule clustering method, we computationally generated random clusters with known parameters such as number of clusters, number of molecules per cluster, and inter-cluster distance. The generation of test data (random clusters) is discussed in Supplementary S3. Subsequently, three different clustering methods (point-clustering, Gaussian mixture, and K-means) were employed for analysing clusters. The first method is point-clustering that uses Euclidean distance () to identify the next point in the cluster and, depending on the distance cut-off, determines if the point belongs to the cluster [50,51]. We chose nm as the cut-off and minimum number of points to be greater than 200 for it to be considered as a valid cluster. This technique has the distinct advantage of leaving out un-clustered points. This is consistent with the observation that not all molecules in real biological sample form clusters. The second method is based on Gaussian mixture that requires the identification of each cluster (i) by fitting a Gaussian function, , where, and are, respectively, the mean and standard deviation of the Gaussian function [52]. Often, expectation maximization based iterations are carried out for convergence to a stable solution [53,54,55,56]. Due to iterative nature of the Gaussian mixture method, the technique benefits from the feedback mechanism and converges to the most likely solution. The third promising method is K-means in which cluster centroids/means are randomly placed and each point is assigned to the nearest mean based on the least-squared Euclidean distance, , where is the Euclidean distance between and the centroid, (calculated using k-means++ algorithm in Matlab) [57,58]. Iteratively, the centroid for each cluster () is recalculated until convergence. Finally, the simulated data are subjected to cluster-analysis algorithms. The details of algorithms and data processing are detailed in Supplementary S2.
Figure 3A shows the performance of clustering methods on the generated test clusters. We adopted the approach that is often used in microscopy, optical tomography, astronomy, and data science that employs phantoms to evaluate different methods [59,60,61,62]. For quantification of a specific parameter, we have computationally generated random clusters (phantom) that serve as a ground truth (see, Figure 3) and used this as a guide to calculate biophysical parameters: first in the simulated clusters and then in real data. A comparison of estimated value with the known value gives an accurate picture of the efficiency of the clustering method. Biophysical parameters (such as cluster area, cluster density, number of molecules per cluster, and pairwise-distance) relevant to single-molecule clustering are considered. It is observed that k-means clustering and point clustering performs superior compared to that of GMM for determining the cluster area. This is quantified based on the coefficient-of-variation measure for each parameter, where , and and corresponds to mean and standard deviation, respectively. All techniques performed equally well in determining the number of molecules per cluster (). Point-clustering () and K-means () techniques are found to be better suited for estimating cluster density when compared to GMM () (see, Figure 3B). This is broadly due to the fact that K-means use centriod-to-molecule distance based search while GMM is a probabilistic model. However, GMM () and K-means () performed better than point-clustering for accessing pairwise distance (). Once the characteristics of clustering methods are determined, they are used to investigate real data (Dendta2-HA transfected cells).
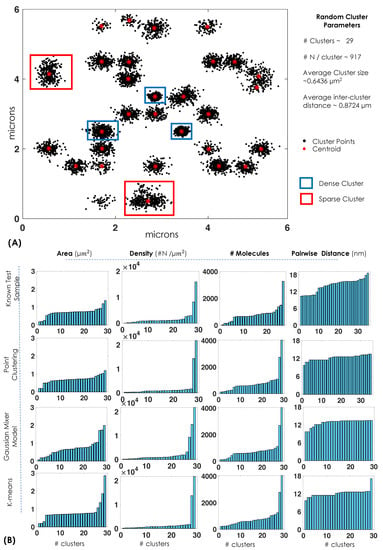
Figure 3.
(A,B) Test samples (random clusters) with specific cluster parameters are generated to evaluate performance of clustering methods. The biophysical parameters (cluster area, cluster density, number of molecules, and pairwise distance) as estimated by clustering methods (K-means, Gaussian-mixture model, and point-clustering) are displayed for 29 clusters.
The analysis was carried out on a large number of cells, and the data were segregated based on weakly (sparse clusters) and strongly (dense clusters) transfected cells. This is due to the fact that weak transfection are known to occur in a variety of biological specimens. A typical cell with dense and sparse HA clustering is shown in Figure 4. For both the cases, three different methods were employed to determine HA clusters and its characteristics. It is evident that, sparse clusters are well-recognized by all the clustering methods ( ), whereas compact clusters are better categorized by point clustering (with a minimum average cluster area, ). This is in line with the known test data. Point clustering has the added advantage of excluding unclustered HA molecules. This is due to the fact that point clustering does not require the initialization of a number of clusters and the necessity to cluster every molecule, which is predominantly due to its point-to-point based search. On the other hand, Gaussian and K-means clustering needs prior knowledge about the number of clusters. In addition, point clustering is found to be the fastest among the clustering methods (Figure 4A,B). K-means assume symmetric clusters whereas point and Gaussian clustering methods are capable of handling random clusters. This is beneficial for identifying clusters that are of arbitrary shape and for calculating biophysical parameters of unknown random clusters. Visualization of clusters shows few large area clusters (5–15 ) and the majority of them are in the moderate range (2–4 ). This observation is consistent with point clustering whereas GMM and K-means suggests a large proportion of larger area clusters (>3 for dense clustering and >6 for sparse clustering cases, respectively) (Figure 4C–F). This is in line with the observation on test sample (Figure 3). Moreover, density analysis indicates the existence of a few high density clusters (>2000 ). This observation is consistent with point-clustering and K-means whereas GMM does not fare well. The number of molecules per cluster is consistent with all clustering methods showing the existence of a few clusters with a large number of HA molecules. These observations indicate that none of the methods are well equipped for determining all the relevant parameters and a suitable combination of them is necessary. Thus, a multimodal approach seems essential.
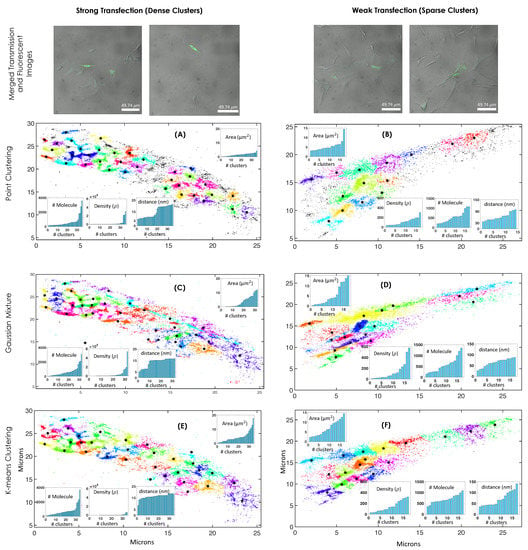
Figure 4.
(A–F) Top row shows merged images (fluorescent and transmission images) of strong and weak transfected cells. Cluster analysis for two chosen single cells from an ensemble of Dendra-2HA transfected NIH3T3 cell. Both strongly and weakly transfected cells are considered, which show dense and weak molecular clusters, respectively. Three different clustering methods (point clustering, Guassian mixture model, and k-means clustering) were employed to determine biophysical parameters (cluster area, cluster density, number of molecules per cluster, and pairwise-distance ). The colors are used to discern clusters.
3. Discussion
A single-molecule localization microscope was developed and integrated with advanced clustering methods for assessment of molecular clusters. In the influenza type A disease model, HA molecules are known to assemble and form HA-assembly post 24 h of transfection (see Figure 2B). A conjugate photoactivable probe (Dendra2-HA) was used to study clustering in transfected NIH3T3 cells. The dynamics of these clusters (virion assembly), including their shape and size, are known to play critical roles that ultimately result in the maturation of the virus [4,63].
The clustering methods identify single-molecule clusters, and critical biophysical parameters are estimated. It is apparent that parameter estimation needs a multimodel approach and a single model is incapable of evaluating all parameters consistent with observation. In order to access the performance of clustering methods, test clusters with known biophysical parameters of interest (such as the number of clusters, number of molecule per cluster, cluster density, and pairwise distance between two nearby molecules) are computationally generated (see Figure 3). All clustering methods (point-clustering, Gaussian mixture model, and k-means) are then used to classify clusters and estimate the parameters. Comparison show point-clustering and k-means as the preferred method for estimating cluster size (area), whereas GMM and k-means are found to be suitable for determining pairwise distance. Both k-means and point-clustering show better estimation of cluster density, and all methods perform equally well for estimating the number of molecules per cluster (see Figure 3). Encouraged by the performance of clustering methods on simulated test data, we anticipate a similar trend for actual data.
The clustering methods are applied to real data (Dendra2HA transfected NIH3T3 cells) and analyzed. Results show that cluster density is better estimated by point-clustering and K-means, whereas cluster area is better estimated by point-clustering (see Figure 4). All clustering techniques perform equally well as far as the number of molecules per cluster is concerned. None of the methods are found to be suitable for determining pairwise distance accurately (see Figure 4). We found a disparity between dense and sparse clusters. Particularly for sparse clusters, cluster density and the number of molecules are better represented by K-means. This shows that accurate estimation of biophysical parameters is dependent on the strength of transfection. Parameter estimation on dense clusters is found to be in line with computational test data.
Overall, the proposed study provides a deeper understanding of single-molecule clustering process in the complex cellular system. It contributes to a better estimation of key biophysical parameters critical for understanding single-molecule complexes, resulting in a better determination of underlying biophysical mechanisms with single-molecule precision.
4. Methods and Protocols
4.1. Cell Culture
NIH3T3 fibroblast cells were thawed and resuspended in complete media ( penicillin streptomycin). The resuspended cells were centrifuged to form a pallete, which is resuspended again in PBS (1X) to remove toxicity caused by the freezing medium ( complete cell medium + DMSO ). Then, the solution was centrifuged to obtain a DMSO free pallete, which is resuspended in complete media and 105 cells were plated in 35 mm dish with 2 mL media (the counting of cells was performed using hemocytometer). The cells were kept undisturbed for 2 days in incubator (at 37 °C) so that the confluence of cells becomes 70–80% in the plate before the split. We have split the cells into three passages followed by transfection with Dendra-2HA plasmid-DNA.
4.2. Cell Transfection and Fixing
NIH 3T3 was used for the study. The cells were seeded in 35 mm dish supplemented with coverslip. The coverslip used was washed with ethanol prior to cell seeding to remove contamination, and then it was washed with PBS to remove leftover ethanol. Then, the cells were transfected with Dendra2-HA after 12–14 h of seeding. It should be noted that the cell count should be not more than 1–1.5 cells per 35 mm dish while seeding so that confluency after 12–14 h is around 60–70%. Lipofectamine 3000 (Life Technologies, Invitrogen) was used for transfecting NIH 3T3 cells with Dendra2–HA as per the Lipo 3000 protocol. The cells were kept in incubation (37 °C + 5% ) for 24 h in antibiotic free complete media (only DMEM and FBS). Subsequently, the cells were washed with PBS and then fixed with . After fixing, the cells were sealed in glass slide using Fluorosave solvent (Invitrogen, Carlsbad, CA, USA) to preserve it for a long duration. The cells were observed through white light to confirm that cells are in shape and subsequently visualized using blue light to observe green fluorescence from transfected cells. Then, the brightest cells (transfected cell) were chosen for single-molecule imaging.
4.3. Optical Setup
The optical system designed for visualizing molecular clusters technically consists of 3 optical arms: (1) blue laser (470–490 nm) for visualizing transfected cells, (2) violet laser (405 nm) for single-molecule activation, and (3) green laser (561 nm) for excitation of activated molecules (see, Figure 1). Dichroic mirror (DM 505) was used to combine the 405 nm and 561 nm laser and directed to the dichroic mirror of inverted fluorescence microscope. On its way, a flip mirror is used to choose either the combined beam (405 nm + 561 nm) or blue light. Blue light is used for identifying transfected cells. Subsequently, the combined beam is used for selectively exciting Dendra2HA single-molecules. A high NA objective (Olympus, 100X, 1.3 NA) is used to tightly focus the light onto the sample in an inverted microscope system (Olympus, IX81 Inverted, Tokoy, Japan). The emitted fluorescence light (570–600 nm) is collected by the same objective, transmits through the dichroic mirror DM 570, and filtered by a set of filters before focusing it on to the EMCCD camera (Andor, iXon 897 Ultra, Belfast, UK). The details of the actual setup and the components are discussed in Supplementary S1.
4.4. Superresolution Imaging and Image Reconstruction
The process begins by recording a large number of images followed by image processing to reconstruct a super-resolved image. For the present study, we have recorded 5000 images for a set of cells that express Dendra2HA. We have considered both weakly and strongly transfected cells. Images are recorded at 33 Hz with an EM-gain of 257. A total of 29,463 and 14,499 single-molecules corresponding to strong and weak transfected cells were recorded. A series of processes were carried out to isolate the single-molecule blinks from the background. This include particle-size filtering to remove false counting and photon-count filtering to remove random backgrounds. Subsequently, the bright spots are identified and fitted with a Gaussian filter. Further analysis is carried out to determine the centroid and variance of the fitted Gaussian. This provides the location and localization precision of the detected single molecules. The single molecules from all 5000 frames are superimposed to reconstruct a super-resolved image.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/photonics9010007/s1. The codes, datasets, and videos acquired for this study are available from the corresponding author upon request. This manuscript incorporates four supplementaries. Supplementary S1: Experimental Optical Setup. Supplementary S2: Data Collection and Analysis. Supplementary S3: Test Sample Generation and Processing.
Author Contributions
Conceptualization, P.J. and P.P.M.; Investigation, P.J. and P.P.M.; Methodology, P.J. and P.P.M.; Validation, P.J. and P.P.M. Both the authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors acknowledge fruitful discussion of fPALM microscopy with Samuel Hess, University of Maine, Orono, ME, USA.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Platzer, R.; Rossboth, B.K.; Schneider, M.C. Unscrambling fluorophore blinking for comprehensive cluster detection via photoactivated localization microscopy. Nat. Commun. 2020, 11, 4993. [Google Scholar] [CrossRef]
- Gudheti, M.V.; Curthoys, N.M.; Gould, T.J.; Kim, D.; Gunewardene, M.S.; Gabor, K.A.; Gosse, J.A.; Kim, C.H.; Zimmerberg, J.; Hess, S.T. Actin mediates the nanoscale membrane organization of the clustered membrane protein influenza hemagglutinin. Biophys. J. 2013, 104, 2182–2192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Civitci, F.; Shangguan, J.; Zheng, T. Fast and multiplexed superresolution imaging with DNA-PAINT-ERS. Nat. Commun. 2020, 11, 4339. [Google Scholar] [CrossRef] [PubMed]
- Curthoys, N.M.; Mlodzianoski, M.J.; Parent, M.; Butler, M.B.; Raut, P.; Wallace, J.; Lilieholm, J.; Mehmood, K.; Maginnis, M.S.; Waters, H.; et al. Influenza Hemagglutinin Modulates Phosphatidylinositol 4, 5-Bisphosphate Membrane Clustering. Biophys. J. 2019, 116, 893–909. [Google Scholar] [CrossRef] [Green Version]
- Deniz, A.A.; Mukhopadhyay, S.; Lemke, E.A. Single-molecule biophysics: At the interface of biology, physics and chemistry. J. R. Soc. Interface 2008, 5, 15–45. [Google Scholar] [CrossRef]
- Mondal, P.P. Probabilistic Optically-Selective Single-molecule Imaging Based Localization Encoded (POSSIBLE) microscopy for ultra-superresolution imaging. PLoS ONE 2020, 15, e0242452. [Google Scholar]
- Yasui, M.; Hiroshima, M.; Kozuka, J.; Sako, Y.; Ueda, M. Automated single-molecule imaging in living cells. Nat. Commun. 2018, 9, 3061. [Google Scholar] [CrossRef] [PubMed]
- Gustavsson, A.K.; Petrov, P.N.; Lee, M.Y.; Shechtman, Y.; Moerner, W.E. 3D single-molecule super-resolution microscopy with a tilted light sheet. Nat. Commun. 2018, 9, 123. [Google Scholar] [CrossRef] [Green Version]
- Mondal, P.P.; Hess, S.T. Total internal reflection fluorescence based multiplane localization microscopy enables super-resolved volume imaging. Appl. Phys. Lett. 2017, 110, 211102. [Google Scholar] [CrossRef]
- Greiss, F.; Deligiannaki, M.; Jung, C.; Gaul, U.; Braun, D. Single-Molecule Imaging in Living Drosophila Embryos with Reflected Light-Sheet Microscopy. Biophys. J. 2016, 110, 939–946. [Google Scholar] [CrossRef] [Green Version]
- Andrecka, J.; Arroyo, J.O.; Lewis, K.; Cross, R.A.; Kukura, P. Label-free Imaging of Microtubules with Sub-nm Precision Using Interferometric Scattering Microscopy. Biophys. J. 2016, 110, 214–217. [Google Scholar] [CrossRef] [Green Version]
- Luo, F.; Qin, G.; Xia, T.; Fang, X. Single-Molecule Imaging of Protein Interactions and Dynamics. Ann. Rev. Anal. Chem. 2020, 13, 337. [Google Scholar] [CrossRef] [PubMed]
- Moerner, W.E.; Kador, L. Optical detection and spectroscopy of single molecules in a solid. Phys. Rev. Lett. 1989, 62, 2535. [Google Scholar] [CrossRef] [Green Version]
- Hess, S.T.; Girirajan, T.P.; Mason, M.D. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys. J. 2006, 91, 4258–4272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valles, M.; Hess, S.T. A Cross Beam Excitation Geometry for Localization Microscopy. iSci. Notes 2017, 2, 1. [Google Scholar]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Rust, M.; Bates, M.; Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 2006, 3, 793–796. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, M.G.L. Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution. Proc. Natl. Acad. Sci. USA 2005, 102, 13081–13086. [Google Scholar] [CrossRef] [Green Version]
- Cella Zanacchi, F.; Lavagnino, Z.; Perrone Donnorso, M.; Del Bue, A.; Furia, L.; Faretta, M.; Diaspro, A. Live-cell 3D super-resolution imaging in thick biological samples. Nat. Methods 2011, 8, 1047–1049. [Google Scholar] [CrossRef]
- Fölling, J.; Bossi, M.; Bock, H.; Medda, R.; Wurm, C.A.; Hein, B.; Jakobs, S.; Eggeling, C.; Hell, S.W. Fluorescence nanoscopy by ground-state depletion and single-molecule return. Nat. Methods 2008, 5, 943–945. [Google Scholar] [CrossRef] [PubMed]
- Dertinger, T.; Colyer, R.; Iyer, G.; Weiss, S.; Enderlein, J. Fast, background-free, 3D super-resolution optical fluctuation imaging (SOFI). Proc. Natl. Acad. Sci. USA 2009, 106, 22287–22292. [Google Scholar] [CrossRef] [Green Version]
- Sharonov, A.; Hochstrasser, R.M. Wide-field subdiffraction imaging by accumulated binding of diffusing probes Alexey Sharonov and Robin M. Hochstrasser. Proc. Natl. Acad. Sci. USA 2006, 103, 18911–18916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giannone, G.; Hosy, E.; Levet, F.; Constals, A.; Schulze, K.; Sobolevsky, A.I.; Rosconi, M.P.; Gouaux, E.; Tampé, R.; Choquet, D.; et al. Dynamic superresolution imaging of endogenous proteins on living cells at ultra-high density. Biophys. J. 2010, 99, 1303–1310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mondal, P.P. Simultaneous multiplane imaging-based localization encoded (SMILE) microscopy for super-resolution volume imaging. Microsc. Res. Tech. 2017, 80, 333. [Google Scholar] [CrossRef]
- Gwosch, K.C.; Pape, J.K.; Balzarotti, F.; Hoess, P.; Ellenberg, J.; Ries, J.; Hell, S.W. MINFLUX nanoscopy delivers 3D multicolor nanometer resolution in cells. Nat. Methods 2020, 217–224. [Google Scholar] [CrossRef]
- Zhang, Y.; Schroeder, L.K.; Lessard, M.D.; Kidd, P.; Chung, J.; Song, Y.; Benedetti, L.; Li, Y.; Ries, J.; Grimm, J.B.; et al. Nanoscale subcellular architecture revealed by multicolor three-dimensional salvaged fluorescence imaging. Nat. Methods 2020, 17, 225–231. [Google Scholar] [CrossRef]
- AbuZineh, K.; Joudeh, L.I.; Al Alwan, B.; Hamdan, S.M.; Merzaban, J.S.; Habuchi, S. Microfluidics-based super-resolution microscopy enables nanoscopic characterization of blood stem cell rolling. Sci. Adv. 2018, 4, eaat5304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mlodzianoski, M.J. Future Considerations for Localizationbased Super-resolution Fluorescence Microscopy. iSci. NoteS 2016, 1, 5. [Google Scholar]
- Thevathasan, J.V.; Kahnwald, M.; Cieśliński, K.; Hoess, P.; Peneti, S.K.; Reitberger, M.; Heid, D.; Kasuba, K.C.; Hoerner, S.J.; Li, Y.; et al. Nuclear pores as versatile reference standards for quantitative superresolution microscopy. Nat. Methods 2019, 16, 1045–1053. [Google Scholar] [CrossRef]
- Habuchi, S. Microfluidics-based Super-Resolution Imaging: A New Tool for Nanoscopic Charactertization of Cellular Interactions. iSci. Notes 2019, 4, 1. [Google Scholar] [CrossRef]
- Ma, H.; Xu, J.; Liu, Y. WindSTORM: Robust online image processing for high-throughput nanoscopy. Sci. Adv. 2019, 5, eaaw0683. [Google Scholar] [CrossRef] [Green Version]
- Turcotte, R.; Liang, Y.; Tanimoto, M.; Zhang, Q.; Li, Z.; Koyama, M.; Betzig, E.; Ji, N. Dynamic super-resolution structured illumination imaging in the living brain. Proc. Natl. Acad. Sci. USA 2019, 116, 9586–9591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.; Taki, M.; Sato, Y.; Tamura, Y.; Yaginuma, H.; Okada, Y.; Yamaguchi, S. A photostable fluorescent marker for the superresolution live imaging of the dynamic structure of the mitochondrial cristae. Proc. Natl. Acad. Sci. USA 2019, 116, 15817–15822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chlanda, P.; Zimmerberg, J. Protein–lipid interactions critical to replication of the influenza A virus. FEBS Lett. 2016, 590, 1940. [Google Scholar] [CrossRef] [Green Version]
- Hess, S.T.; Gould, T.J.; Gudheti, M.V.; Maas, S.A.; Mills, K.D.; Zimmerberg, J. Dynamic clustered distribution of hemagglutinin resolved at 40 nm in living cell membranes discriminates between raft theories. Proc. Natl. Acad. Sci. USA 2007, 104, 17370–17375. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, R.; Blanco, M.R.; Kahlscheuer, M.L.; Abelson, J.; Guthrie, C.; Walter, N.G. Biased Brownian ratcheting leads to pre-mRNA remodeling and capture prior to first-step splicing. Nat. Struct. Mol. Biol. 2013, 20, 1450–1457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voicu, A.; Duteanu, N.; Voicu, M.; Vlad, D.; Dumitrascu, V. The rcdk and cluster R packages applied to drug candidate selection. J. Cheminform. 2020, 12, 3. [Google Scholar] [CrossRef] [Green Version]
- Lemmer, M.; Inkpen, M.S.; Kornysheva, K.; Long, N.J.; Albrecht, T. Unsupervised vector-based classification of single-molecule charge transport data. Nat. Commun. 2016, 7, 12922. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.; Park, S.; Challapalli, S.D.; Fei, J.; Wang, Y. Robust nonparametric quantification of clustering density of molecules in single-molecule localization microscopy. PLoS ONE 2017, 12, e0179975. [Google Scholar] [CrossRef] [Green Version]
- Ripley, B.D. Modelling spatial patterns. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 172–192. [Google Scholar] [CrossRef]
- Kiskowski, M.A.; Hancock, J.F.; Kenworthy, A.K. On the use of Ripley’s K-function and its derivatives to analyze domain size. Biophys. J. 2009, 97, 1095–1103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Parent, M.; Hess, S.T. Quantification of Mitochondrial Membrane Curvature by Three-Dimensional Localization Microscopy. iSci. Notes 2019, 4, 3. [Google Scholar] [CrossRef]
- Mondal, P.P. Spatio-Temporal Super-resolution Optical Fluorescence Microscopy. iSci. Notes 2016, 1, 4. [Google Scholar] [CrossRef]
- Joshi, P.; Mondal, P.P. Adaptable single molecule localization microscopy (aSMLM) for superresolution optical fluorescence imaging. Appl. Phys. Lett. 2021, 119, 173703. [Google Scholar] [CrossRef]
- Thompson, R.E.; Larson, D.R.; Webb, W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002, 82, 2775–2783. [Google Scholar] [CrossRef] [Green Version]
- Veit, M.; Serebryakova, M.V.; Kordyukova, L.V. Palmitoylation of influenza virus proteins. Biochem. Soc. Trans. 2013, 41, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Veit, M.; Kretzschmar, E.; Kuroda, K.; Garten, W.; Schmidt, M.F.; Klenk, H.D.; Rott, R. Site-specific mutagenesis identifies three cysteine residues in the cytoplasmic tail as acylation sites of influenza virus hemagglutinin. J. Virol. 1991, 65, 2491–2500. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. In Proceedings of the 1999 ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 31 May–3 June 1999. [Google Scholar]
- Marcon, Y. Distance-Based Clustering of a Set of XY Coordinates. MATLAB Central File Exchange. 2021. Available online: https://www.mathworks.com/matlabcentral/fileexchange/56150-distance-based-clustering-of-a-set-of-xy-coordinates (accessed on 22 October 2021).
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745. [Google Scholar] [CrossRef] [Green Version]
- Mondal, P.P.; Vicidomini, G.; Diaspro, A. Image reconstruction for multiphoton fluorescence microscopy. Appl. Phys. Lett. 2008, 92, 103902. [Google Scholar] [CrossRef]
- Mondal, P.P. Markov random field aided Bayesian approach for image reconstruction in confocal microscopy. J. Appl. Phys. 2007, 102, 044701. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; p. 1027. [Google Scholar]
- Lloyd, S.P. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129. [Google Scholar] [CrossRef]
- Fraix-Burnet, D.; Thuillard, M.; Chattopadhyay, A.K. Multivariate approaches to classification in extragalactic astronomy. Front. Astron. Space Sci. 2015, 2, 3. [Google Scholar] [CrossRef] [Green Version]
- Perez-Ortega, J.; Almanza-Ortega, N.N.; Romero, D. Balancing effort and benefit of K-means clustering algorithms in Big Data realms. PLoS ONE 2018, 13, e0201874. [Google Scholar] [CrossRef] [PubMed]
- Okawa, S.; Yano, A.; Uchida, K.; Mitsui, Y.; Yoshida, M.; Takekoshi, M.; Marjono, A.; Gao, F.; Hoshi, Y.; Kida, I.; et al. Phantom and mouse experiments of time-domain fluorescence tomography using total light approach. Biomed. Opt. Exp. 2013, 4, 635–651. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Gaoa, M.; Papadakis, G.Z.; Luna, B.; Jain, S.; Mollura, D.J.; Bagci, U. Joint solution for PET image segmentation, denoising, and partial volume correction. Med. Image Anal. 2018, 46, 229–243. [Google Scholar] [CrossRef] [PubMed]
- Dou, D.; Revol, R.; Östbye, H.; Wang, H.; Daniels, R. Influenza A Virus Cell Entry, Replication, Virion Assembly and Movement. Front Immunol. 2018, 9, 1581. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).