Surface Measurement of a Large Inflatable Reflector in Cryogenic Vacuum
Abstract
:1. Introduction
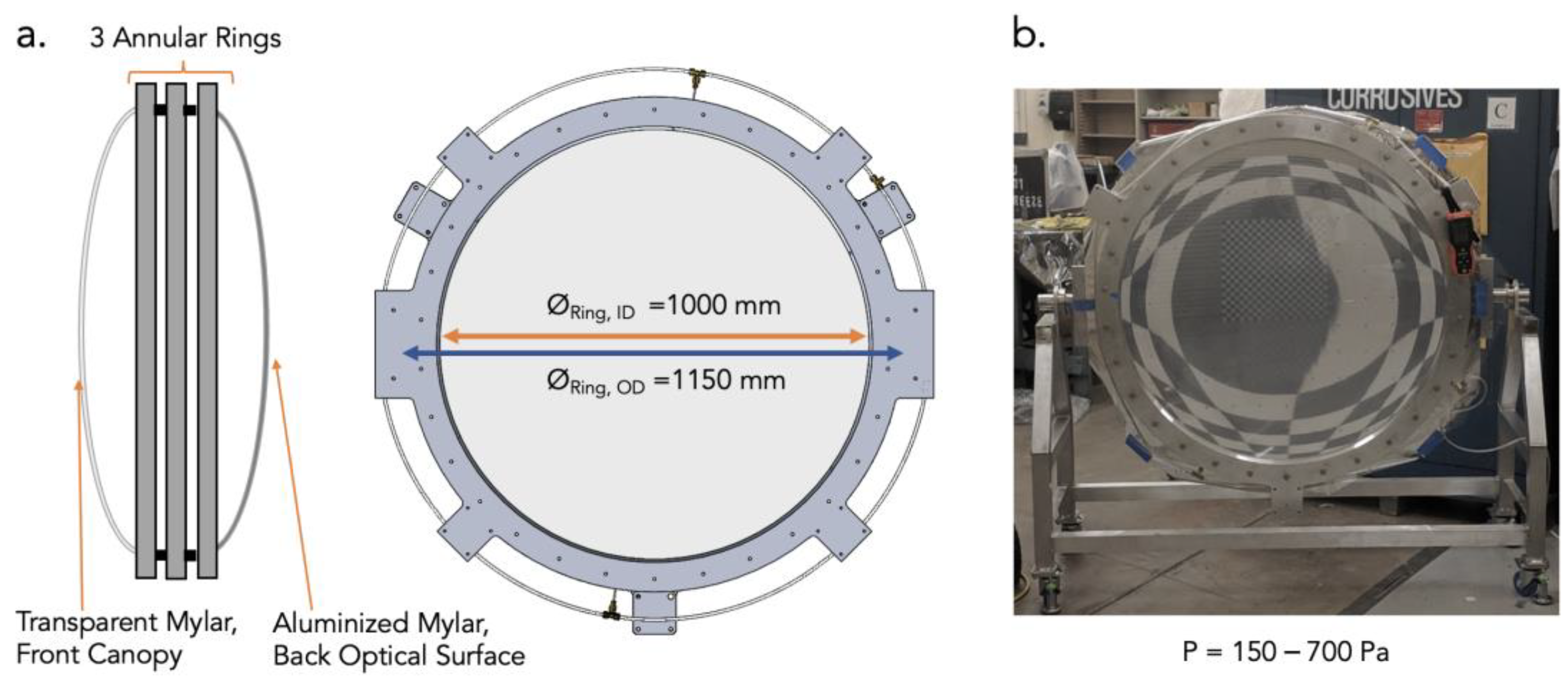
1.1. Geometrical Shape of Pneumatic Membranes
1.2. Thermal Vacuum Chamber Testing and Surface Testing
1.3. Regular Deflectometry Measurement
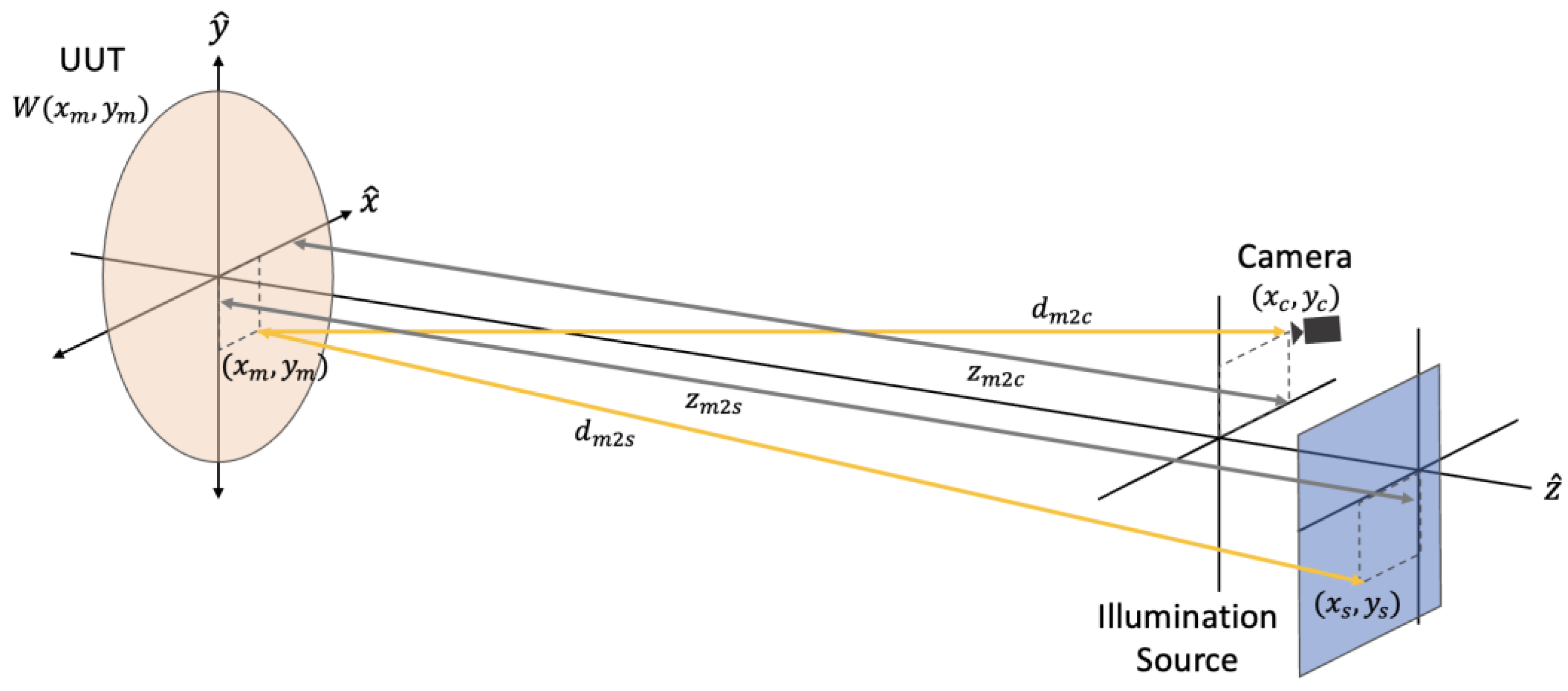
2. Theory and Simulation for Deflectometry Measurement
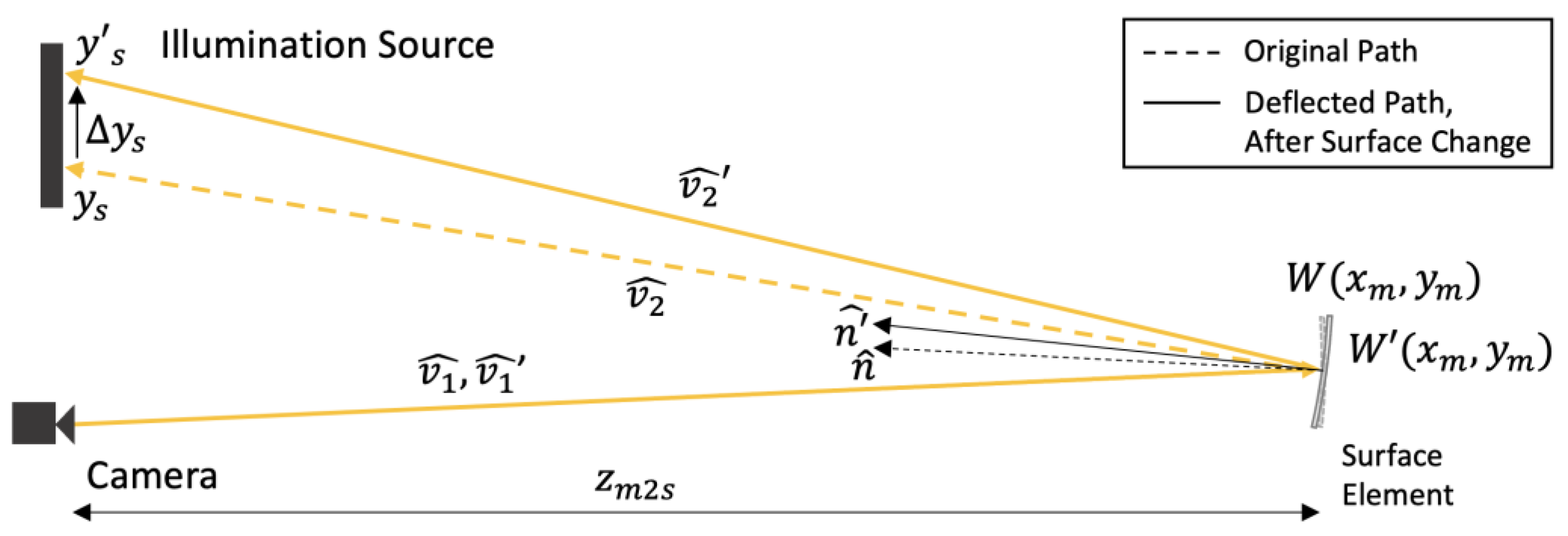
2.1. Differential Deflectometry Measurement
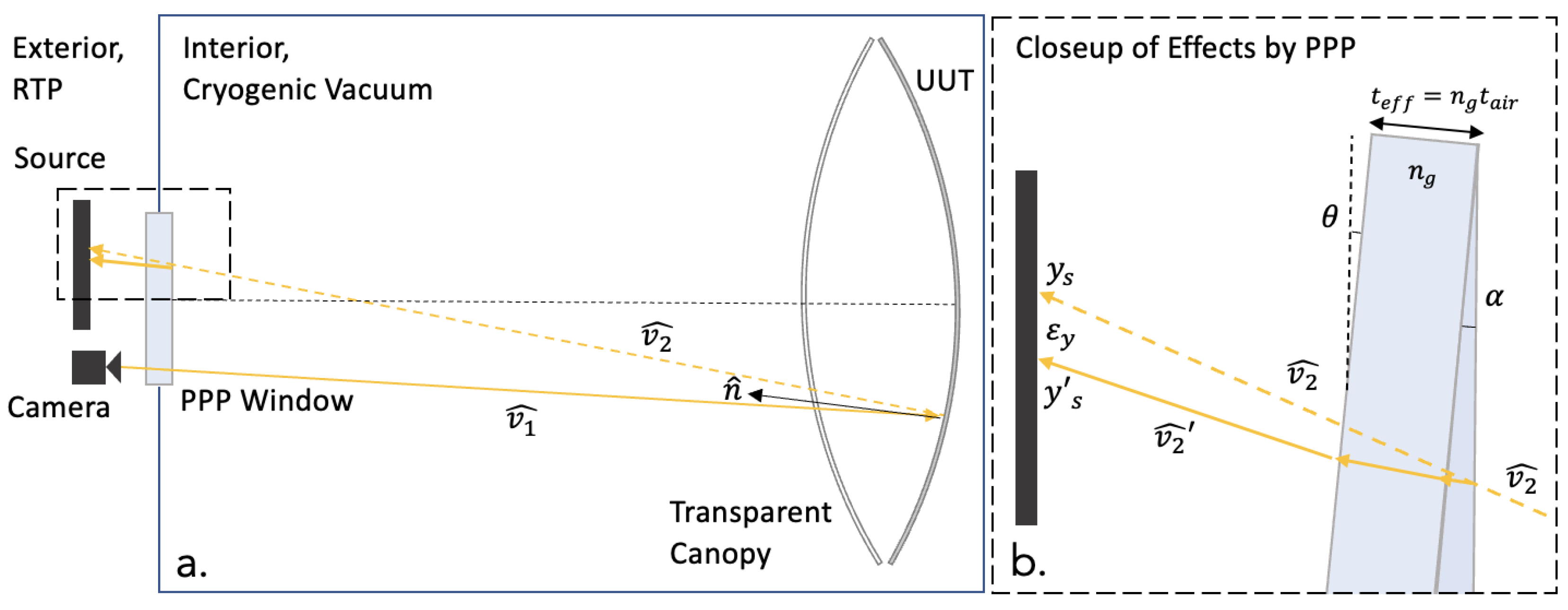
2.2. Unique Geometry of Thermal Vacuum Chamber
2.3. Plane Parallel Plate Geometry with Differential Deflectometry
3. Experimental Setups
4. Experimental Results
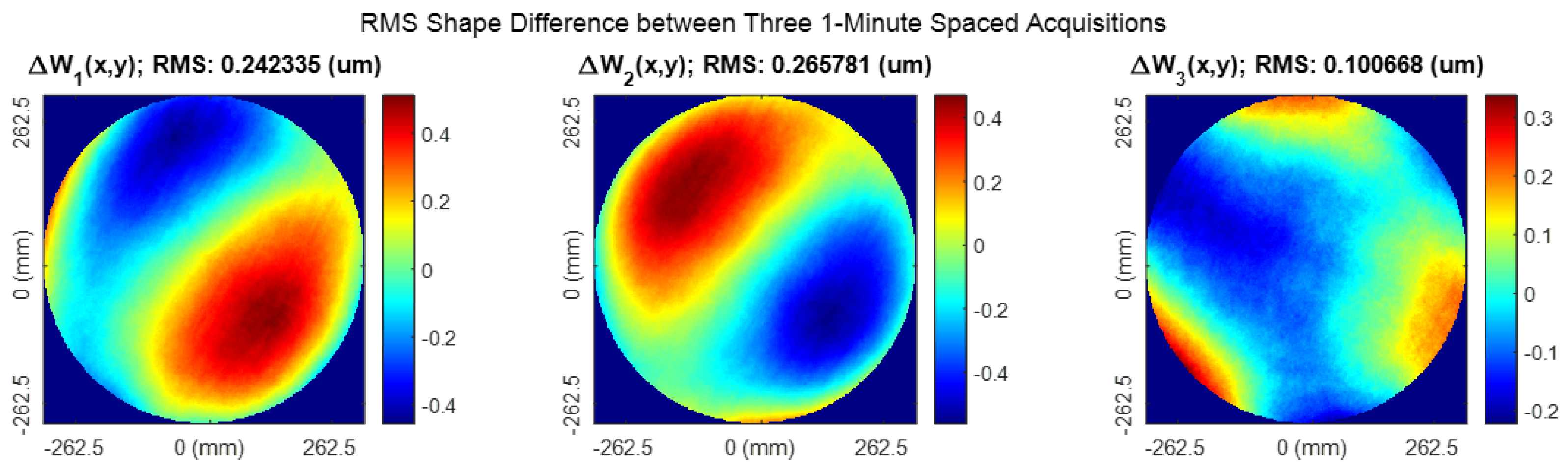
4.1. Deflectometer Repeatability Measurements
4.2. Induced Thermal Gradient by Artifical Sun
4.3. Induced Puncture Response
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Freeland, R.E.; Bilyeu, G. In-Step Inflatable Antenna Experiment. Acta Astronaut. 1993, 30, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Walker, C.K.; Chin, G.; Aalto, S.; Anderson, C.M.; Arenberg, J.W.; Battersby, C.; Bergin, E.; Bergner, J.; Biver, N.; Bjorakerb, G.L.; et al. Orbiting Astronomical Satellite for Investigating Stellar Systems (OASIS): Following the water trail from the interstellar medium to oceans. In Proceedings of the Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems III., San Diego, CA, USA, 1–5 August 2021; p. 26. [Google Scholar] [CrossRef]
- Arenberg, J.W.; Villareal, M.N.; Yamane, J.; Yu, T.; Lazear, J.; Pohner, J.; Sangalis, M.; Jackson, S.L.; Morse, E.; Tyler, R.; et al. OASIS architecture: Key features. In Proceedings of the Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems III., San Diego, CA, USA, 1–5 August 2021; p. 30. [Google Scholar] [CrossRef]
- Palisoc, A.; Pardoen, G.; Takashima, Y.; Chandra, A.; Sirsi, S.; Choi, H.; Kim, D.W.; Quach, H.; Arenberg, J.; Walker, C.K. Analytical and finite element analysis tool for nonlinear membrane antenna modeling for astronomical applications. In Proceedings of the Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems III., San Diego, CA, USA, 1–5 August 2021; p. 32. [Google Scholar] [CrossRef]
- Hencky, H. Über den Spannungszustand in kreisrunden Platten. Z. Angew. Math. Mech. 1915, 63, 311–317. [Google Scholar]
- Quach, H.; Esparza, M.A.; Kang, H.; Chandra, A.; Choi, H.; Berkson, J.; Karrfalt, K.; Sirsi, S.; Takashima, Y.; Palisoc, A.; et al. Deflectometry-based thermal vacuum testing for a pneumatic terahertz antenna. In Proceedings of the Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems III., San Diego, CA, USA, 1–5 August 2021; p. 34. [Google Scholar] [CrossRef]
- Chandra, A.; Walker, C.K. Thermally formed inflatable reflectors for space telescopes. In Proceedings of the Conference 2020 IEEE Aerospace Conference, AERO 2020, Big Sky, MT, USA, 7–14 March 2020. [Google Scholar] [CrossRef]
- Choi, H.; Palisoc, A.; Pandde, A.V.; Esparza, M.A.; Berkson, J.; Takashima, Y.; Kim, D.W.; Walker, C.K. Mid-to-high frequency characterization of inflatable membrane optics. In Proceedings of the Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems III., San Diego, CA, USA, 1–5 August 2021; p. 33. [Google Scholar] [CrossRef]
- Quach, H.; Berkson, J.; Sirsi, S.; Choi, H.; Dominguez, R.; Duffy, B.; Lesser, D.; Takashima, Y.; Palisoc, A.; Walker, C.; et al. Full-aperture optical metrology for inflatable membrane mirrors. In Proceedings of the Optical Manufacturing and Testing XIII., Online Only, 24 August–4 September 2020; p. 20. [Google Scholar] [CrossRef]
- Evans, C.E.; Greenberg, E.S.; Aldridge, D.A.; Santman, J.J. Cryogenic wavefront error measurement for the James Webb Space Telescope fine guidance sensor powered optics. Interferom. XV Tech. Anal. 2010, 7790, 779004. [Google Scholar] [CrossRef]
- Black, J.T.; Pappa, R.S. Photogrammetry and videogrammetry methods for solar sails and other gossamer structures. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; pp. 1671–1681. [Google Scholar] [CrossRef] [Green Version]
- Pappa, R.S.; Giersch, L.R.; Quagliaroli, J.M. Photogrammetry of a 5m inflatable space antenna with consumer-grade digital cameras. Exp. Tech. 2001, 25, 21–29. [Google Scholar] [CrossRef]
- Hayden, J.; Eegholm, B.; Space, S.; Kubalak, D.; Hadjimichael, T.; Ohl, R.; Goddard, N.; Flight, S. Mathematical Corrections Applied to Laser Radar Measurements Made Through a Cryogenic Vacuum Chamber Window. In Proceedings of the Coordinate Metrology Systems Conference, Phoenix, AZ, USA, 25–29 July 2011; p. 6. [Google Scholar]
- Xu, Y.; Wang, Y.; Gao, F.; Jiang, X. Segmentation phase measuring deflectometry for measuring structured specular surfaces. Int. J. Adv. Manuf. Technol. 2021. [Google Scholar] [CrossRef]
- Jain, U.; Gauthier, A.; van der Meer, D. Total-internal-reflection deflectometry for measuring small deflections of a fluid surface. Exp. Fluids 2021, 62, 1–14. [Google Scholar] [CrossRef]
- Willomitzer, F.; Yeh, C.-K.; Gupta, V.; Spies, W.; Schiffers, F.; Katsaggelos, A.; Walton, M.; Cossairt, O. Hand-guided qualitative deflectometry with a mobile device. Opt. Express 2020, 28, 9027. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Opt. Lasers Eng. 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, F.; Jiang, X. A brief review of the technological advancements of phase measuring deflectometry. PhotoniX 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Ritter, R.; Hahn, R. Contribution to analysis of the reflection grating method. Opt. Lasers Eng. 1983, 4, 13–24. [Google Scholar] [CrossRef]
- Su, P.; Parks, R.E.; Wang, L.; Angel, R.P.; Burge, J.H. Software configurable optical test system: A computerized reverse Hartmann test. Appl. Opt. 2010, 49, 4404. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Su, P.; Horne, T.; Brusa, G.; Burge, J.H. Optical metrology of a large deformable aspherical mirror using software configurable optical test system. Opt. Eng. 2014, 53, 085106. [Google Scholar] [CrossRef] [Green Version]
- Kam, J. Differential Phase Measuring Deflectometry for High-Sag Freeform Optics; The University of Arizona: Tucson, AZ, USA, 2019. [Google Scholar]
- Huang, R. High Precision Optical Surface Metrology Using Deflectometry; University of Arizona: Tucson, AZ, USA, 2015. [Google Scholar]
- Smith, W. Modern Optical Engineering, 4th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Esparza, M.A. Stressed Deformable Reflector and Pneumatic Membrane Antenna for Thermal Vacuum Terahertz Wavefront Control and Measurement. In Proceedings of the Astronomical Optics: Design, Manufacture, and Test of Space and Ground Systems III., San Diego, CA, USA, 1–5 August 2021. [Google Scholar] [CrossRef]
- Trumper, I.; Choi, H.; Kim, D.W. Instantaneous phase shifting deflectometry. Opt. Express 2016, 24, 27993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, M.T.; Ghim, Y.S.; Rhee, H.G. Single-shot deflectometry for dynamic 3D surface profile measurement by modified spatial-carrier frequency phase-shifting method. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Sirsi, S. Orbiting Astronomical Satellite for Investigating Stellar Systems (OASIS) Space Telescope; The University of Arizona: Tucson, AZ, USA, 2021. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quach, H.; Kang, H.; Sirsi, S.; Chandra, A.; Choi, H.; Esparza, M.; Karrfalt, K.; Berkson, J.; Takashima, Y.; Palisoc, A.; et al. Surface Measurement of a Large Inflatable Reflector in Cryogenic Vacuum. Photonics 2022, 9, 1. https://doi.org/10.3390/photonics9010001
Quach H, Kang H, Sirsi S, Chandra A, Choi H, Esparza M, Karrfalt K, Berkson J, Takashima Y, Palisoc A, et al. Surface Measurement of a Large Inflatable Reflector in Cryogenic Vacuum. Photonics. 2022; 9(1):1. https://doi.org/10.3390/photonics9010001
Chicago/Turabian StyleQuach, Henry, Hyukmo Kang, Siddhartha Sirsi, Aman Chandra, Heejoo Choi, Marcos Esparza, Karlene Karrfalt, Joel Berkson, Yuzuru Takashima, Art Palisoc, and et al. 2022. "Surface Measurement of a Large Inflatable Reflector in Cryogenic Vacuum" Photonics 9, no. 1: 1. https://doi.org/10.3390/photonics9010001
APA StyleQuach, H., Kang, H., Sirsi, S., Chandra, A., Choi, H., Esparza, M., Karrfalt, K., Berkson, J., Takashima, Y., Palisoc, A., Arenberg, J. W., Walker, C., d’Aubigny, C. D., & Kim, D. (2022). Surface Measurement of a Large Inflatable Reflector in Cryogenic Vacuum. Photonics, 9(1), 1. https://doi.org/10.3390/photonics9010001





