Parametric Mid-Spatial Frequency Surface Error Synthesis
Abstract
:1. Introduction
2. Materials and Methods
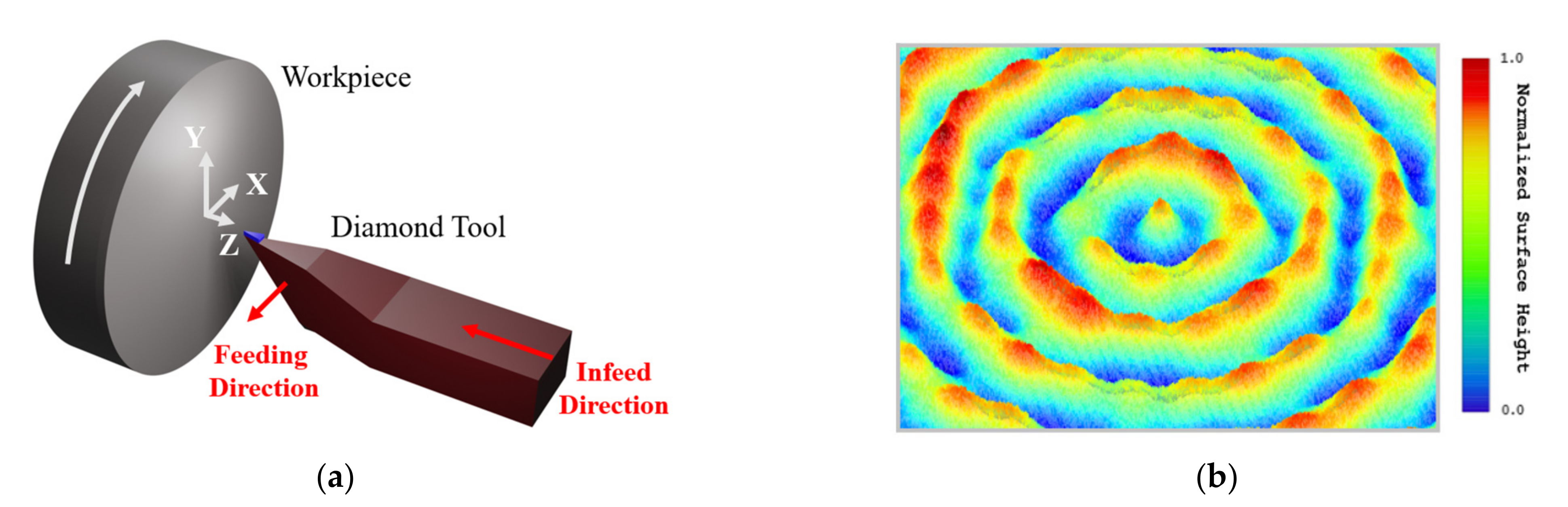
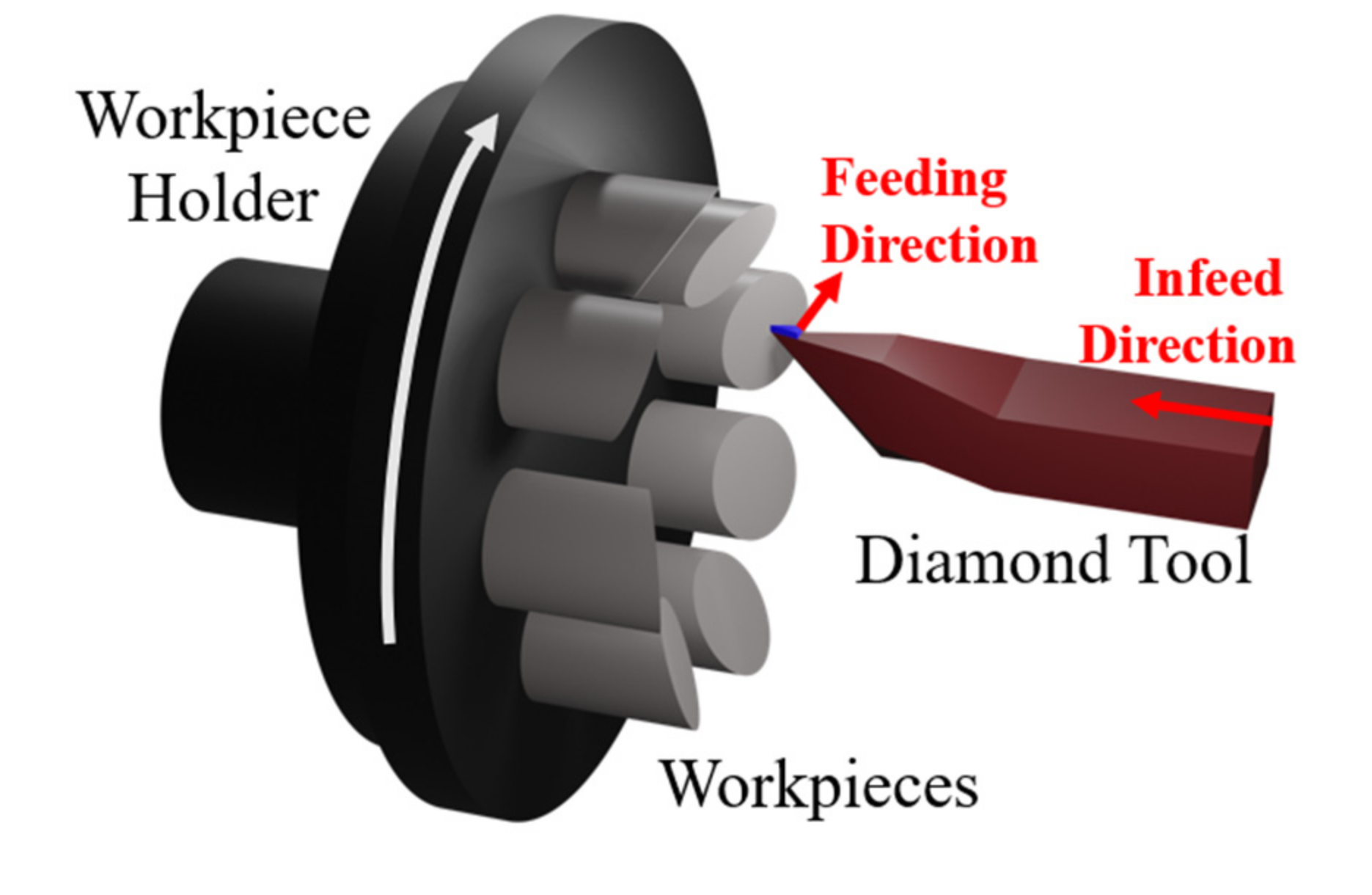
2.1. Single-Point Diamond Turning
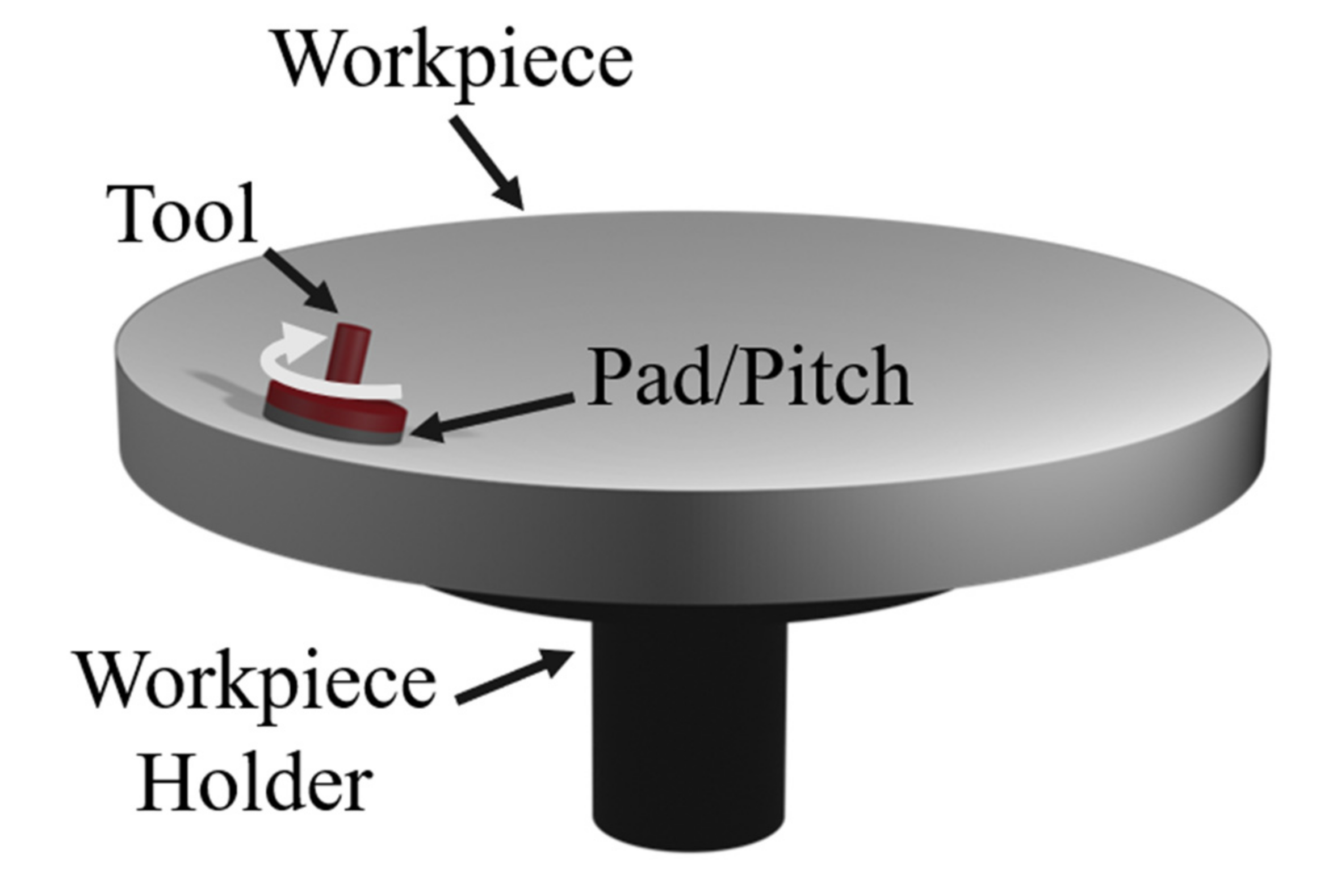
2.2. Sub-Aperture Tool Polishing
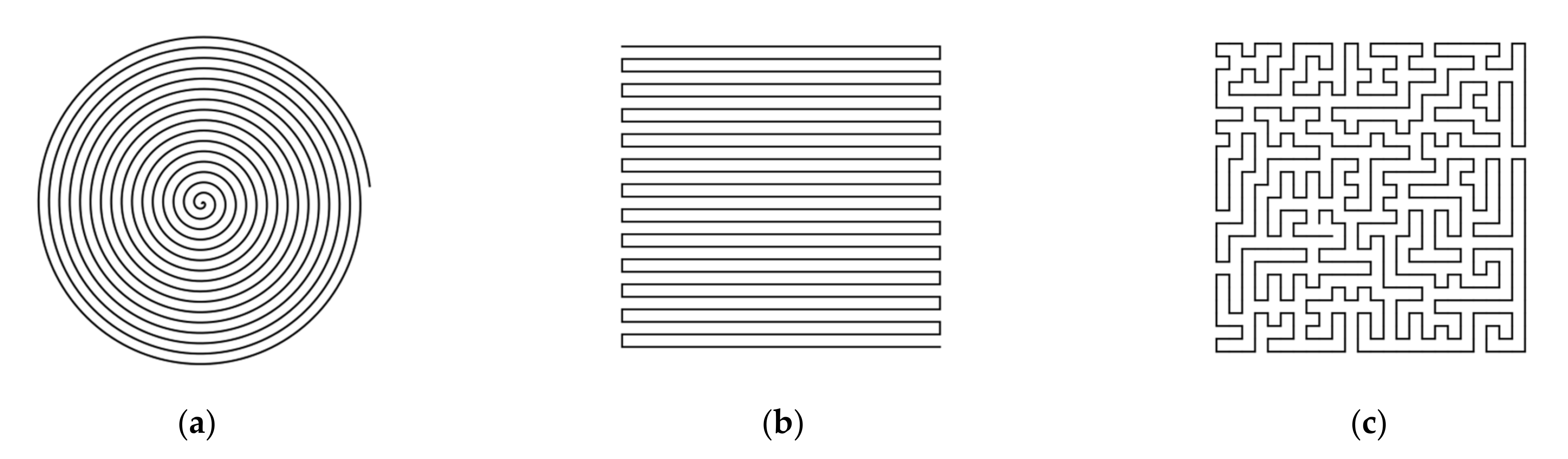
3. Classification of Tooling Mark Features
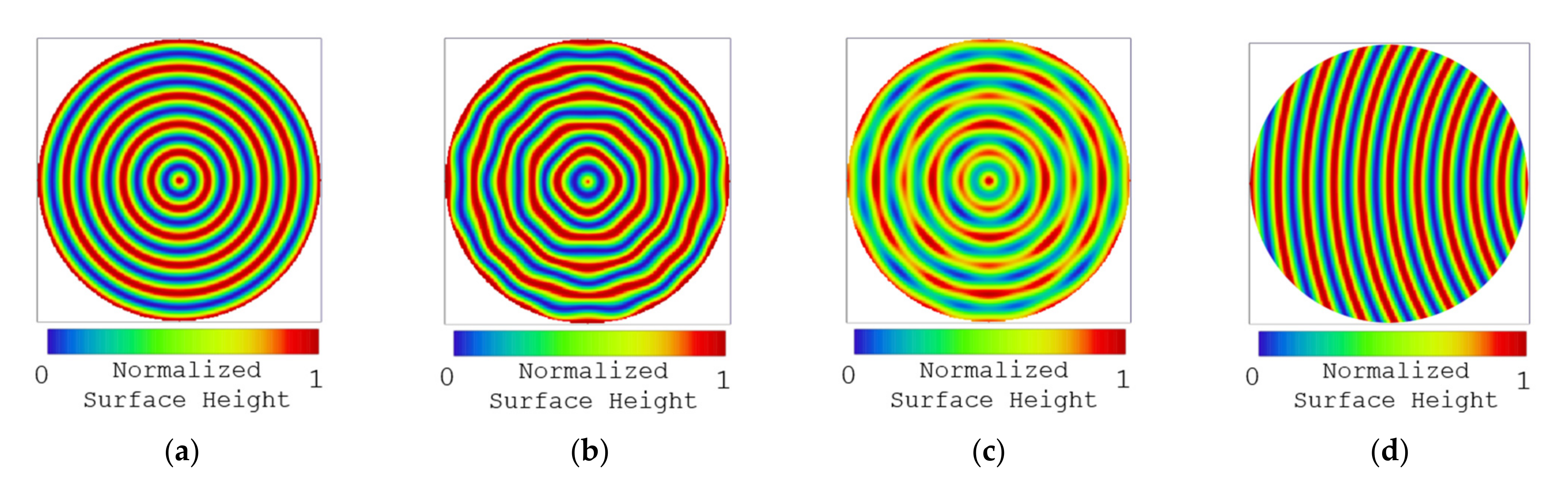
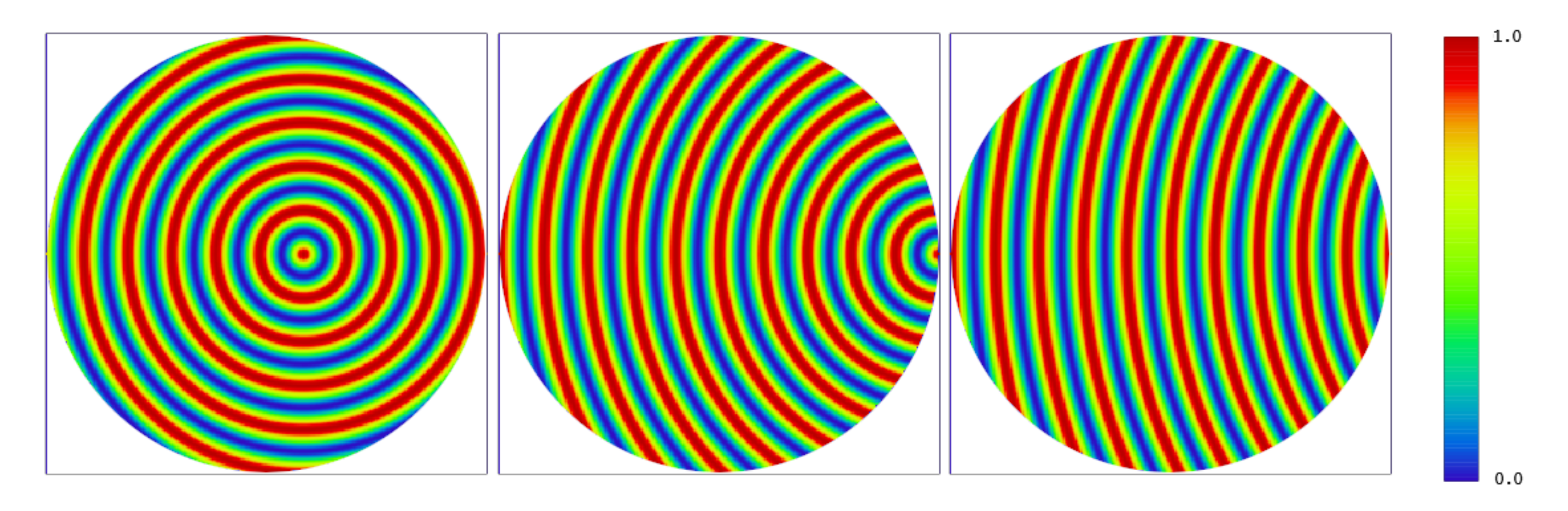
3.1. Radial Rooling Marks, Gρ
3.2. In-Plane Tooling Marks, Gφ
3.3. Out-of-Plane Tooling Marks, Hz
3.4. Off-Axis Radial Tooling Marks
4. Parametric Optical Modelling and Evaluation Criteria
4.1. Optical Model Parametrization
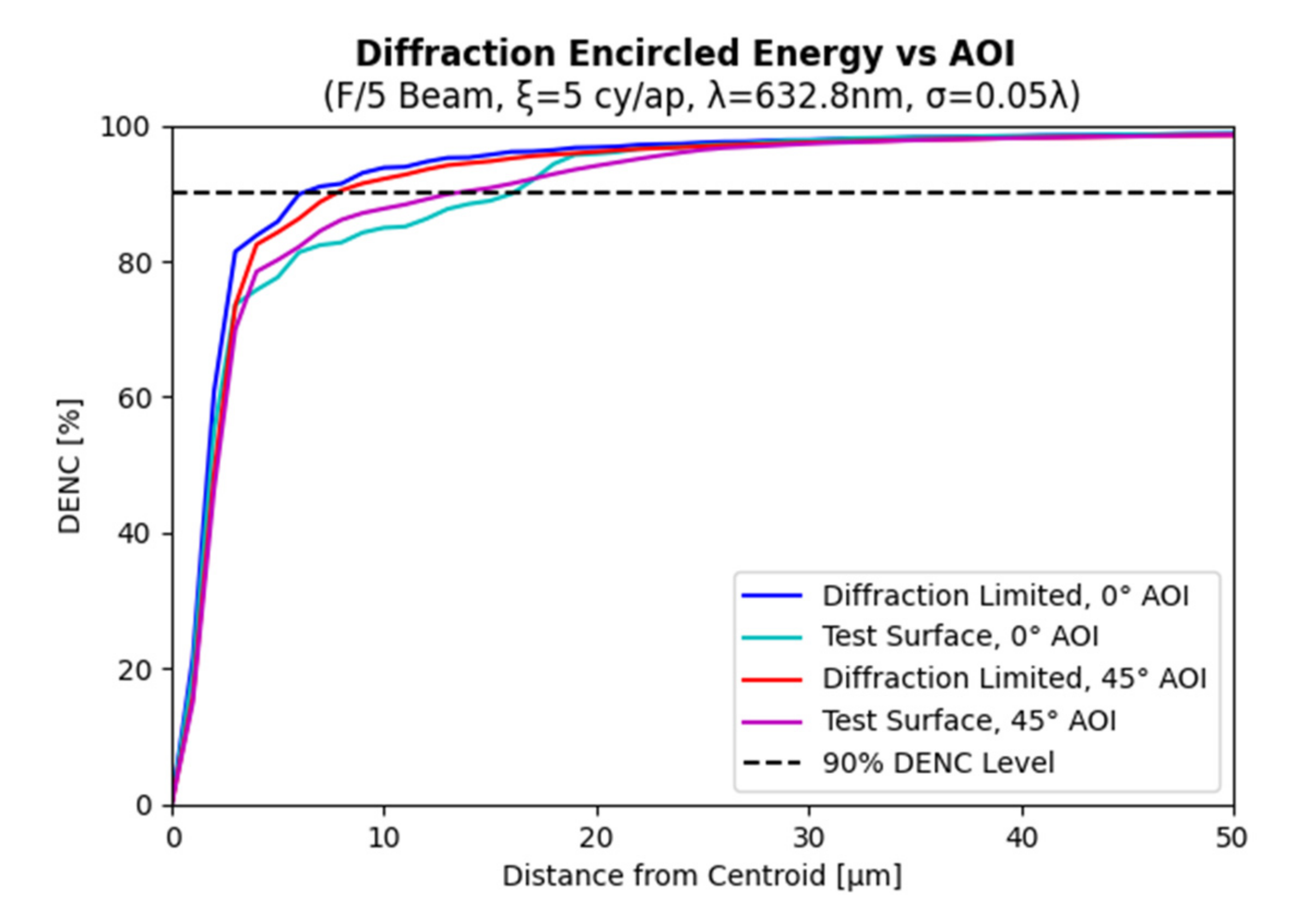
4.2. Performance Metric Calculation Approach
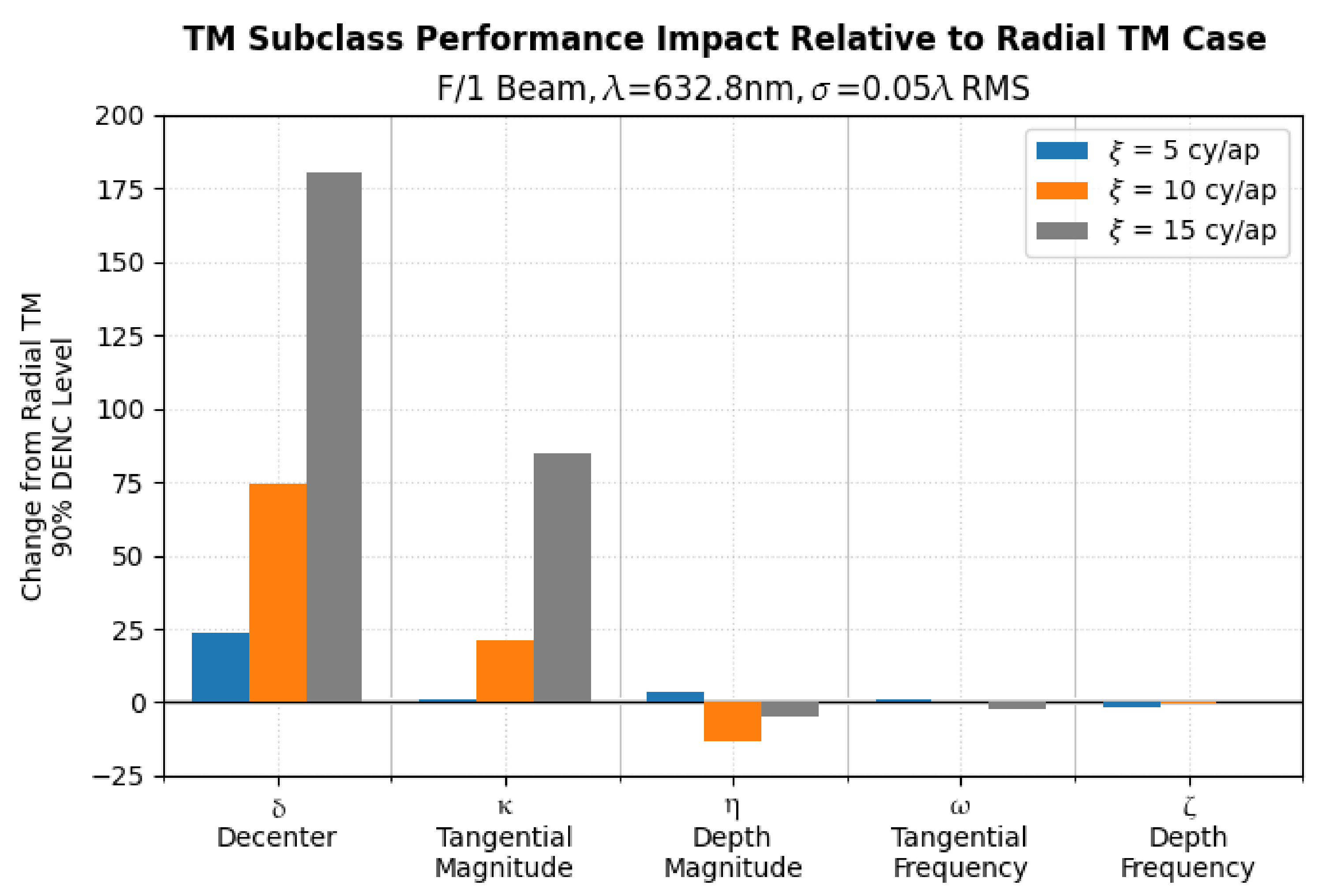
5. Parametric Regression Optical Performance Synthesis
5.1. Form of Parametric Fits
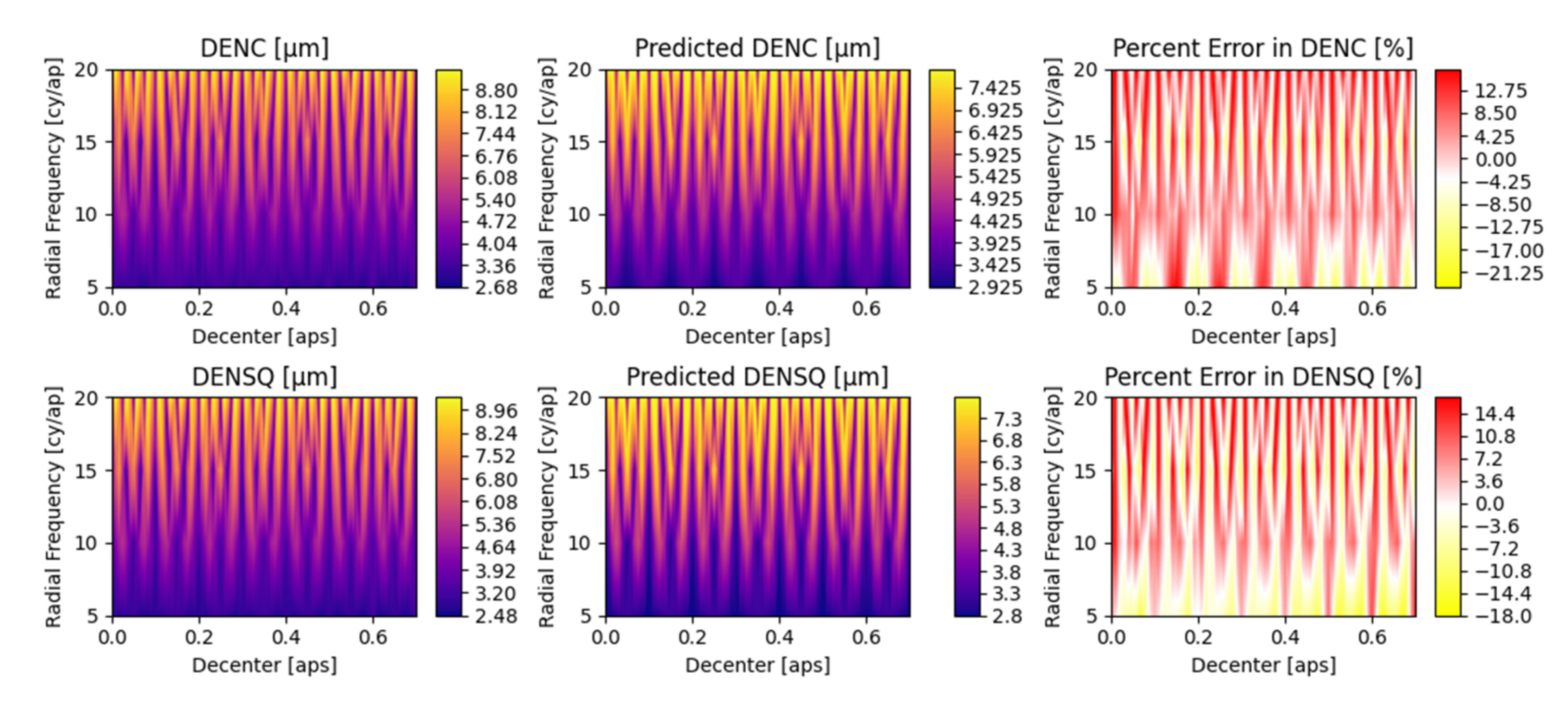
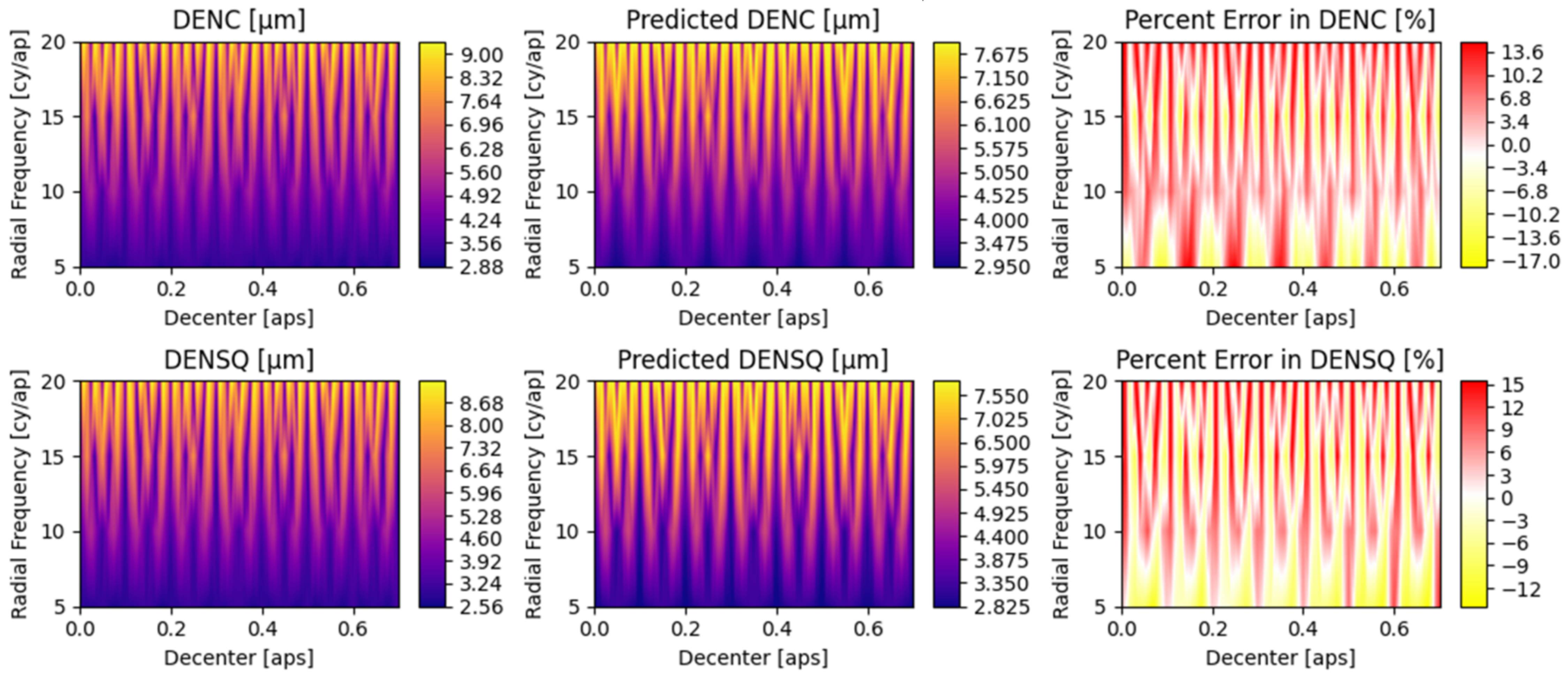
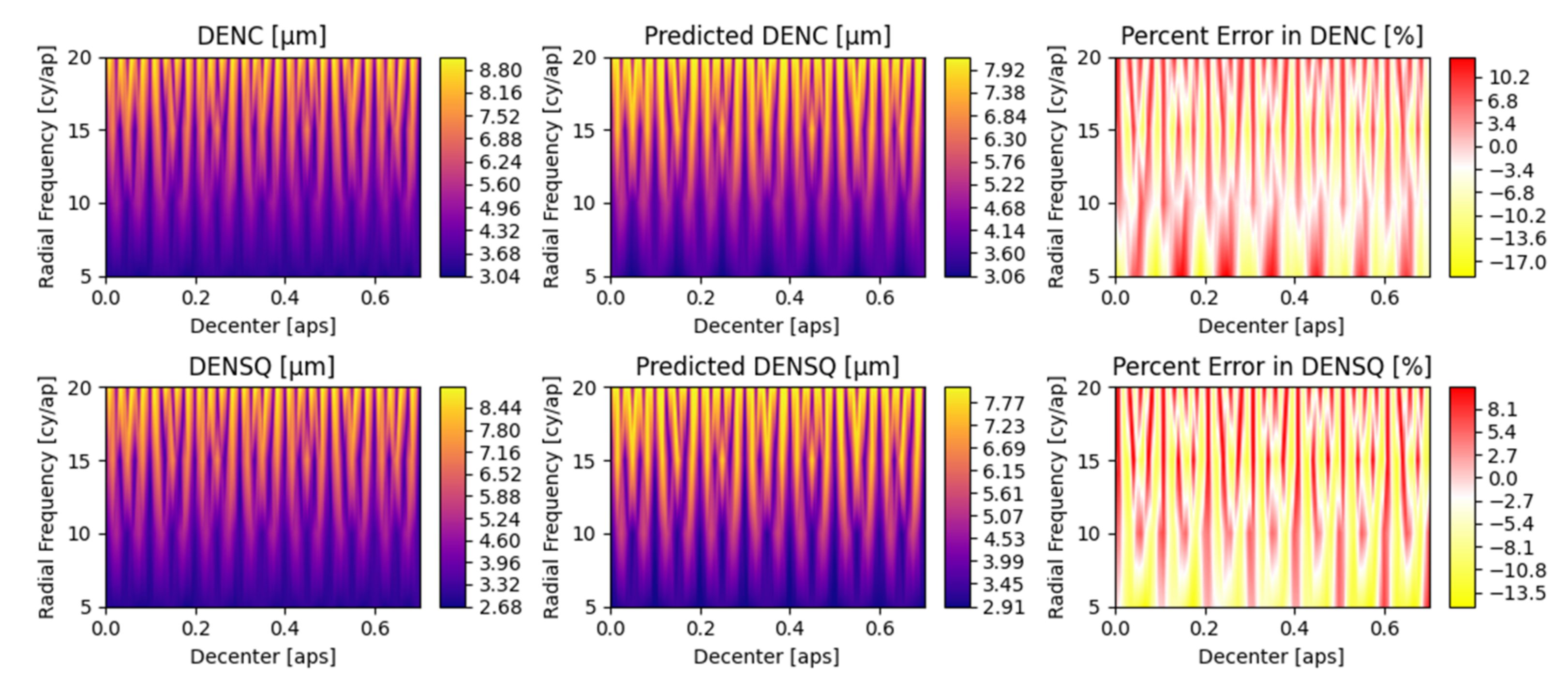
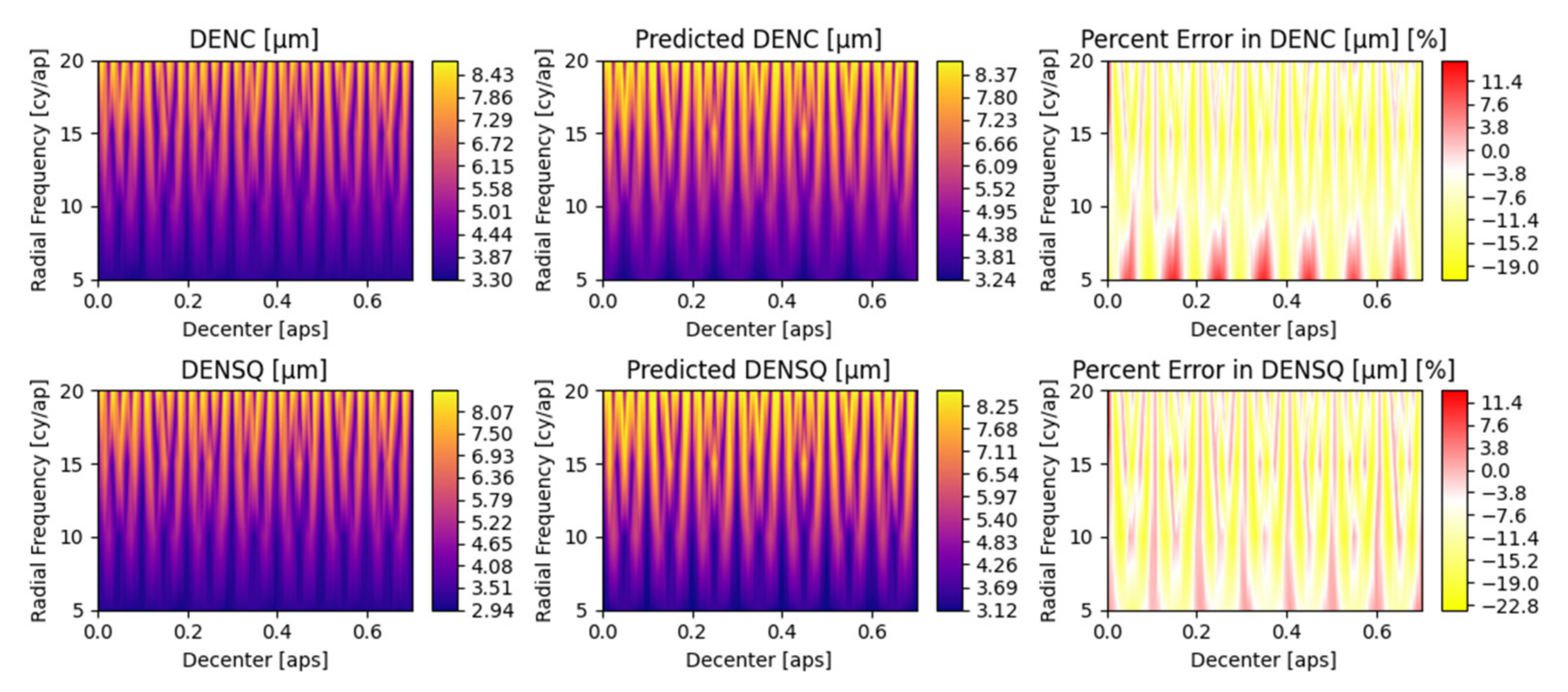
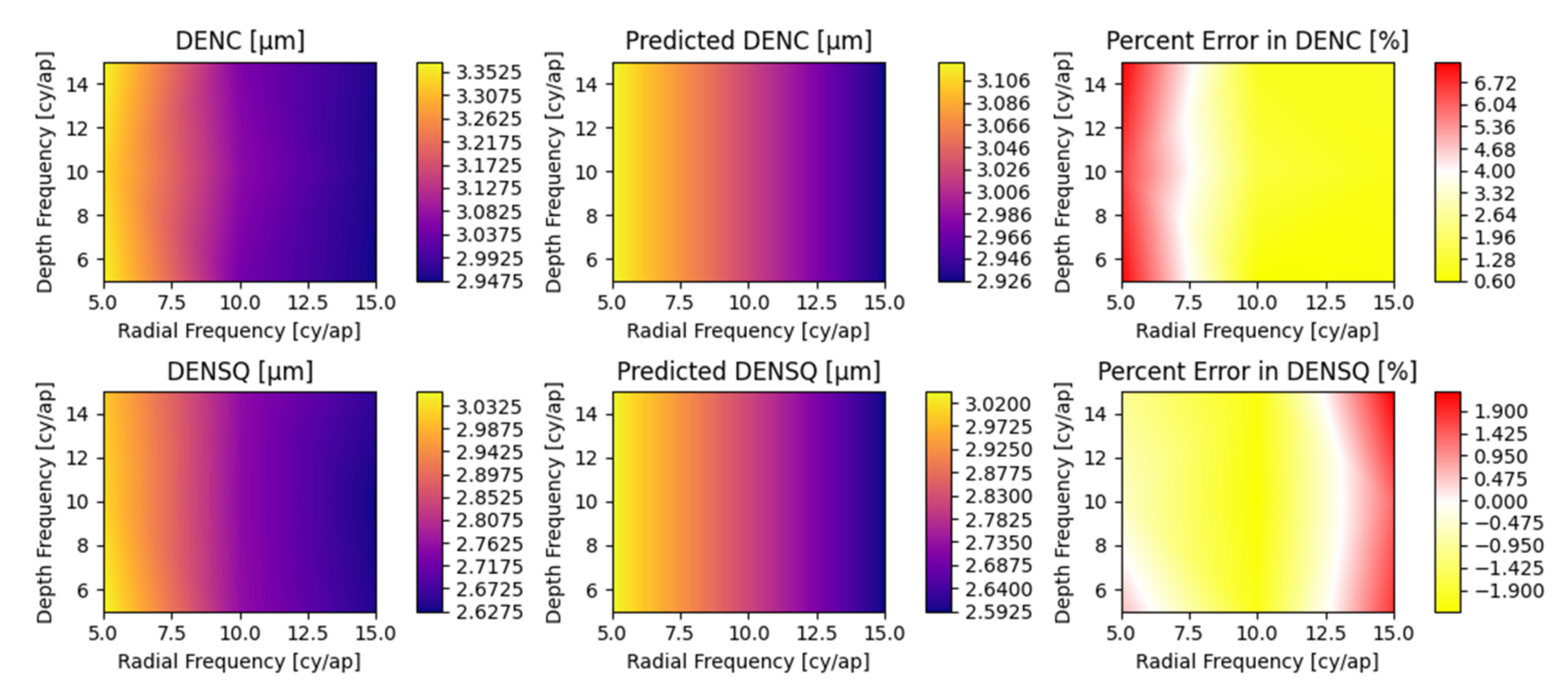
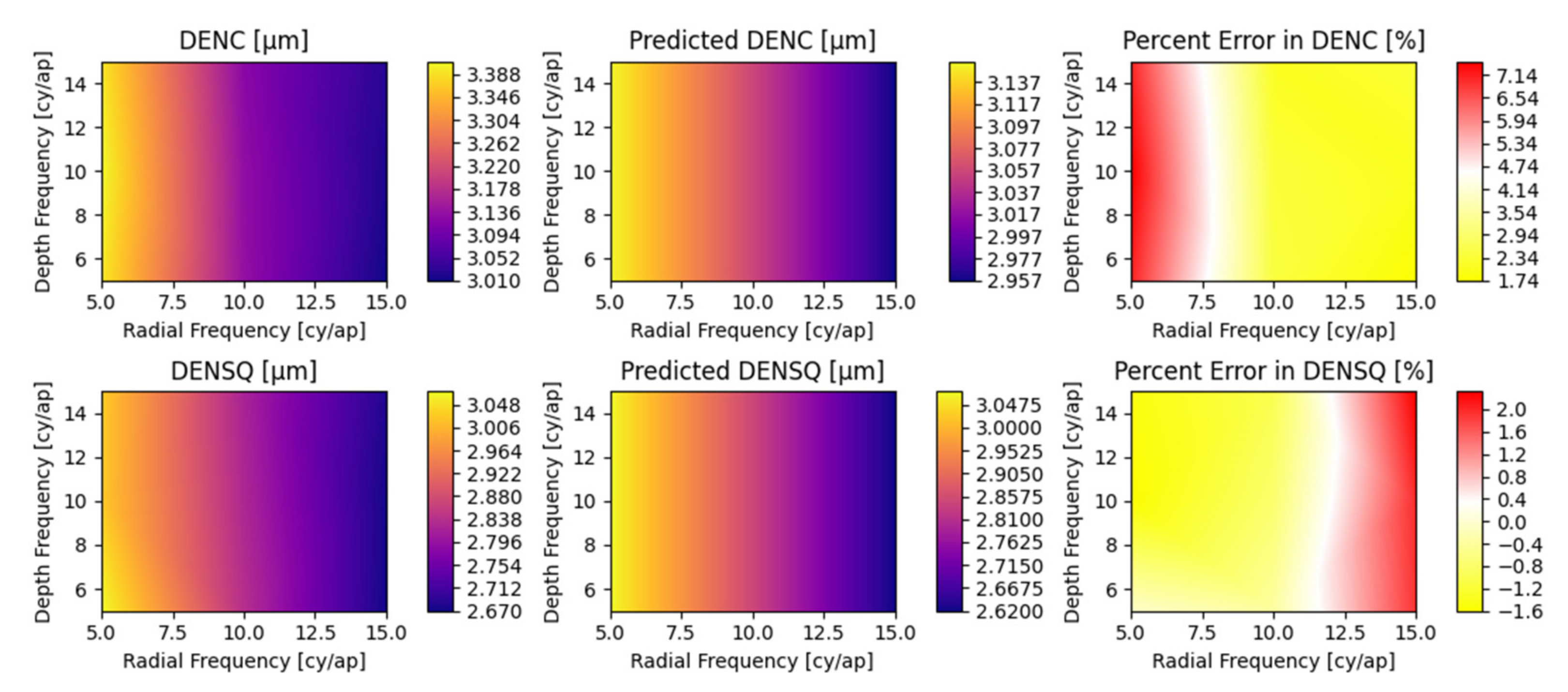
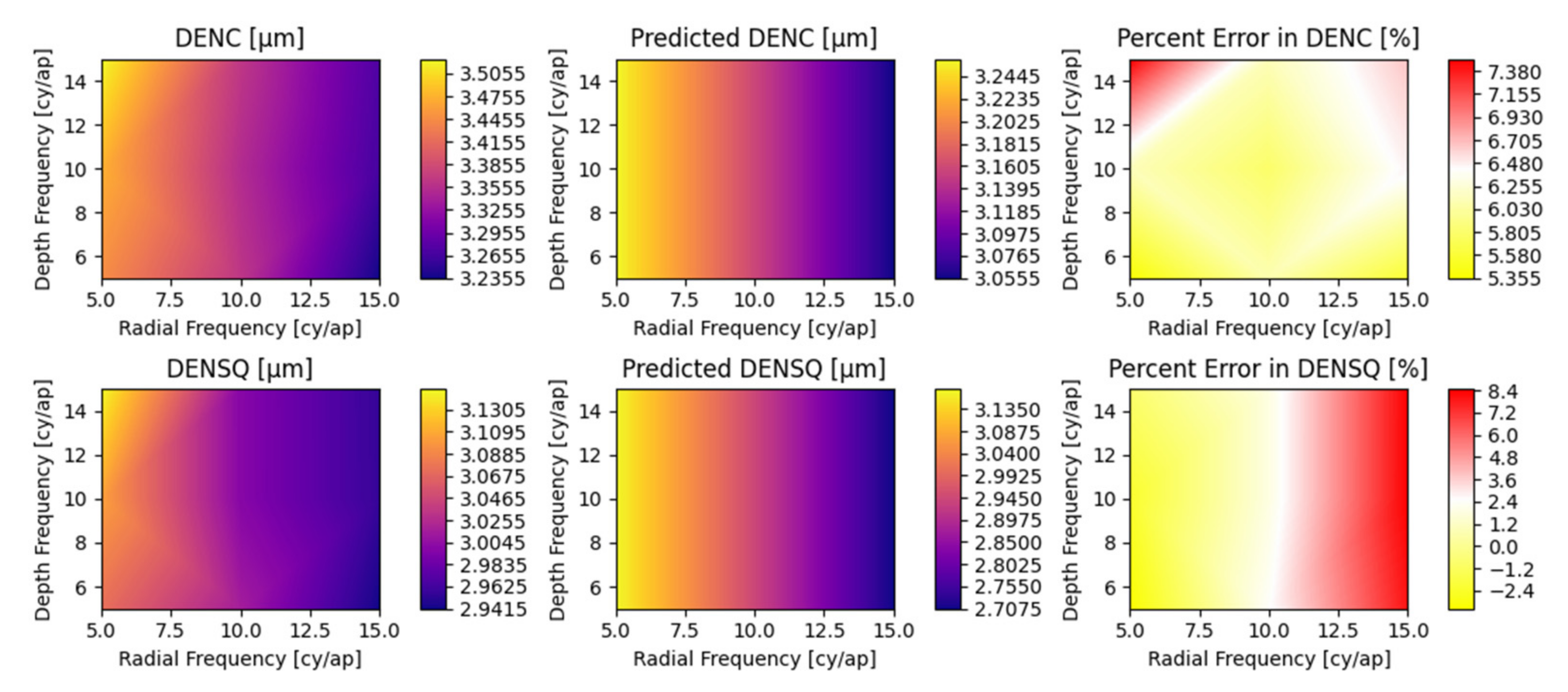
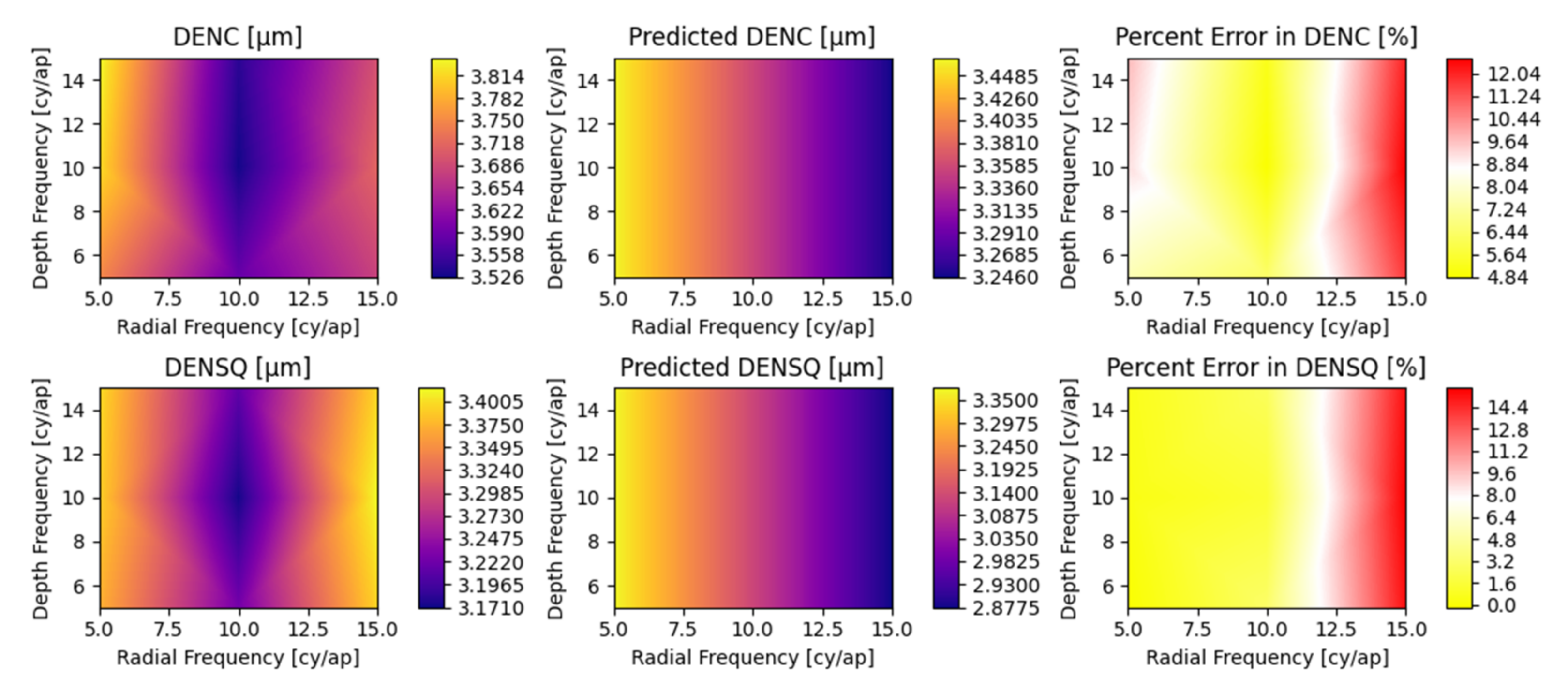
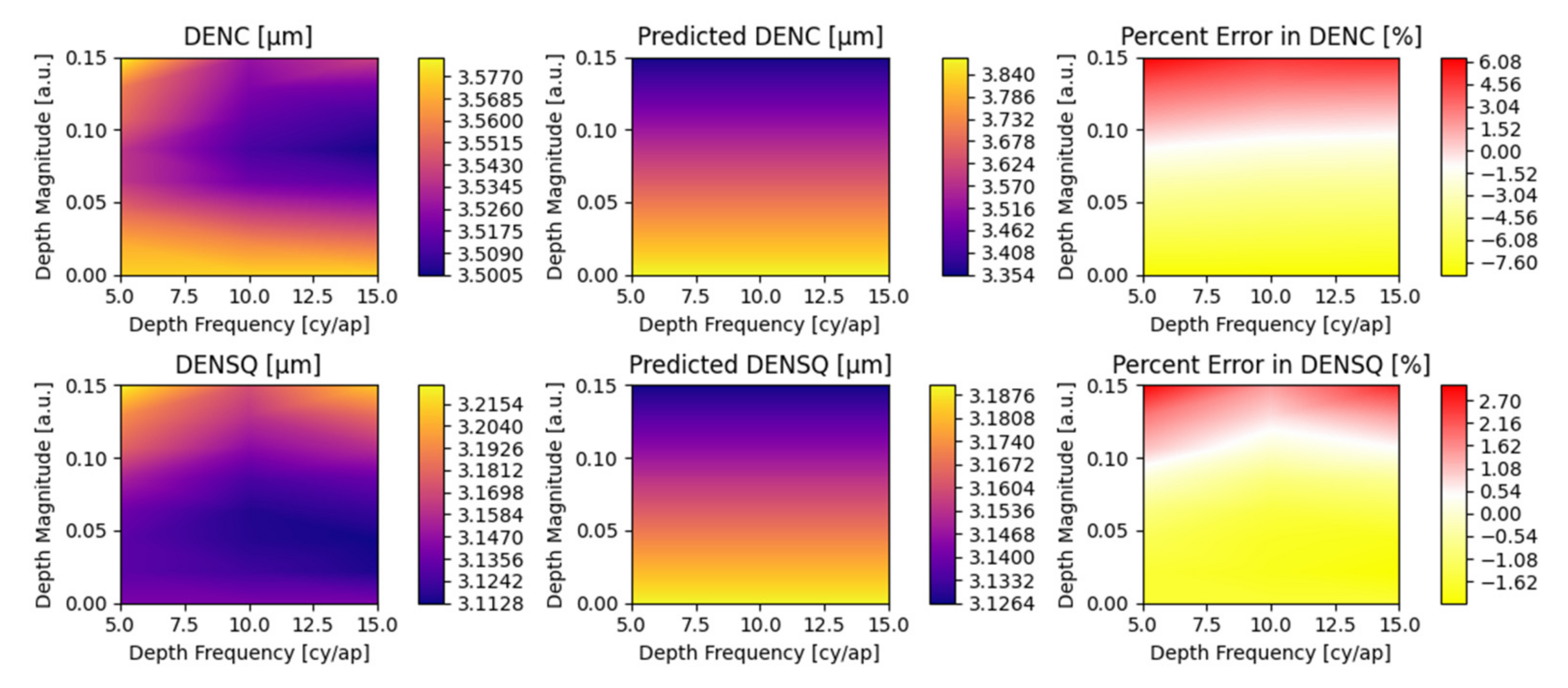
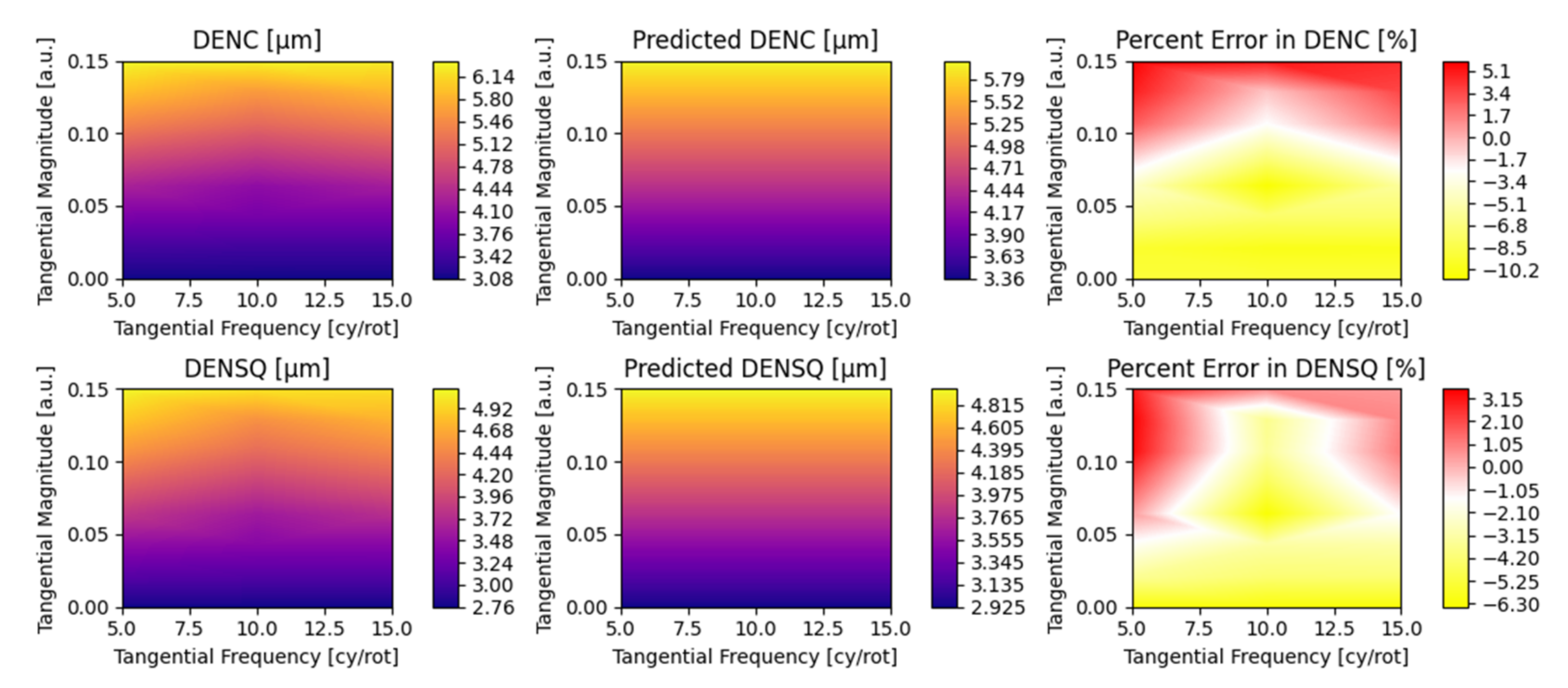
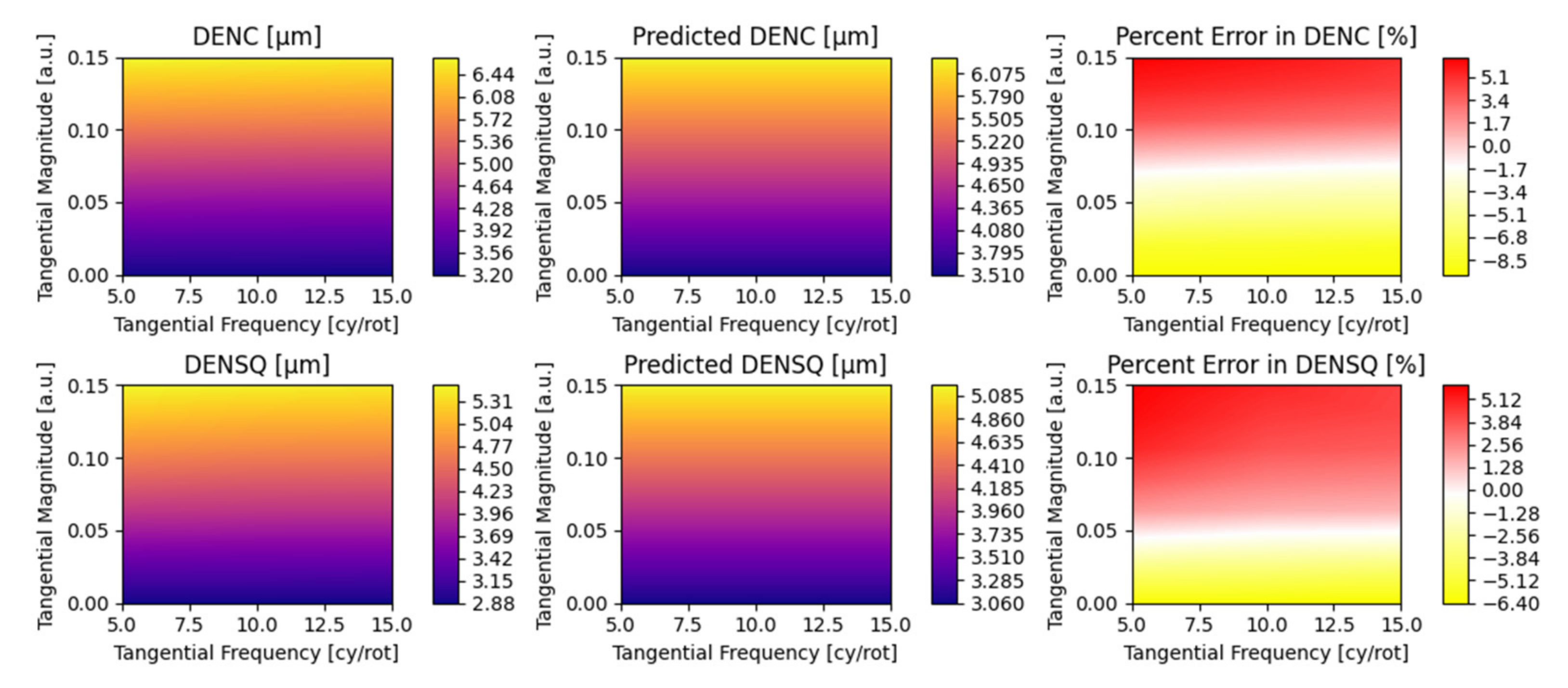
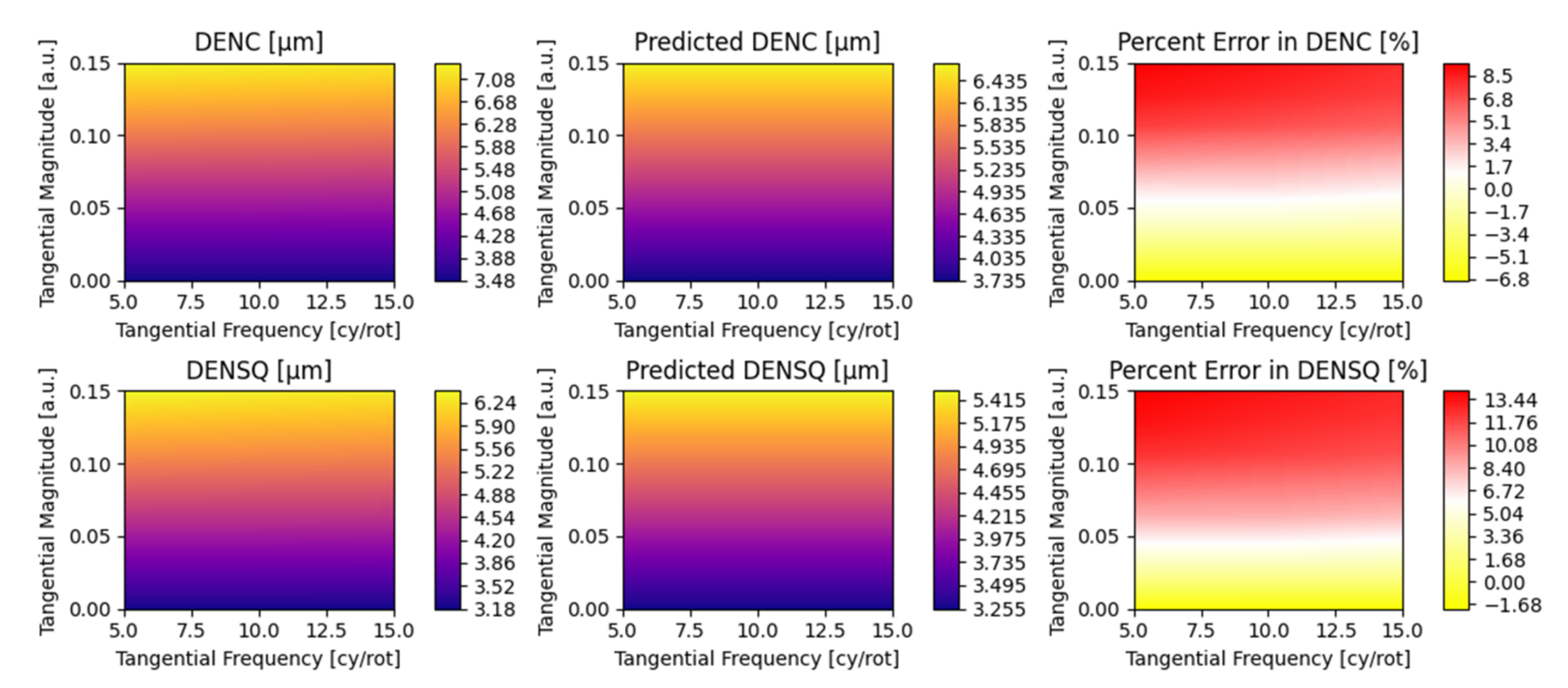
5.2. Parametric Coefficients and Evaluation of Fit Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
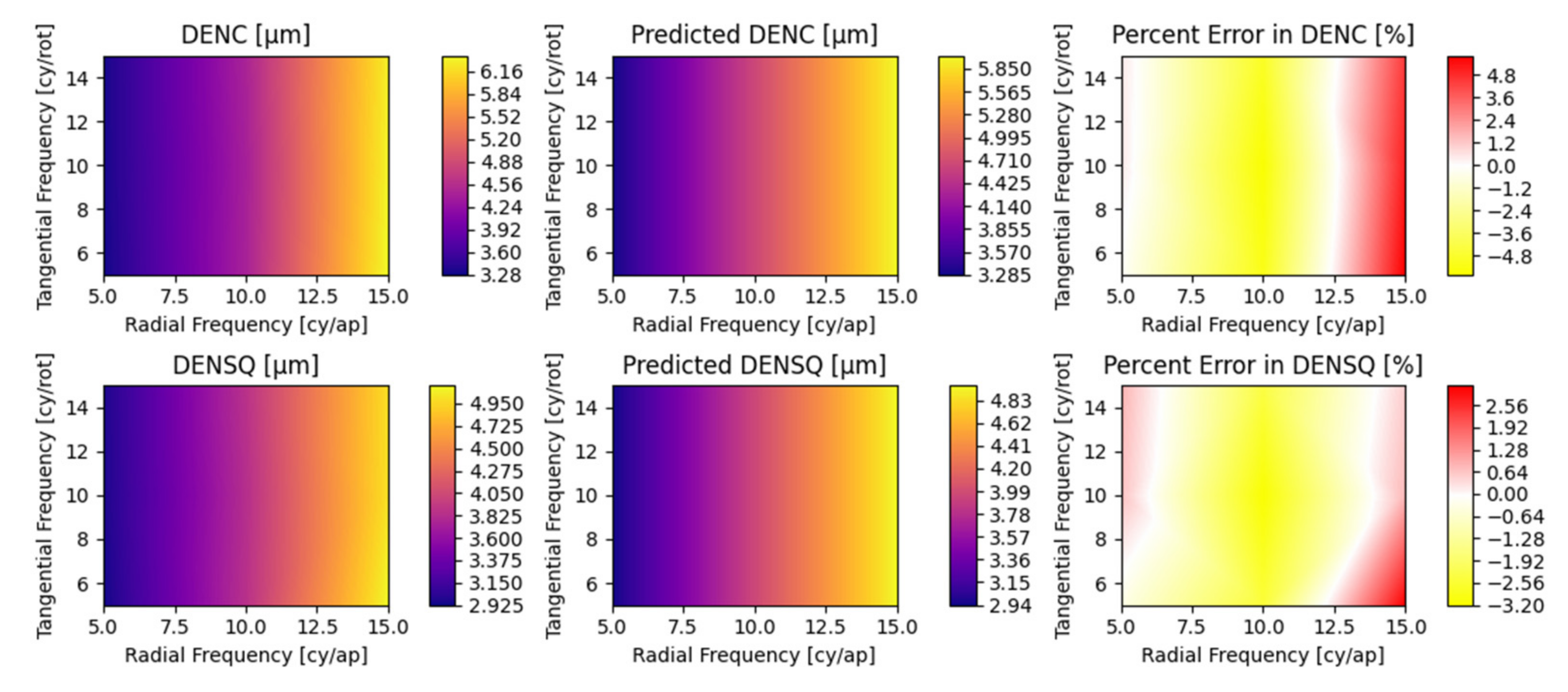
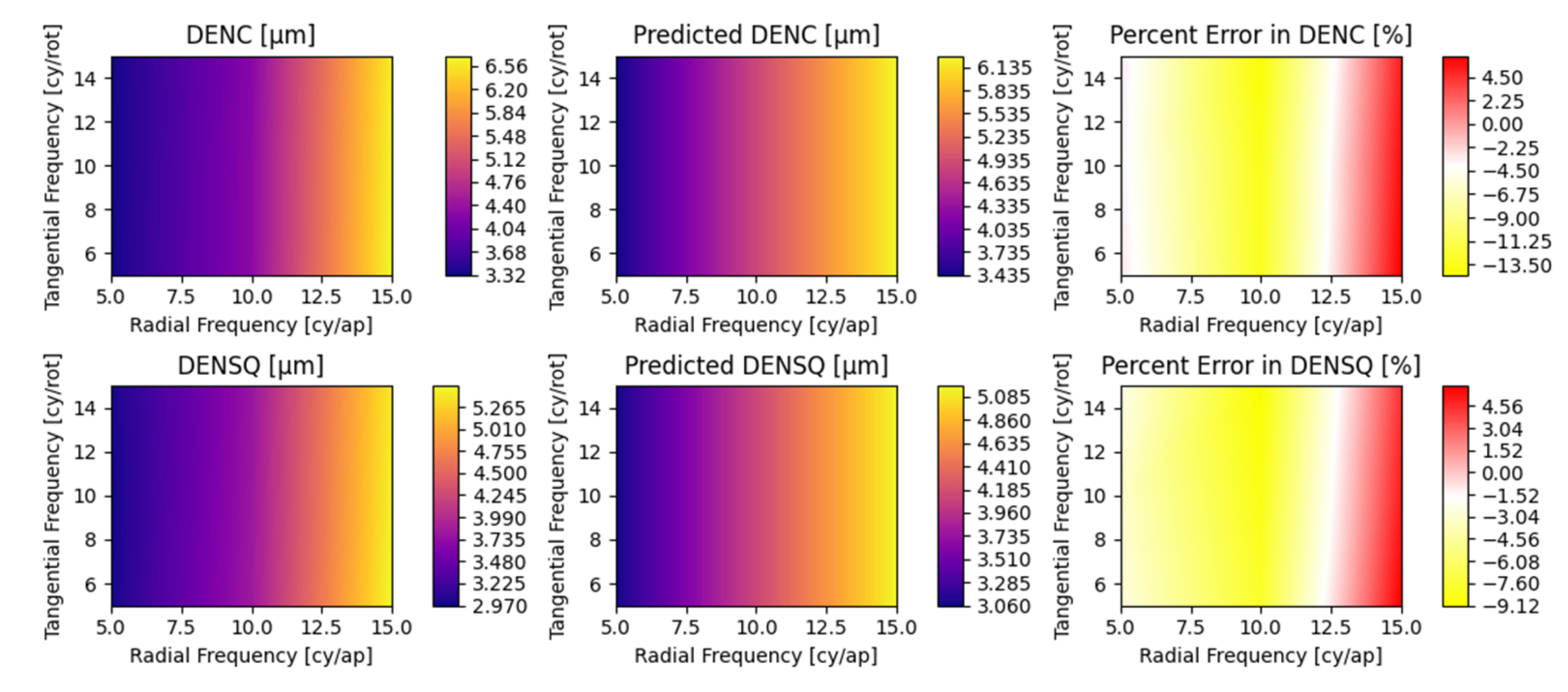
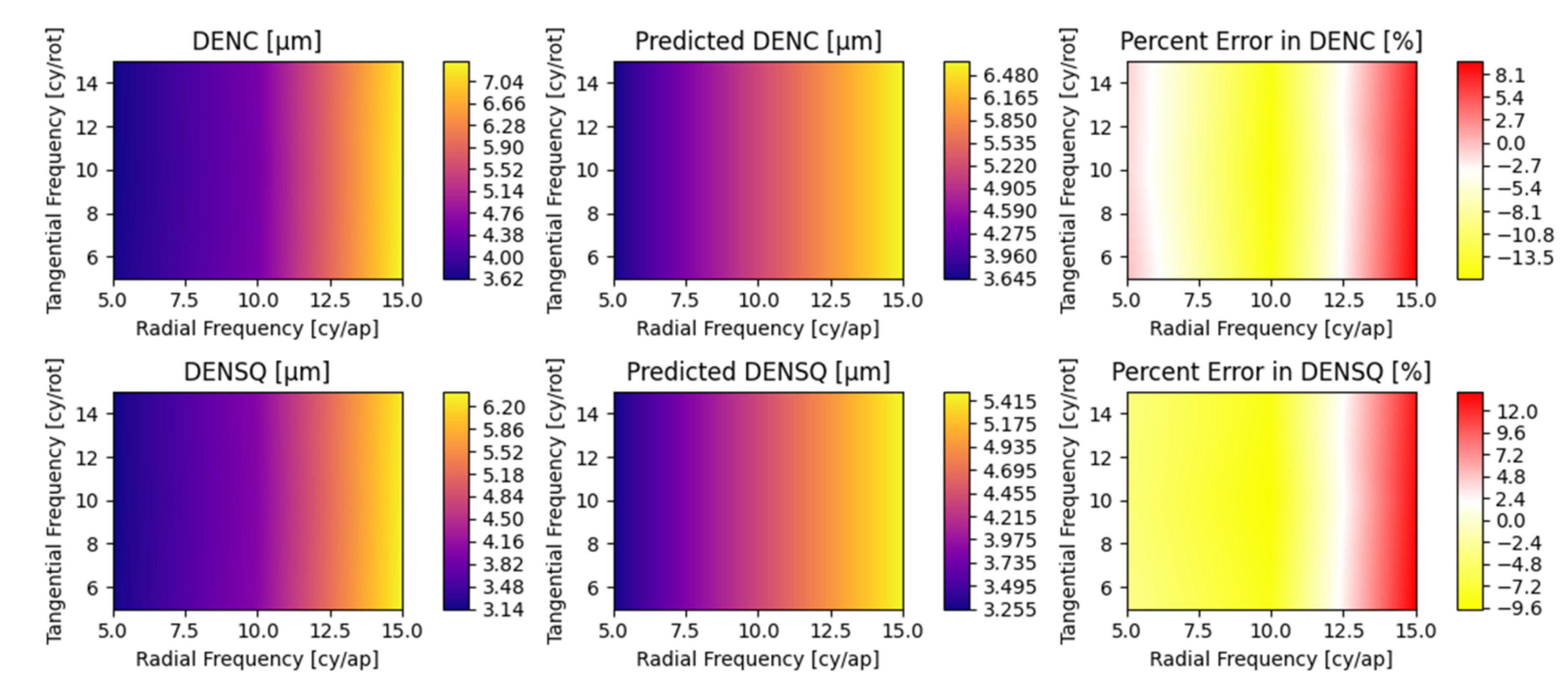
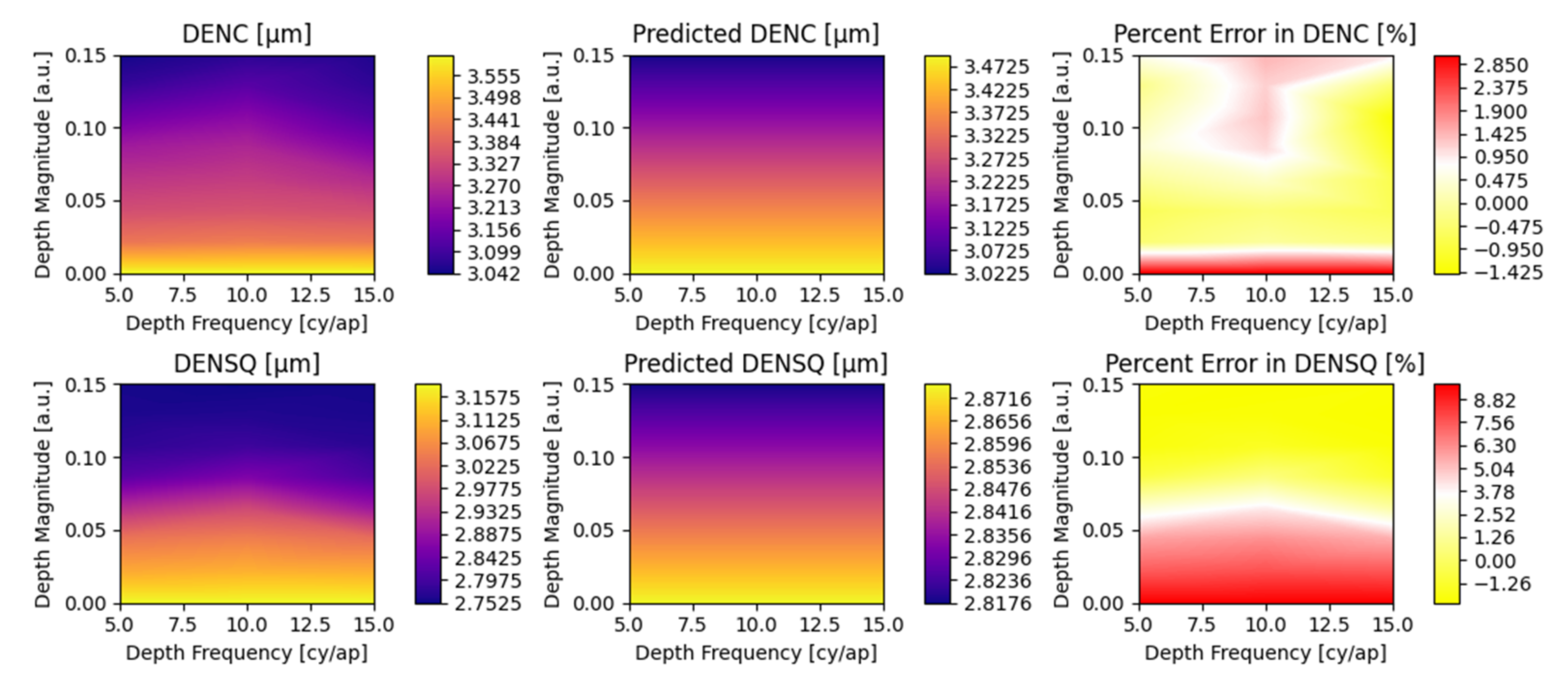
Appendix A. Detailed Parametric Model Fit Error




References
- Risse, S.; Scheiding, S.; Beier, M.; Gebhardt, A.; Damm, C.; Peschel, T. Ultra-precise manufacturing of aspherical and freeform mirrors for high resolution telescopes, Proc. SPIE 9151. In Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation; SPIE: Montréal, QC, Canada, 2014; p. 91510M. [Google Scholar] [CrossRef]
- Tamkin, J.M. A Study of Image Artifacts Caused by Structured Mid-Spatial Frequency Fabrication Errors on Optical Surfaces; The University of Arizona: Tucson, AZ, USA, 2010. [Google Scholar]
- Liang, K.; Alonso, M.A. Understanding the effects of groove structures on the MTF. Opt. Express 2017, 25, 18827–18841. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Yan, F.; Zhang, X. Effects of structured surface errors on MTF of off-axis TMA system, Proc. SPIE 8416. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, Xiamen, China, 16 October 2012; p. 84161B. [Google Scholar] [CrossRef]
- Noll, R.J. Effect of Mid-and High-Spatial Frequencies on Optical Performance. Opt. Eng. 1979, 18, 182137. [Google Scholar] [CrossRef]
- Liang, K.; Alonso, M. Effects on the OTF of MSF structures with random variations. Opt. Express 2019, 27, 34665–34680. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Wei, C.; Hong, Z.; Shao, J. Modeling and analysis of the mid-spatial- frequency error characteristics and generation mechanism in sub-aperture optical polishing. Opt. Express 2020, 28, 8959–8973. [Google Scholar] [CrossRef] [PubMed]
- Aryan, H.; Boreman, G.D.; Suleski, T.J. Simple methods for estimating the performance and specification of optical components with anisotropic mid-spatial frequency surface errors. Opt. Express 2019, 27, 32709–32721. [Google Scholar] [CrossRef] [PubMed]
- Forbes, G.W. Never-Ending Struggles with Mid-Spatial Frequencies. In Optical Measurement Systems for Industrial Inspection IX, 9525:95251B; International Society for Optics and Photonics: Munich, Germany, 2015. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. GUM: Guide to the Expression of Uncertainty in Measurement. In Guide to the Expression of Uncertainty in Measurement Part 6: Developping and Using Measurements Models, Version 2020; JCGM: Sèvres, France, 2020; Available online: https://www.bipm.org/en/publications/guides (accessed on 15 September 2020).
- Doiron, T.; Stoup, J. Uncertainty and Dimensional Calibrations. J. Res. Natl. Inst. Stand. Technol. 1997, 102, 647–676. [Google Scholar] [CrossRef] [PubMed]
- Kacker, R.; Sommer, K.D.; Kessel, R. Evolution of modern approaches to express uncertainty in measurement. Metrologia 2007, 44, 513–529. [Google Scholar] [CrossRef]
- Fang, F.; Xu, F. Recent Advances in Micro/Nano-cutting: Effect of Tool Edge and Material Properties. Nanomanufacturing Metrol. 2018, 1, 4–31. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, N.; Chen, Y.; Fu, Y.; Zhao, Q. Simulation and Experimental Study on the Surface Generation Mechanism of Cu Alloys in Ultra-Precision Diamond Turning. Micromachines 2019, 10, 573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheung, C.F.; Lee, W.B. Modelling and simulation of surface topography in ultra-precision diamond turning. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2000, 214, 463–480. [Google Scholar] [CrossRef]
- Li, L. Investigation of the Optical Effects of Single Point Diamond Machined Surfaces and the Applications of Micro Machining. (Electronic Thesis or Dissertation). 2009. Available online: https://etd.ohiolink.edu/ (accessed on 23 September 2020).
- Shahinian, H.; Mullany, B. Fiber Based Polishing Tools for Optical Applications. In Optical Design and Fabrication; Optical Society of America: Denver, CO, USA, 2017; p. OTu2B.4. [Google Scholar]
- Zha, J.; Zhang, H.; Li, Y.; Chen, Y. Pseudo-random Path Generation Algorithms and Strategies for the Surface Quality Improvement of Optical Aspherical Components. Materials 2020, 13, 1216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunn, C.R.; Walker, D.D. Pseudo-random tool paths for CNC sub-aperture polishing and other applications. Opt. Express 2008, 16, 18942–18949. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.R. Slope error tolerances for optical surfaces. In Optifab 2007: Technical Digest; International Society for Optics and Photonics: Rochester, NY, USA, 2007. [Google Scholar]
- Yip, A. Factors Affecting Surface Topography in Diamond Turning. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2014. [Google Scholar]
- Bittner, R. Tolerancing of single point diamond turned diffractive optical elements and optical surfaces. J. Eur. Opt. Soc.-Rapid Publ. 2007, 2. [Google Scholar] [CrossRef] [Green Version]
- Blalock, T.; Medicus, K.; Nelson, J.D. Fabrication of freeform optics. In Optical Manufacturing and Testing XI; International Society for Optics and Photonics: San Diego, CA, USA, 2015; Volume 9575. [Google Scholar]
- Thorlabs Videos. Single-Point Diamond Turning Capabilities. YouTube, ThorLabs. Available online: http://www.youtube.com/watch?v=6iRohI_jaYg (accessed on 2 April 2015).



| Variable Symbol | Variable Units | Variable Description |
|---|---|---|
| Gρ | μm | Surface profile from radial TMs |
| A | μm | TM amplitude. Varied to achieve desired RMS surface figure requirement. |
| ξ | cycles | Radial frequency of TMs. |
| DUUT | μm | Diameter of unit under test. |
| ρ | μm | Radial spatial coordinate. |
| Gφ | μm | Surface profile contributions from parameters with additional spatial dependence, such as those described in Section 3.2. |
| Variable Symbol | Variable Units | Variable Description |
|---|---|---|
| Gφ | μm | Performance impact from in-plane TMs. |
| κ | μm | Tangential magnitude of TM perturbation into adjacent track. Range of 0 to 0.15 μm under consideration. |
| ω | μm−1 | Seed tangential frequency of in-plane TMs. Range of 0 to 20 μm−1 under consideration. |
| x, y | μm | Cartesian spatial coordinates. |
| Variable Symbol | Variable Units | Variable Description |
|---|---|---|
| Hz | μm | Performance impact from out-of-plane TMs. |
| η | μm | Magnitude of out-of-plane TMs. Range of 0 to 0.15 under consideration. |
| ζ | cycles | Depth seed frequency of out-of-plane TMs. Range of 0 to 20 under consideration |
| DUUT | μm | Diameter of unit under test for conversion to frequencies per aperture. |
| x, y | μm | Cartesian spatial coordinates. |
| Variable Symbol | Variable Units | Variable Description |
|---|---|---|
| ρΔ | μm | Decentered radial spatial coordinate. |
| x, y | μm | Cartesian spatial coordinates. |
| Δx, Δy | μm | Decenter parameter along cartesian spatial coordinates. |
| Variable Symbol | Variable Units | Variable Description |
|---|---|---|
| σ | Waves @ 632.8 nm | RMS Surface Irregularity |
| θ | Degrees | Angle of Incidence |
| f# | Unitless | F-number |
| λ | Nanometers | Wavelength |
| R | Meters | Radius of Curvature (only flat case considered). |
| Surface Type | Comment | Radius | Thickness | Tilt Y |
|---|---|---|---|---|
| STANDARD | OBJECT | ∞ | ∞ | – |
| PARAXIAL | CONVERGER, EFL = τ | – | 0 | – |
| COORDBRK | ELEMENT TILT | – | 0 | θ |
| GRID_SAG | UUT | ∞ | 0 | – |
| COORDBRK | TILT RETURN | – | 0 | -θ |
| STANDARD | FOCUS COMP | ∞ | -τ | – |
| STANDARD | IMG PLANE | ∞ | – | – |
| Regime Limit | RMS Surface Irregularity | Angle of Incidence | Radial Frequency | Tangential Magnitude | Tangential Frequency | Depth Magnitude | Depth Frequency | Decenter |
|---|---|---|---|---|---|---|---|---|
| σ [λ, 632.8 nm] | θ [°] | ξ [cy⁄ap] | κ [a.u.] | ω [cy⁄rot] | η [a.u.] | ζ [cy⁄ap] | δ [aps] | |
| Min | 0.05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Max | 0.1 | 45 | 20 | 0.15 | 15 | 0.15 | 15 | 0.85 |
| Performance Characteristic | Wavelength Scaling Coeff |
|---|---|
| χ [μm/μm] | |
| DENC | 8.102 |
| DENSQ | 5.924 |
| Performance Characteristic | Radial TMs | Off-Axis TMs | ||
|---|---|---|---|---|
| β1 | β2 | ε1 | ε2 | |
| DENC | 118.52 | −0.801 | 14.38 | 6.5 |
| DENSQ | 86.92 | 0.395 | 12.48 | 3.9 |
| Performance Characteristic | In-Plane TMs | Out-of-Plane TMs | ||||||
|---|---|---|---|---|---|---|---|---|
| μ1 | μ2 | μ3 | μ4 | ν1 | ν2 | ν3 | ν4 | |
| DENC | −380.77 | 62.42 | 0 | 0 | −117.34 | 1.343 | 0 | 0 |
| DENSQ | −171.24 | 39.82 | 0 | 0 | 114.57 | −13.432 | 0 | 0 |
| σ [λ,632.8 nm] | θ [°] | ξ [cy/ap] | κ [a.u.] | ω [cy/rot] | η [a.u.] | ζ [cy/ap] | δ [aps] | Simulated DENC [μm] | Predicted DENC [μm] | Percent Error [%] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.048 | 0 | 20 | 0 | 0 | 0 | 0 | 0.79 | 7.385 | 7.457 | −1.0 |
| 0.049 | 0 | 5 | 0.04 | 5 | 0 | 0 | 1.58 | 2.79 | 2.858 | −2.4 |
| 0.043 | 30 | 15 | 0 | 0 | 0 | 5 | 1.83 | 2.696 | 3.061 | −13.5 |
| 0.047 | 15 | 10 | 0 | 0 | 0 | 5 | 0.83 | 4.213 | 4.437 | −5.3 |
| 0.042 | 15 | 15 | 0 | 0 | 0.11 | 5 | 0.83 | 2.456 | 2.531 | −3.1 |
| 0.038 | 45 | 5 | 0 | 10 | 0 | 0 | 0.25 | 2.833 | 2.512 | 11.3 |
| 0.04 | 15 | 15 | 0 | 0 | 0.15 | 5 | 0.92 | 5.836 | 5.397 | 7.5 |
| 0.039 | 30 | 15 | 0 | 0 | 0.09 | 10 | 0.42 | 5.739 | 5.664 | 1.3 |
| σ [λ,632.8 nm] | θ [°] | ξ [cy/ap] | κ [a.u.] | ω [cy/rot] | η [a.u.] | ζ [cy/ap] | δ [aps] | Simulated Char [μm] | Predicted Char [μm] | Percent Error [%] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.048 | 0 | 20 | 0 | 0 | 0 | 0 | 0.79 | 7.327 | 7.381 | −0.7 |
| 0.049 | 0 | 5 | 0.04 | 5 | 0 | 0 | 1.58 | 2.63 | 2.618 | 0.5 |
| 0.043 | 30 | 15 | 0 | 0 | 0 | 5 | 1.83 | 2.402 | 2.668 | −11.1 |
| 0.047 | 15 | 10 | 0 | 0 | 0 | 5 | 0.83 | 4.109 | 4.428 | −7.8 |
| 0.042 | 15 | 15 | 0 | 0 | 0.11 | 5 | 0.83 | 2.122 | 2.408 | −13.5 |
| 0.038 | 45 | 5 | 0 | 10 | 0 | 0 | 0.25 | 2.574 | 2.774 | −7.8 |
| 0.04 | 15 | 15 | 0 | 0 | 0.15 | 5 | 0.92 | 5.79 | 5.785 | 0.1 |
| 0.039 | 30 | 15 | 0 | 0 | 0.09 | 10 | 0.42 | 5.681 | 5.919 | −4.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hefferan, T.; Graves, L.; Trumper, I.; Pak, S.; Kim, D. Parametric Mid-Spatial Frequency Surface Error Synthesis. Photonics 2021, 8, 584. https://doi.org/10.3390/photonics8120584
Hefferan T, Graves L, Trumper I, Pak S, Kim D. Parametric Mid-Spatial Frequency Surface Error Synthesis. Photonics. 2021; 8(12):584. https://doi.org/10.3390/photonics8120584
Chicago/Turabian StyleHefferan, Timothy, Logan Graves, Isaac Trumper, Soojong Pak, and Daewook Kim. 2021. "Parametric Mid-Spatial Frequency Surface Error Synthesis" Photonics 8, no. 12: 584. https://doi.org/10.3390/photonics8120584
APA StyleHefferan, T., Graves, L., Trumper, I., Pak, S., & Kim, D. (2021). Parametric Mid-Spatial Frequency Surface Error Synthesis. Photonics, 8(12), 584. https://doi.org/10.3390/photonics8120584





