Surface Shape Distortion Online Measurement Method for Compact Laser Cavities Based on Phase Measuring Deflectometry
Abstract
:1. Introduction
2. Configuration and Principle of the COPMD
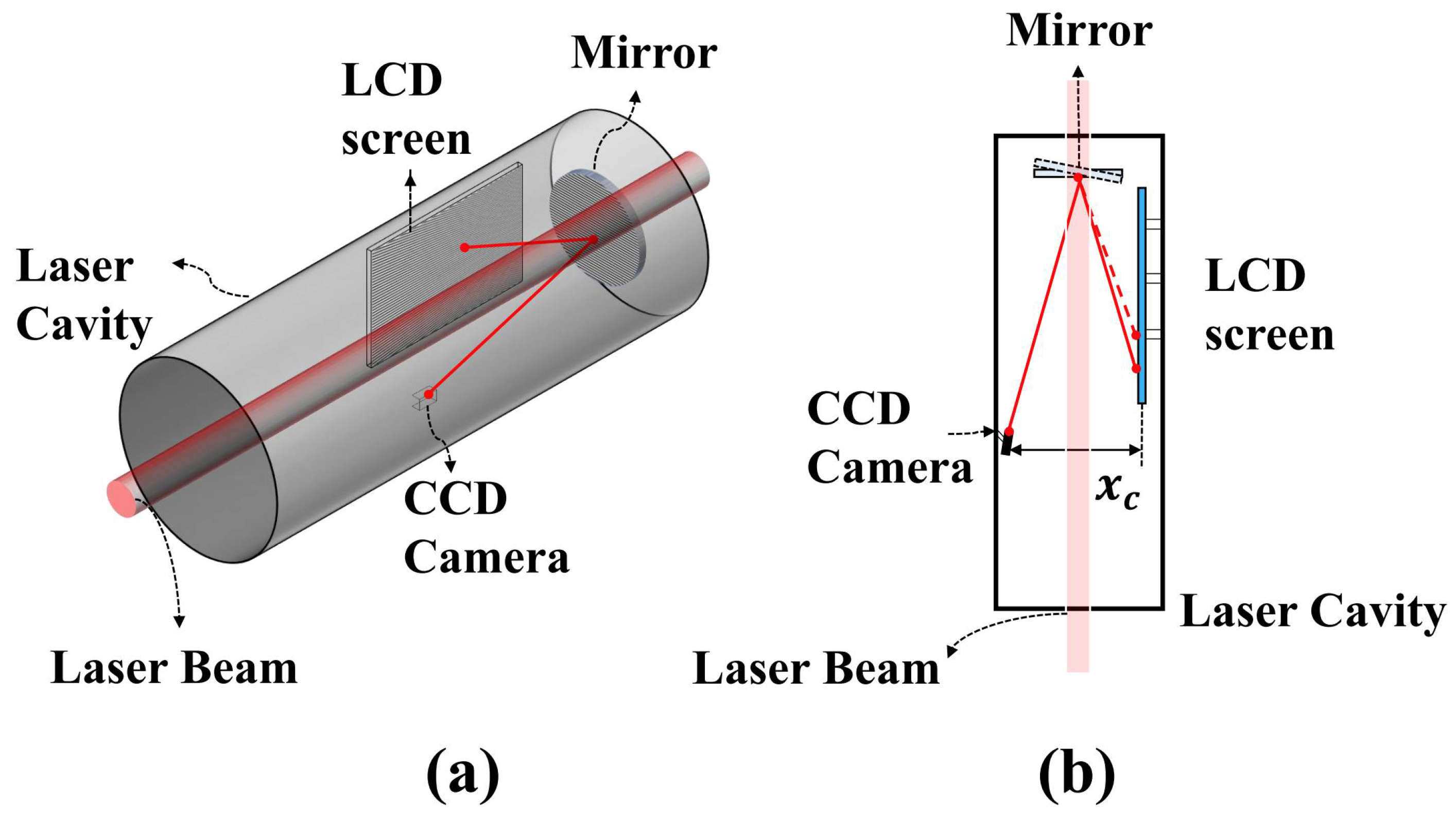
2.1. Configuration of the COPMD
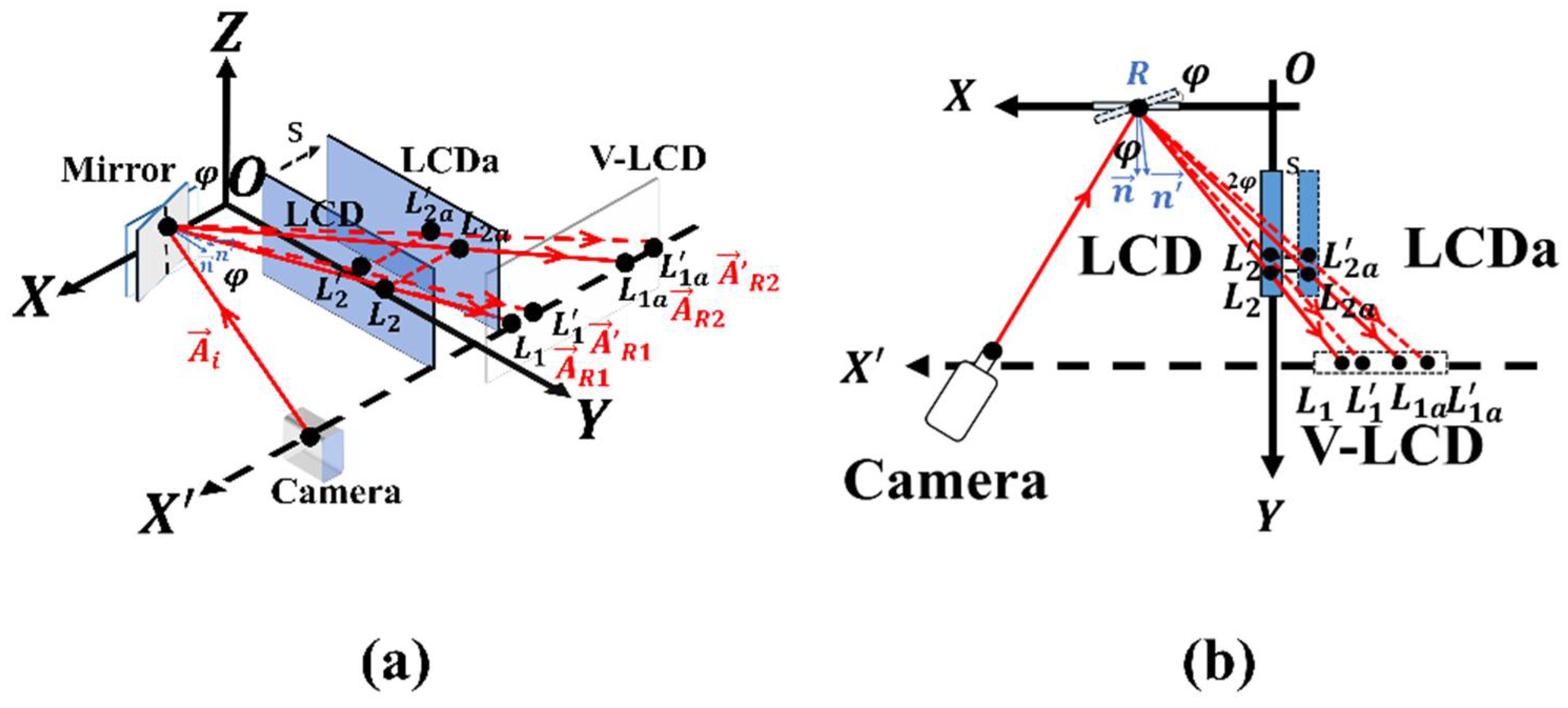
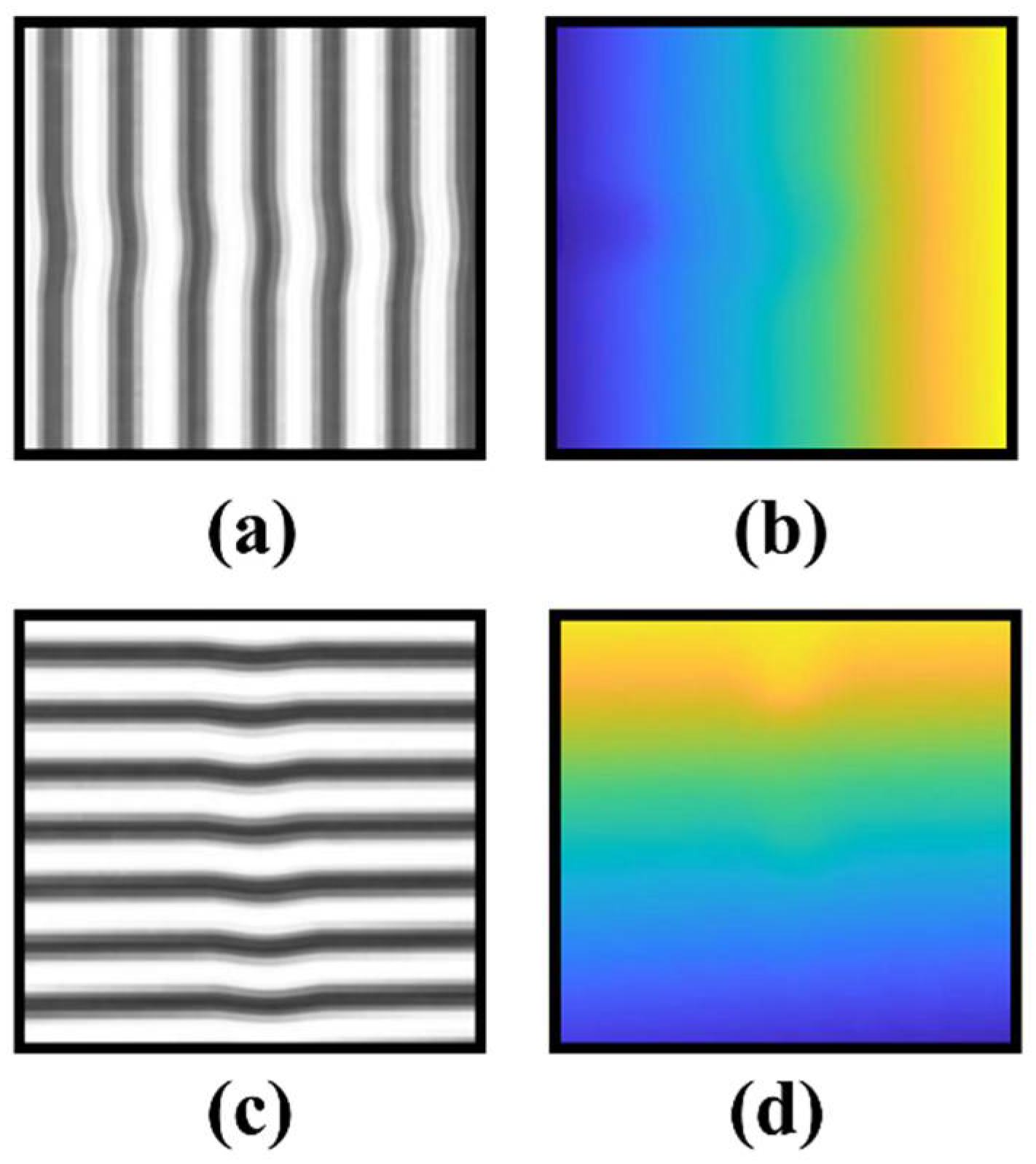
2.2. The Acquisition of Reflection Fringes Irradiance
2.3. The Reconstruction of Wavefront Distortion
3. Measurement Errors Analysis
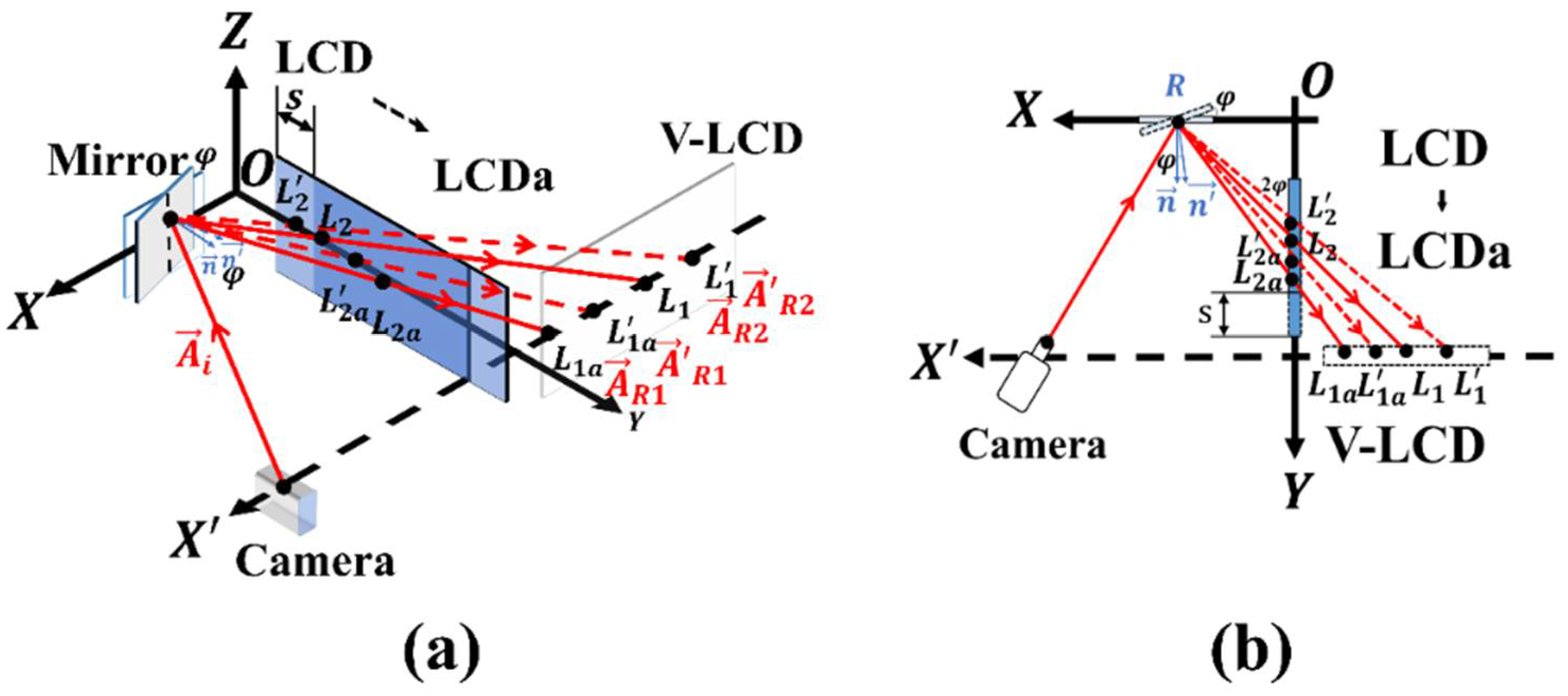
3.1. Measurement Error Due to the LCD Screen Translation along the X-Axis
3.2. Measurement Error Due to the LCD Screen Translation along the Y-Axis
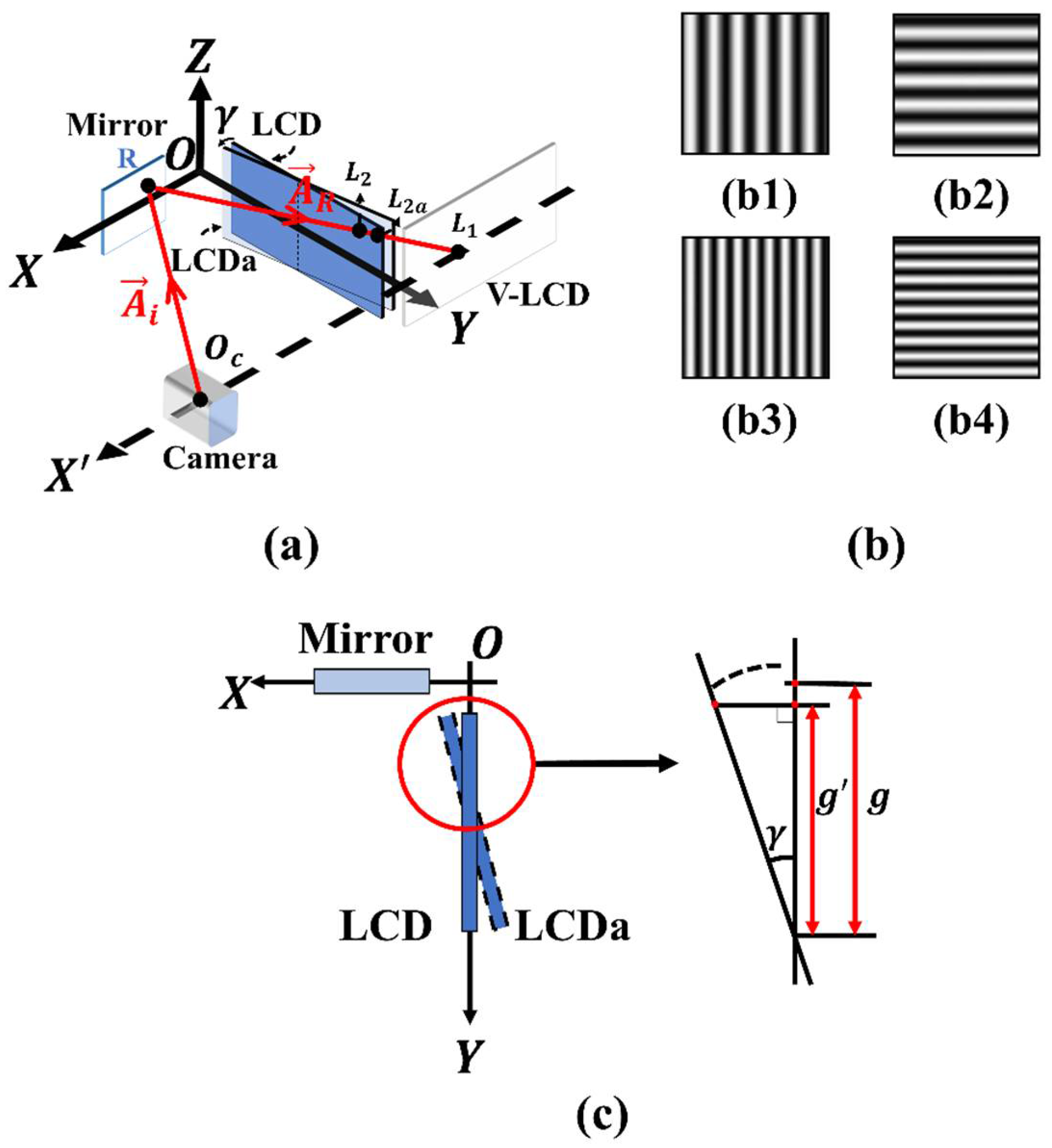
3.3. Measurement Error Due to the LCD Screen Rotation around the Y-Axis
3.4. Measurement Error Due to the LCD Screen Rotation around the Z-Axis
4. Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fedotov, S.I.; Feoktistov, L.P.; Osipov, M.V.; Starodub, A.N. Lasers for ICF with a controllable function of mutual coherence of radiation. Laser Res. 2004, 25, 79–92. [Google Scholar] [CrossRef]
- Koechner, W. Properties of solid-state laser materials. Solid-State Laser Eng. 1999, 1, 28–87. [Google Scholar]
- Chen, Y.F.; Liao, T.S.; Kao, C.F.; Huang, T.M.; Lin, K.H.; Wang, S.C. Optimization of fiber-coupled laser-diode end-pumped lasers: Influence of pump-beam quality. Quantum Electron. 1996, 32, 2010–2016. [Google Scholar] [CrossRef]
- Xiaolu, S.; Zhen, G.; Bingbin, L.; Shiyu, W.; Defang, C.; Jianguo, W. Thermal relaxation time of crystal in pulsed laser diode end-pumped solid-state laser. Chin. J. Lasers 2008, 35, 1132. [Google Scholar] [CrossRef]
- Wynne, R.; Daneu, J.L.; Fan, T.Y. Thermal coefficients of the expansion and refractive index in YAG. Appl. Opt. 1999, 38, 3282–3284. [Google Scholar] [CrossRef]
- Zacharias, R.A.; Beer, N.R.; Bliss, E.S.; Burkhart, S.C.; Cohen, S.J.; Sutton, S.B.; Arnold, T.J. Alignment and wavefront control systems of the National Ignition Facility. Opt. Eng. 2004, 43, 2873–2884. [Google Scholar] [CrossRef]
- Homoelle, D.; Bowers, M.W.; Budge, T.; Haynam, C.; Heebner, J.; Hermann, M.; Jancaitis, K.; Jarboe, J.; LaFortune, K.; Salmon, J.T.; et al. Measurement of the repeatability of the prompt flashlamp-induced wavefront aberration on beamlines at the National Ignition Facility. Appl. Opt. 2011, 50, 4382–4388. [Google Scholar] [CrossRef]
- Aleksandrov, A.G.; Zavalova, V.E.E.; Kudryashov, A.V.E.; Rukosuev, A.L.V.; Sheldakova, Y.V.; Samarkin, V.V.E.; Romanov, P.N. Shack—Hartmann wavefront sensor for measuring the parameters of high-power pulsed solid-state lasers. Quantum Electron. 2010, 40, 321. [Google Scholar] [CrossRef]
- Zheng, W.; Wei, X.; Zhu, Q.; Jing, F.; Hu, D.; Su, J.; Deng, X. Laser performance of the SG-III laser facility. High Power Laser Sci. Eng. 2016, 4, 21. [Google Scholar] [CrossRef] [Green Version]
- Platt, B.C.; Shack, R. History and principles of Shack-Hartmann wavefront sensing. J. Refract. Surg. 2001, 17, S573–S577. [Google Scholar] [CrossRef]
- Seifert, L.; Liesener, J.; Tiziani, H.J. The adaptive shack–hartmann sensor. Opt. Commun. 2003, 216, 313–319. [Google Scholar] [CrossRef]
- Knauer, M.C.; Kaminski, J.; Hausler, G. Phase measuring deflectometry: A new approach to measure specular free-form surfaces. Opt. Metrol. Prod. Eng. 2004, 5457, 366–376. [Google Scholar]
- Xu, Y.; Gao, F.; Jiang, X. A brief review of the technological advancements of phase measuring deflectometry. PhotoniX 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Speck, A.; Zelzer, B.; Kannengießer, M.; Langenbucher, A.; Eppig, T. Inspection of freeform intraocular lens topography by phase measuring deflectometric methods. Appl. Opt. 2013, 52, 4279–4286. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, C.; Liu, X.; Li, Z.; Shi, Y.; Gao, N.; Meng, Z. Phase measuring deflectometry for obtaining 3D shape of specular surface: A review of the state-of-the-art. Opt. Eng. 2021, 60, 020903. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Gao, N.; Meng, Z. 3D shape measurement of diffused/specular surface by combining fringe projection and direct phase measuring deflectometry. Opt. Express 2020, 28, 27561–27574. [Google Scholar] [CrossRef] [PubMed]
- Sironi, G.; Canestrari, R.; Pareschi, G.; Pelliciari, C. Deflectometry for optics evaluation: Free form segments of polynomial mirror. Adv. Opt. Mech. Technol. Telesc. Instrum. 2014, 9151, 91510T. [Google Scholar]
- Häusler, G.; Knauer, M.C.; Faber, C.; Richter, C.; Peterhänsel, S.; Kranitzky, C.; Veit, K. Deflectometry Challenges Interferometry: 3D-Metrology from Nanometer to Meter. In Proceedings of the Digital Holography and Three-Dimensional Imaging, Vancouver, BC, Canada, 26–30 April 2009; p. DMC4. [Google Scholar]
- Faber, C.; Olesch, E.; Krobot, R.; Häusler, G. Deflectometry challenges interferometry: The competition gets tougher! Interferom. XVI Tech. Anal. 2012, 8493, 84930. [Google Scholar]
- Su, P.; Khreishi, M.; Huang, R.; Su, T.; Burge, J.H. Precision aspheric optics testing with SCOTS: A deflectometry approach. Opt. Meas. Syst. Ind. Insp. 2013, 8788, 392–398. [Google Scholar]
- Ye, J.; Niu, Z.; Zhang, X.; Wang, W.; Xu, M. Simultaneous measurement of double surfaces of transparent lenses with phase measuring deflectometry. Opt. Eng. 2021, 137, 106356. [Google Scholar] [CrossRef]
- Zhao, P.; Gao, N.; Zhang, Z.; Gao, F.; Jiang, X. Performance analysis and evaluation of direct phase measuring deflectometry. Opt. Lasers Eng. 2018, 103, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Trumper, I.; Choi, H.; Kim, D.W. Instantaneous phase shifting deflectometry. Opt. Express 2016, 24, 27993–28007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, M.T.; Ghim, Y.S.; Rhee, H.G. Single-shot deflectometry for dynamic 3D surface profile measurement by modified spatial-carrier frequency phase-shifting method. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Su, X.; Liu, Y.; Zhang, Q. Testing an aspheric mirror based on phase measuring deflectometry. Opt. Eng. 2009, 48, 103603. [Google Scholar] [CrossRef]
- Burge, J.H.; Benjamin, S.; Caywood, D.; Noble, C.; Novak, M.; Oh, C.; Zhao, C. Testing of 1.4-m convex off-axis aspheric optical surfaces. Opt. Manuf. Test. 2009, 7426, 74260L. [Google Scholar]
- Yan, M.; Huang, L.; Sun, L.; Fan, J. Laser thermal distortion all-time metrology system for solid-state laser based on phase measuring deflectometry. Opt. Commun. 2018, 423, 134–139. [Google Scholar] [CrossRef]
- Zhou, P.; Martin, H.M.; Zhao, C.; Burge, J.H. Mapping distortion correction for GMT interferometric test. In Proceedings of the Optical Fabrication and Testing, Monterey, CA, USA, 24–28 June 2012; p. OW3D-2. [Google Scholar]
- Huang, R.; Su, P.; Horne, T.; Zappellini, G.B.; Burge, J.H. Measurement of a large deformable aspherical mirror using SCOTS (Software Configurable Optical Test System). Opt. Manuf. Test. 2013, 8838, 883807. [Google Scholar]
- Bian, P.; Shao, X.; Du, J. Finite element analysis of thermal stress and thermal deformation in typical part during SLM. Appl. Sci. 2019, 9, 2231. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Su, X.; Zhang, Q. Wavefront measurement based on active deflectometry. Opt. Test Meas. Technol. Equip. 2008, 6723, 67232N. [Google Scholar]
- Bothe, T.; Li, W.; Von Kopylow, C.; Juptner, W.P. High-resolution 3D shape measurement on specular surfaces by fringe reflection. Opt. Metrol. 2004, 5457, 411–422. [Google Scholar]
- Canabal, H.A.; Alonso, J. Automatic wavefront measurement technique using a computer display and a charge-coupled device camera. Opt. Eng. 2002, 41, 822–826. [Google Scholar] [CrossRef]
- Ghiglia, D.C. Two-Dimentional Phase Unwrapping: Theory. Algorithms Softw. 1998, 4, 21–24. [Google Scholar]
- Massig, J.H. Measurement of phase objects by simple means. Appl. Opt. 1999, 38, 4103–4105. [Google Scholar] [CrossRef]
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Opt. Lasers Eng. 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Huang, S.; Liu, Y.; Chang, C.; Gao, F.; Jiang, X. Three-dimensional shape measurements of specular objects using phase-measuring deflectometry. Sensors 2017, 17, 2835. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Yue, H.; Yi, J.; Li, M.; Liu, Y. Phase error analysis and reduction in phase measuring deflectometry. Opt. Eng. 2015, 54, 064103. [Google Scholar] [CrossRef]
- Dhanotia, J.; Bhatia, V.; Prakash, S. Collimation testing using deflectometry in conjunction with windowed Fourier transform analysis. Appl. Opt. 2017, 56, 2346–2352. [Google Scholar] [CrossRef]
- Höfer, S.; Burke, J.; Heizmann, M. Infrared deflectometry for the inspection of diffusely specular surfaces. Adv. Opt. Technol. 2016, 5, 377–387. [Google Scholar] [CrossRef]
- Liu, Y.; Olesch, E.; Yang, Z.; Häusler, G. Fast and accurate deflectometry with crossed fringes. Adv. Opt. Technol. 2014, 3, 441–445. [Google Scholar] [CrossRef] [Green Version]
- Pehkonen, J.; Palojarvi, P.; Kostamovaara, J. Receiver channel with resonance-based timing detection for a laser range finder. IEEE Trans. 2006, 53, 569–577. [Google Scholar] [CrossRef]
- Nitzan, D.; Brain, A.E.; Duda, R.O. The measurement and use of registered reflectance and range data in scene analysis. Proc. IEEE 1977, 65, 206–220. [Google Scholar] [CrossRef]
- Beheim, G.; Fritsch, K. Remote displacement measurements using a laser diode. Electron. Lett. 1985, 21, 93–94. [Google Scholar] [CrossRef]
- Reza, S.A.; Khwaja, T.S.; Mazhar, M.A.; Niazi, H.K.; Nawab, R. Improved laser-based triangulation sensor with enhanced range and resolution through adaptive optics-based active beam control. Appl. Opt. 2017, 56, 5996–6006. [Google Scholar] [CrossRef] [PubMed]
- Trudel, V.; St-Amant, Y. One-and two-dimensional single-mode differential fiber-optic displacement sensor for submillimeter measurements. Appl. Opt. 2008, 47, 1082–1089. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Y.; Zheng, Y.; Lin, S.; Wang, D.; Zhang, Y.; Huang, L. Surface Shape Distortion Online Measurement Method for Compact Laser Cavities Based on Phase Measuring Deflectometry. Photonics 2022, 9, 151. https://doi.org/10.3390/photonics9030151
Zhuang Y, Zheng Y, Lin S, Wang D, Zhang Y, Huang L. Surface Shape Distortion Online Measurement Method for Compact Laser Cavities Based on Phase Measuring Deflectometry. Photonics. 2022; 9(3):151. https://doi.org/10.3390/photonics9030151
Chicago/Turabian StyleZhuang, Yongchen, Yamin Zheng, Shibing Lin, Deen Wang, Yifan Zhang, and Lei Huang. 2022. "Surface Shape Distortion Online Measurement Method for Compact Laser Cavities Based on Phase Measuring Deflectometry" Photonics 9, no. 3: 151. https://doi.org/10.3390/photonics9030151
APA StyleZhuang, Y., Zheng, Y., Lin, S., Wang, D., Zhang, Y., & Huang, L. (2022). Surface Shape Distortion Online Measurement Method for Compact Laser Cavities Based on Phase Measuring Deflectometry. Photonics, 9(3), 151. https://doi.org/10.3390/photonics9030151





