Optical Amplification and Fast-Slow Light in a Three-Mode Cavity Optomechanical System without Rotating Wave Approximation
Abstract
:1. Introduction
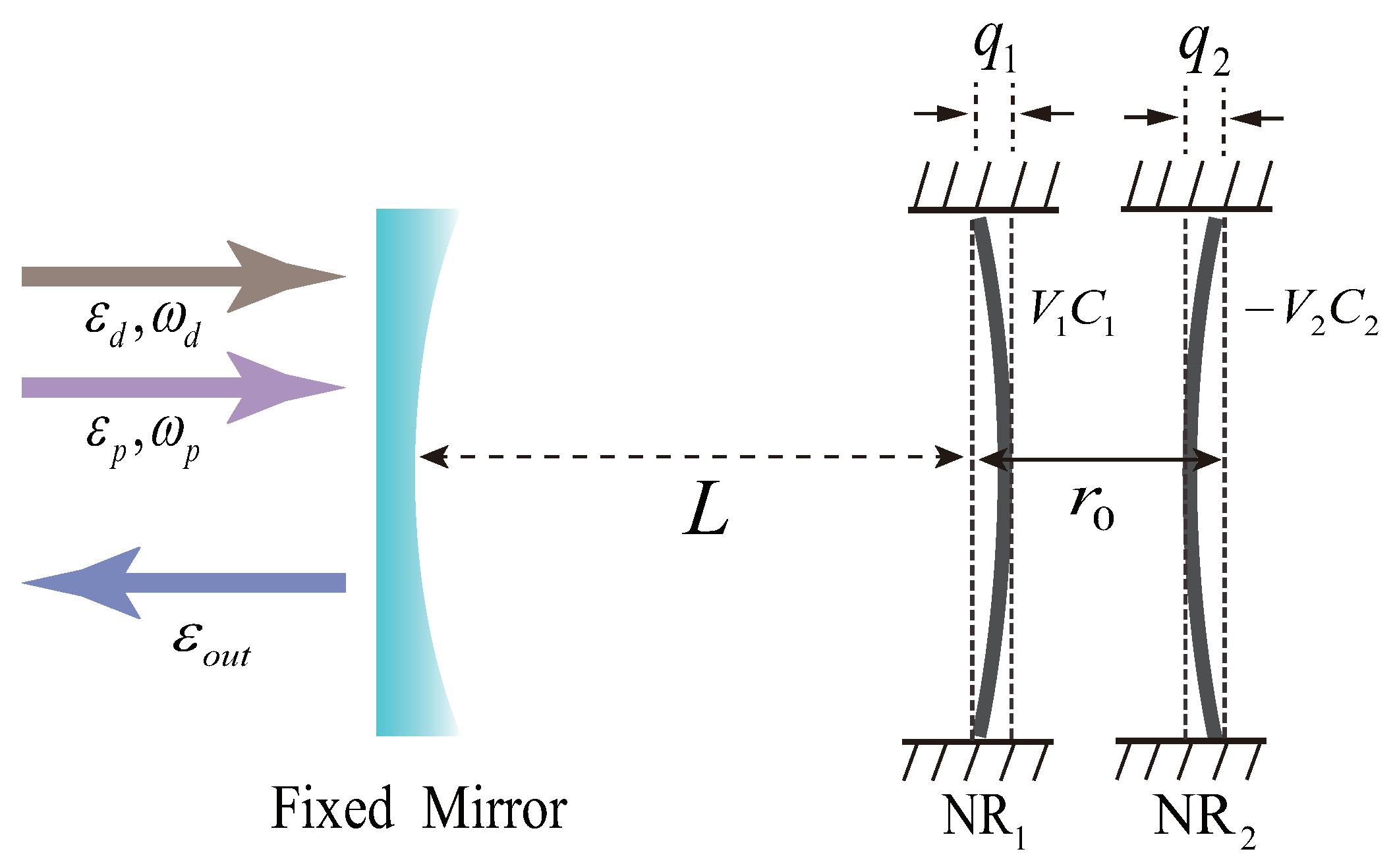
2. System and Hamiltonian
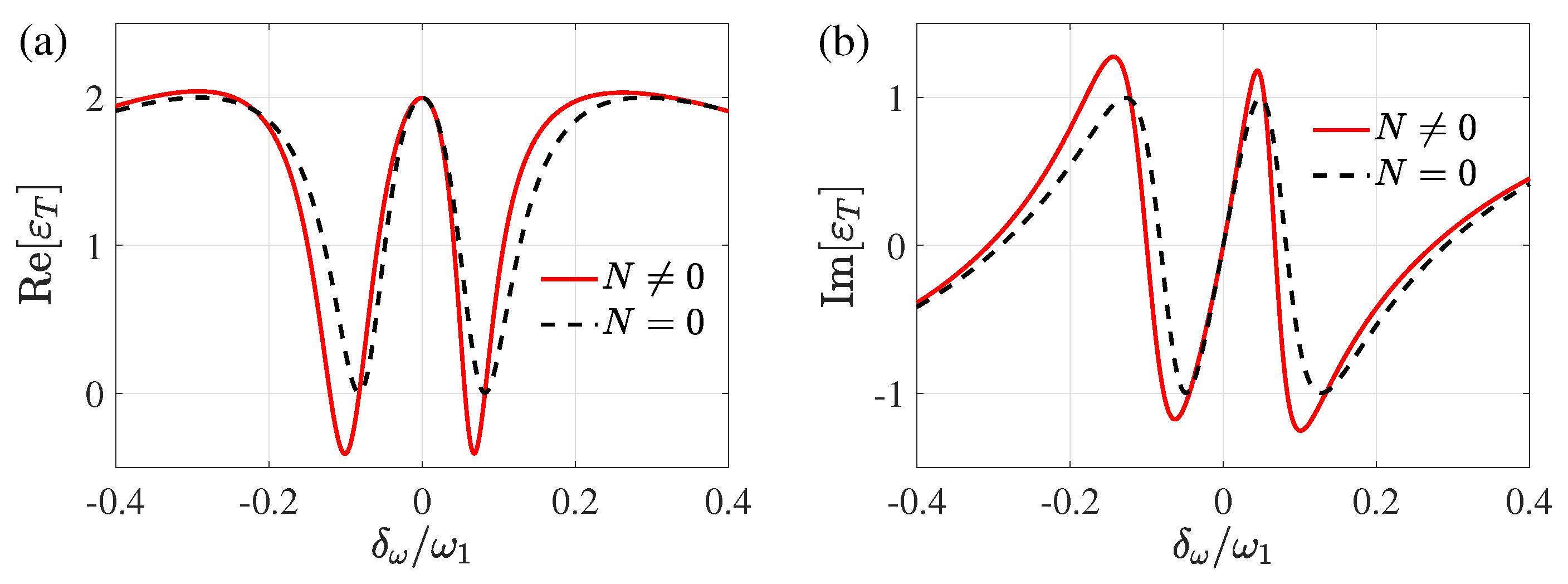
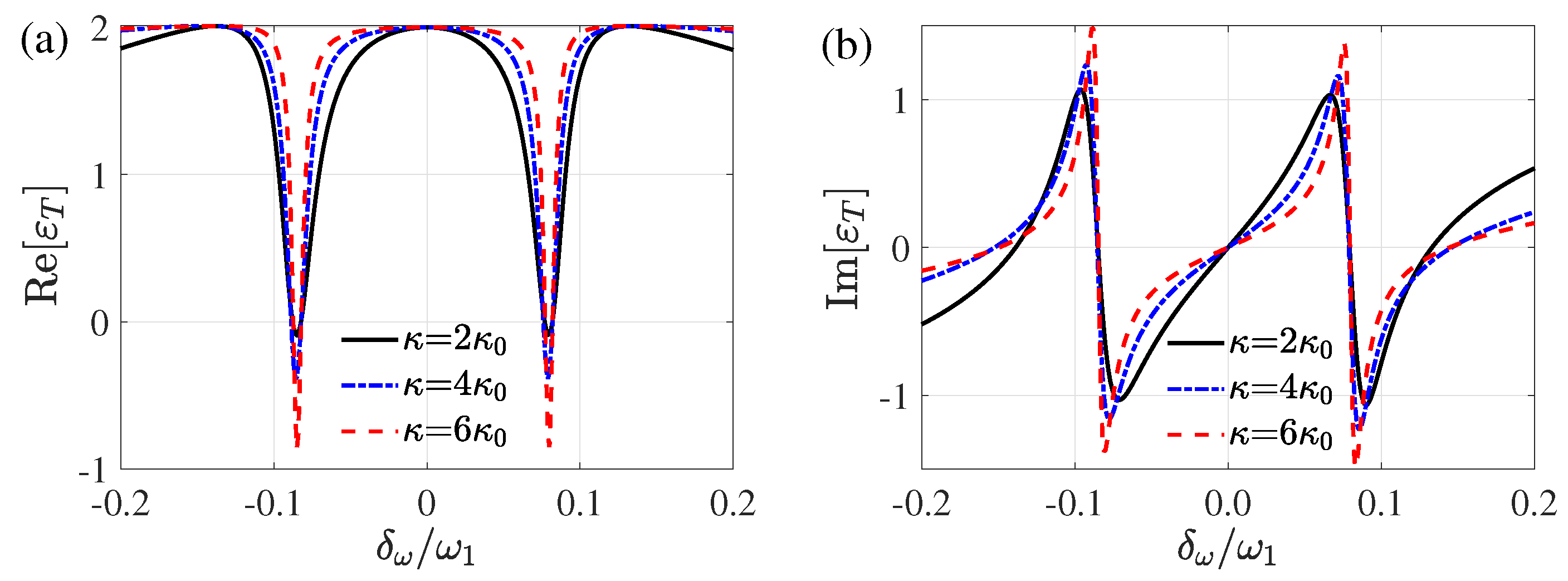
3. Influence of the Counterrotating Term
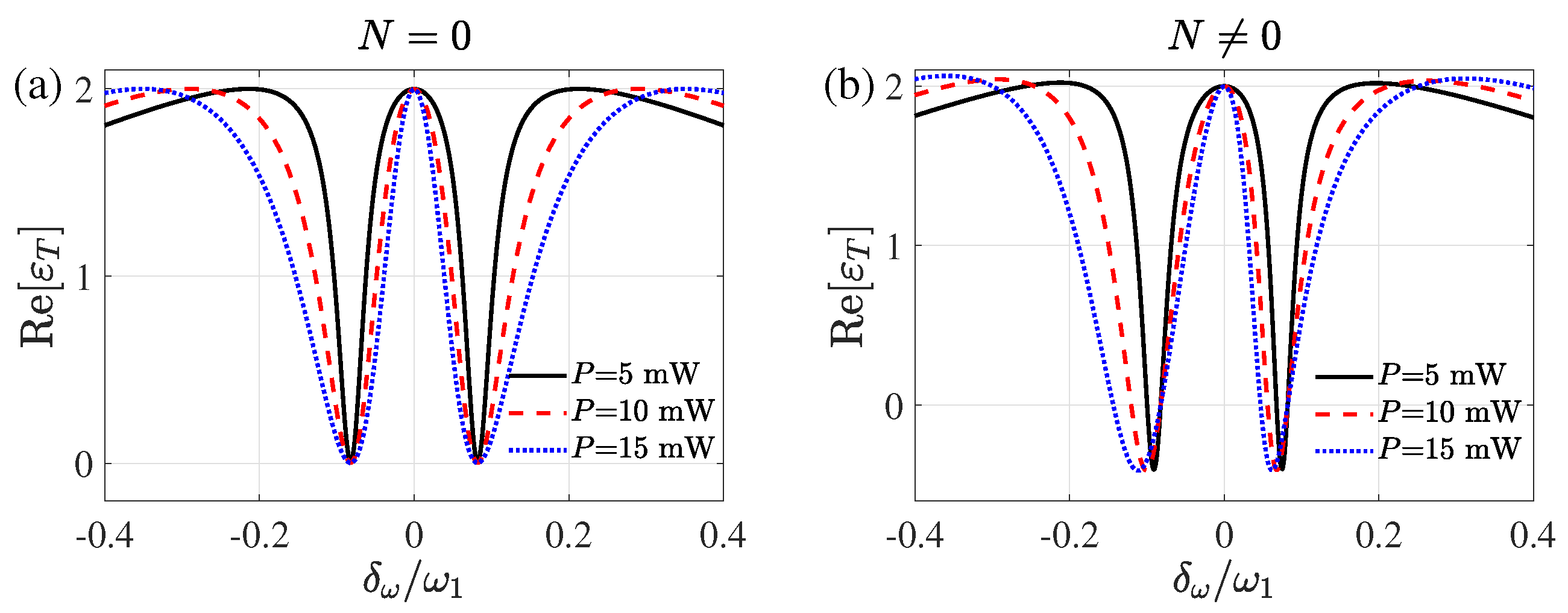
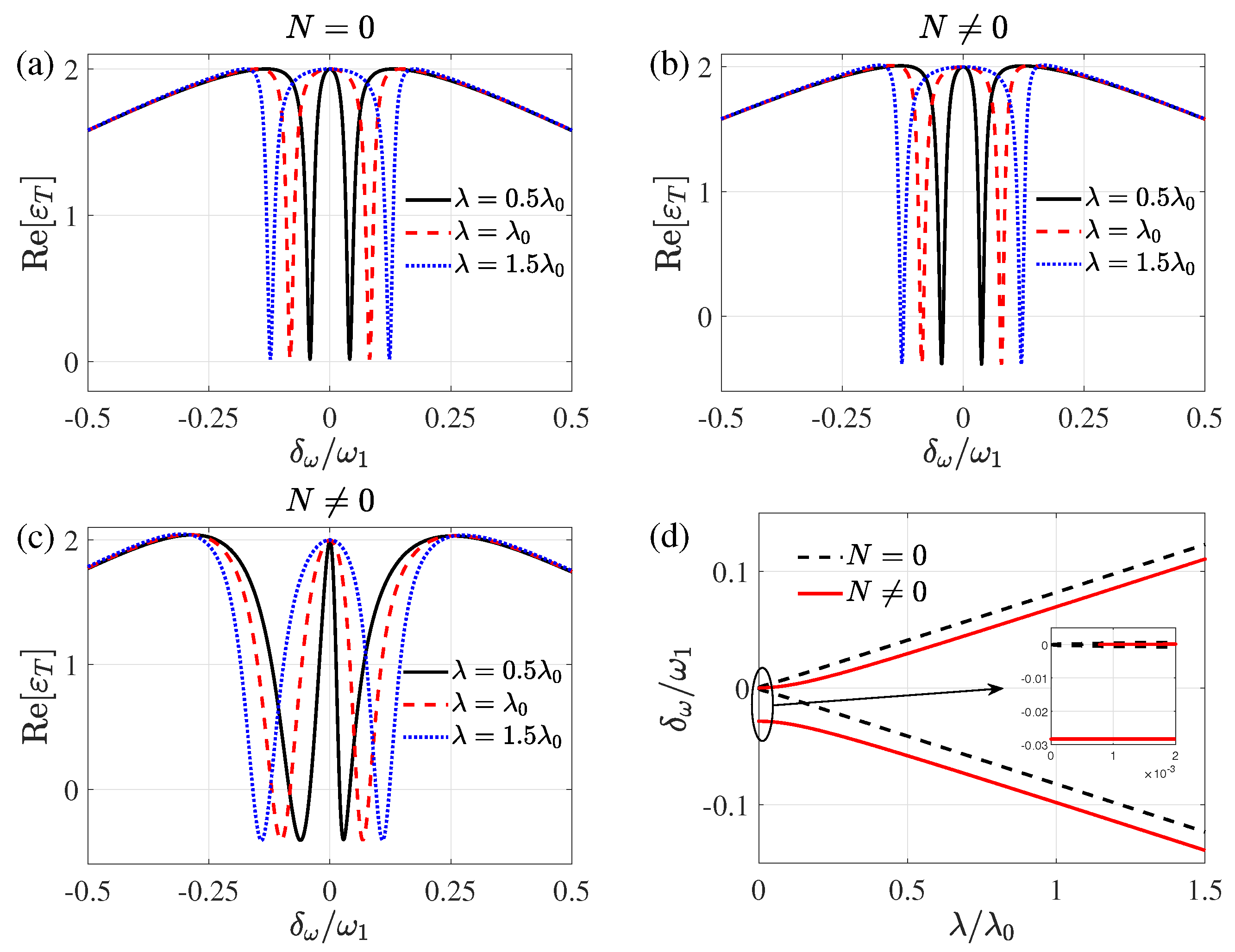
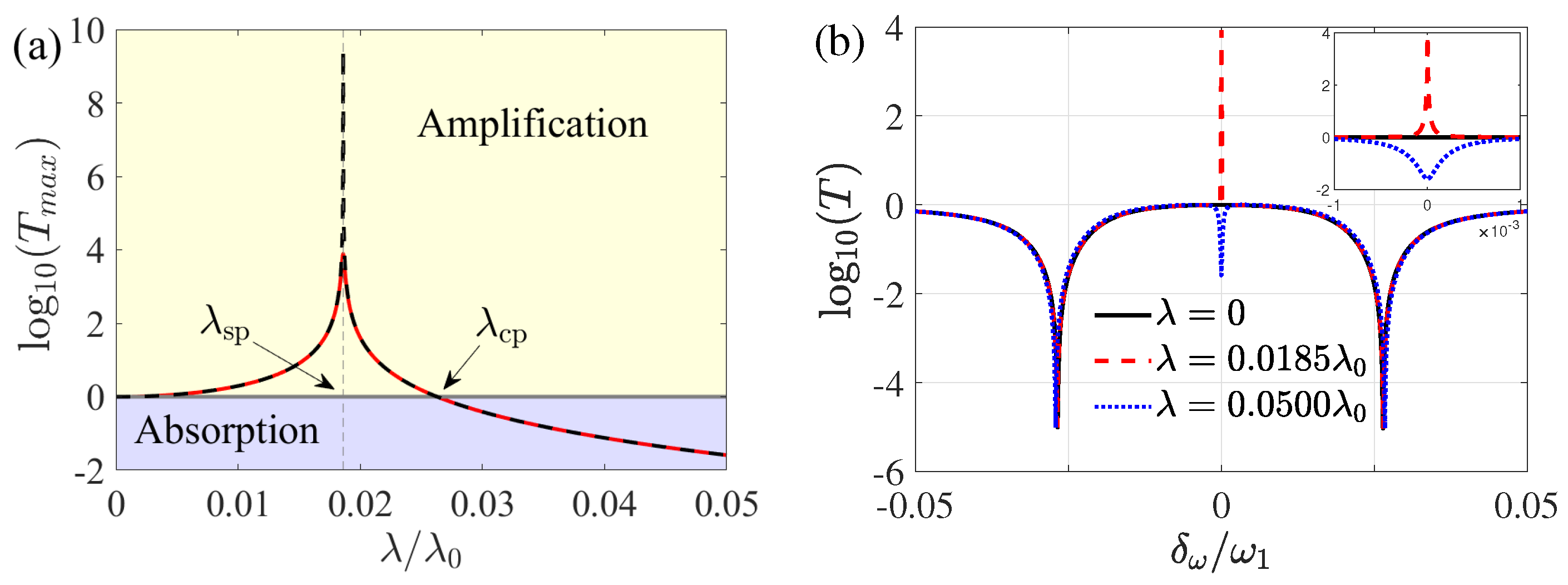
3.1. Asymmetry of Double Optomechanically Induced Amplification
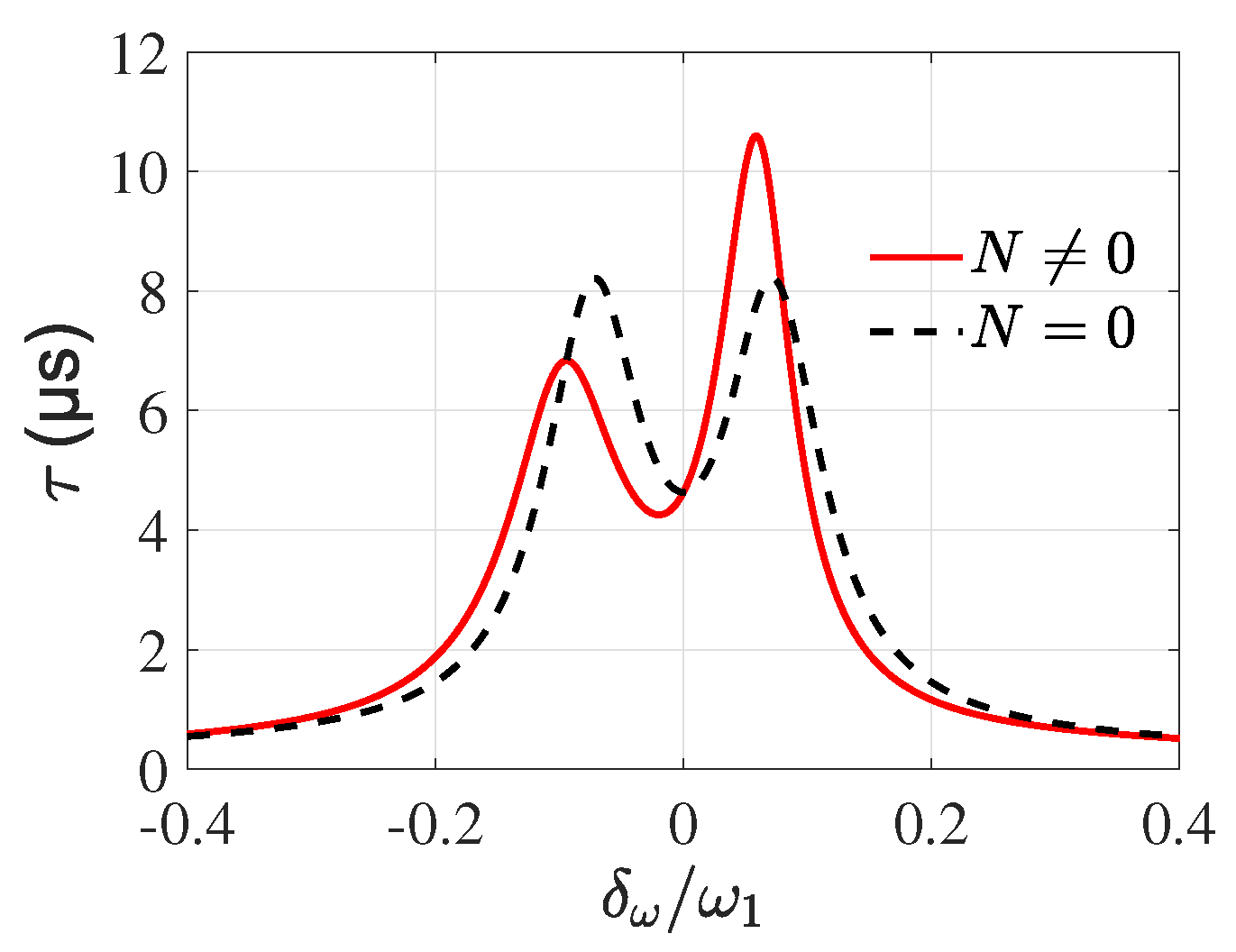
3.2. Fast-Slow Light Effect
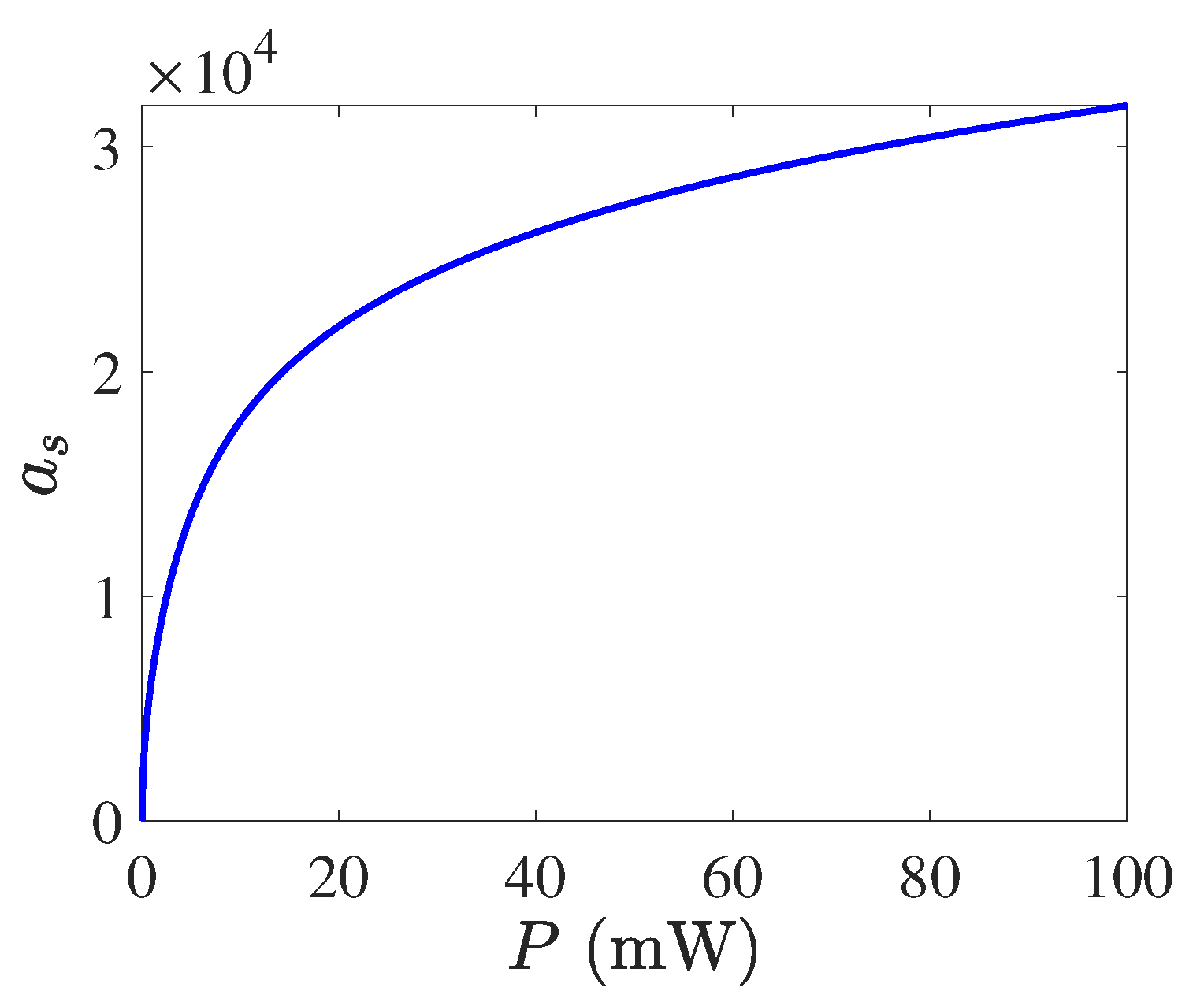
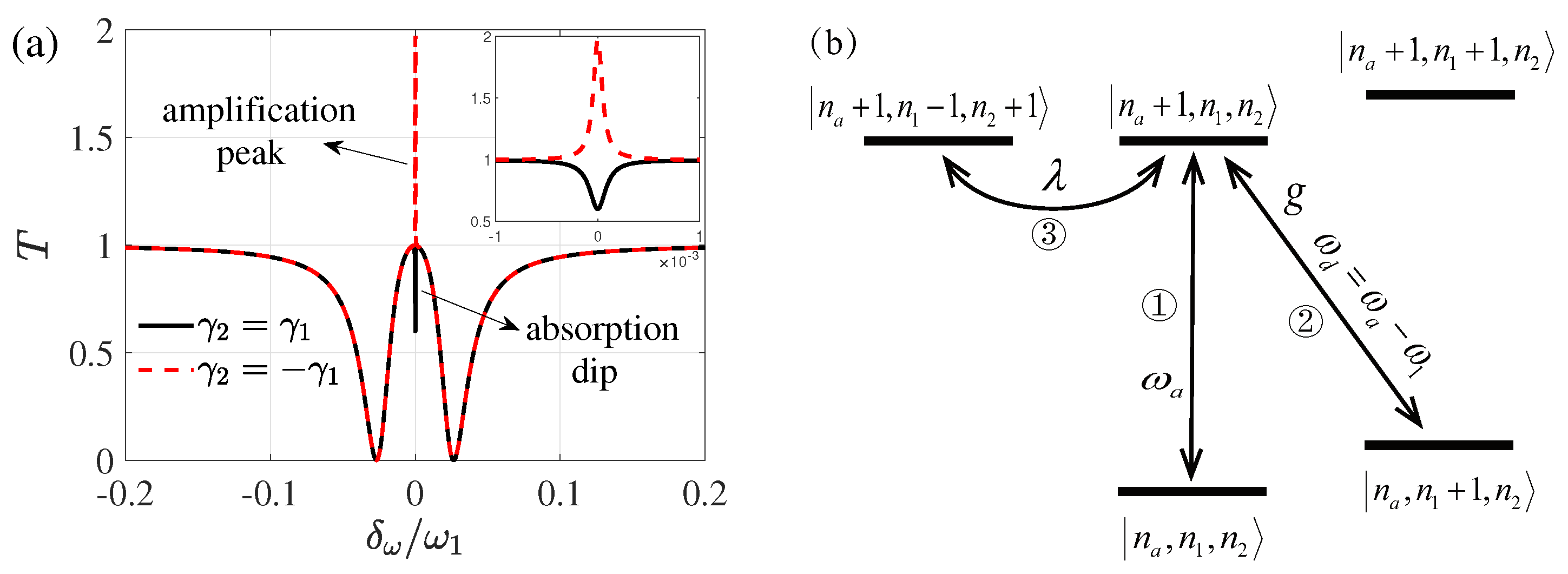
4. Application of the Counterrotating Term to the System with Mechanical Gain
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Probe Output Field
Appendix B. Stability Analysis of the Three-Mode Cavity Optomechanical System
References
- Bowen, W.P.; Milburn, G.J. Quantum Optomechanics; Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
- Brandes, T. Feedback Control of Quantum Transport. Phys. Rev. Lett. 2010, 105, 060602. [Google Scholar] [CrossRef] [Green Version]
- Grimsmo, A.L. Time-Delayed Quantum Feedback Control. Phys. Rev. Lett. 2015, 115, 060402. [Google Scholar] [CrossRef] [Green Version]
- Nunnenkamp, A.; Børkje, K.; Girvin, S.M. Single-Photon Optomechanics. Phys. Rev. Lett. 2011, 107, 063602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leijssen, R.; La Gala, G.R.; Freisem, L.; Muhonen, J.T.; Verhagen, E. Nonlinear cavity optomechanics with nanomechanical thermal fluctuations. Nat. Commun. 2017, 8, ncomms16024. [Google Scholar] [CrossRef] [Green Version]
- Pang, B.; Chen, Y.B. Fundamental relations between measurement, radiation, and decoherence in gravitational wave laser interferometer detectors. Phys. Rev. D 2019, 99, 124016. [Google Scholar] [CrossRef] [Green Version]
- Verlot, P.; Tavernarakis, A.; Briant, T.; Cohadon, P.F.; Heidmann, A. Backaction Amplification and Quantum Limits in Optomechanical Measurements. Phys. Rev. Lett. 2010, 104, 133602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braunstein, S.L. Quantum limits on precision measurements of phase. Phys. Rev. Lett. 1992, 69, 3598–3601. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef] [Green Version]
- Mahajan, S.; Kumar, T.; Bhattacherjee, A.B.; ManMohan. Ground-state cooling of a mechanical oscillator and detection of a weak force using a Bose-Einstein condensate. Phys. Rev. A 2013, 87, 013621. [Google Scholar] [CrossRef]
- Bai, C.H.; Wang, D.Y.; Zhang, S.; Wang, H.F. Qubit-assisted squeezing of mirror motion in a dissipative cavity optomechanical system. Sci. China Phys. Mech. Astron. 2019, 62, 970311. [Google Scholar] [CrossRef]
- Lü, X.Y.; Liao, J.Q.; Tian, L.; Nori, F. Steady-state mechanical squeezing in an optomechanical system via Duffing nonlinearity. Phys. Rev. A 2015, 91, 013834. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, G.S.; Huang, S.M. Strong mechanical squeezing and its detection. Phys. Rev. A 2016, 93, 043844. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.Y.; Bai, C.H.; Wang, H.F.; Zhu, A.D.; Zhang, S. Steady-state mechanical squeezing in a hybrid atom-optomechanical system with a highly dissipative cavity. Sci. Rep. 2016, 6, 2045–2322. [Google Scholar] [CrossRef] [Green Version]
- Bai, C.H.; Wang, D.Y.; Zhang, S.; Liu, S.; Wang, H.F. Engineering of strong mechanical squeezing via the joint effect between Duffing nonlinearity and parametric pump driving. Photon. Res. 2019, 7, 1229–1239. [Google Scholar] [CrossRef]
- Arcizet, O.; Cohadon, P.F.; Briant, T.; Pinard, M.; Heidmann, A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 2006, 444, 71–74. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.C.; Xiao, Y.F.; Luan, X.S.; Wong, C.W. Dynamic Dissipative Cooling of a Mechanical Resonator in Strong Coupling Optomechanics. Phys. Rev. Lett. 2013, 110, 153606. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.X.; Wang, L.; Liu, Y.M.; Wang, D.Y.; Bai, C.H.; Zhang, S.; Wang, H.F. Ground state cooling of magnomechanical resonator in PT-symmetric cavity magnomechanical system at room temperature. Front. Phys. 2020, 15, 52504. [Google Scholar] [CrossRef]
- Marquardt, F.; Chen, J.P.; Clerk, A.A.; Girvin, S.M. Quantum Theory of Cavity-Assisted Sideband Cooling of Mechanical Motion. Phys. Rev. Lett. 2007, 99, 093902. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Gu, X.; Liu, Y.X.; Miranowicz, A.; Nori, F. Tunable photon blockade in a hybrid system consisting of an optomechanical device coupled to a two-level system. Phys. Rev. A 2015, 92, 033806. [Google Scholar] [CrossRef] [Green Version]
- Qiu, L.; Gan, L.; Ding, W.; Li, Z.Y. Single-photon generation by pulsed laser in optomechanical system via photon blockade effect. J. Opt. Soc. Am. B 2013, 30, 1683–1687. [Google Scholar] [CrossRef]
- Wang, D.Y.; Bai, C.H.; Xing, Y.; Liu, S.; Zhang, S.; Wang, H.F. Enhanced photon blockade via driving a trapped Λ-type atom in a hybrid optomechanical system. Phys. Rev. A 2020, 102, 043705. [Google Scholar] [CrossRef]
- Hartmann, M.J.; Plenio, M.B. Steady State Entanglement in the Mechanical Vibrations of Two Dielectric Membranes. Phys. Rev. Lett. 2008, 101, 200503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mari, A.; Eisert, J. Gently Modulating Optomechanical Systems. Phys. Rev. Lett. 2009, 103, 213603. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.X.; Shen, L.T.; Yang, Z.B.; Wu, H.Z.; Zheng, S.B. Enhancement of entanglement in distant mechanical vibrations via modulation in a coupled optomechanical system. Phys. Rev. A 2014, 89, 023843. [Google Scholar] [CrossRef]
- Bai, C.H.; Wang, D.Y.; Wang, H.F.; Zhu, A.D.; Zhang, S. Robust entanglement between a movable mirror and atomic ensemble and entanglement transfer in coupled optomechanical system. Sci. Rep. 2016, 6, 33404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dobrindt, J.M.; Wilson Rae, I.; Kippenberg, T.J. Parametric Normal-Mode Splitting in Cavity Optomechanics. Phys. Rev. Lett. 2008, 101, 263602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, S.M.; Agarwal, G.S. Normal-mode splitting in a coupled system of a nanomechanical oscillator and a parametric amplifier cavity. Phys. Rev. A 2009, 80, 033807. [Google Scholar] [CrossRef] [Green Version]
- He, B.; Yang, L.; Jiang, X.S.; Xiao, M. Transmission Nonreciprocity in a Mutually Coupled Circulating Structure. Phys. Rev. Lett. 2018, 120, 203904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.W.; Li, Y. Optical nonreciprocity and optomechanical circulator in three-mode optomechanical systems. Phys. Rev. A 2015, 91, 053854. [Google Scholar] [CrossRef] [Green Version]
- Shahidani, S.; Naderi, M.H.; Soltanolkotabi, M. Control and manipulation of electromagnetically induced transparency in a nonlinear optomechanical system with two movable mirrors. Phys. Rev. A 2013, 88, 053813. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.X.; Davanço, M.; Aksyuk, V.; Srinivasan, K. Electromagnetically Induced Transparency and Wideband Wavelength Conversion in Silicon Nitride Microdisk Optomechanical Resonators. Phys. Rev. Lett. 2013, 110, 223603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, W.Z.; Wei, L.F.; Li, Y.; Liu, Y.X. Phase-dependent optical response properties in an optomechanical system by coherently driving the mechanical resonator. Phys. Rev. A 2015, 91, 043843. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.B.; Cui, C.L.; Gu, K.H.; Tian, X.D.; Fu, C.B.; Wu, J.H. Coherent perfect absorption, transmission, and synthesis in a double-cavity optomechanical system. Opt. Express 2014, 22, 4886–4895. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Zhou, Y.H.; Guo, Y.Q.; Yi, X.X. Optomechanically induced transparency in optomechanics with both linear and quadratic coupling. Phys. Rev. A 2018, 98, 053802. [Google Scholar] [CrossRef]
- Zhang, H.; Saif, F.; Jiao, Y.; Jing, H. Loss-induced transparency in optomechanics. Opt. Express 2018, 26, 25199–25210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ullah, K.; Naseem, M.T.; Müstecaplıoğlu, O.E. Tunable multiwindow magnomechanically induced transparency, Fano resonances, and slow-to-fast light conversion. Phys. Rev. A 2020, 102, 033721. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, C.; Zhu, K.D. Slow light in a cavity optomechanical system with a Bose-Einstein condensate. Phys. Rev. A 2011, 83, 055803. [Google Scholar] [CrossRef]
- Si, L.G.; Xiong, H.; Zubairy, M.S.; Wu, Y. Optomechanically induced opacity and amplification in a quadratically coupled optomechanical system. Phys. Rev. A 2017, 95, 033803. [Google Scholar] [CrossRef]
- Hao, H.; Kuzyk, M.C.; Ren, J.J.; Zhang, F.; Duan, X.K.; Zhou, L.; Zhang, T.C.; Gong, Q.H.; Wang, H.L.; Gu, Y. Electromagnetically and optomechanically induced transparency and amplification in an atom-assisted cavity optomechanical system. Phys. Rev. A 2019, 100, 023820. [Google Scholar] [CrossRef]
- Nunnenkamp, A.; Sudhir, V.; Feofanov, A.K.; Roulet, A.; Kippenberg, T.J. Quantum-Limited Amplification and Parametric Instability in the Reversed Dissipation Regime of Cavity Optomechanics. Phys. Rev. Lett. 2014, 113, 023604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massel, F.; Heikkilä, T.T.; Pirkkalainen, J.M.; Cho, S.U.; Saloniemi, H.; Hakonen, P.J.; Sillanpää, M.A. Microwave amplification with nanomechanical resonators. Nature 2011, 480, 351–354. [Google Scholar] [CrossRef] [Green Version]
- He, Y. Optomechanically induced transparency associated with steady-state entanglement. Phys. Rev. A 2015, 91, 013827. [Google Scholar] [CrossRef]
- Kronwald, A.; Marquardt, F. Optomechanically Induced Transparency in the Nonlinear Quantum Regime. Phys. Rev. Lett. 2013, 111, 133601. [Google Scholar] [CrossRef] [Green Version]
- Hou, B.P.; Wei, L.F.; Wang, S.J. Optomechanically induced transparency and absorption in hybridized optomechanical systems. Phys. Rev. A 2015, 92, 033829. [Google Scholar] [CrossRef]
- Teufel, J.D.; Li, D.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Simmonds, R.W. Circuit cavity electromechanics in the strong-coupling regime. Nature 2011, 471, 204–208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lü, H.; Wang, C.Q.; Yang, L.; Jing, H. Optomechanically Induced Transparency at Exceptional Points. Phys. Rev. Appl. 2018, 10, 014006. [Google Scholar] [CrossRef] [Green Version]
- Boller, K.J.; Imamoğlu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Yang, X.X. Electromagnetically induced transparency in V-, Λ-, and cascade-type schemes beyond steady-state analysis. Phys. Rev. A 2005, 71, 053806. [Google Scholar] [CrossRef]
- Harris, S.E. Electromagnetically Induced Transparency in an Ideal Plasma. Phys. Rev. Lett. 1996, 77, 5357–5360. [Google Scholar] [CrossRef] [Green Version]
- Ma, P.C.; Zhang, J.Q.; Xiao, Y.; Feng, M.; Zhang, Z.M. Tunable double optomechanically induced transparency in an optomechanical system. Phys. Rev. A 2014, 90, 043825. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.C.; Qin, L.G.; Lu, J.; Wang, Z.Y. Phase-dependent double optomechanically induced transparency in a hybrid optomechanical cavity system with coherently mechanical driving. Chin. Phys. B 2019, 28, 074204. [Google Scholar] [CrossRef] [Green Version]
- Lei, F.C.; Gao, M.; Du, C.G.; Jing, Q.L.; Long, G.L. Three-pathway electromagnetically induced transparency in coupled-cavity optomechanical system. Opt. Express 2015, 23, 11508–11517. [Google Scholar] [CrossRef]
- Wang, H.; Gu, X.; Liu, Y.X.; Miranowicz, A.; Nori, F. Optomechanical analog of two-color electromagnetically induced transparency: Photon transmission through an optomechanical device with a two-level system. Phys. Rev. A 2014, 90, 023817. [Google Scholar] [CrossRef] [Green Version]
- Yellapragada, K.C.; Pramanik, N.; Singh, S.; Lakshmi, P.A. Optomechanical effects in a macroscopic hybrid system. Phys. Rev. A 2018, 98, 053822. [Google Scholar] [CrossRef]
- Wang, T.; Bai, C.H.; Wang, D.Y.; Liu, S.; Zhang, S.; Wang, H.F. Optical response based on Stokes and anti-Stokes scattering processes in cavity optomechanical system. Quantum Inf. Process. 2021, 20, 126. [Google Scholar] [CrossRef]
- Karuza, M.; Biancofiore, C.; Bawaj, M.; Molinelli, C.; Galassi, M.; Natali, R.; Tombesi, P.; Di Giuseppe, G.; Vitali, D. Optomechanically induced transparency in a membrane-in-the-middle setup at room temperature. Phys. Rev. A 2013, 88, 013804. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.M.; Agarwal, G.S. Electromagnetically induced transparency from two-phonon processes in quadratically coupled membranes. Phys. Rev. A 2011, 83, 023823. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.L.; Wu, R.B.; Zhang, J.; Özdemir, Ş.K.; Yang, L.; Nori, F.; Liu, Y.X. Controllable optical response by modifying the gain and loss of a mechanical resonator and cavity mode in an optomechanical system. Phys. Rev. A 2017, 95, 013843. [Google Scholar] [CrossRef] [Green Version]
- Safavi Naeini, A.H.; Alegre, T.P.M.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef] [Green Version]
- Chang, D.E.; Naeini, A.H.S.; Hafezi, M.; Painter, O. Slowing and stopping light using an optomechanical crystal array. New J. Phys. 2011, 13, 023003. [Google Scholar] [CrossRef]
- Zheng, M.H.; Wang, T.; Wang, D.Y.; Bai, C.H.; Zhang, S.; An, C.S.; Wang, H.F. Manipulation of multi-transparency windows and fast-slow light transitions in a hybrid cavity optomechanical system. Sci. China Phys. Mech. Astron. 2019, 62, 950311. [Google Scholar] [CrossRef]
- Fiore, V.; Yang, Y.; Kuzyk, M.C.; Barbour, R.; Tian, L.; Wang, H.L. Storing Optical Information as a Mechanical Excitation in a Silica Optomechanical Resonator. Phys. Rev. Lett. 2011, 107, 133601. [Google Scholar] [CrossRef] [Green Version]
- Børkje, K.; Nunnenkamp, A.; Teufel, J.D.; Girvin, S.M. Signatures of Nonlinear Cavity Optomechanics in the Weak Coupling Regime. Phys. Rev. Lett. 2013, 111, 053603. [Google Scholar] [CrossRef] [PubMed]
- Buters, F.M.; Luna, F.; Weaver, M.J.; Eerkens, H.J.; Heeck, K.; de Man, S.; Bouwmeester, D. Straightforward method to measure optomechanically induced transparency. Opt. Express 2017, 25, 12935–12943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, J.Y.; Zhou, Y.H.; Yin, X.L.; Huang, J.F.; Liao, J.Q. Quantum entanglement maintained by virtual excitations in an ultrastrongly-coupled-oscillator system. Sci. Rep. 2020, 10. [Google Scholar] [CrossRef]
- Yan, X.B. Optomechanically induced transparency and gain. Phys. Rev. A 2020, 101, 043820. [Google Scholar] [CrossRef]
- Wang, Y.Z.; He, S.; Duan, L.W.; Chen, Q.H. Quantum phase transitions in the spin-boson model without the counterrotating terms. Phys. Rev. B 2019, 100. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.H.; Yu, Y.F.; Zhang, Z.M. Nonreciprocal transmission and fast-slow light effects in a cavity optomechanical system. Opt. Express 2019, 27, 15382–15390. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Guo, Y.Q.; Pei, P.; Yi, X.X. Optomechanically induced absorption in parity-time-symmetric optomechanical systems. Phys. Rev. A 2017, 95, 063825. [Google Scholar] [CrossRef]
- Gardiner, C.; Zoller, P. Quantum Noise; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Agarwal, G.S.; Huang, S.M. Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 2010, 81, 041803. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.B. Optomechanically induced optical responses with non-rotating wave approximation. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 035401. [Google Scholar] [CrossRef]
- Hill, J.T.; Safavi Naeini, A.H.; Chan, J.; Painter, O. Coherent optical wavelength conversion via cavity optomechanics. Nat. Commun. 2012, 3, 1196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, D.G.; Wang, X.; Qin, W.; Hou, B.P.; Nori, F.; Liao, J.Q. Tunable optomechanically induced transparency by controlling the dark-mode effect. Phys. Rev. A 2020, 102, 023707. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Tian, L.; Li, Y. Optomechanical transistor with mechanical gain. Phys. Rev. A 2018, 97, 043818. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.-N.; Wang, T.; Wang, D.-Y.; Han, X.; Zhang, S.; Wang, H.-F. Optical Amplification and Fast-Slow Light in a Three-Mode Cavity Optomechanical System without Rotating Wave Approximation. Photonics 2021, 8, 384. https://doi.org/10.3390/photonics8090384
Zhao Y-N, Wang T, Wang D-Y, Han X, Zhang S, Wang H-F. Optical Amplification and Fast-Slow Light in a Three-Mode Cavity Optomechanical System without Rotating Wave Approximation. Photonics. 2021; 8(9):384. https://doi.org/10.3390/photonics8090384
Chicago/Turabian StyleZhao, Yan-Na, Tie Wang, Dong-Yang Wang, Xue Han, Shou Zhang, and Hong-Fu Wang. 2021. "Optical Amplification and Fast-Slow Light in a Three-Mode Cavity Optomechanical System without Rotating Wave Approximation" Photonics 8, no. 9: 384. https://doi.org/10.3390/photonics8090384
APA StyleZhao, Y.-N., Wang, T., Wang, D.-Y., Han, X., Zhang, S., & Wang, H.-F. (2021). Optical Amplification and Fast-Slow Light in a Three-Mode Cavity Optomechanical System without Rotating Wave Approximation. Photonics, 8(9), 384. https://doi.org/10.3390/photonics8090384




