An Improved Large-Field Microscopic Speckle Interferometry System for Dynamic Displacement Measurement of MEMS

Abstract

The traditional microscopic speckle interferometer has limited applications in engineering due to its small field of view. In this paper, we propose a large-field microscopic speckle interferometer which embeds two doublet lens groups in the improved Mach–Zehnder optical path structure to expand its field of view. At the same time, the new system can reduce the coherent noise of reflected light in the optical path. We use this new system to measure the dynamic displacement process of the entire surface of the microchips. The experimental results show that our improved measurement system can achieve large-field, real-time and high-precision dynamic measurement of micro-electromechanical systems (MEMS).

1. Introduction

Microscopic interferometry is a combination of an electronic speckle pattern interferometry (ESPI) system and a microscopic optical path. It has the advantages of non-contact, full-field and high precision, and is widely used in dynamic and static measurement of micro devices [1,2,3,4,5]. ESPI has been developed for many years and is very popular in the field of non-contact measurement. By analyzing the interferograms, we can obtain the phase information of the measured object, and then the static morphology or dynamic deformation can be measured. Researchers have designed a variety of optical measurement configurations and phase processing algorithms for different measurement targets. In 1971, Butters, J.N. and Lecndcrtz, J.A. used a camera instead of a holographic dry plate to record the interference phenomenon of speckles. This series of speckle images can be electronically processed to compare the speckle images before and after deformation [6]. Jones, R. comprehensively analyzed the conditions for obtaining the best performance of the ESPI, such as camera characteristic, laser power, interferometer type and operation mode, which provide a general theoretical basis for the system design and optimization of various interferometers [7]. In reference [8], a detailed analysis of the vibration fringes obtained by phase stepping on a time-averaged electronic speckle pattern interferometer was presented. Moore, A.J. presented two phase-stepping algorithms that can calculate phase from ESPI fringes: the subtraction method and the addition method. Corresponding interference experiments were carried out, combining a piezoelectric transducer (PZT) and pulse laser, and the function of the algorithms was demonstrated through the collected interferograms [9]. One-shot phase-shifting optical and speckle interferometry with modulation of polarization was described in reference [10]. The system has the ability to record multiple phase-shifting optical or speckle patterns at the same time, so it can afford to measure rapid changes generated from rapid varying phenomena. However, this method reduced the spatial resolution while increasing the time resolution. Reference [11] reported a simple, compact ESPI incorporating a holographic optical system for the study of out-of-plane vibration. The subtraction method was used to generate the fringe pattern. The background speckle noise was eliminated by introducing a phase shift between consecutive images, and finally the amplitude and phase image were obtained through path difference modulation. D. Malacara summarized and described common phase-detection algorithms in interferometry, such as the least square method, quadrature phase method and discrete low-pass filtering, etc. [12]. These theories are very helpful for us to obtain the phase under a variety of different measurement conditions.

With the rapid development and wider application of MEMS, there are more and more studies on the measurement of micro devices. The measurement of micro devices can be achieved by introducing the microscopic optical path into the interferometry system. Reference [13] described an optoelectronic holography microscope (OEHM) for measuring static and dynamic modes of MEMS accelerometers with submicron accuracy. After obtaining the intensity patterns obtained by the phase-stepping algorithm, the phase value was obtained by the phase-shifting algorithm. Preliminary results indicate that the MEMS accelerometer considered in this study deforms by 1.48 µm. Kumar, U.P. presented a two-wavelength micro-interferometric setup for 3-D surface profile characterization of smooth and rough micro-specimens. The method removed ambiguity associated with the single-wavelength data and also extended the phase measurement range compared to the conventional single-wavelength interferometry. A seven-phase step algorithm was used for quantitative fringe analysis. The experimental results on rough silicon membrane and smooth sample were presented [14]. Reference [15] proposed a multiple-wavelength microscopic holographic configuration. This system used sequentially recorded phase-shifted frames at three different wavelengths to evaluate the relatively large deformation fields at the effective wavelengths. The phase distribution before and after loading the object was obtained by using the eight-phase step algorithm. The design of the system along with the experimental results on small-scale rough specimens under static load was presented.

In addition to the above several configurations, according to the optical path structure and the position of the microscope, the commonly used microscopic interferometry systems can be divided into three types: Michelson type [16,17,18,19], Mirau type [20,21,22,23,24] and Linnik type [25,26,27,28,29,30,31,32,33]. For example, Wiersma, J.T. used the Michelson microscopic system and synchronous phase sensor to realize high precision and repeatable measurement of common vibration [19]; Schmit, J. proposed an improved Mirau interferometer, which can generate orthogonally polarized output beams, and can obtain better fringe contrast by introducing achromatic phase shift [21]; Somekh, M.G. realized a plasmon microscope with sub-micron resolution by using the Linnik interferometer with speckle illumination [26]; Li, X.D. of Tsinghua University measured the thermal deformation of copper microbridges with different sizes (the maximum size is 2175 µm × 1009 µm) in real time using the Linnik microscopic interferometry system, and the accuracy reached submicron level [33].

Compared with ESPI, the microscopic interferometry system can achieve high-resolution measurement of micro devices. However, at the same time, the microscopic system is limited by the field of view of microscope, and the measurement range is very small. Considering that the size of MEMS is in the micron level to the millimeter level, especially after packaging, the size of many MEMS is in the millimeter level. For micro devices in this size range, the microscopic interferometry system is no longer sufficient to achieve full-field measurement. In this paper, a large-field microscopic speckle interferometry system based on an improved Mach–Zehnder structure is proposed. Our measurement system has two main advantages: 1. under the conditions of using the same microscope objective, compared with the traditional Linnik structure, the new system expands the field of view from a circular area with a diameter of 2.4 mm to a rectangular area of 6 mm × 8 mm; 2. it can reduce the reflected light beam in the optical path, thereby reducing the reflected coherent noise.

The phase extraction algorithm used in our work is the wavelet transform (WT) method, which is described in detail in our previous article [34]. Compared with the phase shifting method that appears many times in the above references, the WT does not need to introduce multiple steps by PZT, which saves a lot of time. Additionally, WT can directly convert the phase change signal from the spatial domain to the frequency domain to realize real-time measurement of the displacement or deformation of the measured object. We used the new system and WT to perform real-time and large-field measurement on a large area of MEMS. Detailed principles and experiments will be introduced below.

2. Principle

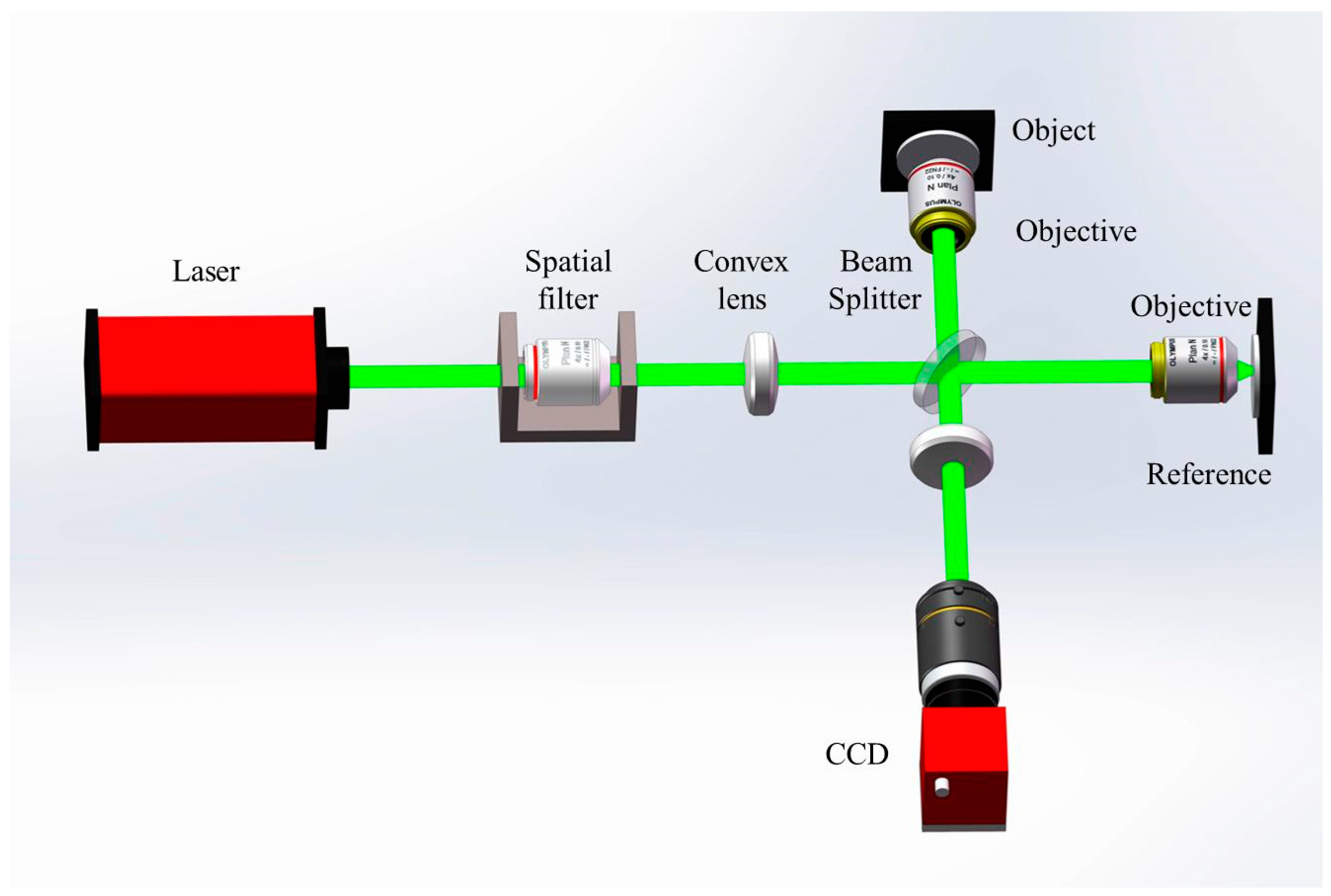
2.1. Traditional Linnik Microscopic Interferometry System

The Linnik microscopic interferometry system is a very common interferometry structure used to measure micro devices. We choose the Linnik microscopic interferometry system as a comparison for later analysis of the effectiveness of expanding the field of view of the new system. This system mainly includes the laser, Linnik microscopic interference structure and CCD. The Linnik microscopic interference structure is composed of a beam splitter and two identical microscope objectives. The laser beam is divided into two arms by the beam splitter. One beam enters the measurement arm and focuses on the measured object through the microscope objective, and the other beam enters the reference arm and focuses on the reference object. The speckle interferograms formed by the two beams is captured by the CCD. We can obtain the displacement or deformation information by processing and analyzing these interferograms. The diagram of the Linnik microscopic interferometry system is shown in Figure 1.

The intensity distribution of speckle interferograms can be expressed as:

$$\mathrm{I}(\mathrm{x},\mathrm{y},{\mathrm{t}}_0)=I_1+I_2+2\sqrt{I_1{I}_2}\cos [{\phi }_0-{\phi }_r]$$

(1)

where I₁ and I₂ are the light intensities of the object beam and the reference beam, respectively, and ${\phi }_0-{\phi }_r$ represents the initial phase difference between them. In the measurement process, when the measured object undergoes continuous out-of-plane displacement, the optical path difference between the object arm and the reference arm changes correspondingly, and the light intensity distribution of the speckle interferogram becomes:

$${\mathrm{I}}^{\prime }(\mathrm{x},\mathrm{y},\mathrm{t})=I_1+I_2+2\sqrt{I_1{I}_2}\cos [{\phi }_0-{\phi }_r+{\Delta }\phi ]$$

(2)

where ${\Delta }\phi$ indicates the phase change caused by the displacement of the measured object.

The speckle fringe pattern can be obtained by subtraction mode, and the output intensity can be expressed as:

$$\begin{array}{l}\mathrm{I}(\mathrm{x},\mathrm{y},\mathrm{t})=\left|{\mathrm{I}}^{\prime }(\mathrm{x},\mathrm{y},\mathrm{t})-\mathrm{I}(\mathrm{x},\mathrm{y},{\mathrm{t}}_0)\right|\\ =4\sqrt{I_1{I}_2}\sin [({\phi }_0-{\phi }_r)+{\Delta }\phi (\mathrm{t})/2]\cdot \sin [{\Delta }\phi (\mathrm{t})/2]\end{array}$$

(3)

where $\sin [({\phi }_0-{\phi }_r)+{\Delta }\phi (\mathrm{t})/2]$ is a high frequency term, which is far beyond the acquisition frequency of CCD; $\sin [{\Delta }\phi (\mathrm{t})/2]$ indicates the fringes related to the change in the measured object.

In our previous research, we introduced the WT to solve the wrapped phase. The continuous WT is defined as:

$$W_I(\mathrm{a},\mathrm{b})=\langle I\left(t\right),{\psi }_{a,b}\left(t\right)\rangle ={\left|a\right|}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\displaystyle {\int }_{-\infty }^{+\infty }I\left(t\right)\psi *\left(\frac{t-b}{a}\right)dt}$$

(4)

where a is the scale parameter, b is the shift parameter, I(t) is the signal to be analyzed, $\psi \left(t\right)$ is the mother wavelet, and $\psi *\left(\frac{t-b}{a}\right)$ is the conjugate function. The amplitude and the phase are given by:

$$A\left(a,b\right)=\sqrt{{\left\{\mathrm{Im}\left[W_I\left(\mathrm{a},\mathrm{b}\right)\right]\right\}}^2+{\left\{\mathrm{Re}\left[W_I\left(\mathrm{a},\mathrm{b}\right)\right]\right\}}^2}$$

(5)

$$\phi \left(a,b\right)=\arctan \left\{\mathrm{Im}\left[W_I\left(\mathrm{a},\mathrm{b}\right)\right]/\mathrm{Re}\left[W_I\left(\mathrm{a},\mathrm{b}\right)\right]\right\}$$

(6)

where $\mathrm{Re}\left[W_I(\mathrm{a},\mathrm{b})\right]$ is the real part of the wavelet coefficient, and $\mathrm{Im}\left[W_I(\mathrm{a},\mathrm{b})\right]$ is the imaginary part. Then, the final phase can be obtained by the phase unwrapping algorithm, and for:

$${\Delta }z(\mathrm{t})=({\Delta }\phi \times \lambda )/4\pi$$

(7)

we can find that ${\Delta }z(\mathrm{t})$, that is, the real-time displacement information of the measured object.

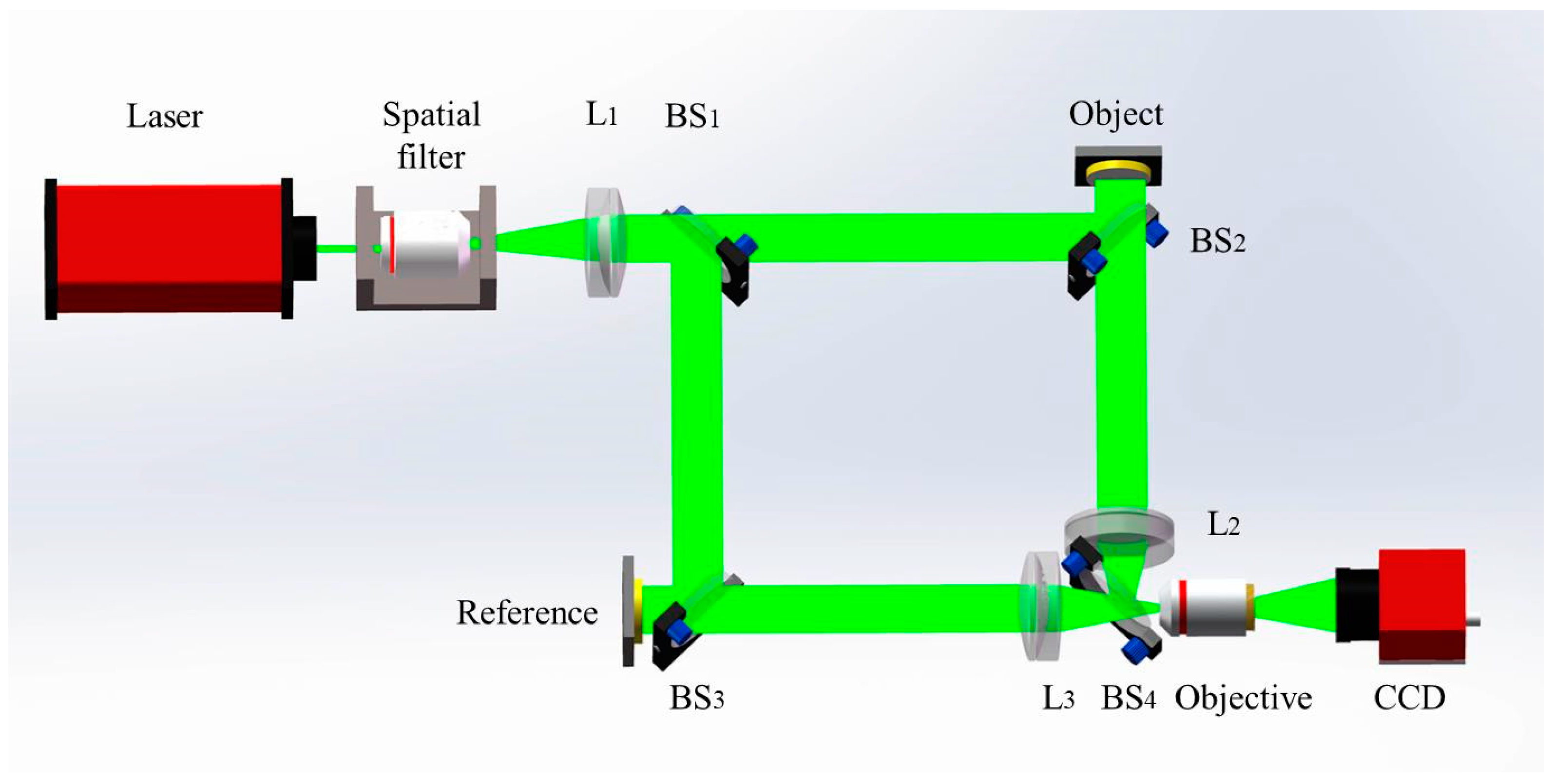
2.2. Large-Field Microscopic Speckle Interferometry System

In this paper, we introduce a new type of large-field microscopic speckle interferometry system. The optical path diagram of the system is shown in Figure 2. In the process of measurement, the laser beam is expanded by the spatial filter and converted into parallel light by the first doublet lens L₁. Then, it is split into the measurement beam and reference beam by beam splitter (BS) BS₁. The measurement beam illuminates the measured object through BS₂, and then reflects back to BS₂, and converges into the field of view of microscope objective through doublet lens L₂ and BS₄. In the experiment, considering that the light is scattered on the rough surface of the measured object, the reflected light intensity gradually weakens as the distance increases, so the distance between BS₂ and L₂ needs to be as small as possible to ensure sufficient light intensity converges into L₂. Therefore, the lens is placed in front of the BS₃. Similarly, the reference beam illuminates the reference object through the BS₃, and finally converges into the field of view of the microscope objective through doublet lens L₃ and BS₄. Two beams converge and interfere in front of the microscope objective, and the time-series interferograms amplified by the microscope objective are collected by CCD.

Our system effectively solves the two problems of small field of view and large reflected light coherent noise mentioned above.

The first step is to reduce the coherent noise of reflected light. The system is improved on the basis of the Mach–Zehnder structure and greatly reduces the influence of reflected light compared to the Linnik system (Michelson structure), for the Mach–Zehnder structure does not have the light returning to the light source, and the light beam only passes through the microscope objective once, which reduces the back-and-forth reflection phenomenon inside the microscope objective and further reduces the reflection coherent noise. Generally, the reduction in the multiple reflected light in the optical path can improve the image quality. However, it is difficult to carry out a comparative experiment to study how much the coherent noise of reflected light is reduced quantitatively.

Then, we need to expand the field of view while ensuring high imaging quality. The system introduces two doublet lens groups: L₁ and L₂ are one group, and L₁ and L₃ are the second group. Take the L₁ and L₂ group as an example. The two doublet lenses are the same. The light beam is converted into parallel light by the lens L₁ to illuminate the surface of the measured object, and the reflected light is transmitted to the lens L₂ in the manner of parallel light to be converged, then all the information enters the microscope objective. Similarly, the light beam modulated by another doublet lens group illuminates the surface of the reference object. Through the collimation and convergence process of the doublet lens group, more information will enter the microscope objective, and then the expansion of the field of view is realized.

In order to verify that the field of view is effectively expanded while ensuring the high imaging quality, we conducted three sets of comparative experiments. Three imaging modes are used to image the resolution board, respectively:

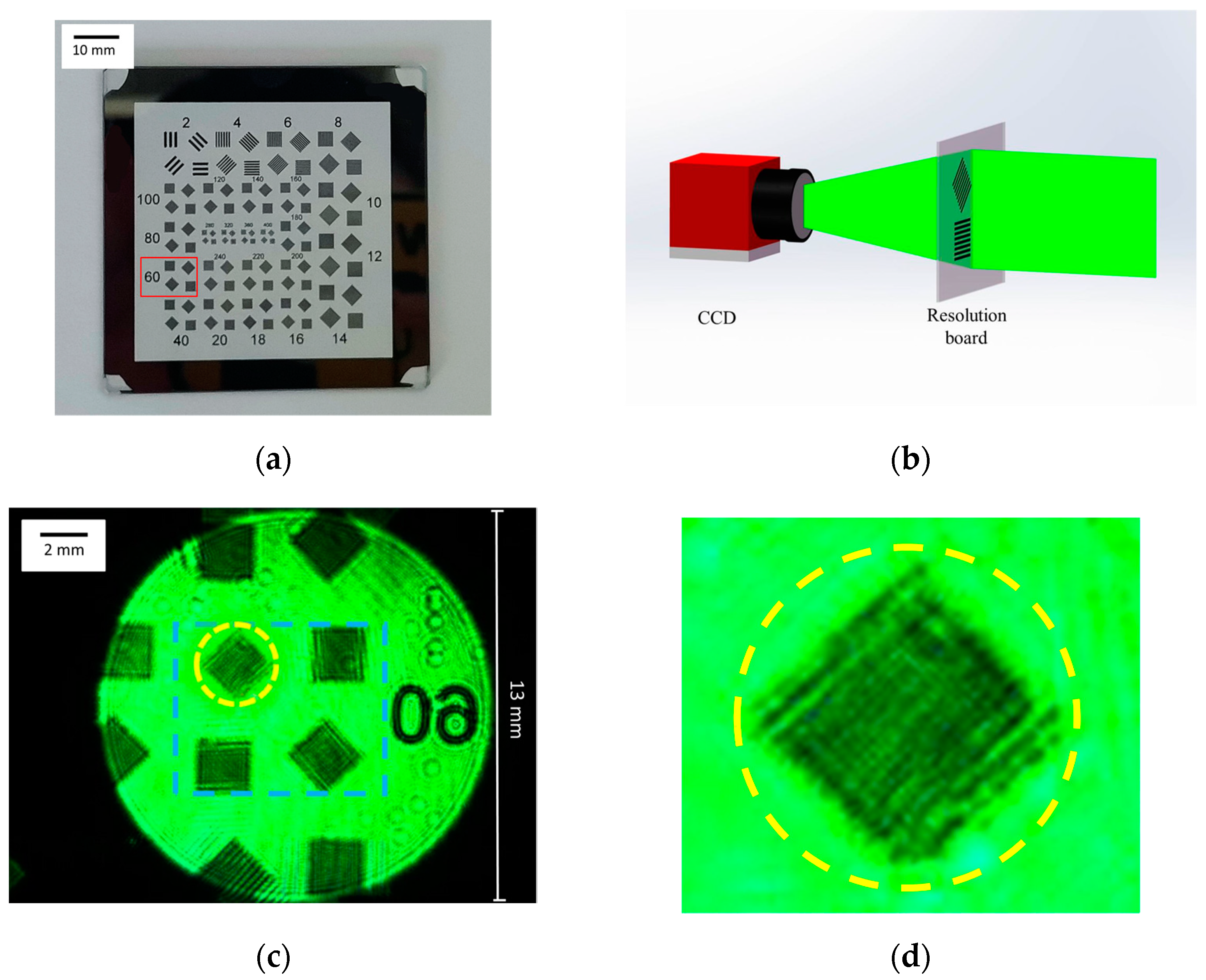
• First, the CCD is directly used for imaging. By adjusting the CCD lens, it can image the pattern numbered 60 on the resolution board, as shown in Figure 3. The field of view is a circle with a diameter of 13 mm. It can be seen that a lot of detailed information is lost in the collected image and the stripes cannot be distinguished. It is obvious that only using ordinary CCD can not distinguish the clear imaging of a small object, as shown in Figure 3d;
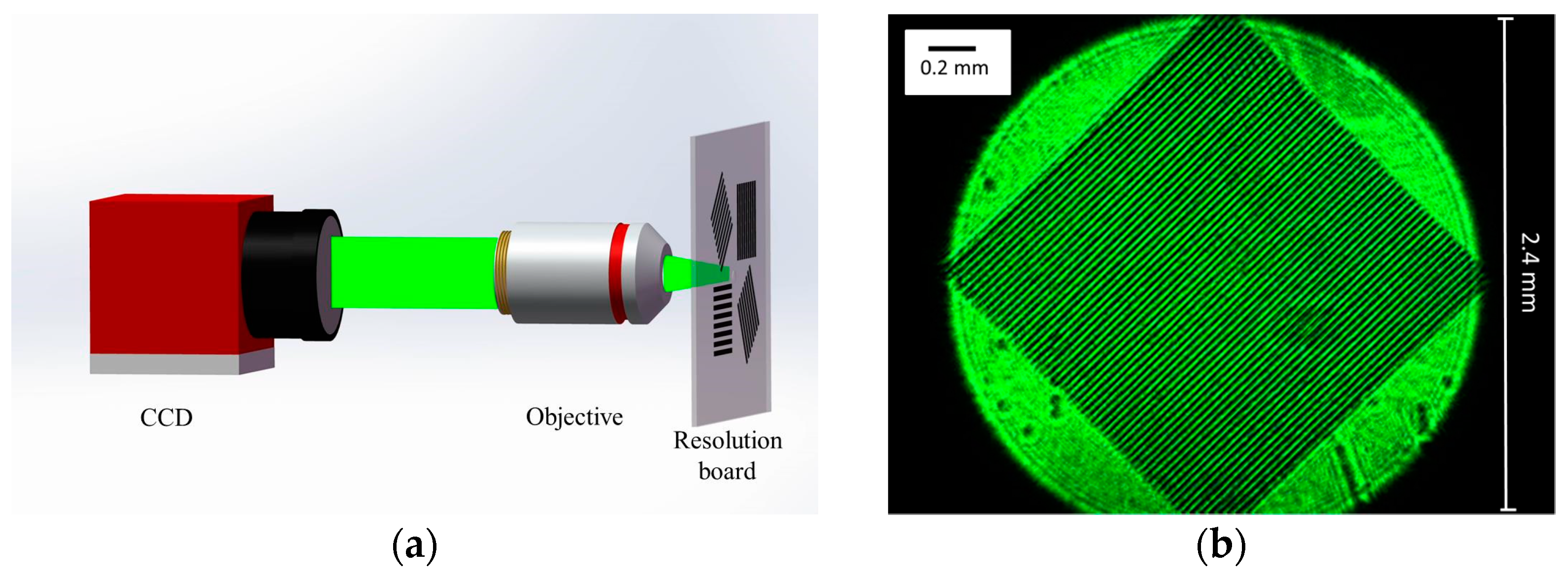
• Then, a microscope objective is added to simulate the field of view of Linnik structure. The pattern numbered 60 of the resolution board is imaged by CCD. As shown in Figure 4, the imaging region corresponds to the yellow contour region of Figure 3 We can find that by adding a microscope objective, 60 obvious stripes and clear details can be observed. At this time, the field of view is modulated by the imaging field of the microscope objective, which is approximately a circle with a diameter of 2.4 mm;
• Finally, the doublet lens group is introduced, and the field of view is shown in Figure 5. At this time, the field of view is modulated by the microscope objective, doublet lens group and the spatial resolution of the CCD together. It is a rectangular with an area of 6 mm × 8 mm, and its imaging area corresponds to the blue contour region in Figure 3. When we enlarge the selected area in the upper left corner, 60 stripes can also be clearly observed. Therefore, by introducing doublet lens groups, we not only expand the field of view, but also ensure the detailed information of the object.

By imaging the resolution board, it is proved that the field of view is effectively enlarged by adding the doublet lens group while ensuring high imaging quality, without distortion or field curvature.

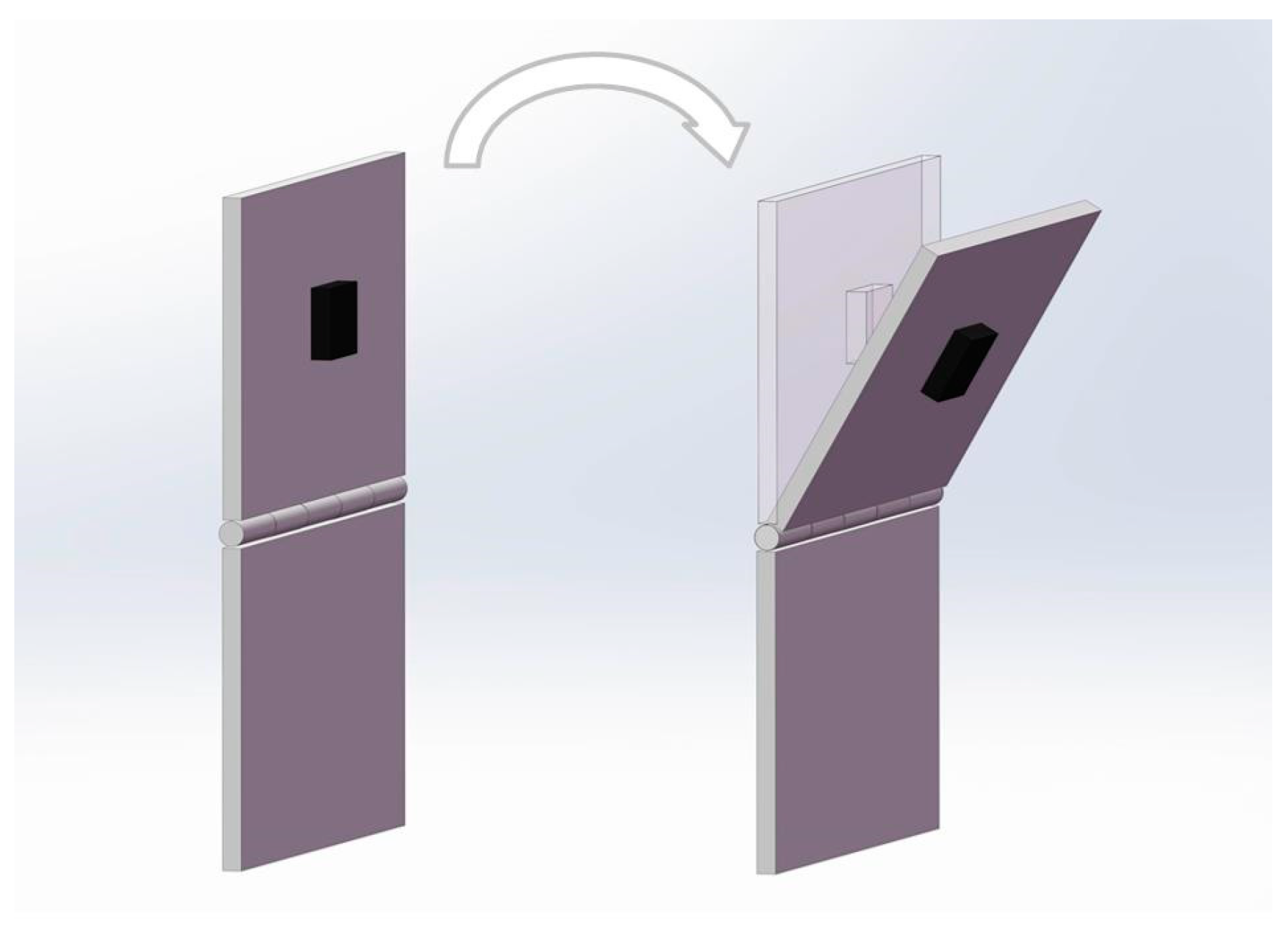
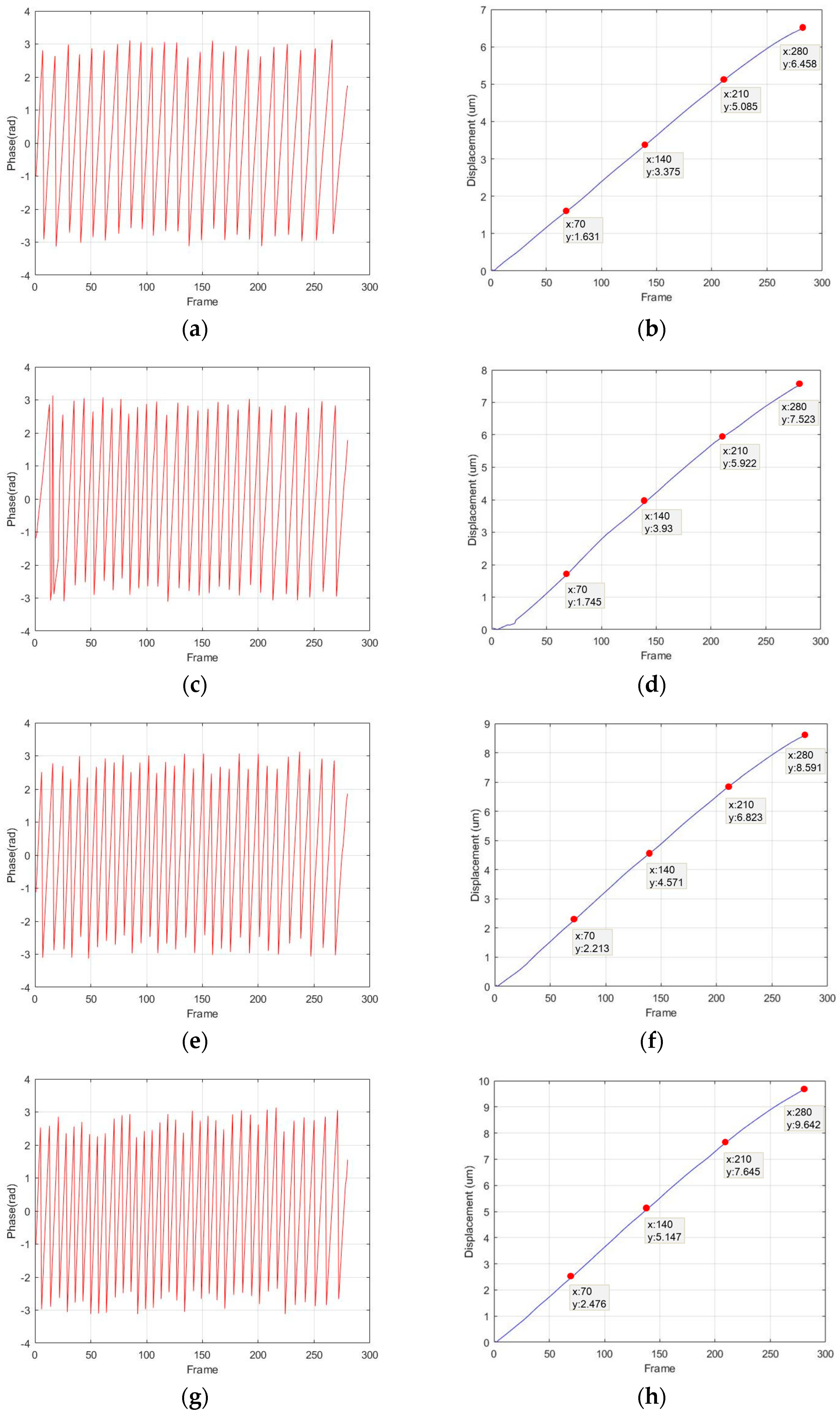
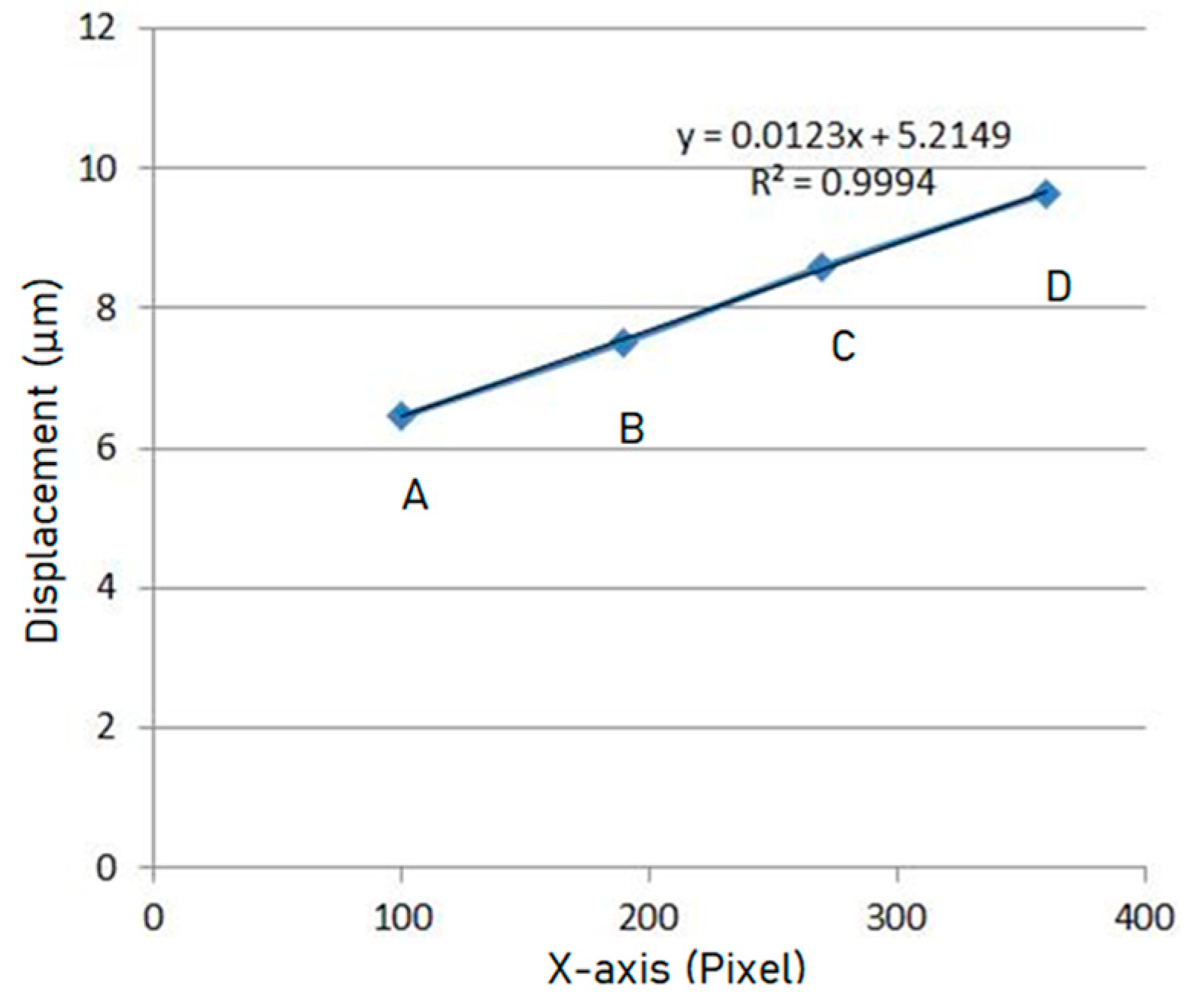
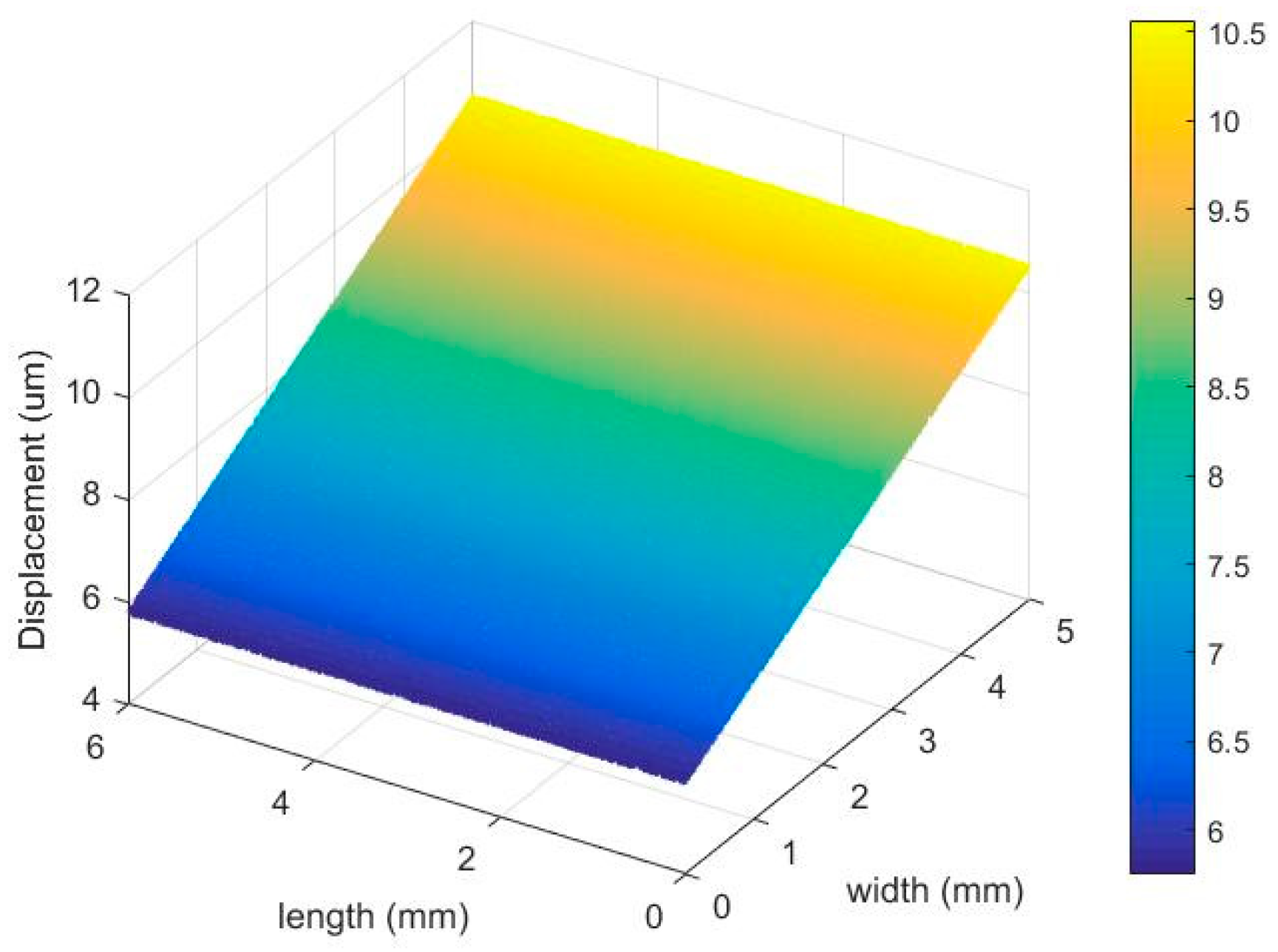
3. Experiment

We built the measurement system according to the light path diagram, as shown in Figure 6. The light source is a single longitudinal mode laser with a wavelength of 532 nm and an output power of 100 mW. The spatial resolution of CCD is 640 × 480. The pixel size of the CCD is 4.8 µm × 4.8 µm. The exposure time in the experiment is 200 microseconds and the acquisition frame rate is 70 frames/s. The numerical aperture of the microscope objective is 0.1 and the magnification is 4×. The focal length of the doublet lens is 50 mm.

The traditional Mach–Zehnder uses two mirrors, and the utilization rate of light is really high. Considering that the measured object is not transparent, we use two beam splitters to replace the two mirrors in our optical path, resulting in only half of the light entering the transmission optical path. However, this phenomenon has little effect, for the current laser power is very high. As in our experiment, the CCD exposure time is only 200 microseconds, and a clear and bright interferogram can be observed.

The measured object and reference object in the experiment are microchips with the size of 5 mm × 6 mm × 1 mm (W × L × H), as shown in Figure 7. We need to measure the displacement of the whole microchip. Because the microchip is similar to a rigid body, it is difficult to generate deformation by heating or loading force. The method we adopt here is to place the measured object on the hinge, the hinge axis is fixed, and the blade is pushed by the Physik Instrumente (PI) displacement platform to simulate the displacement of the measured object. The accuracy of the PI displacement platform is 10 nm. The specific process is shown in Figure 8.

The entire displacement process is 4 s, and 280 speckle interferograms can be collected. One of the speckle interferogram collected by CCD during the displacement process is shown in Figure 9, and the interference fringe patterns obtained by the subtraction mode are shown in Figure 10.

Using the WT phase extraction algorithm mentioned above, the time series phase value of each pixel can be calculated. Then, the continuous phase value is obtained by unwrapping, and the corresponding displacement value is finally obtained.

Taking pixels A (100, 260), B (190, 260), C (280, 260), D (370, 260) as examples, we show the phase and displacement maps of these four pixels over time, as shown in Figure 11. The acquisition frame rate of CCD is 70 frames/s. We can obtain the displacements of these four points at 1, 2, 3, and 4 s from the displacement diagrams. The corresponding dynamic displacement map of the microchip is shown in Figure 12.

It should be noted here that when imaging with a doublet lens group, the object and the image are in opposite directions. Therefore, the smaller the x coordinate of the pixel, the closer to the fixed axis of the hinge it is, and the displacement value of the four pixels gradually becomes smaller. The final displacement range calculated from the experimental results is 5.75–10.47 µm, which, respectively, corresponds to the displacement value of the low end and the top end of the microchip.

In order to verify the accuracy of the results, we first use the displacement value introduced by the PI displacement platform to judge whether the displacement range of the measured object is reasonable. The width of the hinge is 16 mm, the width of the measured object is 5 mm, and the distance between the measured object and the low end and top end of the hinge is 6 and 5 mm, respectively; the displacement value introduced by the PI displacement platform at the top of the hinge is 15 μm, which can be used to judge that our measurement range is generally reasonable.

Then, the linear relationship of four points is used in further judgment. Because the four points are selected with an equal pixel interval, and the measured object is approximate to the rigid body and will not deform easily, so the four points should have a linear correlation. The final displacement values of the four points are connected and the correlation coefficient R² is calculated to be 0.9994, as shown in Figure 13, which indicates that the linearity is very good. That is, our experimental results have high accuracy.

In order to verify the full-field performance of the system and the measurement accuracy of different positions, 16 arbitrary pixels were selected to display their displacement values, as shown in Figure 14. Among them, 12 points are in the same row with points A, B, C, D, respectively. According to the displacement direction, the displacement values of these pixels in the same row should be the same. The measuring result is shown in Figure 14, and the maximum relative error of the 12 points is 0.46%. After traversing all the pixels that record the interference information, the full-field displacement map of the object can be obtained. After calculating the displacement values of all pixels and removing individual dead pixels through smoothing operations, the overall displacement map can be obtained, as shown in Figure 15. In our research, we use MATLAB to calculate the displacement information of each pixel and finally realize the full-field measurement. The entire processing process takes less than 15 s.

4. Discussion

When introducing displacement through the hinge, it is necessary to consider whether the introduced inclination will affect the measurement result. In our experiment, the inclination is very small and has little effect on the measurement of the out-of-plane displacement. The maximum displacement of the top end of the microchip is 9.6 µm, and the distance from the top end to the fixed axis is 11 mm. Thus, the inclination angle is about 0.00087°. Through further calculation, the change in the vertical beam propagation direction does not exceed one pixel, so it will not affect the measurement results. In order to understand the displacement process easily, the angles drawn in Figure 8 and Figure 12 are exaggerated and much larger than the actual angle.

If we want to measure the displacement in the case of a large inclination angle, we can no longer calculate the out-of-plane displacement only by Equation (7), but should consider the influence of the inclination angle and the in-plane displacement [35,36,37]. Yang, L.X. has summarized various out-of-plane displacement and in-plane displacement measurement methods and applicable conditions in detail [35].

5. Conclusions

In this paper, a new type of large-field microscopic speckle interferometry system based on Mach-Zehnder structure is proposed. By introducing doublet lens groups, the new system expands the field of view from a circular area with a diameter of 2.4 mm to a rectangular area of 6 mm × 8 mm. Additionally, our system effectively reduces the reflected light beam in the optical path, thereby reducing the reflected coherent noise. The experimental results show that our improved measurement system can achieve large-field and high-precision dynamic measurement of MEMS.

There are still some details that need to be further improved. The first limitation of our system is the need to obtain proper field of view with different sizes of measured object. To achieve this purpose, we can combine different microscope objectives and doublet lenses, which require a series of experiments to summarize. At the same time, the measurement accuracy is not very high. We can improve the measurement accuracy by optimizing the algorithm (such as phase subdivision) and adding the anti-reflection film on the surface of optical components to further reduce the coherent noise.