Measurement of Focal Length and Radius of Curvature for Spherical Lenses and Mirrors by Using Digital-Grating Moiré Effect

Abstract

This paper proposes the use of digital-grating moiré effect for measuring the focal lengths and radius of curvatures of biconvex and biconcave spherical simple lenses and spherical mirrors. Based on Fresnel diffraction, the equation for the electric field of propagated light passing through the test samples was derived. Through digital image post processing, the recorded intensity on an observation screen was superimposed on a digital grating to generate a moiré pattern. On substituting the slant angle of the moiré pattern into the derived equation, the focal lengths and radius of curvatures could be determined. The experimental results successfully demonstrated the feasibility of the proposed method; the percent errors for focal length and radius of curvature measurement were less than 0.5%. The measurement uncertainty was analyzed and the correctness of the derived equation was confirmed through simulation. Because of the use of digital image post processing, the proposed method has advantages such as a simple set up, easy operation, high stability, high accuracy, and low cost. Thus, the method has considerable potential in relevant application.

1. Introduction

Focal length and radius of curvature, the most important parameters of spherical lenses and mirrors, have been widely used to design optical systems and commercial electro-optical products. The measurement of focal length and radius of curvature is necessary to ensure the quality and performance of lenses and mirrors. Methods such as nodal slide and image magnification have been proposed for these measurements [1]. These methods have been successfully applied to measure the lenses with short focal lengths or large numerical apertures. Modern methods mainly use the Talbot effect and moiré technique to measure focal length [2,3,4,5,6,7,8]. In both these methods, two Ronchi gratings are required. After the test light passes through the test lens and mirror, the magnified self-image of the first grating is superimposed on the second grating to generate moiré fringes. By rotating one grating with respect to the other, the slant angle of the moiré fringes can be used to estimate to the curvature and focal length of the test samples. However, the rotation of the grating can introduce mechanical vibrations. In addition, two gratings are required; therefore, measurement using these two methods is complex and time-consuming. Digital image post processing, a recent trend in relevant applications, has several advantages [9,10]. The technique proposed by Angelis et al. for the automated analysis of moiré fringes for accurate measurement of the focal length of lenses is based on the fast Fourier transform (FFT) and least-squares fit methods [11]. Lee proposed a Talbot interferometry-based digital image method for measuring the focal length of lenses without using moiré fringes. In this method, only one grating is required and the original Fourier transform is used to access the spectrum beyond the limitations of the usual fast Fourier transform [12]. However, using the original Fourier transform can be time-consuming.

In this paper, a method based on digital-grating moiré effect is proposed for measuring the focal lengths and radius of curvatures of spherical lenses and mirrors. The measurement system consists of a test light source, a Ronchi grating, a digital camera, and a personal computer. Based on Fresnel diffraction, the electric fields of the test light at various positions and the intensity at an observation screen were derived using the kernel equation for the method. After the test light passed through the grating and sample, the light intensity was projected on the observation screen and captured by the digital camera. This light intensity was superimposed on a digital grating to generate a moiré fringe. Using the slant angle of the moiré fringe, the focal length and radius of curvature of the test sample were determined. To demonstrate the feasibility of the proposed method, the focal lengths of three convex mirrors and two concave lenses were measured. The measurement percent errors for the focal lengths and radius of curvatures were less than 0.5%. Because the method applied digital image post processing, only a single digital image was required to be captured during measurement. Therefore, this method is time saving and free of mechanical vibrations. In addition, only one grating is required in this method. Consequently, this method has merits such as a simple establishment, easy operation, high stability, high accuracy, and low cost. Thus, it has considerable potential in relevant applications.

2. Principles

Figure 1a,b schematically represent the measurements for the reflection spherical mirrors and transmission spherical lenses (bi-convex or bi-concave), respectively. To facilitate understanding, an x–y–z coordinate system is introduced in the figures. A collimated and expanded laser beam with a wavelength of λ passes through the Ronchi grating (G), located at (x₀, y₀); the transmittance of the grating can be written as

$$t_0(x_0,y_0)=\frac{1}{2}(1+\cos \frac{2\pi x_0}{p_1}),$$

(1)

where p₁ is the period of the grating in the x–direction. The electric field behind the grating is denoted as U₀ (x₀, y₀, 0) (at z = 0) and the intensity can be expressed as

$$I_0={\left|U_0(x_0,y_0,0)\right|}^2=\frac{1}{4}(1+2\cos \frac{2\pi x_0}{p_1}+{\cos }^2\frac{2\pi x_0}{p_1}),$$

(2)

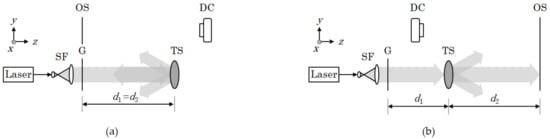
Figure 1. Schematic of the measurement setup for (a) reflection and (b) transmission samples. SF, spatial light filter; G, Ronchi grating; TS, test sample; OS, observation screen; DC, digital camera.

According to Fresnel diffraction, the electric field U₁ (x₁, y₁, d₁) of the test light reaching the test sample (TS) after propagating a distance of d₁ can be expressed as

$$U_1(x_1,y_1,d_1)=\frac{e^{jk{d}_1}}{j\lambda d_1}{\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }{t}_0(x_0,y_0)e^{j\frac{k}{2d_1}[{(x_1-x_0)}^2+{(y_1-y_0)}^2]}d}{x}_{0}d{y}_0}.$$

(3)

Meanwhile, the transmittance of the test sample, t₁ (x₁, y₁), can be expressed as [13]

$$t_1(x_1,y_1)=e^{-j\frac{k}{2f}(x_1^2+y_1^2)},$$

(4)

where k = 2πn/λ is the propagation number, n is the refractive index of the environmental medium, and f is the focal length of the test sample. For converging lenses or concave mirrors, the focal length has a positive sign. By contrast, for diverging lenses or convex mirrors, the focal length has a negative sign.

As shown in Figure 1a,b, respectively, the reflected and transmitted electric field $U_1^{\prime }$ can be written as

$$U_1^{\prime }(x_1,y_1,d_1)=\frac{e^{jk{d}_1}}{j\lambda d_1}{\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }{t}_0(x_0,y_0)}{e}^{j\frac{k}{2d_1}[{(x_1-x_0)}^2+{(y_1-y_0)}^2]}{e}^{-j\frac{k}{2f}(x_1^2+y_1^2)}d{x}_{0}d}{y}_0.$$

(5)

Again, the test light travels an additional distance of propagation d₂ and reaches the observation screen (OS), as shown in Figure 1a,b, respectively. According to Fresnel diffraction, the electric field of the test light on the observation screen can be written as

$$U_2(x_2,y_2,d_2)=\frac{e^{jk{d}_2}}{j\lambda d_2}{\displaystyle \int {\displaystyle {\int }_{-\infty }^{\infty }{U}_1^{\prime }}(x_1,y_1,d_1)e^{j\frac{k}{2d_2}[{(x_2-x_1)}^2+{(y_2-y_1)}^2]}}d{x}_{1}d{y}_1.$$

(6)

With extensive substitution, Equation (6) can be expressed as [13]

$$U_2(x_2,y_2,d_2)=\frac{1}{2}\left\{1+\cos \left[2\pi \frac{x_2}{p_1\left(1-\frac{d_2}{f}\right)}\right]\times \exp \left[-j\frac{\pi \lambda d_1}{p_1^2}\left(\frac{\frac{1}{d_1}-\frac{1}{f}+\frac{1}{d_2}}{\frac{1}{d_2}-\frac{1}{f}}\right)\right]\right\}.$$

(7)

Accordingly, the intensity on the observation screen, recorded using a digital camera (DC), can be expressed as follows:

$$I(x_2,y_2,d_2)=|U_2(x_2,y_2,d_2){|}^2=\frac{1}{4}\left\{1+2\cos \frac{2\pi x_2}{p_1(1-\frac{d_2}{f})}\cos \frac{\pi \lambda d_1}{p_1{}^2}(\frac{\frac{1}{d_1}-\frac{1}{f}+\frac{1}{d_2}}{\frac{1}{d_2}-\frac{1}{f}})+{\cos }^2\frac{2\pi x_2}{p_1(1-\frac{d_2}{f})}\right\}.$$

(8)

The captured intensity with a period of mp₁ and a grating vector K₁ = (2π/mp₁)$\widehat{i}$ is superimposed on a digital grating with a period of p₂ and a grating vector K₂ = (2π cosθ/p₂)$\widehat{i}$−(2π sinθ/p₂)$\widehat{j}$, as shown in Figure 2. The value of p₂ is determined by the captured pattern described in Equation (8) and is set as p₂ ≅ mp₁. Therefore, a moiré pattern with a slant angle α can be obtained. The slant angle α is defined as the angle between the grating vector K₃ of moiré pattern and the y-axis which can be written as [14]

$$\alpha ={\tan }^{-1}\left(\frac{p_2-m{p}_{1}cos\theta }{m{p}_1\sin \theta }\right)={\tan }^{-1}\left(\frac{p_2-\left|1-\frac{{\mathrm{d}}_2}{\mathrm{f}}\right|p_1\cos \theta }{\left|1-\frac{{\mathrm{d}}_2}{\mathrm{f}}\right|p_1\sin \theta }\right)={\tan }^{-1}\left(\frac{1-M\cos \theta }{M\sin \theta }\right),$$

(9)

where m = |1 − d₂/f| is the imaging magnification for grating G, θ is the angle between the practical and digital gratings, and M is the period ratio of the two period patterns (captured intensity and digital grating) which equals mp₁/p₂. Therefore, the observation plane is in the grid image given by the test sample under study. It results from the setup of Figure 1 and the magnification formula m = |1 − d₂/f|.

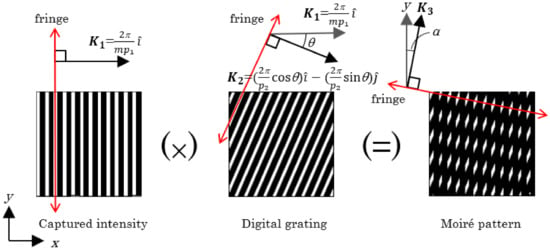
Figure 2. Schematic illustration for the generation of moiré pattern and related orientations.

Accordingly, the focal length of the test samples can be expressed as

$$f=\frac{p_1(\tan \alpha \sin \theta +\cos \theta )d_2}{p_1(\tan \alpha \sin \theta +\cos \theta )-p_2},$$

(10)

and the radius of curvature of the test samples can be written as

$$R=-2f=-\frac{2p_1(\tan \alpha \sin \theta +\cos \theta )d_2}{p_1(\tan \alpha \sin \theta +\cos \theta )-p_2},(\mathrm{for}\mathrm{spherical}\mathrm{mirrors})$$

(11)

and

$$R_1=-R_2=2(n_l-1)f=\frac{2(n_l-1)p_1(\tan \alpha \sin \theta +\cos \theta )d_2}{p_1(\tan \alpha \sin \theta +\cos \theta )-p_2},(\mathrm{for}\mathrm{spherical}\mathrm{lenses})$$

(12)

where R₁ and R₂ are the radius of curvature of the bi-convex or bi-concave lens’s first and second surfaces, and n_l is the refractive index of the lens. Thus, the focal length and radius of curvature of the test samples can be determined using the following experimental parameters: the periods of the practical and digital gratings, p₁ and p₂, respectively; the relative angle between these gratings, θ; the slant angle of the moiré pattern, α; the distance, d₂; and the refractive index of the lens, n_l.

3. Experimental Results and Discussion

To demonstrate the feasibility of the proposed method, three convex mirrors (Edmund Optics) labeled TS1, TS2, and TS3, with focal lengths of −7.751, −25.80, −52.08 mm, respectively, and radius of curvatures of −15.50, −51.60, and −104.2 mm, respectively, and two BK7 concave lenses (Edmund Optics) (n_l = 1.5151 @ λ = 0.6328 μm) labeled TS4 and TS5, with focal lengths −50.00 and −200.0 mm, respectively, and radius of curvatures of −51.51 and −206.0 mm, respectively, were measured. The photos of experiment setup are shown in Figure 3a,b. A Ronchi grating of laser direct writing photomask (MLA150, HEIDELBERG INSTRUMENTS) with a period of 0.2822 mm was used. A 0.6328 μm helium–neon laser was used as the test light source and a digital camera (Canon EOS 650D) was used to capture the intensity of the test light field. The vertical pixel array of the camera was aligned to the pattern of light field along y-direction. For convenience, the distances d₁ and d₂ were both set at 251.7 mm. The captured intensities of TS1–5 (on the observation screen) are illustrated in Figure 4a–e, respectively. The gray-level transformed pictures are illustrated in Figure 4f–j, respectively. The corresponding digital gratings with periods of 9.480, 3.072, 1.659, 1.720, and 0.6410 mm which were set similar to that of the gray-level transformed patterns are shown in Figure 4k–o. The angle θ between the practical and digital grating was set as 30°. Accordingly, the superimposed moiré patterns were obtained as illustrated in Figure 4p–t, respectively. With these moiré patterns, the obtained slant angles, α, of TS1–5 were 15.46°, 15.35°, 15.79°, 15.83°, and 15.50°, respectively. After substituting the relevant parameters into Equations (10)–(12), as listed in Table 1, the focal lengths of TS1–5 were −7.757, −25.67, −52.05, −49.85, and −199.6 mm, respectively, and the radius of curvatures were −15.51, −51.34, −104.1, −51.36, and −205.6 mm, respectively. Compared with commercial reference values, the results exhibited a high accuracy of measurement of the focal lengths and radius of curvatures, and the percent errors were less than 0.5%.

Figure 3. Experiment setup for measuring (a) reflection and (b) transmission samples. SF, spatial light filter; G, Ronchi grating; TS, test sample; OS, observation screen.

Figure 4. Captured intensities on the screen for test samples (TSs): (a) TS1, (b) TS2, (c) TS3, (d) TS4, and (e) TS5. Gray-level transformed images of the captured intensity for the TSs: (f) TS1, (g) TS2, (h) TS3, (i) TS4, and (j) TS5. Digital gratings with a slant angle of 30° for TSs: (k) TS1, (l) TS2, (m) TS3, (n) TS4, and (o) TS5. Moiré patterns obtained with digital image post processing of the TSs: (p) TS1, (q) TS2, (r) TS3, (s) TS4, and (t) TS5.

Table 1. Relevant parameters, experimental results, and percent errors for focal length and radius of curvature measurement.

Test Samples	Angle θ (°)	Slant Angle α (°)	Experimental Value of Focal Length (mm)	Reference Value of Focal Length (mm)	Percent Error (%)
			Experimental Value of Radius of Curvature (mm)	Reference Value of Radius of Curvature (mm)	Percent Error (%)
TS1	30.00	15.46	−7.757	−7.751	0.0774
			−15.51	−15.50	0.0645
TS2	30.00	15.35	−25.67	−25.80	0.5039
			−51.34	−51.60	0.5039
TS3	30.00	15.79	−52.05	−52.08	0.0576
			−104.1	−104.2	0.0960
TS4	30.00	15.83	−49.85	−50.00	0.3000
			−51.36 (R1)	−51.51 (R1)	0.2912
TS5	30.00	15.50	−199.6	−200.0	0.2000
			−205.6 (R1)	−206.0 (R1)	0.1942

3.1. Determination of the Slant Angle for the Digital Gratings

The relationships between the slant angle α of the moiré pattern and the angle θ between the practical and digital gratings were simulated according to Equation (9). These relationships are associated with the value of M (the adapted period ratio for two period patterns), as shown in Figure 5. When M = 1, the relationship between α and θ is linear. In practice, the period of the digital grating typically is slightly different from that of the captured pattern. Bending curves are generated, which gradually deviate from the linear (M = 1) according to the deviation of the value of M from 1. When M < 1, the curves lie above the linear line. By contrast, when M > 1, the curves lie below the linear line. The values of M for TS1–TS5 were 0.9964, 0.9881, 0.9922, 0.9900, and 0.9943, respectively (Figure 5). The value of the slant angle α varies significantly with small variations in the angle θ when θ < 2.5°. By contrast, α has a gentle slope when θ > 10°. In addition, a large value of α, approaching 90° (with a small angle θ), should be avoided to avert an extreme value of the tangent function of α in Equations (10)–(12). Therefore, the ideal angle θ was set as 30°, as illustrated in Figure 5 and Table 1.

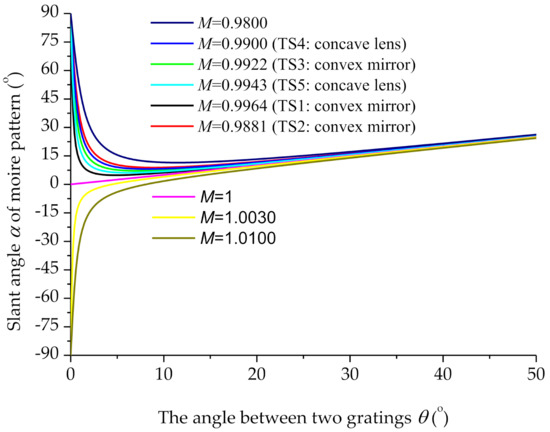
Figure 5. The relationships between the slant angle α of moiré pattern and the angle θ between practical and digital gratings.

3.2. Analysis of Measurement Uncertainty

With Equation (10), the measurement uncertainty of the focal length can be expressed as

$$\Delta f=\sqrt{{\left(\frac{\partial f}{\partial p_1}\Delta p_1\right)}^2+{\left(\frac{\partial f}{\partial p_2}\Delta p_2\right)}^2+{\left(\frac{\partial f}{\partial d_2}\Delta d_2\right)}^2+{\left(\frac{\partial f}{\partial \alpha }\Delta \alpha \right)}^2+{\left(\frac{\partial f}{\partial \theta }\Delta \theta \right)}^2},$$

(13)

with

$$\frac{\partial f}{\partial p_1}=\frac{-p_2{d}_2(\tan \alpha \sin \theta +\cos \theta )}{{\left[p_1(\tan \alpha \sin \theta +\cos \theta )-p_2\right]}^2},$$

(14)

$$\frac{\partial f}{\partial p_2}=\frac{p_1{d}_2(\tan \alpha \sin \theta +\cos \theta )}{{\left[p_1(\tan \alpha \sin \theta +\cos \theta )-p_2\right]}^2},$$

(15)

$$\frac{\partial f}{\partial d_2}=\frac{p_1(\tan \alpha \sin \theta +\cos \theta )}{p_1(\tan \alpha \sin \theta +\cos \theta )-p_2},$$

(16)

$$\frac{\partial f}{\partial \alpha }=\frac{-p_1{p}_2{d}_2{\sec }^2\alpha \sin \theta }{{\left[p_1(\tan \alpha \sin \theta +\cos \theta )-p_2\right]}^2},$$

(17)

$$\frac{\partial f}{\partial \theta }=\frac{-p_1{p}_2{d}_2(\tan \alpha \cos \theta -\sin \theta )}{{\left[p_1(\tan \alpha \sin \theta +\cos \theta )-p_2\right]}^2},$$

(18)

where Δp₁, Δp₂, Δd₂, Δα, andΔθ are errors of the periods of the practical and digital gratings, the distance d₂, the slant angle of the moiré pattern, and the relative angle between these gratings, respectively. The value of Δp₁ equals to 0.005 mm which corresponds to the fabrication line width of photomask (MLA150, HEIDELBERG INSTRUMENTS). With the assistance of a laser rangefinder (GCL 25, Bosch), the distance from the grating to the vertex of test samples was measured which was used to determine the value of d₂ and therefore Δd₂ equals to 0.3 mm. For spherical mirrors, d₂ equals the measured value. For spherical lenses, d₂ equals the distance from the grating to the lens principal point. Therefore, the distance from the vertex to the principal point which can be estimated as one-third the lens center thickness must be added into the measured value. Because the period p₂, the angles α and θ were measured on digital images, the measurement values and deviations are related to the number of pixels, and the physical scale corresponding to one pixel. Shown in Figure 6 is a digital image of captured pattern with 15 megapixel (5184 pixel × 2912 pixel) in which an area with 1200 pixel × 1200 pixel and a scale bar of 50 mm with 1761 pixels are marked. Therefore, the value of Δp₂ equals to 0.028 mm. Figure 7a,b illustrate how to estimate an angle $\Theta$ and an angle deviation $\Delta \Theta$ on a digital image with K × J pixels. The angle $\Theta$ can be expressed as

$$\Theta ={\tan }^{-1}\left[\frac{K(\mathrm{pixels})}{J(\mathrm{pixels})}\right],$$

(19)

and the angle deviation $\Delta \Theta$ can be written as

$$\Delta \Theta ={\tan }^{-1}\left[\frac{1(\mathrm{pixel})}{\sqrt{K^2+J^2}(\mathrm{pixels})}\right].$$

(20)

Figure 6. A digital image (5184 pixel × 2912 pixel) of captured pattern marked with scale bar and number of pixels.

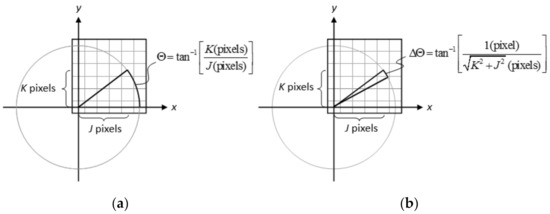
Figure 7. Schematic of the evaluation of (a) angle and (b) angle deviation on a digital image.

Therefore, with Equation (20), considering the digital image with 1200 × 1200 pixels (K = J = 1200) in Figure 6, the angle deviations of Δα and Δθ equal to 0.03°. According to Equation (13), the measurement uncertainty Δf of the focal length for TS1–5 can be evaluated with values of 0.2, 0.8, 2.0, 1.9, 18.3 mm, respectively. The values of relevant terms, parameters, and measurement uncertainty Δf are summarized in Table 2. In order to clarify the large measurement uncertainty of TS5, from Equations (14)–(18), we can find that when p₁ and p₂ have close values, the term of [p₁(tanαsinθ + cosθ) − p₂]² in the denominator will magnify introduced errors of Δp₁, Δp₂, Δα, and Δθ (due to tanαsinθ + cosθ ≅ 1, when α ≅ 15° and θ = 30°). By contrast, in the cases of TS1 and TS2, p₂ has a value much larger than p₁ (>>1), therefore the measurement uncertainty can reach sub-millimeter.

Table 2. Values for relevant terms and parameters for the measurement uncertainty of focal length.

Test Samples	$\left|\frac{\partial \mathit{f}}{\partial {\mathit{p}}_1}\right|$	${\mathit{p}}_1$$\mathbf{\Delta }{\mathit{p}}_1 \left(\mathbf{mm}\right)$	$\left|\frac{\partial \mathit{f}}{\partial {\mathit{p}}_2}\right|$	${\mathit{p}}_2$$\mathbf{\Delta }{\mathit{p}}_2 \left(\mathbf{mm}\right)$	$\left|\frac{\partial \mathit{f}}{\partial {\mathit{d}}_2}\right|$	${\mathit{d}}_2$$\mathbf{\Delta }{\mathit{d}}_2 \left(\mathbf{mm}\right)$	$\left|\frac{\partial \mathit{f}}{\partial \mathit{\alpha }}\right|$	$\mathit{\alpha }$$\mathbf{\Delta }\mathit{\alpha } (\mathbf{°})$	$\left|\frac{\partial \mathit{f}}{\partial \mathit{\theta }}\right|$	$\mathbf{\Delta }\mathit{\theta } (\mathbf{°})$	$\mathbf{\Delta }\mathit{f} \left(\mathbf{mm}\right)$
TS1	0.1417	0.282 0.005	0.0236	9.480 0.028	0.0092	251.7 0.3	0.1414	15.46 0.03	0.0684	0.03	0.2
TS2	0.4987	0.282 0.005	0.2565	3.072 0.028	0.0305	251.7 0.3	0.4978	15.35 0.03	0.2428	0.03	0.8
TS3	1.1130	0.282 0.005	1.0602	1.659 0.028	0.0620	251.7 0.3	1.1111	15.79 0.03	0.5249	0.03	2.0
TS4	1.0585	0.282 0.005	0.9725	1.720 0.028	0.0594	251.7 0.3	1.0567	15.83 0.03	0.4978	0.03	1.9
TS5	6.3423	0.282 0.005	15.6363	0.641 0.028	0.2379	251.7 0.3	6.3309	15.50 0.03	3.0550	0.03	18.3

Furthermore, with Equation (9) and condition of $M\approx 1$, Equations (14)–(18) can be rewritten as

$$\frac{\partial f}{\partial p_1}=\frac{-(p_2/M)d_2}{{\left[(p_1/M)-p_2\right]}^2}\approx \frac{-p_2{d}_2}{{(p_1-p_2)}^2}=\frac{f}{p_1}\cdot S_1,$$

(21)

$$\frac{\partial f}{\partial p_2}=\frac{(p_1/M)d_2}{{\left[(p_1/M)-p_2\right]}^2}\approx \frac{p_1{d}_2}{{(p_1-p_2)}^2}=\frac{f}{p_1}\cdot S_2,$$

(22)

$$\frac{\partial f}{\partial d_2}=\frac{p_1/M}{(p_1/M)-p_2}\approx \frac{p_1}{p_1-p_2}=S_3,$$

(23)

$$\frac{\partial f}{\partial \alpha }=\frac{-p_1{p}_2{d}_2{\sec }^2\alpha \sin \theta }{{\left[(p_1/M)-p_2\right]}^2}\approx \frac{-p_1{p}_2{d}_2{\sec }^2\alpha \sin \theta }{{(p_1-p_2)}^2}=f({\sec }^2\alpha \cdot \sin \theta )\cdot S_1,$$

(24)

$$\frac{\partial f}{\partial \theta }=\frac{-p_1{p}_2{d}_2(\tan \alpha \cos \theta -\sin \theta )}{{\left[(p_1/M)-p_2\right]}^2}\approx \frac{-p_1{p}_2{d}_2(\tan \alpha \cos \theta -\sin \theta )}{{(p_1-p_2)}^2}=-f(\tan \alpha \cos \theta -\sin \theta )\cdot S_2,$$

(25)

with

$$S_1=\frac{-d_r\left|1-d_r\right|}{{\left[1-\left|1-d_r\right|\right]}^2},$$

(26)

$$S_2=\frac{d_r}{{\left[1-\left|1-d_r\right|\right]}^2},$$

(27)

and

$$S_3=\frac{1}{1-\left|1-d_r\right|},$$

(28)

where d_r is defined as relative distance which equals d₂/f. In Equations (21)–(25) (with ${\sec }^2\alpha \sin \theta <1$ and $(\tan \alpha \cos \theta -\sin \theta )<1$) it is obvious that smaller absolute values of S₁, S₂, and S₃ ensure relatively small introduced errors which are directly related to the relative distance in Equations (26)–(28). Therefore, the relationships between S₁, S₂, and S₃ to the relative distance d_r are plotted in Figure 8a–c. The simulation results reveal that a smaller measurement uncertainty can be achieved with increasing the distance of d₂ for cases of f > 0 and f < 0. In the case of f > 0, a smaller measurement uncertainty can also be obtained when d₂ is near the focal length; meanwhile, the distance of d₂ = 2f must be avoided. In addition, from Equations (21) and (22), properly increasing the period p₁ of the grating can also reduce the measurement uncertainty. Because a small measurement uncertainty ultimately relies on a high-precision control of experimental conditions. Considering errors of Δp₁ = 0.001 mm, Δp₂ = 0.01 mm, Δd₂ = 0.01 mm, Δα = Δθ = 0.01° under accurate controls, theoretical evaluations for the measurement uncertainty of focal length under different focal lengths, relative distances, and periods of grating are summarized in Table A1, in Appendix A. Accordingly, this method could be applied to regular commercial spherical lenses and mirrors (−200 mm< f < +200 mm) with Δf < 1.6 mm within a measurement distance of 2 m. Considering the limited length of optical benches, there must be a trade-off between measurement resolution and measurement distance. In addition, distortion of the grid image may occur on the observation screen during measurement which is a function of the off-axis image distance. Therefore, it is necessary to capture the image of the paraxial area to avoid introducing additional errors on the moiré fringes.

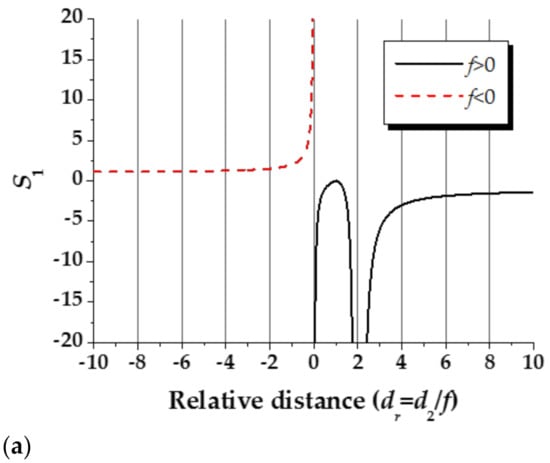
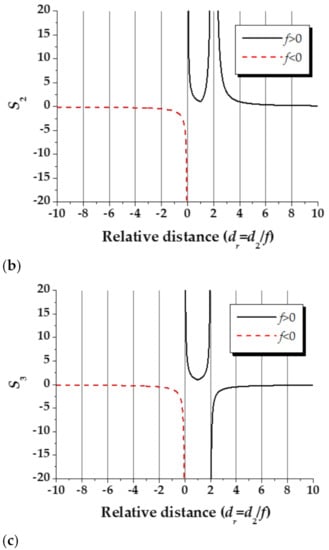
Figure 8. Relationships of (a) S₁ versus relative distance d_r, (b) S₂ versus relative distance d_r, and (c) S₃ versus relative distance d_r.

3.3. Simulation of Light Field Distributions

The intensity behind the grating (with a period p₁ = 0.2822 mm) and its intensity profile were simulated according to Equation (2), as shown in Figure 9. The intensities on the observation screen, and their intensity profiles, the corresponding digital grating with θ = 30°, and their moiré pattern for TS1–5 were simulated (p₁ = 0.2822 mm, d₁ = d₂ = 251.7 mm, and θ = 30°) according to Equation (8), as shown in Figure 10. The simulation results corresponded suitably with the experimental results shown in Figure 4, thus confirming the correctness of the derived equations.

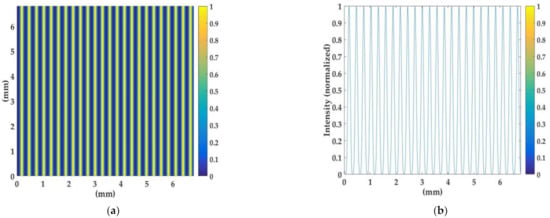
Figure 9. Simulated (a) intensities behind the grating (with a period of p₁ = 0.2822 mm) and (b) the intensity profile.

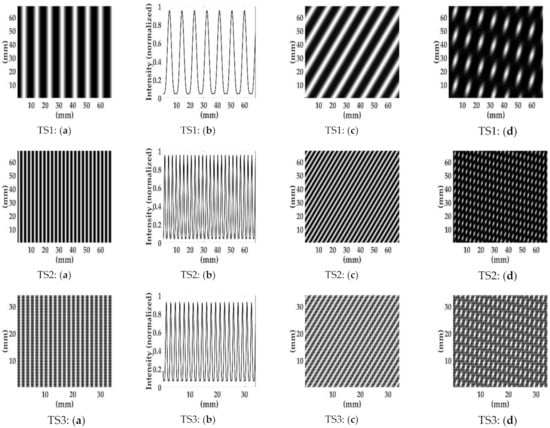
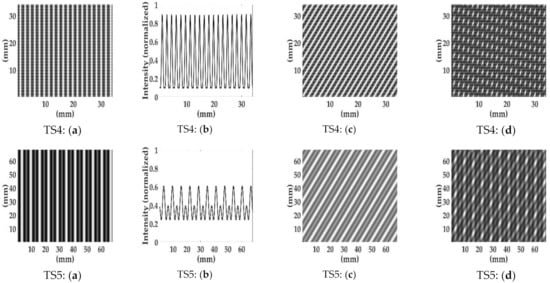
Figure 10. Simulated (a) intensities on the observation screen and (b) intensity profiles, (c) corresponding digital gratings, and (d) the moiré patterns for samples: TS1–TS5.

Compared to Equation (2), Equation (8) contains a cosine modulation term, which varies the intensity distribution on the observation screen. Therefore, the principal maximum of the intensity profile decreased and a subsidiary maximum occurred (Figure 10). The energy splitting reduced the intensity contrast. The period of the principal maximum of the intensity profile on the observation screen was p₁ (1 − d₂/f). When the Gaussian law was followed, (i.e., 1/f = 1/d₁ + 1/d₂), Equation (8) degenerated to Equation (2) with an imaging magnification of m = |1 − d₂/f |. Because of advancements in the technology used in personal computers, the field intensity distribution of light propagation can be visualized. Considering a special case of d₁ = z_T + 2f and d₂ = 2f, where z_T = 2p₁²/λ is the Talbot distance, Equation (8) degenerates to Equation (2) with an imaging magnification of m = 1, and the simulation of the intensity carpet (d₂ versus x₂) is shown in Figure 11a (with λ = 0.6328 μm, p₁ = 0.2822 mm, f = 100 mm). As shown in Figure 11b, at a distance d₂ = 2f = 200 mm, the intensity profile is exactly equal to that in Figure 9b, which is the self-image of grating G at z_T = 251.7 mm with m = 1. In the case of TS5, a sub-moiré pattern was observed (Figure 10 TS5: (d)) because of the subsidiary maximum of the intensity profile. The sub-moiré pattern was parallel to the principal moiré pattern, which did not affect the determination of the slant angle α of the moiré pattern. Because of the introduction of digital-grating, measurements taken using this method require only one practical grating and a single photograph with digital image post-processing. The proposed method could be applied to regular commercial spherical mirrors and lenses (bi-convex or bi-concave).

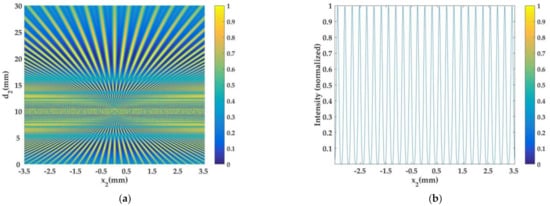
Figure 11. Simulated (a) intensity carpet (with λ = 0.6328 μm, p₁ = 0.2822 mm, f = 100 mm) and (b) the intensity profiles at d₂ = 200 mm.

4. Conclusions

By applying digital image post-processing, digital-grating moiré effect was successfully used to measure the focal length and curvature with percent errors lower than 0.5%. The measurement uncertainty and conditions were analyzed and discussed. The field intensity distribution was derived and visualized using simulations, leading to simplified measurements. The proposed method has the advantages of a simple set up, easy operation, high stability, high accuracy, and low cost, and it can be applied to various spherical simple lenses and mirrors.