Design and Dispersion Control of Microstructured Multicore Tellurite Glass Fibers with In-Phase and Out-of-Phase Supermodes
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
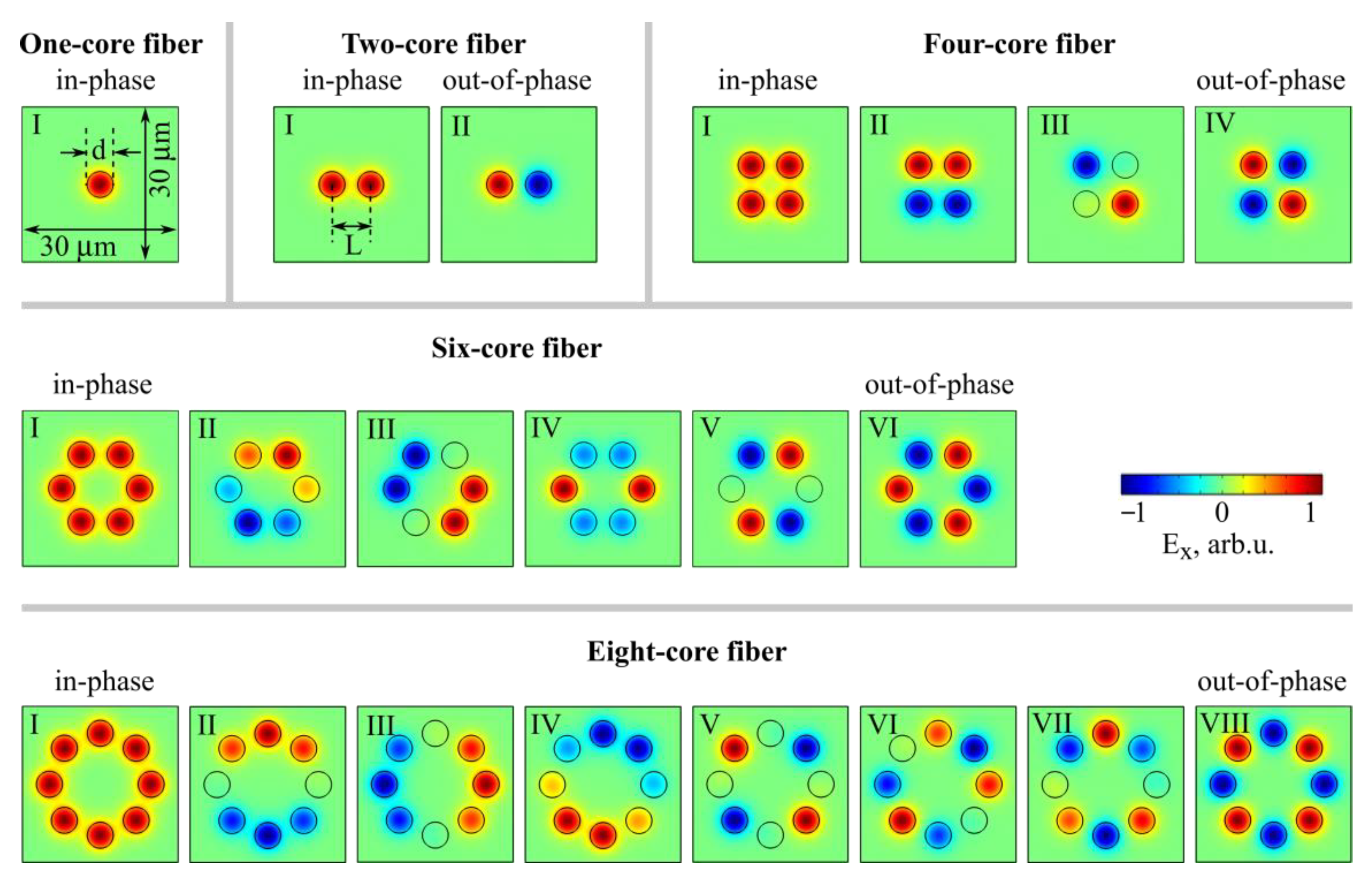
2.2. Fiber Geometry and Mode Structures
2.3. Numerical Methods
3. Results
3.1. One-Core Fibers
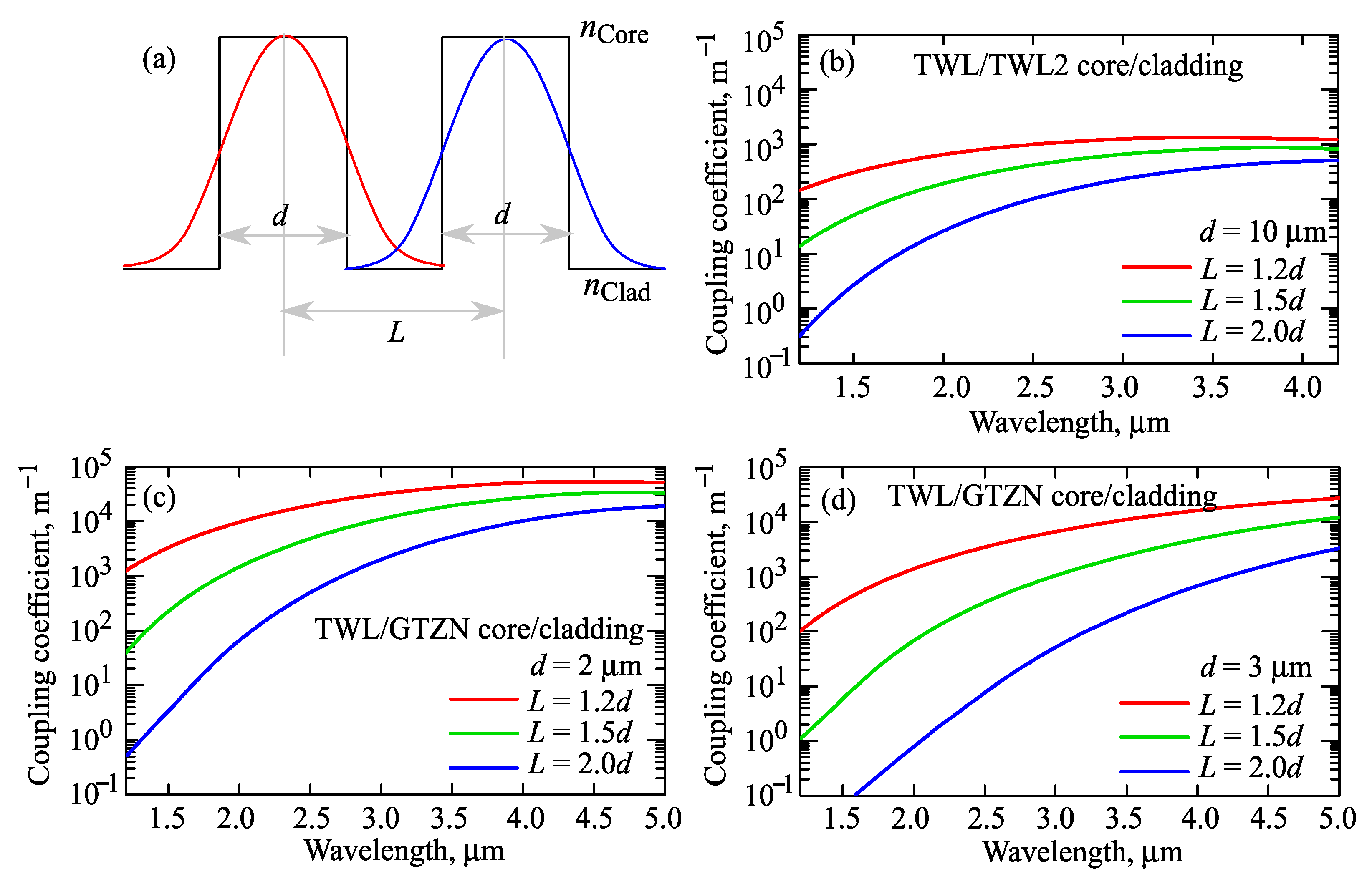
3.2. Mode Coupling in Two-Core Fibers
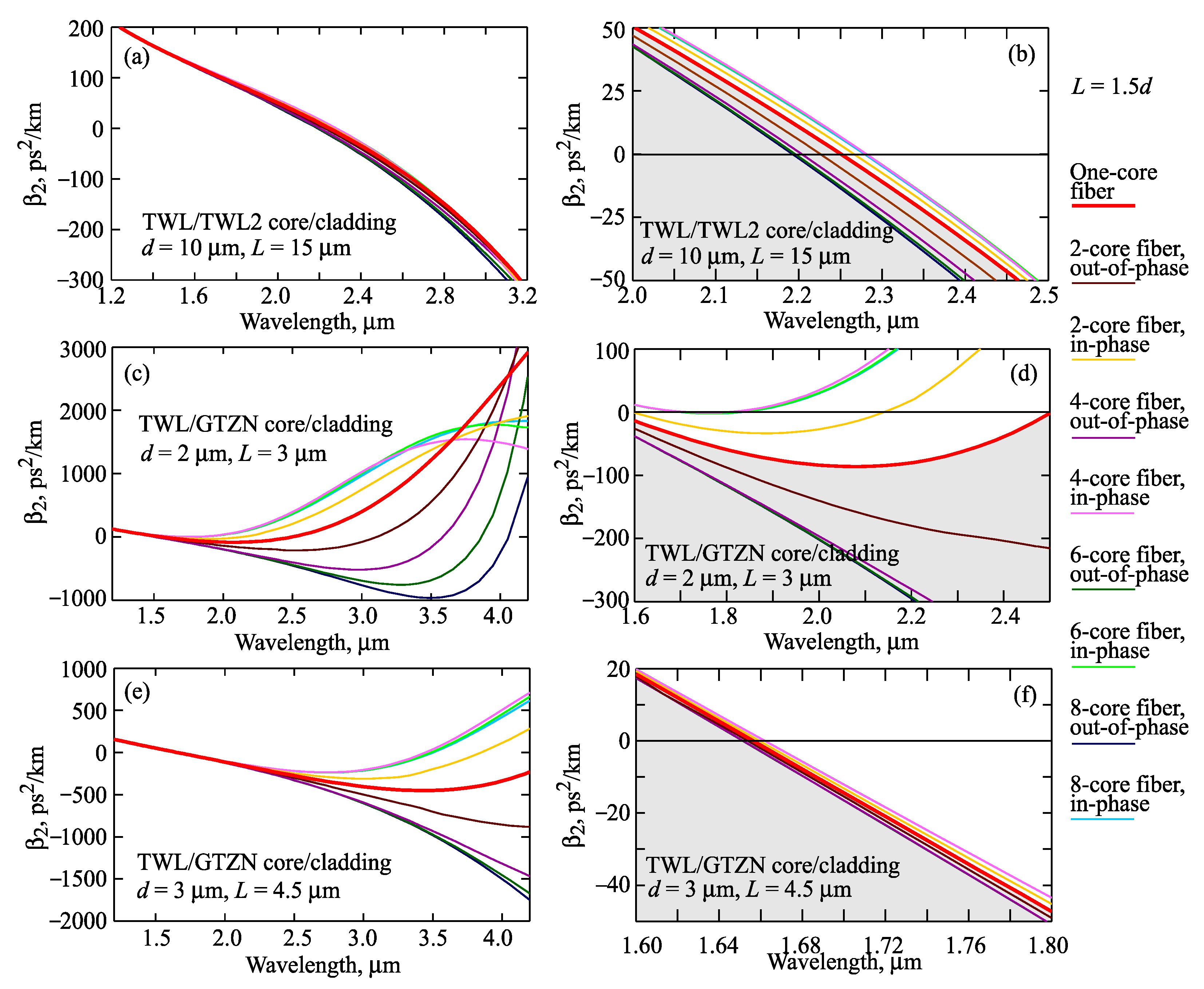
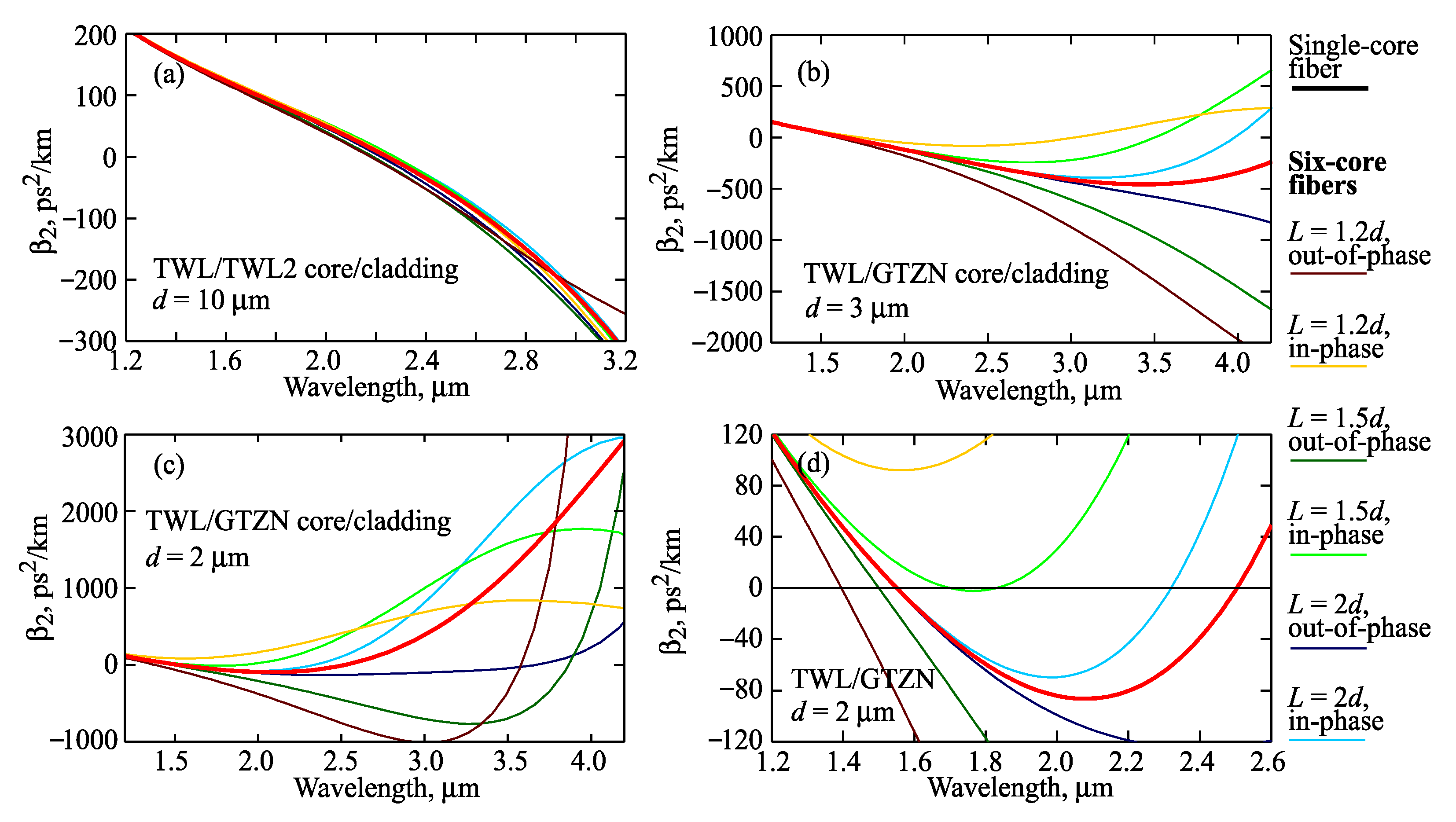
3.3. Multicore Fibers with Different Numbers of Cores and Constant L/d Ratio
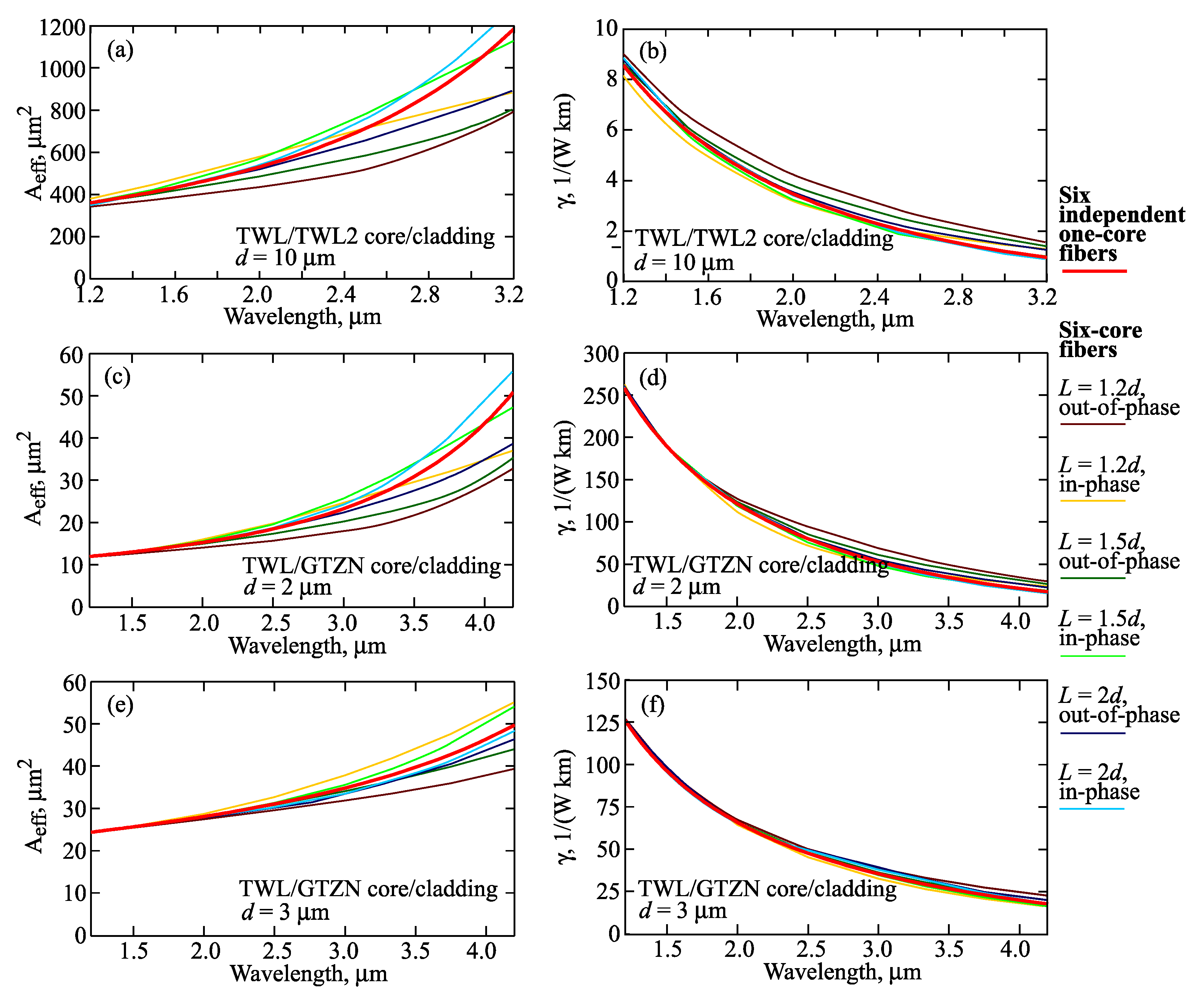
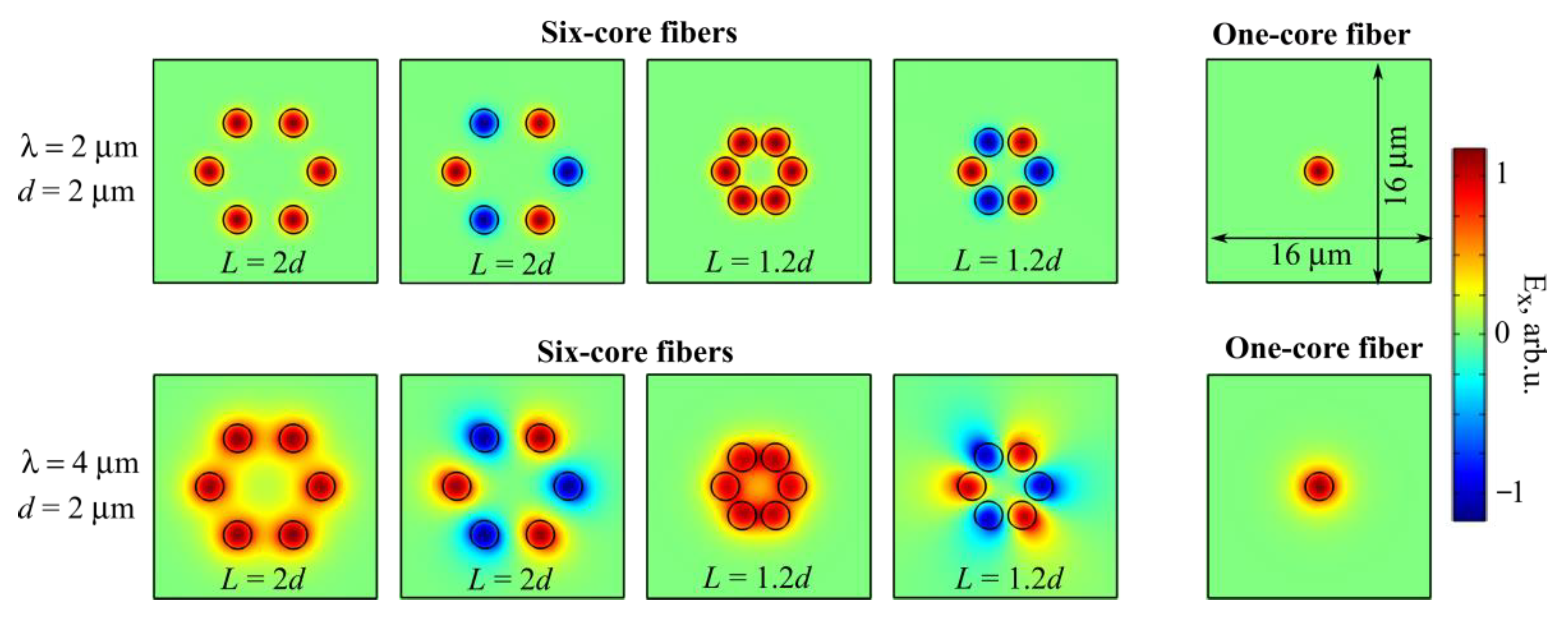
3.4. Six-Core Fibers
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics; Academic Press: London, UK, 2001. [Google Scholar]
- Fermann, M.E.; Hartl, I. Ultrafast fiber laser technology. IEEE J. Sel. Topics Quantum Electron. 2009, 15, 191–206. [Google Scholar] [CrossRef]
- Shi, W.; Fang, Q.; Zhu, X.; Norwood, R.A.; Peyghambarian, N. Fiber lasers and their applications. Appl. Opt. 2014, 53, 6554–6568. [Google Scholar] [CrossRef] [PubMed]
- Bronnikov, K.; Wolf, A.; Yakushin, S.; Dostovalov, A.; Egorova, O.; Zhuravlev, S.; Semjonov, S.; Wabnitz, S.; Babin, S. Durable shape sensor based on FBG array inscribed in polyimide-coated multicore optical fiber. Opt. Express 2019, 27, 38421–38434. [Google Scholar] [CrossRef] [PubMed]
- Supe, A.; Zakis, K.; Gegere, L.; Redka, D.; Porins, J.; Spolitis, S.; Bobrovs, V. Raman Assisted Fiber Optical Parametric Amplifier for S-Band Multichannel Transmission System. Fibers 2021, 9, 9. [Google Scholar] [CrossRef]
- Braunfelds, J.; Senkans, U.; Skels, P.; Janeliukstis, R.; Salgals, T.; Redka, D.; Lyashuk, I.; Porins, J.; Spolitis, S.; Haritonovs, V.; et al. FBG-Based Sensing for Structural Health Monitoring of Road Infrastructure. J. Sens. 2021, 2021, 8850368. [Google Scholar] [CrossRef]
- Kozdrowski, S.; Żotkiewicz, M.; Sujecki, S. Ultra-Wideband WDM Optical Network Optimization. Photonics 2020, 7, 16. [Google Scholar] [CrossRef]
- Supe, A.; Olonkins, S.; Udalcovs, A.; Senkans, U.; Mūrnieks, R.; Gegere, L.; Prigunovs, D.; Grube, J.; Elsts, E.; Spolitis, S.; et al. Cladding-Pumped Erbium/Ytterbium Co-Doped Fiber Amplifier for C-Band Operation in Optical Networks. Appl. Sci. 2021, 11, 1702. [Google Scholar] [CrossRef]
- Sojka, L.; Pajewski, L.; Lamrini, S.; Farries, M.; Benson, T.M.; Seddon, A.B.; Sujecki, S. Experimental Investigation of Actively Q-Switched Er3+: ZBLAN Fiber Laser Operating at around 2.8 µm. Sensors 2020, 20, 4642. [Google Scholar] [CrossRef]
- Currey, R.; Khademian, A.; Shiner, D. Development of a Thulium Fiber Laser for an Atomic Spectroscopy Experiment. Fibers 2020, 8, 12. [Google Scholar] [CrossRef]
- Tang, M.; Granger, G.; Lesparre, F.; Wang, H.; Qian, K.; Lecaplain, C.; Oudar, J.-L.; Jaouen, Y.; Gabet, R.; Gaponov, D.; et al. Large Normal Dispersion Mode-Locked Erbium-Doped Fiber Laser. Fibers 2019, 7, 97. [Google Scholar] [CrossRef]
- Braunfelds, J.; Murnieks, R.; Salgals, T.; Brice, I.; Sharashidze, T.; Lyashuk, I.; Ostrovskis, A.; Spolitis, S.; Alnis, J.; Porins, J.; et al. Frequency comb generation in WGM microsphere based generators for telecommunication applications. Quantum Electron. 2020, 50, 1043–1049. [Google Scholar] [CrossRef]
- Santos, D.; Guerreiro, A.; Baptista, J.M. Evaluation of Nanoplasmonic Optical Fiber Sensors Based on D-Type and Suspended Core Fibers with Metallic Nanowires. Photonics 2019, 6, 100. [Google Scholar] [CrossRef]
- Cheng, T.; Zhang, F.; Tanaka, S.; Li, S.; Yan, X.; Zhang, X.; Suzuki, T.; Ohishi, Y. Ultrafast All-Optical Signal Modulation Induced by Optical Kerr Effect in a Tellurite Photonic Bandgap Fiber. Photonics 2019, 6, 113. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Okhrimchuk, A.G.; Pryamikov, A.D.; Gladyshev, A.V.; Alagashev, G.K.; Smayev, M.P.; Likhov, V.V.; Dorofeev, V.V.; Motorin, S.E.; Yatsenko, Y.P. Direct Laser Written Waveguide in Tellurite Glass for Supercontinuum Generation in 2 μm Spectral Range. J. Lightwave Technol. 2020, 38, 1492–1500. [Google Scholar] [CrossRef]
- Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef] [PubMed]
- Zheltikov, A.M. Nonlinear optics of microstructure fibers. Phys. Uspekhi 2004, 47, 69. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Dunn, S.C.; Usner, B.; Eggleton, B.J.; White, T.P.; McPhedran, R.C.; de Sterke, C.M. Resonances in microstructured optical waveguides. Opt. Express 2003, 11, 1243–1251. [Google Scholar] [CrossRef]
- Price, J.H.V.; Monro, T.M.; Ebendorff-Heidepriem, H.; Poletti, F.; Horak, P.; Finazzi, B.; Leong, J.Y.Y.; Petropoulos, P.; Flanagan, J.C.; Brambilla, G.; et al. Mid-IR Supercontinuum Generation from Nonsilica Microstructured Optical Fibers. IEEE J. Sel. Topics Quantum Electron. 2007, 13, 738–748. [Google Scholar] [CrossRef]
- Yatsenko, Y.P.; Kosolapov, A.F.; Levchenko, A.E.; Semjonov, S.L.; Dianov, E.M. Broadband wavelength conversion in a germanosilicate-core photonic crystal fiber. Opt. Lett. 2009, 34, 2581–2583. [Google Scholar] [CrossRef]
- El-Amraoui, M.; Gadret, G.; Jules, J.C.; Fatome, J.; Fortier, C.; Désévédavy, F.; Skripatchev, I.; Messaddeq, Y.; Troles, J.; Brilland, L.; et al. Microstructured chalcogenide optical fibers from As2S3 glass: Towards new IR broadband sources. Opt. Express 2010, 18, 26655–26665. [Google Scholar] [CrossRef] [PubMed]
- Domachuk, P.; Wolchover, N.A.; Cronin-Golomb, M.; Wang, A.; George, A.K.; Cordeiro, C.M.B.; Knight, J.C.; Omenetto, F.G. Over 4000 nm bandwidth of mid-IR supercontinuum generation in sub-centimeter segments of highly nonlinear tellurite PCFs. Opt. Express 2008, 16, 7161–7168. [Google Scholar] [CrossRef] [PubMed]
- Bi, W.; Li, X.; Xing, Z.; Zhou, Q.; Fang, Y.; Gao, W.; Xiong, L.; Hu, L.; Liao, M. Wavelength conversion through soliton self-frequency shift in tellurite microstructured fiber with picosecond pump pulse. J. Appl. Phys. 2016, 119, 43102. [Google Scholar] [CrossRef]
- Tao, G.; Ebendorff-Heidepriem, H.; Stolyarov, A.M.; Danto, S.; Badding, J.V.; Fink, Y.; Ballato, J.; Abouraddy, A.F. Infrared fibers. Adv. Opt. Photonics 2015, 7, 379–458. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Switkowski, K.; Filipkowski, A.; Kasztelanic, R.; Pysz, D.; Van Le, H.; Stepien, R.; Krolikowski, W.; Buczynski, R. Fiber microprobe with integrated gradient index vortex mask. Opt. Commun. 2020, 477, 126345. [Google Scholar] [CrossRef]
- Bouwmans, G.; Bigot, L.; Quiquempois, Y.; Lopez, F.; Provino, L.; Douay, M. Fabrication and characterization of an all-solid 2D photonic bandgap fiber with a low-loss region (<20 dB/km) around 1550 nm. Opt. Express 2005, 13, 8452–8459. [Google Scholar] [CrossRef]
- Klimczak, M.; Siwicki, B.; Skibiński, P.; Pysz, D.; Stępień, R.; Heidt, A.; Radzewicz, C.; Buczyński, R. Coherent supercontinuum generation up to 2.3 µm in all-solid soft-glass photonic crystal fibers with flat all-normal dispersion. Opt. Express 2014, 22, 18824–18832. [Google Scholar] [CrossRef]
- Dong, L.; Thomas, B.K.; Fu, L. Highly nonlinear silica suspended core fibers. Opt. Express 2008, 16, 16423–16430. [Google Scholar] [CrossRef]
- Mouawad, O.; Picot-Clemente, J.; Amrani, F.; Strutynski, C.; Fatome, J.; Kibler, B.; Desevedavy, F.; Gadret, G.; Jules, J.-C.; Deng, D.; et al. Multioctave midinfrared supercontinuum generation in suspendedcore chalcogenide fibers. Opt. Lett. 2014, 39, 2684–2687. [Google Scholar] [CrossRef]
- Møller, U.; Yu, Y.; Kubat, I.; Petersen, C.R.; Gai, X.; Brilland, L.; Méchin, D.; Caillaud, C.; Troles, J.; Luther-Davies, B.; et al. Multi-milliwatt mid-infrared supercontinuum generation in a suspended core chalcogenide fiber. Opt. Express 2015, 23, 3282–3291. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Shiryaev, V.S.; Koptev, M.Y.; Stepanov, B.S.; Muravyev, S.V. Development of As-Se tapered suspended-core fibers for ultra-broadband mid-IR wavelength conversion. J. Non Cryst. Solids 2018, 480, 43–50. [Google Scholar] [CrossRef]
- Karpate, T.; Stepniewski, G.; Pysz, D.; Rampur, A.; Stepanenko, Y.; Buczynski, R.; Klimczak, M. Soliton detuning of 68.5 THz in the near-infrared in a highly nonlinear suspended core tellurite fiber. J. Opt. Soc. Am. B 2020, 37, 1502–1509. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Dorofeev, V.V.; Skobelev, S.A.; Balakin, A.A.; Motorin, S.E.; Kosolapov, A.F.; Andrianov, A.V. Microstructured fibers Based on tellurite glass for nonlinear conversion of mid-IR ultrashort optical pulses. Photonics 2020, 7, 51. [Google Scholar] [CrossRef]
- Liao, M.; Chaudhari, C.; Qin, G.; Yan, X.; Kito, C.; Suzuki, T.; Ohishi, Y.; Matsumoto, M.; Misumi, T. Fabrication and characterization of a chalcogenide-tellurite composite microstructure fiber with high nonlinearity. Opt. Express 2009, 17, 21608–21614. [Google Scholar] [CrossRef]
- Ortiz, A.M.; Sáez, R.L. Multi-core optical fibers: Theory applications and opportunities. In Selected Topics on Optical Fiber Technologies and Applications; IntechOpen Limited: London, UK, 2017. [Google Scholar] [CrossRef]
- Xia, C.; Bai, N.; Ozdur, I.; Zhou, X.; Li, G. Supermodes for optical transmission. Opt. Express 2011, 19, 16653–16664. [Google Scholar] [CrossRef]
- Rubenchik, A.M.; Chekhovskoy, I.S.; Fedoruk, M.P.; Shtyrina, O.V.; Turitsyn, S.K. Nonlinear pulse combining and pulse compression in multi-core fibers. Opt. Lett. 2015, 40, 721–724. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Rubenchik, A.M.; Fedoruk, M.P.; Tkachenko, E. Coherent propagation and energy transfer in low-dimension nonlinear arrays. Phys. Rev. A 2012, 86, 31804. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Anashkina, E.A.; Andrianov, A.V.; Litvak, A.G. Coherent propagation of laser beams in a small-sized system of weakly coupled optical light-guides. Phys. Rev. A 2018, 98, 43857. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Andrianov, A.V.; Anashkina, E.A.; Litvak, A.G. Coherent propagation and amplification of intense laser pulses in hexagonal multicore fibers. Opt. Lett 2020, 45, 3224–3227. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Kalinin, N.A.; Anashkina, E.A.; Egorova, O.N.; Lipatov, D.S.; Kim, A.V.; Semjonov, S.L.; Litvak, A.G. Selective excitation and amplification of peak-power-scalable out-of-phase supermode in Yb-doped multicore fiber. J. Light. Technol. 2020, 38, 2464–2470. [Google Scholar] [CrossRef]
- Balakin, A.A.; Litvak, A.G.; Skobelev, S.A. Stability of out-of-phase solitons and laser pulse self-compression in active multicore fibers. Phys. Rev. A 2019, 100, 53834. [Google Scholar] [CrossRef]
- Chiang, K.S. Intermodal dispersion in two-core optical fibers. Opt. Lett. 1995, 20, 997–999. [Google Scholar] [CrossRef] [PubMed]
- Peterka, P.; Honzatko, P.; Kanka, J.; Matejec, V.; Kasik, I. Generation of high-repetition-rate pulse trains in a fiber laser through a twin-core fiber. In Photonics, Devices, and Systems II, Proceedings of the SPIE, Prague, Czech Republic 26–29 May 2002; SPIE: Bellingham, DC, USA, 2003; Volume 5036, pp. 376–381. [Google Scholar] [CrossRef]
- Benton, C.J.; Skryabin, D.V. Coupling induced anomalous group velocity dispersion in nonlinear arrays of silicon photonic wires. Opt. Express 2009, 17, 5879–5884. [Google Scholar] [CrossRef]
- De Nobriga, C.E.; Hobbs, G.D.; Wadsworth, W.J.; Knight, J.C.; Skryabin, D.V.; Samarelli, A.; Sorel, M.; De La Rue, R.M. Supermode dispersion and waveguide-to-slot mode transition in arrays of silicon-on-insulator waveguides. Opt. Lett. 2010, 35, 3925–3927. [Google Scholar] [CrossRef]
- Peterka, P.; Kasik, I.; Kanka, J.; Honzatko, P.; Matejec, V.; Hayer, M. Twin-core fiber design and preparation for easy splicing. IEEE Photonics Technol. Lett. 2000, 12, 1656–1658. [Google Scholar] [CrossRef]
- Castro, C.; Jain, S.; De Man, E.; Jung, Y.; Hayes, J.; Calabro, S.; Pulverer, K.; Bohn, M.; Alam, S.; Richardson, D.J.; et al. 100-Gb/s transmission over a 2520-km integrated MCF system using cladding-pumped amplifiers. IEEE Photonics Technol. Lett. 2017, 29, 1187–1190. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.F.; Tam, H.Y.; Tao, X. Multifunctional smart optical fibers: Materials, fabrication, and sensing applications. Photonics 2019, 6, 48. [Google Scholar] [CrossRef]
- Bookey, H.T.; Lousteau, J.; Jha, A.; Gayraud, N.; Thomson, R.R.; Psaila, N.D.; Li, H.; MacPherson, W.N.; Barton, J.S.; Kar, A.K. Multiple rare earth emissions in a multicore tellurite fiber with a single pump wavelength. Opt. Express 2007, 15, 17554–17561. [Google Scholar] [CrossRef]
- Cheng, T.; Duan, Z.; Gao, W.; Asano, K.; Liao, M.; Deng, D.; Suzuki, T.; Ohishi, Y. A novel seven-core multicore tellurite fiber. J. Light. Technol. 2013, 31, 1793–1796. [Google Scholar] [CrossRef]
- Cheng, T.; Duan, Z.; Liao, M.; Gao, W.; Deng, D.; Suzuki, T.; Ohishi, Y. A simple all-solid tellurite microstructured optical fiber. Opt. Express 2013, 21, 3318–3323. [Google Scholar] [CrossRef] [PubMed]
- Dorofeev, V.V.; Moiseev, A.N.; Churbanov, M.F.; Kotereva, T.V.; Chilyasov, A.V.; Kraev, I.A.; Pimenov, V.G.; Ketkova, L.A.; Dianov, E.M.; Plotnichenko, V.G.; et al. Production and properties of high purity TeO2–WO3–(La2O3, Bi2O3) and TeO2–ZnO–Na2O–Bi2O3 glasses. J. Non Cryst. Solids 2011, 357, 2366–2370. [Google Scholar] [CrossRef]
- Boivin, M.; El-Amraoui, M.; Ledemi, Y.; Morency, S.; Vallée, R.; Messaddeq, Y. Germanate-tellurite composite fibers with a high-contrast step-index design for nonlinear applications. Opt. Mater. Express 2014, 4, 1740–1746. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Dorofeev, V.V.; Koltashev, V.V.; Kim, A.V. Development of Er3+-doped high-purity tellurite glass fibers for gain-switched laser operation at 2.7 μm. Opt. Mater. Express 2017, 7, 4337–4351. [Google Scholar] [CrossRef]
- Kedenburg, S.; Strutynski, C.; Kibler, B.; Froidevaux, P.; Désévédavy, F.; Gadret, G.; Jules, J.-C.; Steinle, T.; Mörz, F.; Steinmann, A.; et al. High repetition rate mid-infrared supercontinuum generation from 1.3 to 5.3 μm in robust step-index tellurite fibers. J. Opt. Soc. Am. B 2017, 34, 601–607. [Google Scholar] [CrossRef]
- Snyder, A.W.; Love, J. Optical Waveguide Theory; Chapman and Hall: New York, NY, USA, 1983. [Google Scholar]
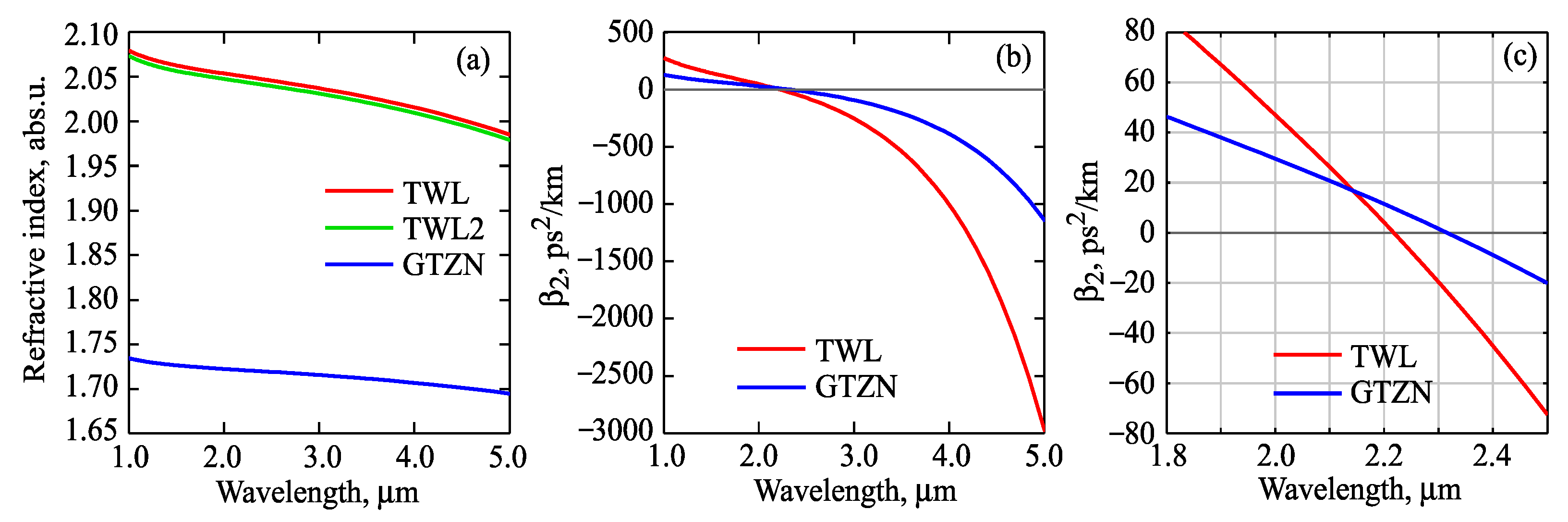
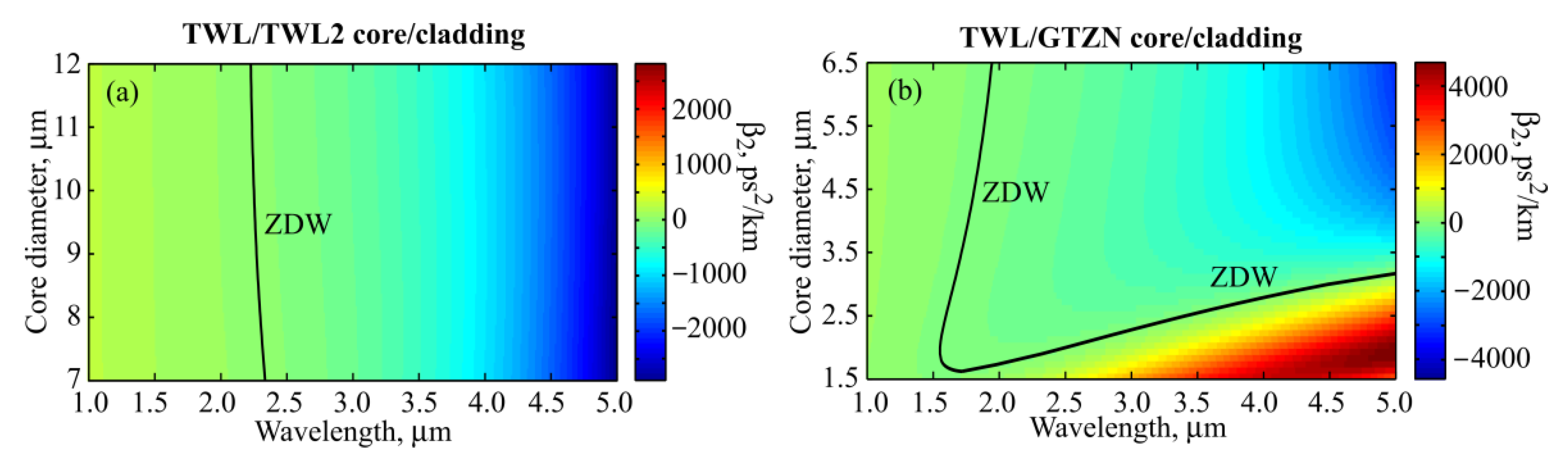
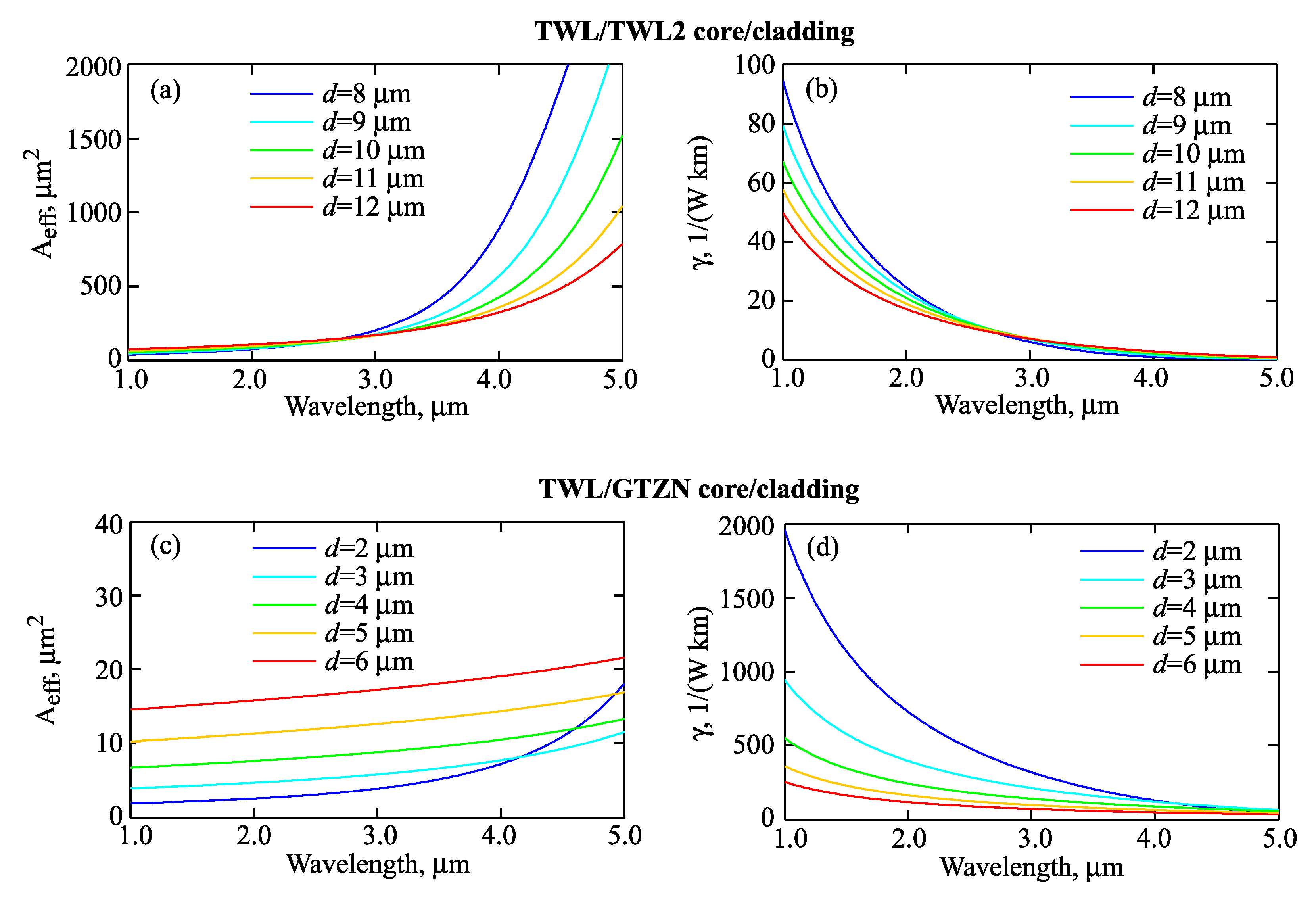
| Glass | B | C1 | C2 | D1, μm2 | D2, μm2 |
|---|---|---|---|---|---|
| TWL | 2.225 | 2.009 | 1.475 | 0.04767 | 149.20 |
| GTZN | 1.679 | 1.292 | 0.500 | 0.03045 | 149.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Andrianov, A.V. Design and Dispersion Control of Microstructured Multicore Tellurite Glass Fibers with In-Phase and Out-of-Phase Supermodes. Photonics 2021, 8, 113. https://doi.org/10.3390/photonics8040113
Anashkina EA, Andrianov AV. Design and Dispersion Control of Microstructured Multicore Tellurite Glass Fibers with In-Phase and Out-of-Phase Supermodes. Photonics. 2021; 8(4):113. https://doi.org/10.3390/photonics8040113
Chicago/Turabian StyleAnashkina, Elena A., and Alexey V. Andrianov. 2021. "Design and Dispersion Control of Microstructured Multicore Tellurite Glass Fibers with In-Phase and Out-of-Phase Supermodes" Photonics 8, no. 4: 113. https://doi.org/10.3390/photonics8040113
APA StyleAnashkina, E. A., & Andrianov, A. V. (2021). Design and Dispersion Control of Microstructured Multicore Tellurite Glass Fibers with In-Phase and Out-of-Phase Supermodes. Photonics, 8(4), 113. https://doi.org/10.3390/photonics8040113






