1. Introduction
When a rough surface is illuminated with a highly coherent light, scattered light is generated from the measured surface. The scattered lights interfere with each other and produce speckle, which is a grain interference fringe whose diameter depends on the size of the aperture of the objective in the optical system [
1,
2,
3].
In interference measurements, speckle is sometimes treated as noise present in fringe images. Therefore, a reduction in the influence of speckle noise is important in speckle interference measurement technology [
4,
5]. Filtering technology has been studied and further developed to address speckle noise [
5,
6,
7]. In addition, high-resolution measurements using techniques such as fringe scanning [
3] have been widely employed in speckle interferometry. Several high-resolution measurement methods for deformation or displacement have been developed by analyzing the recorded phase distribution in the speckle [
8,
9,
10,
11,
12,
13]. Speckle is currently considered a significant phenomenon in the optical field. Furthermore, speckle interferometry has been used for three-dimensional (3D) shape measurements [
14,
15]. A 3D structure beyond the diffraction limit of the objective lens can be measured by using the scattered light as the illumination light and by detecting the phase of the light recorded in the speckle formed by the scattered light [
15].
The principle of this method [
14,
15] can be validated by comparing its measurement results with those of other techniques, such as atomic force microscopy (AFM), using the grating of the periodic structure as the measurement object. In this case, because the same structure exists everywhere, the same situation of the same measured object can be measured [
14,
15,
16]. However, if only the periodic structure is measured, misunderstandings and misconceptions can emerge if the speckle interference measurement technology is not well understood. It has been misunderstood that the proposed method can be used only for measuring the periodic structure. In addition, a misconception emerged that this method has the same principle as that of scatterometry [
17,
18,
19,
20], which is used to measure periodic structures.
To clarify such misunderstandings and misconceptions, this study demonstrates that the proposed measurement method can measure three-dimensional structures that exist randomly in space. Furthermore, the same measured object at the same sample position was measured under different conditions of the diffraction limit by installing an aperture in front of the objective lens. Accordingly, the results were analyzed based on whether the diffraction limit exceeded. As a result of comparing the results under the two situations, it was confirmed that the proposed method can measure beyond the diffraction limit.
Furthermore, this paper explains the mechanism of the measurement process based on the principle of this measurement method using scattered light as illumination.
This paper provides an understanding of the processing of the method, which makes it possible to perform three-dimensional measurements by analyzing only the phase change of the scattered light from the object without using the higher-order diffracted light based on conventional imaging theory [
21].
2. Method
In a conventional speckle interferometer [
1], the laser beam was divided by half mirrors. One of the obtained beams was irradiated onto the measurement object with a rough surface. The other was irradiated onto a rough reference surface to produce the reference light. An interference is generated between the scattered lights from the rough surfaces. The interference fringes, displayed on the image sensor, are captured through lens [
1,
11,
12,
13].
When such an optical system is used, the sampled speckle pattern has a bias component and original signal component in the low-frequency region in the intensity distribution. This phenomenon is the same as the interference fringe intensity distribution for a general interferometer because speckle is also an interference phenomenon. Therefore, an image in which the significant signal component in the frequency domain superimposes on the bias is obtained [
6]. Such an image with a high resolution can be processed and a high phase component can be extracted using temporal fringe scanning technique [
1,
2,
3].
However, this analysis technique cannot be used for dynamic analysis because three sheets of speckle patterns are required. In addition, because each speckle before and after the deformation must overlap in the speckle interference measurement [
1,
22,
23], the relationship between the deformation and speckle size poses a problem in large-deformation measurements when the three speckle patterns are captured [
24].
However, when a plane wave is used as the reference beam and the wave plane is angled with respect to the object beam [
5], a carrier signal can be provided in the speckle. By providing such a carrier signal and performing a Fourier transform on the captured speckle pattern, the bias and signal components can be separated in the frequency domain [
6,
7,
23,
24,
25,
26]. The bias component can be removed by extracting only the signal components in this process. Thus, the phase component can be obtained using only two speckle patterns before and after deformation [
22,
23].
Furthermore, the phase distribution of the specklegram between images was analyzed using the basic speckle interferometry [
5]. The noise in the low-frequency region of these images was removed by a filter using the Fourier transform.
However, when lasers were used, speckles in images were historically treated as noise components, and methods to reduce speckle noise have been extensively studied. In the analysis method used in this study, the noise components in the speckle are reduced by a two-step filtering technique to ensure that they do not affect the analysis. Through this processing [
7], phase analysis is achieved without affecting the signal components.
Using such filtering technologies, the phase information in speckle interferometry can be extracted smoothly by a camera and computer technology, such as electronic speckle pattern interferometry (ESPI) [
1,
2]. Deformation measurements with a resolution of several tens of nanometers were conducted using such technologies [
22,
23].
On the contrary, in terms of the fine structure used in this study, it is believed that it is impossible to obtain the final shape unless filtering is performed. In this study, as described above, processing using filtering technology for noise components in two different frequency bands is performed in two steps [
14,
15,
16]. Therefore, it is possible to observe the fine structure smoothly.
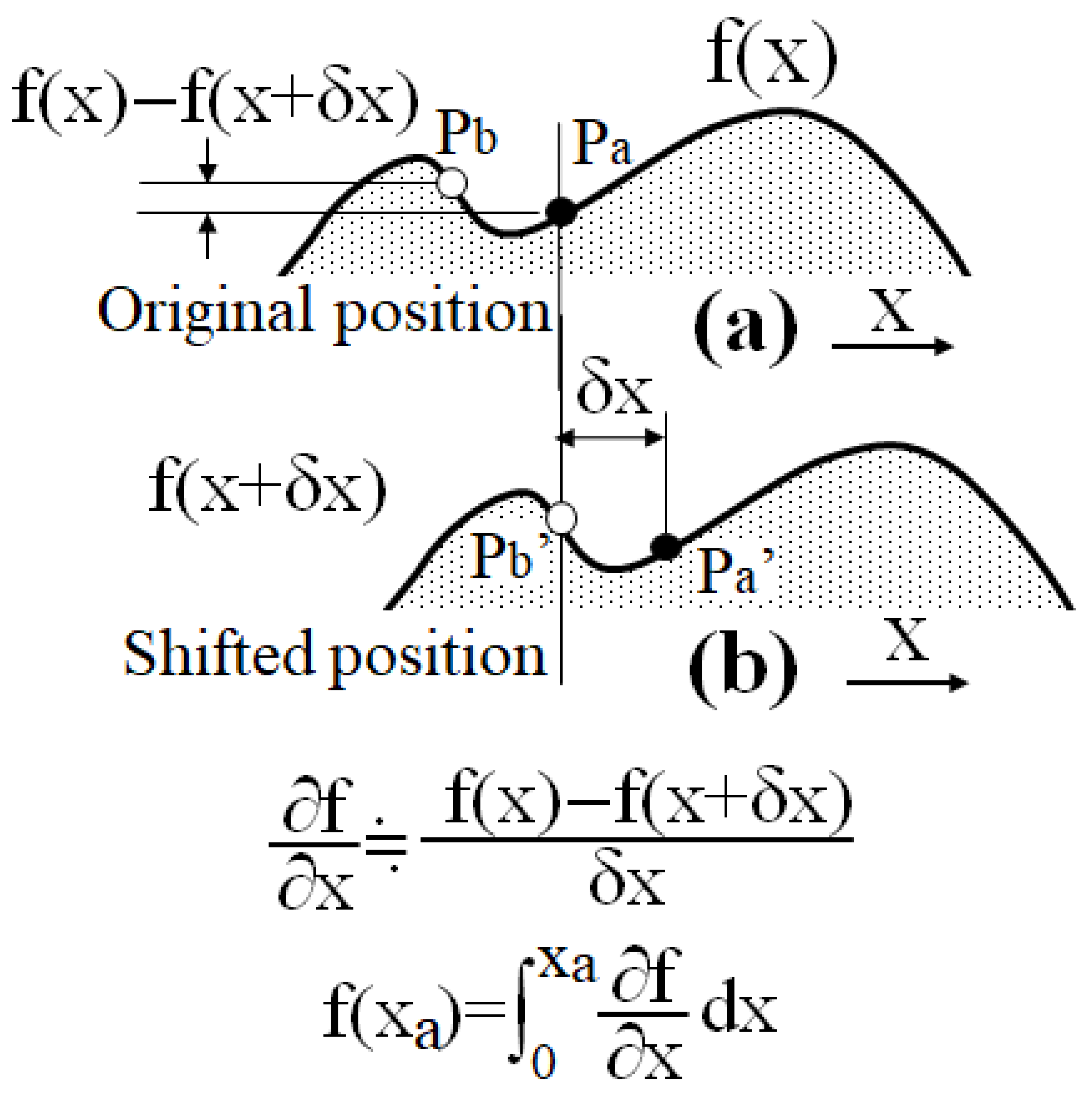
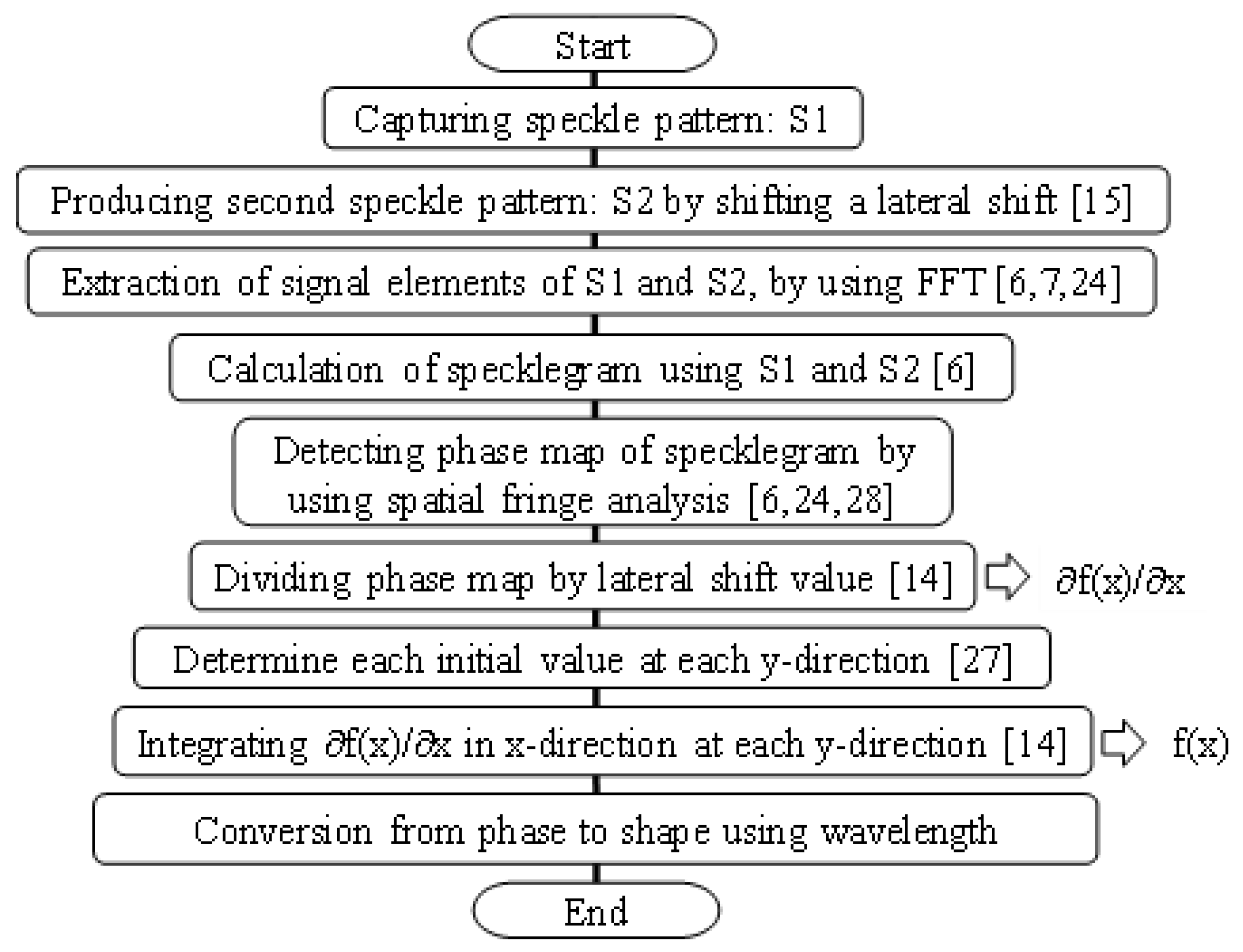
The cross-section of the measured object is shown in
Figure 1. In
Figure 1a, the phase cross-section of the speckle pattern is shown when the measured object is set to the original position of the speckle interferometer. In
Figure 1b, the phase cross-section of the speckle pattern is set at the time when the measured object is shifted by a small amount (
δx). When a specklegram is calculated between these two speckle patterns, the phase change at each position can be analyzed with high resolution using speckle interferometry. Assuming that the phase distribution related to the shape of the measured object is f(
x), as shown in
Figure 1a, the phase change caused by the lateral shift (
δx) at Pa in the original position is the difference between Pa and Pb, i.e., f(
x) − f(
x +
δx). If this phase change is divided by the shift (
δx), the pseudo-differential value (
∂f/
∂x) of the phase distribution f(
x) related to the shape can be obtained, as shown in
Figure 1. By integrating this differential value with respect to the shifted coordinates, the phase distribution f(
x) related to the shape of the original object can be obtained.
As mentioned earlier, the lateral shift of the measured object is believed to be an “advantageous deformation for the speckle deformation measurement” for measurements of 3D shapes based on speckle interferometry. In addition, a piezo element was used in the initial experiment set for achieving lateral shift [
14]. However, as the shift is several tens of nanometers, although the speckle pattern data collected without horizontal shifting are virtually shifted in the computer, it was reported that the result of the virtual shift produces the same effect as the result of the shift using the piezo element [
15]. Therefore, in this analysis, only one speckle pattern was captured instead of collecting two speckle patterns before and after the horizontal shift. A second speckle pattern is produced as image data by virtually shifting in the memory of the computer [
16].
Thus, the 3D shape can be measured using only one speckle pattern without any influence, such as mechanical vibration and fluctuation in air, from the experimental environment. In the 3D shape measurement, when a plane wave is used as the illumination light in the speckle interferometer, the scattered light from the measured object surface is largely affected by diffraction when the structure of the measurement surface becomes finer. Thus, the distribution of the diffracted light increases. When the higher-order diffracted light cannot pass through the lens area, the amount of scattered light passing through the lens from the surface of the measured object decreases. However, the decrease in the amount of scattered light poses a problem in this method, based on the phase analysis of scattered light. In such a case, it is advantageous to use scattered light with many light direction vectors as illumination light to obtain more scattered light through the lens. Accordingly, scattered light was used as the illumination light at the time of measurement in this study.
The speckle interferometer used in this experiment is shown in
Figure 2. In this optical system, scattered light generated after passing through the ground glass was used as the illumination light. The reflected scattered light from the surface of the object was collected by an objective lens (product number: M Plan Apo200×, NA: 0.62, magnification: 200×, Mitutoyo Co. Ltd.: Kawasaki, Japan). The scattered light, including the phase information, reaches the image sensor (pixel size: 1.6 µm, number of pixels: 1024 × 1024) through the pinhole, as shown in
Figure 2.
The beam emitted from the same laser (wavelength: 532 nm, 150 mW) is split by a polarizing beam splitter, collimated by a collimator, and used as the reference light. The camera captures the speckle pattern originating from the interference between the scattered light from the measured object and the reference light. The carrier fringes in the speckle are generated with the object light from the object surface and reference beam by setting the angle of mirror-1 to remove the bias component of the speckle pattern. The frequency of the carrier fringes is set considering the speckle diameter, transmission characteristics of the optical system, and camera characteristics shown in a previous report [
24].
Furthermore, in this optical system, an aperture with a diameter of 8 mm on the rail and a thickness of 0.5 mm was installed in front of the objective lens using a micrometer. The NA of the lens is the original value of 0.62, when the aperture is not inserted. When the aperture was inserted, the aperture diameter of the lens changed from 13 to 8 mm, resulting in an NA of 0.29. Using such an aperture, the diffraction limit of the optical system can be changed without involving the measured object or the construction of the optical system [
16]. In other words, the optical system can be used under two measurement conditions, except for the introduction of apertures. Therefore, an object on the order of several hundred nanometers can be observed by exceeding and not exceeding the diffraction limit. In this optical system, this can be achieved by changing the diffraction limit at the same measurement position of the same camera. The measurement results under different conditions are compared.
It is usually challenging to measure the microstructure (on the order of hundreds of nanometers) of the measured object at the same location using different measuring instruments. Therefore, in previous studies [
14,
15,
16], the principle was validated by overcoming this problem using a diffraction grating with a periodic structure by comparing it with other measurement techniques, such as AFM. This study verifies that this method can measure not only the shapes of periodic structures but also the shapes of randomly distributed 3D objects.
In this study, the shape of the microstructure randomly distributed in 3D was measured. The measured objects were silica spheres, whose shapes were not periodic. In addition, the diameter of the spheres was standardized. Here, because it is challenging to measure the same position of a random object using different measuring instruments, the measurement method was validated by comparing the measured diameters of the silica sphere, which has a standardized diameter under different measurement conditions. The diameter of the silica sphere was measured under different conditions of the diffraction limit without changing the position of the object.
The silica spheres used in this experiment were KMP-590 and X-52-854 manufactured by Shin-Etsu Chemical (Tokyo, Japan). The former is a sphere with a standard diameter of 2 µm (diameter distribution: 1–4 µm), while the latter is a sphere with a standard diameter of 700 nm (diameter distribution: 0.2–5 µm). As shown in
Figure 3, the powdered sample microsphere was fixed to a 10 mm × 5 mm test piece with an adhesive to prepare the sample for measurement. In addition, the surface of the object was coated with platinum with a thickness of several nanometers by sputtering.
The diameter distribution of the measured object was observed using scanning electron microscopy (SEM) before performing the measurements. The results are shown in
Figure 4.
The SEM image shows that the average diameter of the KMP-590 spheres was approximately 2 µm, while that of X-52-854 was approximately 700 nm. The measured diameter of the sphere was consistent with that in the official product catalog. Although the measured object is approximately spherical, it is not necessarily an ideal sphere; some ellipsoids as distorted spheres are observed.
4. Discussion
The above discussion confirms the possibility of measuring the shape of microstructures beyond the diffraction limit of the objective lens by using scattered light as illumination light. Next, the logical mechanism of the measurement process is analyzed.
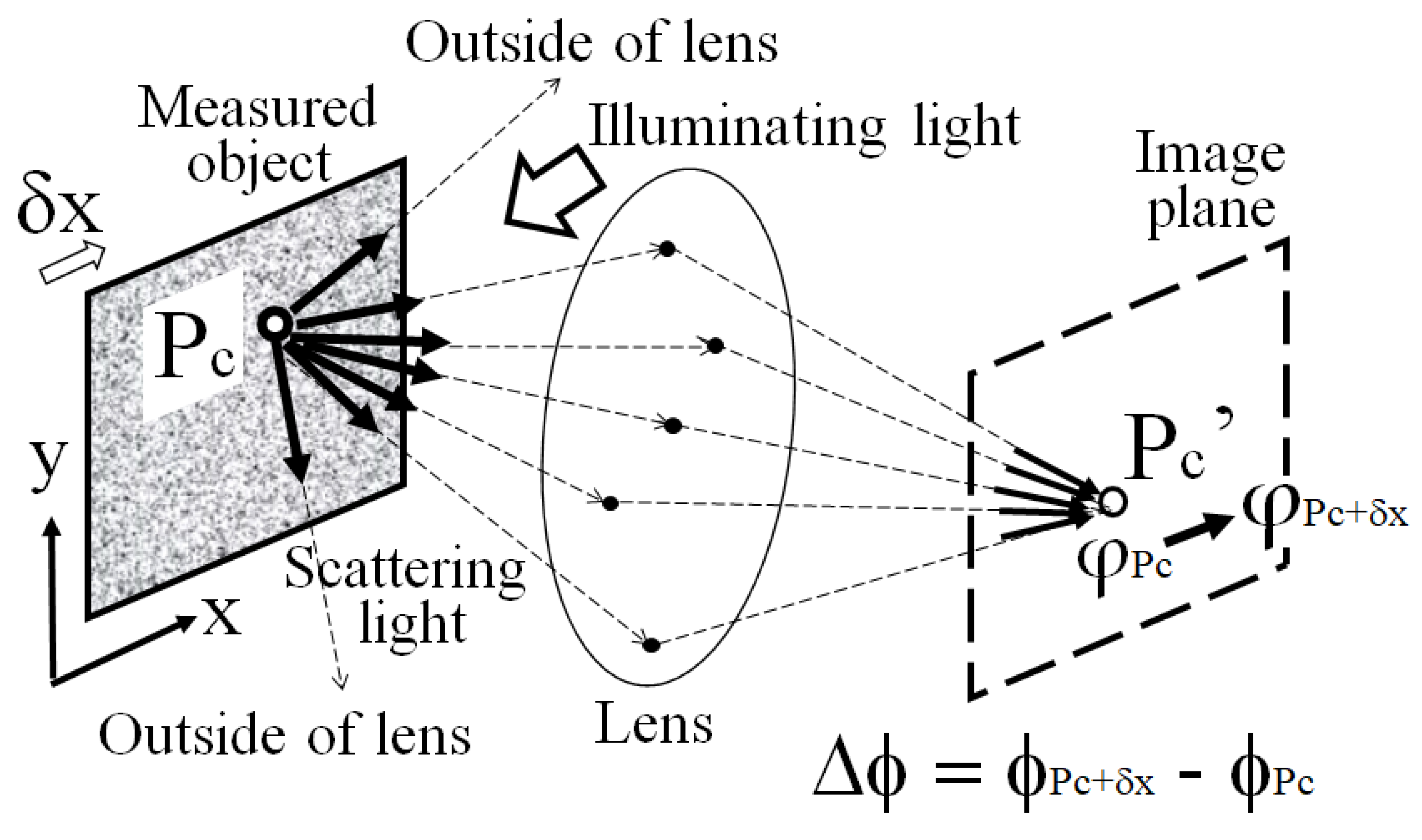
In an optical system based on the concept of perfect imaging [
21], scattered lights are emitted from a point Pc on the object surface when illumination light is applied to a rough object surface, as shown in
Figure 11.
Some of the reflected scattered lights converge to Pc’ on the image plane of the lens after passing through random positions in the lens aperture. Therefore, when the measured object is set farther than the focal length of the lens on the optical axis, the reflected light from the point (Pc) on the surface of the measured object passes through the lens and converges at the corresponding point (Pc’) of the surface of the measured object. The light emitted from one point on the object surface is focused on the conjugate point considering a perfect optical system. In this case, if the higher-order diffracted light from the measurement object passes through the lens and reaches the image plane, a clear focused image is observed, in accordance with Abbe’s imaging theory [
21].
However, when a fine structure beyond the diffraction limit of the objective lens is observed, higher-order diffracted light extends to the outside of the aperture of the lens and cannot pass through the lens, as shown in
Figure 11. Therefore, such light cannot reach the image plane. Thus, a focused image could not be captured. According to traditional image theory [
21], this imaging process can be attributed to an analysis method based on the formation of a light intensity distribution called an image.
When the measurement object is illuminated using scattered light, it is considered that a part of the scattered light from the measured object can pass through the lens aperture, even if the measurement object has a fine structure. As shown by the broken line after scattering at Pc in
Figure 11, coherent light passing through various paths interfere with each other. Such scattered light information from each point on the measurement surface is aligned on the conjugate point of the measured surface under the concept of perfect optics.
In other words, because the speckle pattern reaches the image sensor through the lens under the perfect optical system, it is assumed that two-dimensional phase information (i.e., shape information) that has a one-to-one correspondence with the position of the measured surface is spatially aligned in a regular manner on the image sensor. Because this method uses phase information, it does not require higher-order diffracted lights for shape measurement analysis, as in the conventional imaging theory based on light intensity distribution. If a light with phase information reaches each pixel of the camera through the lens, the phase of the light on each pixel is analyzed with a high resolution, and two-dimensional shape information can be detected on the image sensor using speckle interferometry. If the measured object is laterally shifted by δx and the phase of the speckle from the neighbor point (Pc + δx) of the measured surface can be accurately detected, the two-phase information (ϕPc before the lateral shift and ϕPc + δx after the lateral shift) at Pc’ can be sequentially detected according to the principle of the 3D shape measurement.
The difference (Δϕ) of these phases is equal to the phase value at Pc’ of the specklegram. This specklegram can be calculated between the speckle patterns captured before and after the lateral shift. The derivative value of the shape at Pc can be obtained by dividing the difference in phase by the lateral shift δx. By this operation, the two-dimensional distribution of the derivative of the phase regarding the shape of the measured object can be constructed by the computer. This information has a spatial one-to-one correspondence with the surface of the measured object. The original phase distribution f(x) can be reconstructed by integrating the derivative value in the x-direction.
As stated above, it is considered that the 3D shape of the fine structure exceeding the diffraction limit can be analyzed by this method without the influence of diffraction and without using the concept of image formation, which is based primarily on intensity distribution. In addition, the scattered light with multiple ray vectors in various directions is indispensable as illumination light to perform this operation.