Numerical Simulations on Polarization Quantum Noise Squeezing for Ultrashort Solitons in Optical Fiber with Enlarged Mode Field Area
Abstract
1. Introduction
2. Methods
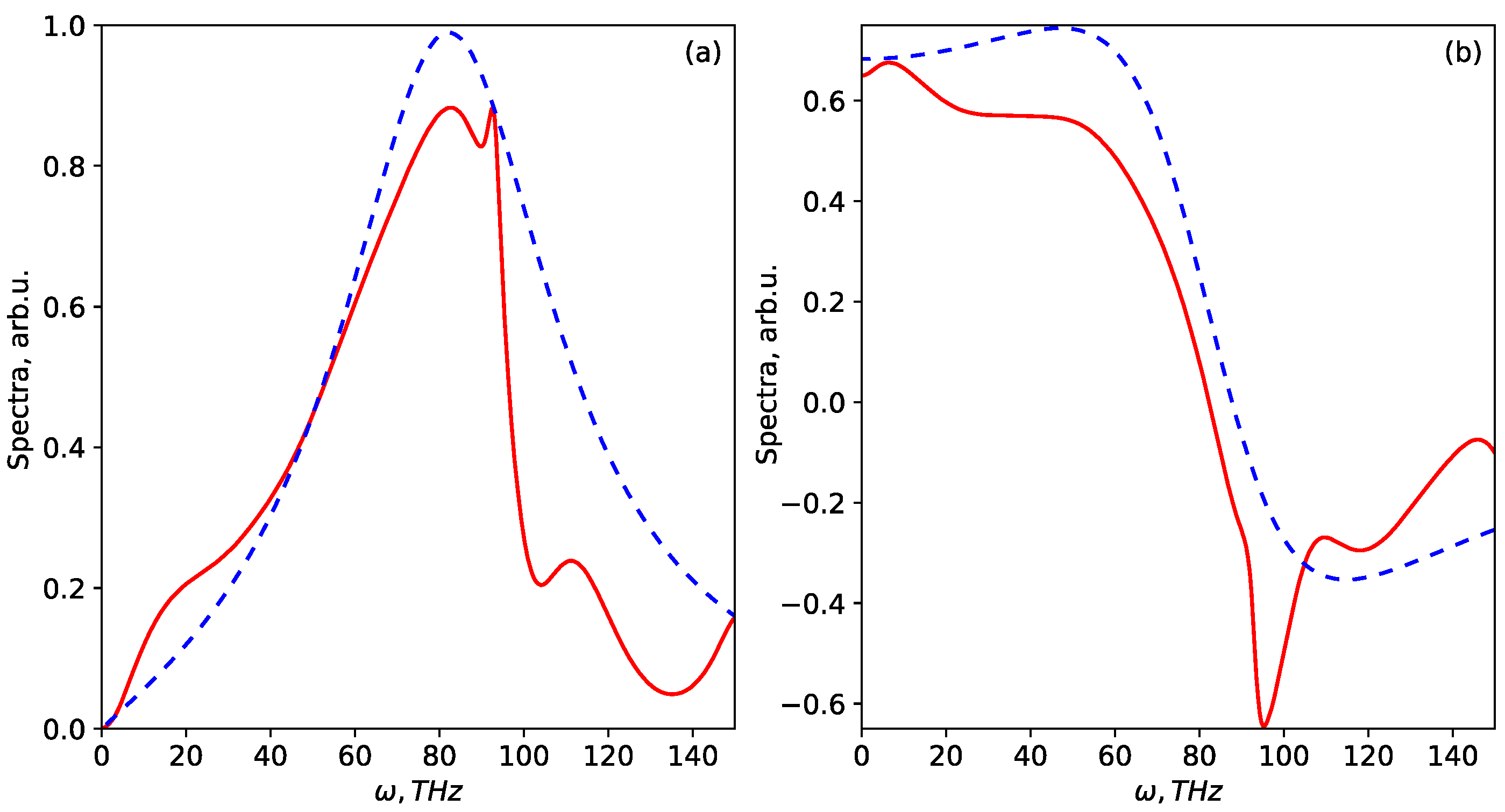
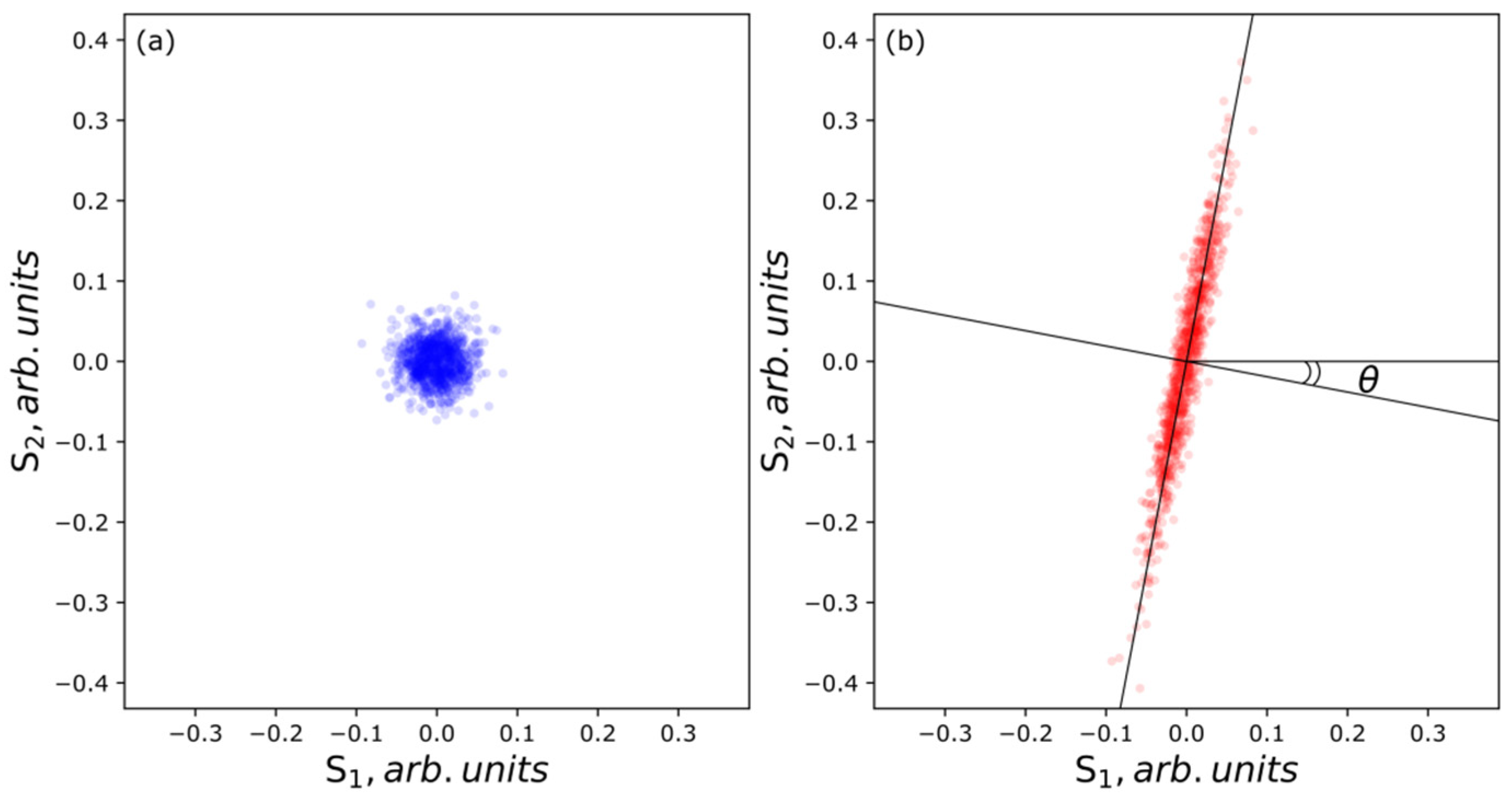
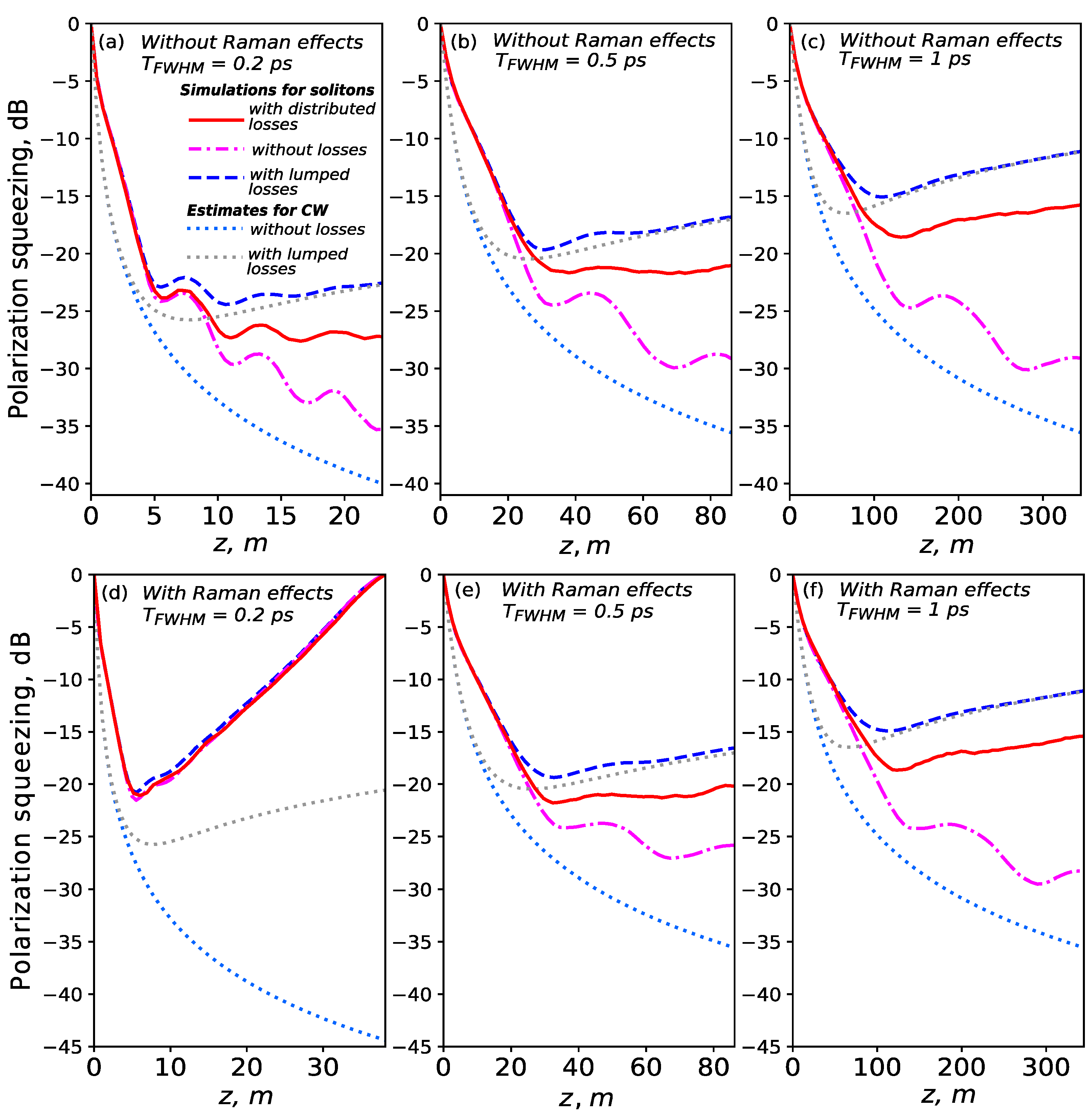
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andersen, U.L.; Gehring, T.; Marquardt, C.; Leuchs, G. 30 years of squeezed light generation. Phys. Scr. 2016, 91, 053001. [Google Scholar] [CrossRef]
- Grote, H.; Danzmann, K.; Dooley, K.L.; Schnabel, R.; Slutsky, J.; Vahlbruch, H. First long-term application of squeezed states of light in a gravitational-wave observatory. Phys. Rev. Lett. 2013, 110, 181101. [Google Scholar] [CrossRef]
- Mansell, G.L.; McRae, T.G.; Altin, P.A.; Yap, M.J.; Ward, R.L.; Slagmolen, B.J.J.; Shaddock, D.A.; McClelland, D.E. Observation of Squeezed Light in the 2 μm Region. Phys. Rev. Lett. 2018, 120, 203603. [Google Scholar] [CrossRef]
- Kaiser, F.; Fedrici, B.; Zavatta, A.; d’Auria, V.; Tanzilli, S. A fully guided-wave squeezing experiment for fiber quantum networks. Optica 2016, 3, 362–365. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Mitschke, F.M.; Mollenauer, L.F. Discovery of the soliton self-frequency shift. Opt. Lett. 1986, 11, 659–661. [Google Scholar] [CrossRef] [PubMed]
- Boutabba, N.; Eleuch, H.; Bouchriha, H. Thermal bath effect on soliton propagation in three-level atomic system. Synth. Met. 2009, 159, 1239–1243. [Google Scholar] [CrossRef]
- Drummond, P.D.; Shelby, R.M.; Friberg, S.R.; Yamamoto, Y. Quantum solitons in optical fibres. Nature 1993, 365, 307–313. [Google Scholar] [CrossRef]
- Leuchs, G.; Korolkova, N.V. Entangling Fiber Solitons: Quantum Noise Engineering for Interferometry and Communication. Opt. Photonics News 2002, 13, 64–69. [Google Scholar] [CrossRef]
- Ritze, H.-H.; Bandilla, A. Quantum effects of a nonlinear interferometer with a Kerr cell. Opt. Commun. 1979, 29, 126–130. [Google Scholar] [CrossRef]
- Imoto, N.; Haus, H.A.; Yamamoto, Y. Quantum nondemolition measurement of the photon number via the optical Kerr effect. Phys. Rev. A 1985, 32, 2287–2292. [Google Scholar] [CrossRef] [PubMed]
- Kitagawa, M.; Yamamoto, Y. Number-phase minimum-uncertainty state with reduced number uncertainty in a Kerr nonlinear interferometer. Phys. Rev. A 1986, 34, 3974–3988. [Google Scholar] [CrossRef]
- Milburn, G.J. Quantum and classical Liouville dynamics of the anharmonic oscillator. Phys. Rev. A 1986, 33, 674–685. [Google Scholar] [CrossRef]
- Stobinska, M.; Milburn, G.J.; Wodkiewicz, K. Wigner function evolution of quantum states in the presence of self-Kerr interaction. Phys. Rev. A 2008, 78, 013810. [Google Scholar] [CrossRef]
- Rudnicki, Ł.; Sánchez-Soto, L.L.; Leuchs, G.; Boyd, R.W. Fundamental quantum limits in ellipsometry. Opt. Lett. 2020, 45, 4607–4610. [Google Scholar] [CrossRef] [PubMed]
- Machida, S.; Yamamoto, Y.; Itaya, Y. Observation of amplitude squeezing in a constant-current–driven semiconductor laser. Phys. Rev. Let. 1987, 58, 1000. [Google Scholar] [CrossRef]
- Wu, L.A.; Kimble, H.J.; Hall, J.L.; Wu, H. Generation of squeezed states by parametric down conversion. Phys. Rev. Lett. 1986, 57, 2520. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Mehmet, M.; Danzmann, K.; Schnabel, R. Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency. Phys. Rev. Lett. 2016, 117, 110801. [Google Scholar] [CrossRef] [PubMed]
- Sizmann, A.; Horowicz, R.J.; Wagner, G.; Leuchs, G. Observation of amplitude squeezing of the up-converted mode in second harmonic generation. Opt. Commun. 1990, 80, 138–142. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Mehmet, M.; Chelkowski, S.; Hage, B.; Franzen, A.; Lastzka, N.; Goßler, S.; Danzmann, K.; Schnabel, R. Observation of squeezed light with 10-dB quantum-noise reduction. Phys. Rev. Lett. 2008, 100, 033602. [Google Scholar] [CrossRef]
- Mehmet, M.; Ast, S.; Eberle, T.; Steinlechner, S.; Vahlbruch, H.; Schnabel, R. Squeezed light at 1550 nm with a quantum noise reduction of 12.3 dB. Opt. Express 2011, 19, 25763–25772. [Google Scholar] [CrossRef]
- Shelby, R.M.; Levenson, M.D.; Perlmutter, S.H.; DeVoe, R.G.; Walls, D.F. Broad-band parametric deamplification of quantum noise in an optical fiber. Phys. Rev. Lett. 1986, 57, 691. [Google Scholar] [CrossRef]
- Corney, J.F.; Heersink, J.; Dong, R.; Josse, V.; Drummond, P.D.; Leuchs, G.; Andersen, U.L. Simulations and experiments on polarization squeezing in optical fiber. Phys. Rev. A 2008, 78, 023831. [Google Scholar] [CrossRef]
- Fiorentino, M.; Sharping, J.E.; Kumar, P.; Porzio, A.; Windeler, R.S. Soliton squeezing in microstructure fiber. Opt. Lett. 2002, 27, 649–651. [Google Scholar] [CrossRef]
- Fiorentino, M.; Sharping, J.E.; Kumar, P.; Levandovsky, D.; Vasilyev, M. Soliton squeezing in a Mach-Zehnder fiber interferometer. Phys. Rev. A 2001, 64, 031801. [Google Scholar] [CrossRef]
- Dong, R.; Heersink, J.; Corney, J.F.; Drummond, P.D.; Andersen, U.L.; Leuchs, G. Experimental evidence for Raman-induced limits to efficient squeezing in optical fibers. Opt. Lett. 2008, 33, 116–118. [Google Scholar] [CrossRef]
- Wang, E.; Verma, G.; Tinsley, J.N.; Poli, N.; Salvi, L. Method for the differential measurement of phase shifts induced by atoms in an optical ring cavity. Phys. Rev. A 2021, 103, 022609. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A.V.; Corney, J.F.; Leuchs, G. Chalcogenide fibers for Kerr squeezing. Opt. Lett. 2020, 45, 5299–5302. [Google Scholar] [CrossRef] [PubMed]
- Bogatskaya, A.; Schegolev, A.; Klenov, N.; Popov, A. Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide. Photonics 2019, 6, 84. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Serena, P.; Meseguer, A.C.; Poli, F.; Bononi, A.; Antona, J.C. Scaling properties of guided acoustic-wave Brillouin scattering in single-mode fibers. Opt. Express 2021, 29, 15528–15540. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.M.; Levenson, M.D.; Bayer, P.W. Guided acoustic-wave Brillouin scattering. Phys. Rev. B 1985, 31, 5244–5252. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Kalinin, N.A.; Anashkina, E.A.; Egorova, O.N.; Lipatov, D.S.; Kim, A.V.; Semjonov, S.L.; Litvak, A.G. Selective excitation and amplification of peak-power-scalable out-of-phase supermode in Yb-doped multicore fiber. J. Light. Technol. 2020, 38, 2464–2470. [Google Scholar] [CrossRef]
- Lin, R.; Udalcovs, A.; Ozolins, O.; Pang, X.; Gan, L.; Tang, M.; Fu, S.; Popov, S.; da Silva, T.F.; Xavier, G.B.; et al. Telecommunication Compatibility Evaluation for Co-existing Quantum Key Distribution in Homogenous Multicore Fiber. IEEE Access 2020, 8, 78836–78846. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Anashkina, E.A.; Andrianov, A.V.; Litvak, A.G. Coherent propagation of laser beams in a small-sized system of weakly coupled optical light guides. Phys. Rev. A 2018, 98, 043857. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A.V. Design and Dispersion Control of Microstructured Multicore Tellurite Glass Fibers with In-Phase and Out-of-Phase Supermodes. Photonics 2021, 8, 113. [Google Scholar] [CrossRef]
- Folkenberg, J.R.; Nielsen, M.D.; Mortensen, N.A.; Jakobsen, C.; Simonsen, H.R. Polarization maintaining large mode area photonic crystal fiber. Opt. Express 2004, 12, 956–960. [Google Scholar] [CrossRef]
- Stone, J.M.; Yu, F.; Knight, J.C. Highly birefringent 98-core fiber. Opt. Lett. 2014, 39, 4568–4570. [Google Scholar] [CrossRef] [PubMed]
- Mansuryan, T.; Rigaud, P.; Bouwmans, G.; Kermène, V.; Quiquempois, Y.; Desfarges-Berthelemot, A.; Armand, P.; Benoist, J.; Barthélémy, A. Spatially dispersive scheme for transmission and synthesis of femtosecond pulses through a multicore fiber. Opt. Express 2012, 20, 24769–24777. [Google Scholar] [CrossRef]
- Drummond, P.D.; Corney, J.F. Quantum noise in optical fibers. I. Stochastic equations. J. Opt. Soc. Am. B 2001, 18, 139–152. [Google Scholar] [CrossRef]
- Corney, J.F.; Drummond, P.D. Quantum noise in optical fibers. II. Raman jitter in soliton communications. J. Opt. Soc. Am. B 2001, 18, 153–161. [Google Scholar] [CrossRef]
- Bonetti, J.; Hernandez, S.M.; Grosz, D.F. Master equation approach to propagation in nonlinear fibers. Opt. Lett. 2021, 46, 665–668. [Google Scholar] [CrossRef]
- Kong, Q.; Ying, H.; Chen, X. Shortcuts to Adiabaticity for Optical Beam Propagation in Nonlinear Gradient Refractive-Index Media. Entropy 2020, 22, 673. [Google Scholar] [CrossRef] [PubMed]
- Stolen, R.H.; Ippen, E.P. Raman gain in glass optical waveguides. Appl. Phys. Lett. 1937, 22, 276–278. [Google Scholar] [CrossRef]
- Bachor, H.A.; Ralph, T.C.; Lucia, S.; Ralph, T.C. A Guide to Experiments in Quantum Optics; Wiley-vch: Weinheim, Germany, 2004. [Google Scholar]
- Kunz, L.; Paris, M.G.A.; Banaszek, K. Noisy propagation of coherent states in a lossy Kerr medium. J. Opt. Soc. Am. B 2018, 35, 214–222. [Google Scholar] [CrossRef]
- Corney, J.F.; Drummond, P.; Heersink, J.; Josse, V.; Leuchs, G.; Andersen, U.L. Many-Body Quantum Dynamics of Polarization Squeezing in Optical Fibers. Phys. Rev. Lett. 2006, 97, 023606. [Google Scholar] [CrossRef]
- Hirosawa, K.; Furumochi, H.; Tada, A.; Kannari, F. Photon Number Squeezing of Ultrabroadband Laser Pulses Generated by Microstructure Fibers. Phys. Rev. Lett. 2005, 94, 203601. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Value |
|---|---|
| β2 | −28.0 ps2/km |
| Aeff | 960 μm2 |
| γ | 0.093 (W∙km)−1 |
| α | 1.0 dB/km |
| λ0 | 1.5 μm |
| T | 300 K |
| i | Fi | ωi, THz∙rad. | Di, THz∙rad. |
|---|---|---|---|
| 1 | −0.3545 | 0.3341 | 8.0078 |
| 2 | 1.2874 | 26.1129 | 46.6540 |
| 3 | −1.4763 | 32.7138 | 33.0592 |
| 4 | 1.0422 | 40.4917 | 30.2293 |
| 5 | −0.4520 | 45.4704 | 23.6997 |
| 6 | 0.1623 | 93.0111 | 2.1382 |
| 7 | 1.3446 | 99.1746 | 26.7883 |
| 8 | −0.8401 | 100.274 | 13.8984 |
| 9 | −0.5613 | 114.6250 | 33.9373 |
| 10 | 0.0906 | 151.4672 | 8.3649 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorokin, A.A.; Anashkina, E.A.; Corney, J.F.; Bobrovs, V.; Leuchs, G.; Andrianov, A.V. Numerical Simulations on Polarization Quantum Noise Squeezing for Ultrashort Solitons in Optical Fiber with Enlarged Mode Field Area. Photonics 2021, 8, 226. https://doi.org/10.3390/photonics8060226
Sorokin AA, Anashkina EA, Corney JF, Bobrovs V, Leuchs G, Andrianov AV. Numerical Simulations on Polarization Quantum Noise Squeezing for Ultrashort Solitons in Optical Fiber with Enlarged Mode Field Area. Photonics. 2021; 8(6):226. https://doi.org/10.3390/photonics8060226
Chicago/Turabian StyleSorokin, Arseny A., Elena A. Anashkina, Joel F. Corney, Vjaceslavs Bobrovs, Gerd Leuchs, and Alexey V. Andrianov. 2021. "Numerical Simulations on Polarization Quantum Noise Squeezing for Ultrashort Solitons in Optical Fiber with Enlarged Mode Field Area" Photonics 8, no. 6: 226. https://doi.org/10.3390/photonics8060226
APA StyleSorokin, A. A., Anashkina, E. A., Corney, J. F., Bobrovs, V., Leuchs, G., & Andrianov, A. V. (2021). Numerical Simulations on Polarization Quantum Noise Squeezing for Ultrashort Solitons in Optical Fiber with Enlarged Mode Field Area. Photonics, 8(6), 226. https://doi.org/10.3390/photonics8060226







