Quantum Optical Experiments Modeled by Long Short-Term Memory
Abstract
:1. Introduction
2. Methods
2.1. Target Values
2.2. Loss Function
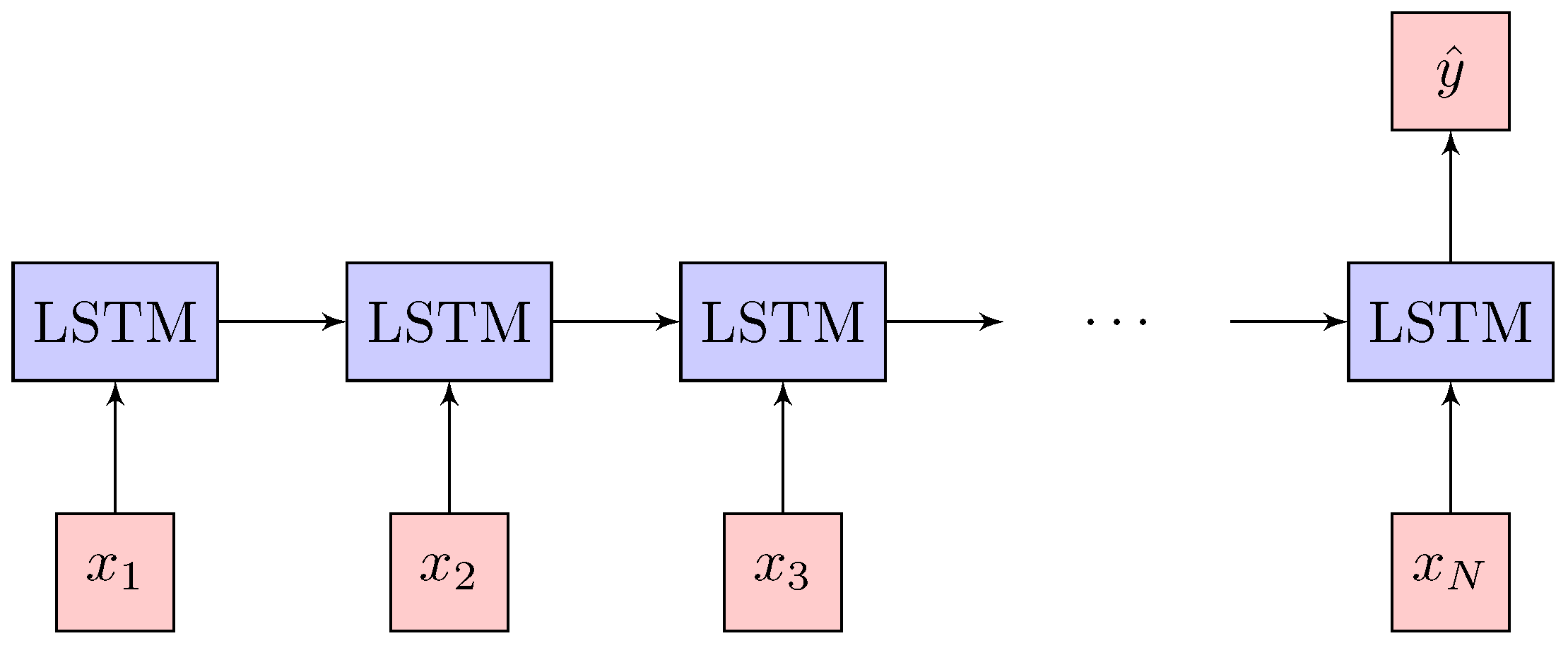
2.3. Network Architecture
3. Experiments
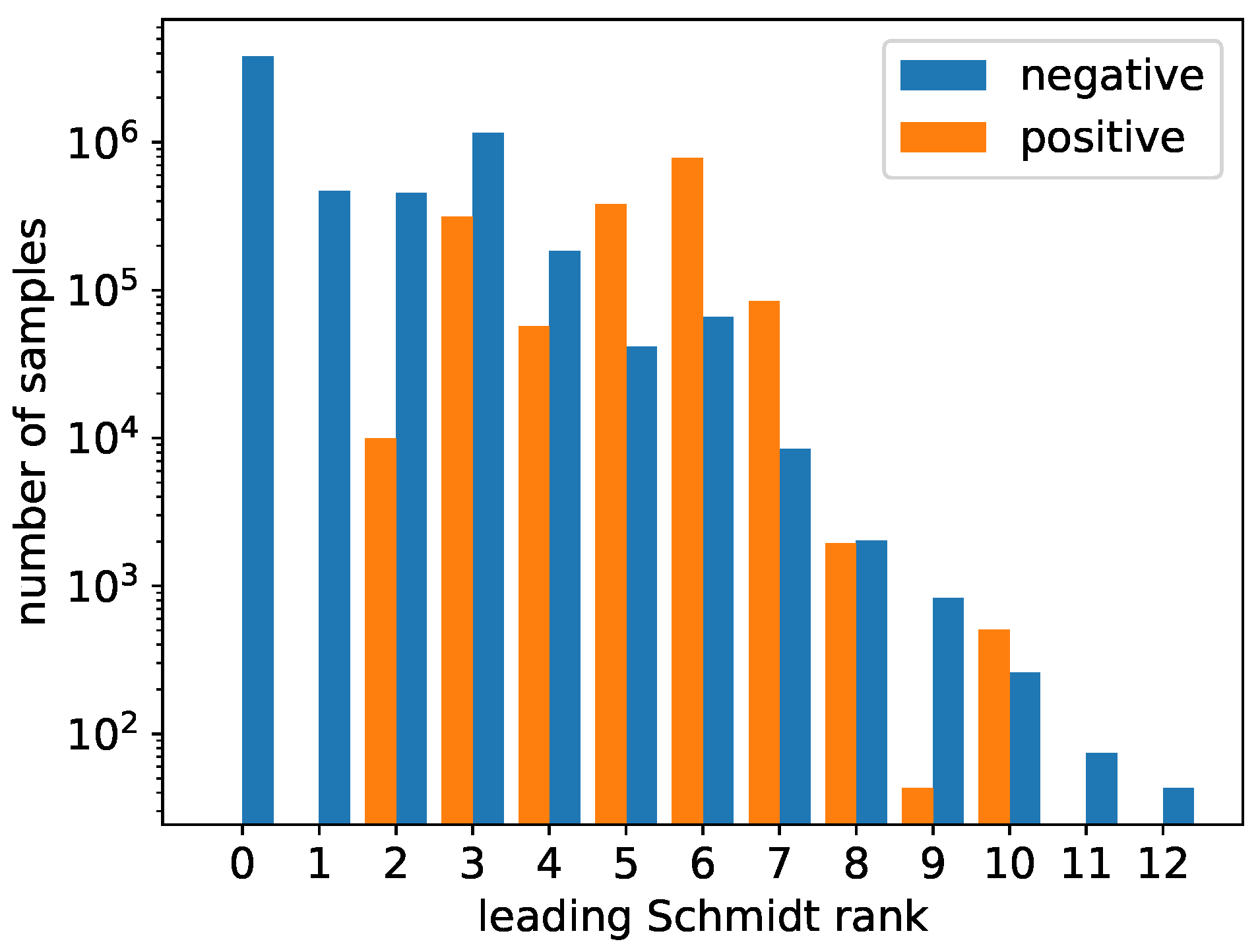
3.1. Dataset
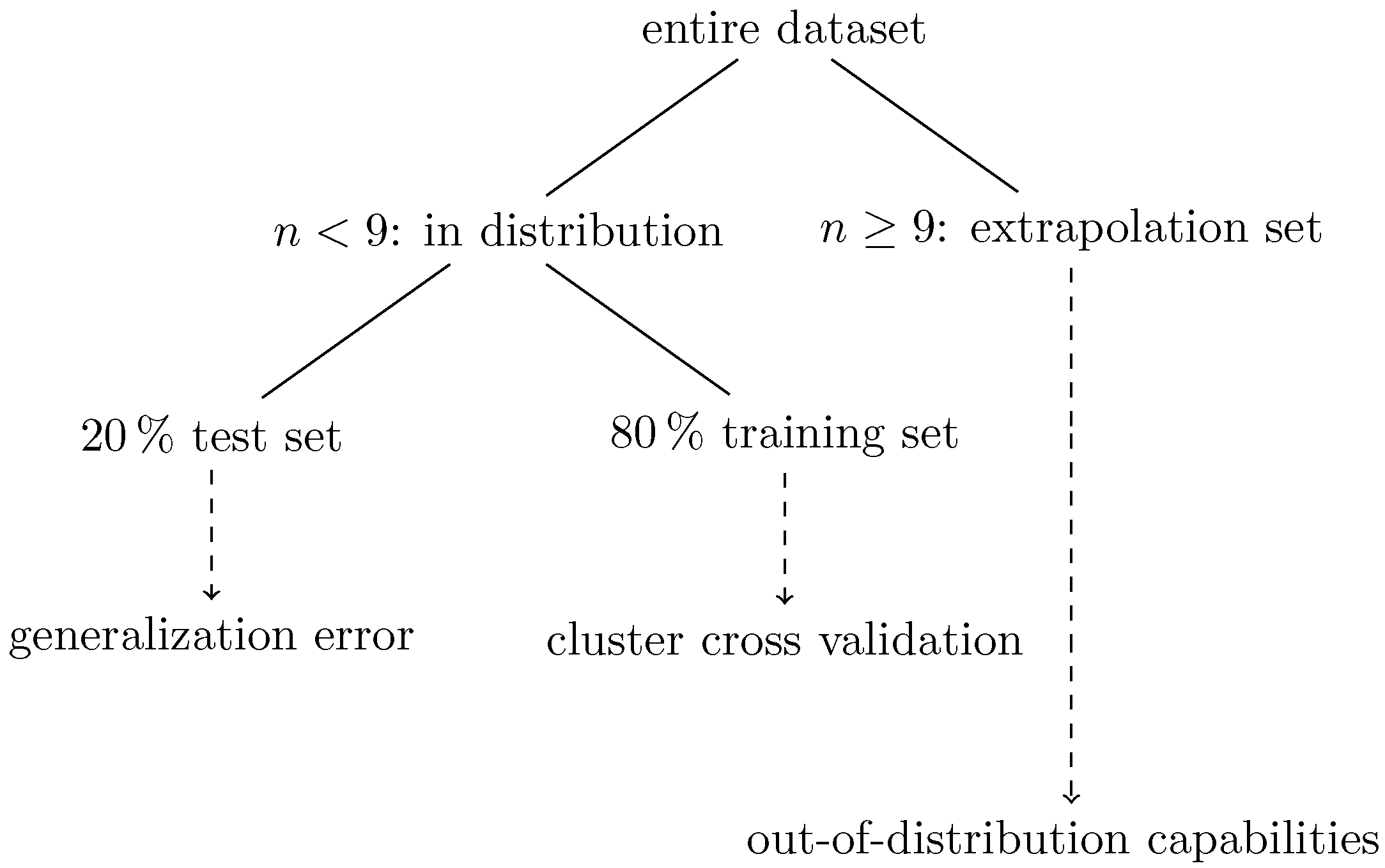
3.2. Workflow
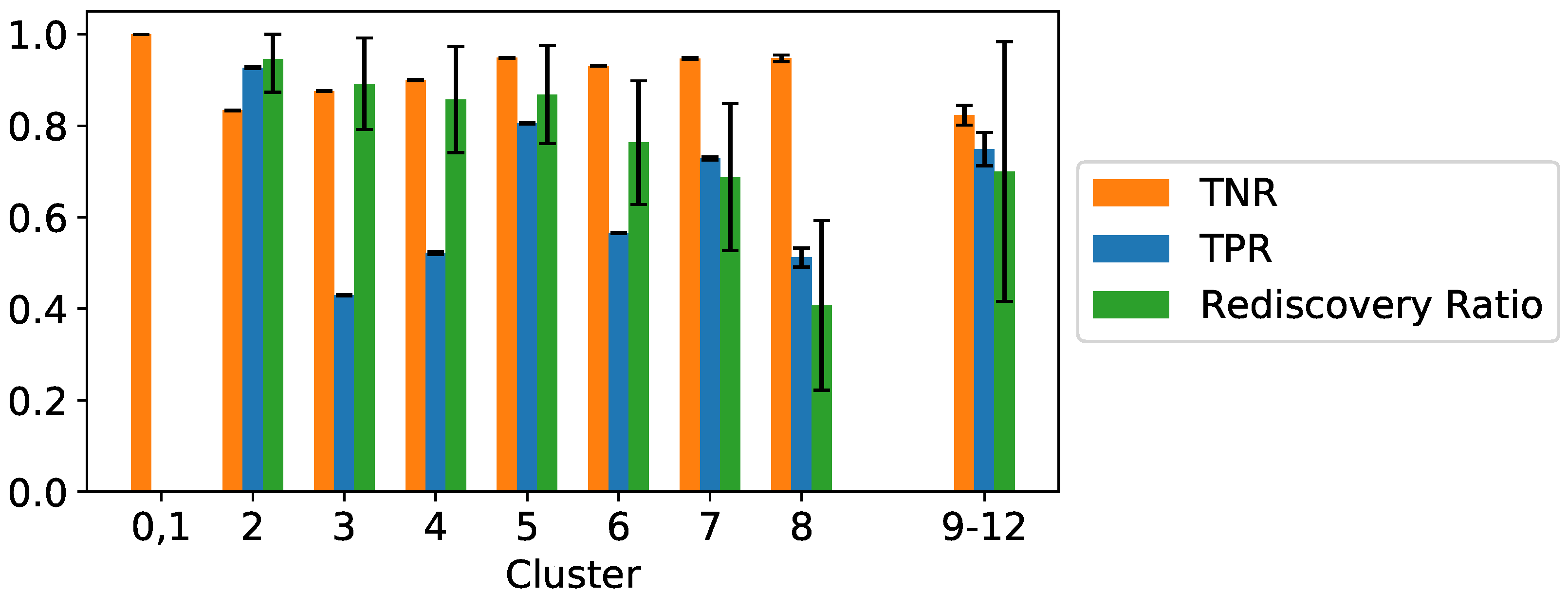
3.3. Results
4. Outlook
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Hochreiter, S. Untersuchungen zu Dynamischen Neuronalen Netzen. Master’s Thesis, Technical University of Munich, Munich, Germany, 1991. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems 27; Curran Associates, Inc.: San Jose, CA, USA, 2014; pp. 3104–3112. [Google Scholar]
- Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 2000, 52, R2493–R2496. [Google Scholar] [CrossRef] [PubMed]
- Kaszlikowski, D.; Gnacínski, P.; Zukowski, M.; Miklaszewski, W.; Zeilinger, A. Violations of local realism by two entangled N-dimensional systems are stronger than for two qubits. Phys. Rev. Lett. 2000, 86, 4418–4421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krenn, M.; Malik, M.; Fickler, R.; Lapkiewicz, R.; Zeilinger, A. Automated Search for new Quantum Experiments. Phys. Rev. Lett. 2016, 116, 090405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malik, M.; Erhard, M.; Huber, M.; Krenn, M.; Fickler, R.; Zeilinger, A. Multi-photon entanglement in high dimensions. Nat. Photonics 2016, 10, 248–252. [Google Scholar] [CrossRef] [Green Version]
- Erhard, M.; Malik, M.; Krenn, M.; Zeilinger, A. Experimental GHZ entanglement beyond qubits. Nat. Photonics 2018, 12, 759–764. [Google Scholar] [CrossRef] [Green Version]
- Knott, P. A search algorithm for quantum state engineering and metrology. New J. Phys. 2016, 18, 073033. [Google Scholar] [CrossRef] [Green Version]
- Nichols, R.; Mineh, L.; Rubio, J.; Matthews, J.C.; Knott, P.A. Designing quantum experiments with a genetic algorithm. Quantum Sci. Technol. 2019, 4, 045012. [Google Scholar] [CrossRef] [Green Version]
- O’Driscoll, L.; Nichols, R.; Knott, P.A. A hybrid machine learning algorithm for designing quantum experiments. Quantum Mach. Intell. 2019, 1, 5–15. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, A.A.; Nautrup, H.P.; Krenn, M.; Dunjko, V.; Tiersch, M.; Zeilinger, A.; Briegel, H.J. Active learning machine learns to create new quantum experiments. Proc. Natl. Acad. Sci. USA 2018, 115, 1221–1226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arrazola, J.M.; Bromley, T.R.; Izaac, J.; Myers, C.R.; Brádler, K.; Killoran, N. Machine learning method for state preparation and gate synthesis on photonic quantum computers. Quantum Sci. Technol. 2019, 4, 024004. [Google Scholar] [CrossRef] [Green Version]
- Zhan, X.; Wang, K.; Xiao, L.; Bian, Z.; Zhang, Y.; Sanders, B.C.; Zhang, C.; Xue, P. Experimental quantum cloning in a pseudo-unitary system. Phys. Rev. A 2020, 101, 010302. [Google Scholar] [CrossRef]
- Krenn, M.; Kottmann, J.S.; Tischler, N.; Aspuru-Guzik, A. Conceptual understanding through efficient automated design of quantum optical experiments. Phys. Rev. X 2021, 11, 031044. [Google Scholar] [CrossRef]
- Flam-Shepherd, D.; Wu, T.; Gu, X.; Cervera-Lierta, A.; Krenn, M.; Aspuru-Guzik, A. Learning Interpretable Representations of Entanglement in Quantum Optics Experiments using Deep Generative Models. arXiv 2021, arXiv:2109.02490. [Google Scholar]
- Krenn, M.; Erhard, M.; Zeilinger, A. Computer-inspired quantum experiments. Nat. Rev. Phys. 2020, 2, 649–661. [Google Scholar] [CrossRef]
- Mayr, A.; Klambauer, G.; Unterthiner, T.; Hochreiter, S. DeepTox: Toxicity Prediction using Deep Learning. Front. Environ. Sci. 2016, 3. [Google Scholar] [CrossRef] [Green Version]
- Mayr, A.; Klambauer, G.; Unterthiner, T.; Steijaert, M.; Wegner, J.K.; Ceulemans, H.; Clevert, D.A.; Hochreiter, S. Large-scale comparison of machine learning methods for drug target prediction on ChEMBL. Chem. Sci. 2018, 9, 5441–5451. [Google Scholar] [CrossRef] [Green Version]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef] [Green Version]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light. Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huber, M.; de Vicente, J.I. Structure of multidimensional entanglement in multipartite systems. Phys. Rev. Lett. 2013, 110, 030501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huber, M.; Perarnau-Llobet, M.; de Vicente, J.I. Entropy vector formalism and the structure of multidimensional entanglement in multipartite systems. Phys. Rev. A 2013, 88, 042328. [Google Scholar] [CrossRef] [Green Version]
- Good, I.J. Rational Decisions. J. R. Stat. Soc. Ser. B 1952, 14, 107–114. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning, 5th ed.; Information Science and Statistics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27; Curran Associates, Inc.: San Jose, CA, USA, 2014; pp. 2672–2680. [Google Scholar]
- Lowerre, B.T. The Harpy speech recognition system. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1976. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved Training of Wasserstein GANs. In Advances in Neural Information Processing Systems 30; Curran Associates, Inc.: San Jose, CA, USA, 2017; pp. 5767–5777. [Google Scholar]
- Yu, L.; Zhang, W.; Wang, J.; Yu, Y. SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient. arXiv 2016, arXiv:1609.05473. [Google Scholar]
- Fedus, W.; Goodfellow, I.; Dai, A.M. MaskGAN: Better Text Generation via Filling in the------. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bengio, S.; Vinyals, O.; Jaitly, N.; Shazeer, N. Scheduled Sampling for Sequence Prediction with Recurrent Neural Networks. In Advances in Neural Information Processing Systems 28; Curran Associates, Inc.: San Jose, CA, USA, 2015; pp. 1171–1179. [Google Scholar]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Karpathy, A.; Li, F.-F. Deep visual-semantic alignments for generating image descriptions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–15 June 2015; pp. 3128–3137. [Google Scholar]
| 0,1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9–12 |
| 0,1 |
| Training | Test | |
|---|---|---|
| BCE loss | 10.2 | 10.4 |
| TNR | 0.9271 ± 2.4 | 0.9261 ± 3.8 |
| TPR | 0.9469 ± 4.1 | 0.9427 ± 6.5 |
| SRV loss | 2.247 | 2.24 |
| SRV accuracy | 0.9382 | 0.938 |
| SRV mean distance | 1.3943 | 1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adler, T.; Erhard, M.; Krenn, M.; Brandstetter, J.; Kofler, J.; Hochreiter, S. Quantum Optical Experiments Modeled by Long Short-Term Memory. Photonics 2021, 8, 535. https://doi.org/10.3390/photonics8120535
Adler T, Erhard M, Krenn M, Brandstetter J, Kofler J, Hochreiter S. Quantum Optical Experiments Modeled by Long Short-Term Memory. Photonics. 2021; 8(12):535. https://doi.org/10.3390/photonics8120535
Chicago/Turabian StyleAdler, Thomas, Manuel Erhard, Mario Krenn, Johannes Brandstetter, Johannes Kofler, and Sepp Hochreiter. 2021. "Quantum Optical Experiments Modeled by Long Short-Term Memory" Photonics 8, no. 12: 535. https://doi.org/10.3390/photonics8120535
APA StyleAdler, T., Erhard, M., Krenn, M., Brandstetter, J., Kofler, J., & Hochreiter, S. (2021). Quantum Optical Experiments Modeled by Long Short-Term Memory. Photonics, 8(12), 535. https://doi.org/10.3390/photonics8120535





