Abstract
With the rapid development of optical communication systems, more advanced techniques conventionally used in long-haul transmissions have gradually entered systems covering shorter distances below 100 km, where higher-speed connections are required in various applications, such as the optical access networks, inter- and intra-data center interconnects, mobile fronthaul, and in-building and indoor communications. One of the techniques that has attracted intensive interests in short-reach optical communications is machine learning (ML). Due to its robust problem-solving, decision-making, and pattern recognition capabilities, ML techniques have become an essential solution for many challenging aspects. In particular, taking advantage of their high accuracy, adaptability, and implementation efficiency, ML has been widely studied in short-reach optical communications for optical performance monitoring (OPM), modulation format identification (MFI), signal processing and in-building/indoor optical wireless communications. Compared with long-reach communications, the ML techniques used in short-reach communications have more stringent complexity and cost requirements, and also need to be more sensitive. In this paper, a comprehensive review of various ML methods and their applications in short-reach optical communications are presented and discussed, focusing on existing and potential advantages, limitations and prospective trends.
1. Introduction
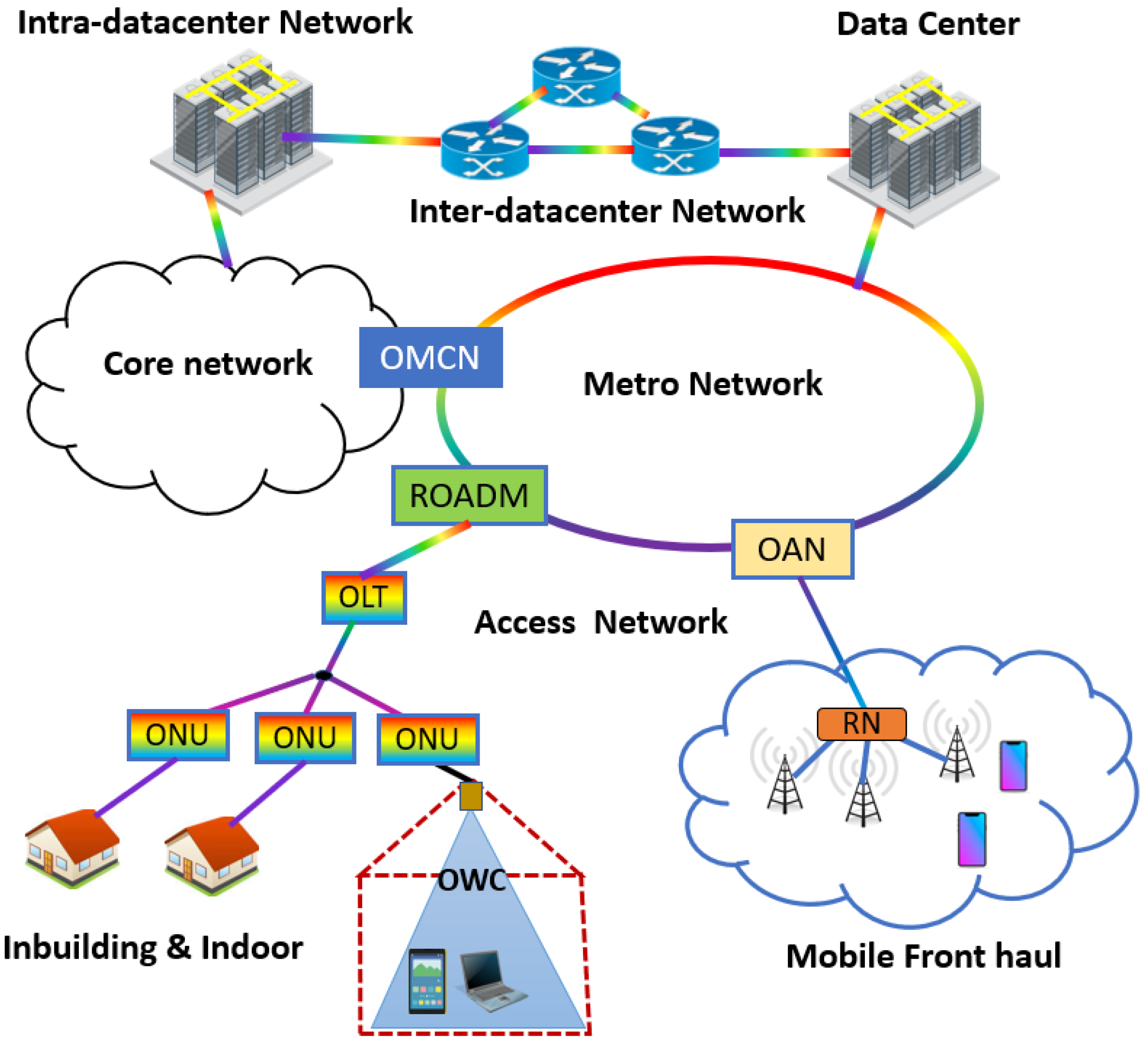
In recent years, short-reach optical communication systems have attracted intensive interests from both the industry and the academia. The criteria we use in this paper to determine whether an optical communication system is a short-reach or a long-reach is based on the transmission distance. We use the short-reach to refer to the communication system and network with a transmission distance of shorter than 100 km, which are cost-sensitive due to their large deployment scale [1]. In short-reach optical communications, in addition to broadband optical access networks, the emergence of 5G and future beyond-5G (also called 6G), new distributed edge cloud computing networks, large-scale machine-to-machine communications, inter- or intra-datacenter communications and mobile fronthaul, also impose new stringent requirements [1,2,3]. The typical architecture and application of the short-reach communications is shown in Figure 1. For the ease of discussion, based on the transmission distance and function, here we divide short-reach communication systems and networks into five categories: inter-datacenter networks, intra-datacenter networks, optical access networks, in-building and indoor optical wireless communications, and mobile fronthaul communications.
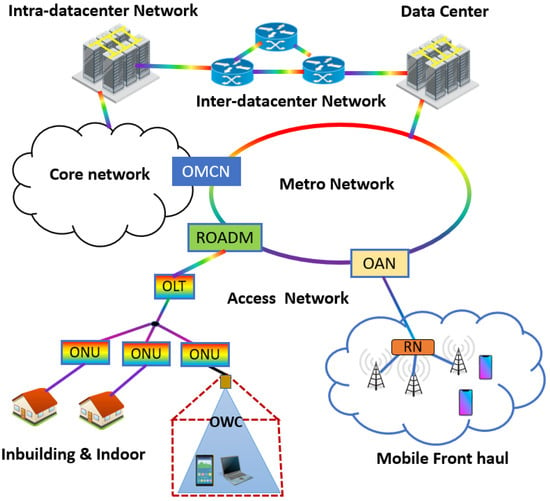
Figure 1.
Short-reach optical communication system. OMCN: optical metro-core node, OAN: optical aggregation node, ROADM: reconfigurable optical add-drop node, ONU: optical network unit, RN: remote node, OLT: optical line termination, OWC: optical wireless communication.
In the past decade, large-scale data centers that promoted the development of information technology has greatly changed our lives [4]. Internet traffic within and between data centers is growing rapidly, particularly driven by the demand for bandwidth-intensive applications such as cloud computing, live streaming, and online games. Therefore, there is an urgent need for the design and deployment of higher capacity optical communication links in inter- and intra-datacenter networks (DCNs), where the intra-DCN link is usually up to hundreds of meters long, and the length of datacenter inter connection (DCI) link is usually up to tens of kilometers [5]. For the sake of solving the bandwidth limitation of traditional wavelength division multiplexing (WDM) networks, flexible bandwidth optical networking has been applied to intra and inter datacenter networking. Due to the low-cost requirement and the short transmission distance property, the multi-mode fiber has been widely used in intra-data center links. To enhance the channel capacity in multi-mode fiber intra-data center links, higher symbol rates and multi-level modulation formats have been used [6]. In addition, the latest standard can use four-level pulse amplitude modulation (PAM-4) to achieve a signal transmission rate of 25 Gbaud to support shortwave wavelength division multiplexing (SWDM) for intra-DCN [5]. Multi-mode fiber links with SWDM technology can help data centers to further upgrade to 40 G and 100 G Ethernet by using vertical-cavity surface-emitting lasers (VCSELs) and lasers optimized OM3/OM4 multi-mode optical fibers [7]. On the other hand, for DCI (with longer transmission distance and higher data rate requirements compared with intra-data center links), 100-Gbaud PAM-4 intensity-modulation direct detection (IM/DD) transceiver has been developed, which supports up to 200 Gb/s data rate [8]. Whilst being cost-effective, IM/DD transmission technologies struggle to further increase the capacity and reach of DCI links to meet even higher requirements, whilst completely coherent solutions are currently too costly. Gratifyingly, in 2020, the use of single side band (SSB) direct detection reached a data rate of more than 400 Gb/s per channel, where 5 WDM channels each with over 400 Gb/s (64-QAM at 85 GBaud/s) have been realized for the first time [9].
The information processed and exchanged in the data center needs to be transmitted to users through the optical access network. As shown in Figure 1, passive optical network (PON) is a typical optical access network architecture that uses un-powered optical splitters for the fiber to premises connections [10]. A PON consists of an optical line terminal (OLT) located at the central office of the service provider and several optical network units (ONUs) located close to customers. High-speed PON can increase the network capacity and improve QoS metrics [11]. ITU-T and IEEE have boosted the nominal line rate of PON systems to more than 10 Gbps (XG(S)-PON) in recent years [12]. Following XG-PON, 40 Gbps-capable PON (NG-PON2) have added solutions to meet higher speed, and larger bandwidth demands [13]. There are three types of higher-speed PON systems: time division multiplexing PON (TDM-PON), time and wavelength division multiplexing PON (TWDM-PON), and WDM-PON [12]. TDM-PON uses time division multiple access (TDMA) to connect multiple ONUs to the same OLT. The commercially widely used TDM-PON technology can provide a symmetrical bit rate of up to 10 Gbps [14]. According to IEEE and ITU definitions, the next-generation TDM-PON will deliver bit rates of 25 Gbps and 50 Gbp, which can cost-effectively accommodate xhaul traffic [14]. To further increase the capacity, WDM-PON has been proposed and studied. The ONUs coexist in the same fiber with light sources operated at various wavelengths, boosting the overall network bandwidth and the number of users serviced in the optical access network [15]. In terms of network connections, the WDM-PON may employ point-to-point, point-to-multipoint, or hybrid systems, which is widely used for FTTx (Fiber to the x, x = home, building, curb or node) [16]. The spectral efficiency of WDM-PON would also have to be improved in order to enhance system capacity and the number of users serviced, where narrowing the inter-channel spacing and reusing WDM channels are two possible strategies [17]. On the other hand, different from TDM-PON and WDM-PON, TWDM-PON is a multi-wavelength PON that uses TDM/TDMA to share each wavelength channel across multiple ONUs. The details of 50G TWDM-PON such as the wavelength plan and channel information are gradually being standardized under the research of ITU-T [12]. Recently, several studies have focused on the energy efficiency of TWDM-PON equipment such as the protocol design for energy efficient OLT [18,19].
The radio access network (RAN) adds a new network section known as fronthaul, which is the link between a radio digital unit (DU; also called a baseband unit, BBU) and a remote radio unit (RRU) [20]. Various functional splits are being specified in the recently proposed next-generation fronthaul interface (NGFI) to allow varied trade-offs between the RRU complexity, fronthaul bandwidth-efficiency, and system performance [20]. Mobile-PON, a high bandwidth efficiency, low latency mobile fronthaul architecture based on functional split and TDM-PON with combined mobile and PON scheduler, has also been presented [21]. In addition, ref. [22] presents a type of mobile fronthaul architecture design plan that uses WDM-PON in addition to the wireless multi-hop and point-to-point optical links to lower fronthaul deployment costs. Furthermore, the 5G RAN architecture of a optical fronthaul network using ultra dense WDM-PON (UDWDM-PON) combined with phased array fed (PAF) reflector antenna systems for radio frequency transmission and reception is also under active research [23].
With broadband access delivered to the doorstep, high-speed in-building and indoor communications have attracted intensive interests. Compared with wired connections, the wireless in-building and indoor communications are more attractive due to the mobility feature. The optical wireless communication (OWC) has been widely used in indoor and in-building communications. As a new type of communication technology, compared with conventional RF wireless technologies, the OWC has the advantages of realizing broadband transmission, flexible networking, low latency, anti-electromagnetic interference and high communication security [24,25,26]. Both the visible range and near-infrared wavelength band have been studied in OWC systems, and both line-of-sight (LOS) and non-line-of-sight (NLOS) links have been explored [27]. In addition, the use of OWC technology for in-building and indoor user positioning has also been proposed and studied [28,29,30,31]. Recently, instead of using dedicated photo-detectors (PDs), the use of optical camera as the receiver in in-building and indoor OWC systems has attracted intensive interests as well [32,33,34]. Using OWC in in-building and indoor environments, over Gbps wireless connections have been demonstrated [35,36].
In the various types of short-reach optical communication systems and networks described above, the communication requirement becomes increasingly stringent and the complexity and requirements of the system increases substantially. To cope with the increasing complexity of various short-reach communication applications, the use of artificial intelligence (AI) technologies in short-reach optical communications has been proposed and widely studied. AI simulate sophisticated biological processes such as learning, extrapolating, and self-correction to enable computer programming to solve problems. In the past few decades, improving the performance of optical communication systems and networks through the application of AI-based technologies has become a field of extensive research, including the fields of transmission, switching, and network management. In particular, machine learning, as a branch of the AI learning method, has been widely studied as it enables the agent to improve its performance in future tasks through learning from the experience gained [37].
In general, there are four types of machine learning algorithms: supervised, unsupervised, semi-supervised and reinforcement learning. The most commonly used ML algorithm in the field of optical communication is the supervised learning, which uses known output features to derive the computational relationship between the input training data and the output data [38]. The neural networks as a supervised machine learning method, such as the artificial neural networks (ANN), convolutional neural network (CNN), and recurrent neural network (RNN), have been widely applied in optical communication systems and networks.
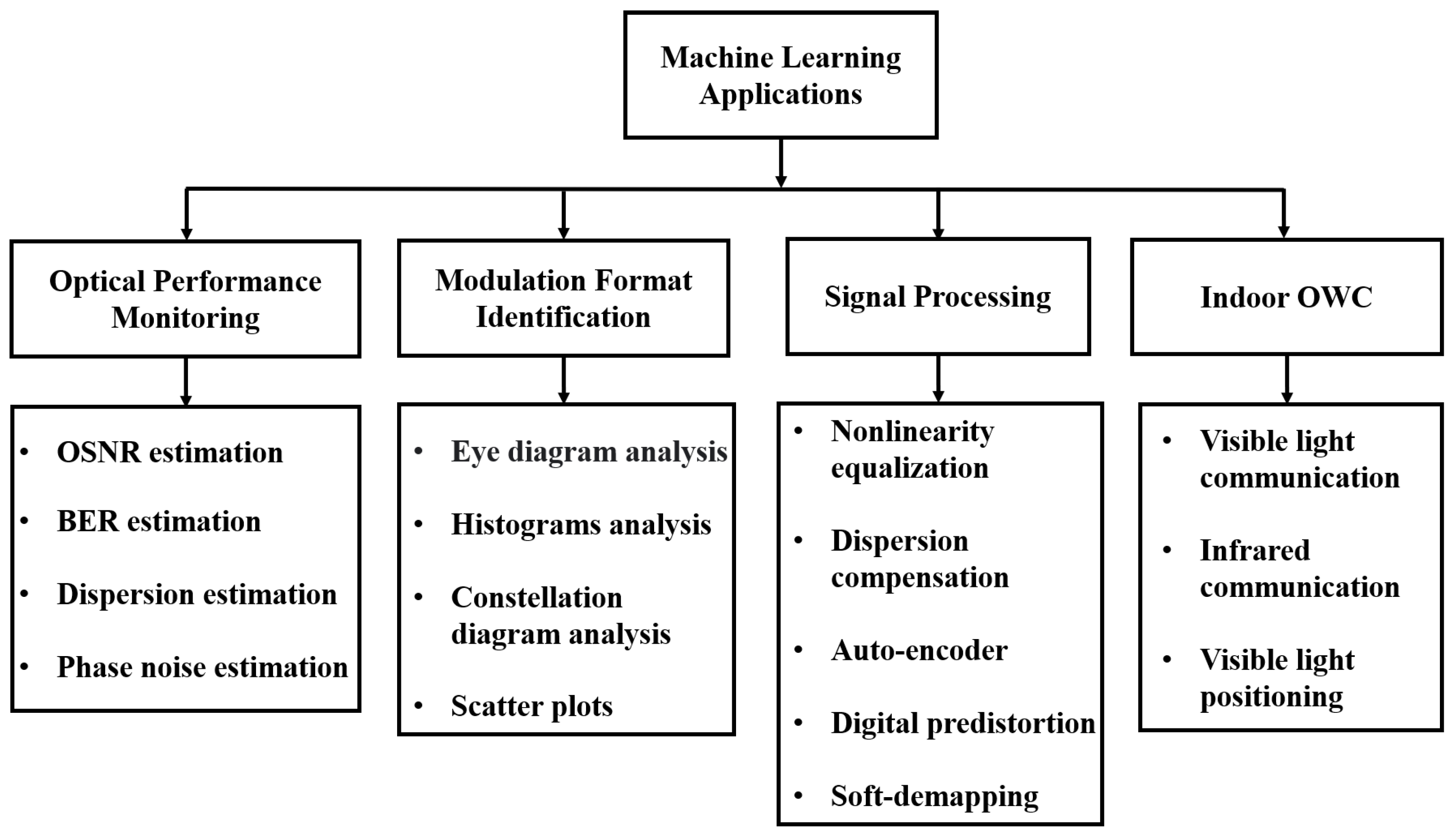
The ML and neural networks have been used in different tasks in optical communication systems and networks. A summary is shown in Figure 2. At the system level, ML is mainly applied in the signal processing to optimize the signal reception and detection after propagating through the highly nonlinear optical communication channels. On the other hand, at the network level, optical networks are facing more challenges due to increasing data switching and routing. From the optical network point of view, the data plane and the control plane both contribute to the increased complexity [39]. The optical network transforms from the traditional static network to the dynamic network, with no predefined spectrum grid or modulation format, and with reconfigurable network topologies, such as the elastic optical networks (EON). Although the overall performance, flexibility and efficiency of the new dynamic network have been greatly improved, it is facing challenges in terms of network reliability, heterogeneity, latency, availability, complexity, quality assurance, capacity, etc. [38]. With the ability of learning and adapt to changes in the environment, the ML technology can well cope with the challenges brought by dynamic optical networks and can even deal with unforeseen scenarios when the ML algorithm is designed [40]. Therefore, the ML algorithm is a promising solution to dynamic optical networks, with applications in optical performance monitoring [41,42,43,44,45,46,47,48,49], modulation format identification [50,51,52] and nonlinearity mitigation [53,54]. In the control plane, ML techniques have been used to achieve the highly demand dynamic control, reconfiguration, and optical network virtualization [39]. For example, the support vector machines (SVM) and clustering algorithms have been employed for detecting soft failures, and data virtualization of optical networks [55]. Meanwhile, the software-defined networking (SDN) has become an important tool for network virtualization and a flexible network traffic controller in recent years. Therefore, ML techniques have been combined with SDN to solve routing and wavelength assignment problems in the WDM systems [56].
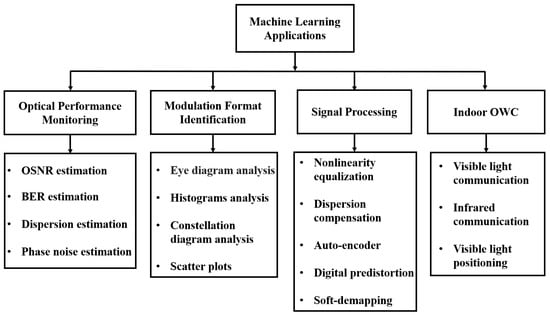
Figure 2.
Machine learning applications in optical communications.
In the field of short-reach optical communication, the EON is a promising flexible grid technology that efficiently allocate the spectrum resource to satisfy the ever-increasing end-user bandwidth demand [57]. The application of EON makes the short-reach optical networks more transparent and dynamic. However, in the meantime, it also leads to more complicated network architectures and operations. Therefore, the real-time monitoring of miscellaneous channel impairments ubiquitous in the network, also known as OPM, is essential for the reliable operation and efficient management of such complex optical networks. Unfortunately, independently monitoring multi-channel is a difficult task because the effects of various impairments are usually mixed and they are almost physically indivisible [58]. Therefore, the use of ML techniques has been widely investigated in OPM, focusing on different key parameters, such as the chromatic dispersion (CD) and polarization-mode dispersion (PMD) monitoring [59,60], fiber nonlinearity monitoring [61], bit error rate (BER) estimation [62], and optical signal to noise ratio (OSNR) monitoring [63,64,65,66].
Another key requirement in short-reach optical communication is the ability to autonomously identify the optical modulation formats deployed. This is particularly required by the OPM units in the intermediate network nodes, because the algorithms used in these devices are dependent on the modulation format utilized [42]. Thus, reliable and accurate MFI is highly demanded. However, the analytical modeling and analysis of MFI in short-reach communication is challenging due to the high hardware cost and complex algorithms. On the other hand, ML algorithms can learn from historical data without the need of accurate analytical framework. As a result, we have also seen several attempts to apply ML methods for the MFI in short-reach optical communication networks [51,52,67,68,69].
When applying ML techniques for OPM and MFI, the requirements and focus in short-reach and long-reach scenarios are different. First, the ML-based OPM in short-reach optical communications need to be less complicated and have higher sensitivity. For example, the CD and OSNR estimations in short-reach systems require higher accuracy than long-reach due to the reduced transmission distance. In addition, the major impairments that can affect the BER are different. Long-reach systems are mainly affected by the amplified spontaneous emission (ASE) noise, accumulated dispersion and nonlinear interference generated by the fiber Kerr effect [70,71]. However, in many short-reach systems, optical amplifiers are not used, and hence, the dominating noise source is no longer ASE. Hence, the system configuration should be considered while determining which impairment parameters are the priorities, since nonlinearity, fiber dispersion, laser phase noise, and relative intensity noise (RIN) can all be the dominant impairment [1]. In terms of MFI, most ML-based MFI technologies are deployed in coherent communication systems to identify modulation formats, such as QPSK, 16-QAM and 64-QAM. These ML based MFI models are normally trained with phase constellation diagrams, which are suitable for both long-reach systems and short-reach systems with coherent receivers. However, the intensity modulation with direct detection is also widely used in short-reach communications. Hence, ML-based MFI technologies in short-reach optical communications also need to be able to recognize intensity-only modulation formats, such as non-return-to-zero (NRZ) and return to zero (RZ) on-off keying (OOK), PAM-4 and PAM-8. Thus, asynchronous amplitude histograms (AAH) [72] and eye-diagram [65] based ML technologies have been proposed for the MFI in short-reach optical systems.
In addition to the application of ML in the field of OPM and MFI, ML techniques are also promising solutions in the signal processing for short-reach optical communications. In optical communication systems, digital signal processing (DSP) is widely used to compensate various transmission impairments, such as the linear impairments (e.g., CD and PMD) [53,73]. For example, the ML-based equalizer has been used as the digital part of a tunable optical signal processor for CD compensation, which can reduce the footprint and attenuation compared with the solution based on fiber Bragg grating and dispersion compensation fibers [74]. In addition to the linear impairments, the nonlinear effects, such as stimulated Brillouin scattering (SBS), four-wave mixing (FWM) and self-phase modulation (SPM), also limit the performance of high-speed optical communication systems. For example, the interactions between laser phase noise and CD generate equalization enhanced phase noise (EEPN) [75], which is challenging to compensate. Furthermore, impairments caused by optical/electrical components with nonlinear memory effects are also difficult to compensate [76]. Therefore, high-speed DSP has been developed for the compensation of nonlinear impairments, such as the Volterra nonlinear equalizers [77]. While Volterra equalizers are known to be effective for removing nonlinear distortions, the implementation and computation complexity is very high. In order to find an alternative solution, the ML-based equalization has been proposed to provide better system performance or reduced complexity with comparable performance [78], since ML techniques can effectively reduce nonlinear distortion and accurately estimate various key parameters in optical networks [58].
In even shorter-reach in-building/indoor OWC systems, the ML technique has also been widely studied. In both visible light communication (VLC) and near-infrared indoor OWC systems, the ML technique has been applied to improve the data transmission performance, mainly by suppressing the inter-symbol interference and nonlinear effects existing in the system [79,80]. In addition, the ML technique has also been widely applied in OWC-based in-building/indoor positioning systems, where better positioning accuracy, as well as simultaneous positioning and receiver orientation estimations, have been realized [81].
In recent years, several reviews and surveys about ML or short-reach communications have been published, such as the ML for OPM and MFI [37], recent developments of shot-reach optical communications [1] and ML-based equalization for short-reach transmission [82]. Unlike the previous survey papers, our survey provides a comprehensive review focusing on various ML-based applications in short-reach communications, including ML-based OPM and MFI techniques, signal processing techniques and in-building/indoor OWC systems. Compared with [37], our paper focuses on short-reach communications, and we not only review ML-based applications for OPM and MFI, but also review the application of ML in signal processing and OWC in-building and indoor positioning. Compared with [1], our paper reviews the recent developments of ML-based techniques in short-reach communications instead of introducing various impairments and related theories that affect the transmission of short-reach systems. Compared to [82], our paper not only covers ML-based equalization techniques in short-reach communications, but also introduces the application of ML in OPM, MFI, and in-building and indoor positioning. The following is a list of our contributions:
- Review the state-of-the-art of short-reach optical communication systems and networks including inter-datacenter networks, intra-datacenter networks, optical access networks, mobile front-haul communications, and in-building and indoor optical wireless communications.
- Comprehensively review ML-based OPM and MFI related research in short-reach optical communications, including the comparison of the different ML techniques, how the OPM task is formulated and the ML technique is utilized, and our analysis of, advantages and limitations of these studies.
- Comprehensively review the recent progress on ML-based signal processing techniques in short-reach optical communications, including ML-based equalization techniques as well as other ML-based signal processors, such as auto encoder/decoder, digital pre-distortion and soft-demapping applications.
- Review the ML-based applications in in-building/indoor OWC systems, including the ML-based signal processing techniques, and the application of ML algorithms in indoor user positioning.
The remainder of this survey is organized as follows. In Section 2, we first describe and compare different ML-based OPM and MFI techniques. Then, we discuss the applications in direct detect and coherent short-reach optical communications in two subsections. In Section 3, we provide a review of recent progress on ML-based signal processing techniques for short-reach optical communications, including different ML-based linear and nonlinear equalizers, auto-encoder, digital predistortion and soft demapping. In Section 4, we review and discuss recent ML-based applications in in-building/indoor OWC systems, including both wireless signal processing and user positioning. Finally, in Section 5, we summarize this paper and provide our views on the potential future research directions.
2. Machine Learning for OPM and MFI in Short Reach Optical Communications
With the development of advanced optical communication systems and networks, the critical role of OPM in the system and network operation has emerged. OPM can optimize the system performance, shorten the system installation time, increase the transmission rate, and reduce operation costs. Advanced OPM methods also have the potential to enable fault management and enhance the quality of service (QoS) in the optical domain [83]. In optical communications and networks, the key parameters that need to be monitored in the optical domain include the total power, OSNR, CD, PMD and fiber nonlinearity [62]. Whilst the transmission distance is shorter, the OPM in short-reach needs to be less complicated and more sensitive. Recently, ML techniques, particularly the deep learning for implementing OPM have been proposed. Deep learning represents a ML method based on the concept of a deep and hierarchical representation of data, which can automatically learn the function of data at multiple levels of abstraction [84]. Once the deep learning algorithm, typically based on neural networks, is fully operational, the difference between the received system feature (including eye diagram, histogram, constellation diagram, power spectrum, and time/frequency domain signal) and the ideal data/ground truth can be attributed to specific physical parameters, which can be derived from previous training process, to realize the OPM function [85]. In addition, the parameters mentioned before (e.g., OSNR), MFI is an important parameter that needs to be monitored during the OPM implementation. Most of the non-machine learning technologies for MFI, such as AAH [86] and asynchronous delayed tap sampling (ADTP) [87], require additional hardware components, which can significantly increase the complexity and cost of implementation. Since neural networks can perform automatic feature extraction and conversion of the channel information required by MFI, the neural networks such as ANN, CNN, and RNN are also good candidates for MFI.
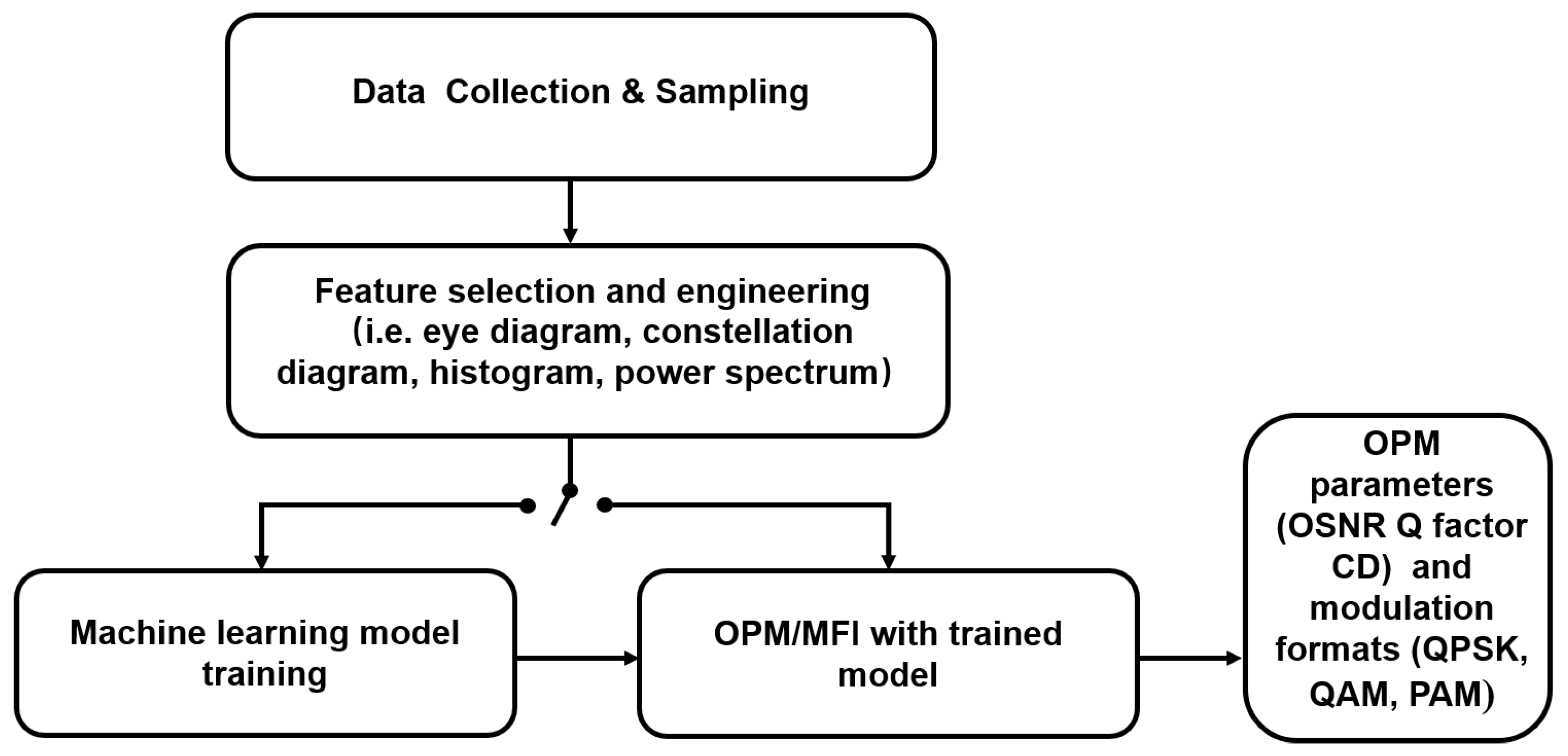
Figure 3 summarizes the generic approach for conducting OPM and MFI using ML techniques. The first step is typically creating a data set for training the deep learning algorithm. Traditionally, the optical signal is converted to the electrical domain at the receiving end and then sampled to construct a data set. Another method to obtain the data set is directly monitoring the optical signal from the transmission link, such as measuring the OSNR using an optical spectrum analyzer (OSA), which does not require optical-to-electrical conversion and can be detected online without interrupting the regular data transmission. The second step is to extract the specific characteristics of the signal, which contains information about the impairments in the system or the modulation format. The eye diagram, power spectrum, constellation diagram, and histogram are examples of such features. These features are then employed in the final step for ML algorithm training to execute OPM, or MFI [37]. Currently, the training is typically implemented offline and after training, the trained model and feature extraction steps can be used for online OPM parameters estimation and MFI. During the system or network operation, the transmission conditions and the corresponding impairments may change over time, and hence, the ML models used may need to be retrained using a newly collected training dataset [88]. Therefore, the effective retraining of ML models is also highly desirable.
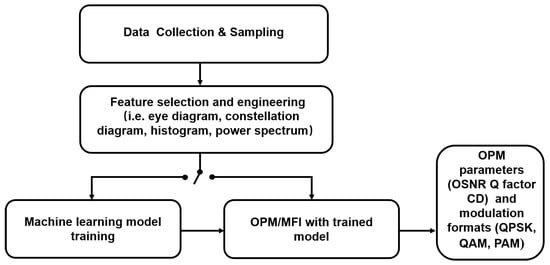
Figure 3.
Procedure for OPM and MFI using machine learning.
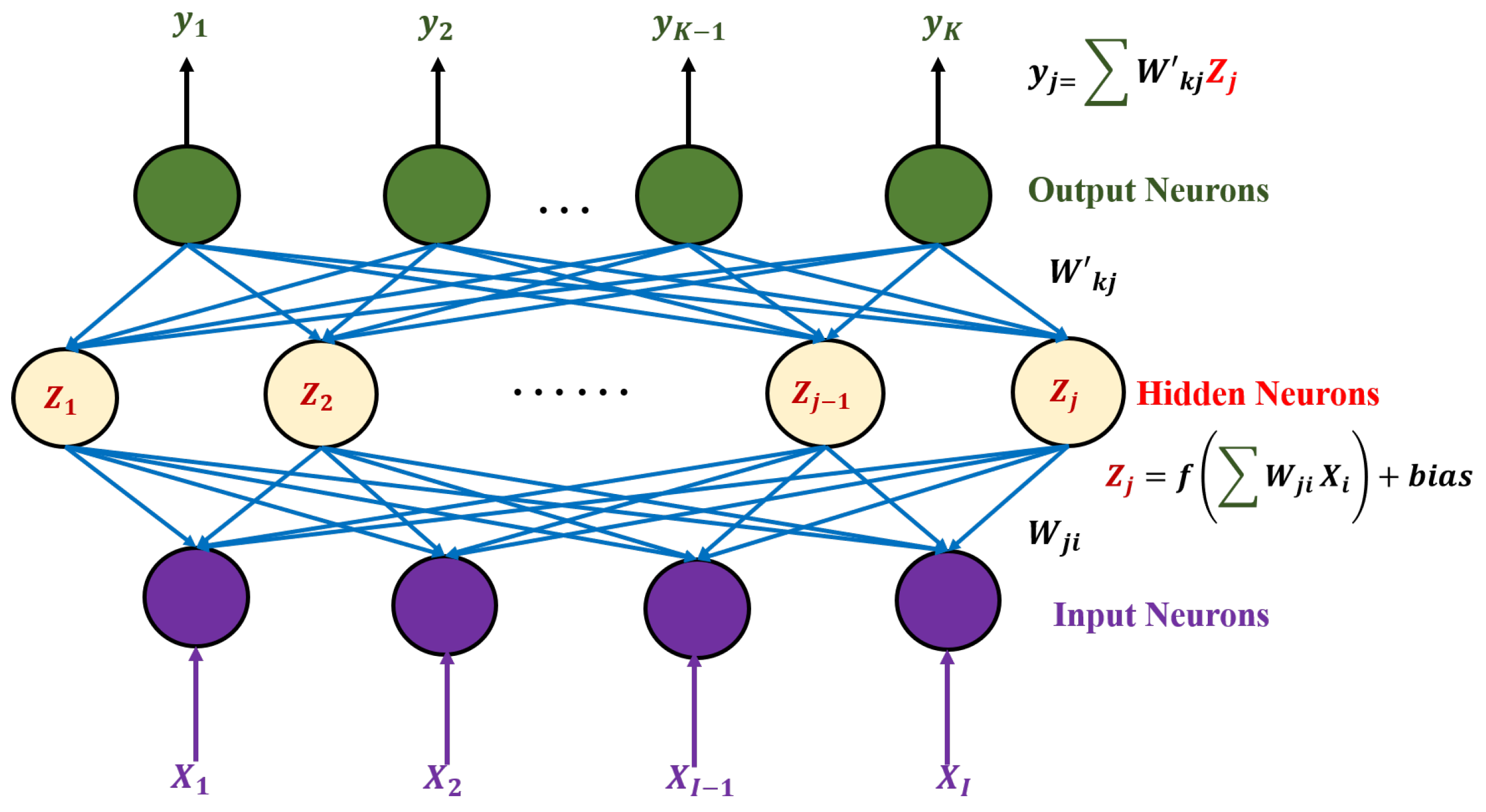
The most popular deep learning is now based on the use of neural networks, so here we start with a summary of different neural networks that have been widely used in OPM and MFI in short-reach optical communications. ANN can be used to model the general relationship between the input and output data sets and are simple to implement [84,89]. The initial application of ANN in OPM can be traced back to 2006, which was used for the OSNR monitoring. It combines wavelet transform (WT) and ANN attributes to detect and classify fast power transients in optical networks [90]. The typical structure of an ANN is shown in Figure 4. The ANN model simulates the electrical activity of neurons in brains and the nervous systems. Generally, processing elements (neurons) are arranged in a layer or vector, and the output of one layer is used as the input of the next layer. A neuron can connect to all or part of the neurons in the next layer. Synaptic connections in the brain are modeled by these connections. The weighted data signal that enters the neuron mimics the nerve cell’s electrical excitation to simulate information transfer in the network. The input value of the processing unit is multiplied by the connection weight , which simulates the learning in ANN by adjusting the strength or weight of the connection. The input-output relationship is then modeled as a more complicated model in the hidden layer under the influence of the activation function (e.g., sigmoid, tanh and Relu), whose input is multiplied by the weight and shifted by the bias, allowing the ANN algorithm to learn almost any function. The activation function f is applied as follows:
Then, a vector of summation function () is used to aggregate all of the weight-adjusted values to generate the output vector.
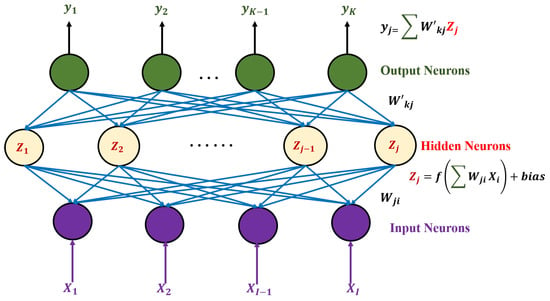
Figure 4.
ANN architecture.
An ANN with many hidden layers between its input layer and output layer is called a deep neural network (DNN). With the increase of unstructured data such as images and videos that need to be processed, feature engineering becomes more complex and time-consuming, making DNN a more powerful tool than the single hidden layer ANN. This is because the DNN can eliminate the need for manual feature engineering by self-learning through training. In 2016, a study showed that a DNN could learn the function of the feature extractor of the incoming digital-to-analogue converters (DAC) sampled signal without manual feature engineering and form itself as an OSNR estimator [63].
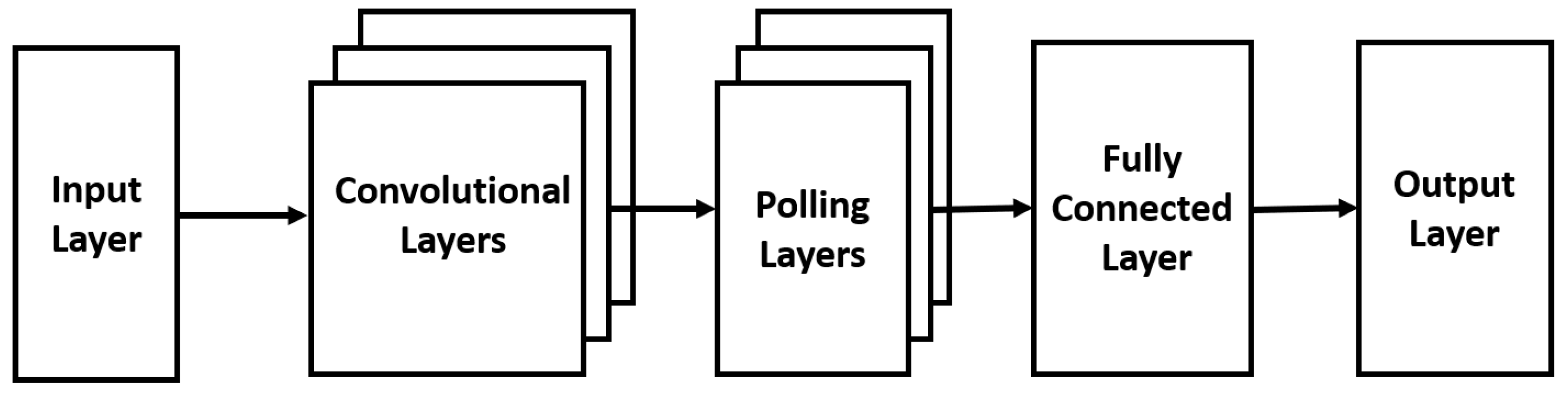
The ANN discussed above is also called the multi-layer perception (MLP) neural network. When the node in each layer is connected to all nodes in the next layer, it is referred to as the fully-connected neural network. In addition to MLP, another type of neural network that has been widely studied for high-speed OPM and MFI is the CNN, which uses one or more layers of convolution units. As shown in Figure 5, CNN is composed of several pairs of convolutional and pooling layers.
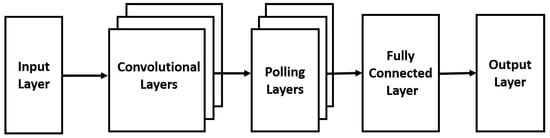
Figure 5.
CNN Architecture.
The function of the convolutional layer is to extract and learn spatial features in the input data, which is typically arranged into the matrix format. This layer is generated by applying a series of different filters to the input. These filters are called convolution kernels. The filter slides element by element on the input matrix to generate a filtered output of the same size as the input. Multiple kernels will produce different filtered outputs. For the convolution of an input matrix A with kernel F to produce a convolved output O, the process can be expressed as [91]:
CNN has been shown to be particularly suitable for image recognition and classification due to its ability of self-learning, which can automatically extract the features from different patterns without human supervision and prior knowledge [65,92]. Hence, CNN has been widely applied in OPM and MFI to process images such as eye diagrams, histograms and constellation diagrams.
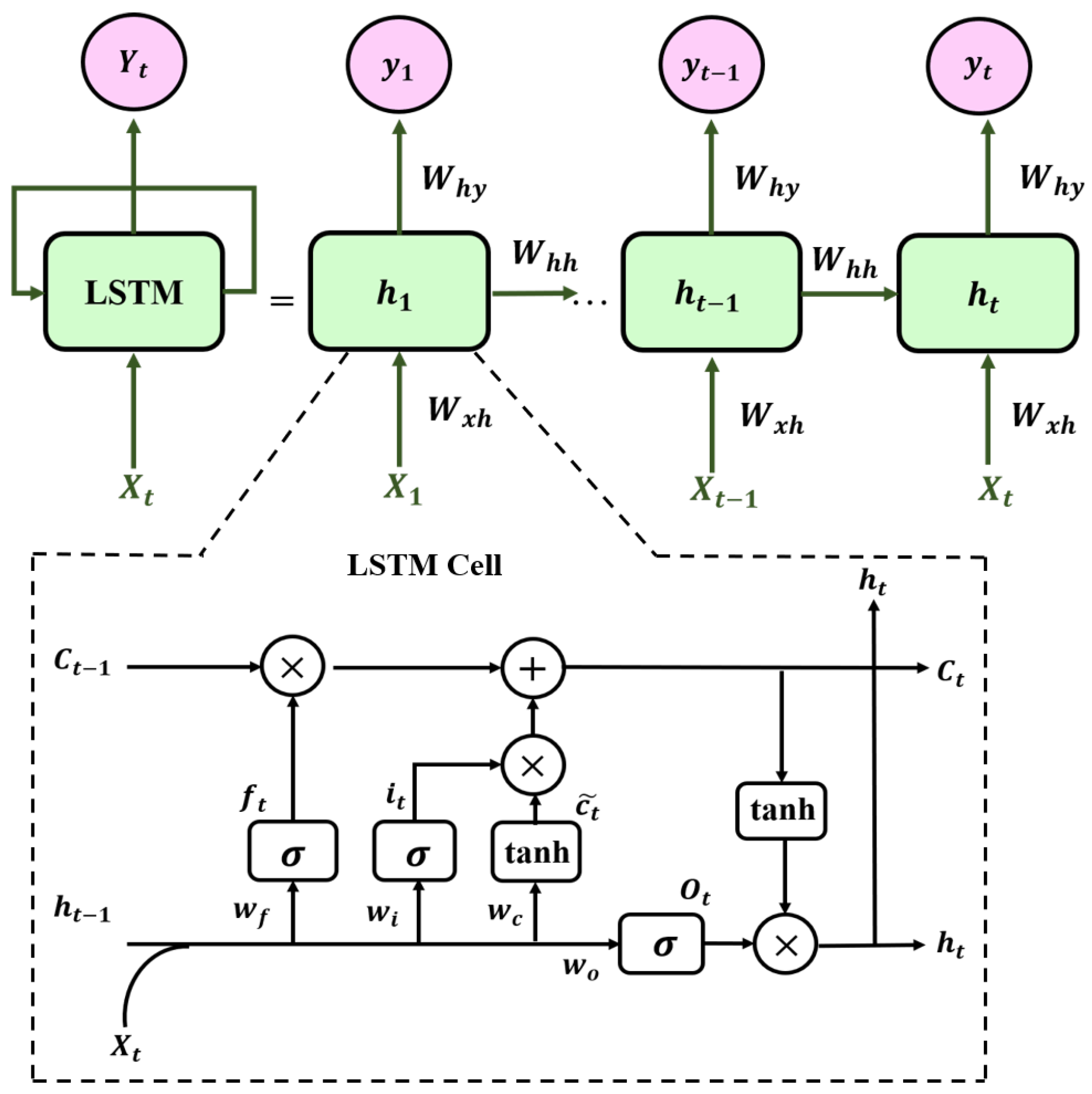
In addition to the MLP and CNN discussed above, RNN has also been studied for OPM and MFI in short-reach optical communication systems and networks. Different from the previous feedforward neural networks, RNN can maintain information from the previous input using its internal memory to affect the current input and output. In addition, RNN has good performance in the correlation modeling of time-varying data and is suitable for processing the signals of optical fiber communication systems received in the time sequence format. RNN has different architectures, and the long short-term memory (LSTM) is a special RNN that can model both long-term and short-term time dependence of time-varying data. The basic structure of LSTM is shown in Figure 6. At time t, the hidden state is updated according to the current input and the hidden state of the previous time step , which can be expressed as [89]:
where the weight between two successive hidden states is , the weight at the input neuron is , is the activation function and is the connection bias vector. LSTM uses three different gates (a forget gate, an input gate, and an output gate) in the LSTM cell (Figure 6) to control the information transmission, and internal self-loops to retain the long-term dependencies already learned from prior input data. Therefore, it can boost the modeling accuracy of long-term dependencies. The forget gate calculates the information about the cell state at time that needs to be forgotten at time t, according to and . The input gate then identifies what information needs to be updated, and the nonlinear function produces the unit input state . Then, the updated cell state at time t is calculated. Finally, the cell state is used to determine the output , which is then filtered by the output gate to produce the output sequence . The forget gate (), input gate (), output gate (), input state (), cell state () and hidden state () calculations at time t in the forwards pass of an LSTM cell are [89]:
where matrices , , are the weights between the hidden layer and the three gates, is the weight between the hidden layer and the input state, , , and are the bias, and ∗ is the convolutional operator. The activation function of the three gates are , which is typically based on a sigmoid function. In 2019, an OSNR monitoring scheme based on LSTM to evaluate the relationship of the time-varying data and the OSNR without the need for extracting features manually has been proposed and demonstrated [89].
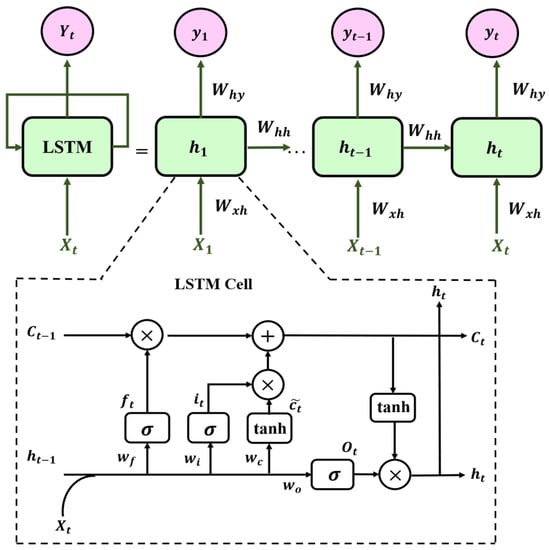
Figure 6.
LSTM network structure.
In addition to long-haul systems and networks, OPM and MFI technologies based on machine learning have also gained popularity in short-reach optical communication systems and networks recently. Due to the channel configuration, where the modulation format, symbol rate, interval and transmit power have become diversified, the ML technology has become a reliable tool, under the accumulated fiber propagation impairments during signal propagation [93]. Table 1 summarizes recent studies on ML-based OPM and MFI in short-reach optical communication systems and networks. Specifically, we listed key information of the system/network considered, the extracted feature used as the input to the ML models, and the ML model structures. In addition, key advantages and limitations of these studies are also summarized in the table.

Table 1.
OPM and MFI applications based on machine learning.
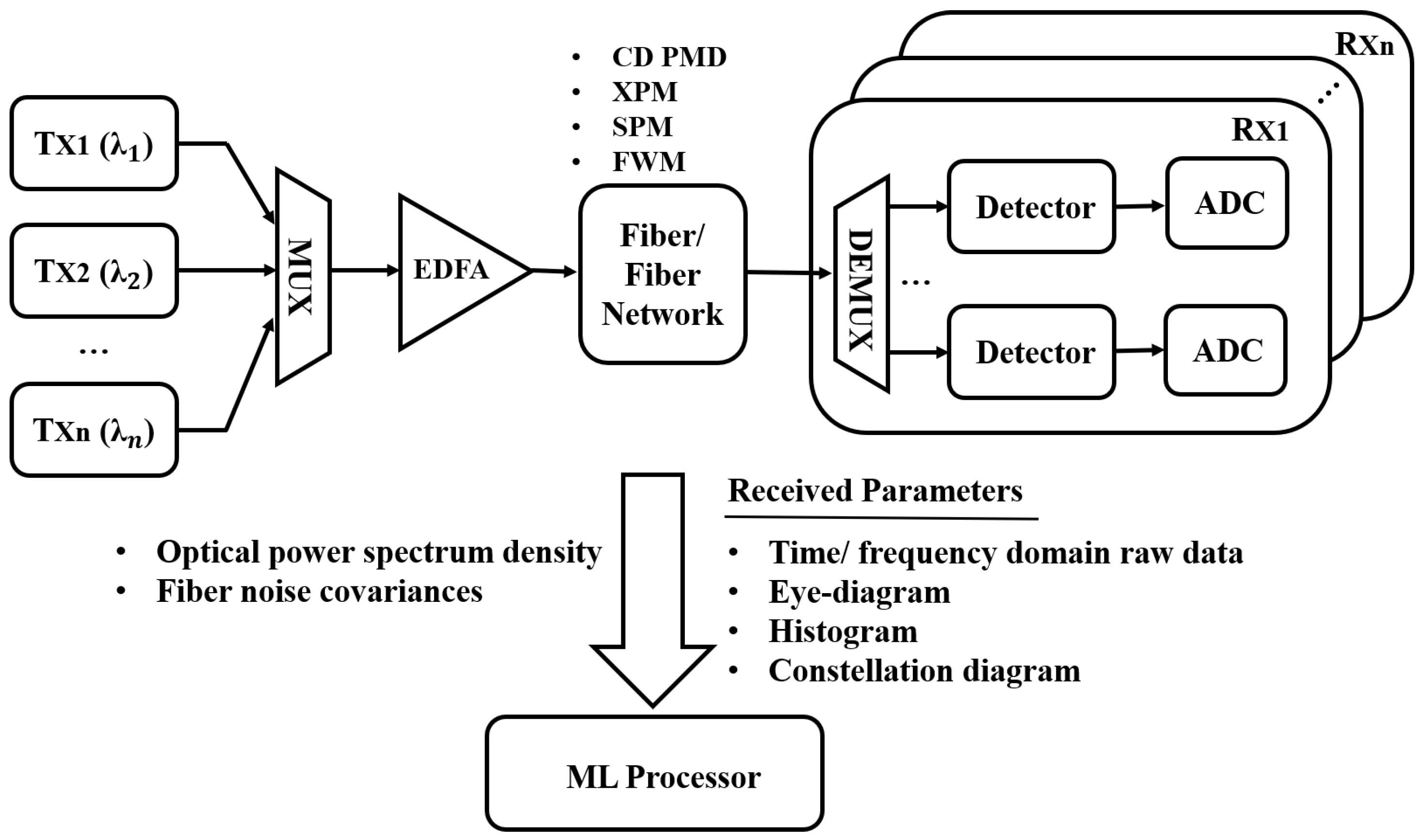
For easier overview and discussion, we classify the above approaches into direct detection and coherent detection categories according to their receiver detection method. The typical application of ML models in OPM and MFI in short-reach optical communications is summarized in Figure 7. At the transmitter side, the data to be transmitted is modulated onto the optical carrier, where both single optical carrier or multiple optical carriers via WDM can be used. The optical carriers are normally generated by laser diodes (LDs) and modulated using Mach-Zehnder modulators (MZMs). When WDM is used, the multiple output signals are then combined by the multiplexer (MUX) and can be optionally amplified by Erbium-doped fiber amplifier (EDFA) before being transmitted through the fiber or fiber network (e.g., PON). During the fiber transmission, the optical signals experience different types of impairments, such as CD and PMD dispersion, cross-phase modulation (XPM), FWM and SPM. After fiber transmission, the data-carrying optical signal is then demultiplexed (if needed in WDM) and detected by the photodetector using either direct or coherent receiver. The converted electrical signal is then sampled for processing via the ML model.
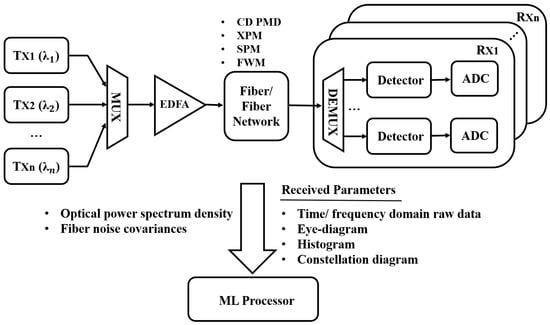
Figure 7.
Typical application of ML models for MFI and OPM in short-reach optical systems and networks; MUX: multiplexer; EDFA: erbium-doped fiber amplifier; ADC: analog to digital converter XPM: cross-phase modulation; FWM: four-wave mixing; SPM: self-phase modulation.
The ML studies can be split into two cases: the first case is using in-line data, such as OSNR, and the second case is using the received data at the receiver side. In the second case, most of the approaches require feature extraction generated diagrams such as the eye diagrams, histograms and constellation diagrams to train the ML algorithm. Some schemes do not require this step, where the raw received data are directly imported to the neural networks [92].
2.1. Direct Detection System
Direct detection is commonly used in short-reach optical communications, such as intra-/inter-datacenter linkages, metro, and access networks, due to its convenience for large-scale deployment, low-cost optical transceivers, and low power consumption [1,98]. The initial attempt to apply ML technology to the OPM in short-reach communications can be dated back to 2006. The authors apply the SVM and pattern recognition methods on eye diagrams to diagnose optical impairments, including CD, PMD and non-coherent crosstalk [50]. However, this approach requires noise filtering on the eye diagram before training, which increases the system’s complexity. Then in 2009, ref. [84] proposed a ML application on a direct detection system using ANN for OPM. 40 Gb/s RZ-OOK/RZ-DPSK signal is transmitted over a direct detection system. Eye diagrams of the received signal sampled by the oscilloscope are then generated, which are used as the input to the ML model. The ML model is based on the ANN, which has one hidden layer with 8 hidden neurons. The eye diagram is used to estimate OSNR, CD, and PMD. The mean squared error (MSE) is used during the training process, which can be expressed as [84]:
where and are the inputs and the desired outputs of the neural network, is the index sequence of the training data, is the element of and is the neural network output for input . Based on the experimental verification, the authors extended this approach to a WDM system for OSNR, fiber nonlinearity and dispersion measurement, where the average measurement errors of OSNR, CD and DGD are 0.77 dB, 4.74 ps/nm and 0.92 ps Gb/s for 40 Gb/s RZ-DPSK signal, respectively [84]. However, the input of the ANN comes from the eye diagram, which requires clock recovery and feature extraction, resulting in higher cost and complexity.
Based on prior studies that verified the feasibility of applying ML techniques for OPM and MFI, several multi-functional models that can provide both OPM and MFI simultaneously have been proposed. Ref. [99] proposed a multi-task model using SVM to perform MFI and ANN for OSNR monitoring on a 32 GBaud/s 64-QAM direct detection system. The SVM part for MFI is trained by the direct detected data, due to its kernel-based functions, which capture the similarities between any two pairings of raw input data. Meanwhile, the neural network part for OSNR monitoring is trained by eye-diagrams. Results show that the MFI accuracy is 94% and within the OSNR range of 4–17 dB, the mean OSNR estimation error is 0.2 dB.
Works like [99] require different ML models to implement MFI and OSNR monitoring separately. Hence, they have the drawbacks of high computational complexity and slow response. In [95], a multi-task deep neutral network (MT-DNN) has been proposed to monitor multiple optical performances in the system simultaneously. In this work, polarization division multiplexed QAM (PDM-QAM) signals are considered, and the asynchronous amplitude histogram after direct detection is selected as the feature input to the ML model. Using MT-DNN, simultaneous MFI, baud rate identification (BRI) and OSNR monitoring are realized. Since the OPM of this work contains multiple tasks, a weighted and hybrid loss function L is used in the MT-DNN, where the loss function of each OPM parameter is based on ether cross-entropy or MSE [95]:
where , and are the loss functions of MFI, BRI and OSNR monitoring, respectively, , and are the adjustable weights for the three tasks to optimize the overall monitoring results, m is the number of samples, is the actual output, and is the prediction from MT-DNN. The MT-DNN includes 5 layers with 80, 160, 80, 40, 6 neurons in each layer. The first three layers’ activation function is ReLU, whereas in the last two layers, softmax is used for BRI and MFI, and the linear function is used for OSNR monitoring. The accuracy rates of MFI and BRI can reach 100% and 96.8%, respectively [95]. However, the OSNR measurement range of this work is reduced when compared with previous works, limiting to 10–20 dB.
Meanwhile, ref. [65] also proposed a multi-functional ML model based on CNN, where MFI and OSNR estimation are realized simultaneously. Different from the use of asynchronous amplitude histogram [95], the eye diagram of the received signal is used as the feature input. Since CNN has the ability of self-feature extraction, it can process the eye diagram in its original form (the pixel value of the image) without having to know other eye diagram parameters (i.e., amplitude, eye histogram, jitter, rise time, fall time) or the original bit information. Therefore, the cost of manual intervention is reduced. In this scheme, the CNN consists of two convolution layers and two pooling layers. The outputs are then mapped into a one-dimensional layer, which is further fully connected to the output layer with 20 neutrons (4 for MFI and 16 for OSNR estimation) [65]. Results show that with 1600 training data, the OSNR estimation accuracy can reach 100%. In addition, 100% accuracy for MFI is also obtained with 800 training data.
2.2. Coherent Detection System
With the rapid technology development, the cost of coherent receivers is declining. In recent years, the application of coherent detection in short-reach optical communication systems and networks to improve spectral efficiency and data rate has also become a new development direction. For example, due to the high receiver sensitivity, frequency selectivity, and scalability, the coherent long-reach PON (LRPON) is regarded as a good choice for providing beyond 100 Gbit/s access, which typically targets at up to 20 km distance connection between the OLT and the ONU [59].
Several reported studies are showing the capability of ANN-based OPM and MFI for short-reach coherent systems [100,101]. In [101], the authors proposed a method based on the combination of ANN and AAH evaluation for OPM, and it can also identify the symbol rate and modulation format at the same time. The ANN model of this work consists of three layers, where there are 200 neurons and 25 neurons in the input layer and the hidden layer, respectively. The MSE was used to train the neural network to improve classification performance. The results reveal that this scheme can monitor CD in the range of 200–1600 ps/nm, with a DP-QPSK OSNR of 9–19 dB and a DP-16QAM OSNR of 14–26 dB. The estimation accuracy can reach after 40 training epochs.
However, the data set for training typical ANN-based OPM techniques is often manually selected [93,101], which limits the scalability to more broad signal sets with different symbol rates and modulation formats. The authors of [49] compared the effectiveness of various ML models for OSNR estimation and center wavelength detection of a QPSK coherent system with up to 80 km transmission distance by analyzing the OSA detected optical spectrum. Thirty optical pre-processed spectral data from 1551 to 1554 nm are collected as the training data set. Each spectral consists of 4096 samples. This work compared the training time and detection accuracy of four ML algorithms (k-nearest neighbor (KNN), decision tree (DT), SVM, ANN) with the same parameters. Results show that SVM has the highest estimation accuracy and lowest training time compared with KNN, ANN and DT. However, the author did not give the details of these ML models, such as the number of nodes in each layer of ANN and the loss function used.
In order to save the cost of feature extraction, a WDM system using the DNN trained with time-domain raw data for OSNR monitoring is proposed [94]. Since the multiple hidden layer units of DNN can automatically extract the input features for modeling complex data, the asynchronously sampled raw data from the coherent receiver is used as a feature vector for DNN training. The five layer DNN contains 2048 neurons in the input layer and is trained with 400,000 data obtained through experiments. Results show that the OSNR of a 16 GBaud/s DP-QPSK signal is successfully estimated with an average error of 1.23 dB and a range of 12 to 32 dB [94]. However, compared with the method based on the eye-diagram [101], the OSNR estimation error of this method is higher. In addition to the time domain data, the frequency domain raw data has also been explored for OSNR monitoring directly [66], where a CNN model is utilized in a single channel cohere system. The total number of training data is 1,000,000. The structure is a typical CNN consisting of an input layer, two convolutional layers, two pooling layers, and two fully connected layers (2048 nodes). The loss function for training is based on MSE. For different combinations of modulation formats and symbol rates (14- and 16-GBaud/s DP-QPSK, 16-QAM, and 64-QAM signals), the bias errors and standard deviations of the OSNR estimator are analyzed. Results show that the proposed OSNR estimator can achieve accurate estimation results with a 0.4 dB average error.
However, many ANN-, DNN- or CNN-based studies only considered the ASE noise or CD without the effects of fiber nonlinearity, such as SPM, XPM and FWM [66,84,94]. Furthermore, some of these studies are limited to single-channel systems [49,101]. Nonlinear distortion will accumulate as the fiber transmission distance increases, which is usually manifested as the crosstalk between symbols in the time domain and the spectrum broadening in the frequency domain. A method based on the LSTM network to estimate OSNR and nonlinear noise power simultaneously by using the strong long-term dependency capturing and learning capabilities of LSTM is reported, which is capable of extracting the relationship between historical and current data [97]. The proposed LSTM network has two hidden layers, each of which has double LSTM memory cells, and each cell contains 15 nodes. The coherent detected signal is translated to the frequency domain by fast Fourier transform (FFT) and then fed to the LSTM network to account for the interdependence of frequency components in a signal with nonlinear distortion. The linear function is employed as the activation function in the output layer of the LSTM network to produce the estimated OSNR and nonlinear noise power. The 5-channel system is simulated through VPI software, and results show that the OSNR estimation error is less than 1.0 dB, with the reference OSNR ranging from 15 to 30 dB for QPSK, 16-QAM and 64-QAM signals [97].
3. Machine Learning for Short-Reach Optical Communication System Signal Processing
DSP in optical communications has seen rapid and significant developments during the past couple of decades to compensate for various types of impairments, and the performance of optical communications has been substantially improved [78]. For short-reach systems, due to the widely use of receiver configurations based on the direct detection and other low-cost and small-size components, innovative signalling and DSP are critical to allow these components to reach their full potential and to meet the data rate demand in a cost-effective manner. ML-based techniques are considered to be a viable alternative to classic DSP due to their capability in solving nonlinear problems. For example, the neural network can be used to optimize the DSP function of the transmitter or the receiver [47]. In particular, in low-cost IM/DD short-reach optical fiber communication systems, where the combination of dispersion that introduces intersymbol interference (ISI) and nonlinear signal detection by a photodiode imposes severe impairments, the ML technique has been seen as a viable DSP solution to improve the system performance [1,102], where it has been applied in different manners, mainly including linear and nonlinear equalization, dispersion compensation, auto-encoder, and nonlinear predistortion, as summarized in Table 2. In this section, we review recent related studies.

Table 2.
Signal processing applications based on machine learning.
3.1. Machine-Learning-Based Equalizer for Short-Reach Optical Communications
With the increasing demand for higher speed and longer transmission distance, the impact of ISI, which can be caused by the bandwidth limitation of various devices/components and fiber dispersion, has become a critical limit in short-reach optical communication systems that leads to detection errors [82]. Therefore, a powerful equalizer is needed for high data rate applications. The digital feed-forward equalizers (FFEs) and decision-feedback linear equalizers (DFEs) are typically used. However, in IM/DD systems, due to the interaction among the square-law detection of PD, the laser/modulator chirp, the fiber dispersion and the additive noise, the overall channel response becomes nonlinear, making it difficult for the linear equalizer to perform accurate channel estimation and impairment compensation [103].
As a result, more complex approaches such as the maximum likelihood sequence estimation (MLSE) [112] and ML-based equalizers have been studied. ML techniques, especially neural networks, are now considered as a powerful equalization tool to compensate both linear and nonlinear distortions in optical communications. Some of them use neural networks as an aid to other signal processing steps, while others use the neural network directly as a one-stop equalizer. In these studies, the neural network has shown better performance than traditional equalizers, and hence, it becomes a very useful and popular technology for short-reach applications [113]. Among various proposed neural network architectures, the feedforward neural network (FFNN) [103,104,114], reservoir computing (RC) [82,106,111,115,116,117,118], and RNN [54,105] allow time-dependent processes (e.g., ISI) to be captured and learned effectively. Therefore, they are good candidates for the linear and nonlinear equalization of memory communication systems such as IM/DD systems [82]. Hence, this section will focus on the recent studies of using these neural network techniques for signal equalization in short-reach systems.
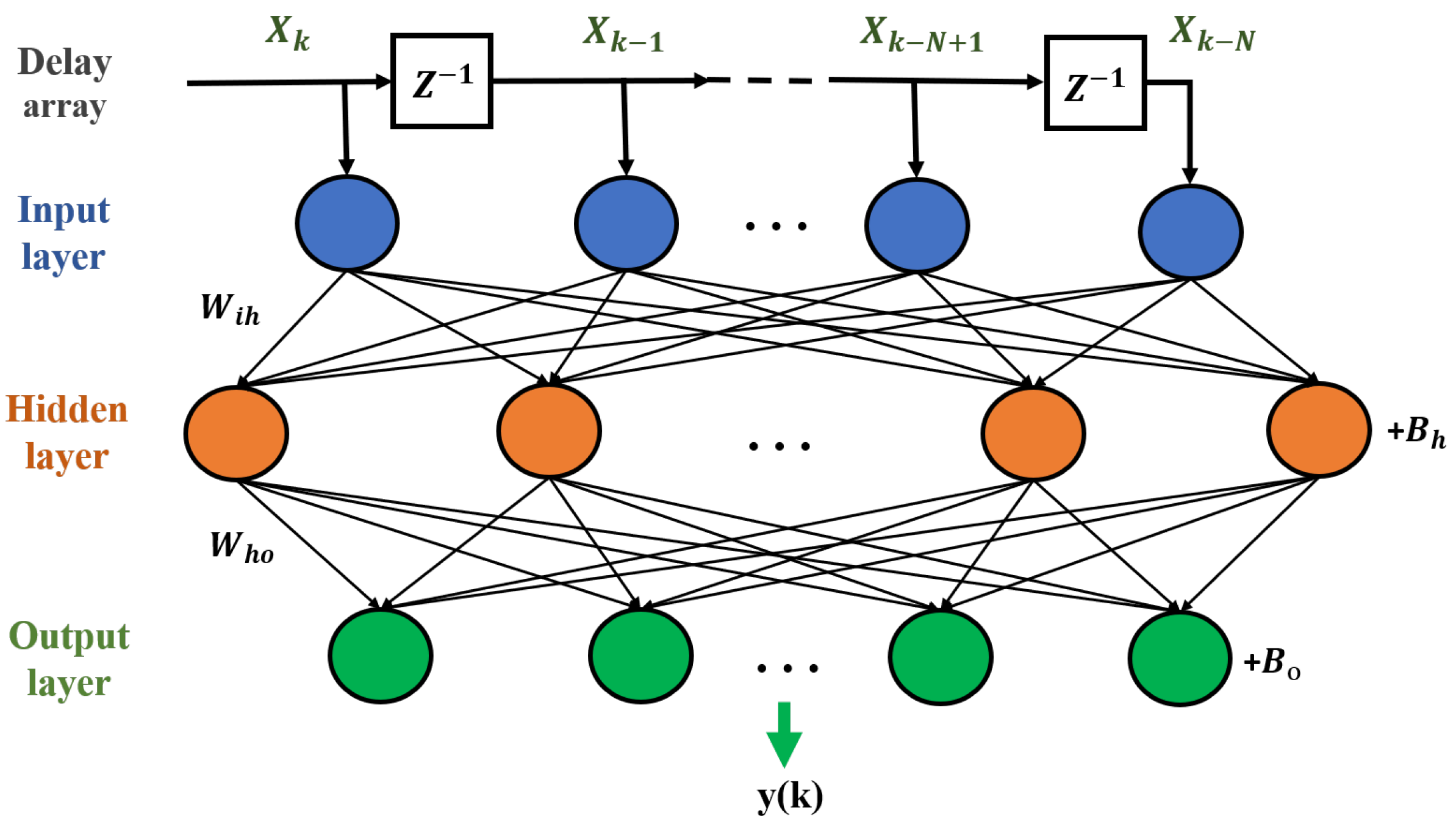
3.1.1. Feed Forward Neural Network Based Equalizer
FFNN has been widely used as the equalizer in short-reach optical communication systems. The FFNN used for equalization applications has the same neural network architecture as the ANN shown in Figure 4, but with a unique input data arrangement. The input of FFNN comes from a tapped delay line, which generates a delayed input time series data. Hence, we use FFNN to refer to the ANN with delayed time series data input when discussing ML-based signal equalization. Figure 8 shows the structure of an FFNN designed for signal equalization, in which the input of the ANN is fed with a time-delayed series of data received in the optical communication system. The FFNN consists of the input layer, the hidden layer and the output layer. Instead of feeding received data to the input layer directly, in FFNN, the sampled signals are fed into the input layer via the time delay array. Such an array creates different time delays, ensuring that FFNN understands both the current and the past information to conduct effective equalization. After the input layer, the received signal is further processed by the hidden layer with a nonlinear activation function to compensate for the nonlinearity in the optical communication system. Then, the distorted signals are reconstructed, and equalization coefficients are obtained at the output layer. The mathematical expression of the FFNN process is:
where is the input signal sequence, is the weight matrix between the input layer and the hidden layer, is the weight matrix between the hidden layer and the output layer, and are the bias metrics of hidden layer and output layer, and f is the activation nonlinear function of the hidden layer.
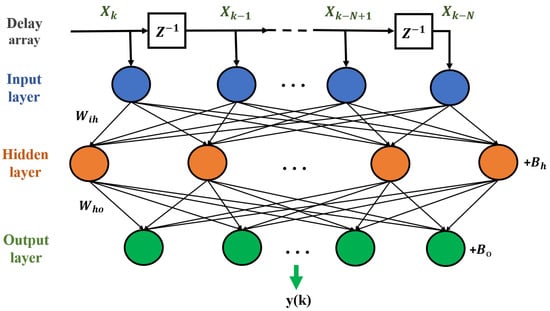
Figure 8.
Feedforward neural network structure.
A nonlinear equalizer based on FFNN has been proposed in an optical communication system with direct detection receivers. A radial basis function (RBF) network, which is based on the FFNN structure, is utilized to perform signal equalization to compensate the dispersion in the system [114]. The RBF method is a nonlinear equalization technology, and it takes the nonlinear transformation function of the photodetector into consideration. Hence, it is well suited for short-reach optical communications, where low cost square-law direct detection is normally used. In this study, the input function of the RBF model is expressed as:
where r is a real vector space with m dimensions expressed as . Then, the expression of output layer after hidden layer is obtained by a to R (scalar) mapping:
where … are the weights of the connections between the hidden layer and the output layer, and the nonlinear activation function is implemented by the hidden nodes , . The nonlinear function selected by this work is:
where is nonlinear function’s input parameter, are the RBF centers, and are positive scalars known as width. In the space, the characteristic of nonlinearity has a response with a radially symmetric shape around the center. In this study, the RBF equalizer is implemented offline and experimentally verified in the on-off keying (OOK) system. Results show that RBF equalizer obtained approximately one order of magnitude lower BER than FFE at 20 dB SNR over up to 100 km fiber length.
Whilst the study in [114] demonstrates the capability of FFNN, in a high-speed short-reach system, multi-level PAM is preferred compared with OOK due to the higher spectral efficiency. Hence, the capability of FFNN in the PAM-based high-speed short-reach optical communication system has also been studied [103], where 32 GBaud/s PAM-8 signal generated by an integrated electro-absorption modulated laser and transmitted over 4 km single mode fiber (SMF) has been equalized. The structures of the neural network-based equalizer is also an FFNN similar to Figure 8. The normalized least-mean-square (NLMS) algorithm minimizes the MSE of the training symbols. In this work, an FFNN with 9 input nodes is used. Results show a better equalization performance (50% lower BER at 2 dBm output power) is achieved compared with the 21-tap conventional symbol space linear FFE. However, this work assumes the channel is static, and the weights of the neural network and input layer time delay are also kept static. Thus, in reality, this FFNN model cannot adapt to possible channel changes over time.
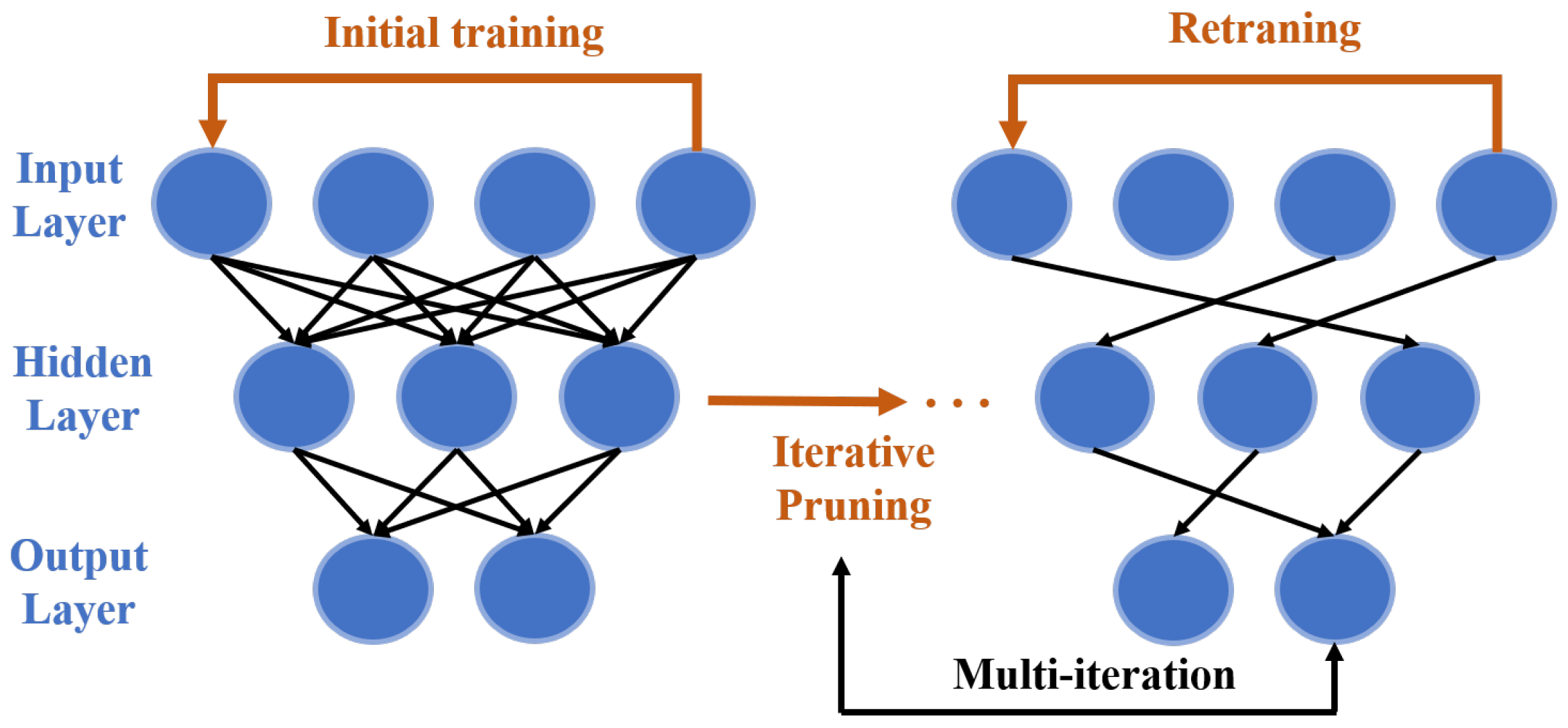
Whilst the capability of FFNN as the signal equalizer has been demonstrated, the complexity of the neural network is an essential practical hurdle that needs to be considered. This is particularly critical in short-reach optical communications due to the more stringent complexity requirement than long-haul transmissions. To reduce the complexity, a compressed neural network equalizer using the iterative pruning approach has been proposed and demonstrated [104]. The pruning procedure is shown in Figure 9, and it reduces the network complexity, whereas the retraining procedure restores performance lost as a result of the pruning. This process of pruning and retraining is conducted recursively, and a sparse neural network structure with few connections can be generated after a number of iterations.
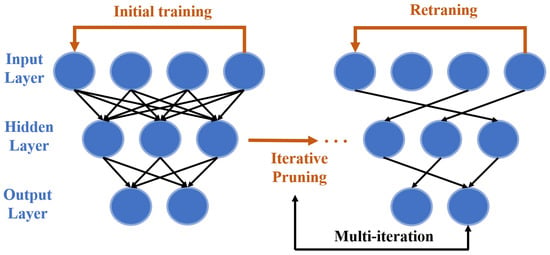
Figure 9.
Iterative pruning process of the compressed FFNN [104].
The compressed neural network is used as the equalizer in a VCSEL-based short-range system with 100 m MMF, and up to 112 Gbps PAM-4 or PAM-8 signals are transmitted. In the compressed neural network, the input and hidden layers have 51 nodes, and the output layer scale is decided by the modulation format, where 4 and 8 output nodes are used for PAM-4 and PAM-8 formats, respectively. The cross-entropy loss function was used to train the neural network to improve the classification performance. Rectified Linear Unit (ReLU), a prominent nonlinear activation function, was chosen as the activation function of a single hidden layer. Results reveal that, using the iterative pruning technique instead of fully connected FFNN, can result in a connection decrease of up to 71% at a BER threshold of [104]. When 2000 connections of the neural network are pruned, the BER of the one-time pruning and iterative pruning algorithms () is lower than that of a fully connected FFNN () in a PAM-8 back-to-back system. This is because that the network’s redundancy is reduced, and hence the network’s generalization ability is improved.
3.1.2. Reservoir Computing Based Equalizer
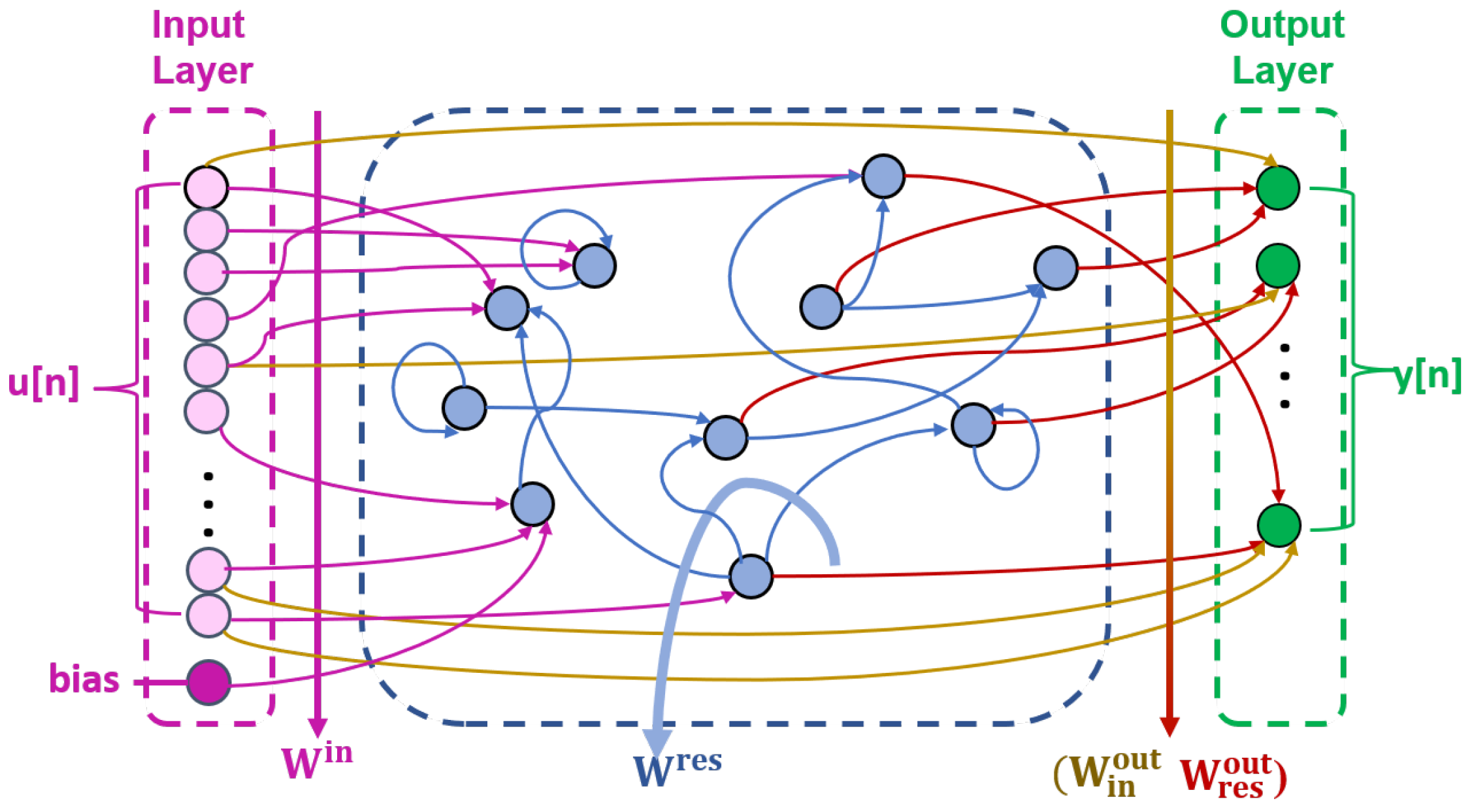
In addition to the FFNN-based equalizers, other types of neural networks have also been studied for signal equalization in short-reach optical communications. In this section, we review the use of RC, which can be considered as a highly redundant RNN with untrained input and hidden parts of the network (reservoir) [82]. RC enables the effective training of the entire neural network by optimizing only the output weights with a single linear regression step, and hence, it avoids typical training problems such as the vanishing gradient problem of typical RNN. The typical structure of the RC based equalizer is shown in Figure 10, and it also consists of the input layer, the hidden layer and the output layer.
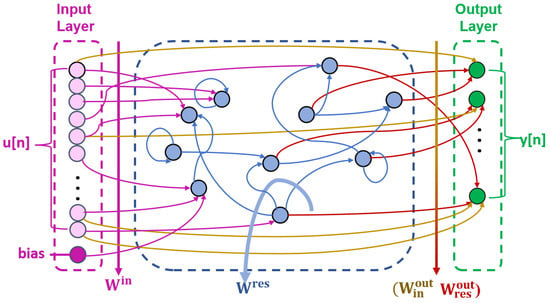
Figure 10.
Reservoir computing general architecture.
Because it resembles nonlinear dynamical systems, the hidden layer is called a reservoir. The inputs are injected into the reservoir via the linear transformation and they drive the reservoir states , which are characterized by the recurrent interconnections within the reservoir and output interconnections [82,116]. Therefore, the reservoir states can be expressed as:
where is the chosen nonlinear activation function and (0 < < 1) is employed to simulate an exponential decay within the reservoir to meet the echo state requirement and replicate realistic physical implementations [118]. The direct connection between the input and the output layers is characterized by . Then, the expression of output layer vector is derived as:
RC are promising tools for channel equalization in short-reach optical communications. In [116], RC are combined with the optical pre-processing, which divides the received optical signal into small sub-bands using an arrayed waveguide grating before entering the PD. RC is then utilized for digital post-processing at the receiver after photodetection. The output layer of this RC model is trained through linear regression with time domain sequences. In this study, 32 GBaud/s OOK modulated signal was transmitted over up to 60 km optical fiber. Compared with the more complex MLSE or FFNN based equalizers, results show that the proposed RC scheme can achieve a compensation distance increase from 10 km to 40 km under 1 dB SNR penalty threshold.
In [117], RC has also been used to achieve channel equalization in a WDM-RoF system. In WDM-RoF systems, due to the linear fiber distortion caused by dispersion, the fiber nonlinearity due to the Kerr effect, and the inelastic scattering of signals, the adjacent channel power ratio (ACPR) performance typically becomes worse after transmission. ACPR refers to the ratio of the overall power of the adjacent channels (i.e., inter-modulation signal) to the power of the main channel (i.e., useful signal), and it is a widely used parameter to characterize the performance of the WDM-RoF system. To overcome the degraded ACPR, RC has been utilized. According to the simulation results, the RC model with 500 nodes can generate 6∼9 dB ACPR gain in a WDM-RoF system. More significantly, the gain is directly proportional to the number of reservoir nodes within a range of 400–800 nodes. As a result, merely increasing the reservoir size can increase performance even further.
3.2. Other Machine-Learning Based Signal Processing Applications for Short-Reach Communication Systems
In addition to serving as the signal equalizer, the ML-based technique has also been extended to other types of signal processing applications, such as auto-encoder [67,109,119,120], digital predistortion [108,121] and soft-demapping [110,122]. In this section, we review recent studies of these ML signal processing applications in short-reach optical communications.
3.2.1. Auto-Encoder
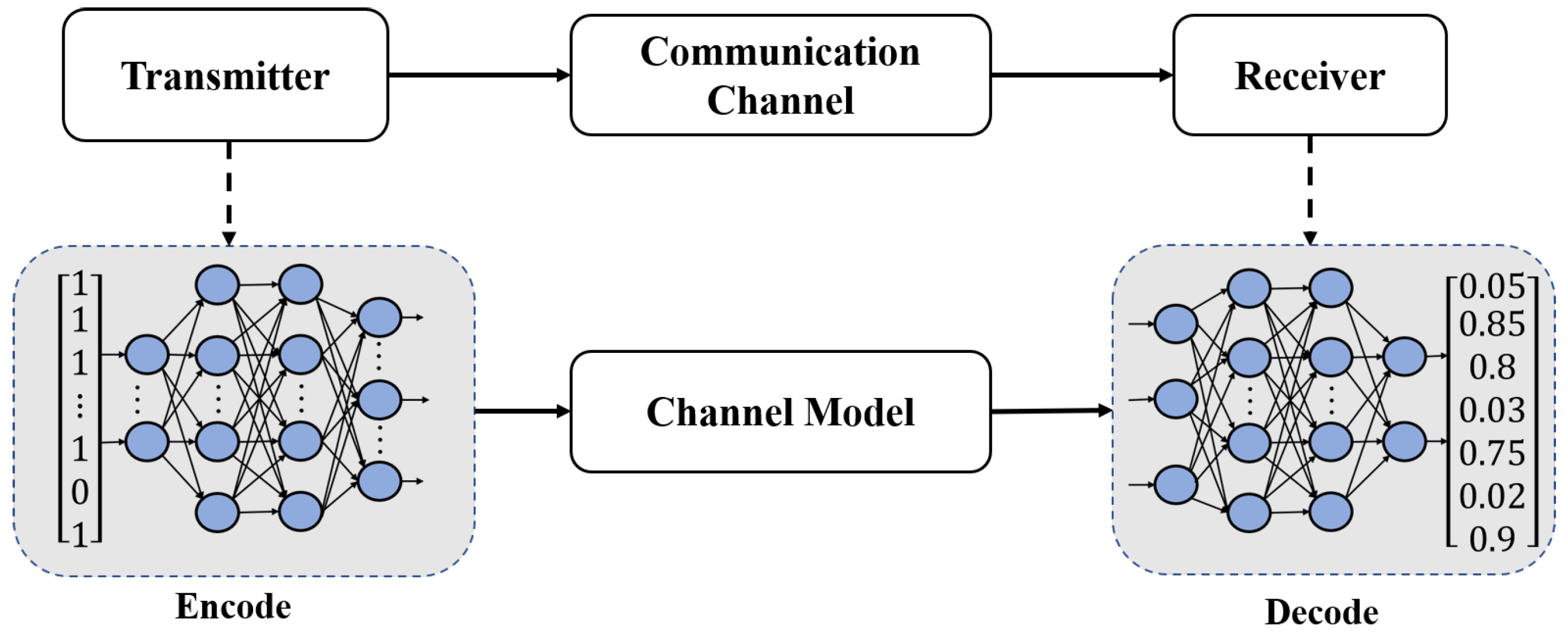
In addition to dealing with the impairments of individual components or sections in optical communication systems, the ML technology can also enable us to construct a communication system by jointly optimizing the transmitter, the receiver and the communication channel in a single end-to-end process. This provides a method to interpret the entire communication system as an auto-encoder [109]. The structure of a fully-connected neural network based auto-encoder is shown in Figure 11.
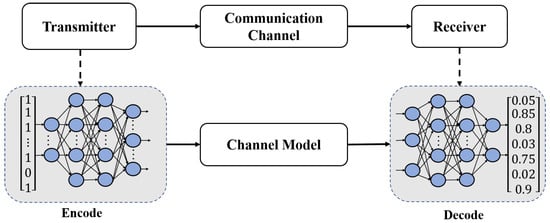
Figure 11.
Implementation of end-to-end system learning using the neural network-based auto-encoder.
The encode and decode sections are the two main parts of the auto-encoder. Encode is used to lower the input dimension, while decode is used to restore the reduced dimension code. The coding process keeps the primary features after dimension reduction, which can effectively reduce the transmission rate and improve the communication system’s reliability [67].
An auto-encoder for the IM/DD systems has been proposed and demonstrated based on the fully connected neural network and the bidirectional LSTM (BiLSTM) channel model [109]. The time domain optical signal characteristics are used, and various factors in the system are incorporated, including the nonlinearity, dispersion, attenuation, and optical-to-electrical square-law conversion. The BiLSTM, which consists of two LSTM sequences in opposite directions, allows bidirectional information to be captured. The BiLSTM network consists of four layers: the input layer, the BiLSTM layer, the hidden layer (a fully connected layer), and the output layer. The input layer consists of 51 neurons for seven classes of optical signals at different transmission distances from 20 to 80 km. The BiLSTM layer has three sub-layers, with each layer containing 32 neurons (16 in each direction). The loss function for training is based on cross-entropy. Using the time domain data for training, the proposed auto-encoder successfully models the channel with variable fiber transmission distance. Simulation results show that the proposed auto-encoder model can achieve one order-of-magnitude lower BER than the traditional PAM-2 and PAM-4 systems with a simple FFNN equalizer at the fiber length of 80 km.
3.2.2. Digital Predistortion
Digital predistortion (DPD) is a method widely used in power amplifiers for both linear and nonlinear impairments compensations. DPD is often realized using Volterra-based algorithms that employ sophisticated indirect and direct learning architectures [121].
In order to find an alternative to the Volterra-based DPD method, a low-complexity DPD based on Extreme Learning Machine (ELM) is proposed, which has the capability of fast adaptive estimation and compensation for any MZM transfer function [108]. The low-complexity ELM-based DPD has been experimentally demonstrated based on an unamplified 40 km DCI link with 400 Gb/s dual-polarization 16-QAM signal. The ELM-DPD achieves the same link budget as the more sophisticated third order Volterra-based nonlinear equalizer. Additionally, an overall link budget gain of 0.85 dB, resulting in a total link budget of 19.1 dB, has been achieved over an unamplified 40 km link when ELM-DPD and Volterra post-equalizer were combined.
ML-based (FFNN-based) DPD has also been used to improve the power efficiency of RoF links for analogue optical front-haul applications [121]. The FFNN-DPD model is trained using the received signal after ADC. The capability of FFNN-DPD is compared with the Volterra-based DPD method in this work. Results show that when the input power is 0 dBm, the FFNN-based DPD reduces the ACPR required in the system by 22 dB, while Volterra based method only reduces it by 14 dB. Since a lower ACPR means the better efficiency of the power amplifier, the FFNN based DPD method improves the RoF link performance with lower complexity compared with the Volterra-based approach.
3.2.3. Soft Demapping
The soft-decision forward error correction (FEC) and higher-order QAM data transmission have been considered as feasible technologies for achieving high-speed and high-spectral efficiency in optical communication systems. In a fading transmission channel such as the optical fiber channel, the bit interleaved code modulation (BICM) is a feasible approach for integrating channel coding and digital modulation, where the modulation constellation can be chosen irrespective of the coding rate. The BICM block’s structure is made up of a series of forwards error correction (FEC) codes, bit interleavers, and constellation mappers [123]. The soft demapper, which evaluates the soft bit (L value), is an important part of the soft decision FEC-BICM system [110]. Due to the high complexity of the Volterra-based equalization, a soft neural network-based method for nonlinear equalization and soft-decision demapping has been presented as an alternative [76].
In [76], the soft DNN (SDNN) architecture is investigated as a solution for nonlinear equalization and soft demapping. The soft DNN design consist of 17 input nodes (8 previous symbols + the current symbol + 8 future symbols) and two hidden layers with 26 and 25 nodes, respectively. The outcomes are then fed into 3 output nodes. The training process is shown in Figure 12. In the training process, symbols , are transmitted through a coherent short-reach optical communication system. An observation value is presented to the SDNN-based demapper, which represents the output of several consecutive channels before and after the ith channel. The calculated soft bit represents the hard decision for soft-decision FEC decoding. If , then the bit is decided to be 0, and if , then it is decided to be 1. The absolute value of indicates the degree of confidence of the soft demapper in its decision. In this work, the bit-wise equivocation is used as the loss function [76]:
where b is the transmitted bit and is the output L value of the neural network. Experiments are conducted to assess the performance and complexity of the proposed SDNN. Back-to-back transmitted 92 GBaud/s data with dual-polarized 64-QAM is utilized. Under the 15% overhead FEC restriction, the proposed bit-wise SDNN equalizer is compared to the fifth-order Volterra equalizer. Results show that the computational complexity is lowered by 65% when the same performance is achieved. Under the same complexity, an OSNR gain of 0.35 dB is achieved using the proposed SDNN, and hence, the system performance is improved.

Figure 12.
Soft DNN model training process.
A bi-directional RNN based soft demapper (BRNN-SD) has also been proposed in [122], which has shown better functionality than the ANN based soft demapper [76,110] on modeling the nonlinear infinite impulse response due to its ability to exhibit temporal dynamic behavior of time sequences. The BRNN-SD model is trained with pre-processed digital signal (a repeated 4096 symbols constant amplitude zero auto-correlation based training sequence). The iterative training is based on gradient descent and the back-propagation method using the adaptive moment estimation (ADAM) optimizer. The loss function is also based on the bit-wise equivocation. The capability of the BRNN has been compared with the reference Volterra based DSP. In the back-to-back system with 92 GBaud/s dual-polarization 32-QAM signals, the proposed BRNN-SD matches the performance of the reference DSP with less complexity. When a 32 channels DWDM system is considered, where each channel has a data rate of 800 Gb/s (DP-32 QAM at 96 GBaud/s), the proposed BRNN-SD method outperforms the reference DSP on the signal recovery.
4. Machine Learning Applications for Indoor Optical Wireless Communication and Positioning
Indoor OWC technology emerges as a complementary method to RF based wireless communication systems with a number of attractive features, such as extremely broad bandwidth, license-free spectrum, high communication security and anti-electromagnetic interference [124]. Among indoor OWC technologies, both the visible and near-infrared spectra have been investigated [125], corresponding to the VLC system and the infrared system, respectively. The infrared system typically adopts the near-infrared LD as the light source and PD as the detector, which have broad modulation bandwidth. However, the deployment of additional infrared transceivers increases the cost, and the maximum power of LD is limited by the laser eye and skin safety regulations [31]. Furthermore, strict alignment between the infrared transmitter and the receiver is typically needed, due to the limited coverage area of light beam and the relatively small reception angular range of the receiver. In contrast, in VLC systems, LED is adopted as the transmitter, and hence, the existing infrastructures can be used to realize illumination and communication simultaneously. Among different types of VLC technologies, optical camera communication (OCC) has recently attractive a lot of interests since it harnesses camera as the receiver with unique features, such as the larger receiver field of view (FOV), spatial and wavelength separation ability and low cost [126,127].
4.1. Machine Learning Applications for Indoor Optical Wireless Communication System
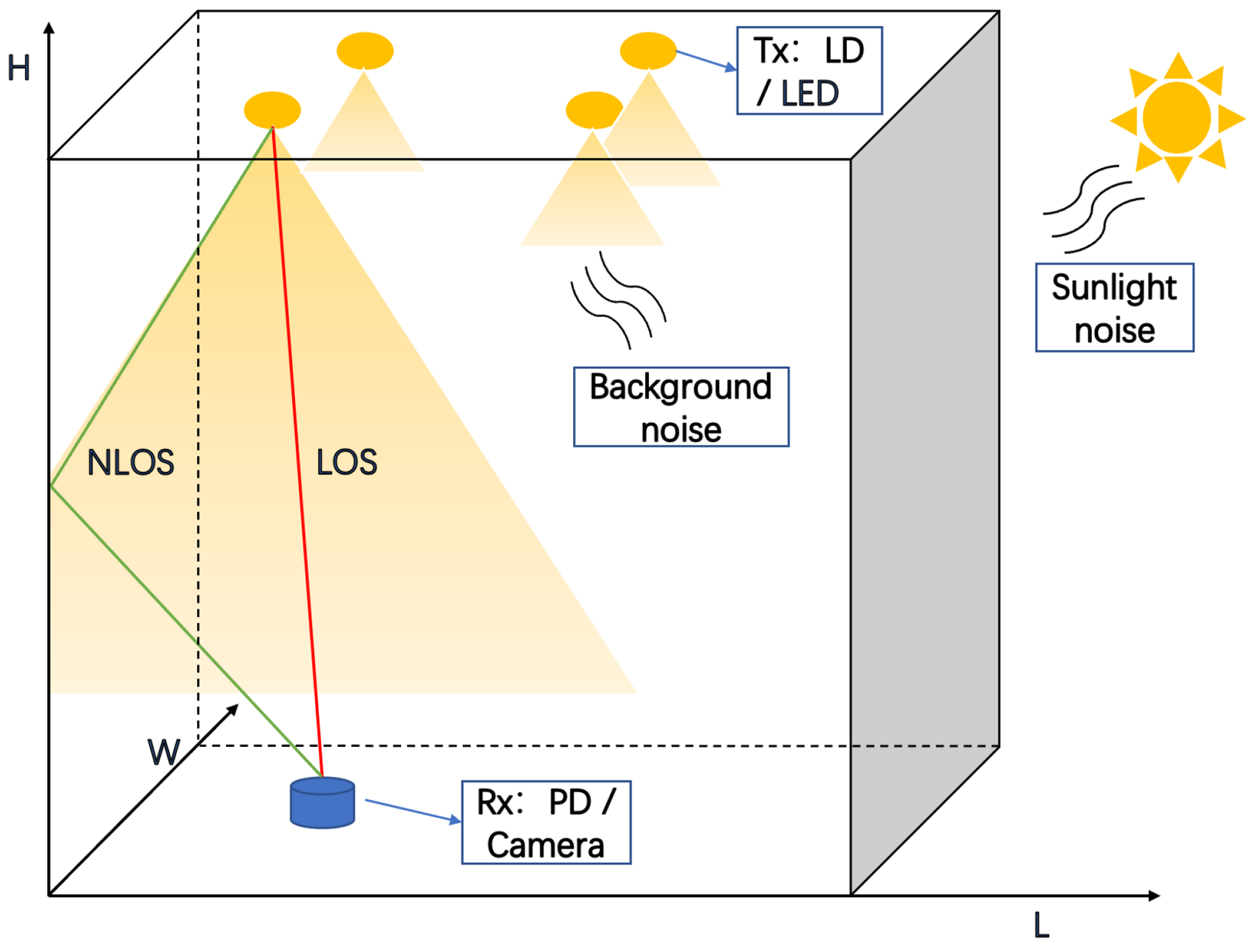
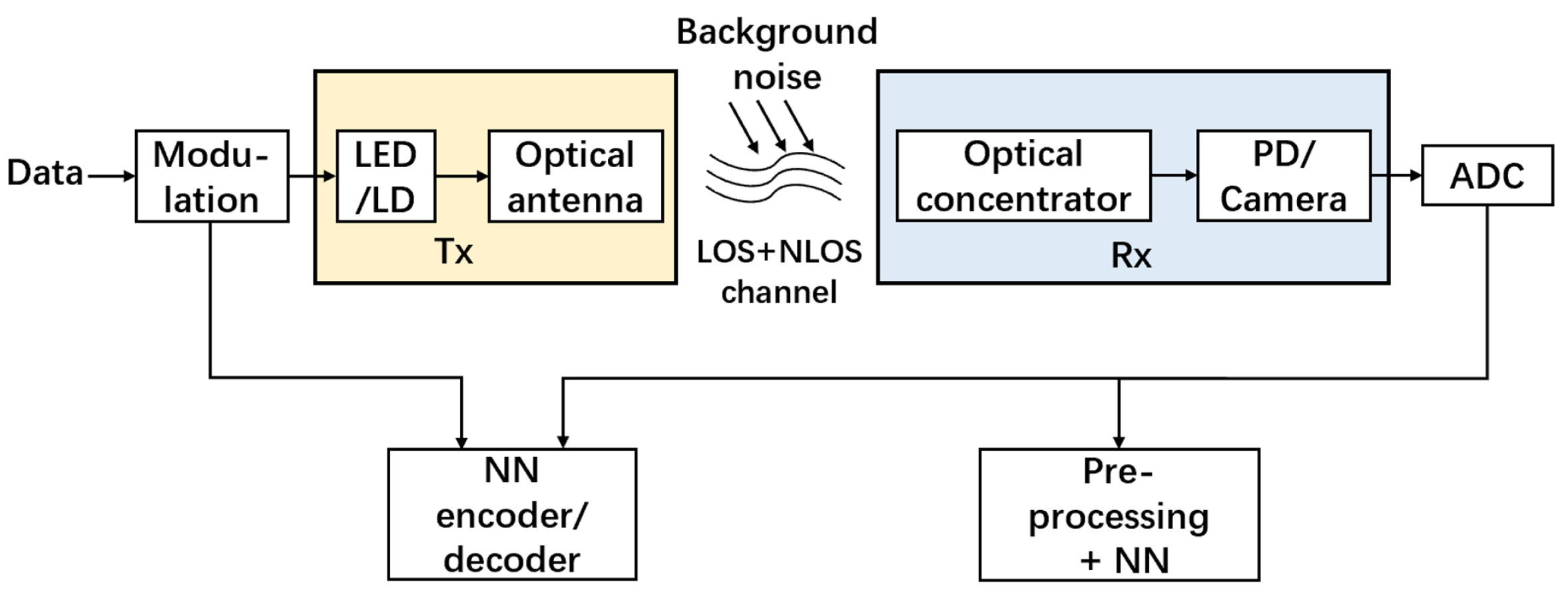
The typical structure of an indoor OWC system is shown in Figure 13, where both LOS signals and non-LOS signals can be used for the wireless data transmission. The background light normally comes from the sunlight or illumination lamps, and it leads to the additional noise of the received data. The limitations imposed by the channel, such as the path loss, ambient noise, inter-symbol interference and multipath propagation, normally affect the system performance. To solve these limitations and to improve the system performance, recently the use of ML technique has been proposed and studied, which has shown outstanding capability.
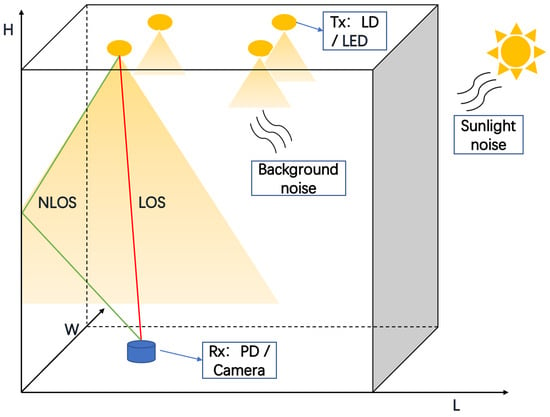
Figure 13.
General architecture of indoor OWC systems.
The typical applications of ML in indoor OWC systems are shown in Figure 14. In indoor OWC systems, the ML technique has mainly been used in two ways: ML-based encoder/decoder and ML-based signal processor.
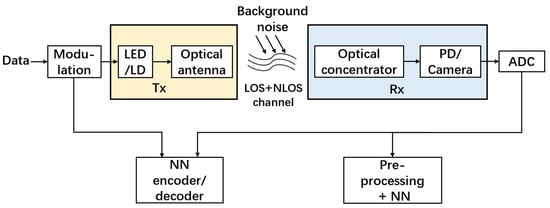
Figure 14.
General applications of ML in indoor OWC systems.
4.1.1. Machine Learning Applications for Indoor Visible Light Communications
As the encoder/decoder, the paper [128] focused on the design of convolutional autoencoder (C-AE) to support the multi-carrier OFDM based OCC system. In the encoder network, one-hot vector that comes from the quantizer passes through the neural network, which includes two dense layers with the ReLU activation function, two convolution and max pooling layers, and another convolution layer with the sigmoid activation function. In the decoder network, the reverse order of the neural network structure is implemented. The results yield a 100% and 99% accuracy at the SNR of 10 dB for 16 QAM and 64 QAM transmitted signals, respectively.
The ML technique is more widely used as the signal processor in indoor VLC systems. A memory-controlled deep LSTM neural network post equalizer to mitigate both linear and nonlinear impairments in a high-speed PAM-based VLC system has been studied [129]. The proposed post equalizer has a hidden layer consisting of a memory controlled deep LSTM neural network (32 layers), and a softmax function-based output layer corresponding to the modulation order. Experiment results show that compared with the conventional FIR-based equalizer, the Q factor can be improved by 1.2 dB using the LSTM-based post-equalizer, and the transmission distance is increased by over 30%. When further compared with the Volterra-based equalization nonlinear scheme, the complexity can be significantly reduced.
In [130], the researchers proposed a Z-Score Averaging neural network (Z-NN) algorithm to reduce the ISI in rolling shutter based OCC system. The raw gray-scale values in R, G, B channels are processed by the Z-score averaging algorithm [131], and then fed into the FFNN, which has a hidden layer with four neurons and a sigmoid activation function output layer. The cross-entropy loss function is used to update the weight parameters. Compared to the results of two classic methods, at a transmission distance of 2.5 m, the traditional Extreme-Value-Averaging (EVA) scheme cannot decode the received pattern, whereas the logistic regression scheme can satisfy the FEC threshold at 960 bit/s, and the Z-NN algorithm can further improve the bit rate to 1200 bit/s. The ISI in rolling shutter based OCC systems has also been suppressed using a more complicated two-dimensional CNN (2D-CNN) to further improve the data transmission performance [132]. This 2D-CNN takes extracted signals in R, G, B channels as the input, followed by two cascaded convolution layers with different numbers of kernels and kernel sizes. Each CNN layer also adopts the ReLU activation function and batch normalization to improve the performance. A fully connected layer with eight neurons is then used for classification, and the softmax function produces the probability distribution of the symbols. The experiment compares the BER performance obtained by the ANN, 1D-CNN and double-equalization [133] at different data rates, and results show the 2D-CNN has the lowest BER.
4.1.2. Machine Learning Applications for Indoor Near-Infrared Communication
In the studies reviewed above, they all use the visible light range for data transmission. In addition to VLC systems, the ML technique has also been explored in OWC systems using the near-infrared wavelength band. In high-speed near-infrared OWC systems, the spatial diversity scheme has been considered to overcome the channel blockage problem and to avoid possible communication interruptions. However, the delay between different channels may cause a severe ISI problem. The ML technique has been investigated to solve this issue, where the study [134] demonstrated a RNN-based symbol decision scheme to solve fractional symbol-period delays (i.e., delays less than one symbol period) induced ISI. The proposed RNN algorithm has three layers: the input layer (IL), the bi-directional LSTM layer (BL) and the output layer (OL). At the IL, each symbol sequence is divided into multiple groups, which are fed into the BL sequentially. BL consists of two LSTM sub-layers: a forward layer and a backward layer for learning the dependency among the data. Finally, the outputs from the BL are cascaded and passed through a softmax layer in the OL to obtain the symbol decision. The capability of RNN has been experimentally demonstrated, where more than one-order-of-magnitude BER improvement has been achieved when compared with traditional method (i.e., selecting the optimum sampling points), and the RNN also performs better than the previously studied FC-NN method.
To handle longer channel delays (i.e., delays more than one symbol period), an attention-augmented long-short term memory (ALSTM) RNN symbol decision scheme has been further developed [135], where an additional attention layer is added before the output layer. The attention layer keeps the states of LSTM cells at all processing steps, and hence, the dependencies among the received symbols can be better captured, especially among non-neighboring symbols. The ALSTM based method shows over one-order-of magnitude BER improvement compared with the RNN without attention layer.
In addition, previous studies mainly implement the ML algorithms using high-end GPUs, which are typically expensive and power hungry, limiting practice applications (particularly the short-range indoor applications). To solve this problem, a FPGA-based RNN hardware accelerator has been proposed for indoor near-infrared OWC systems [136]. Results show that compared with GPU-based implementations, similar BER performance can be obtained, while the latency and power consumption can be reduced by 61% and 58.1%, respectively.
4.1.3. Other Machine Learning Based Applications in Indoor OWC System
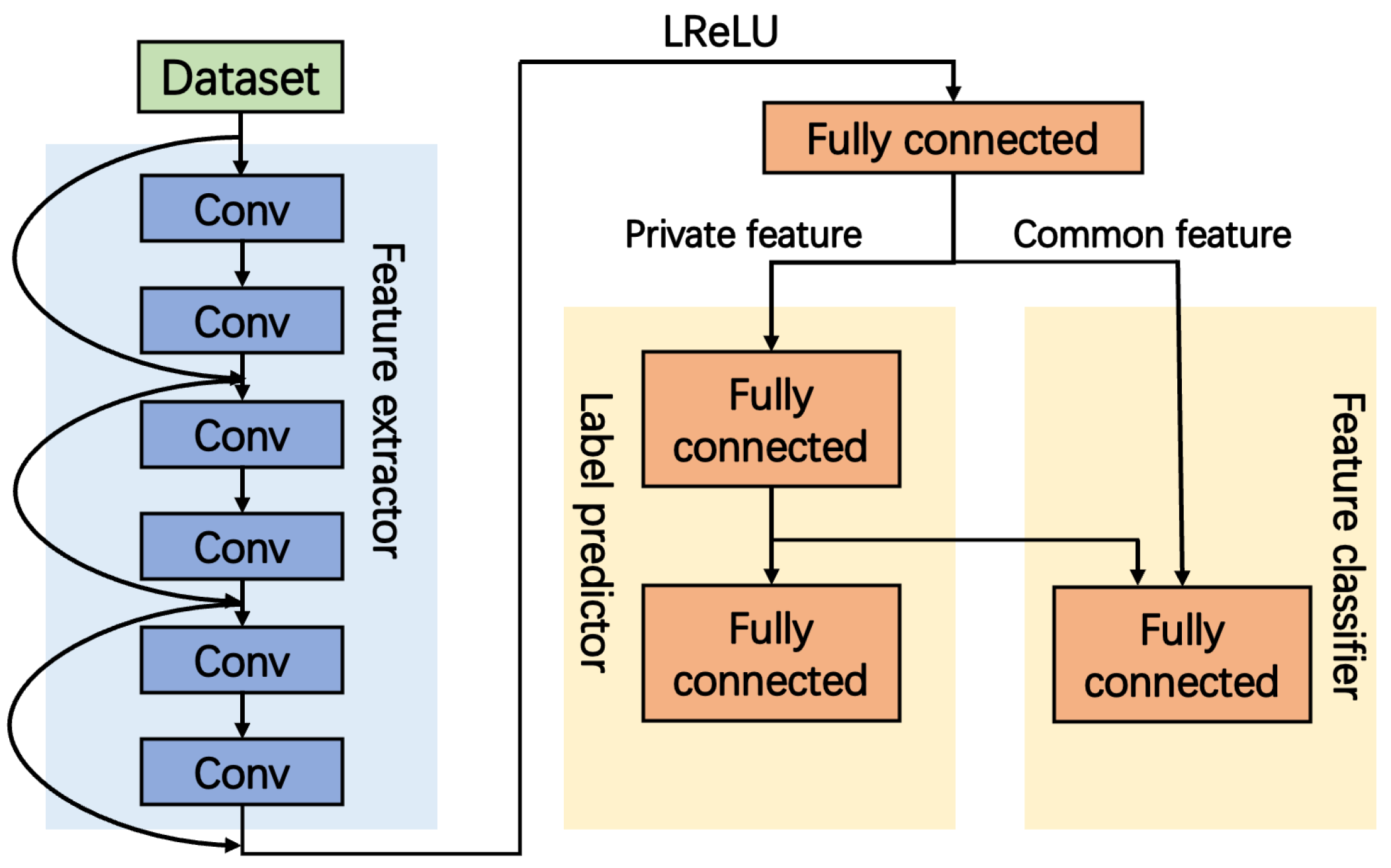
In addition to the applications mentioned above, which focus on signal processing, the ML technique has also been applied in other aspects of indoor OWC systems. In [137], a ML-based feature separation network for transmitter fingerprinting (TF-FSN) to distinguish illegal transmitters and to improve the physical layer security in the indoor VLC system has been proposed.
The proposed neural network structure is depicted in Figure 15. The feature separation network consists of three parts: the feature extractor (FE), the label predictor (LP) and the feature classifier (FC). The FE includes three residual stacks which contain two residual units, and each residual unit contains one convolutional layer, one batch normalization layer and one ReLU activation layer. Then, the outputs are fed into a fully connected layer for dimension reduction, whose output are further evenly divided as the inputs of the LP and FC, respectively. The LP works as a fully connected layer, which classifies the high-dimensional private feature into different labels. At the FC, a loss function with the soft subspace orthogonality constraint is used to optimize the training process, so that the interference of channel effects can be eliminated from the extracted private features. This algorithm is verified by experiment, showing 92.65% and 98% accuracy of identification and verification, respectively. The system also shows strong robustness at different distances over a wide range of SNR.
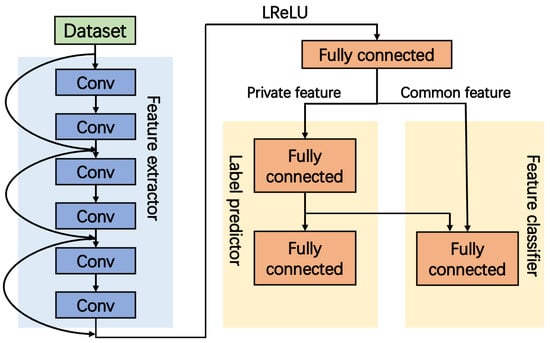
Figure 15.
The structure of the proposed feature separation network.
The ML technique has also been applied to the handover between LiFi access points (APs) and WiFi APs in a heterogeneous indoor wireless system, where a fully-connected neural network with one hidden layer is utilized [138]. Four features including the user’s speed, the separation between LiFi APs, the height of LiFi APs, and the number ratio between LiFi APs and WiFi APs are selected as the input parameters. The tanh activation function is used at the output layer to capture nonlinear effects in the system. Simulation results show that compared to the received signal strength (RSS)-based and trajectory-based handover methods, using the ML based approach can improve the user throughput by up to 260% and 50%, respectively. The Table 3 provides a summary of current ML based applications in indoor OWC system.

Table 3.
A summary of current ML based applications in indoor OWC system.
4.2. Machine Learning Applications for OWC Based Indoor Positioning
Nowadays, indoor localization is an attractive research topic due to its application in the location-based services, such as indoor navigation, opportunistic marketing and smart healthcare [145]. Since the Global Positioning System (GPS) in indoor applications suffers from severe attenuation and multipath dispersion, it is difficult to provide accurate position information. Therefore, alternative solutions have risen including RF-based and OWC-based methods [146]. For indoor localization, the RF-based methods such as Wi-Fi, Bluetooth, RFID and Zigbee have been widely investigated and applied [147]. However, due to the signal attenuation and multipath dispersion, the accuracy for RF-based indoor localization schemes is typically limited to several tens of centimeters. Compared to RF based techniques, the OWC based approaches can provide better accuracy in the centimeter scale and offer immunity to electromagnetic interference in sensitive environment, like hospitals and airplanes [148]. Similar with RF-based positioning systems, the OWC-based indoor positioning can be classified into three categories: the RSS, angle-of-arrival (AOA) and time-of-arrival (TOA)/time difference of arrival (TDOA) based approaches. For RSS-based methods, the received signal intensity reduces as the distance between transmitter and receiver increases, thus providing location estimation at the receiver side. TOA/TDOA explores the absolute or different time of signal arrival from the transmitter to the receiver to calculate the distance for localization. AOA refers to the propagation direction of light incident on the receiver for localization, which can typically be obtained from the image transformation and channel model [149].
However, the aforementioned approaches require precise channel models, accurate time synchronization and low background noise interference to realize accurate indoor localization. Compared to traditional OWC localization methods, the promising ML algorithms can bring better performance and efficiency to indoor OWC positioning applications. The Table 4 provides a summary of current ML based indoor localization performance.

Table 4.
A summary of current ML based indoor localization performance.
The study [150] proposed a TDOA based ANN method for two-dimensional indoor localization. The obtained time difference of the received signal from different LEDs works as the input feature to the ML model. A simple MLP algorithm is used to train the datasets, and a sigmoid activation function is used to map the actual position at the output layer. Simulation results show that 1.662 cm positioning error can be realized in a m room. In [151], the researchers demonstrated a two-layer ANN to achieve RSS-based three-dimensional indoor positioning. The RSS information is collected from three LEDs as the input of the ANN. The sigmoid activation function is applied in the two hidden layers, with 8 nodes and 5 nodes, respectively, and there is no activation function used in the output layer. The Adam optimization algorithm is adopted for training the proposed deep learning model. The measured results show that the average positioning error is less than 1cm within a m unit, which has been significantly improved when compared with the one hidden layer algorithm.
Currently, OWC-based localization schemes mostly assume the receiver and transmitter planes are parallel, which ignore the critical tilt angle of the receiver in practical scenarios. To address this problem, some researchers applied the inertial measurement unit (IMU) to measure the user equipment (UE) tilt angle for positioning [156]. However, the accuracy of IMU in indoor environment may not be guaranteed, and the extra device can increase the cost of the system. From this point of view, ML algorithms can provide a promising solution to estimate the orientation of receiver and to achieve better positioning performance. In [153], the authors employed two deep ANN models, one based on the MLP and the other based on CNN, to map the instantaneous received SNR to the user 3D position and the UE orientation efficiently.
Figure 16 illustrates the proposed simultaneous position and orientation estimation algorithm. For the proposed MLP, the pre-processed SNR of the received signals work as input features. There are d hidden layers where each hidden layer consists of the dense layer, ReLU layer, dropout layer and normalization layer. The proposed CNN has a similar structure except replacing the dense layer by the convolution layer. The output layer consists of six neurons, where each output neuron is related to one of the three position parameters and the three angle parameters (). Results show that for an indoor room with a size of m and considering both LOS and NLOS channels, when compared with the popular KNN algorithm, which achieves estimation accuracies of 29.5 cm, 17.7° and 3.925° for the position, , and , respectively, and the proposed MLP and CNN can realized better performance: the MLP algorithm can achieve 21.4 cm, 15.5° and 2.17°, respectively, and the CNN can achieve 17.15 cm, 12.5° and 2.136°, respectively. Besides, ref. [157] proposed a MLP algorithm to correct the position error caused by the tilt of the receiver in an OCC-based indoor positioning system, since when the tilt angle is different, the features like positions and shapes of the LEDs on the captured images are also different. At the input layer, five features of the projected ellipse image of the LEDs, including two position coordinates (), two axis parameters (major axis and minor axis) and the area, are fed into the MLP. The sigmoid activation function is used to map the nonlinear relationship between the input and the hidden nodes. The output feature is the distance between the transmitter and the receiver. Results show that with different numbers of hidden nodes 10, 30, and 50, the average positioning error is 3.6 cm, 2.1 cm and 1.9 cm, respectively, which significantly reduces the impact caused by the tilt camera.
Figure 16.
The structure of the proposed position and orientation estimation network.
So far, most papers of ML-based indoor OWC localization applications only focus on improving the accuracy of position, while ignoring the importance of LED-ID detection and recognition. In [158], the authors design a ML-based LED identity (LED-ID) detection and recognition method for visible light-based positioning systems. It adopts the pulse width modulation (PWM) method with different frequencies and duty cycles to create unique features for each LED, so that the unique pattern of the image can be captured by camera. Two typical linear classifiers, named fisher classifier and SVM, are applied to classify the captured bright and dark stripes patterns from different LEDs. Experimental results show that the proposed scheme can improve the ability of LED-ID detection to classify a large number of LEDs for large scale indoor positioning systems.
5. Conclusions
In this article, we have provided a comprehensive survey for the recent ML related research in short-reach optical communications (<100 km). This survey covers three fields of the state-of-the-art ML-based applications: OPM and MFI, signal processing and in-building/indoor OWC systems. The structure, advantages and limitations of these ML techniques have been discussed in detail. The emergence and development of ML techniques can save the cost of hardware and integration compared to non-ML techniques. In addition, ML-based OPM techniques are flexible and reconfigurable. Hence, it can adapt to dynamic and increasingly complex network structures and modulation formats. Furthermore, ML-based techniques have been developed to be no longer limited to a single function. In terms of OPM and MFI, some multi-functional approaches have been proposed to undertake the estimation of multiple OPM parameters and perform modulation formats classification simultaneously. In the field of signal processing, ML-based techniques are not limited to simple nonlinear equalization either. Auto-encoders that can optimize the system in an end-to-end manner are under study, and soft-demappers are under reach. In indoor OWC systems, the ML has shown excellent performance to solve the limitations such as pass loss, ambient noise and multipath propagation. For indoor OWC positioning systems, ML has been widely used to improve the position accuracy, realize simultaneous position and orientation estimations, and achieve the recognition of LED-IDs.
However, the capability of many ML-based applications to handle feature extraction and complicated analysis is restricted, which normally require manual feature engineering. As a result, the ML techniques based on multi-layer neural network architectures, such as CNN, DNN, and LSTM, have recently been proposed to automatically learn features from raw data. Nonetheless, these approaches require a large amount of data for training, and some of them need pre-processing the raw data to improve accuracy. The combination of ML technologies and domain expertise offers predictive potential in the absence of big data sets or incompletely representative data, and it may become the critical study direction in the future. On the other hand, ML-based techniques are sensitive to network environment changes. System instability or reconfiguration can result in the requirement of retraining the ML model. How to perform real-time efficient retraining is also an important research topic for future exploration.
Author Contributions
Conceptualization, Y.X. and K.W.; writing—original draft preparation, Y.X., Y.W.; writing—review and editing, Y.X., Y.W., K.W. and S.K.; supervision, K.W. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Australian Research Council (DP170100268).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AAH | Asynchronous Amplitude Histogram |
| ACPR | Adjacent Channel Power Ratio |
| AdaBoost | Adaptive Boosting |
| ADAM | Adaptive Moment Estimation |
| ADTP | Asynchronous Delayed Tap Sampling |
| AI | Artificial Intelligence |
| ALSTM | Attention-Augmented Long Short-Term Memory |
| ANN | Artificial Neural Network |
| AOA | Angle of Arrival |
| AP | Access Point |
| ASE | Amplified Spontaneous Emission |
| BBU | Baseband Unit |
| BICM | Bit Interleaved Code Modulation |
| BiLSTM | Bidirectional Long Short-Term Memory |
| BRI | Baud Rate Identification |
| BRNN-SD | Bidirectional RNN based Soft Demapper |
| BtB | Back to Back |
| C-AE | Convolutional Autoencoder |
| CD | Chromatic Dispersion |
| CNN | Convolutional Neural Network |
| Ch | Channel |
| CV-QKD | Continuous-Variable Quantum Key Distribution |
| DAC | Digital-to-Analogue Converter |
| DBN | Deep Belief Network |
| DCI | Data-center Inter Connection Link |
| DCN | Data-center Network |
| DFE | Decision-Feedback Linear Equalizer |
| DIFF | Difference between Pairs of Signal Strength |
| DNN | Deep Neural Network |
| DNN-LMS | Deep Neural Network-Least Mean Square |
| DPD | Digital Predistortion |
| DSO | Digital Storage Oscilloscope |
| DSP | Digital Signal Processing |
| DT | Decision Tree |
| DU | Digital Unit |
| EDFA | Erbium-Doped Fiber Amplifier |
| EEPN | Equalization Enhanced Phase Noise |
| ELM | Extreme Learning Machine |
| EON | Elastic Optical Network |
| FC | Feature Classifier |
| FC-NN | Fully Convolutional Neural Network |
| FEC | Forward Error Correction |
| FFE | Feed-Forward Equalizer |
| FFNN | Feed-Forward Neural Network |
| FFT | Fast Fourier Transform |
| FIR | Finite Impulse Response |
| FOV | Field of View |
| FPGA | Field Programmable Gate Array |
| FTTx | Fiber to the x, x = Home, Building, Curb or Node |
| FWM | Four-Wave mixing |
| HLF | Hyperbolic Location Fingerprint |
| IM/DD | Intensity Modulation/Direct Detection |
| IMU | Inertial Measurement Unit |
| ISI | Inter-symbol Interference |
| KNN | K-Nearest Neighbor |
| LD | Laser Diode |
| LDBP | Learned Digital Back Propagation |
| LED-ID | LED Identity |
| LOS | Line-of-Sight |
| LP | Label Predictor |
| LRPON | Long-Reach Passive Optical Network |
| LSTM | Long Short-Term Memory |
| MFI | Modulation Format Identification |
| ML | Machine Learning |
| MLP | Multi-Layer Perception |
| MLSE | Maximum Likelihood Sequence Estimation |
| MMF | Multi-Mode Fiber |
| MSE | Mean Squared Error |
| MT-DNN | Multi-Task Deep Neural Network |
| MUX | Multiplexer |
| MZM | Mach-Zehnder Modulator |
| NGFI | Next-Generation Fronthaul Interface |
| NLMS | Normalized Least-Mean-Square |
| NLOS | Non-Line-of-Sight |
| NRZ | Non-Return-to-Zero |
| OCC | Optical Camera Communication |
| OFDM | Orthogonal Frequency Division Multiplexing |
| OLT | Optical Line Terminal |
| ONU | Optical Network Unit |
| OOK | On-Off Keying |
| OPM | Optical Performance Monitoring |
| OSA | Optical Spectrum Analyzer |
| OSNR | Optical Signal to Noise Ratio |
| OWC | Optical Wireless Communication |
| PAF | Phased Array Fed |
| PAM | Pulse Amplitude Modulation |
| PD | Photo-detector |
| PDM-QAM | Polarisation Division Multiplexed Quadrature Amplitude Modulation |
| PDM | Polarisation Division Multiplexed |
| PMD | Polarization-Mode Dispersion |
| PON | Passive Optical Network |
| PWM | Pulse Width Modulation |
| QAM | Quadrature Amplitude Modulation |
| QoS | Quality of Service |
| QPSK | Quadrature Phase Shift Keying |
| RAN | Radio Access Network |
| RBF | Radial Basis Function |
| RC | Reservoir Computing |
| ReLU | Rectified Linear Unit |
| RF | Random Forest |
| RIN | Relative Intensity Noise |
| RNN | Recurrent Neural Network |
| RRU | Remote Radio Unit |
| RSS | Received Signal Strength |
| RZ | Return-to-Zero |
| SBS | Stimulated Brillouin Scattering |
| SDN | Software-Defined Networking |
| SDNN | Soft DNN |
| SMF | Single Mode Fiber |
| SPM | Self-Phase Modulation |
| SSB | Single Side Band |
| SSMF | Standard Single Mode Fiber |
| SVM | Support Vector Machine |
| SWDM | Shortwave Wavelength Division Multiplexing |
| SUI | Stanford University Interim |
| TDM | Time Division Multiplexing |
| TDM-PON | Time Division Multiplexing Passive Optical Network |
| TDMA | Time Division Multiple Access |
| TDOA | Time Difference of Arrival |
| TF-FSN | Transmitter Fingerprinting |
| TLFM | Two-layer Fusion Network |
| TOA | Time of Arrival |
| TWDM | Time and Wavelength Division Multiplexing |
| TWDM-PON | Time and Wavelength Division Multiplexing Passive Optical Network |
| UDWDM-PON | Ultra-Dense Wavelength Division Modulation Passive Optical Network |
| UE | User Equipment |
| VCSEL | Vertical-Cavity Surface-Emitting Laser |
| VLC | Visible Light Communication |
| WDM | Wavelength Division Multiplexing |
| WDM-PON | Wavelength Division Multiplexing Passive Optical Network |
| WT | Wavelet transform |
| XPM | Cross-Phase Modulation |
References
- Chagnon, M. Optical Communications for Short Reach. J. Light. Technol. 2019, 37, 1779–1797. [Google Scholar] [CrossRef]
- Kani, J.I.; Terada, J.; Hatano, T.; Kim, S.Y.; Asaka, K.; Yamada, T. Future optical access network enabled by modularization and softwarization of access and transmission functions [Invited]. IEEE/OSA J. Opt. Commun. Netw. 2020, 12, D48–D56. [Google Scholar] [CrossRef]
- Pang, X.; Ozolins, O.; Lin, R.; Zhang, L.; Udalcovs, A.; Xue, L.; Schatz, R.; Westergren, U.; Xiao, S.; Hu, W.; et al. 200 Gbps/Lane IM/DD Technologies for Short Reach Optical Interconnects. J. Light. Technol. 2020, 38, 492–503. [Google Scholar] [CrossRef] [Green Version]
- Yoo, S.J.B. Energy Efficiency in the Future Internet: The Role of Optical Packet Switching and Optical-Label Switching. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 406–418. [Google Scholar] [CrossRef]
- Koltchanov, I.; Sokolov, E.; Navitskaya, R.; Uvarov, A.; Richter, A. Multimode-Based Short-Reach Optical Communication Systems: Versatile Design Framework; SPIE OPTO; SPIE: Bellingham, WA, USA, 2020; Volume 11308. [Google Scholar]
- Yoo, S.J.B.; Yin, Y.; Wen, K. Intra and inter datacenter networking: The role of optical packet switching and flexible bandwidth optical networking. In Proceedings of the 2012 16th International Conference on Optical Network Design and Modelling (ONDM), Colchester, UK, 17–20 April 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, Y.; Lingle, R.; Shubochkin, R.; McCurdy, A.H.; Balemarthy, K.; Braganza, D.; Kamino, J.; Gray, T.; Fan, W.; Wade, K.; et al. SWDM PAM4 Transmission Over Next Generation Wide-Band Multimode Optical Fiber. J. Light. Technol. 2017, 35, 690–697. [Google Scholar] [CrossRef]
- Mestre, M.A.; Jorge, F.; Mardoyan, H.; Estaran, J.; Blache, F.; Angelini, P.; Konczykowska, A.; Riet, M.; Nodjiadjim, V.; Dupuy, J.Y.; et al. 100-Gbaud PAM-4 Intensity-Modulation Direct-Detection Transceiver for Datacenter Interconnect. In Proceedings of the ECOC 2016 42nd European Conference on Optical Communication, Dusseldorf, Germany, 18–22 September 2016; pp. 1–3. [Google Scholar]
- Le, S.T.; Schuh, K.; Dischler, R.; Buchali, F.; Schmalen, L.; Buelow, H. Beyond 400 Gb/s Direct Detection Over 80 km for Data Center Interconnect Applications. J. Light. Technol. 2020, 38, 538–545. [Google Scholar] [CrossRef]
- Xu, L. Photonic Devices and Subsystems for Future WDM PON and Radio over Fiber Technologies. 2010. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1x190jh0033m08w0u42c00t0ua323937&site=xueshu_se (accessed on 11 November 2021).
- Gupta, A.; Goel, H.; Bohara, V.A.; Srivastava, A. Performance Evaluation of Integrated XG-PON and IEEE 802.11ac based EDCA Networks. In Proceedings of the 2020 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), New Delhi, India, 14–17 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, D.; Wu, X.; Nesset, D. Progress of ITU-T higher speed passive optical network (50G-PON) standardization. J. Opt. Commun. Netw. 2020, 12, D99–D108. [Google Scholar] [CrossRef]
- 40-Gigabit-Capable Passive Optical Networks 2 (NG PON2): Physical Media Dependent (PMD) Layer Specification). ITU-T Recommendation G.989.2. 2019. Available online: https://www.itu.int/rec/T-REC-G.989.2/en (accessed on 11 November 2021).
- Bidkar, S.; Bonk, R.; Pfeiffer, T. Low-Latency TDM-PON for 5G Xhaul. In Proceedings of the 2020 22nd International Conference on Transparent Optical Networks (ICTON), Bari, Italy, 19–23 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Wong, E. Next-Generation Broadband Access Networks and Technologies. J. Light. Technol. 2012, 30, 597–608. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Kartsakli, E.; Papaioannou, S.; Kalfas, G.; Pleros, N.; Antonopoulos, A.; Verikoukis, C. Quality of Service Provisioning in High-Capacity 5G Fronthaul/Backhaul Networks. In Interactive Mobile Communication Technologies and Learning; Auer, M.E., Tsiatsos, T., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 797–804. [Google Scholar]
- Zhang, Z.; Zhang, B.; Chen, Y.; Hua, B.; Chen, X. Channel-reuse IMDD-based 40 Gb/s/λ 16-QAM Nyquist-SCM downstream and 20 Gb/s/λ Nyquist 4 PAM upstream WDM-PON. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016; pp. 1–3. [Google Scholar]
- Dutta, S.; Roy, D.; Das, G. Protocol Design for Energy Efficient OLT in TWDM-EPON Supporting Diverse Delay Bounds. IEEE Trans. Green Commun. Netw. 2021, 5, 1438–1450. [Google Scholar] [CrossRef]
- Dutta, S.; Roy, D.; Das, G. SLA-aware protocol design for energy-efficient OLT transmitter in TWDM-EPON. IEEE Trans. Green Commun. Netw. 2021, 5, 1961–1973. [Google Scholar] [CrossRef]
- Chanclou, P.; Neto, L.A.; Grzybowski, K.; Tayq, Z.; Saliou, F.; Genay, N. Mobile Fronthaul Architecture and Technologies: A RAN Equipment Assessment [Invited]. J. Opt. Commun. Netw. 2018, 10, A1–A7. [Google Scholar] [CrossRef]
- Liu, X.; Effenberger, F. Evolution of mobile fronthaul towards 5G wireless and its impact on time-sensitive optical networking. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–2. [Google Scholar]
- Hisano, D.; Maruta, K.; Nakayama, Y. Low Cost C-RAN and Fronthaul Design with WDM-PON and Multi-hopping Wireless Link. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Konstantinou, D.; Bressner, T.A.; Rommel, S.; Johannsen, U.; Johansson, M.N.; Ivashina, M.V.; Smolders, A.B.; Tafur Monroy, I. 5G RAN architecture based on analog radio-over-fiber fronthaul over UDWDM-PON and phased array fed reflector antennas. Opt. Commun. 2020, 454, 124464. [Google Scholar] [CrossRef]
- Wang, K.; Nirmalathas, A.; Lim, C.; Skafidas, E. High-Speed Optical Wireless Communication System for Indoor Applications. IEEE Photonics Technol. Lett. 2011, 23, 519–521. [Google Scholar] [CrossRef]
- Kavehrad, M. Sustainable energy-efficient wireless applications using light. IEEE Commun. Mag. 2010, 48, 66–73. [Google Scholar] [CrossRef]
- Manor, H.; Arnon, S. Performance of an optical wireless communication system as a function of wavelength. In Proceedings of the 22nd Convention on Electrical and Electronics Engineers in Israel, Tel-Aviv, Israel, 1 December 2002; pp. 287–289. [Google Scholar] [CrossRef]
- Wang, K.; Song, T.; Kandeepan, S.; Li, H.; Alameh, K. Indoor optical wireless communication system with continuous and simultaneous positioning. Opt. Express 2021, 29, 4582–4595. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Yu, H.Y.; Zhu, Y.J.; Sun, Y. On the Ergodic Channel Capacity for Indoor Visible Light Communication Systems. IEEE Access 2017, 5, 833–841. [Google Scholar] [CrossRef]
- Potortì, F.; Palumbo, F.; Crivello, A. Sensors and Sensing Technologies for Indoor Positioning and Indoor Navigation. Sensors 2020, 20, 5924. [Google Scholar] [CrossRef]
- Song, T.; Nirmalathas, A.; Lim, C.; Wong, E.; Lee, K.L.; Hong, Y.; Alameh, K.; Wang, K. Performance Analysis of Repetition-Coding and Space-Time-Block-Coding as Transmitter Diversity Schemes for Indoor Optical Wireless Communications. J. Light. Technol. 2019, 37, 5170–5177. [Google Scholar] [CrossRef]
- Jenila, C.; Jeyachitra, R. Green indoor optical wireless communication systems: Pathway towards pervasive deployment. Digit. Commun. Netw. 2021, 7, 410–444. [Google Scholar] [CrossRef]
- Mahmoodi, K.A.; Gholami, A.; Ghassemlooy, Z. Impact of Number of LEDs on an Optical Camera Communication Based Indoor Positioning System. In Proceedings of the 2020 3rd West Asian Symposium on Optical and Millimeter-Wave Wireless Communication (WASOWC), Tehran, Iran, 24–25 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Shahjalal, M.; Hasan, M.K.; Hossan, M.T.; Chowdhury, M.Z.; Jang, Y.M. Error Mitigation in Optical Camera Communication Based Indoor Positioning System. In Proceedings of the 2018 Tenth International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 3–6 July 2018; pp. 100–103. [Google Scholar] [CrossRef]
- Lin, B.; Tang, X.; Li, Y.; Zhang, M.; Lin, C.; Ghassemlooy, Z.; Wei, Y.; Wu, Y.; Li, H. Experimental demonstration of optical camera communications based indoor visible light positioning system. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Puntsri, K.; Kansaree, E.; Yindeemak, A.; Wongtrairat, W. Experimental Demonstration of Gbps OFDM with 13m long for OWC Systems. In Proceedings of the 2021 9th International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 10–12 March 2021; pp. 241–244. [Google Scholar] [CrossRef]
- Sharma, R.; Sharma, A. IS OWC WDM System Performance Optimization at 40 Gbps Bit Rate with Improved Link Distance of 10000 km. In Proceedings of the 2018 International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018; pp. 795–799. [Google Scholar] [CrossRef]
- Saif, W.S.; Esmail, M.A.; Ragheb, A.M.; Alshawi, T.A.; Alshebeili, S.A. Machine Learning Techniques for Optical Performance Monitoring and Modulation Format Identification: A Survey. IEEE Commun. Surv. Tutor. 2020, 22, 2839–2882. [Google Scholar] [CrossRef]
- Rafique, D.; Velasco, L. Machine learning for network automation: Overview, architecture, and applications [Invited Tutorial]. IEEE/OSA J. Opt. Commun. Netw. 2018, 10, D126–D143. [Google Scholar] [CrossRef] [Green Version]
- Musumeci, F.; Rottondi, C.; Nag, A.; Macaluso, I.; Zibar, D.; Ruffini, M.; Tornatore, M. An Overview on Application of Machine Learning Techniques in Optical Networks. IEEE Commun. Surv. Tutor. 2019, 21, 1383–1408. [Google Scholar] [CrossRef] [Green Version]
- Mata, J.; de Miguel, I.; Durán, R.J.; Merayo, N.; Singh, S.K.; Jukan, A.; Chamania, M. Artificial intelligence (AI) methods in optical networks: A comprehensive survey. Opt. Switch. Netw. 2018, 28, 43–57. [Google Scholar] [CrossRef]
- Cheng, S.; Xiao, D.; Huang, A.; Aibin, M. Machine Learning for Regenerator Placement Based on the Features of the Optical Network. In Proceedings of the 2019 21st International Conference on Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Khan, F.N.; Yu, Y.; Tan, M.C.; Al-Arashi, W.H.; Yu, C.; Lau, A.P.T.; Lu, C. Experimental demonstration of joint OSNR monitoring and modulation format identification using asynchronous single channel sampling. Opt. Express 2015, 23, 30337–30346. [Google Scholar] [CrossRef]
- Jiang, X. Chapter 15-Optical performance monitoring in optical long-haul transmission systems. In Optical Performance Monitoring; Elsevier Inc.: Amsterdam, The Netherlands, 2010; pp. 423–446. [Google Scholar]
- Ramaswami, R.; Sivarajan, K.; Sasaki, G. Optical Networks: A Practical Perspective, 3rd ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2009. [Google Scholar]
- Karout, J.; Agrell, E.; Szczerba, K.; Karlsson, M. Designing Power-Efficient Modulation Formats for Noncoherent Optical Systems. In Proceedings of the 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011, Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Willner, A.; Pan, Z.; Yu, C. Optical performance monitoring. In Optical Fiber Telecommunications V1B; Elsevier Inc.: Amsterdam, The Netherlands, 2008; pp. 233–292. [Google Scholar]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital Signal Processing for Short-Reach Optical Communications: A Review of Current Technologies and Future Trends. J. Light. Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Morawski, R.; Miekina, A. Monitoring of the OSNR in DWDM Systems Using a Low-resolution Spectrometric Transducer. In Proceedings of the 2005 IEEE Instrumentationand Measurement Technology Conference Proceedings, Ottawa, ON, Canada, 16–19 May 2005; Volume 3, pp. 2306–2309. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Zhang, Z.; Li, J.; Gao, H.; Zhang, F.; Chen, X. Machine Learning-Based Multifunctional Optical Spectrum Analysis Technique. IEEE Access 2019, 7, 19726–19737. [Google Scholar] [CrossRef]
- Skoog, R.A.; Banwell, T.C.; Gannett, J.W.; Habiby, S.F.; Pang, M.; Rauch, M.E.; Toliver, P. Automatic Identification of Impairments Using Support Vector Machine Pattern Classification on Eye Diagrams. IEEE Photonics Technol. Lett. 2006, 18, 2398–2400. [Google Scholar] [CrossRef]
- Hong, J.; Chen, L.; Zhu, J.; Zhou, W.; Li, B.; Fu, Y.; Wang, L. Modulation Format Identification and Transmission Quality Monitoring for Link Establishment in Optical Network Using Machine Learning Techniques. In Proceedings of the 2020 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 24–27 October 2020; pp. 1–3. [Google Scholar]
- Khan, F.N.; Zhong, K.; Al-Arashi, W.H.; Yu, C.; Lu, C.; Lau, A.P.T. Modulation Format Identification in Coherent Receivers Using Deep Machine Learning. IEEE Photonics Technol. Lett. 2016, 28, 1886–1889. [Google Scholar] [CrossRef]
- Bütler, R.M.; Häger, C.; Pfister, H.D.; Liga, G.; Alvarado, A. Model-Based Machine Learning for Joint Digital Backpropagation and PMD Compensation. J. Light. Technol. 2021, 39, 949–959. [Google Scholar] [CrossRef]
- Deligiannidis, S.; Bogris, A.; Mesaritakis, C.; Kopsinis, Y. Compensation of Fiber Nonlinearities in Digital Coherent Systems Leveraging Long Short-Term Memory Neural Networks. J. Light. Technol. 2020, 38, 5991–5999. [Google Scholar] [CrossRef]
- Vela, A.P.; Ruiz, M.; Velasco, L. Examples of Machine Learning Algorithms for Optical Network Control and Management. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Martín, I.; Troia, S.; Hernández, J.A.; Rodríguez, A.; Musumeci, F.; Maier, G.; Alvizu, R.; González de Dios, Ó. Machine Learning-Based Routing and Wavelength Assignment in Software-Defined Optical Networks. IEEE Trans. Netw. Serv. Manag. 2019, 16, 871–883. [Google Scholar] [CrossRef]
- Ujjwal, Y.; Thangaraj, J. Review and analysis of elastic optical network and sliceable bandwidth variable transponder architecture. Opt. Eng. 2018, 57, 1–18. [Google Scholar] [CrossRef]
- Khan, F.N.; Lu, C.; Lau, A.P.T. Machine Learning Methods for Optical Communication Systems. In Proceedings of the Advanced Photonics 2017 (IPR, NOMA, Sensors, Networks, SPPCom, PS), Optical Society of America, New Orleans, LA, USA, 24–27 July 2017; p. SpW2F.3. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Zhang, M. Low-Complexity Adaptive Chromatic Dispersion Estimation Scheme Using Machine Learning for Coherent Long-Reach Passive Optical Networks. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Guo, S.; Guo, P.; Yang, A.; Qiao, Y. Deep Neural Network Based Chromatic Dispersion Estimation With Ultra-Low Sampling Rate for Optical Fiber Communication Systems. IEEE Access 2019, 7, 84155–84162. [Google Scholar] [CrossRef]
- Kashi, A.S.; Zhuge, Q.; Cartledge, J.C.; Borowiec, A.; Charlton, D.; Laperle, C.; O’Sullivan, M. Fiber Nonlinear Noise-to-Signal Ratio Monitoring Using Artificial Neural Networks. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Dong, Z.; Khan, F.N.; Sui, Q.; Zhong, K.; Lu, C.; Lau, A.P.T. Optical Performance Monitoring: A Review of Current and Future Technologies. J. Light. Technol. 2016, 34, 525–543. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Wei, J.; Huang, S. Deep neural network based OSNR and availability predictions for multicast light-trees in optical WDM networks. Opt. Express 2020, 28, 10648–10669. [Google Scholar] [CrossRef] [PubMed]
- Pointurier, Y. Machine learning techniques for quality of transmission estimation in optical networks. IEEE/OSA J. Opt. Commun. Netw. 2021, 13, B60–B71. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Li, Z.; Li, J.; Fu, M.; Cui, Y.; Chen, X. Modulation Format Recognition and OSNR Estimation Using CNN-Based Deep Learning. IEEE Photonics Technol. Lett. 2017, 29, 1667–1670. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Kato, T.; Watanabe, S.; Morikawa, H. Convolutional neural network-based optical performance monitoring for optical transport networks. IEEE/OSA J. Opt. Commun. Netw. 2019, 11, A52–A59. [Google Scholar] [CrossRef]
- Karanov, B.; Chagnon, M.; Thouin, F.; Eriksson, T.A.; Bülow, H.; Lavery, D.; Bayvel, P.; Schmalen, L. End-to-End Deep Learning of Optical Fiber Communications. J. Light. Technol. 2018, 36, 4843–4855. [Google Scholar] [CrossRef]
- Fan, X.; Xie, Y.; Ren, F.; Zhang, Y.; Huang, X.; Chen, W.; Zhangsun, T.; Wang, J. Joint Optical Performance Monitoring and Modulation Format/Bit-Rate Identification by CNN-Based Multi-Task Learning. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Wang, D.; Wang, M.; Zhang, M.; Zhang, Z.; Yang, H.; Li, J.; Li, J.; Chen, X. Cost-effective and data size-adaptive OPM at intermediated node using convolutional neural network-based image processor. Opt. Express 2019, 27, 9403–9419. [Google Scholar] [CrossRef]
- Lun, H.; Fu, M.; Liu, X.; Wu, Y.; Yi, L.; Hu, W.; Zhuge, Q. Soft Failure Identification for Long-haul Optical Communication Systems Based on One-dimensional Convolutional Neural Network. J. Light. Technol. 2020, 38, 2992–2999. [Google Scholar] [CrossRef]
- Carena, A.; Curri, V.; Bosco, G.; Poggiolini, P.; Forghieri, F. Modeling of the Impact of Nonlinear Propagation Effects in Uncompensated Optical Coherent Transmission Links. J. Light. Technol. 2012, 30, 1524–1539. [Google Scholar] [CrossRef]
- Huang, L.; Xue, L.; Zhuge, Q.; Hu, W.; Yi, L. Modulation format identification under stringent bandwidth limitation based on an artificial neural network. OSA Contin. 2021, 4, 96–104. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Xu, T. Advanced DSP for Coherent Optical Fiber Communication. Appl. Sci. 2019, 9, 4192. [Google Scholar] [CrossRef] [Green Version]
- Ranzini, S.M.; Da Ros, F.; Bülow, H.; Zibar, D. Tunable Optoelectronic Chromatic Dispersion Compensation Based on Machine Learning for Short-Reach Transmission. Appl. Sci. 2019, 9, 4332. [Google Scholar] [CrossRef] [Green Version]
- Jin, C.; Shevchenko, N.A.; Li, Z.; Popov, S.; Chen, Y.; Xu, T. Nonlinear Coherent Optical Systems in the Presence of Equalization Enhanced Phase Noise. J. Light. Technol. 2021, 39, 4646–4653. [Google Scholar] [CrossRef]
- Schädler, M.; Böcherer, G.; Pachnicke, S. Soft-Demapping for Short Reach Optical Communication: A Comparison of Deep Neural Networks and Volterra Series. J. Light. Technol. 2021, 39, 3095–3105. [Google Scholar] [CrossRef]
- Li, D.; Song, H.; Cheng, W.; Deng, L.; Cheng, M.; Fu, S.; Tang, M.; Liu, D. 180 Gb/s PAM8 Signal Transmission in Bandwidth-Limited IMDD System Enabled by Tap Coefficient Decision Directed Volterra Equalizer. IEEE Access 2020, 8, 19890–19899. [Google Scholar] [CrossRef]
- Kuschnerov, M.; Schaedler, M.; Bluemm, C.; Calabro, S. Advances in Deep Learning for Digital Signal Processing in Coherent Optical Modems. In Proceedings of the Optical Fiber Communication Conference (OFC) 2020, Optical Society of America, San Diego, CA, USA, 8–12 March 2020; p. M3E.2. [Google Scholar] [CrossRef]
- Hsu, C.W.; Liu, S.; Lu, F.; Chow, C.W.; Yeh, C.H.; Chang, G.K. Accurate Indoor Visible Light Positioning System utilizing Machine Learning Technique with Height Tolerance. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Chen, Y.; Guan, W.; Li, J.; Song, H. Indoor Real-Time 3-D Visible Light Positioning System Using Fingerprinting and Extreme Learning Machine. IEEE Access 2020, 8, 13875–13886. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Ji, T.; Manton, J.H.; Shieh, W. Computational complexity comparison of feedforward/radial basis function/recurrent neural network-based equalizer for a 50-Gb/s PAM4 direct-detection optical link. Opt. Express 2019, 27, 36953–36964. [Google Scholar] [CrossRef] [PubMed]
- Ros, F.D.; Ranzini, S.M.; Dischler, R.; Cem, A.; Aref, V.; Bülow, H.; Zibar, D. Machine-learning-based equalization for short-reach transmission: Neural networks and reservoir computing. In Metro and Data Center Optical Networks and Short-Reach Links IV; Srivastava, A.K., Glick, M., Akasaka, Y., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11712, pp. 1–8. [Google Scholar] [CrossRef]
- Kilper, D.C.; Bach, R.; Blumenthal, D.J.; Einstein, D.; Landolsi, T.; Ostar, L.; Preiss, M.; Willner, A.E. Optical Performance Monitoring. J. Light. Technol. 2004, 22, 294. [Google Scholar] [CrossRef]
- Wu, X.; Jargon, J.A.; Skoog, R.A.; Paraschis, L.; Willner, A.E. Applications of Artificial Neural Networks in Optical Performance Monitoring. J. Light. Technol. 2009, 27, 3580–3589. [Google Scholar]
- Zhang, Y.; Ren, Y.; Wang, Z.; Liu, B.; Zhang, H.; Li, S.; Fang, Y.; Huang, H.; Bao, C.; Pan, Z.; et al. Joint OSNR, Skew, ROF Monitoring of Coherent Channel using Eye Diagram Measurement and Deep Learning. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; pp. 1–2. [Google Scholar]
- Zhang, S.; Peng, Y.; Sui, Q.; Li, Z. Modulation format identification using sparse asynchronous amplitude histograms. In Proceedings of the Advanced Photonics 2015, Optical Society of America, Boston, MA, USA, 27 June–1 July 2015; p. SpM4E.3. [Google Scholar] [CrossRef]
- Dods, S.; Anderson, T. Optical performance monitoring technique using delay tap asynchronous waveform sampling. In Proceedings of the 2006 Optical Fiber Communication Conference and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 5–10 March 2006; p. 3. [Google Scholar] [CrossRef]
- Klabjan, D.; Zhu, X. Neural Network Retraining for Model Serving. arXiv 2020, arXiv:2004.14203. [Google Scholar]
- Wang, C.; Fu, S.; Xiao, Z.; Tang, M.; Liu, D. Long Short-Term Memory Neural Network (LSTM-NN) Enabled Accurate Optical Signal-to-Noise Ratio (OSNR) Monitoring. J. Light. Technol. 2019, 37, 4140–4146. [Google Scholar] [CrossRef]
- Ben-Ezra, Y.; Mahlab, U.; Lembrikov, B.I.; Dolev, E. Application of Wavelet Networks for Identification of Transients in Optical Networks. In Proceedings of the 2006 International Conference on Transparent Optical Networks, Nottingham, UK, 18–22 June 2006; Volume 1, pp. 111–114. [Google Scholar]
- Bangari, V.; Marquez, B.A.; Miller, H.; Tait, A.N.; Nahmias, M.A.; de Lima, T.F.; Peng, H.; Prucnal, P.R.; Shastri, B.J. Digital Electronics and Analog Photonics for Convolutional Neural Networks (DEAP-CNNs). IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Zhuge, Q.; Zeng, X.; Lun, H.; Cai, M.; Liu, X.; Yi, L.; Hu, W. Application of Machine Learning in Fiber Nonlinearity Modeling and Monitoring for Elastic Optical Networks. J. Light. Technol. 2019, 37, 3055–3063. [Google Scholar] [CrossRef]
- Tanimura, T.; Hoshida, T.; Rasmussen, J.C.; Suzuki, M.; Morikawa, H. OSNR monitoring by deep neural networks trained with asynchronously sampled data. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016; pp. 1–3. [Google Scholar]
- Cheng, Y.; Fu, S.; Tang, M.; Liu, D. Multi-task deep neural network (MT-DNN) enabled optical performance monitoring from directly detected PDM-QAM signals. Opt. Express 2019, 27, 19062–19074. [Google Scholar] [CrossRef]
- Cho, H.J.; Varughese, S.; Lippiatt, D.; Desalvo, R.; Tibuleac, S.; Ralph, S.E. Optical performance monitoring using digital coherent receivers and convolutional neural networks. Opt. Express 2020, 28, 32087–32104. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, A.; Guo, P.; He, P. OSNR and nonlinear noise power estimation for optical fiber communication systems using LSTM based deep learning technique. Opt. Express 2018, 26, 21346–21357. [Google Scholar] [CrossRef]
- Yi, L.; Liao, T.; Huang, L.; Xue, L.; Li, P.; Hu, W. Machine Learning for 100 Gb/s/λ Passive Optical Network. J. Light. Technol. 2019, 37, 1621–1630. [Google Scholar] [CrossRef]
- Thrane, J.; Wass, J.; Piels, M.; Diniz, J.C.M.; Jones, R.; Zibar, D. Machine Learning Techniques for Optical Performance Monitoring From Directly Detected PDM-QAM Signals. J. Light. Technol. 2017, 35, 868–875. [Google Scholar] [CrossRef] [Green Version]
- Zhuge, Q.; Hu, W. Application of Machine Learning in Elastic Optical Networks. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Guesmi, L.; Ragheb, A.M.; Fathallah, H.; Menif, M. Experimental Demonstration of Simultaneous Modulation Format/Symbol Rate Identification and Optical Performance Monitoring for Coherent Optical Systems. J. Light. Technol. 2018, 36, 2230–2239. [Google Scholar] [CrossRef]
- Karanov, B.; Chagnon, M.; Aref, V.; Ferreira, F.; Lavery, D.; Bayvel, P.; Schmalen, L. Experimental Investigation of Deep Learning for Digital Signal Processing in Short Reach Optical Fiber Communications. In Proceedings of the 2020 IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, 20–22 October 2020. [Google Scholar]
- Gaiarin, S.; Pang, X.; Ozolins, O.; Jones, R.T.; Da Silva, E.P.; Schatz, R.; Westergren, U.; Popov, S.; Jacobsen, G.; Zibar, D. High Speed PAM-8 Optical Interconnects with Digital Equalization Based on Neural Network. In Proceedings of the 2016 Asia Communications and Photonics Conference (ACP), Wuhan, China, 2–5 November 2016; pp. 1–3. [Google Scholar]
- Ge, L.; Zhang, W.; Liang, C.; He, Z. Compressed Neural Network Equalization Based on Iterative Pruning Algorithm for 112-Gbps VCSEL-Enabled Optical Interconnects. J. Light. Technol. 2020, 38, 1323–1329. [Google Scholar] [CrossRef]
- Lavania, S.; Kumam, B.; Matey, P.S.; Annepu, V.; Bagadi, K. Adaptive channel equalization using recurrent neural network under SUI channel model. In Proceedings of the 2015 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 19–20 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Argyris, A.; Bueno, J.; Fischer, I. Photonic machine learning implementation for signal recover in optical communications. Sci. Rep. 2018, 8, 8487. [Google Scholar] [CrossRef] [PubMed]
- Chin, H.M.; Jain, N.; Zibar, D.; Andersen, U.L.; Gehring, T. Machine learning aided carrier recovery in continuous-variable quantum key distribution. npj Quantum Inf. 2021, 7. [Google Scholar] [CrossRef]
- Schaedler, M.; Kuschnerov, M.; Calabrò, S.; Pittalà, F.; Bluemm, C.; Pachnicke, S. AI-Based Digital Predistortion for IQ Mach-Zehnder Modulators. In Proceedings of the 2019 Asia Communications and Photonics Conference (ACP), Chengdu, China, 2–5 November 2019; pp. 1–3. [Google Scholar]
- Li, M.; Wang, D.; Cui, Q.; Zhang, Z.; Deng, L.; Zhang, M. End-to-end Learning for Optical Fiber Communication with Data-driven Channel Model. In Proceedings of the 2020 Opto-Electronics and Communications Conference (OECC), Taipei, Taiwan, 4–8 October 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Schaedler, M.; Calabrò, S.; Pittalà, F.; Bluemm, C.; Kuschnerov, M.; Pachnicke, S. Neural Network-Based Soft-Demapping for Nonlinear Channels. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Ranzini, S.M.; Dischler, R.; Da Ros, F.; Bülow, H.; Zibar, D. Experimental Investigation of Optoelectronic Receiver With Reservoir Computing in Short Reach Optical Fiber Communications. J. Light. Technol. 2021, 39, 2460–2467. [Google Scholar] [CrossRef]
- Yu, Y.; Che, Y.; Bo, T.; Kim, D.; Kim, H. Reduced-state MLSE for an IM/DD system using PAM modulation. Opt. Express 2020, 28, 38505–38515. [Google Scholar] [CrossRef]
- Chandra Kumari Kalla, S.; Ann Rusch, L. Recurrent neural nets achieving MLSE performance in bandlimited optical channels. In Proceedings of the 2020 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 28 September–1 October 2020; pp. 1–2. [Google Scholar] [CrossRef]
- Katz, G.; Sadot, D. Radial Basis Function Network Equalizer for Optical Communication OOK System. J. Light. Technol. 2007, 25, 2631–2637. [Google Scholar] [CrossRef]
- Katumba, A.; Yin, X.; Dambre, J.; Bienstman, P. A Neuromorphic Silicon Photonics Nonlinear Equalizer For Optical Communications With Intensity Modulation and Direct Detection. J. Light. Technol. 2019, 37, 2232–2239. [Google Scholar] [CrossRef] [Green Version]
- Da Ros, F.; Ranzini, S.M.; Bülow, H.; Zibar, D. Reservoir-Computing Based Equalization With Optical Pre-Processing for Short-Reach Optical Transmission. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Lyu, Y.; Li, X.; Wang, T.; Dong, X. Reservoir Computing Based Equalization for Radio over Fiber System. In Proceedings of the 2021 23rd International Conference on Advanced Communication Technology (ICACT), PyeongChang, Korea, 7–10 February 2021; pp. 85–90. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Talreja, V.; Koike-Akino, T.; Wang, Y.; Millar, D.S.; Kojima, K.; Parsons, K. End-to-End Deep Learning for Phase Noise-Robust Multi-Dimensional Geometric Shaping. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 6–10 December 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Karanov, B.; Chagnon, M.; Aref, V.; Lavery, D.; Bayvel, P.; Schmalen, L. Optical Fiber Communication Systems Based on End-to-End Deep Learning: (Invited Paper). In Proceedings of the 2020 IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 28 September–1 October 2020; pp. 1–2. [Google Scholar] [CrossRef]
- Hadi, M.U.; Awais, M.; Raza, M.; Khurshid, K.; Jung, H. Neural Network DPD for Aggrandizing SM-VCSEL-SSMF-Based Radio over Fiber Link Performance. Photonics 2021, 8, 19. [Google Scholar] [CrossRef]
- Schädler, M.; Böcherer, G.; Pittalà, F.; Calabrò, S.; Stojanovic, N.; Bluemm, C.; Kuschnerov, M.; Pachnicke, S. Recurrent Neural Network Soft-Demapping for Nonlinear ISI in 800Gbit/s DWDM Coherent Optical Transmissions. J. Light. Technol. 2021, 39, 5278–5286. [Google Scholar] [CrossRef]
- Michael, L.; Gomez-Barquero, D. Bit-Interleaved Coded Modulation (BICM) for ATSC 3.0. IEEE Trans. Broadcast. 2016, 62, 181–188. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, M.Z.; Hossan, M.T.; Islam, A.; Jang, Y.M. A Comparative Survey of Optical Wireless Technologies: Architectures and Applications. IEEE Access 2018, 6, 9819–9840. [Google Scholar] [CrossRef]
- Cahyadi, W.A.; Chung, Y.H.; Ghassemlooy, Z.; Hassan, N.B. Optical Camera Communications: Principles, Modulations, Potential and Challenges. Electronics 2020, 9, 1339. [Google Scholar] [CrossRef]
- Takai, I.; Ito, S.; Yasutomi, K.; Kagawa, K.; Andoh, M.; Kawahito, S. LED and CMOS Image Sensor Based Optical Wireless Communication System for Automotive Applications. IEEE Photonics J. 2013, 5, 6801418. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, M.; Ghassemlooy, Z.; Le Minh, H.; Tsai, H.M.; Tang, X.; Png, L.C.; Han, D. Experimental Demonstration of RGB LED-Based Optical Camera Communications. IEEE Photonics J. 2015, 7, 1–12. [Google Scholar] [CrossRef]
- Walter, I.; Khadr, M.H.; Elgala, H. Deep Learning Based Optical Camera Communications. In Proceedings of the OSA Advanced Photonics Congress (AP) 2019 (IPR, Networks, NOMA, SPPCom, PVLED), Optical Society of America, Burlingame, CA, USA, 29 July–1 August 2019; p. SpTh3E.2. [Google Scholar] [CrossRef]
- Lu, X.; Lu, C.; Yu, W.; Qiao, L.; Liang, S.; Lau, A.P.T.; Chi, N. Memory-controlled deep LSTM neural network post-equalizer used in high-speed PAM VLC system. Opt. Express 2019, 27, 7822–7833. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.S.; Liu, Y.; Chow, C.W.; Chang, Y.H.; Lin, D.C.; Song, S.H.; Hsu, K.L.; Yeh, C.H. Z-Score Averaging Neural Network and Background Content Removal for High Performance Rolling Shutter based Optical Camera Communication (OCC). In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 6–10 June 2021; pp. 1–3. [Google Scholar]
- Ismail, N.; Rahiman, M.H.F.; Taib, M.N.; Ali, N.A.M.; Jamil, M.; Tajuddin, S.N. Classification of the quality of agarwood oils from Malaysia using Z-score technique. In Proceedings of the 2013 IEEE 3rd International Conference on System Engineering and Technology, Shah Alam, Malaysia, 19–20 August 2013; pp. 78–82. [Google Scholar] [CrossRef]
- Liu, L.; Deng, R.; Chen, L.K. 47-kbit/s RGB-LED-based optical camera communication based on 2D-CNN and XOR-based data loss compensation. Opt. Express 2019, 27, 33840–33846. [Google Scholar] [CrossRef]
- Liu, L.; Deng, R.; Chen, L.K. Spatial and Time Dispersions Compensation With Double-Equalization for Optical Camera Communications. IEEE Photonics Technol. Lett. 2019, 31, 1753–1756. [Google Scholar] [CrossRef]
- He, J.; Lee, J.; Song, T.; Li, H.; Kandeepan, S.; Wang, K. Recurrent neural network (RNN) for delay-tolerant repetition-coded (RC) indoor optical wireless communication systems. Opt. Lett. 2019, 44, 3745–3748. [Google Scholar] [CrossRef]
- He, J.; Lee, J.; Song, T.; Li, H.; Kandeepan, S.; Wang, K. Delay-Tolerant Indoor Optical Wireless Communication Systems Based on Attention-Augmented Recurrent Neural Network. J. Light. Technol. 2020, 38, 4632–4640. [Google Scholar] [CrossRef]
- Lee, J.; Song, T.; He, J.; Kandeepan, S.; Wang, K. Recurrent neural network FPGA hardware accelerator for delay-tolerant indoor optical wireless communications. Opt. Express 2021, 29, 26165–26182. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Huang, Z.; Wang, X. Transmitter Fingerprinting for VLC Systems via Deep Feature Separation Network. IEEE Photonics J. 2021, 13, 1–7. [Google Scholar] [CrossRef]
- Wu, X.; O’Brien, D.C. A Novel Machine Learning-Based Handover Scheme for Hybrid LiFi and WiFi Networks. In Proceedings of the 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, 7–11 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ma, S.; Dai, J.; Lu, S.; Li, H.; Zhang, H.; Du, C.; Li, S. Signal Demodulation With Machine Learning Methods for Physical Layer Visible Light Communications: Prototype Platform, Open Dataset, and Algorithms. IEEE Access 2019, 7, 30588–30598. [Google Scholar] [CrossRef]
- Pham, T.L.; Nguyen, H.; Nguyen, T.; Jang, Y.M. A Novel Neural Network-Based Method for Decoding and Detecting of the DS8-PSK Scheme in an OCC System. Appl. Sci. 2019, 9, 2242. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Zhao, M.; Qiao, L.; Chi, N. Non-linear Compensation of Multi-CAP VLC System Employing Pre-Distortion Base on Clustering of Machine Learning. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Shi, D.; Zhang, X.; Vladimirescu, A.; Shi, L.; Huang, Y.; Liu, Y. A Device Identification Method Based on LED Fingerprint for Visible Light Communication System. In Proceedings of the 15th International Conference on Availability, Reliability and Security (ARES ’20), Dublin, Ireland, 25–28 August 2020; Association for Computing Machinery: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Alotaibi, N.M.; Alwakeel, S.S. A Neural Network Based Handover Management Strategy for Heterogeneous Networks. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 1210–1214. [Google Scholar] [CrossRef]
- Ben Zineb, A.; Ayadi, M.; Tabbane, S. QoE-based vertical handover decision management for cognitive networks using ANN. In Proceedings of the 2017 Sixth International Conference on Communications and Networking (ComNet), Hammamet, Tunisia, 29 March–1 April 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Chavez-Burbano, P.; Guerra, V.; Rabadan, J.; Jurado-Verdu, C.; Perez-Jimenez, R. Novel Indoor Localization System Using Optical Camera Communication. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Drawil, N.M.; Amar, H.M.; Basir, O.A. GPS Localization Accuracy Classification: A Context-Based Approach. IEEE Trans. Intell. Transp. Syst. 2013, 14, 262–273. [Google Scholar] [CrossRef]
- Luo, J.; Fan, L.; Li, H. Indoor Positioning Systems Based on Visible Light Communication: State of the Art. IEEE Commun. Surv. Tutor. 2017, 19, 2871–2893. [Google Scholar] [CrossRef]
- IEEE Standard for Local and metropolitan area networks–Part 15.7: Short-Range Optical Wireless Communications-Redline. IEEE Std 802.15.7-2018 (Revision of IEEE Std 802.15.7-2011)-Redline. 2019, pp. 1–670. Available online: https://ieeexplore.ieee.org/document/8751172 (accessed on 11 November 2021).
- Taylor, M.T.; Hranilovic, S. Angular diversity approach to indoor positioning using visible light. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 1093–1098. [Google Scholar] [CrossRef]
- Li, X.; Cao, Y.; Chen, C. Machine Learning Based High Accuracy Indoor Visible Light Location Algorithm. In Proceedings of the 2018 IEEE International Conference on Smart Internet of Things (SmartIoT), Xi’an, China, 17–19 August 2018; pp. 198–203. [Google Scholar] [CrossRef]
- He, J.; Hsu, C.W.; Zhou, Q.; Tang, M.; Fu, S.; Liu, D.; Deng, L.; Chang, G.K. Demonstration of High Precision 3D Indoor Positioning System Based on Two-Layer Ann Machine Learning Technique. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Lin, C.; Lin, B.; Tang, X.; Zhou, Z.; Zhang, H.; Chaudhary, S.; Ghassemlooy, Z. An Indoor Visible Light Positioning System Using Artificial Neural Network. In Proceedings of the 2018 Asia Communications and Photonics Conference (ACP), Hangzhou, China, 26–29 October 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Arfaoui, M.A.; Soltani, M.D.; Tavakkolnia, I.; Ghrayeb, A.; Assi, C.M.; Safari, M.; Haas, H. Invoking Deep Learning for Joint Estimation of Indoor LiFi User Position and Orientation. IEEE J. Sel. Areas Commun. 2021, 39, 2890–2905. [Google Scholar] [CrossRef]
- Tran, H.Q.; Ha, C. Improved Visible Light-Based Indoor Positioning System Using Machine Learning Classification and Regression. Appl. Sci. 2019, 9, 1048. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Hu, F.; Elikplim, N.R.; Li, L. Indoor Localization Using Visible Light via Two-Layer Fusion Network. IEEE Access 2019, 7, 16421–16430. [Google Scholar] [CrossRef]
- Poulose, A.; Eyobu, O.S.; Han, D.S. An Indoor Position-Estimation Algorithm Using Smartphone IMU Sensor Data. IEEE Access 2019, 7, 11165–11177. [Google Scholar] [CrossRef]
- Yuan, T.; Xu, Y.; Wang, Y.; Han, P.; Chen, J. A Tilt Receiver Correction Method for Visible Light Positioning Using Machine Learning Method. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Xie, C.; Guan, W.; Wu, Y.; Fang, L.; Cai, Y. The LED-ID Detection and Recognition Method Based on Visible Light Positioning Using Proximity Method. IEEE Photonics J. 2018, 10, 1–16. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).