Abstract
Hydrogen (H2) sensing is crucial for modern energy storage technology, which looks to hydrogen as the most promising alternative to fossil fuels. In this respect, magnesium (Mg) offers unique possibilities, since magnesium and hydrogen easily undergo a reversible hydrogenation reaction where Mg reversibly converts into MgH2. From an optical point of view, this process produces an abrupt refractive index change, which can be exploited for sensing applications. To maximize this opportunity, we envision an architecture composed of two Ag/ITO/Mg metal/dielectric resonators facing each other and displaced by 200 nm of vacuum. This structure forms a so-called Epsilon-Near-Zero (ENZ) multi-cavity resonator, in which the two internal Mg layers, used as tunneling coupling metals, are accessible to environmental agents. We demonstrate that the hydrogenation of the two Mg layers leads to substantial changes in the strong coupling between the cavities composing the entire resonator, with a consequent abrupt modification of the spectral response, thus enabling the sensing mechanism. One of the main advantages of the proposed system with respect to previous research is that the proposed multilayered architecture avoids the need for lithographic processes. This feature makes the proposed architecture inexpensive and wafer-to-chip scalable, considering that each kind of substrate from common glass to silicon can be used. Therefore, our sensing architecture offers great promise for applications in embedded H2 sensors.
1. Introduction
The ever-increasing demand for innovative energy sources that can replace fossil fuels is encouraging the scientific community to make increasingly significant efforts in hydrogen-related technology. In this respect, one of the cardinal points is the ability to detect leakages. To this end, hydrogen sensors are crucial. The majority of hydrogen sensors are electronically operated. These sensors usually detect changes in resistivity due to the hydrogenation of the sensing conductive material, which is usually a metal-like palladium (Pd) or even a conductive polymer [1,2,3,4,5,6,7,8,9,10,11,12]. Sensors based on an optical readout can, however, overcome some of the most common drawbacks of electrically driven sensors, such as compactness and operativity in harsh conditions. In this respect, photonic nanotechnology can offer plenty of innovative optical-based solutions, especially those developed in the fields of liquid crystals [13,14,15,16], photonic crystals [17,18,19,20,21], and plasmonics [22,23,24,25,26,27,28,29]. Metals such as Pd constitute a natural bridge between hydrogen sensing and plasmonics. The plasmonic properties of Pd have been largely documented in the past [30,31,32,33,34], making it possible to engineer so-called “metamaterials” (nanoscale structures whose overall optical properties can be engineered at will simply by acting on the optical and geometrical parameters of the subunits with which they are made) ideal for hydrogen sensing. Particularly interesting for hydrogen sensing are so-called hyperbolic metamaterials (HMMs) [35,36,37,38]. HMMs made of Pd nanowires immersed in nanoporous anodized aluminum oxide (AAO) were demonstrated to be useful for low-concentration H2 sensing [39]. Recently, resonant metal/dielectric multilayers have been proposed as refractive index sensors [40]. The optical response of these multilayers has been described in the framework of the analogy between quantum mechanics and classic electromagnetism that revealed that resonances arising in these structures can be considered as resonant tunneling modes, in correspondence to which the multilayer manifests a so-called “Epsilon-Near-Zero” (ENZ) effective permittivity [40]. Moving around a zero-effective-permittivity condition, a small change in the structure can dramatically change the way light interacts with them. Despite its ease of fabrication, however, the single cavity configuration is unsuitable for sensing applications that rely on the refractive index change caused in the metallic layers, since this would imply the effective cancellation of the optical cavity due to the transformation of the metal into a dielectric material. Moreover, the metallic layers are often buried under thick oxides that would passivate them, thus preventing their hydrogenation capability. From this point of view, it can be useful to consider the case of strongly coupled multiple resonators. This is the case, for example, of two metal/dielectric/metal (MDM) cavities sharing the same central metal layer to form a MDMDM double cavity resonator. In this case, the central metal also constitutes the energy exchange channel between the two adjacent cavities, so that we can refer to it as the “tunneling metal”. Its thickness determines the strength with which the cavities are electromagnetically coupled. This configuration is extremely sensitive to any change in the optical properties of the central metal, which immediately translates into a modification of the coupling strength between the two cavities with a consequent substantial spectral variation.
In this paper, we leverage on this concept to propose and numerically investigate a slightly more sophisticated structure consisting of a three-cavity metal/dielectric multilayer. The proposed architecture is composed of two Ag/ITO/Mg MDM cavities facing each other from the Mg side and separated by a vacuum spacer that acts as the central of the three cavities. In this configuration, the two Mg layers are the tunneling metals through which the three cavities are electromagnetically connected. They also remain exposed to environmental conditions; therefore, they are potentially accessible to H2 molecules, whose presence can determine their hydrogenation to form MgH2. This process is reversible and it is responsible for an abrupt refractive index change (Mg is a metal while MgH2 is a dielectric) that switches the system from a three-cavity to a single-cavity resonator. The remarkable change in the spectral response of the structure (detected through its transmittance, reflectance, and absorbance) enables the sensing mechanism. Due to the large number of resonances hosted by the system, it offers the possibility to work in several spectral regions from the visible (VIS) to the near-infrared (NIR). Considering its ease of fabrication, inexpensiveness, and wafer-to-chip-size scalability, the proposed structure holds great promise for applications in embedded H2 sensors.
2. Results and Discussion
The technological core at the basis of the proposed architecture is Mg. Although it is often replaced with more application-friendly metals, Mg offers exceptional photonic properties. In the framework of the well-studied analogy between classic electromagnetism and quantum mechanics, it has indeed been demonstrated that Mg can be considered a so-called “Hermitian metal” [40]. This means that the ratio between the real and imaginary part of its refractive index (shown in Figure 1, together with the dielectric permittivity) is well below 0.2 in the entire visible range. Given that the real part of the refractive index of Mg is included in the (0–1) range, the phase velocity vph = c/n of an electromagnetic wave propagating in a Mg slab is superluminal in the entire visible range. As a result, the electromagnetic wave in the Mg slab manifests a marked exponential profile, which makes Mg ideal as a connection metal between cavities via optical tunneling [40]. The property that profiles Mg as the perfect material for the purposes of this work is its hydrogenation capability. Mg is indeed well known to reversely react with hydrogen to form MgH2. Due to this property, Mg is one of the materials to which the scientific community looks for hydrogen storage. A recent work from Isidorsson et al. elucidated the refractive index change that Mg undergoes during the hydrogenating process, reporting a useful expression for the optical constants of MgH2, which we recall here as well [41]:
with parameters included in the following table (Table 1): .
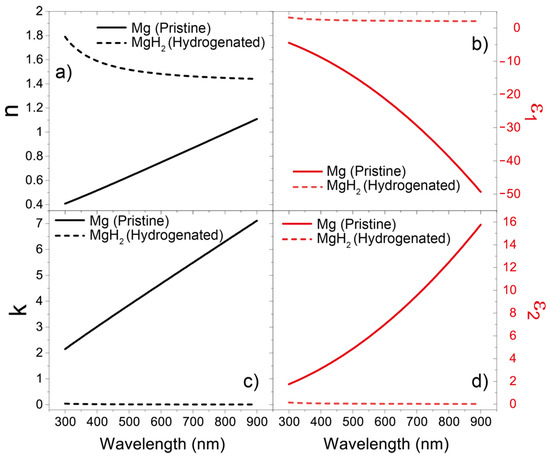
Figure 1.
(a) Real and (b) imaginary part of the refractive index (left panels) and (c) real and (d) imaginary part of dielectric permittivity (right panels) of pure Mg (black and red solid curves) and MgH2 (black and red dashed curves), respectively.

Table 1.
Parameters of the Lorentz model for MgH2.
In the proposed architecture, Mg is used as a connection metal between strongly coupled optical cavities. In particular, the structure, sketched in Figure 2a, consists of a three-cavity metal/dielectric resonator made by two metal/dielectric/metal (MDM) Ag (20 nm)/ITO (200 nm)/Mg (var.) cavities facing each other and displaced by 200 nm of vacuum. The optical constants used for both Ag and ITO have been experimentally measured via spectroscopic ellipsometry measurements and are reported in [42]. In this configuration, the central vacuum layer, obtained by means of two submicron spacers (‘s’ in the sketch of Figure 2a), acts as the central cavity, while the two internal Mg layers act as coupling metals between the two external cavities. Due to the ability of Mg to transmit energy from one cavity to another under the form of exponentially decaying waves, the three cavities constituting the entire system become strongly coupled. The strong interaction between adjacent cavities connected via a shared thin metallic layer has been studied elsewhere, highlighting both the anti-crossing dynamics between resonances and the formation of allowed and forbidden photonic bands [43,44,45,46,47]. Strongly coupled optical cavities manifest a high sensitivity to all the changes in the connection layers that can modify the optical path of a light wave travelling through them. For example, changing the thickness of the central Mg metals substantially modifies the spectral response of the entire structure, as shown in the maps of Figure 2b,c, where both the reflectance and the transmittance of the three-cavity system shown in Figure 2a are reported. It can be observed how, by increasing the thickness of the two central Mg layers, the three resonances present for small thicknesses converge into one single resonance (see the black dip around 500 nm in Figure 2b). This phenomenon appears when thickness of the Mg layers exceeds its skin depth (~11 nm). This dynamic is well known to occur in this kind of strongly coupled resonator and has been described within the framework of the classic/quantum analogy with the states of the H2 molecule as a function of the interatomic distance between the two H atoms [43].

Figure 2.
(a) Sketch of the multilayered structure. (b) p-Polarization reflectance and (c) transmittance map while varying the thickness of the Mg layers.
The spectral response of the multilayered metal/dielectric resonator shown in Figure 2a was calculated via Scattering Matrix Method (SMM) simulations for both p- and s- polarization. The resonances occurring in both polarizations can be understood as effective resonant tunneling modes [40,48], as shown in Section 1 of the Supporting Information.
If exposed to H2 molecules (see, for example, the inlet that could be submerged in the vacuum layer for a H2 flux, Figure 3a,b), the two central Mg layers can undergo a hydrogenation reaction. This process dramatically changes the nature of Mg, which switches from an optical metal to a low-loss dielectric, as documented in Figure 1. Such a transition causes the three-cavities system sketched in Figure 3a to collapse into a single-cavity system, in which the central dielectric layer is a compound dielectric made of ITO/MgH2/vacuum/MgH2/ITO (as sketched in Figure 3b). The spectral response of the new system changes completely. The transmittance/reflectance/absorbance spectra, calculated at an angle of incidence of 50°, of the hydrogenated multilayer are reported in Figure 3c–e.
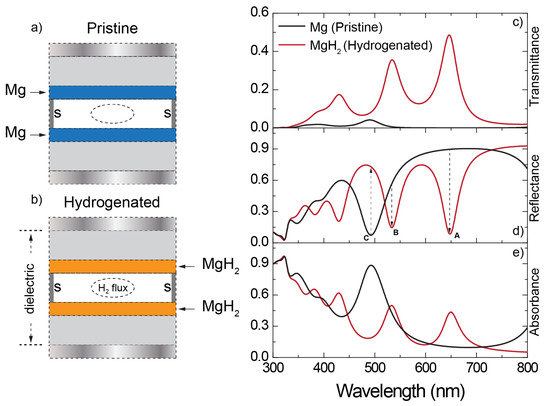
Figure 3.
SMM calculated (c) transmittance, (d) reflectance, and (e) absorbance, for an incident angle of 50°, for the pristine (black curves, sketch in (a)) and hydrogenated (red curves, sketch in (b)) structure. The Mg layer thickness is fixed at 20 nm, and total hydrogenation is considered.
The spectrum of the hydrogenated system manifests several modes, recognizable as peaks in transmittance and absorbance and dips in reflectance, which correspond to higher accessible harmonics due to the large thickness of the new dielectric cavity. This abrupt change introduces several sensing possibilities. For example, considering the mode labeled with A in Figure 3d, the reflectivity switches from 0.89 (pristine) to 0.084 (hydrogenated), resulting in a decrease of about 90.5%. For the modes labeled by B and C in the same figure, we have, respectively, a decrease of about 75% and a tenfold increase. These values highlight the broad sensing margins and versatility introduced by this configuration. However, Mg hydrogenation is a sophisticated process. While the interface of the Mg layer hydrogenates, it is increasingly more difficult for the atoms buried in the bulk of the layer to fully hydrogenate. During this transient phase, the optical response of the multilayer can vary significantly. Let us consider in the model the case of the non-complete hydrogenation of the Mg layers, by including a thin MgH2 layer on top of the exposed interfaces of both the two Mg layers. Of course, the thickness of the MgH2 layers is occasionally subtracted from those of the Mg layers themselves (see sketches in Figure 4a). The thickness of the MgH2 layer spans a range between 0 nm (no hydrogenation at all) to 20 nm (full hydrogenation). The evolution of the calculated p- (Figure 4b) and s-polarization (Figure 4) reflectance and of the p- (Figure 4c) and s-polarization (Figure 4e) transmittance follows the transition from a three-cavity multilayer (no hydrogenation at all), to a single-cavity system. Such a transition is particularly visible in the calculated p-polarization (Figure 4b,c) scattering parameters, when the thickness of the MgH2 layer exceeds 10 nm (50% of the total thickness of the Mg layer). Here, the mode occurring around 500 nm for the pristine three-cavity system splits into two additional modes (see dashed lines in Figure 4b,c). This feature necessitates a careful explanation that can be fully captured only by using the quantum analogy with potential wells.

Figure 4.
(a) Sketch showing the gradual hydrogenation of Mg layers, modeled as two thin MgH2 layers whose thickness gradually replaces that of the remaining Mg layers. (b,c) p- and (d,e) s-polarized reflectance and transmittance spectra calculated via SMM simulations while increasing the thickness of the MgH2 layer. Sketch of the idealization in terms of the classic electromagnetism/quantum mechanics analogy that sees the multicavity system as a series of coupled potential wells in which the central barrier (Mg layer) is (f) thick (very low hydrogenation) and (g) thin (almost complete hydrogenation and replacement of the Mg layer with MgH2). (h) Scheme showing the energy splitting between the bonding and anti-bonding mode with respect to the thickness of the central metallic barrier.
Let us focus on the system constituted by the first Ag-ITO-Mg-MgH2-Vacuum-MgH2-Mg series of layers from top to bottom. This system has been sketched in Figure 4f and constitutes a double-cavity metal/insulator/metal resonator. The spectral properties of this system have been described in detail elsewhere and it has been clarified that such a system resembles the case of the quantum double-potential well, characterized by two modes, one at lower energy (often called the “bonding” mode) and one at higher energy (often called the “anti-bonding” mode) [43,44]. The energy splitting between these two modes has been demonstrated to increase while the thickness of the central metallic layer decreases. While the hydrogenation of the Mg layers also reaches the deeper atoms, the multilayer system evolves from the one sketched in Figure 4f to the one sketched in Figure 4g. This is equivalent to passing from a double potential well with a thick central barrier (see the potential wells idealization sketched in Figure 4f) to a double-potential well with thin central barrier (see the potential wells idealization sketched in Figure 4g). The first configuration (thick Mg layer) is characterized by negligible modal splitting, manifested by a single pronounced dip in reflectance around 500 nm for the thickness of the MgH2 layers below 10 nm (see Figure 4b,d). The second configuration manifests substantial modal splitting, resulting in the two modes visible as two reflectance dips in Figure 4b,d above 10 nm thick MgH2 layers.
In practical applications, Mg is often capped with a passivating Pd layer that hydrogenates before Mg to give rise to PdHx, a highly absorptive metal. This protective layer prevents Mg from oxidizing, thus preserving its hydrogenation capabilities. The optical constants of PdHx can be calculated as shown by Isidorsson et al. [41]. Hereafter, we consider such a case as well, by numerically simulating the configuration depicted in Figure 5a.
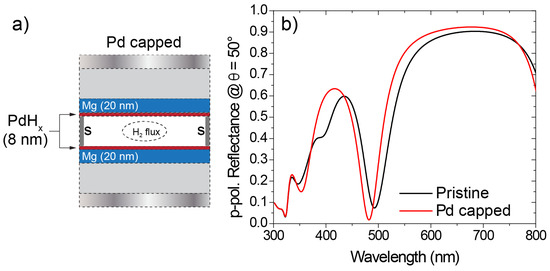
Figure 5.
(a) Sketch of the PdHx capped architecture. (b) Comparison between the p-polarization Reflectance spectra calculated at an angle of incidence of 50° for the pristine and the PdHx-capped architectures.
Here, two PdHx layers (8 nm thickness) are placed on top of each Mg layer. In Figure 5b, a comparison between the p-polarization reflectance, calculated at an angle of incidence of 50°, of the pristine system (the system in Figure 3a) and of the PdHx capped system is provided in Figure 5b, demonstrating that no significant change in the optical response is caused by the inclusion of the capping layers.
3. Conclusions
In this study, we demonstrated the ability of resonant ENZ multilayers to work as hydrogen-sensing devices. The structure we propose consists of a three-cavity architecture produced by two Ag/ITO/Mg metal/dielectric/metal resonators facing each other and displaced by 200 nm vacuum separation spacer, acting as a third, central cavity. The three cavities present in this geometry are therefore strongly coupled through the two Mg layers. As a result, the spectral response of the entire system is extremely sensitive to any refractive index change in the coupling metals. The vacuum spacer leaves the two Mg layers exposed, allowing their accessibility to environmental agents. Therefore, H2 molecules can be absorbed via hydrogenation. The disruptive refractive index change that Mg undergoes after the hydrogenation reaction substantially modifies its optical nature, transforming it from an optical metal to a low-loss dielectric. As a consequence, the overall three-cavity architecture becomes a single-cavity resonator with a compound dielectric layer. The scattering parameter of the former architecture involving the hydrogenated Mg layers are substantially different from the pristine version, thus allowing the H2 sensing mechanism to function. The system we propose here features several strong points, among which its inexpensiveness and ease of fabrication are worth mentioning. The proposed architecture is also chip-to-wafer-size-scalable, making it possible to envision its employment in embedded system applications.
Supplementary Materials
The following are available online at www.mdpi.com/2304-6732/8/12/0537/s1, Figure S1: ffective epsilon-near-zero characteristics of the mulrilayer.
Author Contributions
Conceptualization, V.C.; methodology, V.C.; software, V.C.; validation, V.C. and A.D.L.; writing—original draft preparation, V.C.; writing—review and editing, A.D.L.; supervision, A.D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Öztürk, S.; Kılınç, N. Pd Thin Films on Flexible Substrate for Hydrogen Sensor. J. Alloys Compd. 2016, 674, 179–184. [Google Scholar] [CrossRef]
- Kilinç, N. Resistive Hydrogen Sensors Based on Nanostructured Metals and Metal Alloys. Nanosci. Nanotechnol. Lett. 2013, 5, 825–841. [Google Scholar] [CrossRef]
- Hao, M.; Wu, S.; Zhou, H.; Ye, W.; Wei, X.; Wang, X.; Chen, Z.; Li, S. Room-Temperature and Fast Response Hydrogen Sensor Based on Annealed Nanoporous Palladium Film. J. Mater. Sci. 2016, 51, 2420–2426. [Google Scholar] [CrossRef]
- Arya, S.K.; Krishnan, S.; Silva, H.; Jean, S.; Bhansali, S. Advances in Materials for Room Temperature Hydrogen Sensors. Analyst 2012, 137, 2743–2756. [Google Scholar] [CrossRef]
- Thomas, R.C.; Hughes, R.C. Sensors for Detecting Molecular Hydrogen Based on Pd Metal Alloys. J. Electrochem. Soc. 1997, 144, 3245–3249. [Google Scholar] [CrossRef]
- Noh, J.S.; Lee, J.M.; Lee, W. Low-Dimensional Palladium Nanostructures for Fast and Reliable Hydrogen Gas Detection. Sensors 2011, 11, 825–851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, Y.; Zheng, L.; Zou, K.; Li, C. Enhancing Performances of a Resistivity-Type Hydrogen Sensor Based on Pd/SnO2/RGO Nanocomposites. Nanotechnology 2017, 28, 215501. [Google Scholar] [CrossRef]
- van Lith, J.; Lassesson, A.; Brown, S.A.; Schulze, M.; Partridge, J.G.; Ayesh, A. A Hydrogen Sensor Based on Tunneling between Palladium Clusters. Appl. Phys. Lett. 2007, 91, 181910. [Google Scholar] [CrossRef]
- Ellis, D.L.; Zakin, M.R.; Bernstein, L.S.; Rubner, M.F. Conductive Polymer Films as Ultrasensitive Chemical Sensors for Hydrazine and Monomethylhydrazine Vapor. Anal. Chem. 1996, 68, 817–822. [Google Scholar] [CrossRef]
- Huang, J.; Virji, S.; Weiller, B.H.; Kaner, R.B. Nanostructured Polyaniline Sensors. Chem.—A Eur. J. 2004, 10, 1314–1319. [Google Scholar] [CrossRef]
- Virji, S.; Kaner, R.B.; Weiller, B.H. Hydrogen Sensors Based on Conductivity Changes in Polyaniline Nanofibers. J. Phys. Chem. B 2006, 110, 22266–22270. [Google Scholar] [CrossRef] [PubMed]
- Herkert, E.; Sterl, F.; Strohfeldt, N.; Walter, R.; Giessen, H. Low-Cost Hydrogen Sensor in the Ppm Range with Purely Optical Readout. ACS Sens. 2020, 5, 978–983. [Google Scholar] [CrossRef] [PubMed]
- Mulder, D.J.; Schenning, A.P.H.J.; Bastiaansen, C.W.M. Chiral-Nematic Liquid Crystals as One Dimensional Photonic Materials in Optical Sensors. J. Mater. Chem. C 2014, 2, 6695–6705. [Google Scholar] [CrossRef] [Green Version]
- Esteves, C.; Ramou, E.; Porteira, A.R.P.; Barbosa, A.J.M.; Roque, A.C.A. Seeing the Unseen: The Role of Liquid Crystals in Gas-Sensing Technologies. Adv. Opt. Mater. 2020, 8, 1902117. [Google Scholar] [CrossRef]
- Carlton, R.J.; Hunter, J.T.; Miller, D.S.; Abbasi, R.; Mushenheim, P.C.; Tan, L.N.; Abbott, N.L. Chemical and Biological Sensing Using Liquid Crystals. Liq. Cryst. Rev. 2013, 1, 29. [Google Scholar] [CrossRef]
- De Sio, L.; Caligiuri, V.; Umeton, C. Tuneable Broadband Optical Filter Based on Soft-Composite Materials. J. Opt. 2014, 16, 065703. [Google Scholar] [CrossRef]
- Seidel, J.; Grafström, S.; Eng, L. Stimulated Emission of Surface Plasmons at the Interface between a Silver Film and an Optically Pumped Dye Solution. Phys. Rev. Lett. 2005, 94, 177401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaky, Z.A.; Ahmed, A.M.; Shalaby, A.S.; Aly, A.H. Refractive Index Gas Sensor Based on the Tamm State in a One-Dimensional Photonic Crystal: Theoretical Optimisation. Sci. Rep. 2020, 10, 9736. [Google Scholar] [CrossRef]
- Giessen, H.; Mai, P.; Tittl, A.; Liu, N.; Grossmann, C.; Seidel, A.; Orzekowsky, R.; Meyrath, T. Optical Hydrogen Sensing with Metallic Photonic Crystals and Plasmonic Metamaterials. In Proceedings of the IEEE Sensors, Waikoloa, HI, USA, 1–4 November 2010; pp. 2177–2178. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Recent Advances and Progress in Photonic Crystal-Based Gas Sensors. J. Phys. D Appl. Phys. 2017, 50, 203001. [Google Scholar] [CrossRef]
- Afsari, A.; Sarraf, M.J. Design of a Hydrogen Sulfide Gas Sensor Based on a Photonic Crystal Cavity Using Graphene. Superlattices Microstruct. 2020, 138, 106362. [Google Scholar] [CrossRef]
- Wadell, C.; Syrenova, S.; Langhammer, C. Plasmonic Hydrogen Sensing with Nanostructured Metal Hydrides. ACS Nano 2014, 8, 11925–11940. [Google Scholar] [CrossRef]
- Sil, D.; Gilroy, K.D.; Niaux, A.; Boulesbaa, A.; Neretina, S.; Borguet, E. Seeing Is Believing: Hot Electron Based Gold Nanoplasmonic Optical Hydrogen Sensor. ACS Nano 2014, 8, 7755–7762. [Google Scholar] [CrossRef]
- Langhammer, C.; Zorić, I.; Kasemo, B.; Clemens, B.M. Hydrogen Storage in Pd Nanodisks Characterized with a Novel Nanoplasmonic Sensing Scheme. Nano Lett. 2007, 7, 3122–3127. [Google Scholar] [CrossRef] [PubMed]
- Langhammer, C.; Larsson, E.M.; Zhdanov, V.P.; Zorić, I. Asymmetric Hysteresis in Nanoscopic Single-Metal Hydrides: Palladium Nanorings. J. Phys. Chem. C 2012, 116, 21201–21207. [Google Scholar] [CrossRef]
- Poyli, M.A.; Silkin, V.M.; Chernov, I.P.; Echenique, P.M.; Muiño, R.D.; Aizpurua, J. Multiscale Theoretical Modeling of Plasmonic Sensing of Hydrogen Uptake in Palladium Nanodisks. J. Phys. Chem. Lett. 2012, 3, 2556–2561. [Google Scholar] [CrossRef] [PubMed]
- Policicchio, A.; Conte, G.; Stelitano, S.; Bonaventura, C.P.; Putz, A.-M.; Ianăşi, C.; Almásy, L.; Horváth, Z.E.; Agostino, R.G. Hydrogen Storage Performances for Mesoporous Silica Synthesized with Mixed Tetraethoxysilane and Methyltriethoxysilane Precursors in Acidic Condition. Colloids Surf. A Physicochem. Eng. Asp. 2020, 601, 125040. [Google Scholar] [CrossRef]
- Pedicini, R.; Maisano, S.; Chiodo, V.; Conte, G.; Policicchio, A.; Agostino, R.G. Posidonia Oceanica and Wood Chips Activated Carbon as Interesting Materials for Hydrogen Storage. Int. J. Hydrogen Energy 2020, 45, 14038–14047. [Google Scholar] [CrossRef]
- Policicchio, A.; Putz, A.-M.; Conte, G.; Stelitano, S.; Bonaventura, C.P.; Ianăşi, C.; Almásy, L.; Wacha, A.; Horváth, Z.E.; Agostino, R.G. Hydrogen Storage Performance of Methyl-Substituted Mesoporous Silica with Tailored Textural Characteristics. J. Porous Mater. 2021, 28, 1049–1058. [Google Scholar] [CrossRef]
- Sugawa, K.; Tahara, H.; Yamashita, A.; Otsuki, J.; Sagara, T.; Harumoto, T.; Yanagida, S. Refractive Index Susceptibility of the Plasmonic Palladium Nanoparticle: Potential as the Third Plasmonic Sensing Material. ACS Nano 2015, 9, 1895–1904. [Google Scholar] [CrossRef]
- Langhammer, C.; Yuan, Z.; Zorić, I.; Kasemo, B. Plasmonic Properties of Supported Pt and Pd Nanostructures. Nano Lett. 2006, 6, 833–838. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for Better Plasmonic Materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Marchi, S.D.; Núñez-Sánchez, S.; Bodelón, G.; Pérez-Juste, J.; Pastoriza-Santos, I. Pd Nanoparticles as a Plasmonic Material: Synthesis, Optical Properties and Applications. Nanoscale 2020, 12, 23424–23443. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Tang, S.; Mu, X.; Dai, Y.; Chen, G.; Zhou, Z.; Ruan, F.; Yang, Z.; Zheng, N. Freestanding Palladium Nanosheets with Plasmonic and Catalytic Properties. Nat. Nanotechnol. 2011, 6, 28–32. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic Metamaterials. Nat. Photonics 2013, 7, 958–968. [Google Scholar] [CrossRef]
- Vasilantonakis, N.; Wurtz, G.A.; Podolskiy, V.A.; Zayats, A.V. Refractive Index Sensing with Hyperbolic Metamaterials: Strategies for Biosensing and Nonlinearity Enhancement. Opt. Express 2015, 23, 14329–14343. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic Metamaterials and Their Applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Caligiuri, V.; Pezzi, L.; Veltri, A.; De Luca, A. Resonant Gain Singularities in 1D and 3D Metal-Dielectric Multilayered Nanostructures. ACS Nano 2017, 11, 1012–1025. [Google Scholar] [CrossRef]
- Hierro-Rodriguez, A.; Leite, I.T.; Rocha-Rodrigues, P.; Fernandes, P.; Araujo, J.P.; Jorge, P.A.S.; Santos, J.L.; Teixeira, J.M.; Guerreiro, A. Hydrogen Sensing via Anomalous Optical Absorption of Palladium-Based Metamaterials. Nanotechnology 2016, 27, 185501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caligiuri, V.; Palei, M.; Biffi, G.; Artyukhin, S.; Krahne, R. A Semi-Classical View on Epsilon-Near-Zero Resonant Tunneling Modes in Metal/Insulator/Metal Nanocavities. Nano Lett. 2019, 19, 3151–3160. [Google Scholar] [CrossRef]
- Isidorsson, J.; Giebels, I.A.M.E.; Arwin, H.; Griessen, R. Optical Properties of MgH2 Measured in Situ by Ellipsometry and Spectrophotometry. Phys. Rev. B 2003, 68, 115112. [Google Scholar] [CrossRef] [Green Version]
- Caligiuri, V.; Dhama, R.; Sreekanth, K.V.; Strangi, G.; De Luca, A. Dielectric Singularity in Hyperbolic Metamaterials: The Inversion Point of Coexisting Anisotropies. Sci. Rep. 2016, 6, 20002. [Google Scholar] [CrossRef]
- Caligiuri, V.; Palei, M.; Biffi, G.; Krahne, R. Hybridization of Epsilon-near-Zero Modes via Resonant Tunneling in Layered Metal-Insulator Double Nanocavities. Nanophotonics 2019, 8, 1–8. [Google Scholar] [CrossRef]
- Caligiuri, V.; Biffi, G.; Patra, A.; Pothuraju, R.D.; Luca, A.D.; Krahne, R. One-Dimensional Epsilon-Near-Zero Crystals. Adv. Photonics Res. 2021, 2, 2100053. [Google Scholar] [CrossRef]
- Caligiuri, V.; Pianelli, A.; Miscuglio, M.; Patra, A.; MacCaferri, N.; Caputo, R.; De Luca, A. Near- And Mid-Infrared Graphene-Based Photonic Architectures for Ultrafast and Low-Power Electro-Optical Switching and Ultra-High Resolution Imaging. ACS Appl. Nano Mater. 2020, 3, 12218–12230. [Google Scholar] [CrossRef]
- Kuttruff, J.; Garoli, D.; Allerbeck, J.; Krahne, R.; De Luca, A.; Brida, D.; Caligiuri, V.; Maccaferri, N. Ultrafast All-Optical Switching Enabled by Epsilon-near-Zero-Tailored Absorption in Metal-Insulator Nanocavities. Commun. Phys. 2020, 3, 1–7. [Google Scholar] [CrossRef]
- Gaponenko, S.V. Introduction to Nanophotonics; Cambridge University Press: Cambridge, UK, 2010; p. 465. ISBN 978-0-511-75050-2. [Google Scholar]
- Caligiuri, V.; Palei, M.; Imran, M.; Manna, L.; Krahne, R. Planar Double-Epsilon-Near-Zero Cavities for Spontaneous Emission and Purcell Effect Enhancement. ACS Photonics 2018, 5, 2287–2294. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).