Investigation of Shielding Effects on Picosecond Laser-Induced Copper Plasma Characteristics under Different Focusing Distances
Abstract
:1. Introduction
2. Materials and Methods
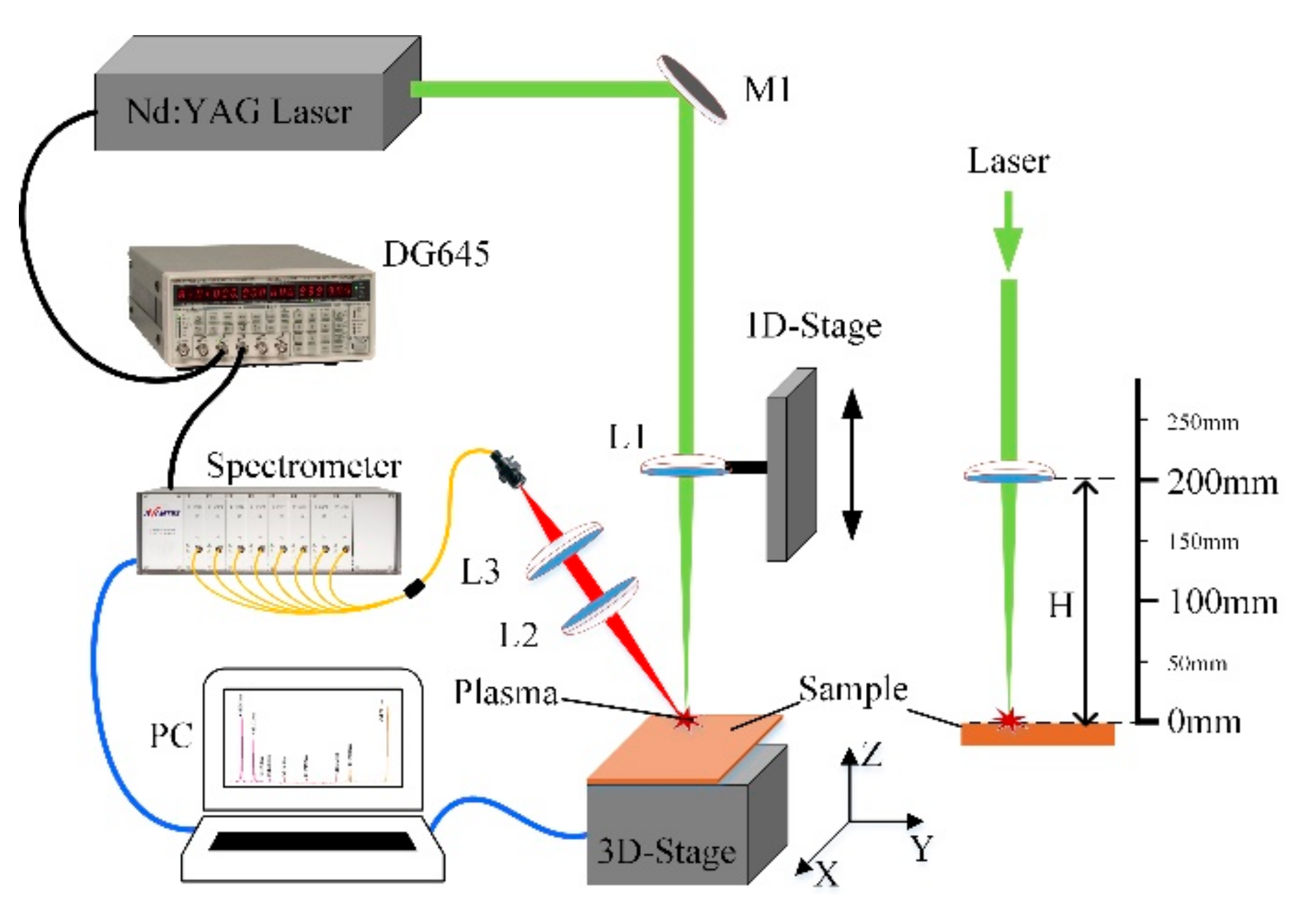
2.1. Instrumentation
2.2. Operating Conditions
3. Results and Discussion
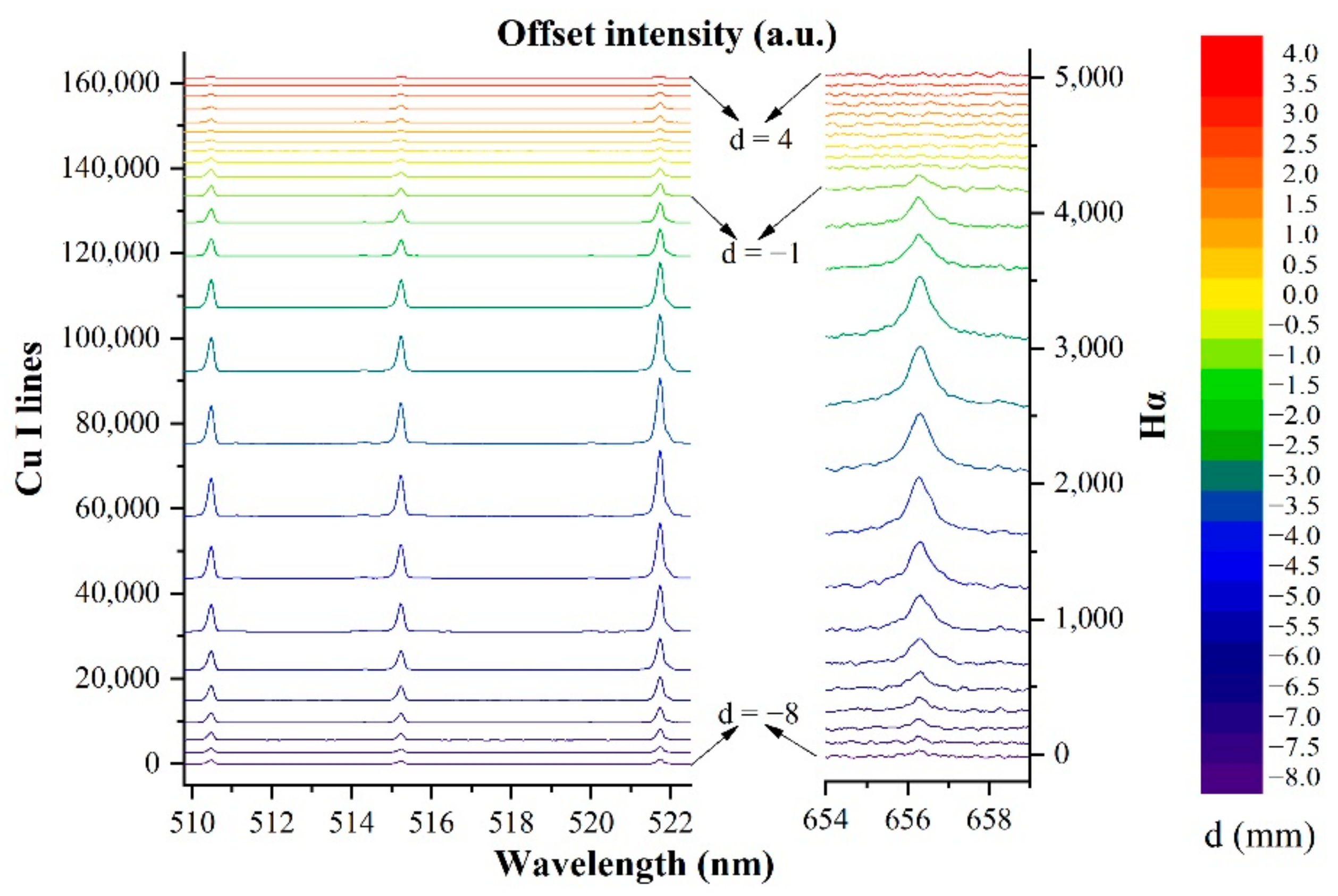
3.1. Emission Spectrum
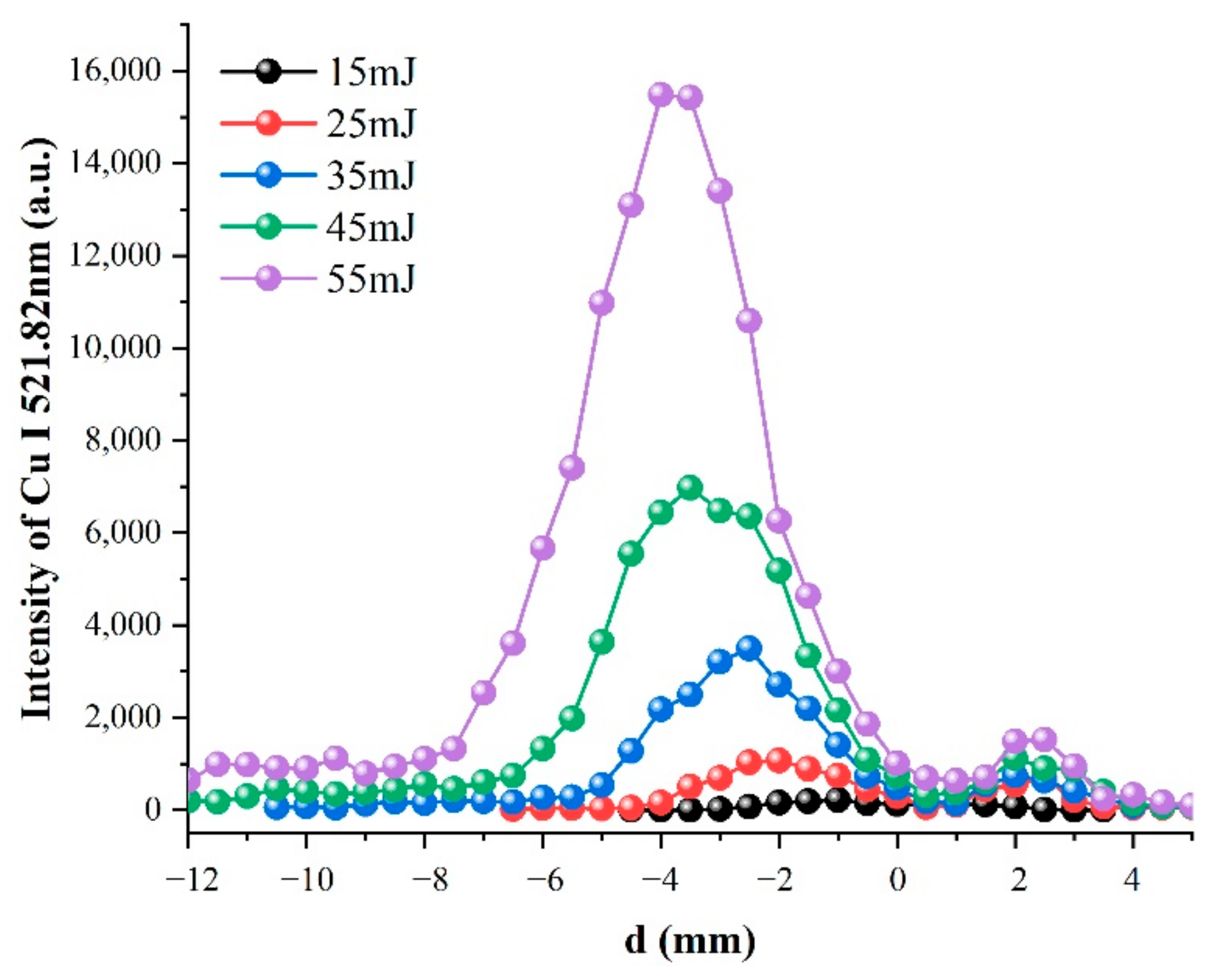
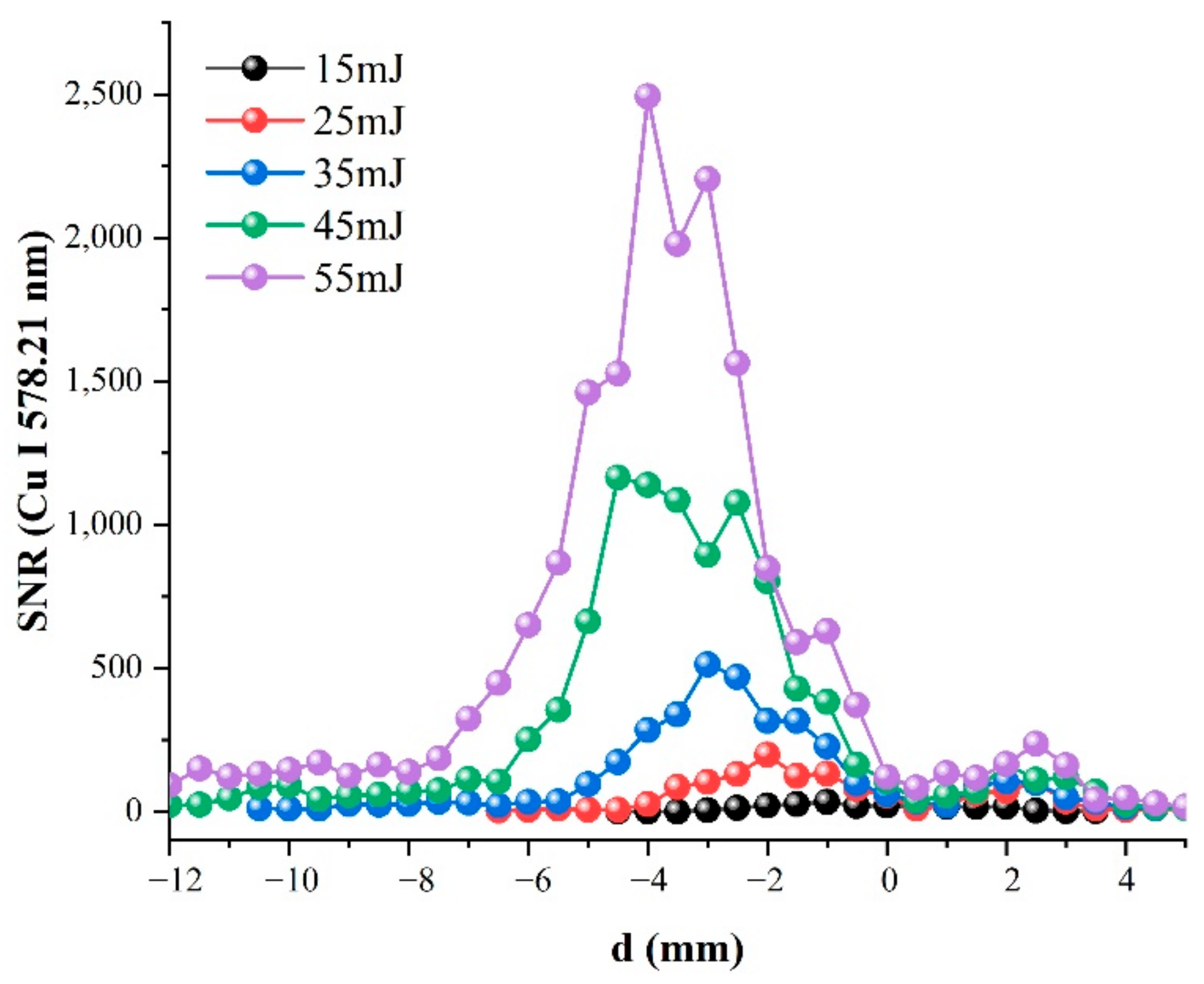
3.2. Effects of Pulse Energy
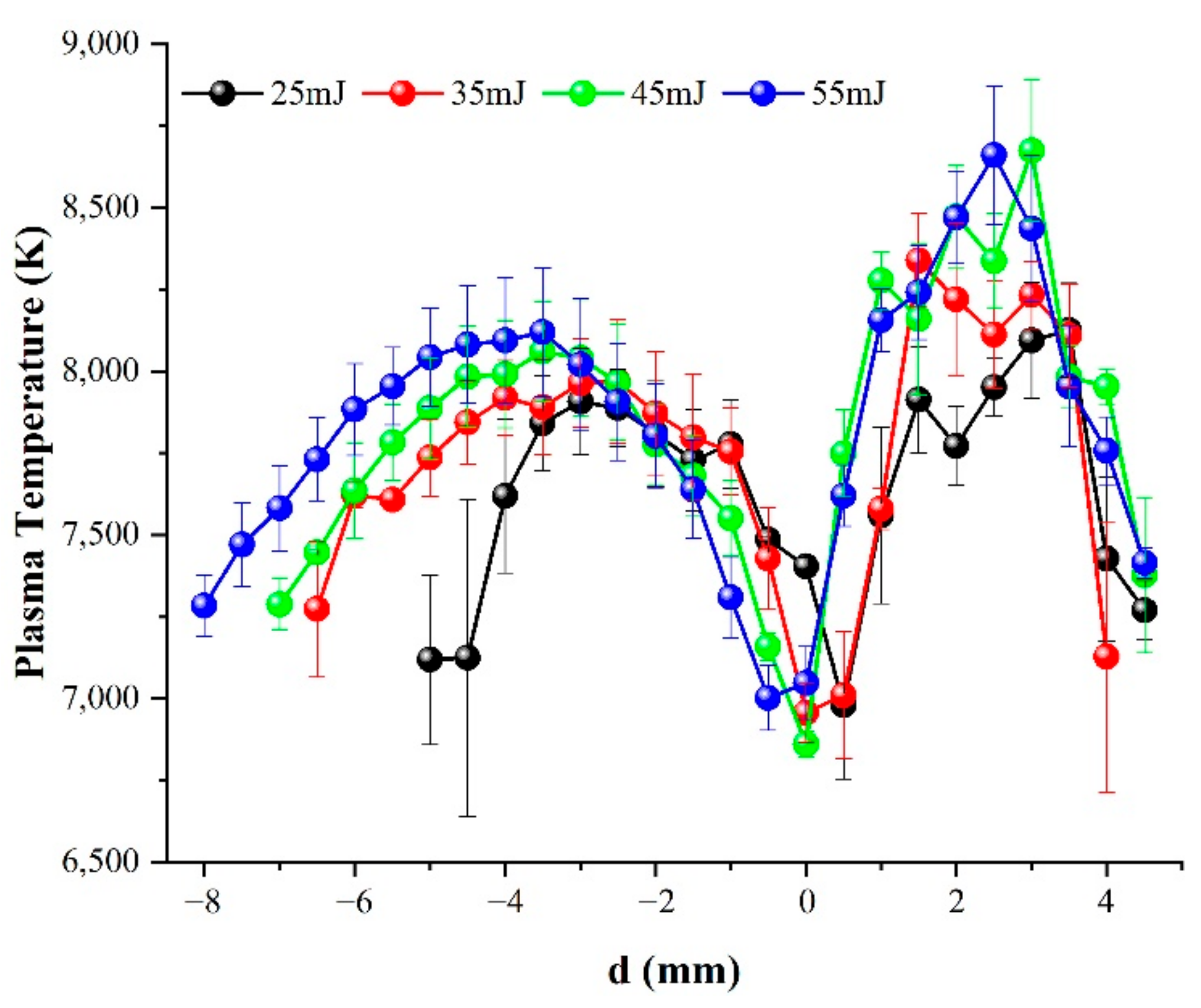
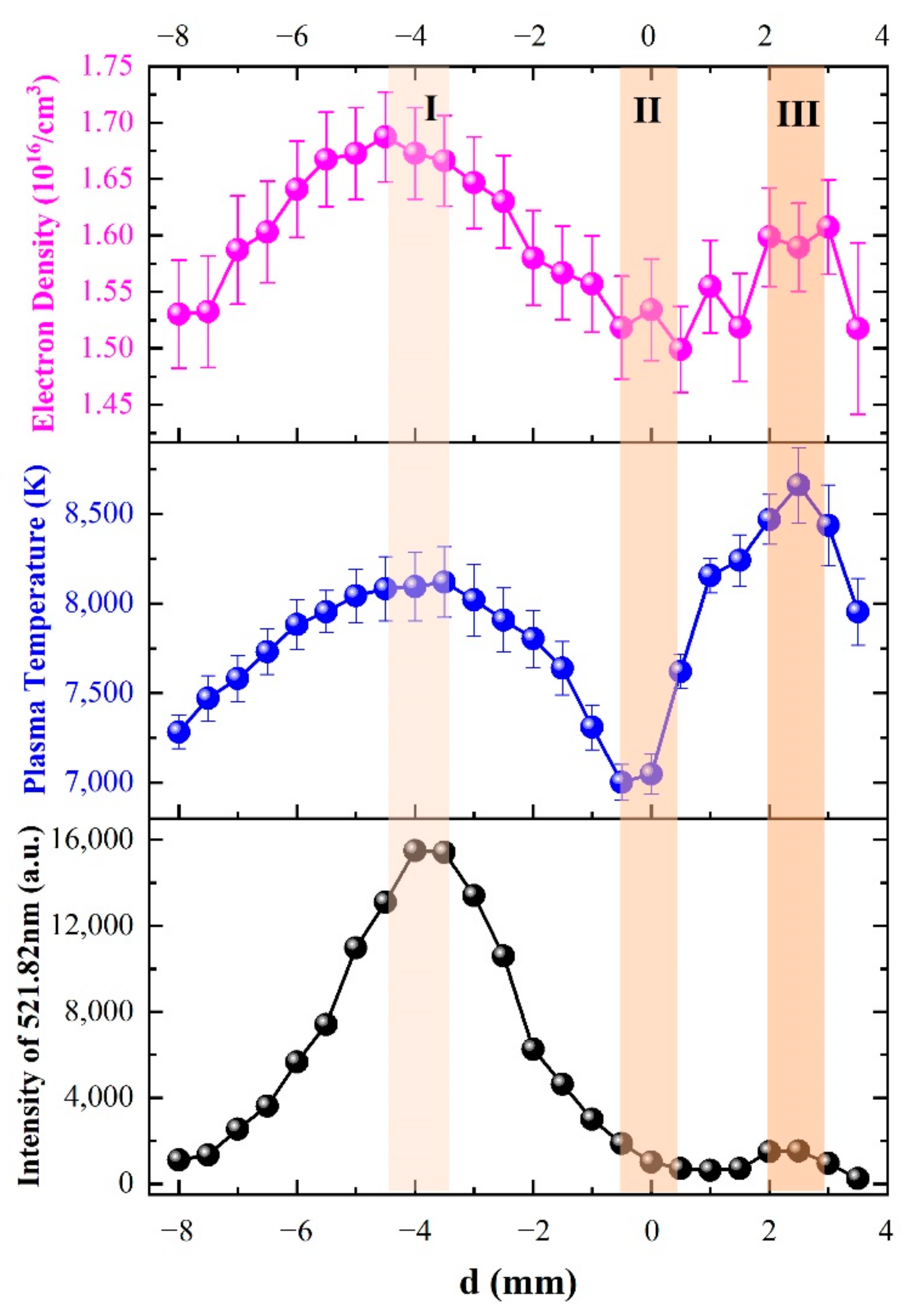
3.3. Plasma Temperature
3.4. Electron Density
3.5. Validity of LTE and Optically Thin
3.6. Internal Relationship
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Ahmed, R.; Iqbal, J.; Baig, M.A. Effects of laser wavelengths and pulse energy ratio on the emission enhancement in dual pulse LIBS. Laser Phys. Lett. 2015, 12, 66102. [Google Scholar] [CrossRef]
- Bredice, F.O.; Di Rocco, H.O.; Sobral, H.M.; Villagrán-Muniz, M.; Palleschi, V. A new method for determination of self-absorption coefficients of emission lines in laser-induced breakdown spectroscopy experiments. Appl. Spectrosc. 2010, 64, 320–323. [Google Scholar] [CrossRef] [PubMed]
- De Lucia, F.C.; Gottfried, J.L.; Miziolek, A.W. Evaluation of femtosecond laser-induced breakdown spectroscopy for explosive residue detection. Opt. Express 2009, 17, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Cremers, D.A.; Radziemski, L.J. Handbook of Laser-Induced Breakdown Spectroscopy, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013; ISBN 9781118567364. [Google Scholar]
- Li, Q.; Tian, Y.; Xue, B.; Li, N.; Ye, W.; Lu, Y.; Zheng, R. Improvement in the analytical performance of underwater LIBS signals by exploiting the plasma image information. J. Anal. At. Spectrom. 2020, 35, 366–376. [Google Scholar] [CrossRef]
- Ruiz, J.; Delgado, T.; Cabalín, L.M.; Laserna, J.J. At-line monitoring of continuous casting sequences of steel using discriminant function analysis and dual-pulse laser-induced breakdown spectroscopy. J. Anal. At. Spectrom. 2017, 32, 1119–1128. [Google Scholar] [CrossRef]
- Rauschenbach, I.; Jessberger, E.K.; Pavlov, S.G.; Hübers, H.-W. Miniaturized Laser-Induced Breakdown Spectroscopy for the in-situ analysis of the Martian surface: Calibration and quantification. Spectrochim. Acta Part B At. Spectrosc. 2010, 65, 758–768. [Google Scholar] [CrossRef]
- Pagnotta, S.; Lezzerini, M.; Ripoll-Seguer, L.; Hidalgo, M.; Grifoni, E.; Legnaioli, S.; Lorenzetti, G.; Poggialini, F.; Palleschi, V. Micro-Laser-Induced Breakdown Spectroscopy (Micro-LIBS) Study on Ancient Roman Mortars. Appl. Spectrosc. 2017, 71, 721–727. [Google Scholar] [CrossRef]
- Yao, M.; Lin, J.; Liu, M.; Xu, Y. Detection of chromium in wastewater from refuse incineration power plant near Poyang Lake by laser induced breakdown spectroscopy. Appl. Opt. 2012, 51, 1552–1557. [Google Scholar] [CrossRef]
- Xu, W.; Chen, A.; Wang, Q.; Zhang, D.; Wang, Y.; Li, S.; Jiang, Y.; Jin, M. Generation of high-temperature and low-density plasma with strong spectral intensity by changing the distance between the focusing lens and target surface in femtosecond laser-induced breakdown spectroscopy. J. Anal. At. Spectrom. 2019, 34, 1018–1025. [Google Scholar] [CrossRef]
- Singh, J.P.; Thakur, S.N. Laser-Induced Breakdown Spectroscopy, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 978-0-444-51734-0. [Google Scholar]
- Liu, D.; Zhang, D. Vaporization and Plasma Shielding during High Power Nanosecond Laser Ablation of Silicon and Nickel. Chin. Phys. Lett. 2008, 25, 1368–1371. [Google Scholar] [CrossRef]
- Mao, X.; Russo, R.E. Invited paper Observation of plasma shielding by measuring transmitted and reflected laser pulse temporal profiles. Appl. Phys. A 1996, 64, 1–6. [Google Scholar] [CrossRef]
- Giannuzzi, G.; Gaudiuso, C.; Di Franco, C.; Scamarcio, G.; Lugarà, P.M.; Ancona, A. Large area laser-induced periodic surface structures on steel by bursts of femtosecond pulses with picosecond delays. Opt. Lasers Eng. 2019, 114, 15–21. [Google Scholar] [CrossRef]
- Aguilera, J.A.; Aragón, C.; Peñalba, F. Plasma shielding effect in laser ablation of metallic samples and its influence on LIBS analysis. Appl. Surf. Sci. 1998, 127-129, 309–314. [Google Scholar] [CrossRef]
- Capon, M.R.; Docchio, F.; Mellerio, J. Nd:YAG laser photodisruption: An experimental investigation on shielding and multiple plasma formation. Graefe’s Arch. Clin. Exp. Ophthalmol. 1988, 226, 362–366. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, D.; Li, Z.; Hou, S.; Yu, B.; Guan, L.; Tan, X.; Li, L. A new model of pulsed laser ablation and plasma shielding. Phys. B Condens. Matter 2005, 362, 82–87. [Google Scholar] [CrossRef]
- Penczak, J.; Kupfer, R.; Bar, I.; Gordon, R.J. The role of plasma shielding in collinear double-pulse femtosecond laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2014, 97, 34–41. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.H.; Kim, T.H.; Jung, E.C.; Yun, J.-I. Shielding effect of laser-induced plasma in glass: Pulse-to-pulse evolution of nitrogen and analyte emission lines. Appl. Phys. A 2011, 104, 863–869. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Li, H.; Li, X.; Li, Z. Lens-to-sample distance effect on the quantitative analysis of steel by laser-induced breakdown spectroscopy. J. Phys. D Appl. Phys. 2020, 53, 255203. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, M.; Liu, X.; Cui, Q.; Zhao, M. The mechanism of effect of lens-to-sample distance on laser-induced plasma. Acta Phys. Sin. 2013, 62, 25203. [Google Scholar] [CrossRef]
- Fu, H.; Ni, Z.; Wang, H.; Jia, J.; Dong, F. Accuracy improvement of calibration-free laser-induced breakdown spectroscopy. Plasma Sci. Technol. 2019, 21, 34001. [Google Scholar] [CrossRef]
- Goncharov, V.K.; Kozadaev, K.V.; Makarov, V.V.; Shchegrikovich, D.V. Occurrence of erosion processes in the near-surface region of metals exposed to intense nanosecond laser pulses. J. Eng. Thermophys. 2013, 86, 798–804. [Google Scholar] [CrossRef]
- Mao, S.S.; Mao, X.; Greif, R.; Russo, R.E. Dynamics of an air breakdown plasma on a solid surface during picosecond laser ablation. Appl. Phys. Lett. 2000, 76, 31–33. [Google Scholar] [CrossRef]
- Zhang, N.; Zhu, X.; Yang, J.; Wang, X.; Wang, M. Time-resolved shadowgraphs of material ejection in intense femtosecond laser ablation of aluminum. Phys. Rev. Lett. 2007, 99, 167602. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Du, X.; Dong, G.; Qiu, J. Influence of laser-induced air breakdown on femtosecond laser ablation of aluminum. Opt. Express 2015, 23, 1370–1376. [Google Scholar] [CrossRef]
- Li, X.; Wei, W.; Wu, J.; Jia, S.; Qiu, A. The Influence of spot size on the expansion dynamics of nanosecond-laser-produced copper plasmas in atmosphere. J. Appl. Phys. 2013, 113, 243304. [Google Scholar] [CrossRef]
- Harilal, S.S.; Coons, R.W.; Hough, P.; Hassanein, A. Influence of spot size on extreme ultraviolet efficiency of laser-produced Sn plasmas. Appl. Phys. Lett. 2009, 95, 221501. [Google Scholar] [CrossRef] [Green Version]
- Vadillo, J.M.; Fernández Romero, J.M.; Rodríguez, C.; Laserna, J.J. Effect of plasma shielding on laser ablation rate of pure metals at reduced pressure. Surf. Interface Anal. 1999, 27, 1009–1015. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Cristoforetti, G.; de Giacomo, A.; Dell’Aglio, M.; Legnaioli, S.; Tognoni, E.; Palleschi, V.; Omenetto, N. Local Thermodynamic Equilibrium in Laser-Induced Breakdown Spectroscopy: Beyond the McWhirter criterion. Spectrochim. Acta Part B At. Spectrosc. 2010, 65, 86–95. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, L.; Yin, W.; Yao, S.; Zhao, Y.; Ma, W.; Dong, L.; Xiao, L.; Jia, S. Development and performance evaluation of self-absorption-free laser-induced breakdown spectroscopy for directly capturing optically thin spectral line and realizing accurate chemical composition measurements. Opt. Express 2017, 25, 23024–23034. [Google Scholar] [CrossRef]
- Hahn, D.W.; Omenetto, N. Laser-induced breakdown spectroscopy (LIBS), part I: Review of basic diagnostics and plasma-particle interactions: Still-challenging issues within the analytical plasma community. Appl. Spectrosc. 2010, 64, 335–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jabbar, A.; Hou, Z.; Liu, J.; Ahmed, R.; Mahmood, S.; Wang, Z. Calibration-free analysis of immersed metal alloys using long-pulse-duration laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2019, 157, 84–90. [Google Scholar] [CrossRef]
- Konjević, N.; Wiese, W.L. Experimental Stark widths and shifts for spectral lines of neutral and ionized atoms. J. Phys. Chem. Ref. Data 1990, 19, 1307–1385. [Google Scholar] [CrossRef]
- Shakeel, H.; Haq, S.U.; Abbas, Q.; Nadeem, A.; Palleschi, V. Quantitative analysis of Ge/Si alloys using double-pulse calibration-free laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2018, 146, 101–105. [Google Scholar] [CrossRef]
- Valenzuela, A.; Munson, C.; Porwitzky, A.; Weidman, M.; Richardson, M. Comparison between geometrically focused pulses versus filaments in femtosecond laser ablation of steel and titanium alloys. Appl. Phys. B 2014, 116, 485–491. [Google Scholar] [CrossRef]
- Zhong, J.; Li, Y.; Lu, X.; Zhang, Y.; Bernhardt, J.; Liu, F.; Hao, Z.; Yu, Q.; Chen, M.; Yuan, X.; et al. Generation of single plasma channel in air. Acta Phys. Sin. 2007, 56, 7114–7119. [Google Scholar] [CrossRef]


| Wavelength | Aki (s−1) | gk | Transition Levels (Up→Low) | Ek (eV) | Ei (eV) |
|---|---|---|---|---|---|
| 510.55 nm | 0.2 × 107 | 4 | 3d104p(2P3/2)→3d94s2(2D5/2) | 3.817 | 1.389 |
| 515.32 nm | 6 × 107 | 4 | 3d104d(2D3/2)→3d104p(2P1/2) | 6.192 | 3.786 |
| 521.82 nm | 7.5 × 107 | 6 | 3d104d(2D5/2)→3d104p(2P3/2) | 6.193 | 3.817 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Deng, H.; Xiong, Z.; Guo, J.; Liu, Q.; Li, G.; Shang, L. Investigation of Shielding Effects on Picosecond Laser-Induced Copper Plasma Characteristics under Different Focusing Distances. Photonics 2021, 8, 536. https://doi.org/10.3390/photonics8120536
Chen L, Deng H, Xiong Z, Guo J, Liu Q, Li G, Shang L. Investigation of Shielding Effects on Picosecond Laser-Induced Copper Plasma Characteristics under Different Focusing Distances. Photonics. 2021; 8(12):536. https://doi.org/10.3390/photonics8120536
Chicago/Turabian StyleChen, Linyu, Hu Deng, Zhonggang Xiong, Jin Guo, Quancheng Liu, Guilin Li, and Liping Shang. 2021. "Investigation of Shielding Effects on Picosecond Laser-Induced Copper Plasma Characteristics under Different Focusing Distances" Photonics 8, no. 12: 536. https://doi.org/10.3390/photonics8120536
APA StyleChen, L., Deng, H., Xiong, Z., Guo, J., Liu, Q., Li, G., & Shang, L. (2021). Investigation of Shielding Effects on Picosecond Laser-Induced Copper Plasma Characteristics under Different Focusing Distances. Photonics, 8(12), 536. https://doi.org/10.3390/photonics8120536





