Ultrafast High-Voltage Kicker System for Ion-Clearing Gaps
Abstract
:1. Introduction
2. Electromagnetic Design
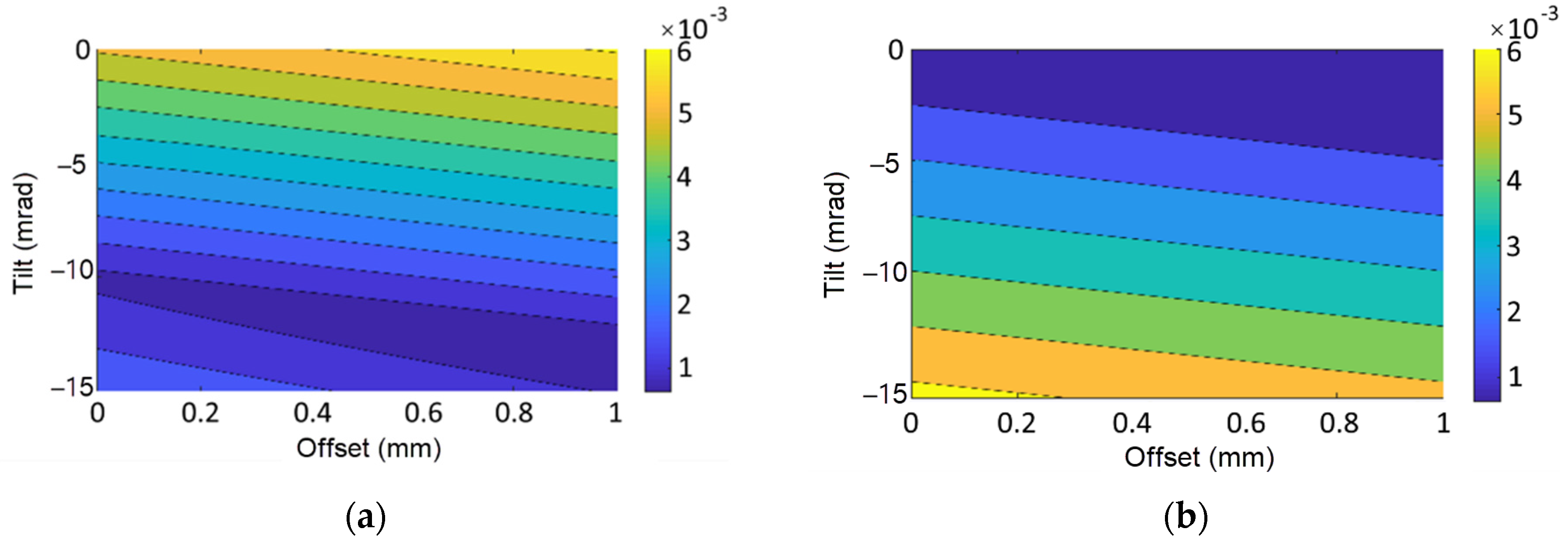
3. Beam Dynamics
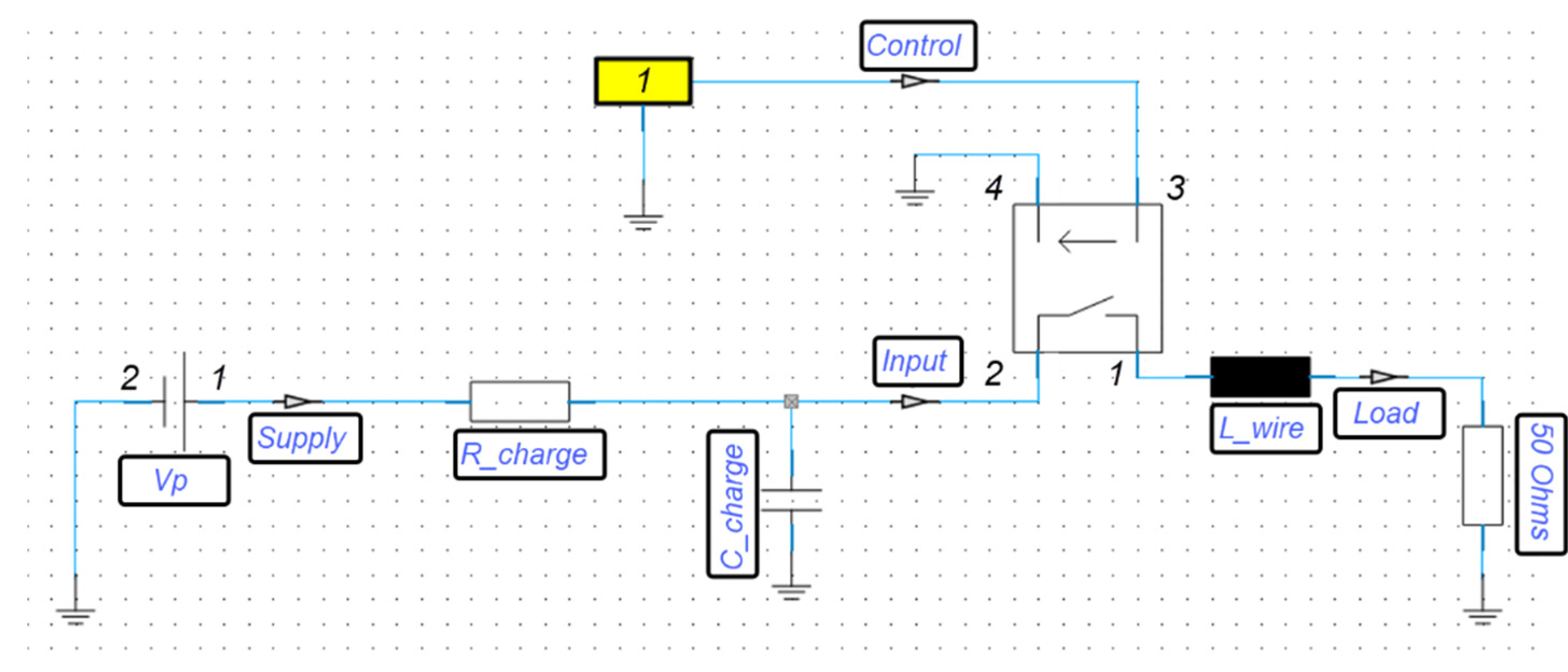
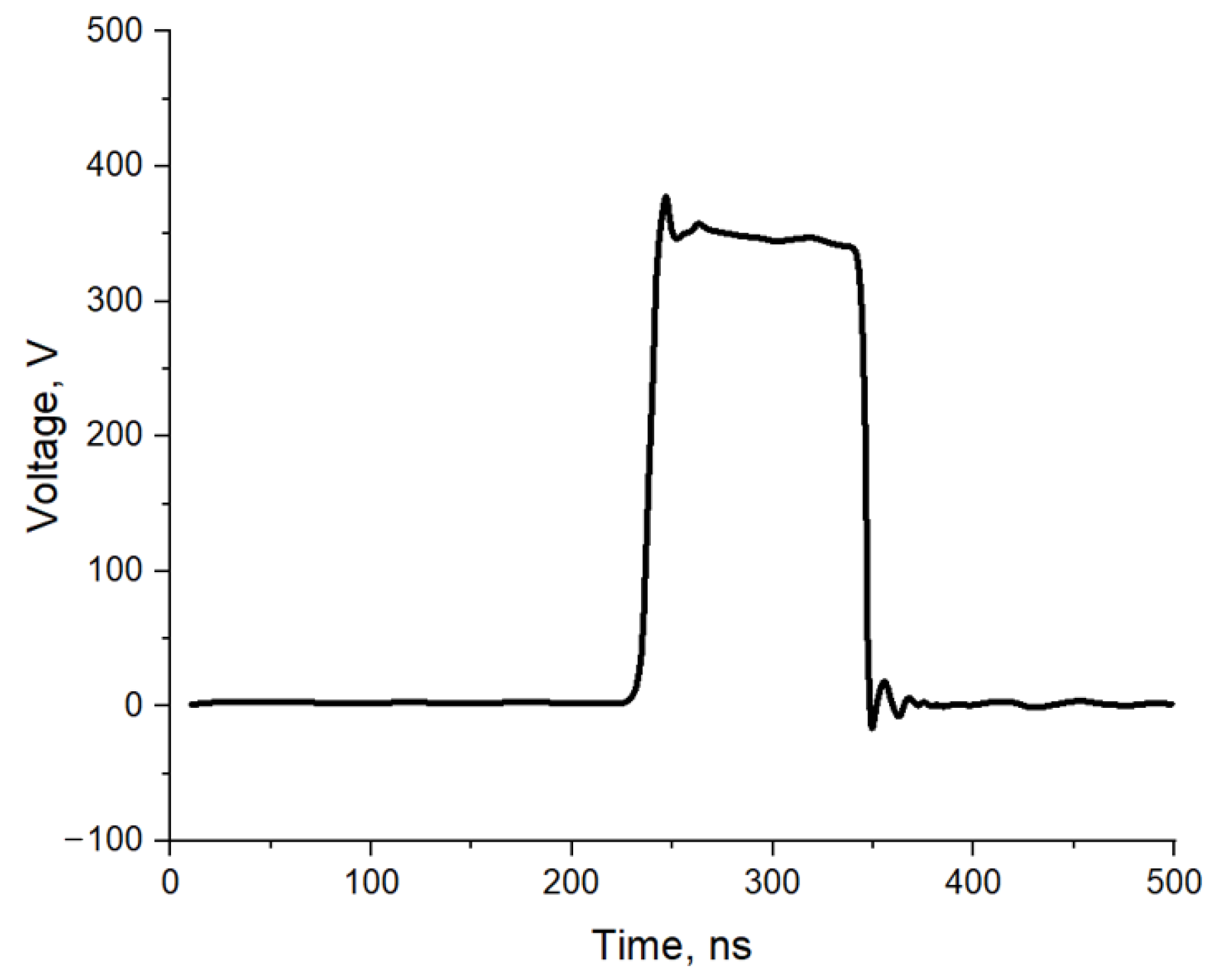
4. High-Voltage Tests
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Accardi, A.; Albacete, J.L.; Anselmino, M.; Armesto, N.; Aschenauer, E.C.; Bacchetta, A.; Boer, D.; Brooks, W.K.; Burton, T.; Chang, N.-B.; et al. Electron-Ion Collider: The next QCD frontier. Eur. Phys. J. A 2016, 52, 268. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, F. Future colliders for particle physics—“Big and small”. Nucl. Instrum. Meth. Phys. Res. A 2018, 909, 33–37. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Derbenev, Y.; Benson, S.; Roblin, Y. Multi-Stage Electron Cooling Scheme for JLEIC. In Proceedings of the 9th International Particle Accelerator Conference (IPAC’18), Vancouver, BC, Canada, 29 April–4 May 2018; pp. 397–399. [Google Scholar]
- Thieberger, P.; Altinbas, Z.; Carlson, C.; Chasman, C.; Costanzo, M.; Degen, C.; Drees, K.A.; Fischer, W.; Gassner, D.; Gu, X.; et al. High energy Coulomb-scattered electrons for relativistic particle beam diagnostics. Phys. Rev. Accel. Beams 2016, 19, 041002. [Google Scholar] [CrossRef] [Green Version]
- Mether, L.; Oeftiger, A.; Rumolo, G. Modeling of fast beam-ion instabilities. CERN Yellow Rep. Conf. Proc. 2018, 1, 63–68. [Google Scholar] [CrossRef]
- Hoffstaetter, G.H.; Liepe, M. Ion clearing in an ERL. Nucl. Instrum. Meth. Phys. Res. A 2006, 557, 205–212. [Google Scholar] [CrossRef]
- Chao, A.W.; Mess, K.H.; Tigner, M.; Zimmermann, F. Handbook of Accelerator Physics and Engineering, 2nd ed.; World Scientific Publishing Co.: Hackensack, NJ, USA, 2013. [Google Scholar]
- Full, S.; Bartnik, A.; Bazarov, I.V.; Dobbins, J.; Dunham, B.; Hoffstaetter, G.H. Detection and clearing of trapped ions in the high current Cornell photoinjector. Phys. Rev. Accel. Beams 2016, 19, 034201. [Google Scholar] [CrossRef] [Green Version]
- Poncet, A. Ion trapping, clearing, beam-ion interactions. In Proceedings of the CERN Accelerator School Course on Vacuum Technology for Particle Accelerators, Copenhagen, Denmark, 28 May–3 June 1999; pp. 165–202. [Google Scholar]
- Dienes, M.; Month, M.; Strasser, B.; Turner, S. Frontiers of Particle Beams: Factories with e+ e− Rings. Lect. Notes Phys. 1994, 425, 202–221. [Google Scholar] [CrossRef]
- Ben-Zvi, I. Superconducting energy recovery linacs. Supercond. Sci. Technol. 2016, 29, 103002. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Roblin, Y.; Zhang, Y.; Derbenev, Y.; Benson, S.; Li, R.; Chen, J.; Huang, H.; Luo, L. Simulation Study on JLEIC High Energy Bunched Electron Cooling. In Proceedings of the North American Particle Accelerator Conference 2016, Chicago, IL, USA, 9–14 October 2016; pp. 568–571. [Google Scholar]
- Hajima, R. Energy Recovery Linacs for Light Sources. Rev. Accel. Sci. Technol. 2012, 3, 121–146. [Google Scholar] [CrossRef]
- Gassner, D.M.; Fedotov, A.; Hulsart, R.; Kayran, D.; Litvinenko, V.; Michnoff, R.; Miller, T. Instrumentation for the Proposed Low Energy RHIC Electron Cooling Project with Energy Recovery. In Proceedings of the 3rd International Beam Instrumentation Conference 2014, Monterey, CA, USA, 14–18 September 2014; pp. 49–54. [Google Scholar]
- Tennant, C.; Alarcon, R.; Balewski, J.; Benson, S.; Bernauer, J.; Bessuille, J.; Blyth, D.; Boyce, J.; Cao, T.; Cervantes, R. LERF-New Life for the Jefferson Lab FEL. In Proceedings of the ERL 2017, the 59th ICFA Advanced Beam Dynamics Workshop on Energy Recovery Linacs, Geneva, Switzerland, 18–23 June 2018; pp. 45–48. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles, 1st ed.; CRC Press: Boca Raton, FL, USA, 1988; ISBN 9780852743928. [Google Scholar]
- Novikov-Borodin, A.V.; Kutuzov, V.A.; Ostroumov, P.N. A fast chopper for intensity adjustment of heavy-ion beams. In Proceedings of the IEEE Particle Accelerator Conference (PAC’05), Knoxville, TN, USA, 16–20 May 2005; Volume 2005, pp. 1692–1694. [Google Scholar]
- Couprie, M.E. New generation of light sources: Present and future. J. Electron. Spectrosc. Relat. Phenom. 2014, 196, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Drebot, I.; Bacci, A.; Bosotti, A.; Broggi, F.; Canella, F.; Cardarelli, P.; Cialdi, S.; Faillace, L.; Galzerano, G.; Gambaccini, M.; et al. BriXs Ultra High Flux Inverse Compton Source Based on Modified Push-Pull Energy Recovery Linacs. Instruments 2019, 3, 49. [Google Scholar] [CrossRef] [Green Version]
- Avreline, N.; Kutsaev, S.V.; Avreline, A.; Murokh, A. Acceleration of heavy ions in inverse free electron laser. Laser Phys. Lett. 2021, 18, 055402. [Google Scholar] [CrossRef]
- Raab, F.H. Class-E, class-C, and class-F power amplifiers based upon a finite number of harmonics. IEEE Trans. Microw. Theory Tech. 2001, 49, 1462–1468. [Google Scholar] [CrossRef]
- Smirnov, A.; Agustsson, R.; Ahmadi, M.; Blanchard, P.; Boucher, S.; Branner, R.; Hartzell, J.; Hoyt, K.; Khodos, V.; Mccann, D. Progress on 1.5 GHz Multi-kW CW Amplifier. In Proceedings of the 9th International Particle Accelerator Conference (IPAC’18), Vancouver, BC, Canada, 29 April–4 May 2018. [Google Scholar]





| Parameter | Value |
|---|---|
| Deflecting angle | 20 mrad (deflecting voltage 140 kV) |
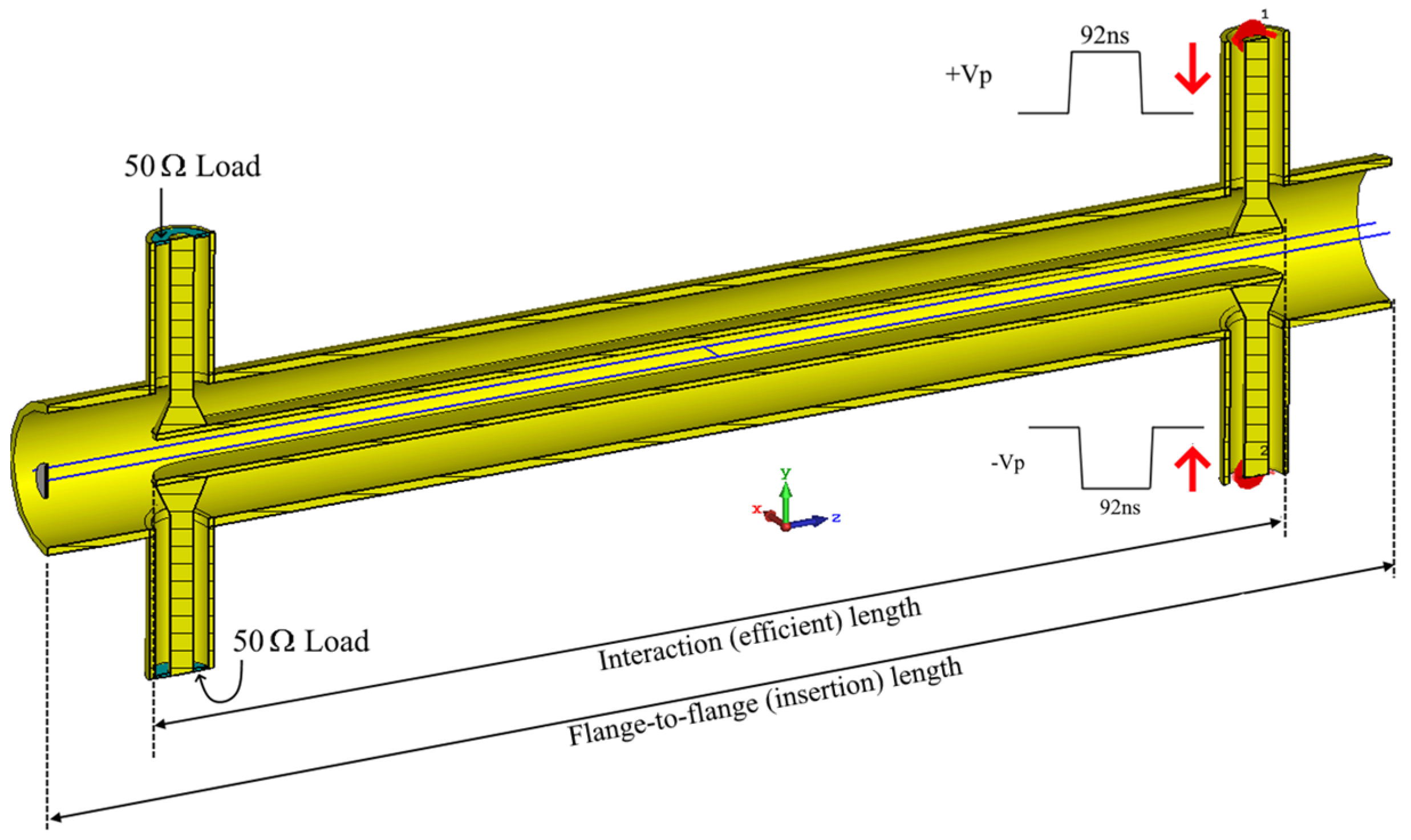
| Flange-to-flange length | 50–60 cm |
| Electron beam energy | 7 MeV |
| Bunch repetition rate | 43.4 MHz |
| Bunch rms transverse size | σ = 1 mm |
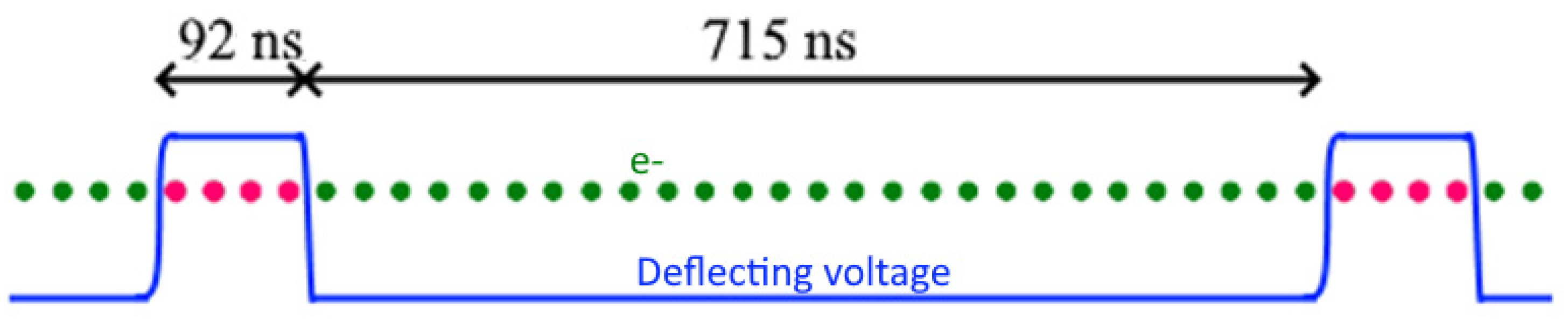
| Deflecting pulse width | 92 ns flat-top required to deflect 4 out of 31 bunches in train |
| Kicker operation per rate | 1.4 MHz (715 ns pulsing period) |
| Rise and fall time | <20 ns (10 ns desired) |
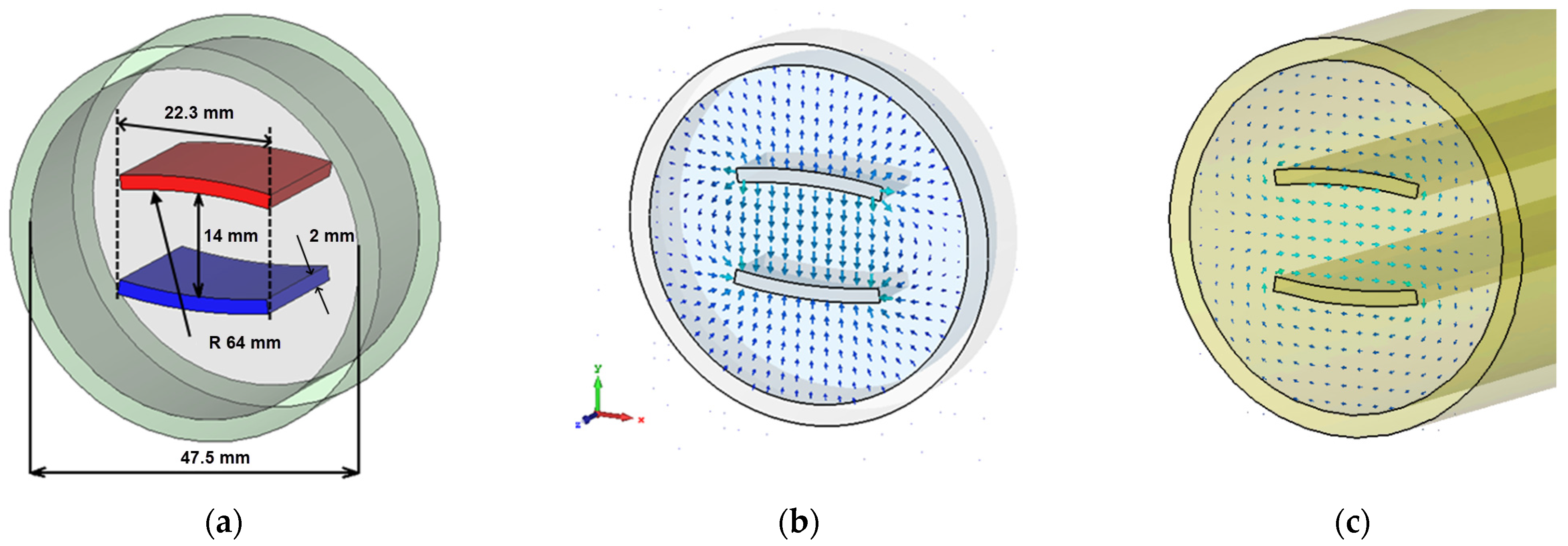
| Aperture (gap) | 14 mm |
| Required pulsed power | 27.6 kW peak power per channel (55.2 kW total) 3.8 kW average power per channel (7.6 kW total) |
| Analytical Evaluation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 20 mrad kick | yes | yes | yes | yes | yes | no | yes | no |
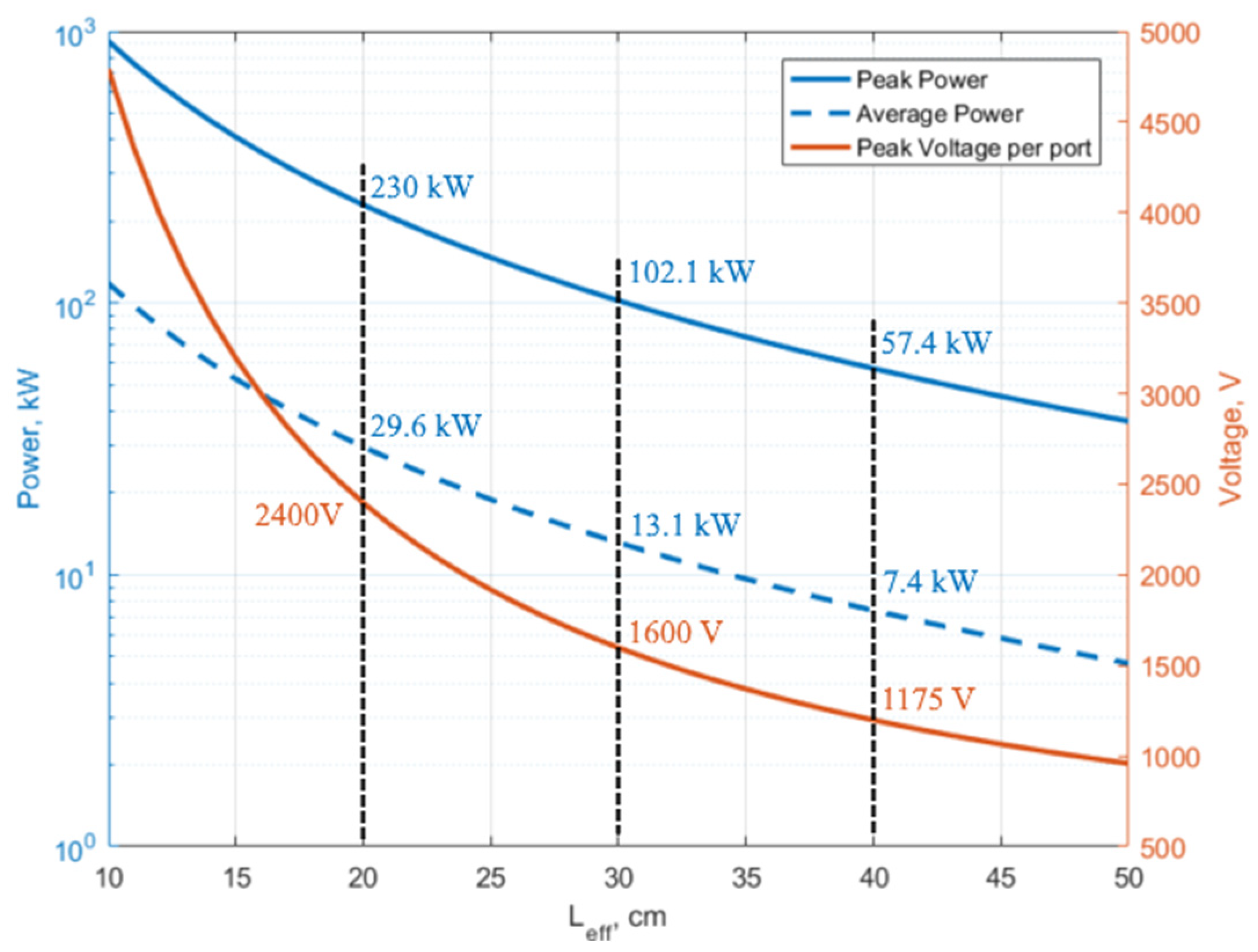
| Leff, mm | 200 | 300 | 400 | 600 | 400 | 400 | 600 | 600 |
| Vp, V | 2275 | 1560 | 1175 | 790 | 1175 | 1175 | 790 | 790 |
| Offset, mm | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Tilt, mm | 0 | 0 | 0 | 0 | −5 | −5 | −6 | −6 |
| Beam loss, % | 10−6 | 8.8 × 10−5 | 0.0027 | 0.21 | 5.4 × 10−5 | 4.7 × 10−5 | 4.6 × 10−3 | 4.8 × 10−3 |
| Pb, W | 0.04 | 2.4 | 104.5 | 8100 | 2.1 | 1.8 | 178 | 176 |
| PRF, kW | 14.5 | 6.8 | 3.85 | 1.75 | 3.85 | 3.85 | 1.75 | 1.75 |
| CST simulations | ||||||||
| Beam loss, % | 7 × 10−6 | 4 × 10−5 | 0.0016 | 0.38 | 4.7 × 10−5 | 4.7 × 10−5 | 3.6 × 10−3 | 3.6 × 10−3 |
| Pb, W | 0.27 | 1.55 | 62 | 14700 | 1.8 | 1.8 | 140 | 140 |
| Space charge | ||||||||
| Beam loss, % | 1.8 × 10−3 | 4.7 × 10−5 | ||||||
| Pb, W | 70 | 1.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, A.Y.; Agustsson, R.; Benson, S.V.; Gavryushkin, D.; Guo, J.; Kutsaev, S.V.; Moro, A.; Park, G.T.; Smirnov, A.V.; Wang, H.; et al. Ultrafast High-Voltage Kicker System for Ion-Clearing Gaps. Photonics 2021, 8, 507. https://doi.org/10.3390/photonics8110507
Smirnov AY, Agustsson R, Benson SV, Gavryushkin D, Guo J, Kutsaev SV, Moro A, Park GT, Smirnov AV, Wang H, et al. Ultrafast High-Voltage Kicker System for Ion-Clearing Gaps. Photonics. 2021; 8(11):507. https://doi.org/10.3390/photonics8110507
Chicago/Turabian StyleSmirnov, Alexander Yu., Ronald Agustsson, Stephen V. Benson, Dmitry Gavryushkin, Jiquan Guo, Sergey V. Kutsaev, Adam Moro, Gunn Tae Park, Alexei V. Smirnov, Haipeng Wang, and et al. 2021. "Ultrafast High-Voltage Kicker System for Ion-Clearing Gaps" Photonics 8, no. 11: 507. https://doi.org/10.3390/photonics8110507
APA StyleSmirnov, A. Y., Agustsson, R., Benson, S. V., Gavryushkin, D., Guo, J., Kutsaev, S. V., Moro, A., Park, G. T., Smirnov, A. V., Wang, H., & Zhang, S. (2021). Ultrafast High-Voltage Kicker System for Ion-Clearing Gaps. Photonics, 8(11), 507. https://doi.org/10.3390/photonics8110507






