Broadband Terahertz Photonic Integrated Circuit with Integrated Active Photonic Devices
Abstract
1. Introduction
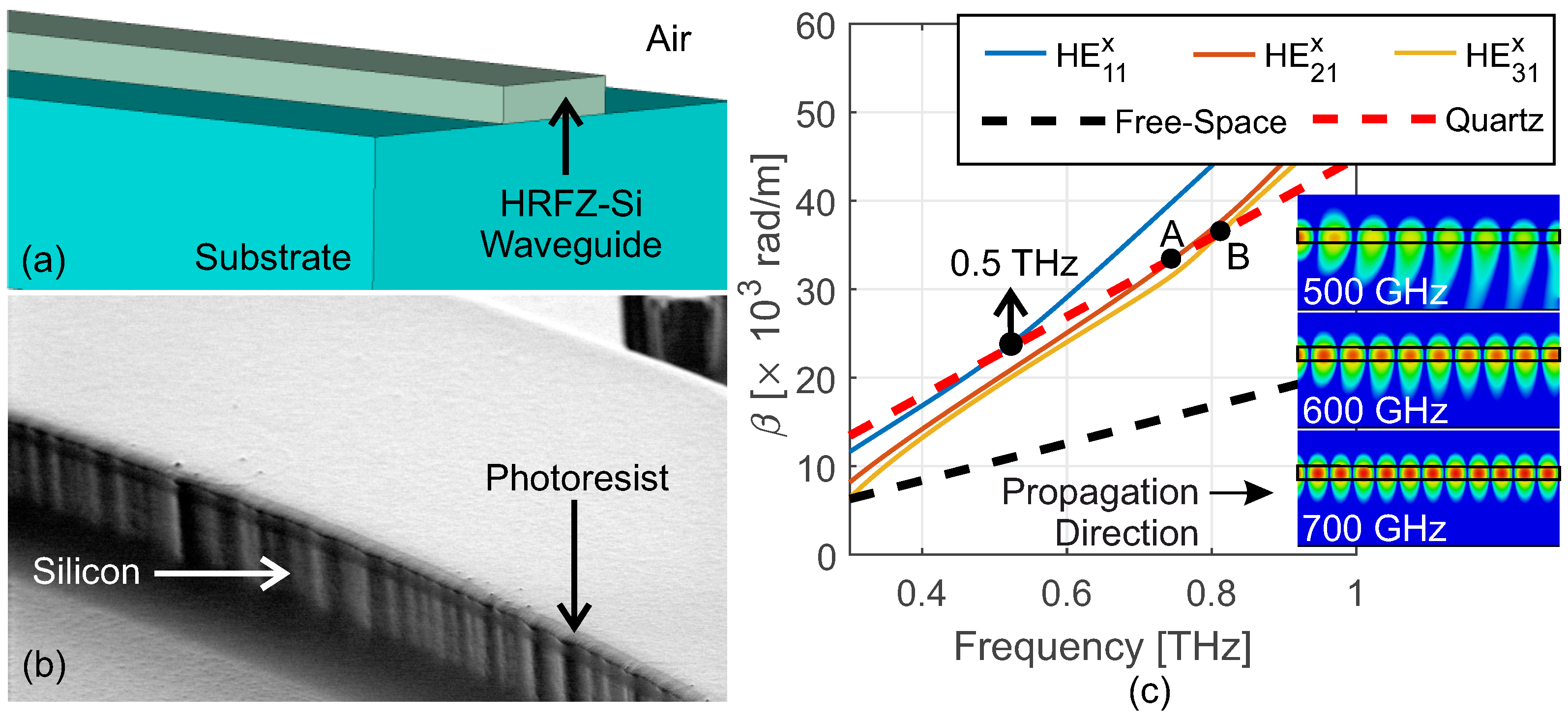
2. Waveguide Architecture
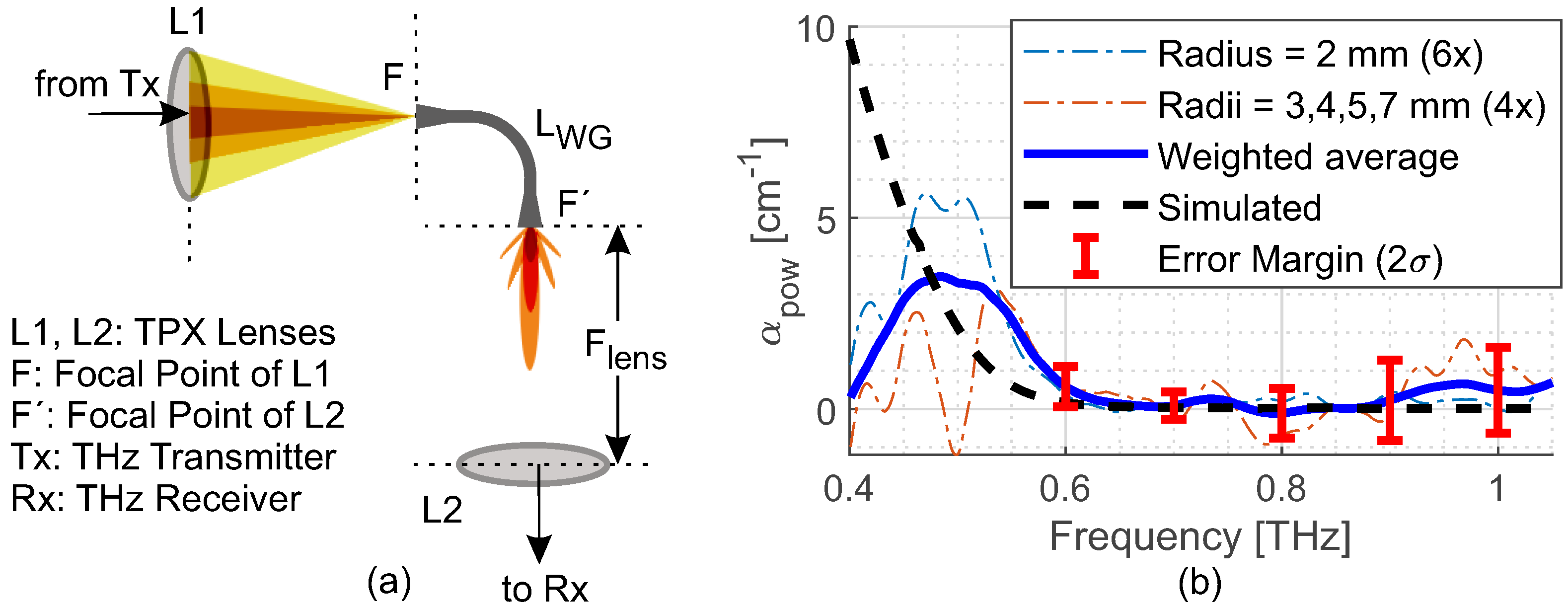
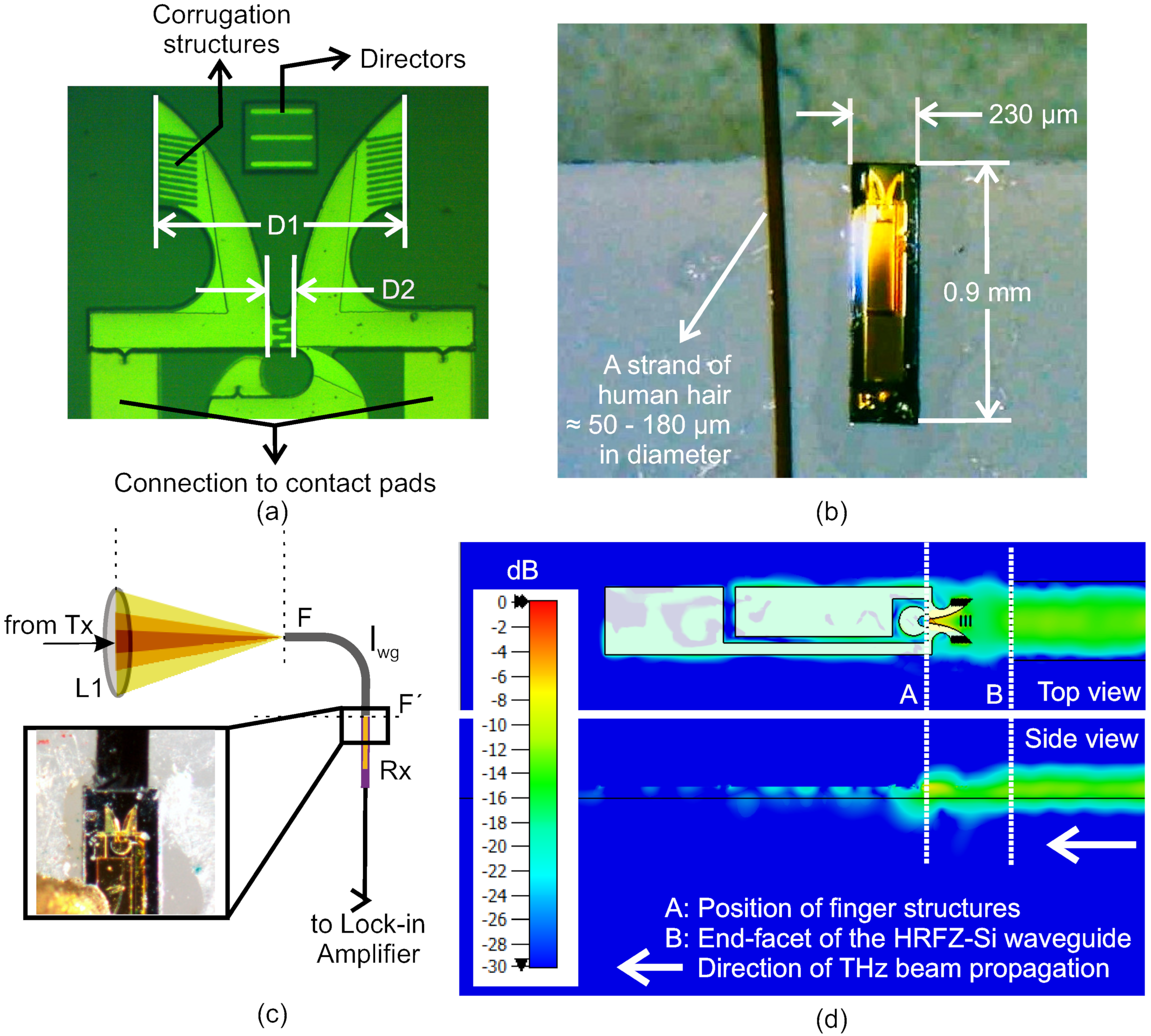
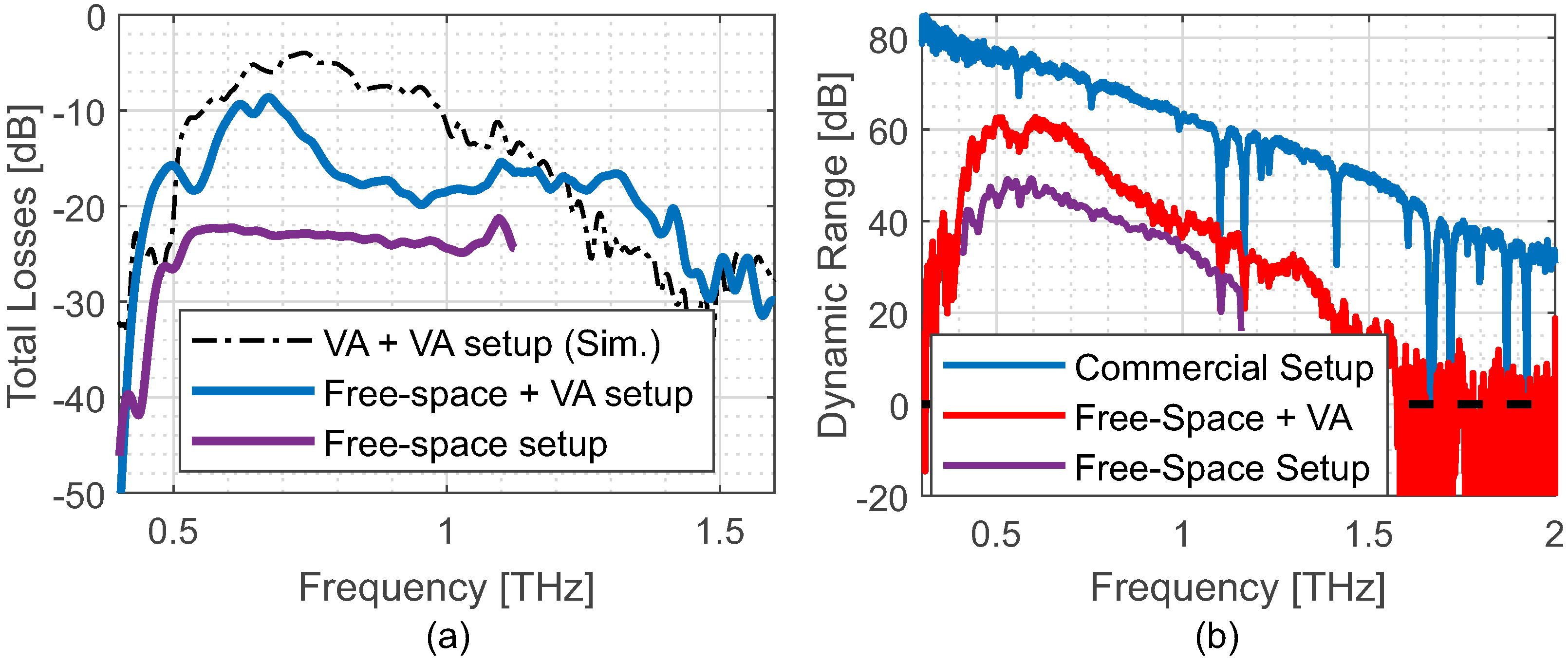
3. Fabrication and Measurement Setup
4. Waveguide Performance
4.1. Transmission Losses through Straight Sections
4.2. Bends
5. Transitions to Active Devices
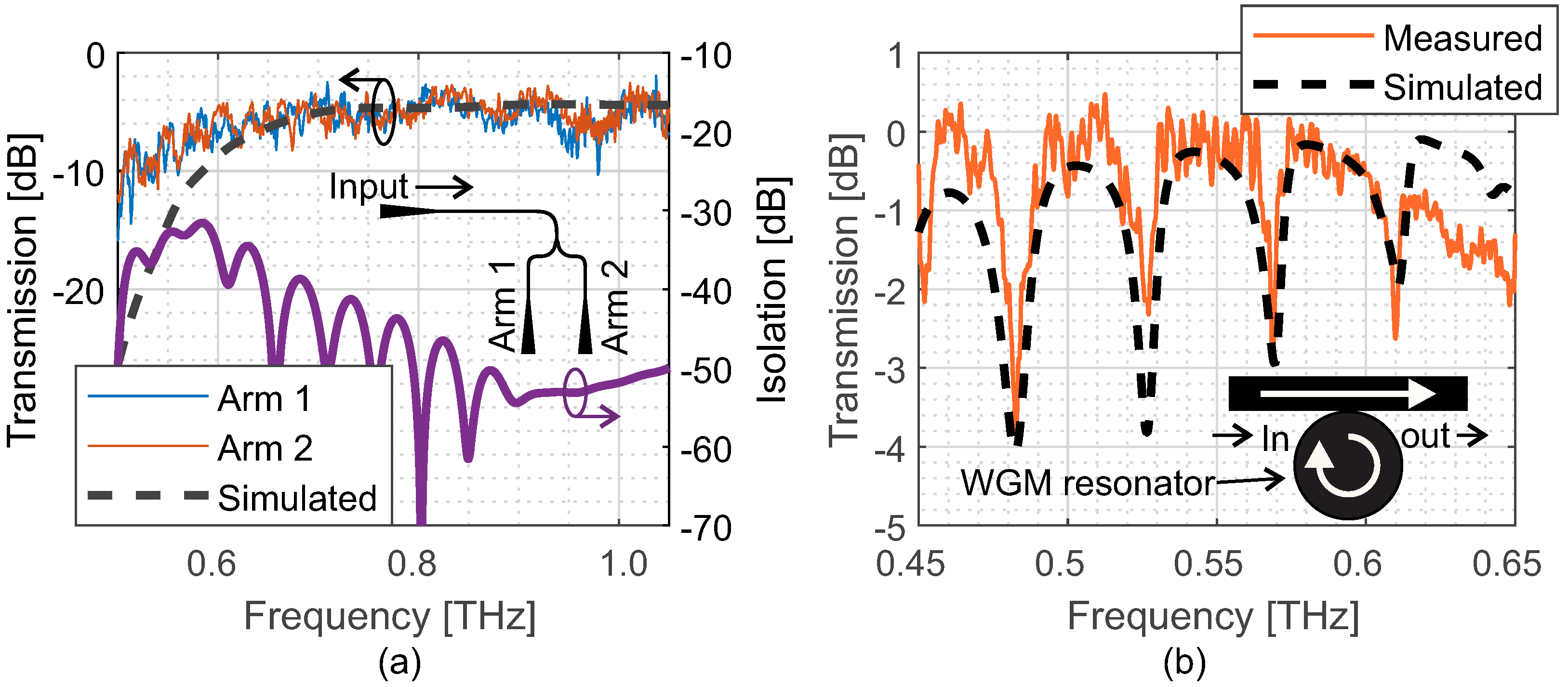
6. Couplers
7. Frequency-Selective Filter Example
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rymanov, V.; Lu, P.; Dülme, S.; Stöhr, A. Lens-assisted quasi-optical THz transmitter employing antenna-integrated triple transit region photodiodes. In Proceedings of the 2017 International Topical Meeting on Microwave Photonics (MWP), Beijing, China, 23–26 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Peytavit, E.; Latzel, P.; Pavanello, F.; Ducournau, G.; Lampin, J. CW Source Based on Photomixing With Output Power Reaching 1.8 mW at 250 GHz. IEEE Electron Device Lett. 2013, 34, 1277–1279. [Google Scholar] [CrossRef]
- Al-Khalidi, A.; Alharbi, K.H.; Wang, J.; Morariu, R.; Wang, L.; Khalid, A.; Figueiredo, J.M.L.; Wasige, E. Resonant Tunneling Diode Terahertz Sources With up to 1 mW Output Power in the J-Band. IEEE Trans. Terahertz Sci. Technol. 2020, 10, 150–157. [Google Scholar] [CrossRef]
- Frequency Multipliers (WR and D Series). Available online: https://www.vadiodes.com/en/frequency-multipliers (accessed on 26 January 2021).
- Lu, P.K.; Turan, D.; Jarrahi, M. High-sensitivity telecommunication-compatible photoconductive terahertz detection through carrier transit time reduction. Opt. Express 2020, 28, 26324–26335. [Google Scholar] [CrossRef] [PubMed]
- N5291A 900 Hz to 120 GHz PNA MM-Wave System. Available online: https://www.keysight.com/de/pdx-2817990-pn-N5291A/900-hz-to-120-ghz-pna-mm-wave-system (accessed on 26 January 2021).
- Lee, T.H.; Wong, S.S. CMOS RF integrated circuits at 5 GHz and beyond. Proc. IEEE 2000, 88, 1560–1571. [Google Scholar] [CrossRef]
- Daulay, O.; Botter, R.; Marpaung, D. On-chip programmable microwave photonic filter with an integrated optical carrier processor. OSA Contin. 2020, 3, 2166–2174. [Google Scholar] [CrossRef]
- Hossain, M.; Boppel, S.; Heinrich, W.; Krozer, V. Efficient active multiplier-based signal source for >300 GHz system applications. Electron. Lett. 2019, 55, 1220–1221. [Google Scholar] [CrossRef]
- Ranjkesh, N.; Amarloo, H.; Gigoyan, S.; Ghafarian, N.; Basha, M.A.; Safavi-Naeini, S. 1.1 THz U-Silicon-On-Glass (U-SOG) Waveguide: A Low-Loss Platform for THz High-Density Integrated Circuits. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 702–709. [Google Scholar] [CrossRef]
- Amarloo, H.; Ranjkesh, N.; Safavi-Naeini, S. Terahertz Silicon–BCB–Quartz Dielectric Waveguide: An Efficient Platform for Compact THz Systems. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 201–208. [Google Scholar] [CrossRef]
- Amarloo, H.; Safavi-Naeini, S. Terahertz Slot Dielectric Waveguide Implemented on the Silicon-BCB-Quartz Platform. IEEE Trans. Terahertz Sci. Technol. 2021, 11, 310–317. [Google Scholar] [CrossRef]
- Crowe, T.W.; Foley, B.; Durant, S.; Hui, K.; Duan, Y.; Hesler, J.L. VNA frequency extenders to 1.1 THz. In Proceedings of the 2011 International Conference on Infrared, Millimeter, and Terahertz Waves, Houston, TX, USA, 2–7 October 2011; p. 1. [Google Scholar] [CrossRef]
- Sengupta, K.; Nagatsuma, T.; Mittleman, D.M. Terahertz integrated electronic and hybrid electronic–photonic systems. Nat. Electron. 2018, 1, 622–635. [Google Scholar] [CrossRef]
- Han, H.; Park, H.; Cho, M.; Kim, J. Terahertz pulse propagation in a plastic photonic crystal fiber. Appl. Phys. Lett. 2002, 80, 2634–2636. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H. A novel low-loss Terahertz waveguide: Polymer tube. Opt. Express 2010, 18, 3762–3767. [Google Scholar] [CrossRef] [PubMed]
- Campion, J.; Li, Y.; Zirath, H.; Oberhammer, J.; Hassona, A.; He, Z.S.; Beuerle, B.; Gomez-Torrent, A.; Shah, U.; Vecchiattini, S.; et al. Toward Industrial Exploitation of THz Frequencies: Integration of SiGe MMICs in Silicon-Micromachined Waveguide Systems. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 624–636. [Google Scholar] [CrossRef]
- Headland, D.; Withayachumnankul, W.; Yu, X.; Fujita, M.; Nagatsuma, T. Unclad Microphotonics for Terahertz Waveguides and Systems. J. Light. Technol. 2020, 38, 6853–6862. [Google Scholar] [CrossRef]
- Zhu, H.; Xue, Q.; Hui, J.; Pang, S.W. Design, Fabrication, and Measurement of the Low-Loss SOI-Based Dielectric Microstrip Line and its Components. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 696–705. [Google Scholar] [CrossRef]
- Ranjkesh, N.; Basha, M.; Taeb, A.; Safavi-Naeini, S. Silicon-on-Glass Dielectric Waveguide—Part II: For THz Applications. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 280–287. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, X.; Zang, X.; Cheng, Q.; Chen, L.; Zhu, Y. Terahertz integrated device: High-Q silicon dielectric resonators. Opt. Mater. Express 2018, 8, 50–58. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, G.; Yuan, S.; Chen, L.; Wu, X.; Zhang, X. Voltage-actuated thermally tunable on-chip terahertz filters based on a whispering gallery mode resonator. Opt. Lett. 2019, 44, 4670–4673. [Google Scholar] [CrossRef] [PubMed]
- Ranjkesh, N.; Gigoyan, S.; Amarloo, H.; Basha, M.; Safavi-Naeini, S. Broadband Single-Mode THz Suspended Silicon-On-Glass Waveguide. IEEE Microw. Wirel. Components Lett. 2018, 28, 185–187. [Google Scholar] [CrossRef]
- Akiki, E.; Verstuyft, M.; Ducournau, G.; Walter, B.; Mairiaux, E.; Faucher, M.; Lampin, J.; Vanwolleghem, M.; Kuyken, B. Low Loss Suspended Silicon Waveguide and Photonic Crystal for THz Regime. In Proceedings of the 2019 Conference on Lasers and Electro-Optics Europe European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 23–27 June 2019; p. 1. [Google Scholar] [CrossRef]
- Rivera-Lavado, A.; García-Muñoz, L.E.; Generalov, A.; Lioubtchenko, D.; Abdalmalak, K.A.; Llorente-Romano, S.; García-Lampérez, A.; Segovia-Vargas, D.; Räisänen, A.V. Design of a Dielectric Rod Waveguide Antenna Array for Millimeter Waves. J. Infrared Millim. Terahertz Waves 2017, 38, 33–46. [Google Scholar] [CrossRef]
- Rivera-Lavado, A.; García-Muñoz, L.E.; Lioubtchenko, D.; Preu, S.; Abdalmalak, K.A.; Santamaría-Botello, G.; Segovia-Vargas, D.; Räisänen, A.V. Planar Lens–Based Ultra-Wideband Dielectric Rod Waveguide Antenna for Tunable THz and Sub-THz Photomixer Sources. J. Infrared Millim. Terahertz Waves 2019, 40, 838–855. [Google Scholar] [CrossRef]
- Bingham, A.L.; Grischkowsky, D.R. Terahertz 2-D Photonic Crystal Waveguides. IEEE Microw. Wirel. Components Lett. 2008, 18, 428–430. [Google Scholar] [CrossRef]
- Amarloo, H.; Safavi-Naeini, S. Terahertz Line Defect Waveguide Based on Silicon-on-Glass Technology. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 433–439. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Fujita, M.; Nagatsuma, T. Integrated Silicon Photonic Crystals Toward Terahertz Communications. Adv. Opt. Mater. 2018, 6, 1800401. [Google Scholar] [CrossRef]
- Yu, X.; Sugeta, M.; Yamagami, Y.; Fujita, M.; Nagatsuma, T. Simultaneous low-loss and low-dispersion in a photonic-crystal waveguide for terahertz communications. Appl. Phys. Express 2019, 12, 012005. [Google Scholar] [CrossRef]
- Gao, W.; Yu, X.; Fujita, M.; Nagatsuma, T.; Fumeaux, C.; Withayachumnankul, W. Effective-medium-cladded dielectric waveguides for terahertz waves. Opt. Express 2019, 27, 38721–38734. [Google Scholar] [CrossRef]
- Waveguide Band Designations. Available online: https://vadiodes.com/VDI/pdf/waveguidechart200908.pdf (accessed on 4 September 2020).
- Seifert, T.; Jaiswal, S.; Martens, U.; Hannegan, J.; Braun, L.; Maldonado, P.; Freimuth, F.; Kronenberg, A.; Henrizi, J.; Radu, I.; et al. Efficient metallic spintronic emitters of ultrabroadband terahertz radiation. Nat. Photonics 2016, 10, 483–488. [Google Scholar] [CrossRef]
- Olvera, A.D.J.F.; Betancour, A.F.; de Dios, C.; Acedo, P.; Preu, S. Architecture and Component Characterization of a High-Resolution Free-Space Vector Network Analyzer for the Terahertz Range. In Proceedings of the 2019 European Microwave Conference in Central Europe (EuMCE), Prague, Czech Republic, 13–15 May 2019; pp. 257–260. [Google Scholar]
- Nandi, U.; Dutzi, K.; Deninger, A.; Lu, H.; Norman, J.; Gossard, A.C.; Vieweg, N.; Preu, S. ErAs:In(Al)GaAs photoconductor-based time domain system with 4.5 THz single shot bandwidth and emitted terahertz power of 164 μW. Opt. Lett. 2020, 45, 2812–2815. [Google Scholar] [CrossRef] [PubMed]
- Liebermeister, L.; Nellen, S.; Kohlhaas, R.; Breuer, S.; Schell, M.; Globisch, B. Ultra-fast, High-Bandwidth Coherent cw THz Spectrometer for Non-destructive Testing. J. Infrared Millim. Terahertz Waves 2019, 40, 288–296. [Google Scholar] [CrossRef]
- Preu, S.; Terahertz Photonic Integrated Circuit. German Patent Request DE 10 2019 104 982 A1 (2019). Available online: https://register.dpma.de/DPMAregister/pat/PatSchrifteneinsicht?docId=DE102019104982A1 (accessed on 2 November 2021).
- Amarloo, H.; Safavi-Naeini, S. Slot plasmonic waveguide based on doped-GaAs for terahertz deep-subwavelength applications. J. Opt. Soc. Am. A 2015, 32, 2189–2194. [Google Scholar] [CrossRef]
- Marcatili, E.A.J. Dielectric rectangular waveguide and directional coupler for integrated optics. Bell Syst. Tech. J. 1969, 48, 2071–2102. [Google Scholar] [CrossRef]
- Olvera, A.F.; Lu, H.; Gossard, A.C.; Preu, S. Continuous-wave 1550 nm operated terahertz system using ErAs:In(Al)GaAs photo-conductors with 52 dB dynamic range at 1 THz. Opt. Express 2017, 25, 29492–29500. [Google Scholar] [CrossRef]
- Jansen, C.; Wietzke, S.; Wang, H.; Koch, M.; Zhao, G. Terahertz spectroscopy on adhesive bonds. Polym. Test. 2011, 30, 150–154. [Google Scholar] [CrossRef]
- Yeh, C.; Shimabukuro, F.I. Propagation Characteristics of Guide. In The Essence of Dielectric Waveguides; Springer: Boston, MA, USA, 2008; pp. 55–98. [Google Scholar] [CrossRef]
- Ramaswami, R.; Sivarajan, K.; Sasaki, G. Optical Networks: A Practical Perspective, 3rd ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2009. [Google Scholar]
- Fernandez Olvera, A.D.J.; Nandi, U.; Norman, J.; Gossard, A.C.; Roskos, H.; Preu, S. Dispersive properties of self-complementary log-periodic antennas in pulsed THz systems. In Proceedings of the 2017 42nd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Cancun, Mexico, 27 August–1 September 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Aller, M.M.; Preu, S. Quasi-Analytical Description of a Double Slit Planar Dielectric Waveguide as Broadband Dispersion Compensating Element. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Colman, P.; Combrié, S.; Lehoucq, G.; Rossi, A.D. Control of dispersion in photonic crystal waveguides using group symmetry theory. Opt. Express 2012, 20, 13108–13114. [Google Scholar] [CrossRef][Green Version]
- Heiblum, M.; Harris, J. Analysis of curved optical waveguides by conformal transformation. IEEE J. Quantum Electron. 1975, 11, 75–83. [Google Scholar] [CrossRef]
- Marcatili, E.A.J. Bends in Optical Dielectric Guides. Bell Syst. Tech. J. 1969, 48, 2103–2132. [Google Scholar] [CrossRef]
- Saijonmaa, J.; Yevick, D. Beam-propagation analysis of loss in bent optical waveguides and fibers. J. Opt. Soc. Am. 1983, 73, 1785–1791. [Google Scholar] [CrossRef]
- Sheehan, R.N.; Horne, S.; Peters, F.H. The design of low-loss curved waveguides. Opt. Quantum Electron. 2008, 40, 1211–1218. [Google Scholar] [CrossRef]
- Smit, M.K.; Pennings, E.C.; Blok, H. Normalized approach to the design of low-loss optical waveguide bends. J. Light. Technol. 1993, 11, 1737–1742. [Google Scholar] [CrossRef]
- Navarro-Cía, M.; Wu, J.; Liu, H.; Mitrofanov, O. Generation of radially-polarized terahertz pulses for coupling into coaxial waveguides. Sci. Rep. 2016, 6, 38926. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Lavado, A.; Preu, S.; García-Muñoz, L.E.; Generalov, A.; Montero-de-Paz, J.; Döhler, G.; Lioubtchenko, D.; Méndez-Aller, M.; Sedlmeir, F.; Schneidereit, M.; et al. Dielectric Rod Waveguide Antenna as THz Emitter for Photomixing Devices. IEEE Trans. Antennas Propag. 2015, 63, 882–890. [Google Scholar] [CrossRef]
- Rumsey, V.H. 3-PLANE-SHEET ANTENNAS. In Frequency Independent Antennas; Rumsey, V.H., Ed.; Academic Press: New York, NY, USA, 1966; pp. 23–37. [Google Scholar] [CrossRef]
- Fernandez Olvera, A.D.J.; Roggenbuck, A.; Dutzi, K.; Vieweg, N.; Lu, H.; Gossard, A.C.; Preu, S. International System of Units (SI) Traceable Noise-Equivalent Power and Responsivity Characterization of Continuous Wave ErAs:InGaAs Photoconductive Terahertz Detectors. Photonics 2019, 6, 15. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Mukherjee, A.K.; Kumar, R.; Preu, S. Vivaldi End-Fire Antenna for THz Photomixers. J. Infrared Millim. Terahertz Waves 2020, 41, 728–739. [Google Scholar] [CrossRef]
- Schaubert, D.; Kollberg, E.; Korzeniowski, T.; Thungren, T.; Johansson, J.; Yngvesson, K. Endfire tapered slot antennas on dielectric substrates. IEEE Trans. Antennas Propag. 1985, 33, 1392–1400. [Google Scholar] [CrossRef]
- Greenberg, M.C.; Virga, K.L.; Hammond, C.L. Performance characteristics of the dual exponentially tapered slot antenna (DETSA) for wireless communications applications. IEEE Trans. Veh. Technol. 2003, 52, 305–312. [Google Scholar] [CrossRef]
- Vogt, D.W.; Leonhardt, R. Ultra-high Q terahertz whispering-gallery modes in a silicon resonator. APL Photonics 2018, 3, 051702. [Google Scholar] [CrossRef]
- Monifi, F.; Friedlein, J.; Ozdemir, Ş.K.; Yang, L. A Robust and Tunable Add–Drop Filter Using Whispering Gallery Mode Microtoroid Resonator. J. Light. Technol. 2012, 30, 3306–3315. [Google Scholar] [CrossRef]
- Gad, M.; Ackert, J.; Yevick, D.; Chrostowski, L.; Jessop, P.E. Ring Resonator Wavelength Division Multiplexing Interleaver. J. Light. Technol. 2011, 29, 2102–2108. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukherjee, A.K.; Xiang, M.; Preu, S. Broadband Terahertz Photonic Integrated Circuit with Integrated Active Photonic Devices. Photonics 2021, 8, 492. https://doi.org/10.3390/photonics8110492
Mukherjee AK, Xiang M, Preu S. Broadband Terahertz Photonic Integrated Circuit with Integrated Active Photonic Devices. Photonics. 2021; 8(11):492. https://doi.org/10.3390/photonics8110492
Chicago/Turabian StyleMukherjee, Amlan Kusum, Mingjun Xiang, and Sascha Preu. 2021. "Broadband Terahertz Photonic Integrated Circuit with Integrated Active Photonic Devices" Photonics 8, no. 11: 492. https://doi.org/10.3390/photonics8110492
APA StyleMukherjee, A. K., Xiang, M., & Preu, S. (2021). Broadband Terahertz Photonic Integrated Circuit with Integrated Active Photonic Devices. Photonics, 8(11), 492. https://doi.org/10.3390/photonics8110492




