Mueller Matrix Polarimetry with Invariant Polarization Pattern Beams

Abstract

A wide class of nonuniformly totally polarized beams that preserve their transverse polarization pattern during paraxial propagation was studied. Beams of this type are of interest, in particular, in polarimetric techniques that use a single input beam for the determination of the Mueller matrix of a homogeneous sample. In these cases, in fact, it is possible to test the sample response to several polarization states at once. The propagation invariance of the transverse polarization pattern is an interesting feature for beams used in these techniques, because the polarization state of the output beam can be detected at any transverse plane after the sample, without the use of any imaging/magnifying optical system. Furthermore, exploiting the great variety of the beams of this class, the ones that better fit specific experimental constrains can be chosen. In particular, the class also includes beams that present all possible polarization states across their transverse section (the full Poincaré beams (FPB)). The use of the latter has recently been proposed to increase the accuracy of the recovered Mueller matrix elements. Examples of FPBs with propagation-invariant polarization profiles and its use in polarimetry are discussed in detail. The requirement of invariance of the polarization pattern can be limited to the propagation in the far field. In such a case, less restrictive conditions are derived, and a wider class of beams is found.

1. Introduction

It is well known that the transverse polarization pattern of a completely coherent and nonuniformly totally polarized (NUTP) beam changes, in general, upon paraxial free propagation. The proposal of new NUTP beams [1,2,3,4,5,6,7,8,9,10] and the study of how they propagate through different systems is a subject of increasing interest (see, for example, [11,12,13,14,15,16,17,18,19,20,21,22,23]). At the same time, researchers have also focused on studying invariance upon propagation of some NUTP beams characteristics, such as their irradiance, state or degree of polarization, coherence, etc. [24,25,26,27,28,29,30,31,32]. Conditions ensuring the polarization invariance in propagation have been studied also for the case of partially coherent electromagnetic beams [26,31,33].

On the other hand, in a variety of applications, such as polarimetry, lidar, microscopy, manipulation of particles, etc., NUTP beams with invariant transverse polarization distributions can be convenient. The most used NUTP beams that remain invariant in polarization during propagation are the spirally polarized beams [2,6,32,34], especially in the particular cases of radial and azimuthal polarization.

Polarimetry is a noninvasive testing technique that provides information about the optical properties of a sample [35]. Since partially polarized light can be described by the $4\times 1$ Stokes vector $\mathbf{S}$, the optical behavior of a sample can be described by its $4\times 4$ Mueller matrix, $\widehat{M}$ [36,37,38]. To measure its Mueller matrix, a sample is generally tested sequentially by at least four different input polarization states [36]. The latter must be represented by four independent $4\times 1$ Stokes vectors, to recover the Mueller matrix elements by means of an inversion procedure [36,37].

A polarimetric technique has recently been proposed for the analysis of linear, deterministic, and homogeneous samples [16]. It uses a single test beam but endowed with nonuniform polarization across its transverse profile, and the response of the sample is then analyzed at different points of the transverse beam profile. To this aim, beams that potentially provide the best performances are those that present all possible polarization states across their profile, because using a large number of input polarization states results in a reduction in the uncertainties on the measured values of the Mueller matrix [39]. Beams of this type were introduced by Beckley et al. [8] and are known as full Poincaré beams (FPBs) [9,40,41]. The term Full-Poincaré Polarimetry (FPP) is used to denote this technique.

It should be recalled that a different technique using FPBs is currently employed in (Stokes) polarimetry. In this case, the polarization state of a beam is recovered from the image of the FPB generated through a stress-engineered optic [42,43,44,45].

In previous experimental verifications of FPP, the input FPB was obtained on exploiting the anisotropy properties of a calcite crystal [39,46]. The transverse dimensions of the tested samples were large enough to allow the use of an input FPB with a spot size of the order of a few millimeters, so that no optical magnifying systems were needed to image the output beam onto a CCD sensor and perform measurements.

For smaller samples, or when their optical properties are not uniform, the input beam needs to be focused onto the region to be tested. Analysis of the output beam would necessarily require the use of optical systems, which could affect the polarization measurements. Therefore, it would be convenient to have a FPB that keeps its polarization profile in free-space propagation, except for a transverse scaling factor, so that the same pattern would be observed at any distance from the sample. The most comfortable beam size for the detection could be selected simply choosing the right distance from the sample to locate the sensor.

In this article, we first present a class of perfectly coherent and NUTP beams [47] that fulfill the above requirements, that is, they retain the shape of their transverse polarization pattern during paraxial propagation, the only change being a scaling of the transverse coordinates as one goes from one transverse plane to another. To the same class belongs all beams that are obtained by transforming one of the above beams by means of a general linear, deterministic, and homogeneous optical element. In other terms, if the input beam fulfills the above requirement, the propagation invariance is also guaranteed for the beam exiting the sample. Within such a class, we identify NUTP beams that are FPB and study their applicability in Mueller matrix polarimetry.

A less strict condition is found if the propagation invariance of the transverse pattern is required only in the far zone. It was shown that in such a case a wider class of fields is obtained and that four different polarization-invariant fields are obtained in a simple way from any pair of Fourier-transformable functions.

The article is structured as follows. This section constitutes the introduction, while, in Section 2, a condition for the invariance of the polarization pattern is reviewed, and some examples are given. Afterward, the fields whose polarization patterns repeat at the far-field is studied in Section 3. The main result of this work is the study of invariant full Poincarè beams and their use in polarimetry, which is presented in Section 4. Finally, the main findings of this work are discussed in Section 5.

2. Invariant Fields

In this section, we review a class of light beams that exhibit a propagation-invariant intensity profile and polarization pattern. A condition ensuring the shape-invariance of the transverse polarization pattern of a field is that the latter be expressible as the superposition of two component fields, having orthogonal and uniform polarizations, chosen in such a way that the ratio between their values at any point of a transverse plane (taking the above scaling factor into account) remains invariant at any propagation distance z. In the trivial case of uniform polarization, this happens because one of the two fields can always be set to zero. Let us denote by ${\mathit{V}}_0\left(\mathit{r}\right)$ a typical vector field across the plane $z=0$, writing it as

$${\displaystyle {\mathit{V}}_0\left(\mathit{r}\right)=\sum _{i=1}^2{V}_0^{\left(i\right)}\left(\mathit{r}\right){\widehat{ϵ}}_i,}$$

(1)

where $\mathit{r}=(r,\theta )$ is a point in the source plane, and ${\widehat{ϵ}}_i$$(i=1,2)$ are unit vectors specifying two orthogonal polarization states, which look for two component fields, $V_0^{\left(i\right)}\left(\mathit{r}\right)$, fulfilling the above condition.

Within the paraxial approximation, the field propagated at any distance z can be evaluated by expressing the initial one in terms of Gaussian modes, whose propagation expression can be given in closed form. This can be made either in rectangular or in polar coordinates, where Hermite–Gaussian (HG) or Laguerre–Gaussian (LG) functions, respectively, can be used [48]. We denote both families of functions by ${\Psi }_h(\mathit{r};w_0)$, regardless of the specific coordinate system we are using, while the meaning of the index h depends on the particular class of functions: it may represent either the indexes (say, n and m) of the two Hermite polynomials involved in the definition of HG functions or the two parameters (say, p and s) specifying a generalized Laguerre polynomial, for the case of LG modes. Both classes of functions depend on a further parameter, namely, the spot size $w_0$, which fixes the transverse extent of the modes at their waist.

Gaussian functions form a complete set in $L^2$. This allows for any paraxial beam to be written as a superposition of modes of the above types, with arbitrary $w_0$. In particular, we have

$${\displaystyle V_0^{\left(i\right)}\left(\mathit{r}\right)=\sum _h{c}_h^{\left(i\right)}{\Psi }_h(\mathit{r};w_0),}$$

(2)

where

$${\displaystyle c_h^{\left(i\right)}=\int V_0^{\left(i\right)}\left(\mathit{r}\right){\Psi }_h^{\ast }(\mathit{r};w_0)\mathrm{d}\mathit{r},}$$

(3)

the integral being extended to the whole plane $z=0$. The field propagated at a distance z is therefore evaluated taking into account the effects of propagation on each of the modes. The latter, in fact, keep their initial form, up to a scaling factor, and acquire both a spherical curvature and a phase depending on the mode indices. More precisely, we have

$$\begin{array}{cc}\hfill V_z^{\left(i\right)}\left(\mathit{r}\right)=& {\displaystyle \frac{w_0}{w_z}{e}^{\mathrm{i}kz}exp\left(\frac{\mathrm{i}k{r}^2}{2R_z}\right)\sum _h{c}_h^{\left(i\right)}{\Psi }_h(\mathit{r};w_z)e^{{\displaystyle -\mathrm{i}(N+1){\Phi }_z}},}\hfill \end{array}$$

(4)

where k is the wave number and

$$\begin{array}{c}\hfill \begin{array}{c}{w}_z=w_0\sqrt{1+{\left(\frac{z}{z_R}\right)}^2};R_z=z\left[1+{\left(\frac{z_R}{z}\right)}^2\right];{\Phi }_z=arctan\left(\frac{z}{z_R}\right),\end{array}\end{array}$$

(5)

with $z_R=k{w}_0^2/2$ being the Rayleigh distance. The parameter N is related to the indexes of the modes. It equals $n+m$ for HG modes and $2p+\left|s\right|$ for LG modes and contributes to the phase term $(N+1){\Phi }_z$ appearing in Equation (4). Such a term is known as phase anomaly or Gouy phase [49]. It is important to stress that, since each of the modes is shape-invariant during propagation, the phase anomaly is the only factor responsible for the fact that a general beam changes in shape during propagation [50,51].

According to Equation (1), the polarization pattern of a beam across a transverse plane is determined by the relative amplitude and phase of the two component fields at any point of the plane and, in general, changes during propagation because the two fields generally change in shape and acquire different phases. On the other hand, from the above results, it turns out that a condition ensuring that the relative amplitudes and phases of the two beams remain unchanged at any point is to require that, in the modal expansion of its component fields (Equation (4)), only those terms are present for which the phase anomaly changes in the same way during propagation [50,51]. This means that either of the two orthogonally polarized components of the beam have to be expressed as the sum of HG (and/or LG) modes with one and the same value of N. This condition implies that, except for overall amplitude and phase terms, the propagated field is an exact replica of the initial one, scaled by the factor $w_0/w_z$.

It is worth recalling here that the LG mode with indices p and s can be expressed as the sum of HG modes for which $n+m=2p+\left|s\right|$ [48,52], and, conversely, the HG mode with indices n and m can be expressed as the sum of LG modes for which $2p+\left|s\right|=n+m$. This means that every beam obtained following the above rule can be thought of equally as a superposition of either HG or LG modes, the involved expansion coefficients being related by linear transformation rules [53].

A significant remark can be made before dealing with particular examples. If a beam presents a propagation-invariant polarization profile, the same property holds for any other beam obtained from the first one by placing in its path a general linear, deterministic, and homogeneous optical element. In fact, any optical element of this kind can be described by a constant Jones matrix, $\widehat{J}$, and its effect on a beam at $z=0$ is to produce at its output the field

$${{\mathit{V}}^{\prime }}_0\left(\mathbf{r}\right)=\widehat{J}{\mathit{V}}_0\left(\mathbf{r}\right).$$

(6)

If we introduce the direct propagator in free space, $K_z(\mathbf{r},\mathit{\rho })$, such that

$${\displaystyle {\mathit{V}}_z\left(\mathbf{r}\right)=\int \int K_z(\mathbf{r},\mathit{\rho }){\mathit{V}}_0\left(\mathit{\rho }\right)\mathrm{d}\mathit{\rho },}$$

(7)

the expression for the propagated field ${\mathit{V}}_z^{\prime }$ reads

$$\begin{array}{cc}\hfill {\mathit{V}}_z^{\prime }\left(\mathbf{r}\right)& {\displaystyle =\int \int K_z(\mathbf{r},\mathit{\rho }){\mathit{V}}_0^{\prime }\left(\mathit{\rho }\right)\mathrm{d}\mathit{\rho }=\int \int K_z(\mathbf{r},\mathit{\rho })\widehat{J}{\mathit{V}}_0\left(\mathit{\rho }\right)\mathrm{d}\mathit{\rho }=}\hfill \\ \\ \hfill & {\displaystyle =\widehat{J}\int \int K_z(\mathbf{r},\mathit{\rho }){\mathit{V}}_0\left(\mathit{\rho }\right)\mathrm{d}\mathit{\rho }=\widehat{J}{\mathit{V}}_z\left(\mathbf{r}\right),}\hfill \end{array}$$

(8)

so that if $\mathit{V}$ preserves its transverse polarization pattern during propagation, the same occurs for ${\mathit{V}}^{\prime }$.

Incidentally, we note that the shape-invariance property holds not only when $K_z$ is the direct propagator in free space but for whatever linear scalar operator. Hence, in particular, it holds for the propagation of the beam through any isotropic optical systems, characterized by an ABCD transformation matrix [49].

Examples

The best known examples of NUTP fields whose polarization pattern remains unchanged on propagation are donut beams with radial or azimuthal polarization. A method to produce them is through the superposition of a ${\mathrm{LG}}_{0,1}$ mode, with circular polarization ${\widehat{ϵ}}_1=(\widehat{x}+\mathrm{i}\widehat{y})/\sqrt{2}$, and a ${\mathrm{LG}}_{0,-1}$ mode, with the same amplitude and orthogonal polarization ${\widehat{ϵ}}_2=(\widehat{x}-\mathrm{i}\widehat{y})/\sqrt{2}$ (in both cases $N=1$) [2,7,54]. An analogous scheme leads to azimuthally polarized beams. Unfortunately, such beams present only linear polarization states across their profile, and this is not enough to perform complete polarimetric characterization. In fact, all linear states present a zero value of the third component of its Stokes vector, $S_3=0$, so that any selection of four different linear polarization states of the input field cannot be independent. The use of a homogeneous anisotropic optical element placed before the sample would not help, because even in this case we could not find four independent states across the beam cross section.

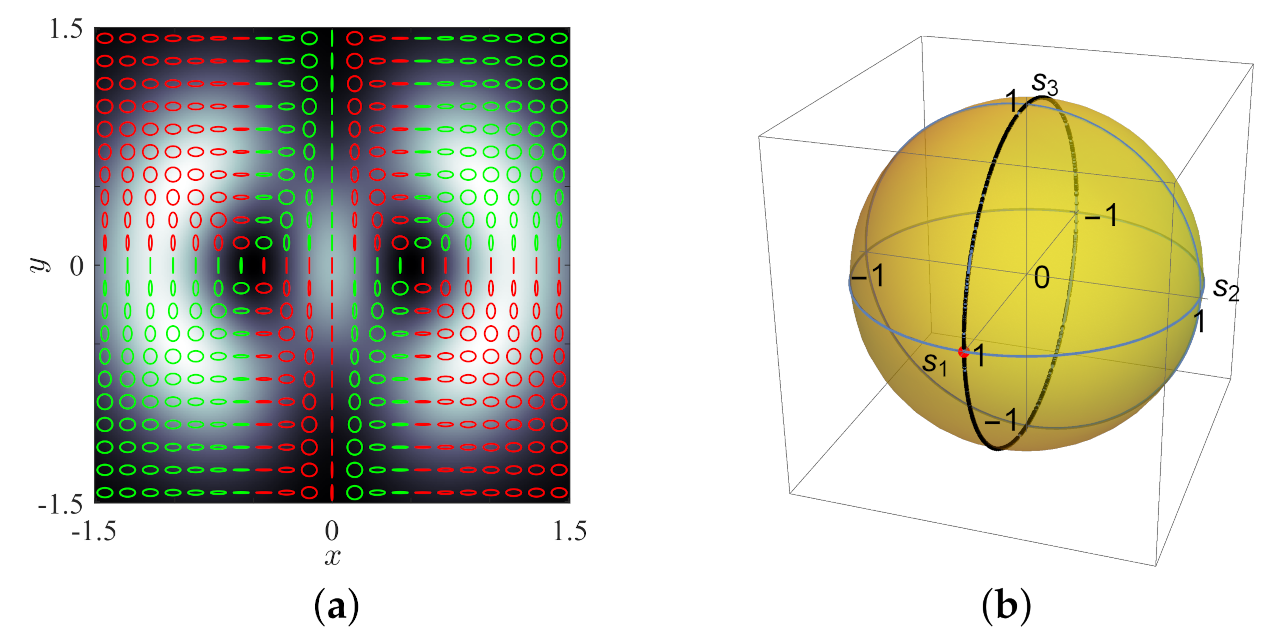
As the first example, consider, for instance, the superposition of two linearly polarized component beams, and take ${\widehat{ϵ}}_1=\widehat{x}$ and ${\widehat{ϵ}}_2=\widehat{y}$. Then, if we choose the field across the plane $z=0$ as

$${\mathit{V}}_0\left(\mathit{r}\right)={\mathrm{HG}}_{11}(\mathit{r},w_0){\widehat{ϵ}}_1+\mathrm{i}{\mathrm{HG}}_{20}(\mathit{r},w_0){\widehat{ϵ}}_2,$$

(9)

where ${\mathrm{HG}}_{nm}(\mathit{r},w_0)$ denotes the HG mode of order $nm$ (here, $N=m+n=2$), we obtain the amplitude and polarization patterns shown in Figure 1a. It can be easily checked that, for the field in Equation (9), its Stokes component $S_2=0$ everywhere, so the states of polarization are distributed on a meridian of the Poincaré sphere as it can be observed in Figure 1b. Here, $21\times 21$ points evenly distributed across the transverse section of the beam in Figure 1a were selected for calculating the corresponding polarization states, which were represented over the intensity map as polarization ellipses. In Figure 1b, every state of polarization is represented as a dot on the Poincaré sphere surface. The same sampling of the polarization pattern will be chosen for the subsequent figures.

A richer polarization pattern can be obtained by selecting a superposition of several modes for at least one of the components, for example,

$${\mathit{V}}_0\left(\mathit{r}\right)={\mathrm{HG}}_{11}(\mathit{r},w_0){\widehat{ϵ}}_1+\left[{\mathrm{HG}}_{20}(\mathit{r},w_0)+\mathrm{i}{\mathrm{HG}}_{02}(\mathit{r},w_0)\right]{\widehat{ϵ}}_2,$$

(10)

whose polarization pattern is shown in Figure 2a. It can be observed in Figure 2b that the polarization states covers a wider area on the Poincaré sphere.

For both previous examples, the intensity profile and the polarization pattern remain invariant, up to a scale factor, in free-space propagation.

To simplify the notations, in the following, we use normalized coordinates, i.e., we adopt units for which $w_0$ is unitary.

3. A Looser Condition: Invariance in the Far Field

A wider class of fields can be identified if the condition of shape invariance of the polarization pattern is required only when the propagated field reaches the far zone. Using the same approach as in the previous case, we require that, in the modal expansion of the component fields (Equation (4)), only those terms for which the phase anomalies take the same value in the far field (i.e., when $z\gg z_R$), up to an integer multiple of $2\pi$, are present. In this case, while in the near zone the mutual phases among the Gaussian modes generally change, thus modifying also the polarization state of the total field, they align again in the far zone. From a mathematical point of view, the phase anomaly of each of the Gaussian modes saturates to the value $(N+1)\pi /2$ in the far field. So, to guarantee shape invariance in the far field, it is sufficient that either of the two orthogonally polarized components of the beam could be expressed as the sum of HG (and/or LG) modes with values of $n+m$ (and/or of $2p+\left|s\right|$) that only differ for $4j$, with integer j, that is to say,

$$N_2-N_1=4j,\mathrm{with}j=0,1,2\dots ,$$

(11)

where $N_1$ and $N_2$ are the orders of the x and y components of the field, respectively.

An interesting aspect of this approach is that, in practice, it is not necessary to resort to superpositions of modes of suitable order to obtain propagation-invariant polarization patterns. In fact, using an analogous procedure as that used to conceive self-Fourier functions [55,56], it can be shown that four different beams of this class can be obtained in a simple way starting from any pair of Fourier-transformable functions.

Let us consider an arbitrary Fourier-transformable function $g(x,y)$ and define the following auxiliary functions:

$$\begin{array}{ccc}\hfill g^{(+)}(x,y)& =& \frac{1}{2}g(x,y),g^{(-)}(x,y)=\frac{1}{2}g(-x,-y),\hfill \\ \\ \hfill {\tilde{g}}^{(+)}(x,y)& =& \frac{1}{2}\tilde{g}(x,y),{\tilde{g}}^{(-)}(x,y)=\frac{1}{2}\tilde{g}(-x,-y),\hfill \\ \hfill \end{array}$$

(12)

where $\tilde{g}(\nu ,\mu )$ is the two-dimensional Fourier transform of $g(x,y)$. Then, four linear combinations of the auxiliary functions, namely, $g_q(x,y)$, with $q=0,1,2,3$, can be defined as

$$\left(\begin{array}{c}{g}_0(x,y)\\ g_1(x,y)\\ g_2(x,y)\\ g_3(x,y)\end{array}\right)=\frac{1}{2}\left(\begin{array}{cccc}1& 1& 1& 1\\ 1& -1& \mathrm{i}& -\mathrm{i}\\ 1& 1& -1& -1\\ 1& -1& -\mathrm{i}& \mathrm{i}\end{array}\right)\left(\begin{array}{c}{g}^{(+)}(x,y)\\ g^{(-)}(x,y)\\ {\tilde{g}}^{(+)}(x,y)\\ {\tilde{g}}^{(-)}(x,y)\end{array}\right).$$

(13)

Such functions are generalized self-Fourier functions, in the sense that they reproduce themselves on Fourier transformation, up to a proportionality factor [56]. More precisely, the relation ${\tilde{g}}_q(\nu ,\mu )={\mathrm{i}}^{-q}{g}_q(\nu ,\mu )$ holds.

Let us now apply this result to the vectorial case and consider the following vectorial function:

$$\mathit{G}(x,y)=\left(\begin{array}{c}{g}^X(x,y)\\ g^Y(x,y)\end{array}\right),$$

(14)

where $g^X(x,y)$ and $g^Y(x,y)$ are two arbitrary Fourier-transformable functions. Then, on applying Equations (12) and (13) to the two components $g^X(x,y)$ and $g^Y(x,y)$, four vector fields are obtained as

$${\mathit{G}}_q(x,y)=\left(\begin{array}{c}{g}_q^X(x,y)\\ g_q^Y(x,y)\end{array}\right),$$

(15)

which present the same polarization pattern profile across the source plane and in the far field, because their components reproduce themselves after Fourier transformation, with the same proportionality factor.

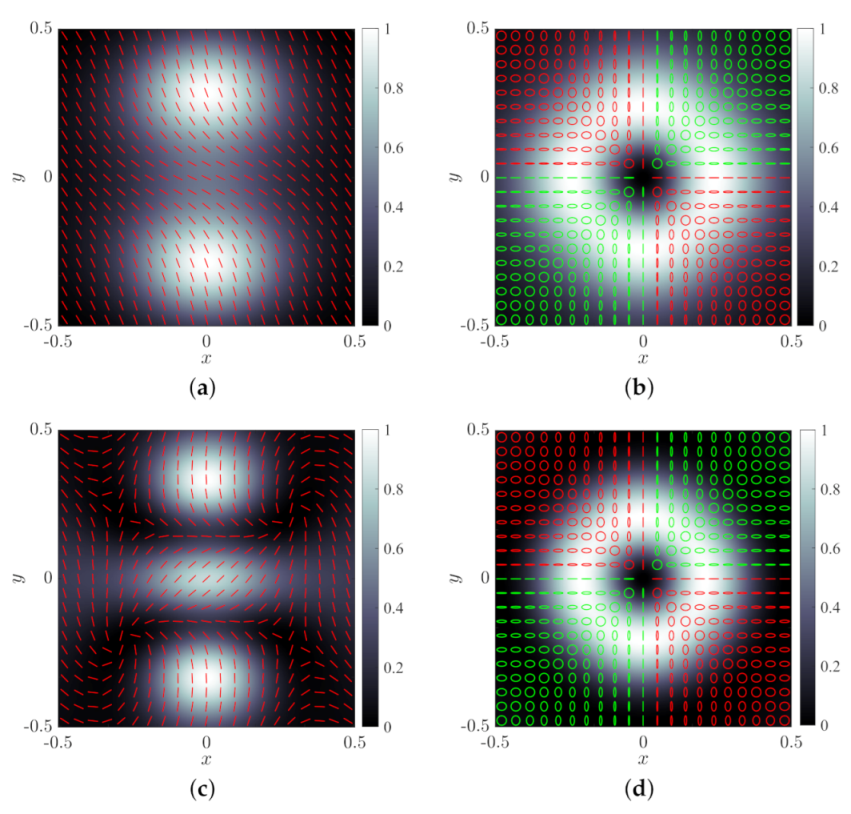
An Example

To give a simple example, let us consider the following field:

$$\mathit{G}(x,y)=\left(\begin{array}{c}{A}_x(1+2x)exp\left(-x^2-y^2\right)\\ \\ A_y(-1+\mathrm{i}y+2y^2)exp\left(-x^2-y^2\right)\end{array}\right),$$

(16)

where $A_j$ are constants whose squares have intensity dimensions. The Fourier transform of $\mathit{G}(x,y)$ is

$$\tilde{\mathit{G}}(\nu ,\mu )=\pi \left(\begin{array}{c}{A}_x\left(1-2\mathrm{i}\pi \nu \right)exp\left[-{\pi }^2\left({\nu }^2+{\mu }^2\right)\right]\\ \\ A_{y}2\pi \mu \left(1-2\pi \mu \right)exp\left[-{\pi }^2\left({\nu }^2+{\mu }^2\right)\right]\end{array}\right).$$

(17)

Note that neither the field given by Equation (16) nor its Fourier transform present an invariant polarization pattern. They are not self-Fourier transform fields either. However, by using Equations (13) and (15), the following four different self-Fourier fields can be built

$${\mathit{G}}_0(x,y)=\left(\begin{array}{c}2A_x\left[exp\left(-r^2\right)+\pi exp\left(-{\pi }^2{r}^2\right)\right]\\ \\ 2A_y\left[(-2+4y^2)exp\left(-r^2\right)+4{\pi }^3{y}^{2}exp\left(-{\pi }^2{r}^2\right)\right]\end{array}\right),$$

(18)

$${\mathit{G}}_1(x,y)=4\left[exp\left(-r^2\right)+{\pi }^{2}exp\left(-{\pi }^2{r}^2\right)\right]\left(\begin{array}{c}{A}_{x}x\\ \\ \mathrm{i}{A}_{y}y\end{array}\right),$$

(19)

$${\mathit{G}}_2(x,y)=\left(\begin{array}{c}2A_x\left[exp\left(-r^2\right)-\pi exp\left(-{\pi }^2{r}^2\right)\right]\\ \\ 2A_y\left[(-2+4y^2)exp\left(-r^2\right)-4{\pi }^3{y}^{2}exp\left(-{\pi }^2{r}^2\right)\right]\end{array}\right),$$

(20)

and

$${\mathit{G}}_3(x,y)=4\left[exp\left(-r^2\right)-{\pi }^{2}exp\left(-{\pi }^2{r}^2\right)\right]\left(\begin{array}{c}{A}_{x}x\\ \\ \mathrm{i}{A}_{y}y\end{array}\right).$$

(21)

The intensity profile and the polarization pattern corresponding to these four self-Fourier fields for $A_x=A_y=1$ are represented in Figure 3. In Figure 3b,d, the polarization varies from linear to circular, moving along the azimuthal direction. Polarization structures of this kind have recently been investigated in the case of focusing of vector beams with polarization singularities [19,20].

Richer self-Fourier polarization patterns and self-Fourier intensity profiles can be obtained by using more complex generating vectorial functions.

4. Full Poincaré Invariant Fields and Their Application in Polarimetry

In the above examples, several polarization states were simultaneously present across the plane $z=0$, and the polarization pattern was preserved during propagation. However, in some cases, such as those concerning polarimetric techniques, it can be useful to have beams that present across a transverse plane the greatest possible number of polarization states. To this aim, the best solution is represented by the full Poincaré beams. Such beams were introduced in [8] as examples of totally but non-uniformly polarized fields that present, across any transverse plane, every possible polarization state. Using the present approach we can find, within the class of FPB’s, those fields that preserve their polarization pattern during propagation. 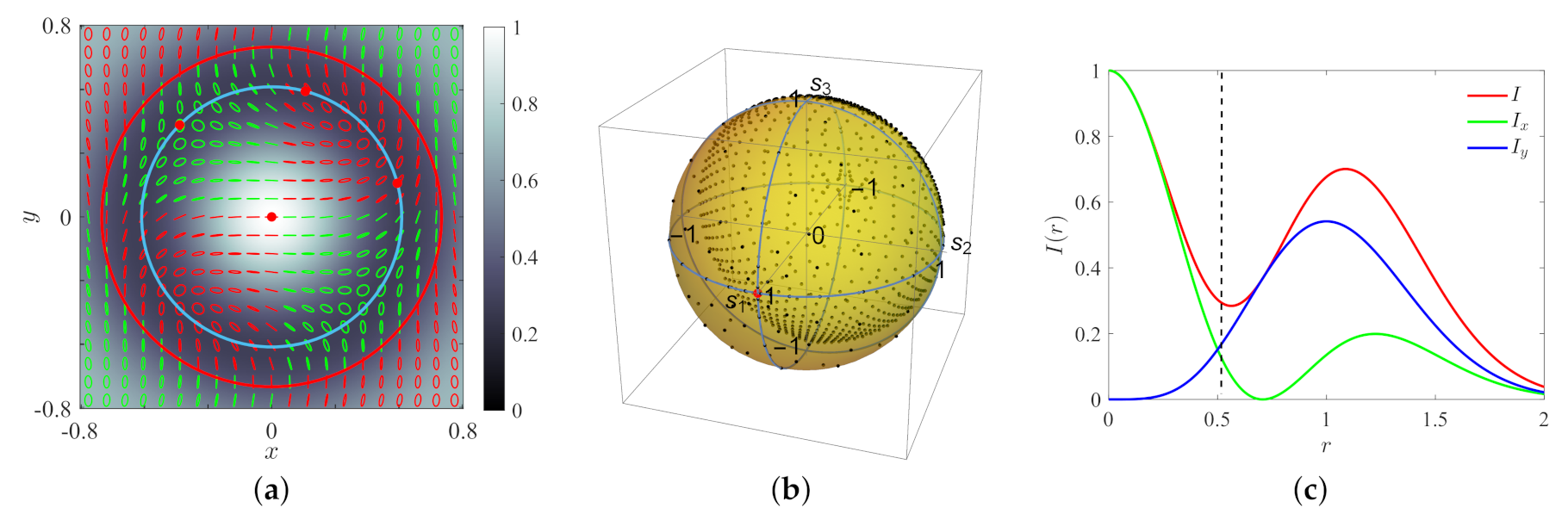An example of these fields with low-order modes in Equation (2) is presented in the following.

We take two linearly polarized component fields: a single LG mode with indices $\ell =1$ and $s=0$ (as the field $V_0^{\left(1\right)}$) and a single LG mode with indices $\ell =0$ and $s=2$ (as $V_0^{\left(2\right)}$). The sum $2\ell +\left|s\right|$ gives 2 in both cases.

Using the definition of LG modes [49], the total field can be written as

$${\mathit{V}}_0\left(\mathit{r}\right)=\left(\begin{array}{c}1-2r^2\\ \alpha r^2{e}^{-2\mathrm{i}\vartheta }\end{array}\right)e^{-r^2},$$

(22)

where common constant factors were omitted, and the coefficient $\alpha$ was introduced to let change the amplitude ratio between the two fields. The intensity distribution, together with the polarization states of the field across the plane, are shown in Figure 4a, for $\alpha =2$.

From Figure 4b, it seems that these states of polarization could cover the entire surface of the Poincaré sphere. It is possible to show that any possible polarization state on the Poincaré sphere is present across the transverse plane and even evaluate the coordinate where it occurs. In fact, from the definition of Stokes parameters [36,37]

$$\begin{array}{c}\hfill S_0\left(\mathit{r}\right)=|V_x{\left(\mathit{r}\right)|}^2+{\left|V_y\left(\mathit{r}\right)\right|}^2\\ \hfill S_1\left(\mathit{r}\right)=|V_x{\left(\mathit{r}\right)|}^2-{\left|V_y\left(\mathit{r}\right)\right|}^2\\ \hfill S_2\left(\mathit{r}\right)=2\Re \left\{V_x\left(\mathit{r}\right)V_y^{\ast }\left(\mathit{r}\right)\right\}\\ \hfill S_3\left(\mathit{r}\right)=2\Im \left\{V_x\left(\mathit{r}\right)V_y^{\ast }\left(\mathit{r}\right)\right\}\end{array}$$

(23)

where $\Re \{·\}$ and $\Im \{·\}$ stand for the real and the imaginary part, respectively, and ${}^{\ast }$ denotes the complex conjugate. It turns out that the elements of the normalized Stokes vector ($s_i=S_i/S_0$, $i=1,\dots ,3$) are

$${\displaystyle s_1=\frac{1-F^2}{1+F^2};s_2=\frac{2Fcos\left(2\vartheta \right)}{1+F^2};s_3=\frac{2Fsin\left(2\vartheta \right)}{1+F^2},}$$

(24)

where the auxiliary function F is defined as

$${\displaystyle F=\frac{\alpha r^2}{1-2r^2}.}$$

(25)

We first note that F can assume all possible values from zero to infinity when r spans the interval $(0,1/\sqrt{2})$. As a consequence, in the same interval, $s_1$ can take any value from $-1$ and 1. Then, on choosing $\vartheta$, all possible values of $s_2$ and $s_3$ can be selected. In the present case, the angles $\vartheta$ and $\vartheta +\pi$ give rise to the same polarization [8,9].

The expressions in Equation (24) can be inverted to obtain the coordinates where a given polarization appears across the transverse plane. Solving for F in the first of these expressions and using Equation (25), the following value is obtained

$${\displaystyle r^2=\frac{1}{2+\alpha \sqrt{{\displaystyle \frac{1+s_1}{1-s_1}}}},}$$

(26)

while, from the second and third expressions, the corresponding values of the angle $\vartheta$ are derived as

$${\displaystyle \vartheta =\frac{1}{2}arg[s_2+\mathrm{i}{s}_3](+\pi ).}$$

(27)

Since we were interested in using an FPB as a parallel polarization state generator, we had to select the four optimum states of polarization to be used in FPP and find the points where they are located. It is well known that the optimal configuration with a minimum number of polarization testing states in a Mueller matrix polarimeter involves four input states that form a regular tetrahedron inscribed in the Poincaré sphere [57,58]. This configuration is optimal in the sense that the errors propagated in the derivation of the Mueller matrix are minimized. A rather natural choice for one of the points is the center of the beam (where a local maximum of the intensity is found), which fixes the Stokes vector of one of the tetrahedron vertices (say, $V_0$) at ${[1,0,0]}^T$. Therefore, the three remaining vertices ($V_i$, with $i=1,2,3$) are located on the circle formed by the intersection of the Poincaré sphere with the plane $s_1=-1/3$.

We introduce, for brevity, the symbol $\sigma$ to denote $s_2\left(V_1\right)$ and assumed that the polarization at vertex $V_1$ is left-handed. As the normalized Stokes parameters satisfy $s_1^2+s_2^2+s_3^2=1$ and $s_1^2=1/9$, then $s_2^2$ cannot exceed $8/9$. As a consequence, $\sigma$ can only take values in the interval $-\sqrt{8}/3\le \sigma \le \sqrt{8}/3$. If we choose a value for $\sigma$, the polarization states of all vertices will become fixed. In particular, the three polarization states with $s_1=-1/3$ are located along a circle with radius

$${\displaystyle r^2=\frac{1}{2+\alpha /\sqrt{2}},}$$

(28)

at values of $\vartheta$ given by the following expressions:

$${\displaystyle cos\left(2{\vartheta }_1\right)=\frac{3\sigma }{2\sqrt{2}},}$$

(29)

$${\displaystyle cos\left(2{\vartheta }_{2,3}\right)=\frac{3}{2\sqrt{2}}\left({\displaystyle \frac{-\sigma }{2}\pm \sqrt{{\displaystyle \frac{2}{3}-\frac{3{\sigma }^2}{4}}}}\right).}$$

(30)

The points across the beam section corresponding to $\sigma =0$ are shown in Figure 4a as red points, together with the intensity and polarization maps. The red circle has radius $\sqrt{2}$ and encloses the region where all polarization states are present (twice). On varying $\sigma$, the three outermost points move along the light blue circle, whose radius is given by Equation (28). For the present case, this radius turns to be $r=0.54$, corresponding to the vertical dashed line in Figure 4c.

For the beam described by Equation (22), it is not easy to find four points of its transverse section whose polarization states form a regular tetrahedron on the Poincaré sphere and show a similar high intensity (see Figure 4c), which is also convenient to reduce the propagated errors in the determination of the Mueller matrix from polarimetric measurements.

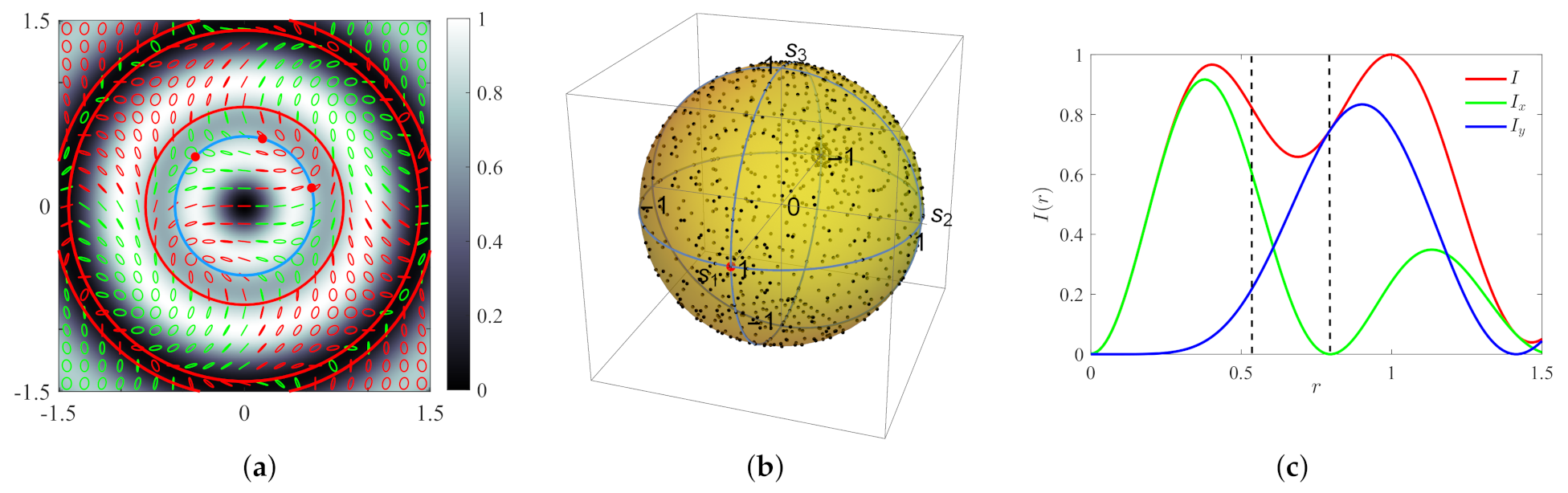
For the next example, we took the following component fields: a single LG mode with indices $p=1$ and $s=3$ (linearly polarized along $\widehat{x}$) and a single LG mode with indices $p=2$ and $s=1$ (linearly polarized along $\widehat{y}$). The sum $2p+\left|s\right|$ gives 5 in both cases. Following the use of normalized coordinates, the total field can be written as

$${\mathit{V}}_0\left(\mathit{r}\right)=\left(\begin{array}{c}2r^4-6r^2+3\\ \alpha r^2\left(2-r^2\right)e^{-2\mathrm{i}\vartheta }\end{array}\right)r{e}^{-\mathrm{i}\vartheta }{e}^{-r^2}.$$

(31)

The intensity distribution together with the polarization states of the field across the plane are shown in Figure 5a for $\alpha =1.25\sqrt{2}$. These states of polarization are also represented on the Poincaré sphere (see Figure 5b).

As in the previous example, it is possible to show that any possible polarization state on the Poincaré sphere is present across the transverse plane and even to evaluate the coordinate where it occurs. In fact, expressions in Equation (24) remain valid only by replacing the value of the auxiliary function F by

$${\displaystyle F=\frac{\alpha r^2\left(2-r^2\right)}{2r^4-6r^2+3}.}$$

(32)

The latter expression takes all possible values from zero to infinity when r spans the interval $[0,r_1]$, where

$$r_1=\sqrt{{\displaystyle \frac{3-\sqrt{3}}{2}}}$$

(33)

is the lowest positive root of the denominator of F. Inverting expressions in Equation (24), with F given by Equation (32), allows us to obtain the polar coordinates where a given polarization (chosen at will) appears across the transverse beam section. For $r\le r_1$ we have:

$${\displaystyle r^2=\frac{1+3\beta -\sqrt{3{\beta }^2+3\beta +1}}{1+2\beta },}$$

(34)

$${\displaystyle \vartheta =\frac{1}{2}arg[s_2+\mathrm{i}{s}_3](+\pi ),}$$

(35)

with

$$\beta =\frac{1}{\alpha }\sqrt{{\displaystyle \frac{1-s_1}{1+s_1}}},$$

(36)

so that the whole Poincaré sphere is mapped twice in the circle $0\le r\le r_1$, regardless of the value of $\alpha$. It can be shown that the Poincaré sphere is mapped again (twice) in the region $r_1\le r\le r_2$ and in the region $r_2\le r\le r_3$, with

$$r_2=\sqrt{2};r_3=\sqrt{{\displaystyle \frac{3+\sqrt{3}}{2}}}.$$

(37)

The three regions are identified by the solid red circles in Figure 5a.

A useful choice for using this beam as a parallel polarization state generator for polarimetry consists of selecting four points where the intensity values are sufficiently high. In this way, a more precise measurement of the Stokes parameters on these points can be obtained. This can be achieved, for instance, by selecting one of the points on the circle of radius $r_1$ (all of them having vertical polarization), then fixing the Stokes vector of one of the tetrahedron vertices (say, $P_0$) at ${[-1,0,0]}^T$.

The three remaining vertices ($P_i$, with $i=1,2,3$) are located at the intersection of the Poincaré sphere with the plane $s_1=1/3$. Using again the parameter $\sigma =s_2\left(P_1\right)$, it turns out that, limiting ourselves to the region $r\le r_1$, the three polarization states with $s_1=1/3$ are located along a circle having radius

$${\displaystyle r^2=\frac{3+\alpha \sqrt{2}-\sqrt{2{\alpha }^2+3\alpha \sqrt{2}+3}}{2+\alpha \sqrt{2}},}$$

(38)

at values of $\vartheta$ given by

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle cos\left(2{\vartheta }_1\right)=\frac{3\sigma }{2\sqrt{2}};cos\left(2{\vartheta }_{2,3}\right)=\frac{3}{2\sqrt{2}}\left({\displaystyle \frac{-\sigma }{2}\pm \sqrt{{\displaystyle \frac{2}{3}-\frac{3{\sigma }^2}{4}}}}\right).}\end{array}\end{array}$$

(39)

More solutions exist for $r>r_1$, but the intensity is lower there.

The measurement points across the beam section, corresponding to $\sigma =0$, are shown in Figure 5 as red dots (together with any point on the smallest red circle). On varying $\sigma$, the three red points move along the blue circle, whose radius is given by Equation (38), but their intensities are always the same. Furthermore, the intensities at all measurement points are very high (always over 75% of the maximum), as can be seen in Figure 5c, where the radii of the blue circle ($r=0.56$) and that of the inner red circle ($r=r_1$, given by Equation (33)) are indicated as vertical dashed lines.

We point out that if a different polarization basis is chosen for the component fields (instead of $\widehat{x},\widehat{y}$), a different polarization pattern is obtained, but the four selected points continue presenting relatively high intensity (more than 75% of the maximum) and polarization states that are on the vertices of a regular tetrahedron inscribed in the Poincaré sphere and can be used profitably for FPP measurements.

The best method to exploit the potential offered by this type of beams is to use a CCD sensor to detect the polarization states across the beam section. Due to the propagation-invariant feature of the transverse polarization pattern, no imaging optical elements are required before the sensor. On taking (at least) four images of the field profile after suitable configurations of linear polarizers and phase plates [36,37] and processing them, the whole maps of the Stokes parameters (without and with the sample, respectively) can be obtained. Therefore, in the evaluation of the Mueller matrix of the sample, all possible input polarization states are available at once. A reduction in the propagated errors can be achieved by averaging the results pertaining to different sets of measurement points or by increasing the number of points used in each measurement [16,39,57,58,59].

5. Discussion

Since in polarimetric techniques at least four linearly independent states of polarization at the input of a sample are required for a complete Mueller matrix characterization [36], NUTP beams can be profitably used as parallel polarization state generators [16,35,39,59,60,61]. Moreover, the invariance upon propagation of the polarization pattern of the input beam can be an advantage in these systems because the sample can be positioned at any transverse plane along the beam path, and no imaging systems are required after the sample [16,39,59]. Here, a class of NUTP beams whose polarization and intensity transverse profiles remain invariant during propagation, up to a scaling factor, were analyzed. In particular, in view of applications in Mueller polarimetric techniques, beams of this class that are also FPBs were studied. Some examples were given for which not only the transverse polarization map had been obtained but also the coordinates of the points where measurements should be taken to reduce the propagated errors in the determination of the Mueller matrix of the sample. Finally, we showed that, when the invariance condition is only required at the far field, a great variety of fields can be envisaged following simple analytical procedures.