Proposal for a Skin Layer-Wise Decomposition Model of Spatially-Resolved Diffuse Reflectance Spectra Based on Maximum Depth Photon Distributions: A Numerical Study
Abstract
1. Introduction
2. Materials and Methods
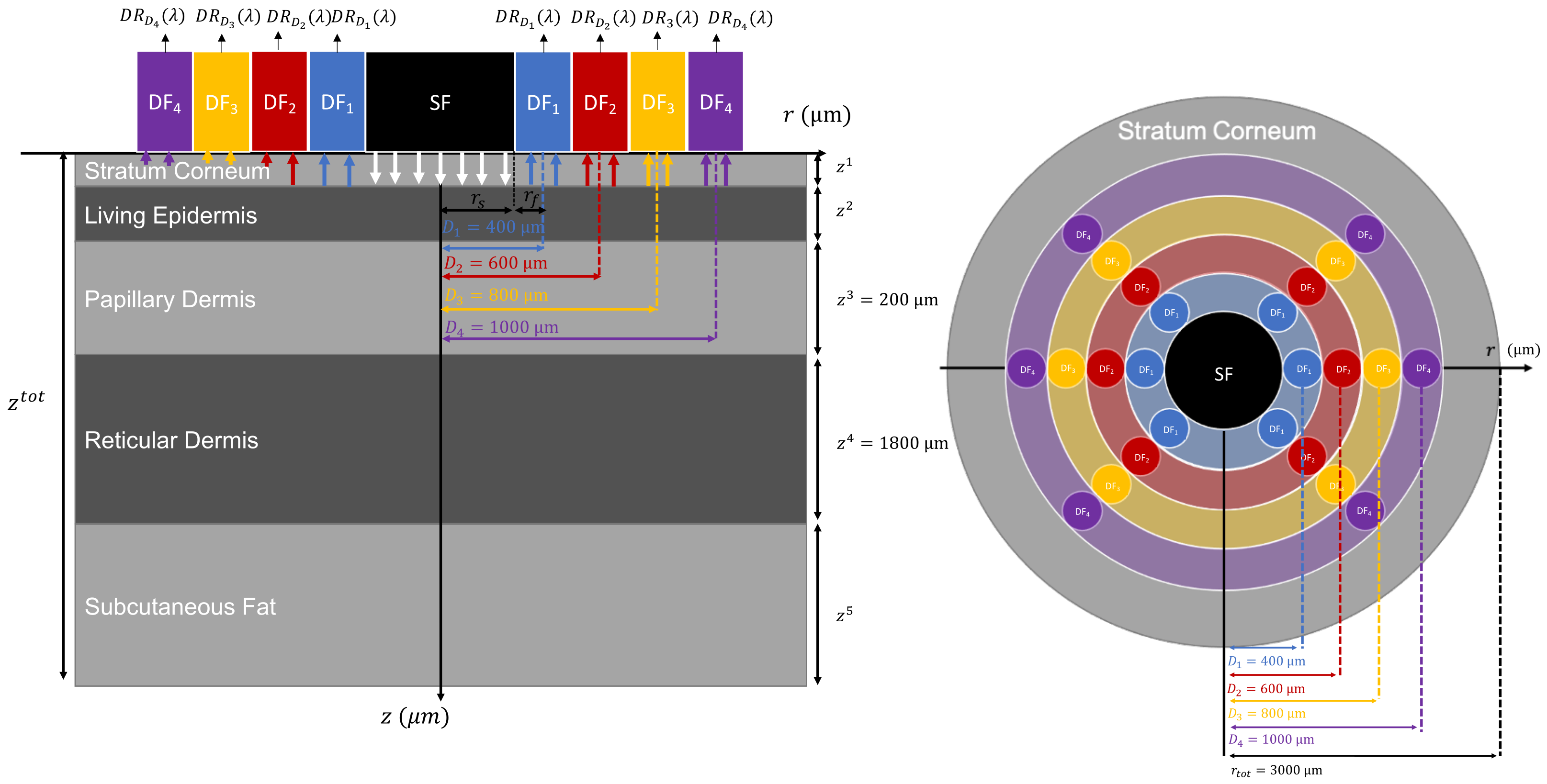
2.1. SR-DRS Probe—Geometrical and Spectral Features Implemented for Simulations
2.2. Skin Five-Layered Model
2.2.1. Layer Thicknesses and Skin Types Modeled
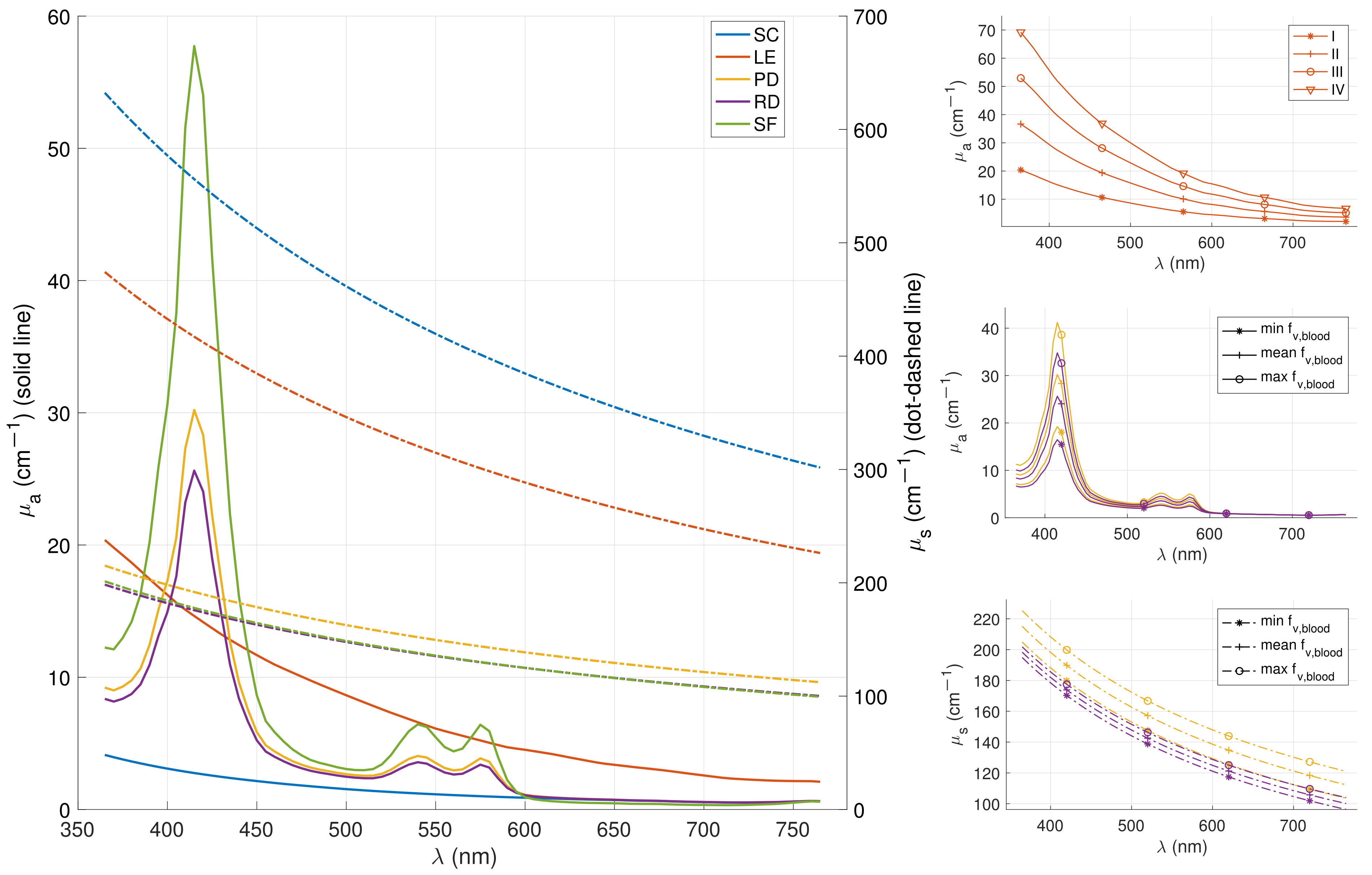
2.2.2. Skin Optical Properties
Absorption Properties
Scattering Properties
Other Optical Parameters
2.3. Simulation Configuration, Method and Tools
2.3.1. Simulation Parameters Description
2.3.2. Probed Depth Histograms
| Algorithm 1: Maximum depth histogram of weighted detected photons |
 |
| 1 Here, the maximal depth is discretized to allow the design of the histogram. The width of the length interval is the spatial resolution in depth i.e., m. |
3. Results and Discussion
3.1. Detailed Results for Healthy Skin Model with Intermediate Thicknesses
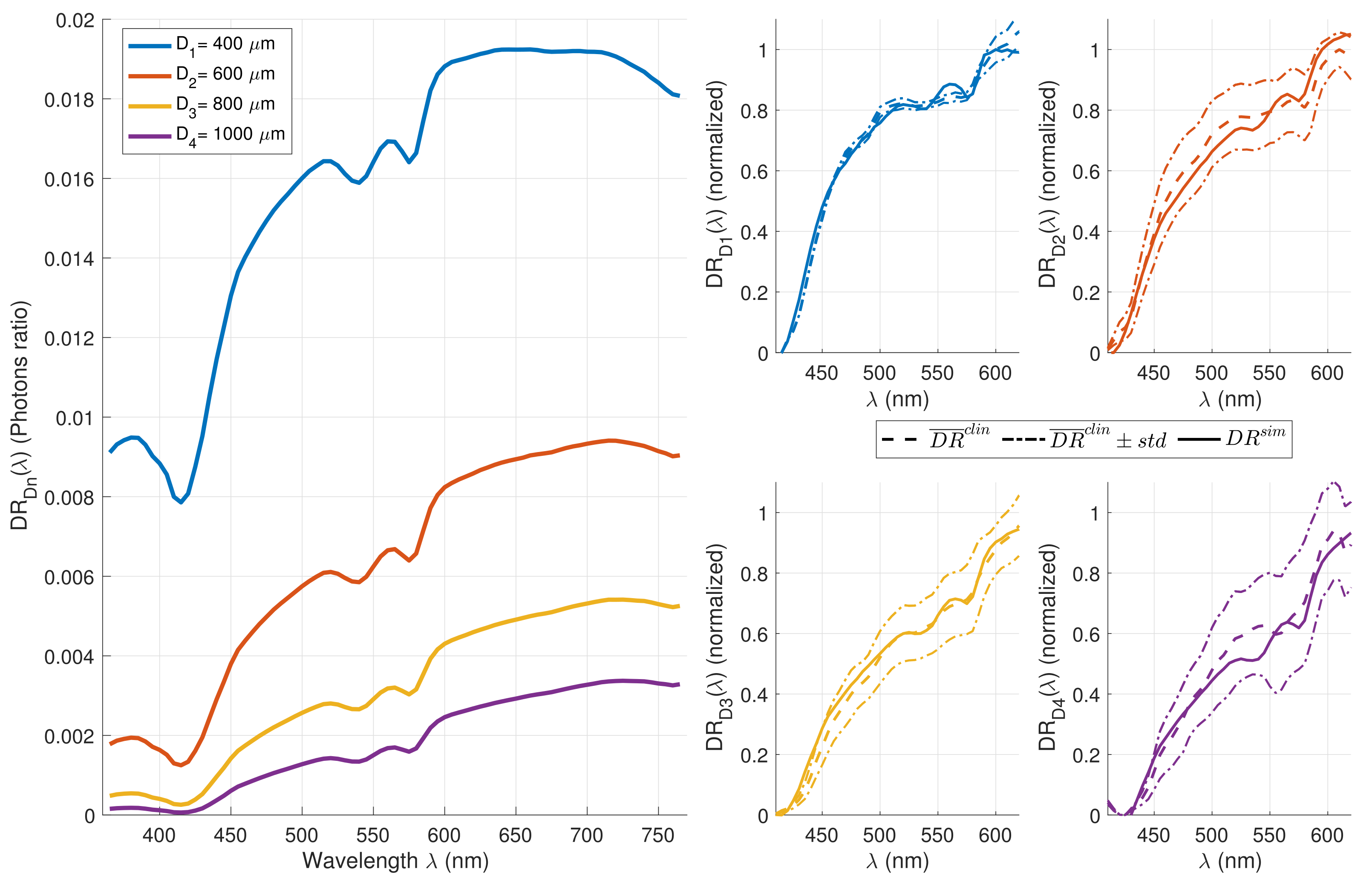
3.1.1. SR-DR Simulated Spectra
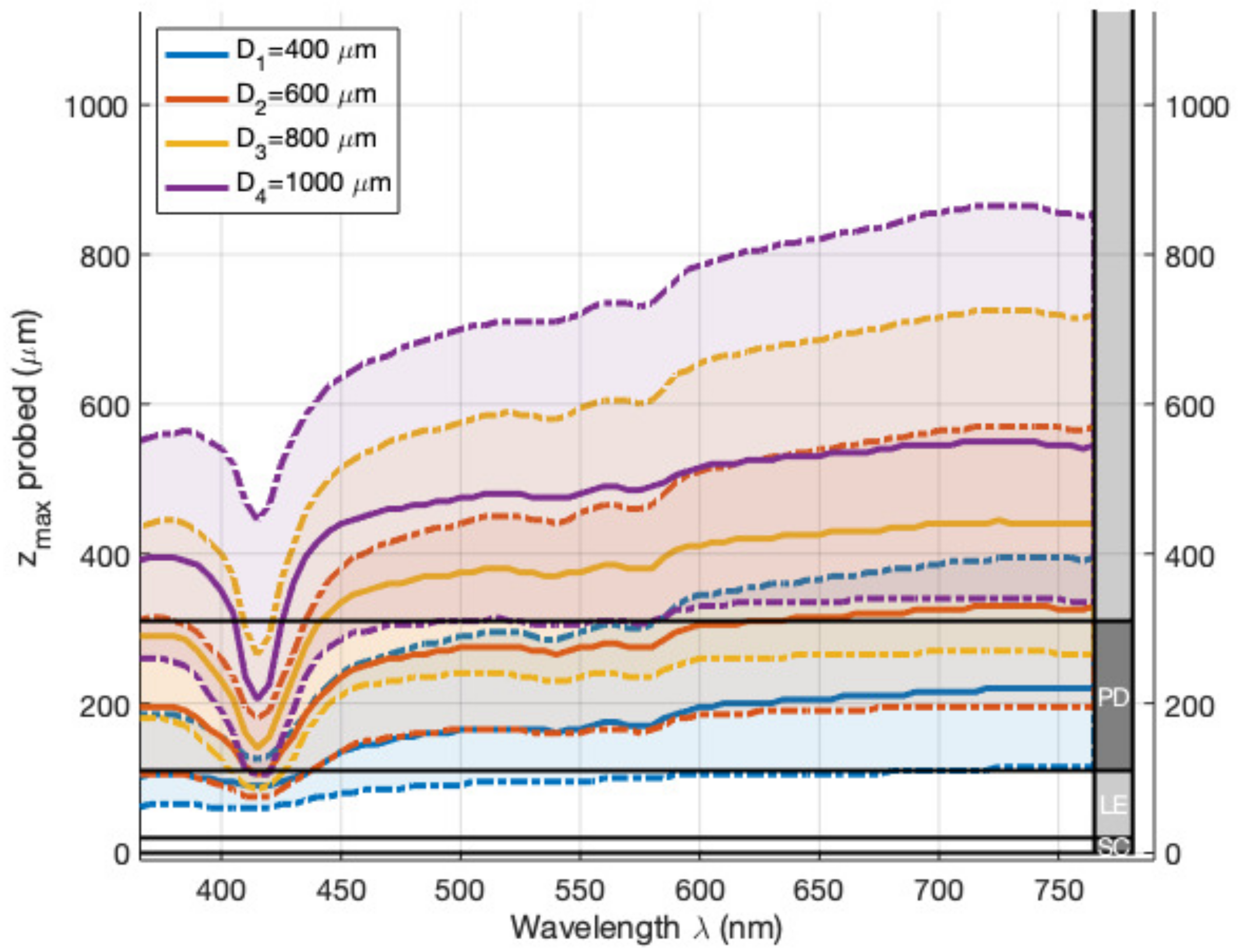
3.1.2. Depth Histogram and Exploitation
Depth Histogram
Extraction of a Typical Probed Depth and Spectral Behavior
3.2. Analysis of Spectral and Probed Depth Data Related to Medium Configuration
3.2.1. Epidermis Thickness Modifications in Healthy Skin Model
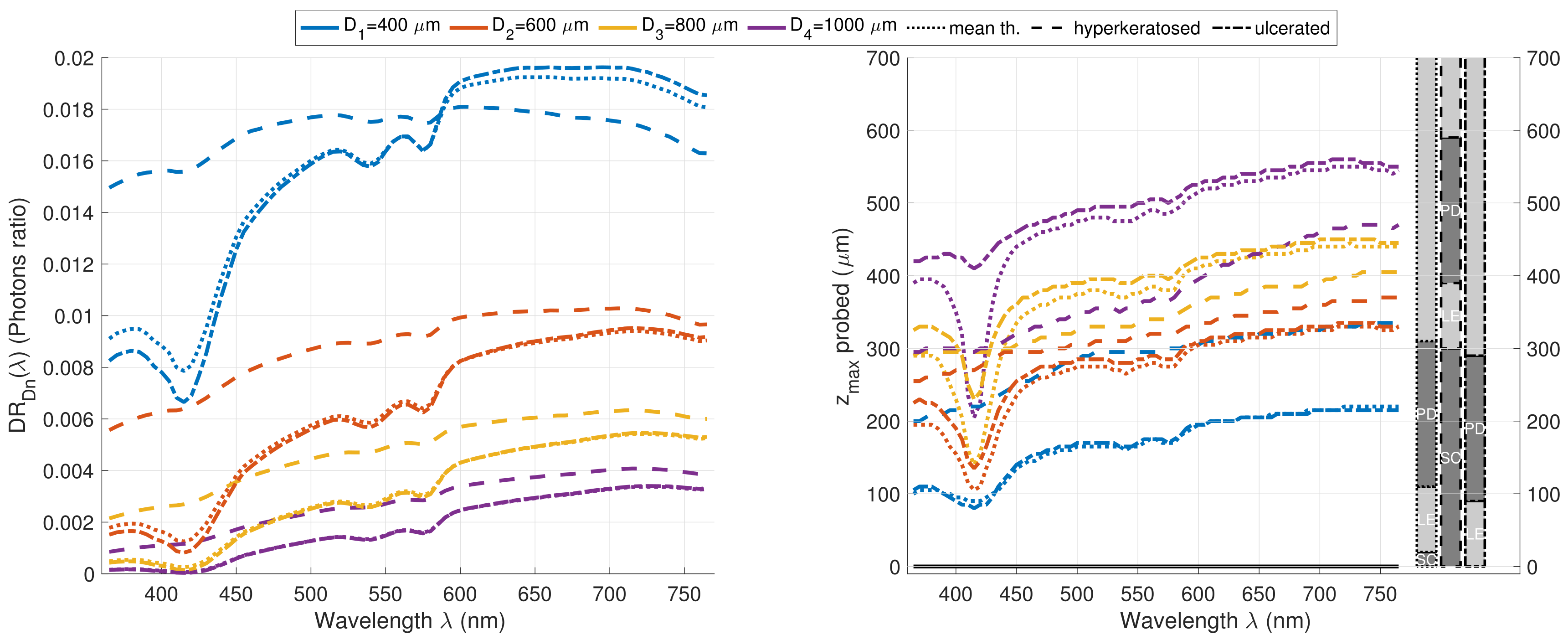
3.2.2. Epidermis Modifications in Healthy and Pathological Skin Models
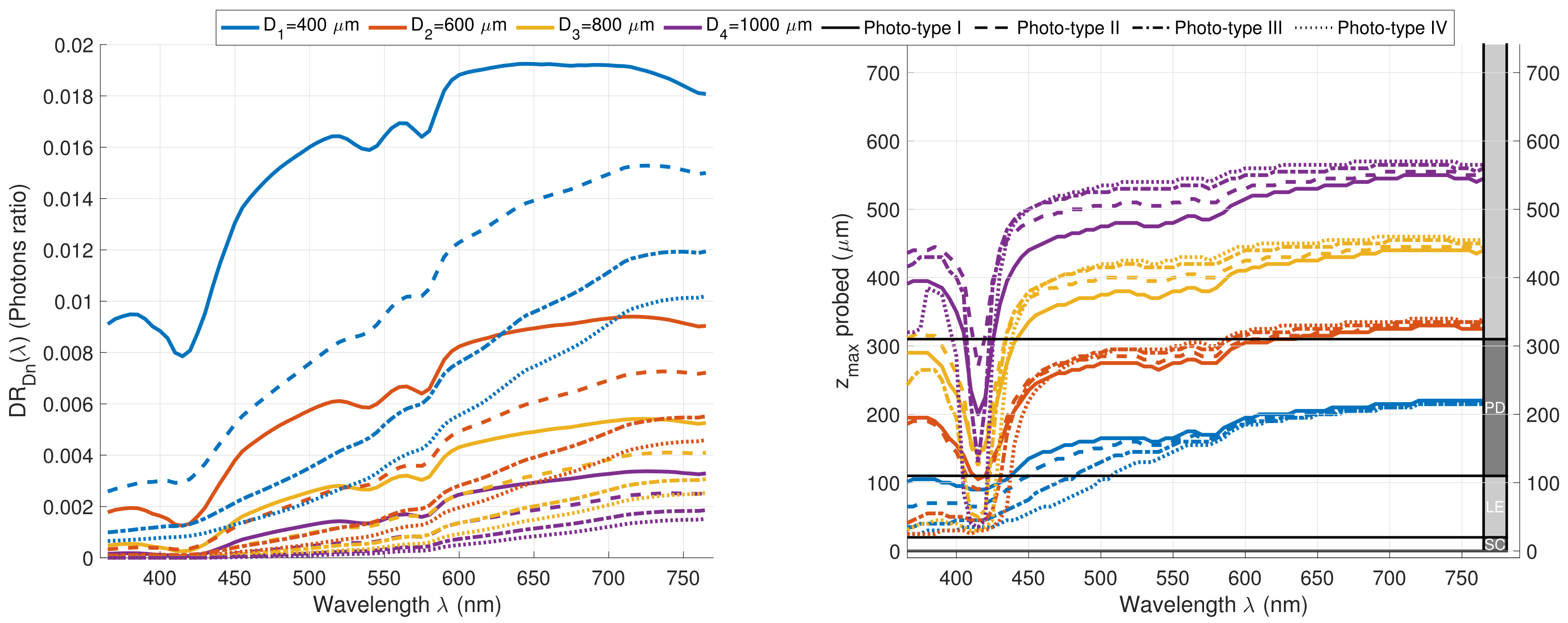
3.2.3. Phototype Modifications in Healthy Skin Model
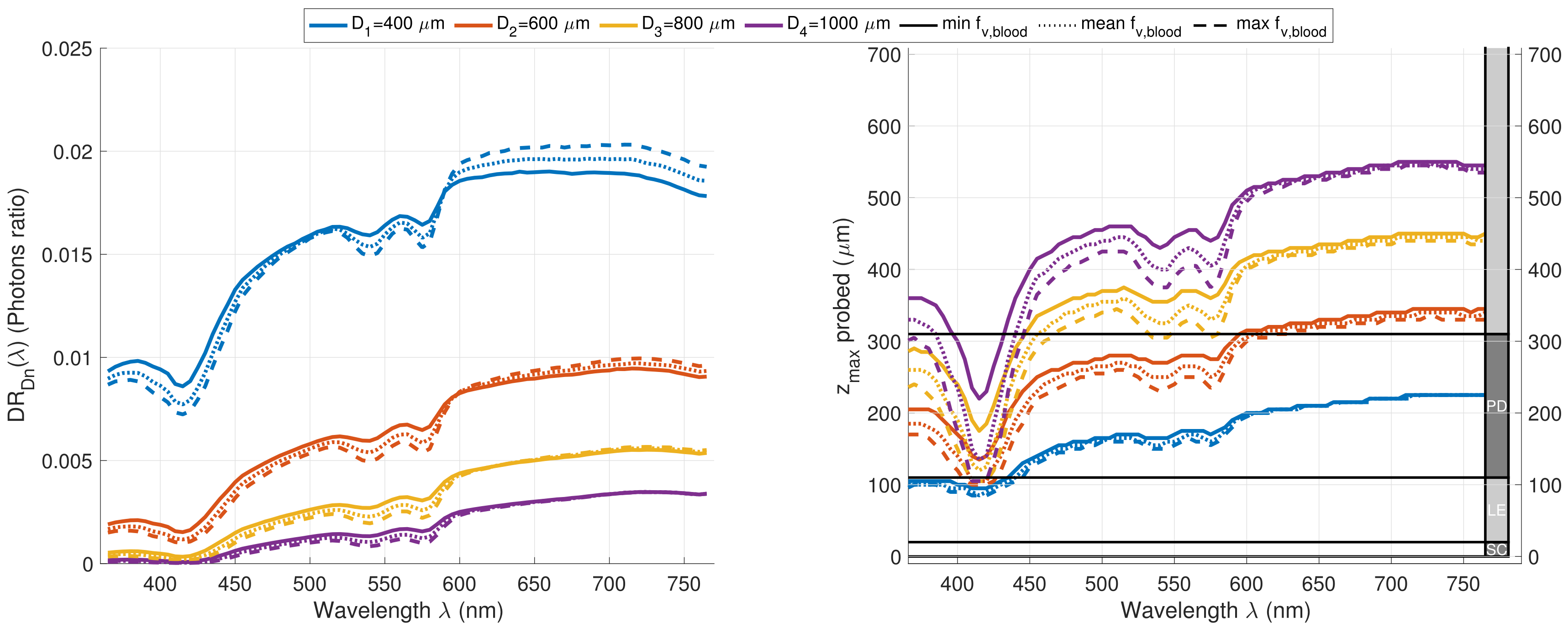
3.2.4. Blood Content in Dermal Layer Modifications in Healthy Skin Model
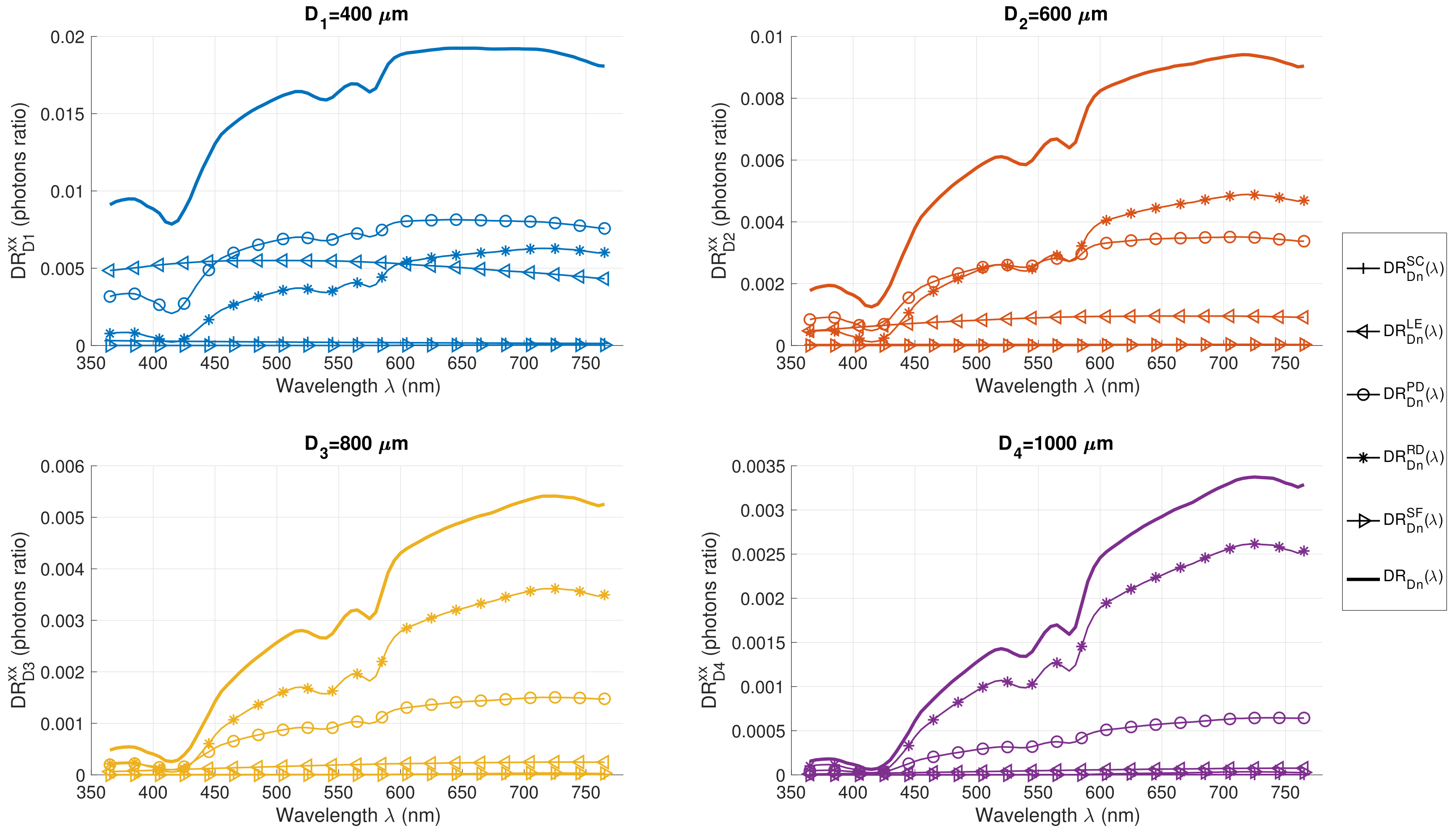
3.3. A Proposal of a Model for DR Signal Decomposition by Skin Layer
4. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bydlon, T.M.; Nachabé, R.; Ramanujam, N.; Sterenborg, H.J.C.M.; Hendriks, B.H.W. Chromophore based analyses of steady-state diffuse reflectance spectroscopy: Current status and perspectives for clinical adoption. J. Biophotonics 2015, 8, 9–24. [Google Scholar] [CrossRef] [PubMed]
- Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical properties of skin, subcutaneous, and muscle tissues: A review. J. Innov. Opt. Health Sci. 2011, 04, 9–38. [Google Scholar] [CrossRef]
- Kollias, N.; Seo, I.; Bargo, P.R. Interpreting diffuse reflectance for in vivo skin reactions in terms of chromophores. J. Biophotonics 2010, 3, 15–24. [Google Scholar] [CrossRef]
- Wilson, R.H.; Nadeau, K.P.; Jaworski, F.B.; Tromberg, B.J.; Durkin, A.J. Review of short-wave infrared spectroscopy and imaging methods for biological tissue characterization. J. Biomed. Opt. 2015, 20, 030901. [Google Scholar] [CrossRef]
- Bruulsema, J.T.; Essenpreis, M.; Heinemann, L.; Hayward, J.E.; Berger, M.; Gries, F.A.; Koschinsky, T.; Sandahl-Christiansen, J.; Orskov, H.; Farrell, T.J.; et al. Detection of Changes in Blood Glucose Concentration in vivo with Spatially Resolved Diffuse Reflectance. In Biomedical Optical Spectroscopy and Diagnostics; Optical Society of America: Orlando, FL, USA, 1996. [Google Scholar]
- Hjalmarsson, P.; Thennadil, S.N. Determination of glucose concentration in tissue-like material using spatially resolved steady-state diffuse reflectance spectroscopy. In Complex Dynamics and Fluctuations in Biomedical Photonics V; Tuchin, V.V., Wang, L.V., Eds.; International Society for Optics and Photonics: San Jose, CA, USA, 2008; Volume 6855, pp. 48–56. [Google Scholar]
- Finlay, J.; Foster, T. Hemoglobin oxygen saturations in phantoms and in vivo from measurements of steady-state diffuse reflectance at a single, short source-detector separation. Med. Phys. 2004, 31, 1949–1959. [Google Scholar] [CrossRef] [PubMed]
- Spliethoff, J.W.; Evers, D.J.; Klomp, H.M.; van Sandick, J.W.; Wouters, M.W.; Nachabe, R.; Lucassen, G.W.; Hendriks, B.H.; Wesseling, J.; Ruers, T.J. Improved identification of peripheral lung tumors by using diffuse reflectance and fluorescence spectroscopy. Lung Cancer 2013, 80, 165–171. [Google Scholar] [CrossRef] [PubMed]
- Arifler, D.; MacAulay, C.E.; Follen, M.; Richards-Kortum, R.R. Spatially resolved reflectance spectroscopy for diagnosis of cervical precancer: Monte Carlo modeling and comparison to clinical measurements. J. Biomed. Opt. 2006, 11, 064027. [Google Scholar] [CrossRef]
- LaRiviere, B.; Garman, K.S.; Ferguson, N.L.; Fisher, D.A.; Jokerst, N.M. Spatially Resolved Diffuse Reflectance Spectroscopy of Tumor and Normal Excised Human Colon with Thin Film Si Sensors. In Proceedings of the Optical Sensors and Sensing Congress (ES, FTS, HISE, Sensors), San Jose, CA, USA, 25–27 June 2019; Optical Society of America: San Jose, CA, USA, 2019; p. STu2D.5. [Google Scholar] [CrossRef]
- Pery, E.; Amouroux, M.; Diaz-Ayil, G.; Blondel, W.C.P.M.; Bourg-Heckly, G.; D’Hallewin, M.; Leroux, A.; Guillemin, F. Multi-modality point spectroscopy: Interests, development and application to in vivo diagnosis of bladder and skin cancers. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 1353–1358. [Google Scholar] [CrossRef]
- Nie, Z.; Du Le, V.N.; Cappon, D.; Provias, J.; Murty, N.; Hayward, J.E.; Farrell, T.J.; Patterson, M.S.; McMillan, W.; Fang, Q. Integrated Time-Resolved Fluorescence and Diffuse Reflectance Spectroscopy Instrument for Intraoperative Detection of Brain Tumor Margin. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 49–57. [Google Scholar] [CrossRef]
- Evers, D.J.; Nachabe, R.; Peeters, M.J.V.; van der Hage, J.A.; Oldenburg, H.S.; Rutgers, E.J.; Lucassen, G.W.; Hendriks, B.H.W.; Wesseling, J.; Ruers, T.J.M. Diffuse reflectance spectroscopy: Towards clinical application in breast cancer. Breast Cancer Res. Treat. 2013, 137, 155–165. [Google Scholar] [CrossRef]
- Georgakoudi, I.; Jacobson, B.C.; Van Dam, J.; Backman, V.; Wallace, M.B.; Müller, M.G.; Zhang, Q.; Badizadegan, K.; Sun, D.; Thomas, G.A.; et al. Fluorescence, reflectance, and light-scattering spectroscopy for evaluating dysplasia in patients with Barrett’s esophagus. Gastroenterology 2001, 120, 1620–1629. [Google Scholar] [CrossRef]
- Garcia-Uribe, A.; Chang, C.C.; Zou, J.; Banerjee, B.; Kuczynski, J.; Wang, L.V. Pancreatic tumor margin detection by oblique incidence diffuse reflectance spectroscopy. In Proceedings of the Optical Biopsy IX, San Francisco, CA, USA, 16 February 2011; Alfano, R.R., Ed.; International Society for Optics and Photonics: San Francisco, CA, USA, 2011; Volume 7895, pp. 110–114. [Google Scholar]
- Garcia-Uribe, A.; Wang, L.V.; Zou, J.; Smith, E.B.; Duvic, M.D.; Prieto, V. In-vivo characterization of optical properties of pigmented skin lesions including melanoma using oblique incidence diffuse reflectance spectrometry. J. Biomed. Opt. 2011, 16, 020501. [Google Scholar] [CrossRef]
- Pires, L.; Demidov, V.; Vitkin, I.A.; Bagnato, V.S.; Kurachi, C.; Wilson, B.C. Optical clearing of melanoma in vivo: Characterization by diffuse reflectance spectroscopy and optical coherence tomography. J. Biomed. Opt. 2016, 21, 081210. [Google Scholar] [CrossRef] [PubMed]
- Amouroux, M.; Blondel, W.; Granel-Brocard, F.; Marchal, F.; Guillemin, F. A preliminary study on skin phantoms to test spatially resolved-Diffuse Reflectance Spectroscopy as a tool to help diagnose cutaneous melanoma: A non-invasive measurement of Breslow index. Bio-Med. Mater. Eng. 2008, 18, 339–343. [Google Scholar] [CrossRef]
- Khairallah, G.; Blondel, W.; Rakotomanga, P.; Soussen, C.; Delconte, A.; Plenat, F.; Marchal, F.; Amouroux, M. Impact of standardization of autofluorescence and diffuse reflectance spectra on diagnosis accuracy of optical spectroscopy used for skin carcinomas diagnosis. In Proceedings of the Saratov Fall Meeting SFM’18 International Symposium”Optics and Biophotonics-V, Saratov, Russia, 24–29 September 2018. [Google Scholar]
- Amouroux, M.; Díaz-Ayil, G.; Blondel, W.C.P.M. Classification of ultraviolet irradiated mouse skin histological stages by bimodal spectroscopy: Multiple excitation autofluorescence and diffuse reflectance. J. Biomed. Opt. 2009, 14, 14011. [Google Scholar] [CrossRef] [PubMed]
- Koenig, A.; Roig, B.; Digabel, J.L.; Josse, G.; Dinten, J.M. Accessing deep optical properties of skin using diffuse reflectance spectroscopy. In Clinical and Biomedical Spectroscopy and Imaging IV; Brown, J.Q., Deckert, V., Eds.; International Society for Optics and Photonics: Munich, Germany, 2015; Volume 9537, pp. 42–49. [Google Scholar]
- Naglič, P.; Pernuš, F.; Likar, B.; Bürmen, M. Estimation of optical properties by spatially resolved reflectance spectroscopy in the subdiffusive regime. J. Biomed. Opt. 2016, 21, 095003. [Google Scholar] [CrossRef]
- Sharma, M.; Marple, E.; Reichenberg, J.; Tunnell, J.W. Design and characterization of a novel multimodal fiber-optic probe and spectroscopy system for skin cancer applications. Rev. Sci. Instruments 2014, 85, 083101. [Google Scholar] [CrossRef] [PubMed]
- Koenig, A.; Grande, S.; Dahel, K.; Planat-Chrétien, A.; Poher, V.; Goujon, C.; Dinten, J.M. Diffuse reflectance spectroscopy: A clinical study of tuberculin skin tests reading. In Biomedical Applications of Light Scattering VII; Wax, A.P., Backman, V., Eds.; International Society for Optics and Photonics: San Francisco, CA, USA, 2013; Volume 8592, pp. 98–105. [Google Scholar] [CrossRef]
- Breslin, T.M.; Ramanujam, N. Autofluorescence and Diffuse Reflectance Properties Malignant and Benign Breast Tissues. Ann. Surg. Oncol. 2003, 11, 65–70. [Google Scholar] [CrossRef]
- Ye Yuan, P.R. Enzymatic degradation of human skin dermis revealed by fluorescence and reflectance spectroscopy. Opt. Exp. 2008, 16, 9857–9868. [Google Scholar]
- Borisova, E.G.; Angelova, L.P.; Pavlova, E.P. Endogenous and Exogenous Fluorescence Skin Cancer Diagnostics for Clinical Applications. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 211–222. [Google Scholar] [CrossRef]
- Zhang, H.; Salo, D.C.; Kim, D.M.; Komarov, S.; Tai, Y.C.; Berezin, M.Y. Penetration depth of photons in biological tissues from hyperspectral imaging in shortwave infrared in transmission and reflection geometries. J. Biomed. Opt. 2016, 21, 126006. [Google Scholar] [CrossRef]
- Martelli, F.; Binzoni, T.; Pifferi, A.; Spinelli, L.; Farina, A.; Torricelli, A. There’s plenty of light at the bottom: Statistics of photon penetration depth in random media. Sci. Rep. 2016, 6, 27057. [Google Scholar] [CrossRef]
- Hidenobu Arimoto, M.E.; Yamada, Y. Depth profile of diffuse reflectance near-infrared spectroscopy for measurement of water content in skin. Skin Res. Technol. 2005, 11, 27–35. [Google Scholar] [CrossRef]
- Arifler, D.; Schwarz, R.A.; Chang, S.K.; Richards-Kortum, R. Reflectance spectroscopy for diagnosis of epithelial precancer: Model-based analysis of fiber-optic probe designs to resolve spectral information from epithelium and stroma. Appl. Opt. 2005, 44, 4291–4305. [Google Scholar] [CrossRef]
- Tseng, S.H.; Tzeng, S.Y.; Liaw, Y.K.; Hsu, C.K.; Lee, J.; Chen, W.R. Noninvasive evaluation of collagen and hemoglobin contents and scattering property of in vivo keloid scars and normal skin using diffuse reflectance spectroscopy: Pilot study. J. Biomed. Opt. 2012, 17, 077005. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nilsson, H.; Larsson, M.; Nilsson, G.; Strömberg, T. Photon pathlength determination based on spatially resolved diffuse reflectance. J. Biomed. Opt. 2002, 7, 475–485. [Google Scholar] [CrossRef][Green Version]
- Larsson, M.; Nilsson, H.; Strömberg, T. In vivo determination of local skin optical properties and photon path length by use of spatially resolved diffuse reflectance with applications in laser Doppler flowmetry. Appl. Opt. 2003, 42, 124–134. [Google Scholar] [CrossRef]
- Liebert, A.; Wabnitz, H.; Steinbrink, J.; Obrig, H.; Möller, M.; Macdonald, R.; Villringer, A.; Rinneberg, H. Time-resolved multidistance near-infrared spectroscopy of the adult head: Intracerebral and extracerebral absorption changes from moments of distribution of times of flight of photons. Appl. Opt. 2004, 43, 3037–3047. [Google Scholar] [CrossRef]
- Fredriksson, I.; Larsson, M.; Strömberg, T. Inverse Monte Carlo method in a multilayered tissue model for diffuse reflectance spectroscopy. J. Biomed. Opt. 2012, 17, 047004. [Google Scholar] [CrossRef] [PubMed]
- Blondel, W.; Delconte, A.; Khairallah, G.; Marchal, F.; Gavoille, A.; Amouroux, M. Spatially-Resolved Multiply-Excited Autofluorescence and Diffuse Reflectance Spectroscopy: SpectroLive Medical Device for Skin In Vivo Optical Biopsy. Electronics 2021, 10, 243. [Google Scholar] [CrossRef]
- Khairallah, G.; Amouroux, M.; Plénat, F.; Rakotomanga, P.; Soussen, C.; Marchal, F.; Delconte, A.; Chen, H.; Blondel, W. Spatially resolved spectroscopy for guiding margin delineation during human skin carcinomas resection: First clinical results on diffuse reflectance and autofluorescence spectra and in vivo skin optical properties. In Biophotonics: Photonic Solutions for Better Health Care VI; Popp, J., Tuchin, V.V., Pavone, F.S., Eds.; International Society for Optics and Photonic: Strasbourg, France, 2018; Volume 10685, pp. 200–206. [Google Scholar]
- Dahlstrand, U.; Sheikh, R.; Nguyen, C.D.; Hult, J.; Reistad, N.; Malmsjö, M. Identification of tumor margins using diffuse reflectance spectroscopy with an extended-wavelength spectrum in a porcine mode. Skin Res. Technol. 2018, 24, 667–671. [Google Scholar] [CrossRef]
- Feng, X.; Fox, M.C.; Reichenberg, J.S.; Lopes, F.C.P.S.; Sebastian, K.R.; Markey, M.K.; Tunnell, J.W. Biophysical basis of skin cancer margin assessment using Raman spectroscopy. Biomed. Opt. Express 2019, 10, 104–118. [Google Scholar] [CrossRef]
- Zelinskyi, Y.; Naglič, P.; Pernuš, F.; Likar, B.; Bürmen, M. Fast and accurate Monte Carlo simulations of subdiffusive spatially resolved reflectance for a realistic optical fiber probe tip model aided by a deep neural network. Biomed. Opt. Express 2020, 11, 3875–3889. [Google Scholar] [CrossRef] [PubMed]
- Maiti, R.; Duan, M.; Danby, S.G.; Lewis, R.; Matcher, S.J.; Carré, M.J. Morphological parametric mapping of 21 skin sites throughout the body using optical coherence tomography. J. Mech. Behav. Biomed. Mater. 2020, 102, 103501. [Google Scholar] [CrossRef]
- Chopra, K.; Calva, D.; Sosin, M.; Tadisina, K.; Banda, A.; Cruz, C.D.L.; Chaudhry, M.; Legesse, T.; Drachenberg, C.; Manson, P.; et al. A comprehensive examination of topographic thickness of skin in the human face. Aesthet. Surg. J. 2015, 35, 1007–1013. [Google Scholar] [CrossRef] [PubMed]
- Robertson, K.; Re, J.L. Variation in Epidermal Morphology in Human Skin at Different Body Sites as Measured by Reflectance Confocal Microscopy. Med. J. Ltd. 2010, 90, 368–373. [Google Scholar]
- Amouroux, M. Caractérisation de la Transformation Néoplasique de la peau par Spectroscopies Optiques sur Fantôme de Mélanome et Carcinome Epidermoïde murin Photo-Induit. Ph.D. Thesis, Université Henri Poincaré, Nancy, France, 2008. [Google Scholar]
- Colas, V.; Daul, C.; Khairallah, G.; Amouroux, M.; Blondel, W. Spatially resolved diffuse reflectance and autofluorescence photon depth distribution in human skin spectroscopy: A modeling study. In Optics in Health Care and Biomedical Optics X; Luo, Q., Li, X., Gu, Y., Zhu, D., Eds.; International Society for Optics and Photonics: Bellingham, Washington, USA, 2020; Volume 11553, pp. 82–96. [Google Scholar] [CrossRef]
- Meglinski, I.V.; Matcher, S.J. Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in the visible and near-infrared spectral regions. Physiol. Meas 2002, 23, 741. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef]
- Prahl, S. A Compendium of Tissue Optical Properties. Available online: http://omlc.ogi.edu/spectra/ (accessed on 1 December 2020).
- Karsten, A.E.; Smit, J.E. Modeling and Verification of Melanin Concentration on Human Skin Type. Photochem. Photobiol. 2012, 88, 469–474. [Google Scholar] [CrossRef]
- Nishidate, I.; Maeda, T.; Aizu, Y.; Niizeki, K. Visualizing depth and thickness of a local blood region in skin tissue using diffuse reflectance images. J. Biomed. Opt. 2007, 12, 054006. [Google Scholar] [CrossRef]
- Krishnaswamy, A.; Baranoski, G. Light and Skin Interactions, 1st ed.; Elsevier: Burlington, MA, USA, 2010. [Google Scholar]
- Altshuler, G.; Smirnov, M.; Yaroslavsky, I. Lattice of optical islets: A novel treatment modality in photomedicine. J. Phys. D Appl. Phys. 2005, 38, 2732. [Google Scholar] [CrossRef]
- Ding, H.; Lu, J.; Wooden, W.; Kragel, P.; Hu, X. Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm. Phys. Med. Biol. 2006, 51, 1479–1489. [Google Scholar] [CrossRef]
- Tsui, S.Y.; Wang, C.Y.; Huang, T.H.; Sung, K.B. Modelling spatially-resolved diffuse reflectance spectra of a multi-layered skin model by artificial neural networks trained with Monte Carlo simulations. Biomed. Opt. Express 2018, 9, 1531–1544. [Google Scholar] [CrossRef]
- Alerstam, E.; Svensson, T.; Andersson-Engels, S. CUDAMCML: User Manual and Implementation Notes. 2009. Available online: http://www.lth.se/fileadmin/atomfysik/Biophotonics/Software/CUDAMCML.pdf (accessed on 1 October 2019).
- Sun, C.; Aernouts, B.; Saeys, W. Bridging the gap between measurement-based and simulation-based metamodels for deriving bulk optical properties from spatially-resolved reflectance profiles: Effect of illumination and detection geometry. Opt. Express 2021, 29, 15882–15905. [Google Scholar] [CrossRef]
- Hennessy, R.; Goth, W.; Sharma, M.; Markey, M.K.; Tunnell, J.W. Effect of probe geometry and optical properties on the sampling depth for diffuse reflectance spectroscopy. J. Biomed. Opt. 2014, 19, 107002. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Greening, G.; Mundo, A.; Rajaram, N.; Muldoon, T.J. Sampling depth of a diffuse reflectance spectroscopy probe for in-vivo physiological quantification of murine subcutaneous tumor allografts. J. Biomed. Opt. 2018, 23, 085006. [Google Scholar] [CrossRef] [PubMed]
- Yudovsky, D.; Pilon, L. Rapid and accurate estimation of blood saturation, melanin content, and epidermis thickness from spectral diffuse reflectance. Appl. Opt. 2010, 49, 1707–1719. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Hennessy, R.; Markey, M.K.; Tunnell, J.W. Verification of a two-layer inverse Monte Carlo absorption model using multiple source-detector separation diffuse reflectance spectroscopy. Biomed. Opt. Express 2014, 5, 40–53. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Zeng, F.A.; Chance, B. Photon migration in the presence of a single defect: A perturbation analysis. Appl. Opt. 1995, 34, 3826–3837. [Google Scholar] [CrossRef]
- Jonasson, H.; Fredriksson, I.; Bergstrand, S.; Östgren, C.J.; Larsson, M.; Strömberg, T. In vivo characterization of light scattering properties of human skin in the 475- to 850-nm wavelength range in a Swedish cohort. J. Biomed. Opt. 2018, 23, 121608. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical assessment of cutaneous blood volume depends on the vessel size distribution: A computer simulation study. J. Biophotonics 2010, 3, 75–81. [Google Scholar]
- Zhu, C.; Liu, Q. Validity of the semi-infinite tumor model in diffuse reflectance spectroscopy for epithelial cancer diagnosis: A Monte Carlo study. Opt. Express 2011, 19, 17799–17812. [Google Scholar] [CrossRef] [PubMed]
- Palmer, G.M.; Ramanujam, N. Monte Carlo-based inverse model for calculating tissue optical properties. Part I: Theory and validation on synthetic phantoms. Appl. Opt. 2006, 45, 1062–1071. [Google Scholar] [CrossRef] [PubMed]
- Cen, H.; Lu, R.; Dolan, K. Optimization of inverse algorithm for estimating the optical properties of biological materials using spatially-resolved diffuse reflectance. Inverse Probl. Sci. Eng. 2010, 18, 853–872. [Google Scholar] [CrossRef]



| (nm) | (m) | (m) | (m) | |
|---|---|---|---|---|
| 400, 600, 800, 1000 | 0.22 | 300 | 100 |
| Skin Categories | SC Thickness (m) | LE Thickness (m) | |
|---|---|---|---|
| Healthy | Smallest thicknesses | 10 | 60 |
| Mean thicknesses | 20 | 90 | |
| Highest thicknesses | 30 | 120 | |
| Carcinoma | Ulcerated | 0 | 90 |
| Hyperkeratosed | 300 | 90 | |
| Skin Type | Very Fair | Fair | Moderately Fair | Dark Skin |
|---|---|---|---|---|
| Phototype | I | II | III | IV |
| Melanosome volume fraction | 0.01 | 0.04 | 0.08 | 0.11 |
| Blood Content | Weak | Mean | Strong |
|---|---|---|---|
| PD blood volume fraction | 0.0144 | 0.024 | 0.0336 |
| RD blood volume fraction | 0.012 | 0.02 | 0.028 |
| Name (Unit) | Symbol | SC | LE | PD | RD | SF |
|---|---|---|---|---|---|---|
| Absorption parameters | ||||||
| Volume fraction (dimensionless) | 0.35 | 0.6 | 0.5 | 0.7 | 0.05 | |
| 0.2 | 0.15 | 0.173 | 0.173 | 0.753 | ||
| 0.45 | 0.24 | 0.303 | 0.125 | 0.141 | ||
| 0 | See Table 3 | 0 | 0 | 0 | ||
| 0 | 0 | See Table 4 | See Table 4 | 0.005 | ||
| Concentration (g/L) | 0 | |||||
| 0 | 80 | 0 | 0 | 0 | ||
| 0 | 12 | 0 | 0 | 0 | ||
| 0 | 0 | 0.05 | 0.05 | 0.05 | ||
| 0 | 0 | 150 | 150 | 150 | ||
| Scattering parameters | ||||||
| Volume fraction | 0 | 0 | See Table 4 | See Table 4 | 0.05 | |
| Vessel diam. (cm) | / | / | ||||
| Scat. coeff. (cm) | 400 | 300 | 120 | 120 | 130 | |
| Other optical properties and medium geometry | ||||||
| Layer thick. (m) | See Table 2 | See Table 2 | 200 | 1800 | See Table 2 | |
| Anisotropy factor | 0.92 | 0.75 | 0.72 | 0.72 | 0.9 | |
| Refractive index | 1.55 | 1.44 | 1.39 | 1.38 | 1.34 | |
| Photon Number | Block Number | Threads per Block | (s) | (s) | |
|---|---|---|---|---|---|
| 28 | 320 | [900–1500] | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colas, V.; Blondel, W.; Khairallah, G.; Daul, C.; Amouroux, M. Proposal for a Skin Layer-Wise Decomposition Model of Spatially-Resolved Diffuse Reflectance Spectra Based on Maximum Depth Photon Distributions: A Numerical Study. Photonics 2021, 8, 444. https://doi.org/10.3390/photonics8100444
Colas V, Blondel W, Khairallah G, Daul C, Amouroux M. Proposal for a Skin Layer-Wise Decomposition Model of Spatially-Resolved Diffuse Reflectance Spectra Based on Maximum Depth Photon Distributions: A Numerical Study. Photonics. 2021; 8(10):444. https://doi.org/10.3390/photonics8100444
Chicago/Turabian StyleColas, Victor, Walter Blondel, Grégoire Khairallah, Christian Daul, and Marine Amouroux. 2021. "Proposal for a Skin Layer-Wise Decomposition Model of Spatially-Resolved Diffuse Reflectance Spectra Based on Maximum Depth Photon Distributions: A Numerical Study" Photonics 8, no. 10: 444. https://doi.org/10.3390/photonics8100444
APA StyleColas, V., Blondel, W., Khairallah, G., Daul, C., & Amouroux, M. (2021). Proposal for a Skin Layer-Wise Decomposition Model of Spatially-Resolved Diffuse Reflectance Spectra Based on Maximum Depth Photon Distributions: A Numerical Study. Photonics, 8(10), 444. https://doi.org/10.3390/photonics8100444






