Topological Charge and Asymptotic Phase Invariants of Vortex Laser Beams
Abstract
:1. Introduction
2. Orbital Angular Momentum and Topological Charge
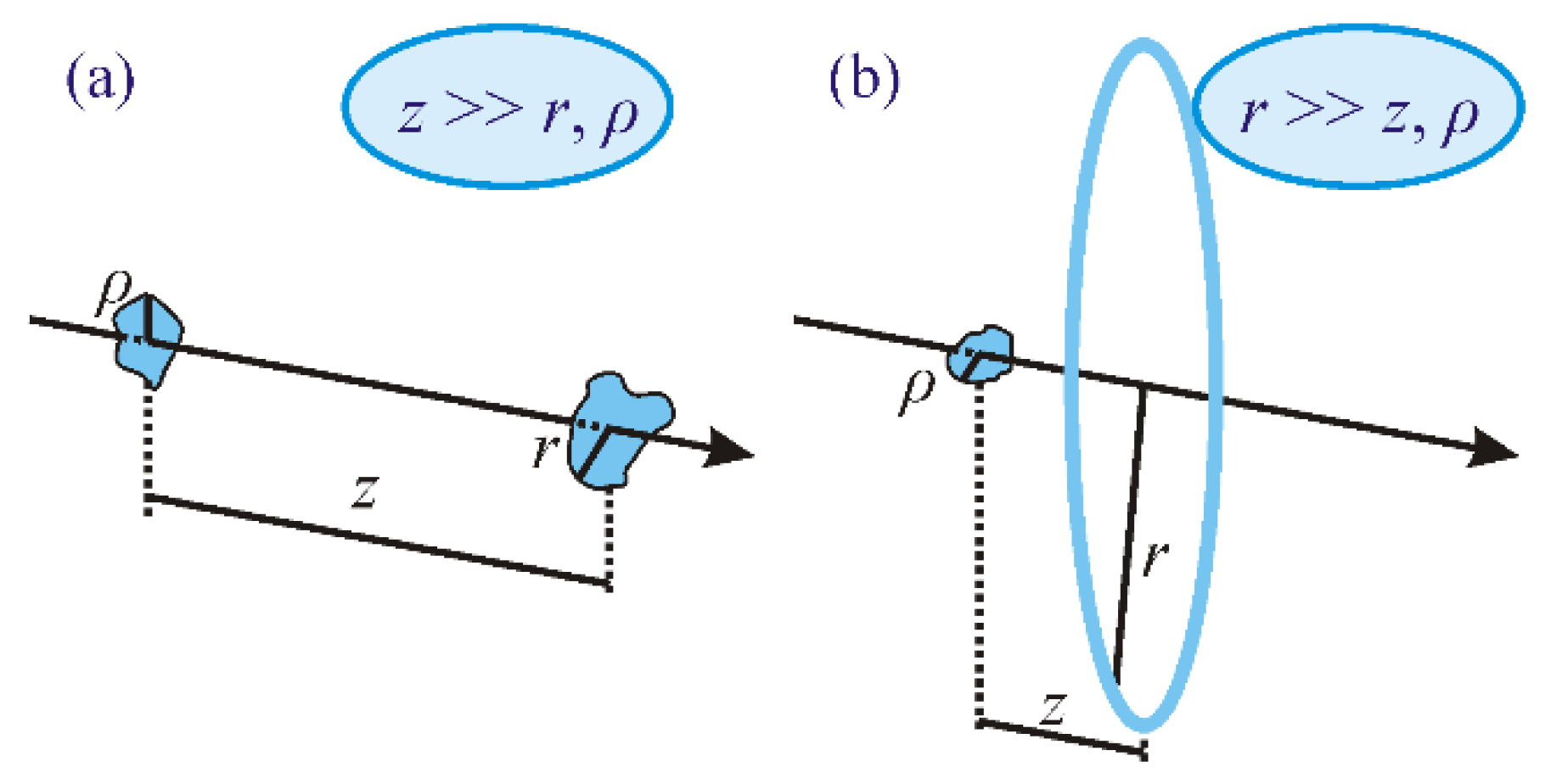
3. Propagation of a Light Field in Free Space and Conservation of Its Orbital Angular Momentum
4. Conservation of the Topological Charge
5. Asymptotic Phase Invariants of Vortex Laser Beams
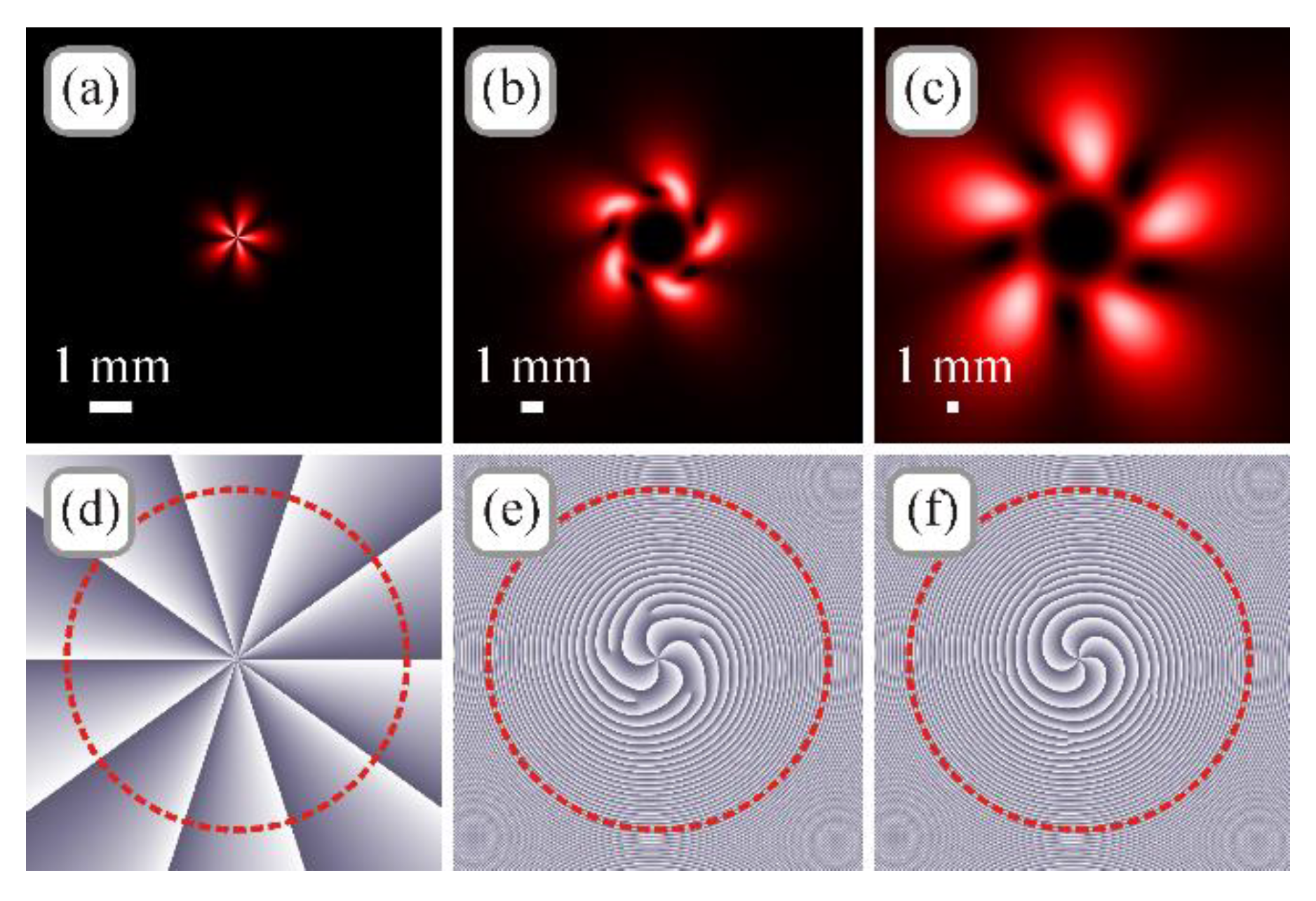
6. Numerical Simulation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef]
- Bandres, M.; Gutiérrez-Vega, J.; Chávez-Cerda, S. Parabolic nondiffracting optical wave fields. Opt. Lett. 2004, 29, 44–46. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Vega, J.; Iturbe-Castillo, M.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science: Mill Valley, CA, USA, 1986. [Google Scholar]
- Efremidis, N.; Chen, Z.; Segev, M.; Christodoulides, D. Airy beams and accelerating waves: An overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Hu, Y.; Li, T.; Cannan, D.; Yin, X.; Morandotti, R.; Chen, Z.; Zhang, X. Nonparaxial Mathieu and Weber Accelerating Beams. Phys. Rev. Lett. 2012, 109, 193901. [Google Scholar] [CrossRef] [Green Version]
- Turunen, J.; Friberg, A.T. Propagation-invariant optical fields. Prog. Opt. 2010, 54, 1–88. [Google Scholar]
- Levy, U.; Derevyanko, S.; Silberberg, Y. Light modes of free space. Prog. Opt. 2016, 61, 237–281. [Google Scholar]
- Xiong, H.; Huang, Y.; Wu, Y. Laguerre-Gaussian optical sum-sideband generation via orbital angular momentum exchange. Phys. Rev. A 2021, 103, 043506. [Google Scholar] [CrossRef]
- Gbur, G.; Tuson, R.K. Vortex beam propagation through atmospheric turbulence and topological charge conservation. J. Opt. Soc. Am. A 2008, 25, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Volyar, A.V.; Bretsko, M.V.; Akimova, Y.E.; Egorov, Y.A.; Milyukov, V.V. Sectorial perturbation of vortex beams: Shannon entropy, orbital angular momentum and topological charge. Comput. Opt. 2019, 43, 723–734. [Google Scholar] [CrossRef]
- Alperin, S.N.; Niederriter, R.D.; Gopinath, J.T.; Siemens, M.E. Quantitative measurement of the orbital angular momentum of light with a single, stationary lens. Opt. Lett. 2016, 41, 5019–5022. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Calculation of fractional orbital angular momentum of superpositions of optical vortices by intensity moments. Opt. Express 2019, 27, 11236–11251. [Google Scholar] [CrossRef]
- Melo, L.A.; Jesus-Silva, A.J.; Chávez-Cerda, S.; Ribeiro, P.H.S.; Soares, W.C. Direct measurement of the topological charge in elliptical beams using diffraction by a triangular aperture. Sci. Rep. 2018, 8, 6370. [Google Scholar] [CrossRef] [Green Version]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017, 56, 4095–4104. [Google Scholar] [CrossRef]
- Allen, L.; Barnett, S.M.; Padgett, M.J. Orbital Angular Momentum; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Gaussian beams with very high orbital angular momentum. Opt. Commun. 1997, 144, 210–213. [Google Scholar] [CrossRef]
- Martinez-Castellanos, I.; Gutiérrez-Vega, J. Shaping optical beams with non-integer orbital-angular momentum: A generalized differential operator approach. Opt. Lett. 2015, 40, 1764–1767. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259. [Google Scholar] [CrossRef]
- Allen, L.; Padgett, M.J.; Babiker, M., IV. The orbital angular momentum of light. Prog. Opt. 1999, 39, 291–372. [Google Scholar]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. Ser. A 1974, 336, 165–190. [Google Scholar]
- Soskin, M.S.; Gorshkov, V.N.; Vasnetsov, M.V.; Malos, J.T.; Heckenberg, N.R. Topological charge and angular momentum of light beams carrying optical vortices. Phys. Rev. A 1997, 56, 4064. [Google Scholar] [CrossRef] [Green Version]
- Kotlyar, V.V.; Kovalev, A.A.; Nalimov, A.G. Optical phase singularities ‘going to’infinity with a higher-than-light speed. J. Opt. 2021, 23, 105702. [Google Scholar] [CrossRef]
- Gori, F. Current Trends in Optics; Dainty, J.C., Ed.; Academic Press: Cambridge, MA, USA, 1994; p. 140. [Google Scholar]
- Humblet, J. Sur le moment d’impulsion d’une onde electromagnetique. Physica 1943, 10, 585–603. [Google Scholar] [CrossRef]
- Sommerfeld, A. Lectures on Theoretical Physics; Academic Press: New York, NY, USA, 1954; pp. 361–373. [Google Scholar]
- Sacks, Z.; Rozas, D.; Swartzlander, G.J. Holographic formation of optical-vortex filaments. Opt. Soc. Am. B 1998, 15, 2226–2234. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Skidanov, R.V.; Moiseev, O.Y.; Soifer, V.A. Diffraction of a finite-radius plane wave and a Gaussian beam by a helical axicon and a spiral phase plate. J. Opt. Soc. Am. A 2007, 24, 1955–1964. [Google Scholar] [CrossRef]
- Dennis, M. Rows of optical vortices from elliptically perturbing a high-order beam. Opt. Lett. 2006, 31, 1325–1327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paroli, B.; Siano, M.; Potenza, M. Measuring the topological charge of orbital angular momentum radiation in single-shot by means of the wavefront intrinsic curvature. Appl. Opt. 2020, 59, 5258–5264. [Google Scholar] [CrossRef]
- Wang, D.; Huang, H.; Toyoda, H.; Liu, H. Topological Charge Detection Using Generalized Contour-Sum Method from Distorted Donut-Shaped Optical Vortex Beams: Experimental Comparison of Closed Path Determination Methods. Appl. Sci. 2019, 9, 3956. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalev, A.A.; Kotlyar, V.V.; Nalimov, A.G. Topological Charge and Asymptotic Phase Invariants of Vortex Laser Beams. Photonics 2021, 8, 445. https://doi.org/10.3390/photonics8100445
Kovalev AA, Kotlyar VV, Nalimov AG. Topological Charge and Asymptotic Phase Invariants of Vortex Laser Beams. Photonics. 2021; 8(10):445. https://doi.org/10.3390/photonics8100445
Chicago/Turabian StyleKovalev, Alexey A., Victor V. Kotlyar, and Anton G. Nalimov. 2021. "Topological Charge and Asymptotic Phase Invariants of Vortex Laser Beams" Photonics 8, no. 10: 445. https://doi.org/10.3390/photonics8100445
APA StyleKovalev, A. A., Kotlyar, V. V., & Nalimov, A. G. (2021). Topological Charge and Asymptotic Phase Invariants of Vortex Laser Beams. Photonics, 8(10), 445. https://doi.org/10.3390/photonics8100445





