Scattering Properties of PT-Symmetric Chiral Metamaterials
Abstract
1. Introduction
2. Physical Model and Main Equations
2.1. PT-Symmetry Conditions in Chiral Systems
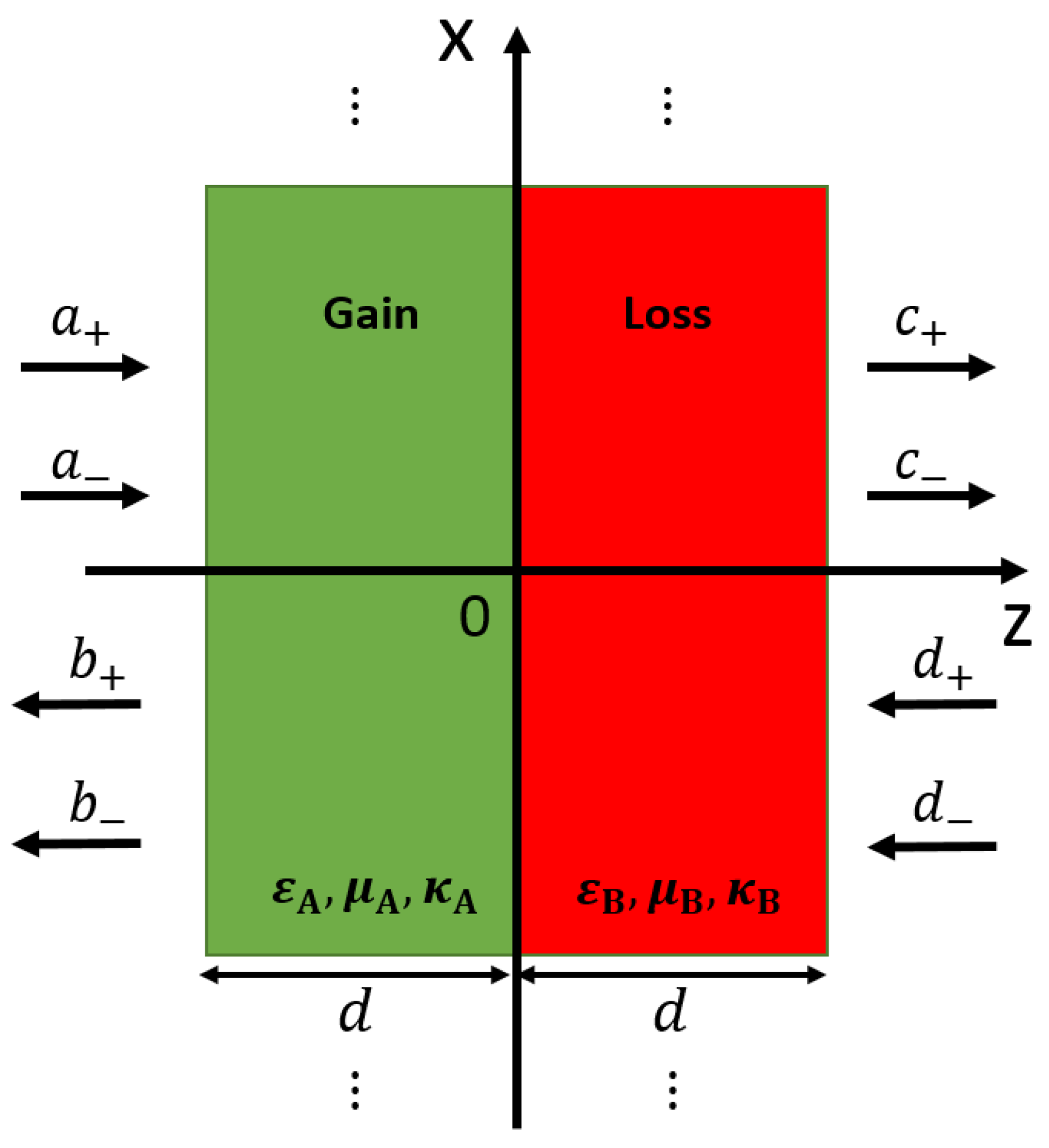
2.2. Chiral Systems in Scattering Configurations under Normal Incidence: The Scattering Matrix
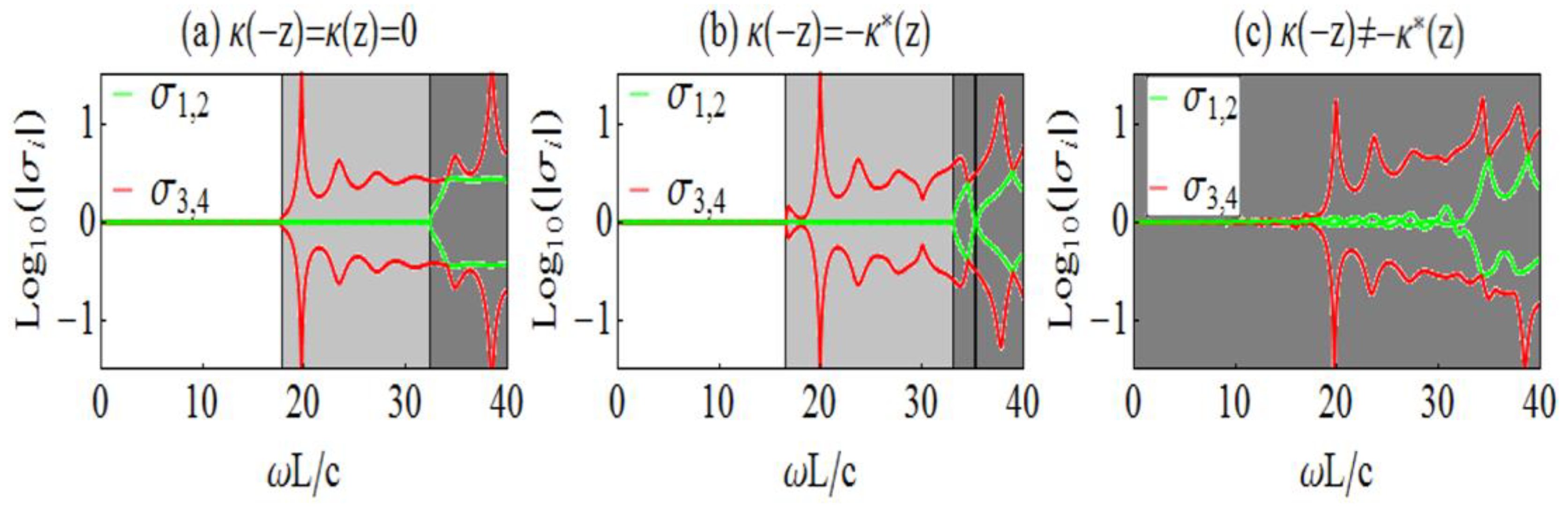
2.3. Generalized Unitarity Relations for Chiral PT-Symmetric Systems
3. Results and Discussion
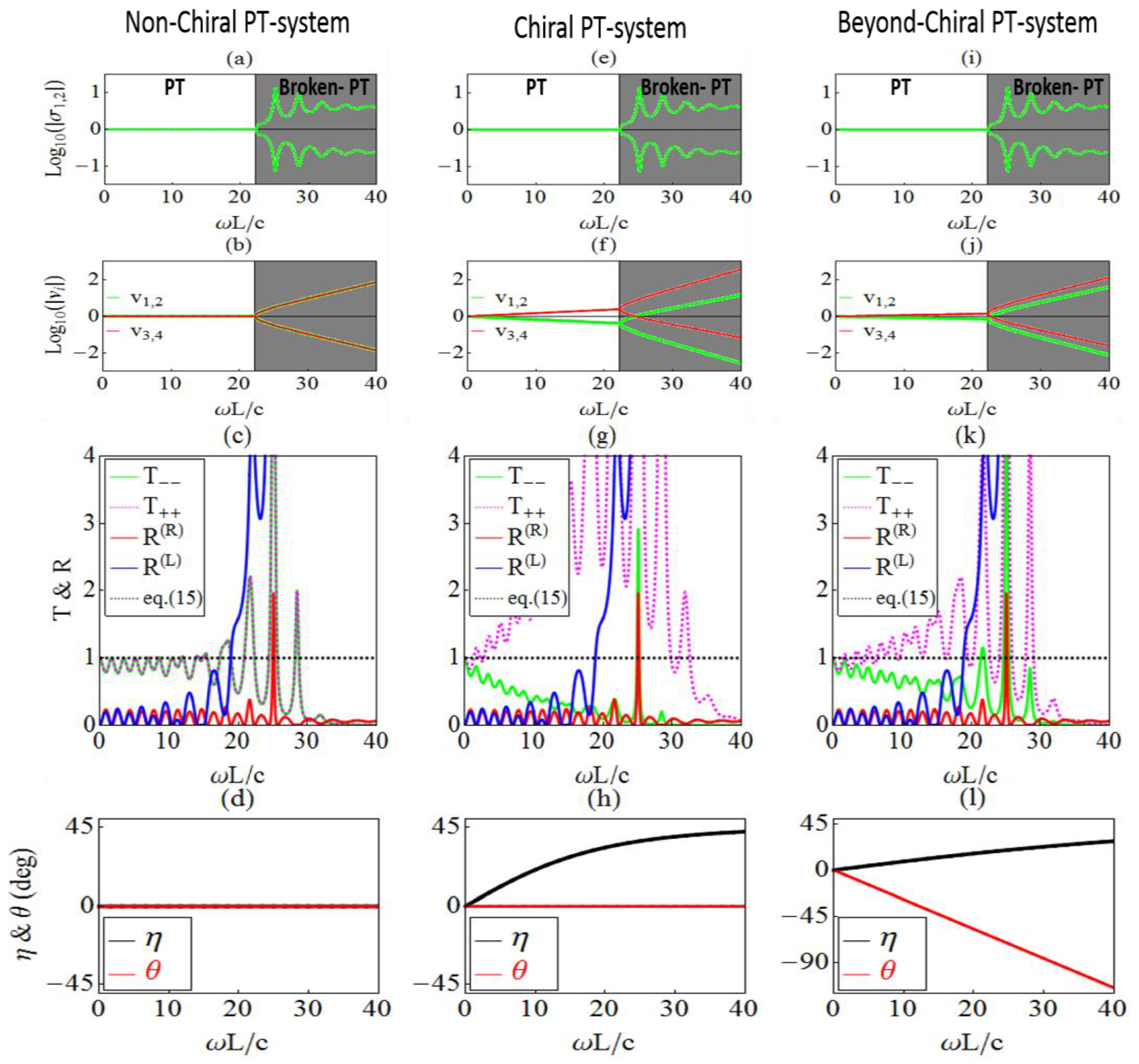
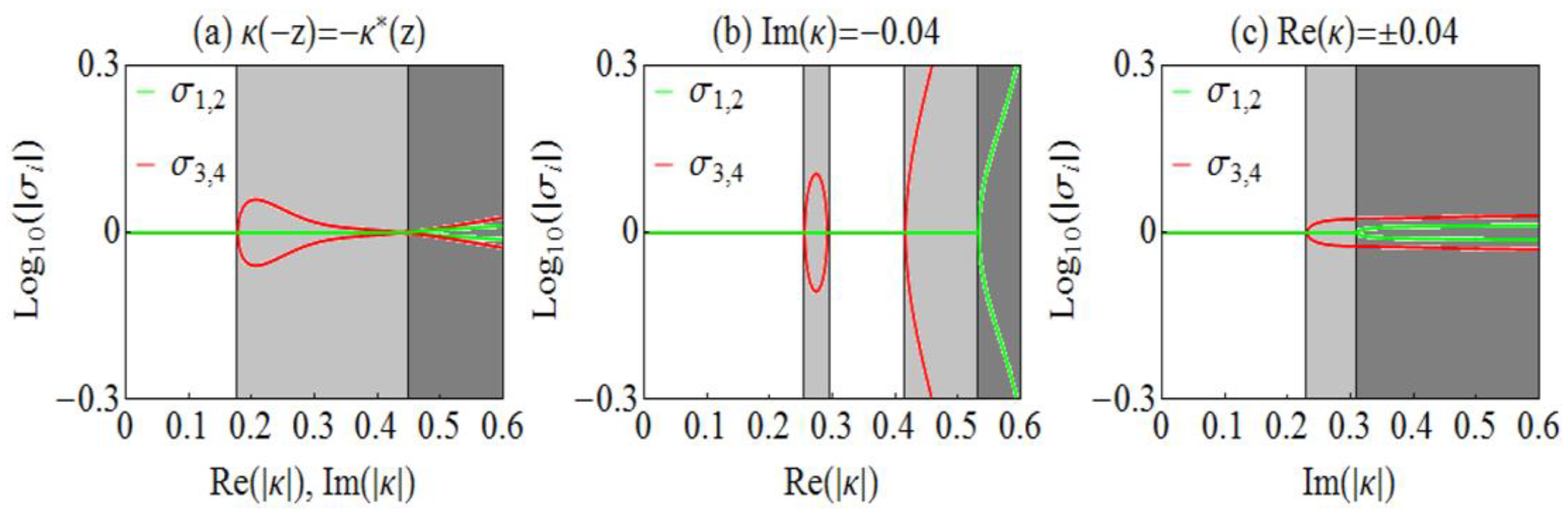
3.1. PT-Symmetric Chiral Bilayer under Normal Incidence: Different PT Phases and Scattering Characteristics
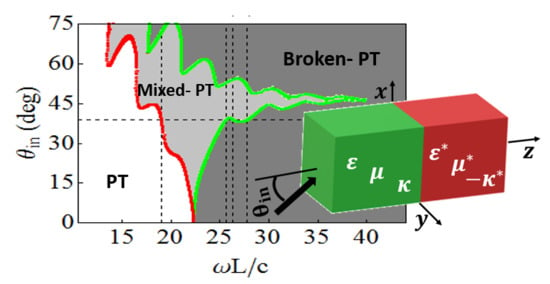
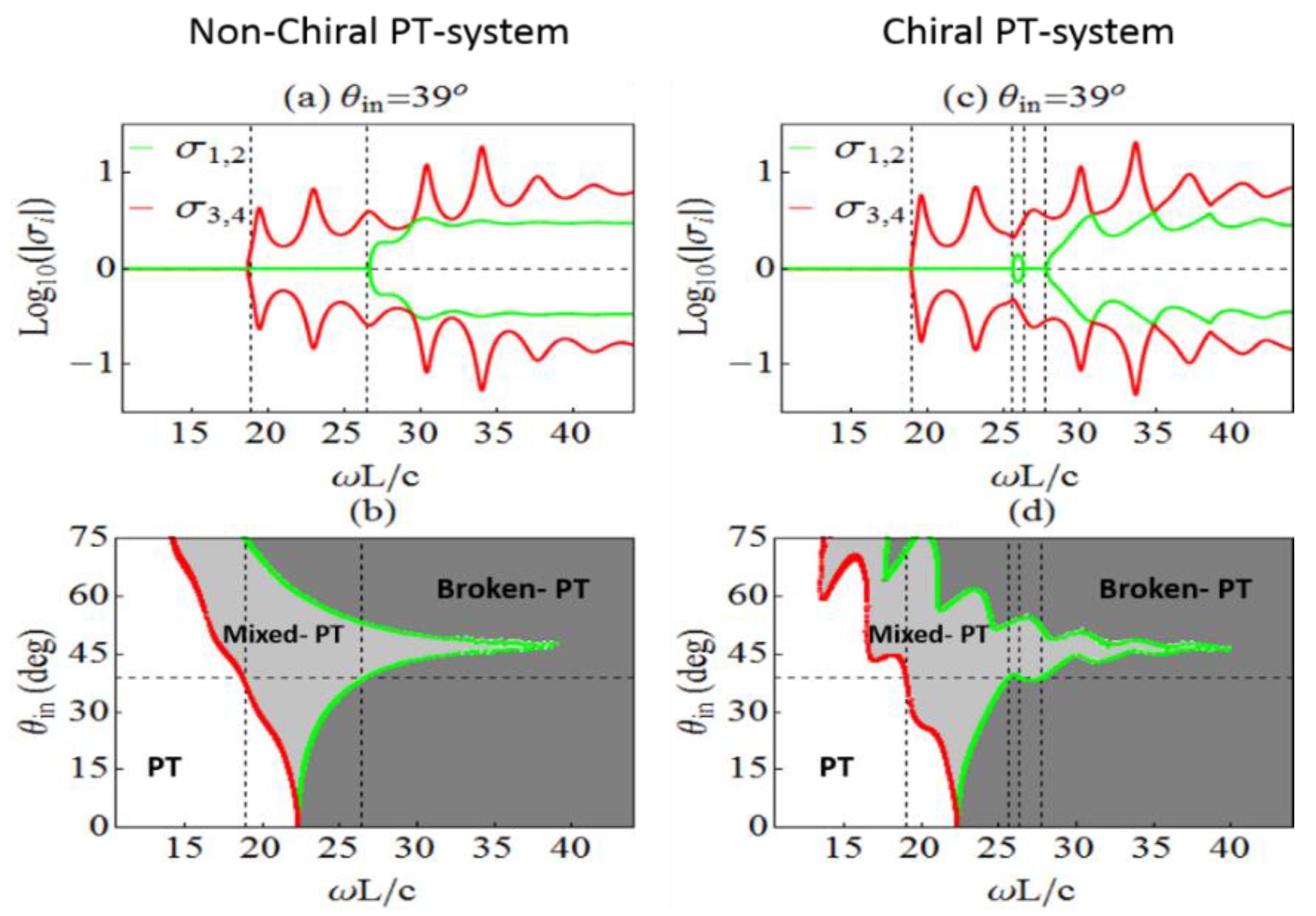
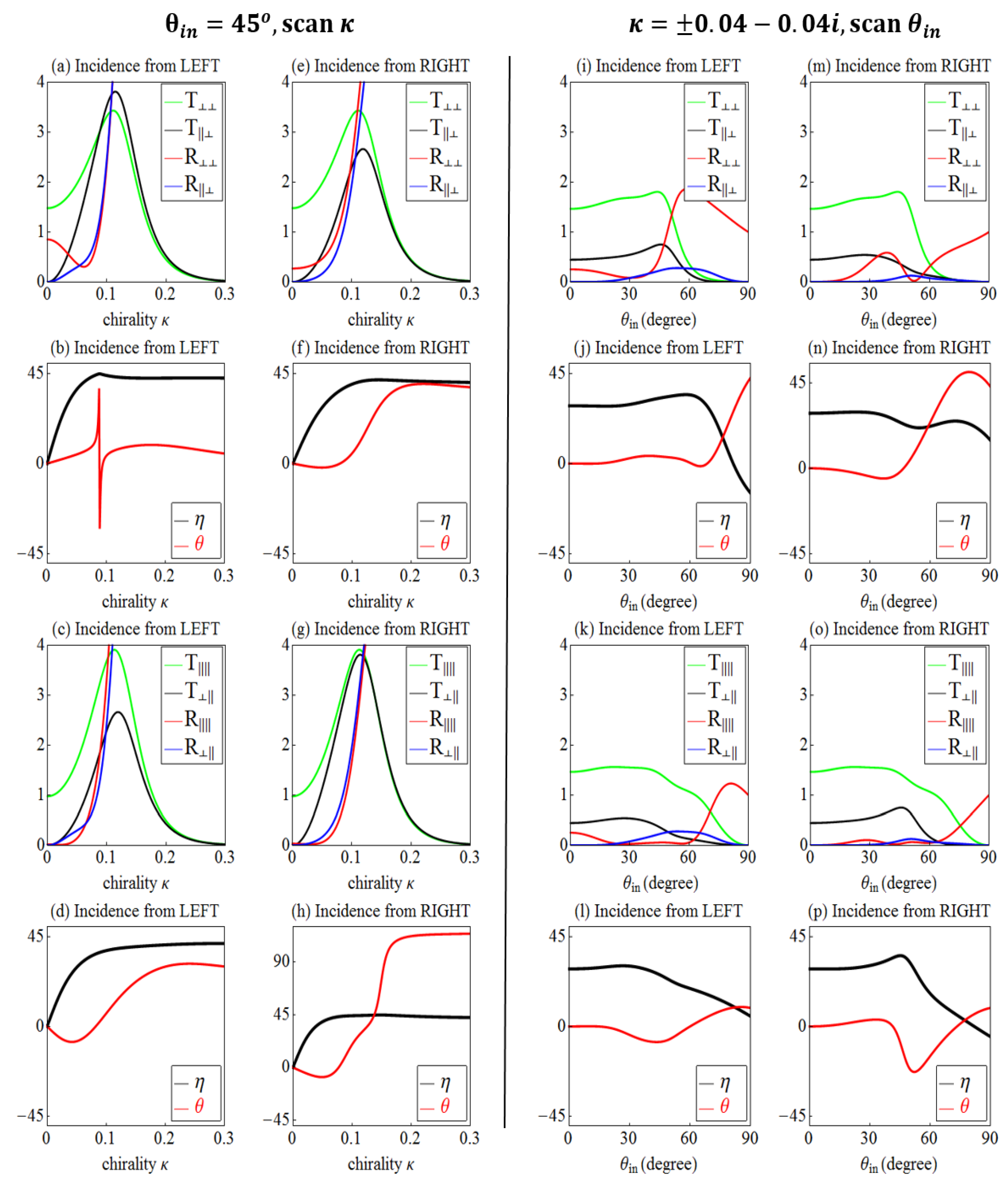
3.2. PT-Symmetric Chiral Bilayer under Oblique Incidence: Controlling the PT-Symmetry Phase
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real Spectra in non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S.; Meisinger, P.N. PT-symmetric quantum mechanics. J. Math. Phys. 1999, 40, 2201. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex Extension of Quantum Mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947. [Google Scholar] [CrossRef]
- Krasnok, A.; Baranov, D.; Li, H.; Ali Miri, M.; Monticone, F.; Alu, A. Anomalies in light scattering. Adv. Opt. Photonics 2019, 11, 892. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Musslimani, Z.H. Beam Dynamics in PT Symmetric Optical Lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Revat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of PT-Symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Sagev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192. [Google Scholar] [CrossRef]
- Feng, L.; Avache, M.; Huang, J.; Xu, Y.; Lu, M.; Chen, Y.; Fainman, Y.; Scherer, A. Nonreciprocal light propagation in a silicon photonic circuit. Science 2011, 333, 729–733. [Google Scholar] [CrossRef]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Uniderectional Invisibility Induced by PT-Symmetric Periodic Structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.H.; Oliveira, J.E.; Almeida, R.; Chen, Y.F.; Scherer, A. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Deng, X.H.; Chen, L. Uniderectional invisibility in a two-layer non-PT-symmetric slab. Opt. Express 2014, 22, 19440. [Google Scholar] [CrossRef] [PubMed]
- Yannopapas, V. Spotaneous PT-symmetry breaking in complex frequency band structures. Phys. Rev. A 2014, 89, 013808. [Google Scholar] [CrossRef]
- Sarisaman, M. Uniderectional reflectionlessness and invisibility in the TE and TM modes of a PT-symmetric slab system. Phys. Rev. A 2017, 95, 013806. [Google Scholar] [CrossRef]
- Tzortzakakis, A.F.; Makris, K.G.; Economou, E.N. Non-Hermitian disorder in two dimensional optical lattices. Phys. Rev. B 2020, 101, 014202. [Google Scholar] [CrossRef]
- Ge, L.; Chong, Y.D.; Stone, A.D. Conservation relations and anisotropic transmission resonances in one-dimensional PT-symmetric photonic heterostructures. Phys. Rev. A 2012, 85, 023802. [Google Scholar] [CrossRef]
- Longhi, S. Spotaneous PT-symmetric laser absorber. Phys. Rev. A 2010, 82, 031801. [Google Scholar] [CrossRef]
- Chong, Y.D.; Ge, L.; Stone, A.D. PT-Symmetry Breaking and Laser-Absorber Modes in Optical Scattering Systems. Phys. Rev. Lett. 2011, 106, 093902. [Google Scholar] [CrossRef]
- Sun, Y.; Tan, W.; Li, H.Q.; Li, J.; Chen, H. Experimental Demonstration of a Coherent Perfect Absorber with PT Phase Transition. Phys. Rev. Lett. 2014, 112, 143903. [Google Scholar] [CrossRef]
- Castaldi, G.; Savoia, S.; Galdi, V.; Alu, A.; Engheta, N. PT Metamaterials via Complex Coordinate Transformation Optics. Phys. Rev. Lett. 2013, 110, 173901. [Google Scholar] [CrossRef] [PubMed]
- Savoia, S.; Castaldi, G.; Galdi, V.; Alu, A.; Engheta, N. Tunneling of obliquely incident waves through PT-symmetric epsilon-near-zero bilayers. Phys. Rev. B 2014, 89, 085105. [Google Scholar] [CrossRef]
- Savoia, S.; Castaldi, G.; Galdi, V.; Alu, A.; Engheta, N. PT-symmetry-induced wave confinement and guiding in ε-near-zero metamaterials. Phys. Rev. B 2015, 91, 115114. [Google Scholar] [CrossRef]
- Shramkova, O.V.; Tsironis, G.P. Gain-Driven Discrete Breathers in PT-Symmetric Nonlinear Metamaterials. J. Opt. 2016, 18, 105101. [Google Scholar] [CrossRef]
- Wang, J.; Dong, H.; Ling, C.; Chan, C.T.; Fung, K.H. Nonreciprocal μ-near-zero mode in PT-symmetric magnetic domains. Phys. Rev. B 2015, 91, 235410. [Google Scholar] [CrossRef]
- Droulias, S.; Katsantonis, I.; Kafesaki, M.; Soukoulis, C.M.; Economou, E.N. Chiral Metamaterials with PT-Symmetry and Beyond. Phys. Rev. Lett. 2019, 122, 213201. [Google Scholar] [CrossRef]
- Katsantonis, I.; Droulias, S.; Soukoulis, C.M.; Economou, E.N.; Kafesaki, M. PT-Symmetry chiral metamaterials: Asymmetric effects and PT-phase control. arXiv 2020, arXiv:2003.07882. [Google Scholar]
- Yu, S.; Park, H.; Piao, X.; Min, B.; Park, N. Low-dimensional optical chirality in complex potentials. Optica 2016, 3, 1025–1032. [Google Scholar] [CrossRef]
- Lindell, I.V.; Sihvola, A.H.; Tretyakov, S.A.; Viitanen, A.J. Electromagnetic Waves in Chiral and Bi-Isotropic Media; Artech House Boston: London, UK, 1994. [Google Scholar]
- Wang, B.; Zhou, J.; Koschny, T.; Kafesaki, M.; Soukoulis, C.M. Chiral Metamaterials: Simulations and Experiments. J. Opt. A 2009, 11, 114003. [Google Scholar] [CrossRef]
- Kenanakis, G.; Economou, E.N.; Soukoulis, C.M.; Kafesaki, M. Controlling THz and far-IR waves with chiral and bianisotropic metamaterials. EPJ. Appl. Metamater. 2016, 2, 15. [Google Scholar] [CrossRef][Green Version]
- Pendry, J.B. A Chiral Route to Negative Refraction. Science 2004, 306, 1353. [Google Scholar] [CrossRef] [PubMed]
- Plum, E.; Zhou, J.; Dong, J.; Fedotov, V.A.; Koschny, T.; Soukoulis, C.M.; Zheludev, N.I. Metamaterials with negative index due to chirality. Phys. Rev. B 2009, 79, 035407. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, J.; Wang, B.; Koschny, T.; Kafesaki, M.; Soukoulis, C.M. Negative refractive index due to chirality. Phys. Rev. B 2009, 79, 121104(R). [Google Scholar] [CrossRef]
- Kenanakis, G.; Zhao, R.; Katsarakis, N.; Kafesaki, M.; Soukoulis, C.M.; Economou, E.N. Optically controllable THz chiral metamaterials. Opt. Express 2014, 22, 12149. [Google Scholar] [CrossRef] [PubMed]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decher, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009, 325, 5947. [Google Scholar] [CrossRef]
- Condon, E.U. Theories of Optical Rotatory Power. Rev. Mod. Phys. 1937, 9, 432. [Google Scholar] [CrossRef]
- Ozgun, E.; Serebryannikov, A.E.; Ozbay, E.; Soukoulis, C.M. Broadband mixing of PT-symmetric and PT-broken phases in photonic heterostructures with a one-dimensional loss/gain bilayer. Sci. Rep. 2017, 7, 15504. [Google Scholar] [CrossRef]
- Kalozoumis, P.A.; Pappas, G.; Diakonos, F.K.; Schmelcher, P. Systematic pathway to PT-symmetry breaking in scattering systems. Phys. Rev. A 2014, 90, 043809. [Google Scholar] [CrossRef]
- Droulias, S.; Katsantonis, I.; Kafesaki, M.; Soukoulis, C.M.; Economou, E.N. Accessible phases via wave impedance engineering with PT-symmetric metamaterials. Phys. Rev. B 2019, 100, 205133. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsantonis, I.; Droulias, S.; M. Soukoulis, C.; N. Economou, E.; Kafesaki, M. Scattering Properties of PT-Symmetric Chiral Metamaterials. Photonics 2020, 7, 43. https://doi.org/10.3390/photonics7020043
Katsantonis I, Droulias S, M. Soukoulis C, N. Economou E, Kafesaki M. Scattering Properties of PT-Symmetric Chiral Metamaterials. Photonics. 2020; 7(2):43. https://doi.org/10.3390/photonics7020043
Chicago/Turabian StyleKatsantonis, Ioannis, Sotiris Droulias, Costas M. Soukoulis, Eleftherios N. Economou, and Maria Kafesaki. 2020. "Scattering Properties of PT-Symmetric Chiral Metamaterials" Photonics 7, no. 2: 43. https://doi.org/10.3390/photonics7020043
APA StyleKatsantonis, I., Droulias, S., M. Soukoulis, C., N. Economou, E., & Kafesaki, M. (2020). Scattering Properties of PT-Symmetric Chiral Metamaterials. Photonics, 7(2), 43. https://doi.org/10.3390/photonics7020043