Generation of Terahertz Radiation by Two-Color Ionizing Laser Pulses with Arbitrary Intensity Ratios

Abstract

The dependence of the terahertz energy generated by two-color femtosecond ionizing pulses on intensities of both one-color components is studied. The numerical calculations are supported with analytical formulas which help to reveal the nature of these dependences. The optimal intensity ratios in the cases when the frequency ratios in two-color pulse are equal to 2, 3/2 and 4 are found.

1. Introduction

Sources of intense broadband terahertz (THz) radiation attract much interest due to various applications: time-domain spectroscopy, remote sensing, terahertz imaging and others [1,2,3]. One of the most widely used methods for THz generation is based on ionizing gases or liquids with intense two-color laser pulses with durations of 10–200 fs [3,4,5,6,7,8]. Typically such two-color pulses consist of a strong main field on fundamental near-infrared frequency with a relatively weak addition of its second harmonic.

A recently discovered possibility of efficient generation of THz radiation with the use of the ionizing two-color pulses with frequency ratios other than 2 [9,10] opened up wide space for research of the optimal parameters of such pulses. These ratios can be equal to any rational fraction $a/b$ with a small odd sum of numerator and denominator, such as 3/2, 4/1 and others. The sum $(a+b+1)$ defines the least order of multiwave mixing required for generation of the near-zero-frequency (THz) components of radiation. However, in the case of ionization-induced multiwave mixing (IMWM), the efficiencies of these higher-order processes can be considerable, and become even more expressed with decrease of intensities of the ionizing pulse components.

For the frequency ratio of 2, the optimal ratio of intensities is known to be $I_2/I_1\approx 0.5÷1$ [7,8]. The other frequency ratios have not been yet researched in this effect.

In this paper the dependence of THz yield on the intensities of both one-color components of the ionizing pulse is investigated at different frequency ratios. It is shown, that the optimal intensity ratio depends on the total intensity of the ionizing pulse, and the causes of these dependences are explained with the use of the developed analytical model.

2. Methods and Analytical Model

The electric field of a two-color pulse consists of two quasimonochromatic components,

$$\mathbf{E}\left(t\right)=\widehat{\mathbf{x}}({\mathcal{E}}_{1}sin{\omega }_{1}t+{\mathcal{E}}_{2}sin[{\omega }_{2}t+\varphi ]),$$

(1)

where ${\mathcal{E}}_{1,2}\left(t\right)=\sqrt{8\pi I_{1,2}/c}exp-\frac{t^{2}ln4}{{\tau }_p^2}$ are the slow envelopes of the field components, $I_{1,2}$ are their peak intensities, ${\tau }_p$ is the pulse FWHM duration, ${\omega }_{1,2}$ are their central frequencies, $\varphi$ is the phase shift between the carriers, $\widehat{\mathbf{x}}$ is the unit vector along the x axis. To find the current density of free electrons $\mathbf{j}$, induced by the field $\mathbf{E}$, here is used the semiclassical approach, which is based on solving the system of equations which can be obtained from the Boltzmann kinetic equation under the condition of a symmetric distribution of born free electrons over the velocities [11]:

$$\frac{\partial N}{\partial t}=(N_g-N)w\left(\right|\mathbf{E}\left|\right),$$

(2)

$$\frac{\partial \mathbf{j}}{\partial t}=\frac{e^2}{m}N\mathbf{E},$$

(3)

with initial conditions $N(t\to -\infty )=0$, $\mathbf{j}(t\to -\infty )=0$. Here N is the concentration of free electrons, $N_g$ is the initial concentration of neutral particles, $w\left(\right|\mathbf{E}\left|\right)$ is the probability of ionization of a neutral particle per unit time in the field $\mathbf{E}$, $\mathbf{j}$ is the current density of free electrons. Since the polarizations are linear, further in the article the projections on x axis for $E=(\mathbf{E}·\widehat{\mathbf{x}})$ and $j=(\mathbf{j}·\widehat{\mathbf{x}})$ will be used. The residual current density (RCD) [6,9], which is proportional to the square root of energy of the radiating plasma oscillations (and THz yield) excited after the passage of the ionizing pulse, can be found from

$$\overline{j}=j(t\to +\infty )=\frac{e^2}{m}{\int }_{-\infty }^{+\infty }A\frac{dN}{dt}dt,$$

(4)

where $A\left(t\right)=-{\int }_{-\infty }^{t}Edt$ is the projection of vector-potential of the laser pulse on x axis, which is proportional to the drift velocity of the born free electrons, if $A(\pm \infty )=0$. Ionization probability per unit time is given by the following equation [12]

$$w\left(E\right)=4{\mathsf{\Omega }}_a\frac{E_a}{\left|E\right|}exp\left(-\frac{2E_a}{3\left|E\right|}-\frac{12\left|E\right|}{E_a}\right),$$

(5)

where $E_a\approx 5·{10}^9$ V/cm and ${\mathsf{\Omega }}_a\approx 2.6\times {10}^{17}$ rad/s are the atomic units of the electric field strength and frequency.

From the common IMWM theory [4,9] it follows that in such two-color pulses the optimal phase shift for THz generation is ${\varphi }_{opt}=0$ in the framework of the semiclassical approach, so further in the article it will be neglected. In derivation of our analytical formulas we will consider the envelopes of the laser pulse components constant inside the period $T=2\pi /\omega$ and imply the relative change of the free electron density over the period to be small. With that we can separate the ’fast’ time inside the period $t^{\prime }\in [0,T)$, through which the parameters of the carrier will be expressed, from the time of the envelope $t=kT+t^{\prime },k\in \mathbb{Z}$, so for the vector potential of the two-color field with the additional second harmonic we can write:

$$A(t,t^{\prime })=-\frac{{\mathcal{E}}_1\left(t\right)}{\omega }cos\omega t^{\prime }-\frac{{\mathcal{E}}_2\left(t\right)}{2\omega }cos2\omega t^{\prime }.$$

(6)

Inside the period T the field modulus $\left|E\right(t^{\prime }\left)\right|$ has two symmetric maxima at time points $t^{\prime }=t_0^{\prime }$ and $t^{\prime }=T-t_0^{\prime }$ which can be found from the conditions $d^{2}A/d{t\prime }^2{|}_{t^{\prime }=t_0^{\prime }}=0$. The value of $t_0^{\prime }$ is determined only by the ratio of the field amplitudes, and can be approximated from expanding the carrier of the field into Taylor series up to the 4th order, which gives

$$\omega t_0^{\prime }\approx \sqrt{\frac{6+12r-\sqrt{3-15r+12r^2}}{1+8r}},$$

(7)

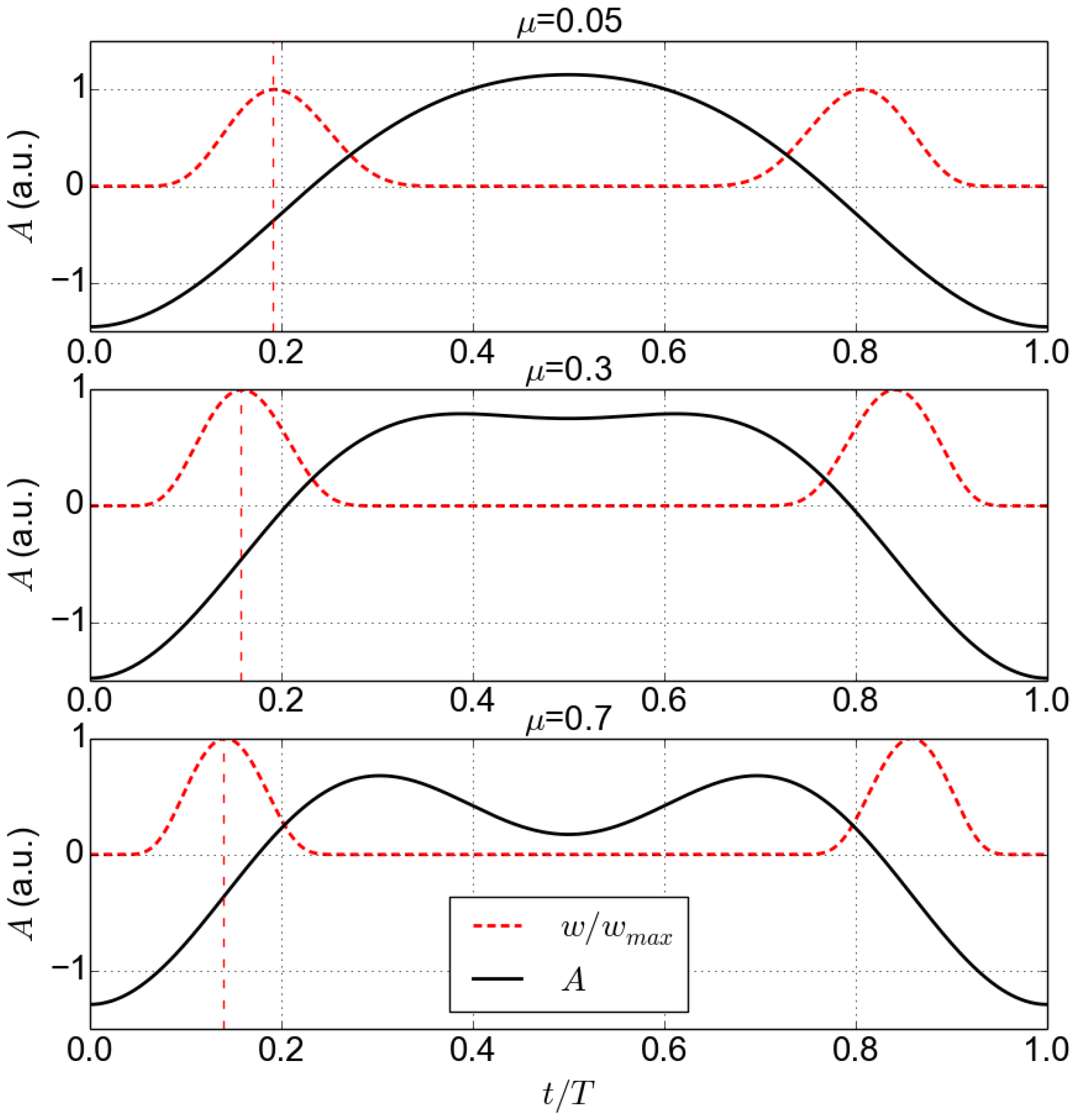
where $r={\mathcal{E}}_2/{\mathcal{E}}_1$. Corresponding $w\left(t^{\prime }\right)$ will have two symmetric peaks, as shown on Figure 1. Since $w\left(\right|E\left|\right)$ is typically a very sharp function of $\left|E\right|$, characterized by the effective exponent $n\left(E\right)=E{w}^{\prime }\left(E\right)/w\left(E\right)\gg 1$, the peaks located at the field global maxima over the period are narrow compared to the scales of $A\left(t^{\prime }\right)$ and strongly dominate the peaks at other local maxima.

The partial RCD ${\overline{j}}_T$ produced over the period T can be calculated with the assumption that $A\left(t^{\prime }\right)$ can be well linearly approximated for a duration of the narrow peak of ionization, then

$${\overline{j}}_T\left(t\right)\approx \frac{e^2{N}_s}{m}{\int }_0^{T}A(t,t^{\prime })w(t,t^{\prime })d{t}^{\prime }\approx \frac{e^2}{m}A(t,t_0^{\prime })N_T,$$

(8)

where $N_T\left(t\right)\approx N_s{\int }_0^{T}w(t,t^{\prime })d{t}^{\prime }$ is the number of ionized particles produced over the period T with the initial number of neutral particles equal to $N_s$. Assuming that we have a long pulse with a smooth envelope, we can derive

$$\overline{j}\approx \frac{e^2}{m}{\int }_{-\infty }^{+\infty }A(t,t_0^{\prime })\frac{d\overline{N}}{dt}dt\approx \frac{e^2{N}_g\sigma }{m}A(t_0,t_0^{\prime }).$$

(9)

Here $\overline{N}$ is found from the equation $d\overline{N}/dt=(N_g-\overline{N})\overline{w}$, and $\overline{w}=N_T/\left(T{N}_g\right)$ is the period-averaged ionization rate, $t_0$ is the time of the maximum of $d\overline{N}/dt$, which at $\sigma <0.9$ coincides with the maximum of the envelope of the laser pulse, $\sigma =N(t\to +\infty )/N_g$ is the final degree of ionization.

To find the optimal intensity ratio with a fixed sum of intensities $I_S=I_1+I_2$, we introduce the parameter $\mu =I_2/I_S\in [0,1]$, from which the field amplitudes are ${\mathcal{E}}_2=\sqrt{\mu }\mathcal{E}$ and ${\mathcal{E}}_1=\sqrt{1-\mu }\mathcal{E}$, where $\mathcal{E}=\sqrt{8\pi I_S/c}exp-\frac{t^{2}ln4}{{\tau }_p^2}$. Substituting these values into Equation (7) to find $t_0^{\prime }\left(\mu \right)$ and simplifying the result we get

$$A_{(2/1)}(t,t_0^{\prime })\approx \frac{9\mathcal{E}\left(t\right)}{20\omega }\sqrt{1-\mu }\sqrt[3]{\mu }.$$

(10)

Equation (10) gives the optimal $\mu =0.4$, or in terms of intensity ratio $I_2/I_1=2/3$ in the case of saturation of ionization $\sigma \left(\mu \right)\equiv 1$. At low values of $I_S$ there appears the factor of final degree of ionization, which can be calculated from

$$\sigma \approx 1-exp\left(-{\int }_{-\infty }^{+\infty }\overline{w}\left(t\right)dt\right),$$

(11)

with $\overline{w}\left(t\right)\approx w\left(E_m\right)/\sqrt{2\pi \eta }$ being the period-averaged ionization rate, employing the maximum field inside period T

$$E_m\left(t\right)\approx \left(\sqrt{\mu }+\sqrt{1-\mu }-\frac{{\pi }^2\sqrt{\mu -{\mu }^2}}{8(4\sqrt{\mu }+\sqrt{1-\mu })}\right)\mathcal{E}\left(t\right),$$

(12)

and the width of the peak of ionization

$$\eta \approx n(4\sqrt{\mu }+\sqrt{1-\mu })\mathcal{E}\left(t\right)/E_m.$$

(13)

The maximum of $E_m\left(\mu \right)$ is reached at $\mu \approx 0.6$, so as the maximum of $\sigma \left(\mu \right)$. With the decrease of $I_S$ the peak of $\sigma \left(\mu \right)$ becomes sharper, affecting the shift of the maximum of $\overline{j}\left(\mu \right)$ from $\mu \approx 0.4$ to $\mu \approx 0.6$ at very low intensities.

For the other frequency ratios, the general equation for RCD seen in Equation (8) remains the same, but with another values of the parameter $A(t,t_0^{\prime })$. Here we provide the equations for the cases when the frequency ratio between components is ${\omega }_2/{\omega }_1=3/2$

$$A_{(3/2)}(t,t_0^{\prime })\approx \frac{3\mathcal{E}\left(t\right)}{20\omega }\sqrt{1-\mu }\sqrt[3]{\mu },$$

(14)

and for the additional 4th harmonic, ${\omega }_2/{\omega }_1=4$,

$$A_{(4/1)}(t,t_0^{\prime })\approx \frac{3\mathcal{E}\left(t\right)}{10\omega }(1-\mu )\sqrt[7]{\mu }.$$

(15)

3. Results and Discussion

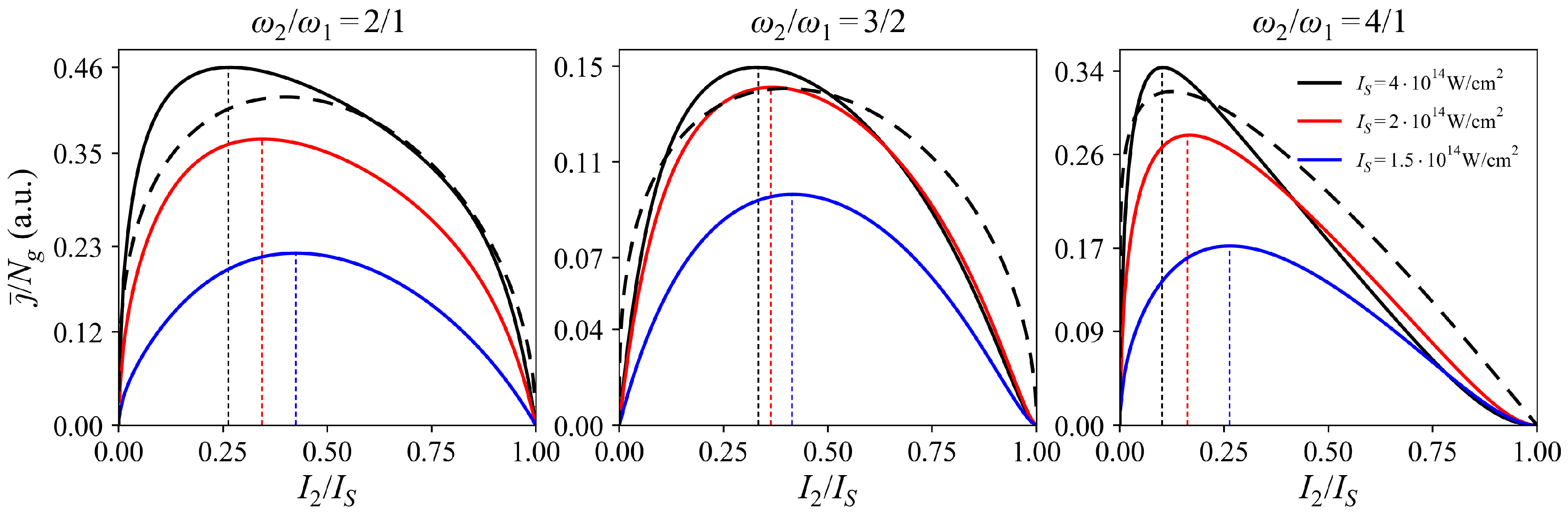
The obtained analytical results were compared with the numerical solutions of Equations (2) and (4) employing the ionization probability of a hydrogen atom in Equation (5) at different intensities of the pulse components (Figure 2). The envelopes of the pulse components in the numerical calculations had Gaussian shapes,

$${\mathcal{E}}_{1,2}=\sqrt{8\pi I_{1,2}/c}exp\left(-\frac{t^{2}ln4}{{\tau }_p^2}\right),$$

(16)

with the pulse FWHM duration ${\tau }_p=$ 50 fs and ${\omega }_1$ corresponding to the wavelength ${\lambda }_1=800$ nm.

Though the particular positions of maxima of $\overline{j}\left(\mu \right)$ slightly differ from the ones predicted by analytical Equation (9), the trend, due to which at lower intensities these maxima shift towards equal intensities can be clearly seen. Such a trend is unusual for the common mechanisms of nonlinear multiwave mixing, such as high-order Kerr effect [13,14]. The low-frequency components of nonlinear polarization at low intensities of two-color fields with the frequency ratio ${\omega }_2/{\omega }_1=a/b$ would have the following dependences on the amplitudes of the components:

$$P_{THz}\propto {\mathcal{E}}_1^a{\mathcal{E}}_2^b,$$

(17)

which means that for the generation of one low-frequency photon there are needed a photons of ${\omega }_1$ and b photons of ${\omega }_2$. If we fix the sum of intensities of the components $I_s$, as has been done for the IMWM mechanism in the previous section, this would give the optimal intensity ratio $I_2/I_s={\mu }_{opt}=b/(a+b)$, or $I_2/I_1=b/a$, so the optimal intensity ratio should be the reversed frequency ratio.

However, for the IMWM, in fact, happens the opposite, and the common optimal intensity ratios are observed at high total intensities. At intensities higher than $I_S\approx 3\times {10}^{14}$ W/cm${}^2$ the dependence of RCD on $I_S$ saturates, since the final degree of ionization $\sigma$ becomes close to unity, and the time $t_0$ shifts towards the front of the laser pulse, keeping almost constant the intensity at which most free electrons appear. The lower the total intensity gets, the more equal the optimal intensities become (up to the limitations of the used semiclassical approach, employing the tunnel ionization regime, which in terms of total intensity would give $I_S\ge 1\times {10}^{14}$ W/cm${}^2$). With decreasing total intensity, the dependence of $\sigma$ on the intensity ratio becomes more pronounced (and its maximum is always close to the point of equal intensities), leading to the shift of the maximum of RCD. For investigating the THz generation at lower intensities of the level of ${10}^{13}$ W/cm${}^2$, which usually occur in two-color filamentation [8,13], a more generic approach, such as solution of three-dimensional time-dependent Shroedinger equation could be used [4,9]. This approach shows good agreement with the semiclassical calculations in the tunneling regime of ionization, but is also capable to describe the wavemixing in the multiphoton regime.

4. Conclusions

The obtained analytical formulas show that the dependence of THz yield on the intensity ratio in the two-color ionizing laser pulse can be represented as a multiplication of two factors. The first one is the value of free-electron drift velocity at the time of local maxima of the electric field, and this factor is usually optimized when the low-frequency component is significantly more intense, than the one with the higher frequency. The second parameter is the final degree of ionization, which at high total intensities ($I_S\ge 3\times {10}^{14}$ W/cm${}^2$) is close to unity with any intensity ratio, but at lower intensities it reaches its maximum when the intensities of the components are close to equal, and therefore the THz yield optimum shifts to equal intensities with the decrease of the total intensity. These analytical results are in good agreement with the numerical calculations and the known experiments.