Size Dependence of the Resonant Third-Order Nonlinear Refraction of Colloidal PbS Quantum Dots

Abstract

Due to their high resonant third-order nonlinear response, lead sulfide quantum dots (QDs) are potential materials for applications in the field of nonlinear optics. In this paper, we implement the Z-scan method to study the resonant nonlinear response of lead sulfide QDs in colloidal solutions. We managed to measure the purely intrinsic resonant nonlinear response, free of thermal contribution. We report that the lead sulfide QD third-order nonlinear response per QD shows an unconventional increase. A figure of merit for QD nonlinearity grows as a power function with a factor of 2.9.

1. Introduction

Semiconductor quantum dots (QDs) can find their use in nonlinear-optical (NLO) applications due to the spike-like density of their electronic states. The concentration of optical transitions in very narrow energy intervals in QDs causes a strong enhancement of the NLO response [1,2]. Third-order nonlinear effects in nanomaterials are extensively studied to this day. Weakly confined QDs have been studied in more detail for a variety of materials (such as CdS, CdSe, Ag₂S or CsPbBr₃) [3,4,5,6]. The available studies of strongly confined QDs are mostly limited to PbSe and PbS [7,8]. Core–shell materials have also been investigated for nonlinearities [8,9,10]. NLO effects should be more pronounced in QDs, which are in a strong confinement regime. In this regime, both electrons and holes are confined, and optical transitions occur between single-particle eigenstates, thus concentrating the optical transitions in a single energy interval. In strongly confined QDs, Coulomb or exchange interactions can be neglected. Hence, absorption saturation may be considered as the saturation of a two-level system. Absolute changes in the refractive index can be large before the saturation of the transition [11].

Lead sulfide (PbS) QDs are an excellent model object for studying physical processes in the strong confinement regime. The large Bohr radius (18 nm) of PbS allows us to investigate the size dependencies of linear and nonlinear optical properties under the strong confinement for a variety of QD sizes, minimizing the contribution from surface-related effects. In addition, the high absorption coefficient of PbS QDs is regarded as offering the possibility of obtaining very high resonant nonlinearities [12]. It is worth noting that the electronic spectra of PbS may be tuned over the entire near-infrared (NIR) region by QD size variation, which makes this material very attractive for utilization in telecommunication systems.

In the absence of one-photon absorption (non-resonant regime) nonlinear response is mostly limited to rather weak Kerr nonlinearity and multiphoton absorption. The resonant regime is defined by the presence of one-photon absorption. Moving to the resonant regime may increase the resulting nonlinear response [12,13]. Very high optical resonant nonlinearities of PbS QDs have been observed for QDs in glass matrices [14], poly vinyl alcohol coating [15], zeolites [16], poly(vinyl acetate) glue [17], in polymer solutions [18,19], and in liquid solutions [8,20,21,22,23,24]. Experimental data on PbS QDs nonlinear properties in the literature deal mainly with particularly sized QDs and may scarcely be generalized. Therefore, a comprehensive analysis of the nonlinear properties of PbS QDs for QDs of different sizes is required to estimate the influence of quantum confinement on semiconductor nonlinearities.

Another issue is the origin of measured nonlinearity. When measuring intrinsic electronic nonlinearity in the presence of a linear absorption, we have to consider the thermo-optical effects. Absorbed excitation energy heats a sample, changing the nonlinear refraction due to the thermo-optical coefficient dn/dT being higher than zero. Most works cited above utilize pumping pulses with kHz or even MHz repetition rates, which lead to the accumulation of heat within the sample.

In this article, we investigate the size dependence of the third-order nonlinear response in PbS QDs in colloidal solutions. Despite the fact that QDs dispersed in various solid matrices are more convenient for NLO applications, the use of colloidal solutions solves the problem of photodarkening and allows more accurate study of intrinsic QD nonlinearities. We also report that, to reduce thermal effects, it is necessary to utilize ultrashort pulses with low repetition rates. To simplify the comparison of results, we quantify the nonlinearity in the microscopic units.

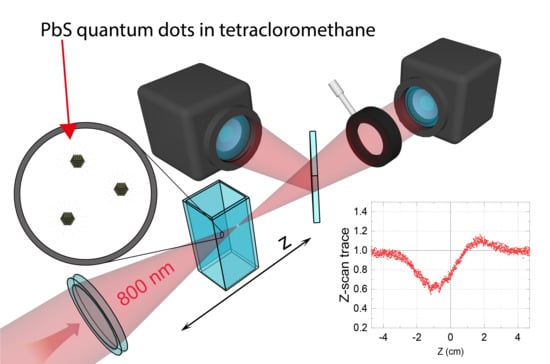
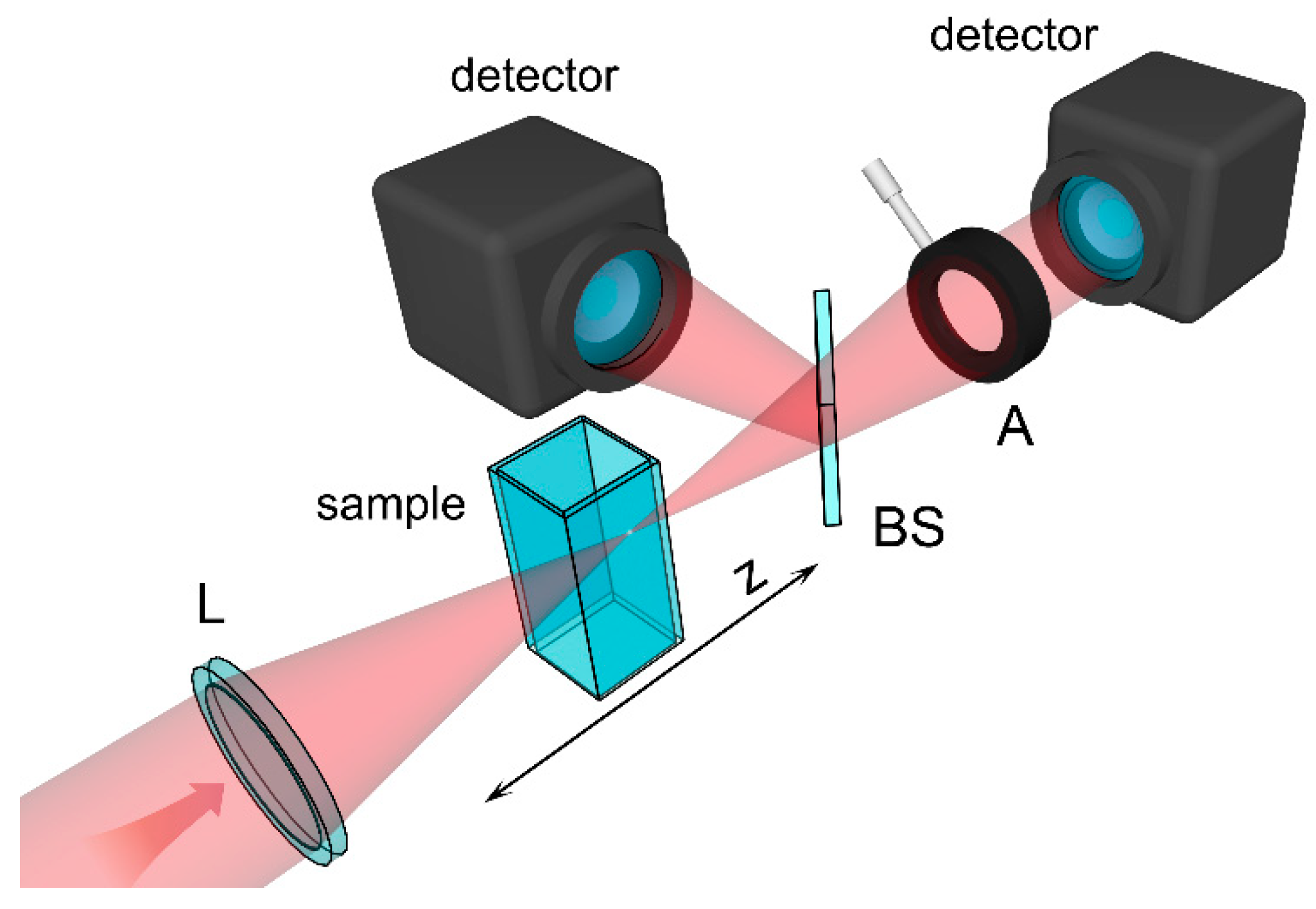
2. Materials and Methods

QDs were synthesized with the hot-injection method, described in detail elsewhere [25]. For all optical measurements, QDs were dispersed in pure tetrachloromethane (CCl₄). QDs were synthesized with radii from 1.5 nm to 4.2 nm, size dispersion gradually decreases with size from 9.6% to 4.5%, respectively. QD size and size dispersion have been estimated from the analysis of the absorbance spectra, namely from first excitonic peak position and full width at half maximum [25]. Spectra were captured with a Shimadzu UV3600 spectrophotometer (Shimadzu, Japan). QD solution absorbance spectra are presented in Figure 1.

The Z-scan technique [26] was employed to study the nonlinear parameters. We used a custom-built Z-scan setup based on a femtosecond (~35 fs) Ti:sapphire laser system (Avesta, Russia) as a probing light source (see Figure 2 for the setup scheme). An additional Pockels cell allowed us to change the pulse repetition rate from 0.1 Hz to 1 kHz. Pulse energy was controlled by a polarization attenuator and varied in the range of 0.9 ÷ 1.32 µJ. A lens with a focal distance of 20 cm was used to concentrate the gaussian laser beam. Two identical photodetector heads (Ophir, Israel) were used to capture the signal.

The nonlinear refractive index (NRI) was calculated using Equation (1) [26]:

$$n_2=\frac{\Delta T}{0.406I_{in}}\frac{\sqrt{2}\lambda }{2\pi L_{\alpha }{\left(1-S\right)}^{0.25}},L_{\alpha }=\left(1-\exp \left[-\alpha \cdot l\right]\right)/\alpha ,S=1-\exp \left(-2r_a^2/w_a^2\right),$$

(1)

where ΔT—difference between minimum and maximum of the Z-scan trace, I_in—laser beam intensity in the absence of the absorption, λ—laser wavelength (800 nm), L_α—effective length, l—sample thickness, α—linear absorption coefficient S—aperture linear transmittance, r_a and w_a are radii of aperture and beam respectively. The laser intensity within the sample was calculated from Equation (1) using the known value of the quartz NRI (3.28 · 10⁻¹⁶ cm²/W).

Z-scan was performed on QD solutions in optical glass cuvettes, which do not absorb at 800 nm. Cuvette contribution to the signal was taken into account by subtracting the Z-scan trace of an empty cuvette from the Z-scan trace of the cuvette with the sample. NRI is connected to the nonlinear susceptibility via Equation (2) [27]:

$$n_2\left[{\mathrm{cm}}^2/\mathrm{W}\right]=\frac{0.0395}{n_0^2}{\chi }^{(3)}\left[\mathrm{esu}\right],$$

(2)

where n₀ is the linear refraction coefficient. Both nonlinear susceptibility and NRI are macroscopic parameters, and to correctly assess the nonlinearities of single QDs we have to use microscopic quantities. For third-order nonlinear processes, such a quantity is second-order hyperpolarizability γ. For a two-component solution, we can apply Equation (3) (in electrostatic system of units - esu) [28]:

$$\begin{array}{l}{\chi }_{solution}^{(3)}=f_{QD}^4{N}_{QD}{\gamma }_{QD}+f_{solvent}^4{N}_{solvent}{\gamma }_{solvent}\equiv f_{QD}^4{N}_{QD}{\gamma }_{QD}+{\chi }_{solvent}^{(3)},\\ f_{solvent}=\frac{n_{solvent}^2+2}{3},f_{QD}^4=\frac{{\left[{\left({\epsilon }_{\mathrm{Re}}+2n_{solvent}^2\right)}^2+{\epsilon }_{\mathrm{Im}}^2\right]}^2}{81n_{solvent}^8},\\ {\gamma }_{QD}=\frac{{\chi }_{solution}^{(3)}-{\chi }_{solvent}^{(3)}}{f_{QD}^4{N}_{QD}}=\frac{n_2^{solution}\frac{n_{eff}^2}{0.0395}-{\chi }_{solvent}^{(3)}}{f_{QD}^4{N}_A{C}_{QD}},\end{array}$$

(3)

where ε_Re and ε_Im are real and imaginary parts of QD dielectric permittivity at the wavelength of 800 nm; f—local field factor, N_QD—number of QD per unit volume; n_eff—effective refractive index, calculated from Maxwell Garnett model, N_a—the Avogadro number, C_QD—QD molar concentration. The QD concentration was kept sufficiently low to have a negligible impact on the refractive index of the solution. For our solvent, CCl₄ (n₀ = 1.4607), we obtained the following macroscopic nonlinear parameters: n₂ = 5.1 × 10⁻¹⁶ cm²/W, χ⁽³⁾ = 2.76 × 10⁻¹⁴ esu. The real and imaginary parts of QD dielectric permittivity were determined from linear absorbance spectra using the Kramers–Kronig relations. The iterative method for Kramers–Kronig calculations was adopted from Moreels et al. [29].

3. Results and Discussion

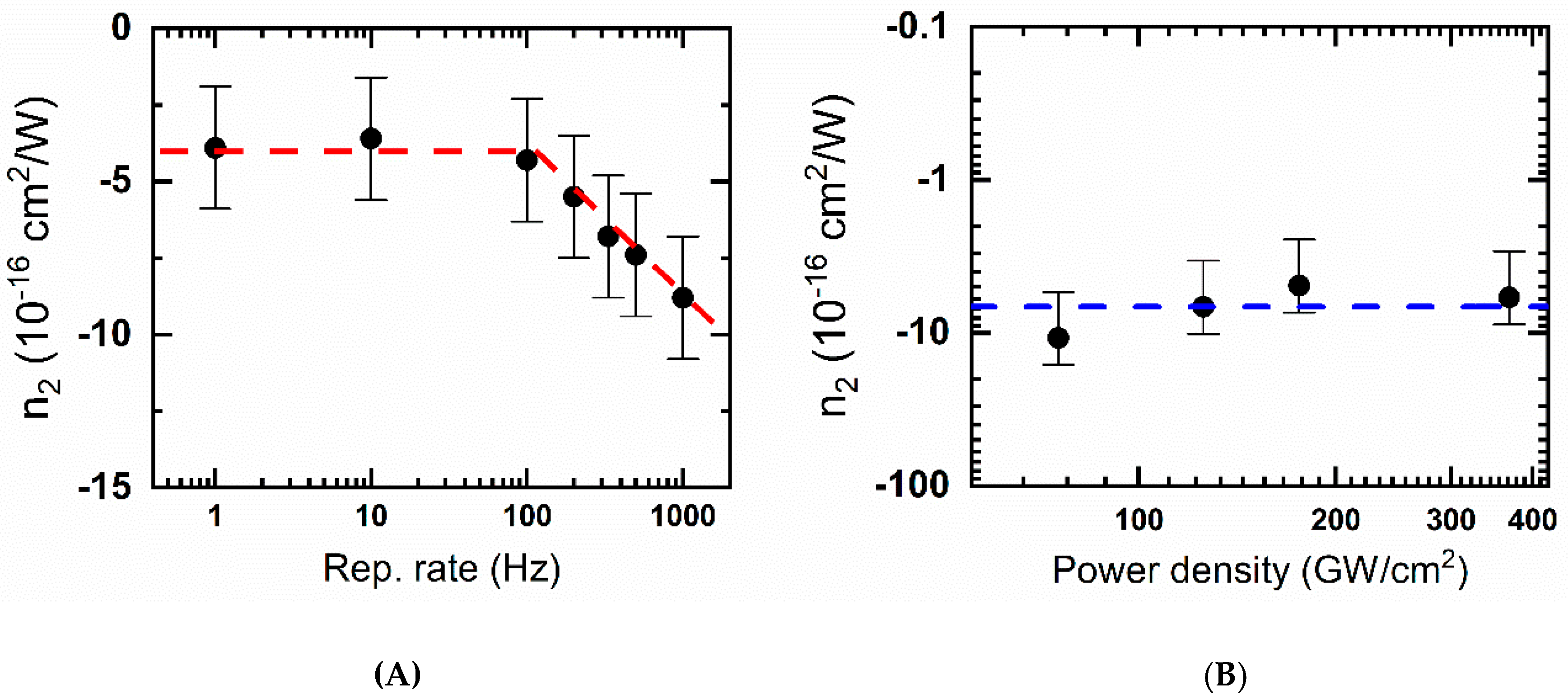
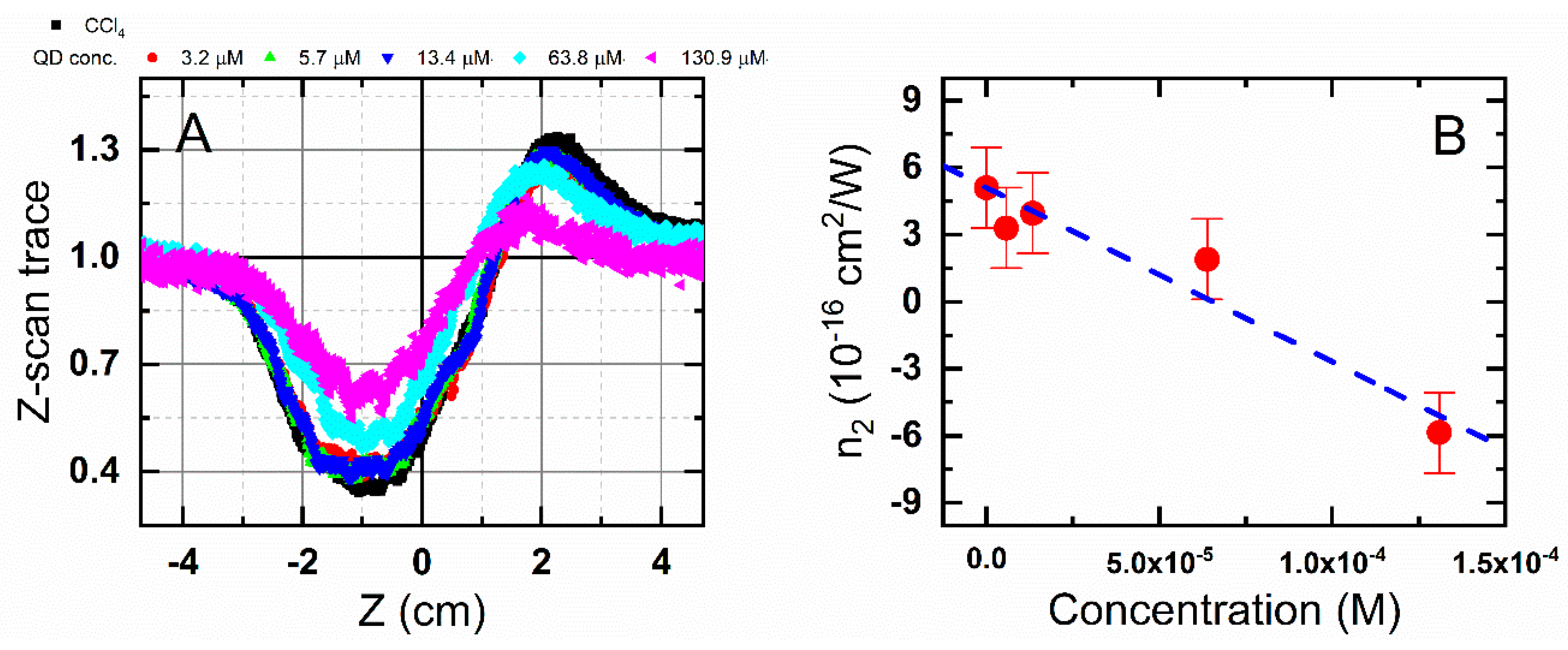
3.1. Thermal Nonlinearity

To measure resonant nonlinearity correctly, we have to tackle the sample heating because of light absorption. Such heating complicates the analysis of the nonlinear response. We assume that our QDs nonlinear response originates from two counterparts: electronic and thermal. Since we are interested in intrinsic electronic nonlinearity, we have to minimize the thermal counterpart.

Thermal nonlinearity can be split into two parts. “Direct” thermal contribution to NRI exceeds the electronic contribution when pumping pulse duration exceeds ~30 ps [27]. To avoid the direct thermal counterpart to NRI, we employ ultrashort pump pulses (~35 fs). In the resonant case, pumping the sample with a high pulse repetition rate (PRR) laser beam may also lead to the appearance of “indirect” thermal nonlinearity. If the pumping pulse arrives before the sample has returned to the equilibrium temperature, it leads to the accumulation of heat in the sample, thus increasing the NRI thermal counterpart. To prove this, we performed NRI measurements for the QD solution (d = 3.3 nm, concentration ~10⁻⁵ M) with PRR ranging from 1 Hz to 1000 Hz (see Figure 3A). We revealed that, for our QD solutions, NRI remains almost unchanged for PRR values of 100 Hz and less. When PRR exceeds 100 Hz, NRI increases, which we assume is a sign of “indirect” thermal nonlinearity. To avoid thermal nonlinearities, all further experiments were performed at a PRR of 10 Hz. NRI values obtained are independent of the beam intensity (see Figure 3B).

We should point out that the sign of PbS NRI is negative, which corresponds to the self-defocusing process. The nonlinear response of a solution should be proportional to a number of active species (in our case QDs) per unit volume [28]. To characterize an individual QD nonlinear response, we use second-order hyperpolarizability γ, which can be derived from the linear fit of NRI concentration dependence. Z-scan traces for QD solutions with concentrations of 5 × 10⁻⁶ M–1.3 × 10⁻⁴ M are shown in Figure 4A. The linear fit for the NRI values can be seen in Figure 4B. The interpolated hyperpolarizability value for 3.3 nm PbS QDs is −(2.5 ± 0.8) × 10⁻³² esu.

3.2. PbS QD Nonlinear Refraction in the Literature

It is complicated to directly compare the magnitudes of the nonlinear response due to the lack of reported microscopic parameters in the literature.

Table 1. Summary of PbS QD nonlinear refractions found in the literature. τ_p—pulse duration.

QD Diameter, nm	n2, cm2/W	n2/C, cm2/(W·M)	τp|PRR	Host	Ref.
3÷8.4	−10−16	−(0.4÷6.8) × 10−10	35 fs|10 Hz	solution	This work
3.8÷6.4	−(5÷35) × 10−12	−(1÷7) × 10−6	150 fs|76 MHz	solution	[20]
4.6÷11	−(0.5÷4.2) × 10−3	−(0.1÷0.8)	300 fs|1 kHz	solution	[22]
10	−3 × 10−14	n/a	~ns|n/a	solution	[21]
10	−(0.9÷3.4) × 10−15	n/a	130 fs|76 MHz	solution	[30]
1.6	−1.05 × 10−9	n/a	cw	solution	[8]
3.8	−3.16 × 10−12	n/a	4 ns|10 Hz	solution	[23]
2.4÷5	−(3.5÷8.4) × 10−11	n/a	cw	solution	[24]
3.5	−2 × 10−23	n/a	~fs|n/a	glass	[14]
<15	−10−16	n/a	50 ps|1 Hz	PVA sol	[15]
<1.3	−(2.8÷7.0) × 10−10	n/a	50 ps|10 Hz	zeolite	[16]

summarizes the literature data for the nonlinear refraction of PbS QDs. The NRI values reported in the literature varied in a wide range that can be explained by several factors. The first factor is that NRI is a macroscopic parameter of the sample. Thus, its magnitude is directly proportional to the concentration of the QDs. When applicable, some comparisons can be made by normalizing the nonlinear refraction index of QDs to the QD concentration in the studied sample. However, the QD host material can also affect the measured NRI. Moreover, the QD size and size distribution should also change the NRI. Besides that, the experimental conditions drastically affect the observed NRI, as shown above. The excitation parameters varied from paper to paper, which complicates the comparison of the results. The contribution from all these factors leads to a wide range of reported NRI values.

Our normalized NRI values are lower than those reported by Omari et al. [20] and Neo et al. [22]. We attribute this to the fact that we measure the purely electronic counterpart of the NRI, which better describes the intrinsic QD nonlinearity.

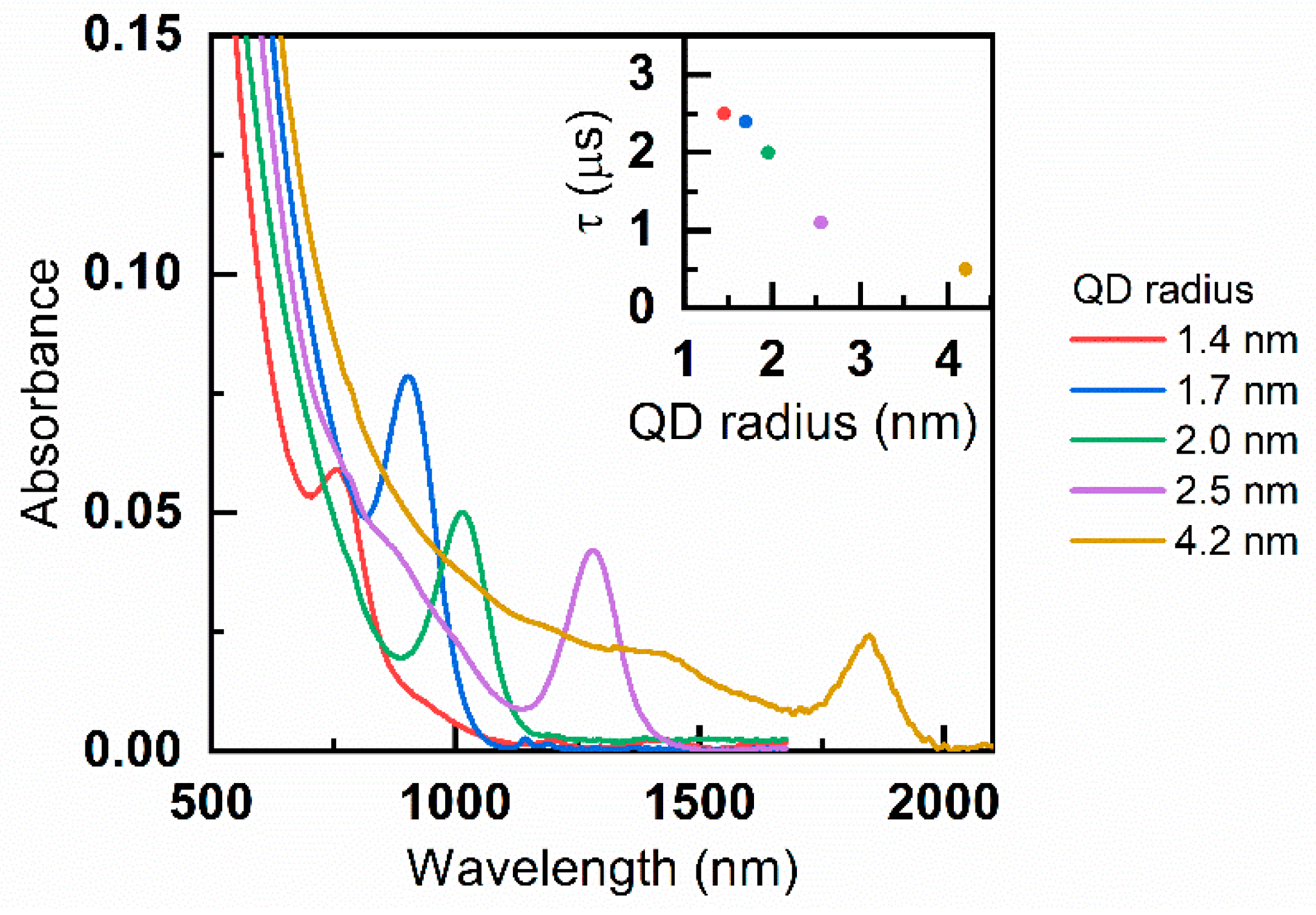
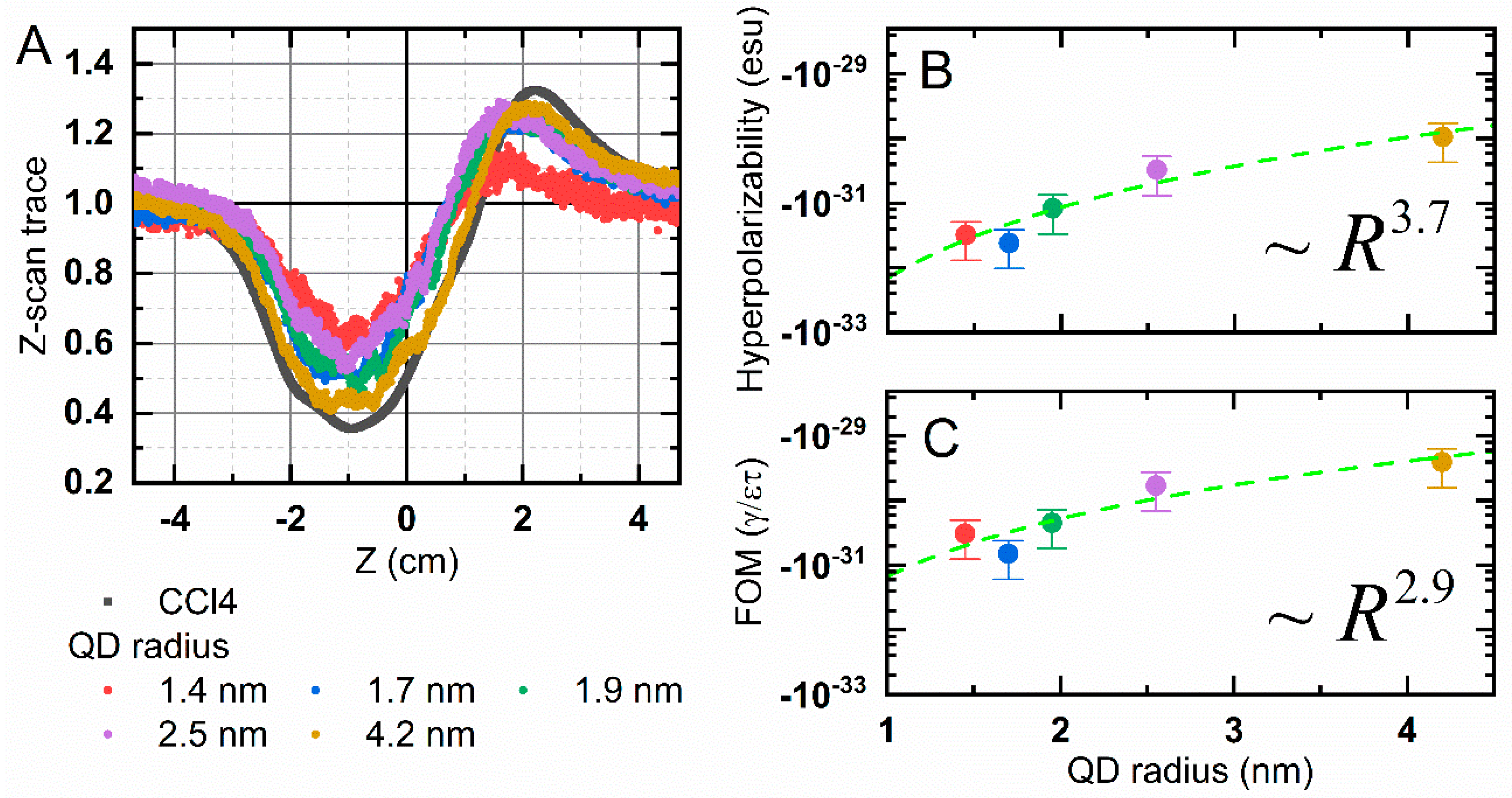
3.3. Size-Dependent Nonlinear Response

In theory, quantum confinement should increase the resonant nonlinear response [11,12]. Moreover, in the strong confinement regime, oscillator strength should increase with confinement; thus, the nonlinear response per QD should decrease with size growth [12]. Neo et al. reported size-dependent NRI of the PbS QDs in the resonant regime [22]. They found that NRI decreases with QD size growth. However, they utilized a laser with a 1-kHz repetition rate, and, as we have shown above, this causes unwanted thermal effects, which alter the results. Increases in the nonlinear response with QD size growth were also observed for CdS_xSe_1−x [31], CuInS and AgInS [32] QDs in the resonant regime, and CdTe QDs in the near-resonant regime [33].

Experimental studies reported deviations from existing theoretical predictions. However, no decent explanation was given for this phenomenon. The reasons for this are poor data generalization and a lack of comprehensive studies of nonlinearity size dependence. In our attempt to fill this gap, we performed Z-scan measurements for the set of QDs with radii from 1.5 nm to 4.2 nm.

Z-scan traces for QDs with different sizes can be seen in Figure 5A. The QD hyperpolarizability size distribution is shown in Figure 5B. We found that QD hyperpolarizability increases with size. Moreover, nonlinear fitting shows that hyperpolarizability grows with the QD radius to the power of ~3.7. To accurately compare the quality of the QD nonlinear response, it is necessary to consider the QD absorption as well as carrier relaxation time [13]. For this purpose, we employed the following figure of merit (FOM) for QD nonlinearity:

$$\mathrm{FOM}=\frac{\gamma }{\epsilon \tau },$$

where γ is QD hyperpolarizability, ε is the QD extinction at pumping wavelength (800 nm), τ—relaxation time, obtained from TRPL measurement (see inset on Figure 1) [25]. Figure 5C shows that obtained FOM also increases with the QD radius to the power of 2.9. Interestingly, the obtained ~R^2.9 FOM growth is similar to the observed cubic χ⁽³⁾ growth for QDs in the weak confinement regime [34].

To understand the unusual experimentally observed dependence, several possible explanations should be considered.

• Both the linear and nonlinear properties of the QD are governed by its electronic structure. The seemingly featureless absorption spectra of PbS QDs contain rich electronic structure [35]. It has been found that PbS QDs electronic structure induce the natural anomalous size dependence of the excited carrier relaxation, which was explained in terms of phonon-induced transitions from the in-gap states to QD fundamental states [25,36]. When the QD size decreases, the relaxation time increases to the power of ~1.4. That intrinsically modifies FOM size dependence. It has recently been proven that PbS QDs possess two emissive states [37]. The number of optically active states should influence the resonant nonlinear response. The influence of PbS QDs’ electronic system aspects on their nonlinear responses was recently pointed out by Padihla et al. They reported unconventional increase in volume-normalized two-photon cross-section with decreasing QD sizes [38];
• The dependence of nonlinear optical responses on QD size distribution has been theoretically predicted [39]. The broadening of the QD size distribution increases the inhomogeneous linewidth of the QD ensemble, thus weakening their nonlinear optical response. In our case, when the QD radius reduces from 4.2 nm to 1.4 nm, QD size distribution increases from 4.5% to 9.6%, respectively. Temperature-dependent photoluminescence analysis can also be applied to extrapolate inhomogeneous broadening, which increases from 149 meV to 176 meV for 4.5 nm and 3.7 nm QD, respectively [40];
• QD surface has a great impact on QD properties [41,42]. The incomplete passivation of the QD surface forms so-called surface trap states. Photoexcited carriers trapped at the QD surface form a static internal field, reducing the oscillator strength, leading to the saturation of the absorption [43] and reducing the nonlinear response. When the QD radius decreases from 4.3 to 1.5 nm, the QD surface-to-volume ratio increases drastically, which makes the impact of the of surface traps even more pronounced, decreasing the nonlinear response further on.
• The formation of biexciton states within the QD may also contribute to the nonlinear response. QD size growth leads to an increase in biexciton oscillator strength, which, in turn, increases the $\left|{\chi }^{(3)}\right|$ [39,44].

In contrast to simplified theoretical predictions, the experimentally observed size dependence of the resonant nonlinear FOM in the strong confinement regime includes many competing mechanisms that require further detailed experimental and theoretical analysis.

For the QDs to be used in NLO devices, it would be beneficial to improve the magnitude of QDs’ nonlinear response. For example, Kerr lens mode-locking operates with materials having n₂~10⁻¹⁶–10⁻¹⁵ cm²/W [45], and all-optical switching devices can work with n₂~10⁻²² cm²/W [46]. To date, such values for QD solutions have already been achieved. Further increases in the magnitude of QD nonlinear response allow us to achieve the same macroscopic nonlinear parameters (n₂ or χ⁽³⁾) with lower QD concentrations, thus lowering the amount of required material. The improvement of the nonlinear response can be achieved by creating QDs with less defects, which will prevent the charge trapping and oscillator strength reduction. The photoluminescence quantum yield of the used QDs was ~25%, which leaves enough room for improving the surface passivation and reducing the defect-state density. Additional increases in the nonlinear response may be achieved by narrowing the QD size distribution [39]. Assuming that inhomogeneous linewidth broadening changes the nonlinear response in the same way as homogeneous broadening, the QDs’ nonlinear response can be increased by three to four times. In summary, the nonlinear response can be enhanced by an order of magnitude that is suitable for the use of non-concentrated media with PbS QDs in most applications. Lastly, the QD ligand shell greatly affects the QD properties, including the nonlinear response; it has been recently shown that changing the shell can even revert the sign of the NRI [21]. However, further studies are required to truly understand the impact of the ligand shell on QDs’ nonlinear properties.

4. Conclusions

In this work, we have studied the nonlinear refraction of PbS QDs in colloidal solution using the Z-scan method. We demonstrated that, to eliminate the thermal nonlinearities in the resonant regime, it is necessary to use ultrashort pulses at pulse repetition rates lower than 100 Hz. We revealed that, contrary to the theory, PbS QDs’ nonlinear refractive index (or their second order hyperpolarizability) increases with size. The particular reason for this behavior is a subject for further investigation. In addition, we have suggested a few possible ways to increase the magnitude of QDs’ nonlinear response.