RF Injection of THz QCL Combs at 80 K Emitting over 700 GHz Spectral Bandwidth
Abstract
1. Introduction
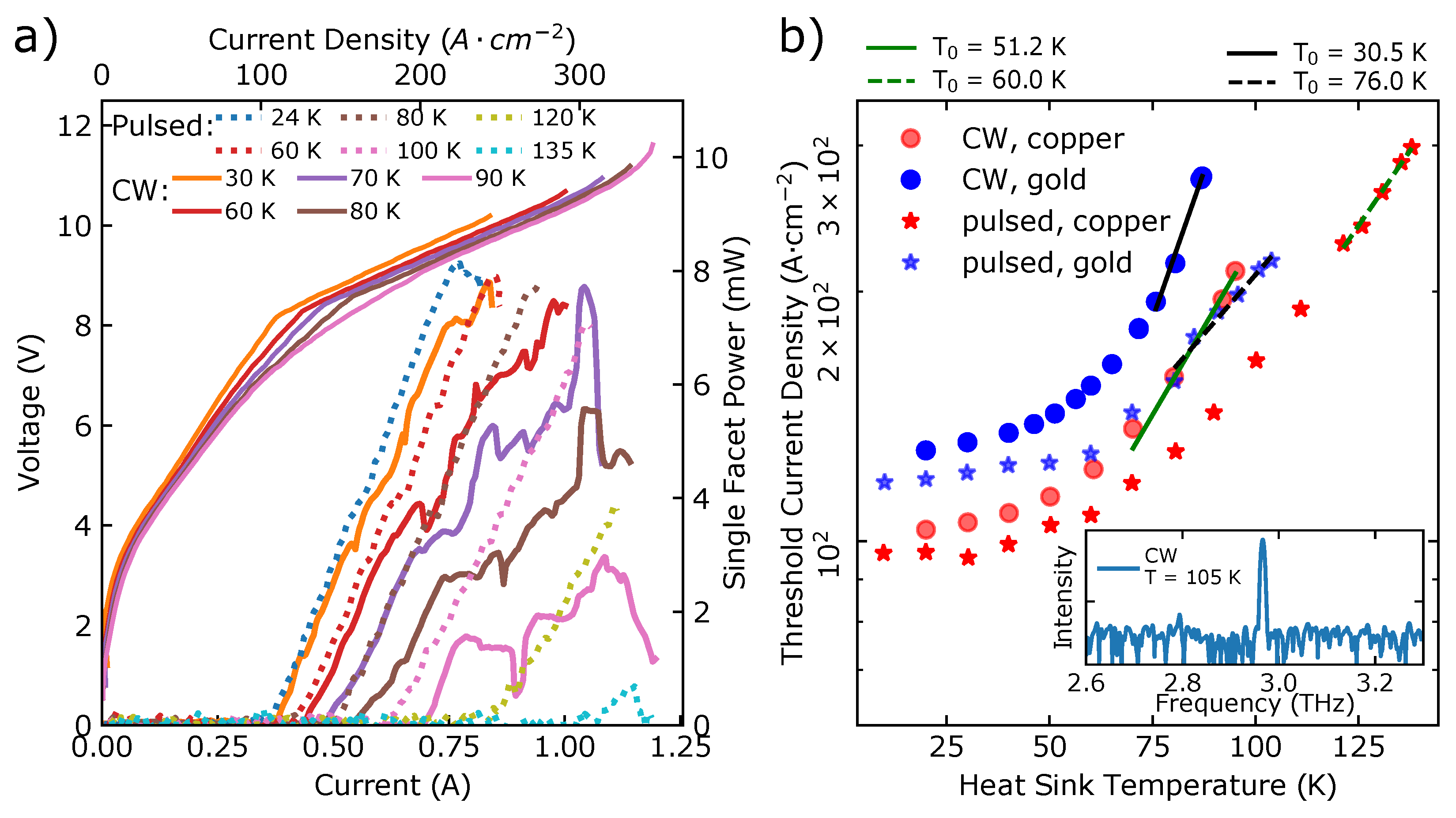
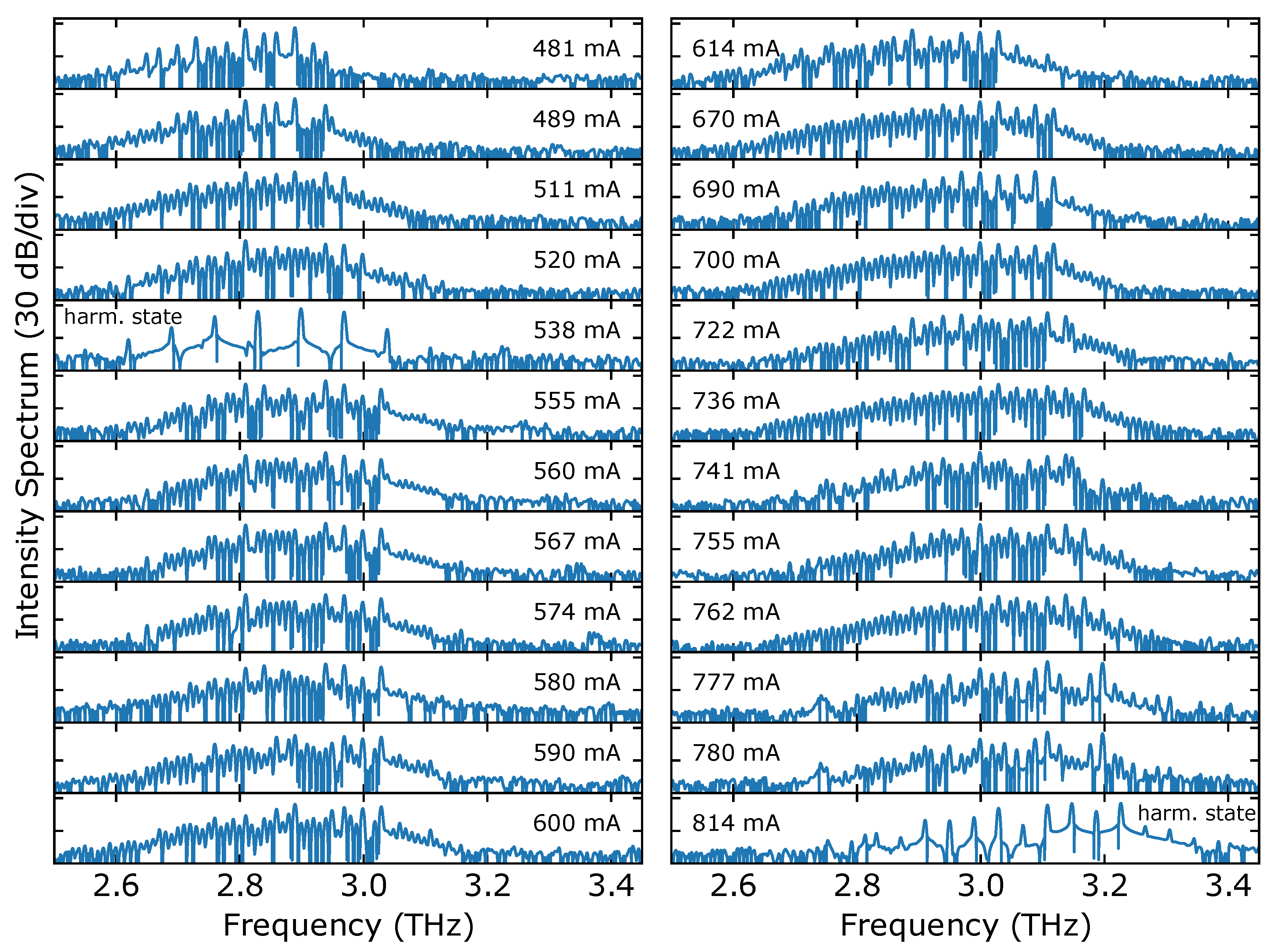
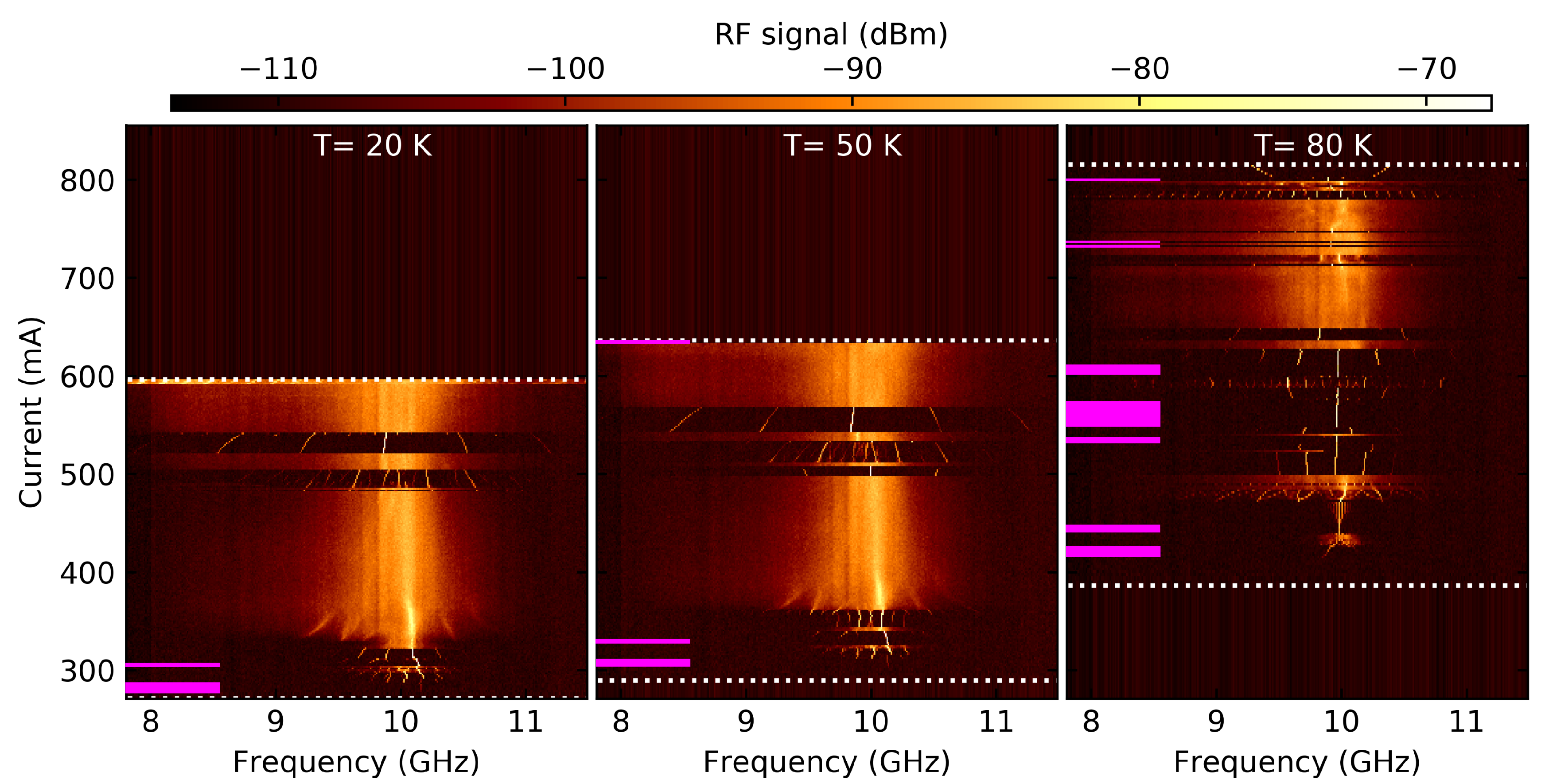
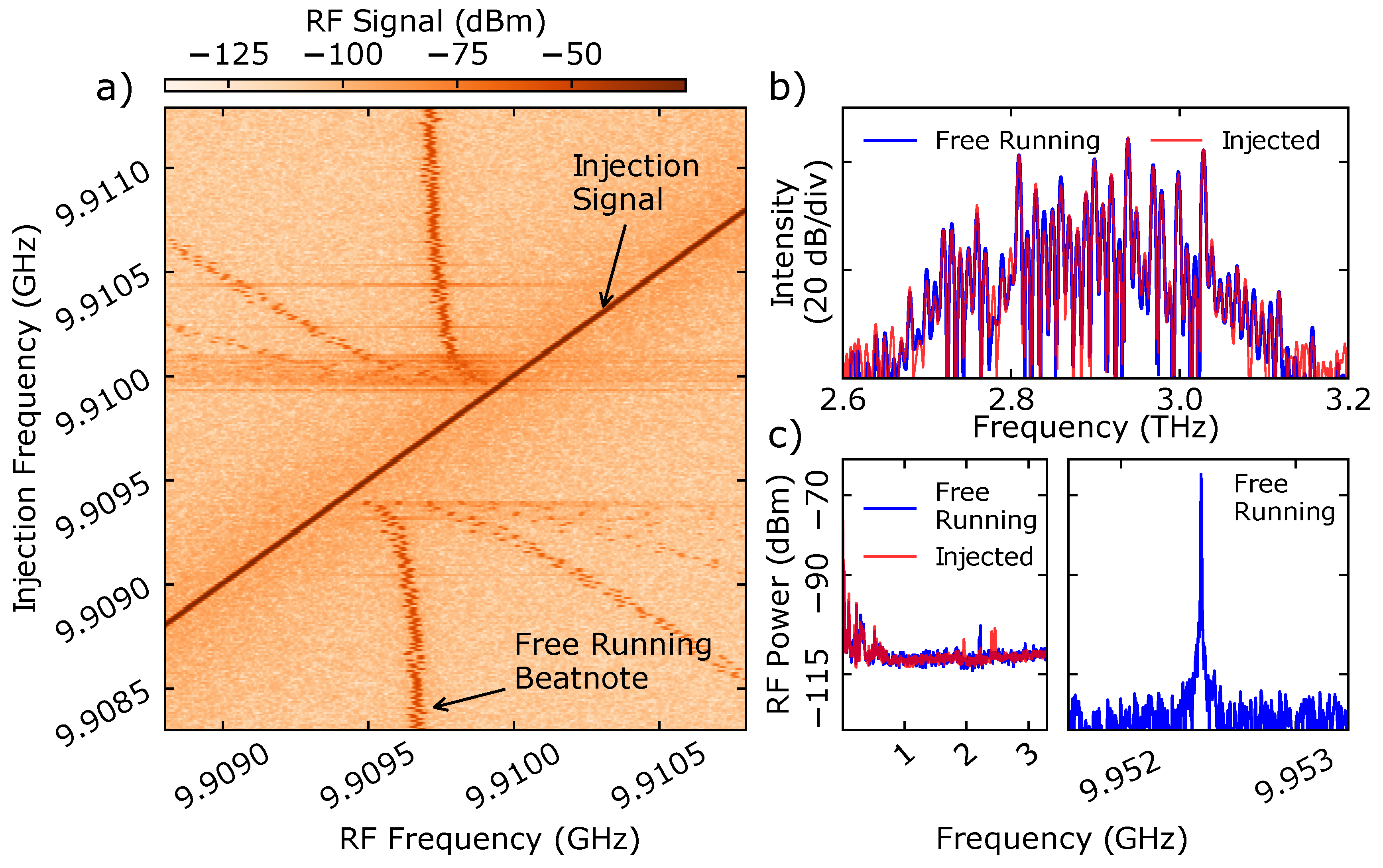
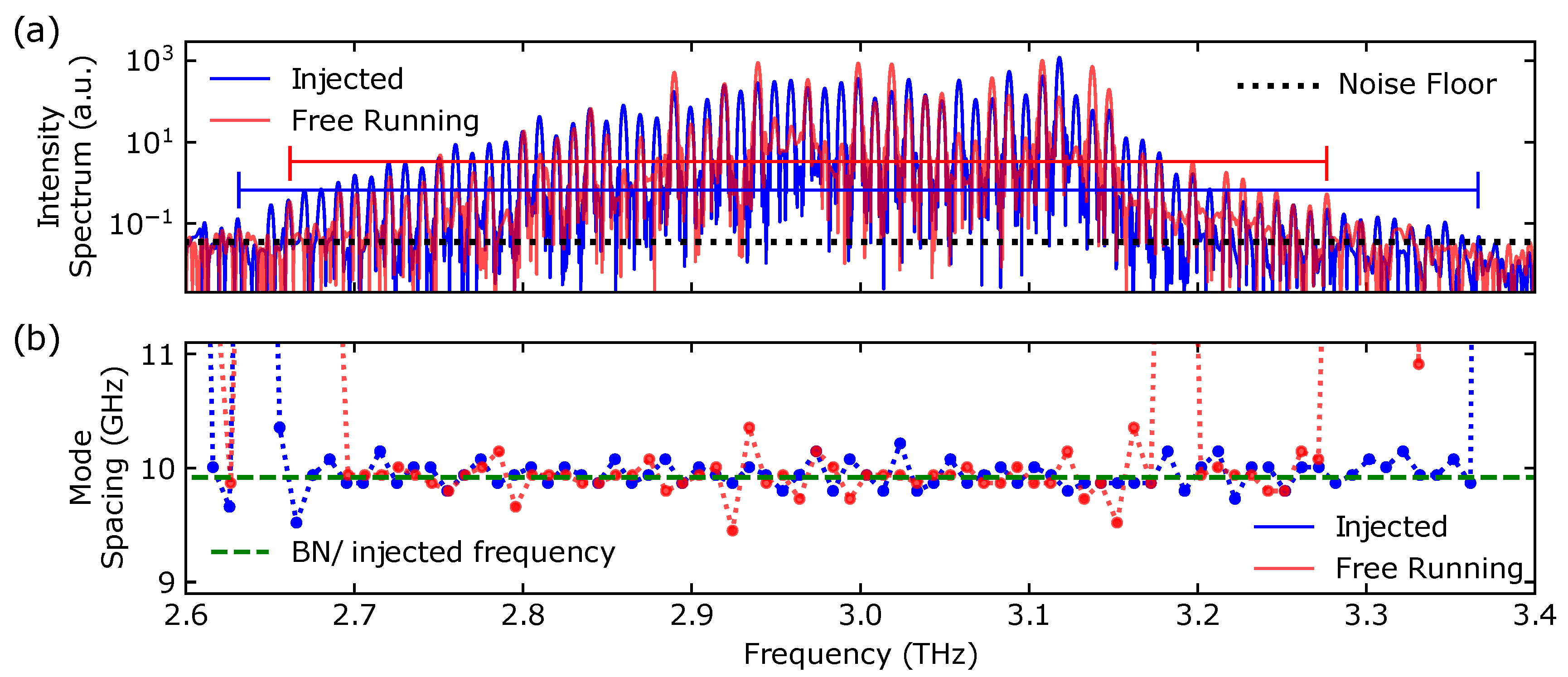
2. Results
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holzwarth, R.; Udem, T.; Hansch, T.; Knight, J.; Wadsworth, W.; Russell, P. Optical frequency synthesizer for precision spectroscopy. Phys. Rev. Lett. 2000, 85, 2264–2267. [Google Scholar] [CrossRef]
- Udem, T.; Holzwarth, R.; Hansch, T. Optical frequency metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef]
- Reichert, J.; Holzwarth, R.; Udem, T.; Hansch, T. Measuring the frequency of light with mode-locked lasers. Opt. Commun. 1999, 172, 59–68. [Google Scholar] [CrossRef]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Hugi, A.; Villares, G.; Blaser, S.; Liu, H.C.; Faist, J. Mid-infrared frequency comb based on a quantum cascade laser. Nature 2012, 492, 229–233. [Google Scholar] [CrossRef] [PubMed]
- Burghoff, D.; Kao, T.Y.; Han, N.; Chan, C.W.I.; Cai, X.; Yang, Y.; Hayton, D.J.; Gao, J.R.; Reno, J.L.; Hu, Q. Terahertz laser frequency combs. Nat. Photonics 2014, 8, 462–467. [Google Scholar] [CrossRef]
- Scalari, G.; Faist, J.; Picqué, N. On-chip mid-infrared and THz frequency combs for spectroscopy. Appl. Phys. Lett. 2019, 114, 150401. [Google Scholar] [CrossRef]
- Faist, J.; Capasso, F.; Sivco, D.; Sirtori, C.; Hutchinson, A.; Cho, A. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef]
- Barbieri, S.; Ravaro, M.; Gellie, P.; Santarelli, G.; Manquest, C.; Sirtori, C.; Khanna, S.P.; Linfield, E.H.; Davies, A.G. Coherent sampling of active mode-locked terahertz quantum cascade lasers and frequency synthesis (vol 5, pg 306, 2011). Nat. Photonics 2011, 5, 378. [Google Scholar]
- Wang, F.; Maussang, K.; Moumdji, S.; Colombelli, R.; Freeman, J.R.; Kundu, I.; Li, L.; Linfield, E.H.; Davies, A.G.; Mangeney, J.; et al. Generating ultrafast pulses of light from quantum cascade lasers. Optica 2015, 2, 944–949. [Google Scholar] [CrossRef]
- Bachmann, D.; Roesch, M.; Süess, M.J.; Beck, M.; Unterrainer, K.; Darmo, J.; Faist, J.; Scalari, G. Short pulse generation and mode control of broadband terahertz quantum cascade lasers. Optica 2016, 3, 1087–1094. [Google Scholar] [CrossRef]
- Forrer, A.; Roesch, M.; Singleton, M.; Beck, M.; Faist, J.; Scalari, G. Coexisting frequency combs spaced by an octave in a monolithic quantum cascade laser. Opt. Express 2018, 26, 23167–23177. [Google Scholar] [CrossRef]
- Roesch, M.; Beck, M.; Süess Martin, J.; Bachmann, D.; Unterrainer, K.; Faist, J.; Scalari, G. Heterogeneous terahertz quantum cascade lasers exceeding 1.9 THz spectral bandwidth and featuring dual comb operation. Nanophotonics 2018, 7, 237. [Google Scholar] [CrossRef]
- Roesch, M.; Scalari, G.; Beck, M.; Faist, J. Octave-spanning semiconductor laser. Nat. Photonics 2014, 9, 42. [Google Scholar] [CrossRef]
- Cappelli, F.; Consolino, L.; Campo, G.; Galli, I.; Mazzotti, D.; Campa, A.; de Cumis, M.S.; Pastor, P.C.; Eramo, R.; Rosch, M.; et al. Retrieval of phase relation and emission profile of quantum cascade laser frequency combs. Nat. Photonics 2019, 13. [Google Scholar] [CrossRef]
- Benea-Chelmus, I.C.; Rösch, M.; Scalari, G.; Beck, M.; Faist, J. Intensity autocorrelation measurements of frequency combs in the terahertz range. Phys. Rev. A 2017, 96, 033821. [Google Scholar] [CrossRef]
- Mezzapesa, F.P.; Pistore, V.; Garrasi, K.; Li, L.; Davies, A.G.; Linfield, E.H.; Dhillon, S.; Vitiello, M.S. Tunable and compact dispersion compensation of broadband THz quantum cascade laser frequency combs. Opt. Express 2019, 27, 20231–20240. [Google Scholar] [CrossRef]
- Wang, F.; Nong, H.; Fobbe, T.; Pistore, V.; Houver, S.; Markmann, S.; Jukam, N.; Amanti, M.; Sirtori, C.; Moumdji, S.; et al. Short Terahertz Pulse Generation from a Dispersion Compensated Modelocked Semiconductor Laser. Laser Photonics Rev. 2017, 11, 1700013. [Google Scholar] [CrossRef]
- Consolino, L.; Nafa, M.; Cappelli, F.; Garrasi, K.; Mezzapesa, F.P.; Li, L.; Davies, A.G.; Linfield, E.H.; Vitiello, M.S.; De Natale, P.; et al. Fully phase-stabilized quantum cascade laser frequency comb. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef]
- Freeman, J.R.; Ponnampalam, L.; Shams, H.; Mohandas, R.A.; Renaud, C.C.; Dean, P.; Li, L.; Davies, A.G.; Seeds, A.J.; Linfield, E.H. Injection locking of a terahertz quantum cascade laser to a telecommunications wavelength frequency comb. Optica 2017, 4, 1059–1064. [Google Scholar] [CrossRef]
- Bosco, L.; Franckié, M.; Scalari, G.; Beck, M.; Wacker, A.; Faist, J. Thermoelectrically cooled THz quantum cascade laser operating up to 210 K. Appl. Phys. Lett. 2019, 115, 010601. [Google Scholar] [CrossRef]
- Forrer, A.; Franckié, M.; Stark, D.; Olariu, T.; Beck, M.; Faist, J.; Scalari, G. Photon-driven broadband emission and RF injection locking of THz quantum cascade laser frequency combs. arXiv 2019, arXiv:1912.00890. [Google Scholar]
- Scalari, G.; Amanti, M.I.; Walther, C.; Terazzi, R.; Beck, M.; Faist, J. Broadband THz lasing from a photon-phonon quantum cascade structure. Opt. Express 2010, 18, 8043–8052. [Google Scholar] [CrossRef] [PubMed]
- Scalari, G.; Terazzi, R.; Giovannini, M.; Hoyler, N.; Faist, J. Population inversion by resonant tunneling in quantum wells. Appl. Phys. Lett. 2007, 91, 032103. [Google Scholar] [CrossRef]
- Piccardo, M.; Chevalier, P.; Mansuripur, T.S.; Kazakov, D.; Wang, Y.; Rubin, N.A.; Meadowcroft, L.; Belyanin, A.; Capasso, F. The harmonic state of quantum cascade lasers: Origin, control, and prospective applications (Invited). Opt. Express 2018, 26, 9464–9483. [Google Scholar] [CrossRef]
- Mansuripur, T.S.; Vernet, C.; Chevalier, P.; Aoust, G.; Schwarz, B.; Xie, F.; Caneau, C.; Lascola, K.; Zah, C.e.; Caffey, D.P.; et al. Single-mode instability in standing-wave lasers: The quantum cascade laser as a self-pumped parametric oscillator. Phys. Rev. A 2016, 94, 063807. [Google Scholar] [CrossRef]
- Wienold, M.; Röben, B.; Schrottke, L.; Grahn, H.T. Evidence for frequency comb emission from a Fabry-Pérot terahertz quantum-cascade laser. Opt. Express 2014, 22, 30410–30424. [Google Scholar] [CrossRef]
- Villares, G.; Faist, J. Quantum cascade laser combs: Effects of modulation and dispersion. Opt. Express 2015, 23, 1651–1669. [Google Scholar] [CrossRef]
- G.Derntl, C.; Scalari, G.; Bachmann, D.; Beck, M.; Faist, J.; Unterrainer, K. Gain dynamics in a heterogeneous terahertz quantum cascade laser. Appl. Phys. Lett. 2018, 113, 81102. [Google Scholar]
- Opačak, N.; Schwarz, B. Theory of frequency modulated combs in lasers with spatial hole burning, dispersion and Kerr. arXiv 2019, arXiv:1905.13635. [Google Scholar] [CrossRef] [PubMed]
- Gellie, P.; Barbieri, S.; Lampin, J.F.; Filloux, P.; Manquest, C.; Sirtori, C.; Sagnes, I.; Khanna, S.P.; Linfield, E.H.; Davies, A.G.; et al. Injection-locking of terahertz quantum cascade lasers up to 35GHz using RF amplitude modulation. Opt. Express 2010, 18, 20799–20816. [Google Scholar] [CrossRef]
- Hillbrand, J.; Beiser, M.; Andrews, A.M.; Detz, H.; Weih, R.; Schade, A.; Höfling, S.; Strasser, G.; Schwarz, B. Picosecond pulses from a mid-infrared interband cascade laser. Optica 2019, 6, 1334–1337. [Google Scholar] [CrossRef]
- Wang, C.Y.; Kuznetsova, L.; Gkortsas, V.M.; Diehl, L.; Kärtner, F.X.; Belkin, M.A.; Belyanin, A.; Li, X.; Ham, D.; Schneider, H.; et al. Mode-locked pulses from mid-infrared Quantum Cascade Lasers. Opt. Express 2009, 17, 12929–12943. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Burghoff, D.; Hayton, D.J.; Gao, J.R.; Reno, J.L.; Hu, Q. Terahertz multiheterodyne spectroscopy using laser frequency combs. Optica 2016, 3, 499–502. [Google Scholar] [CrossRef]
- Sterczewski, L.A.; Westberg, J.; Yang, Y.; Burghoff, D.; Reno, J.; Hu, Q.; Wysocki, G. Terahertz hyperspectral imaging with dual chip-scale combs. arXiv 2018, arXiv:1812.03505. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forrer, A.; Bosco, L.; Beck, M.; Faist, J.; Scalari, G. RF Injection of THz QCL Combs at 80 K Emitting over 700 GHz Spectral Bandwidth. Photonics 2020, 7, 9. https://doi.org/10.3390/photonics7010009
Forrer A, Bosco L, Beck M, Faist J, Scalari G. RF Injection of THz QCL Combs at 80 K Emitting over 700 GHz Spectral Bandwidth. Photonics. 2020; 7(1):9. https://doi.org/10.3390/photonics7010009
Chicago/Turabian StyleForrer, Andres, Lorenzo Bosco, Mattias Beck, Jérôme Faist, and Giacomo Scalari. 2020. "RF Injection of THz QCL Combs at 80 K Emitting over 700 GHz Spectral Bandwidth" Photonics 7, no. 1: 9. https://doi.org/10.3390/photonics7010009
APA StyleForrer, A., Bosco, L., Beck, M., Faist, J., & Scalari, G. (2020). RF Injection of THz QCL Combs at 80 K Emitting over 700 GHz Spectral Bandwidth. Photonics, 7(1), 9. https://doi.org/10.3390/photonics7010009





