Hybrid Integrated Semiconductor Lasers with Silicon Nitride Feedback Circuits
Abstract
:1. Introduction
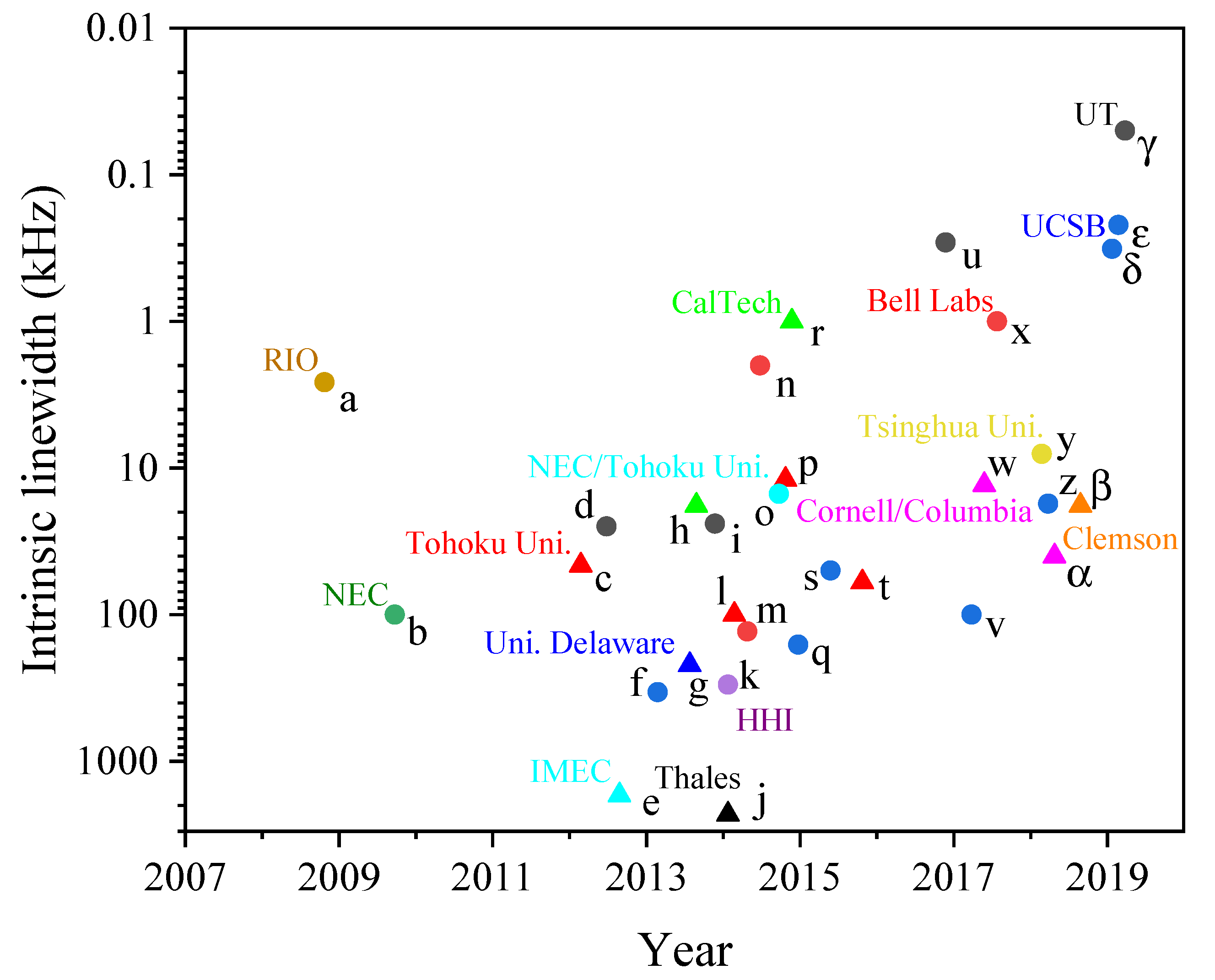
2. State of the Art
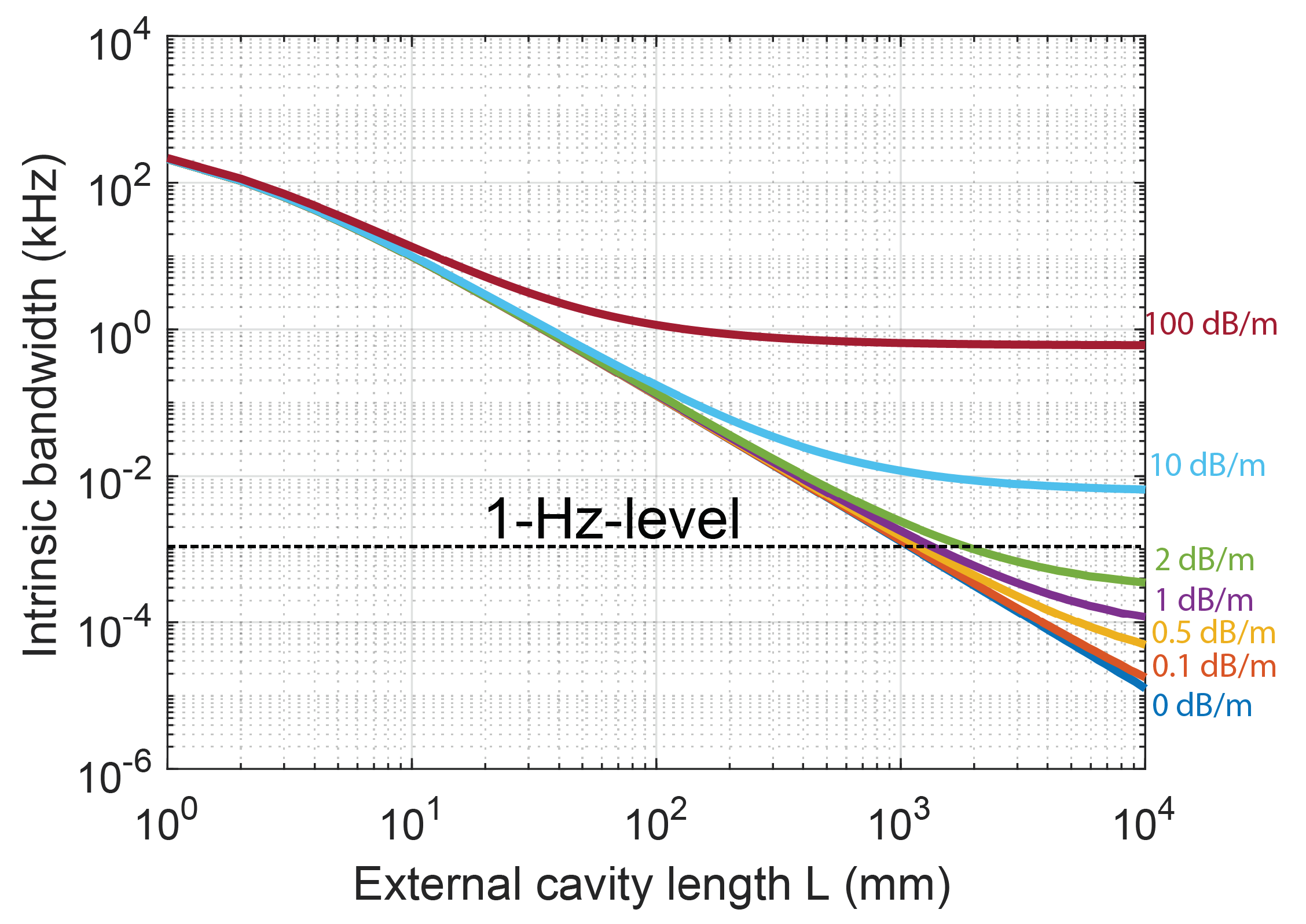
3. Intrinsic linewidth of Extended Cavity Hybrid Integrated Diode Lasers
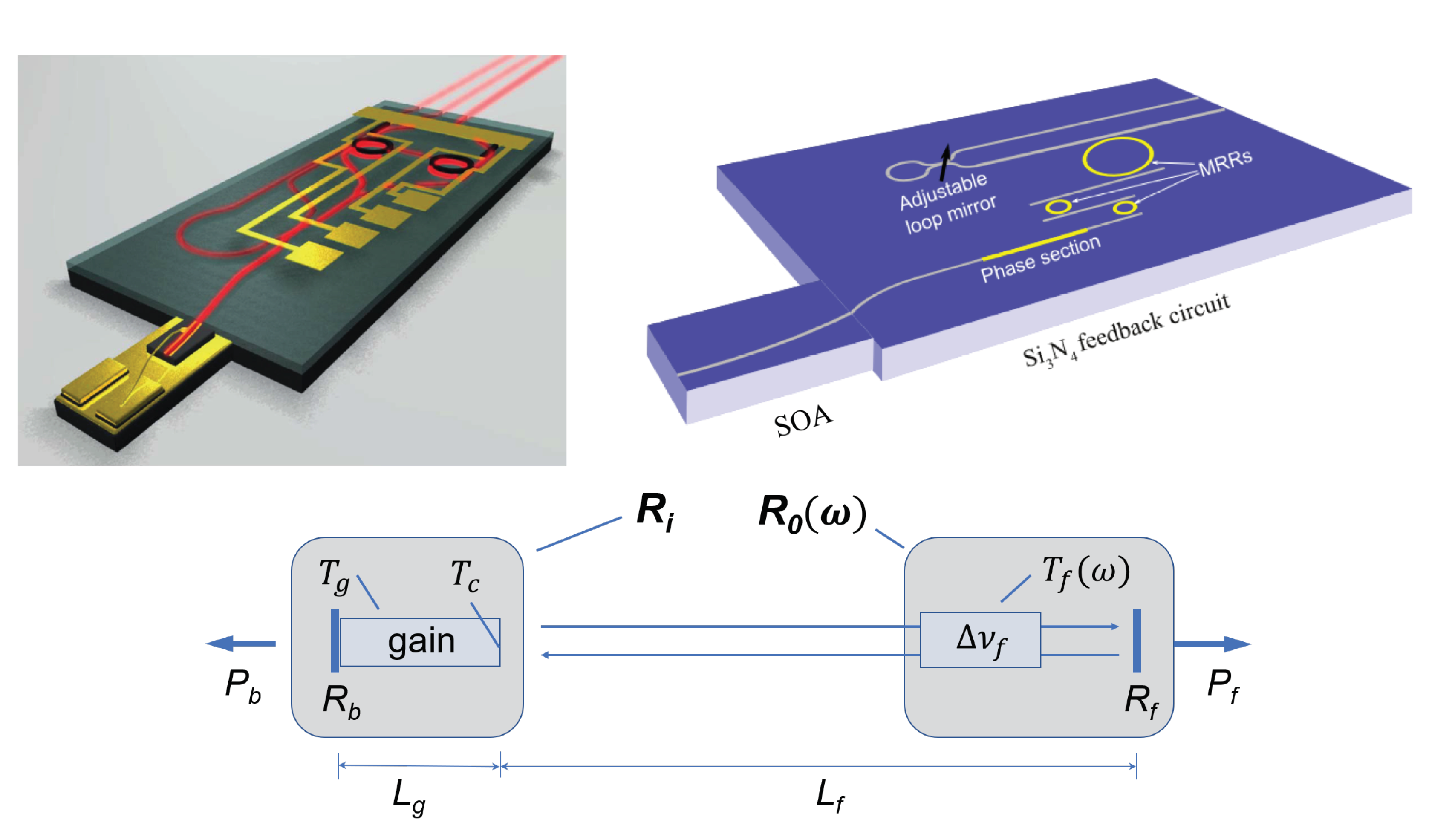
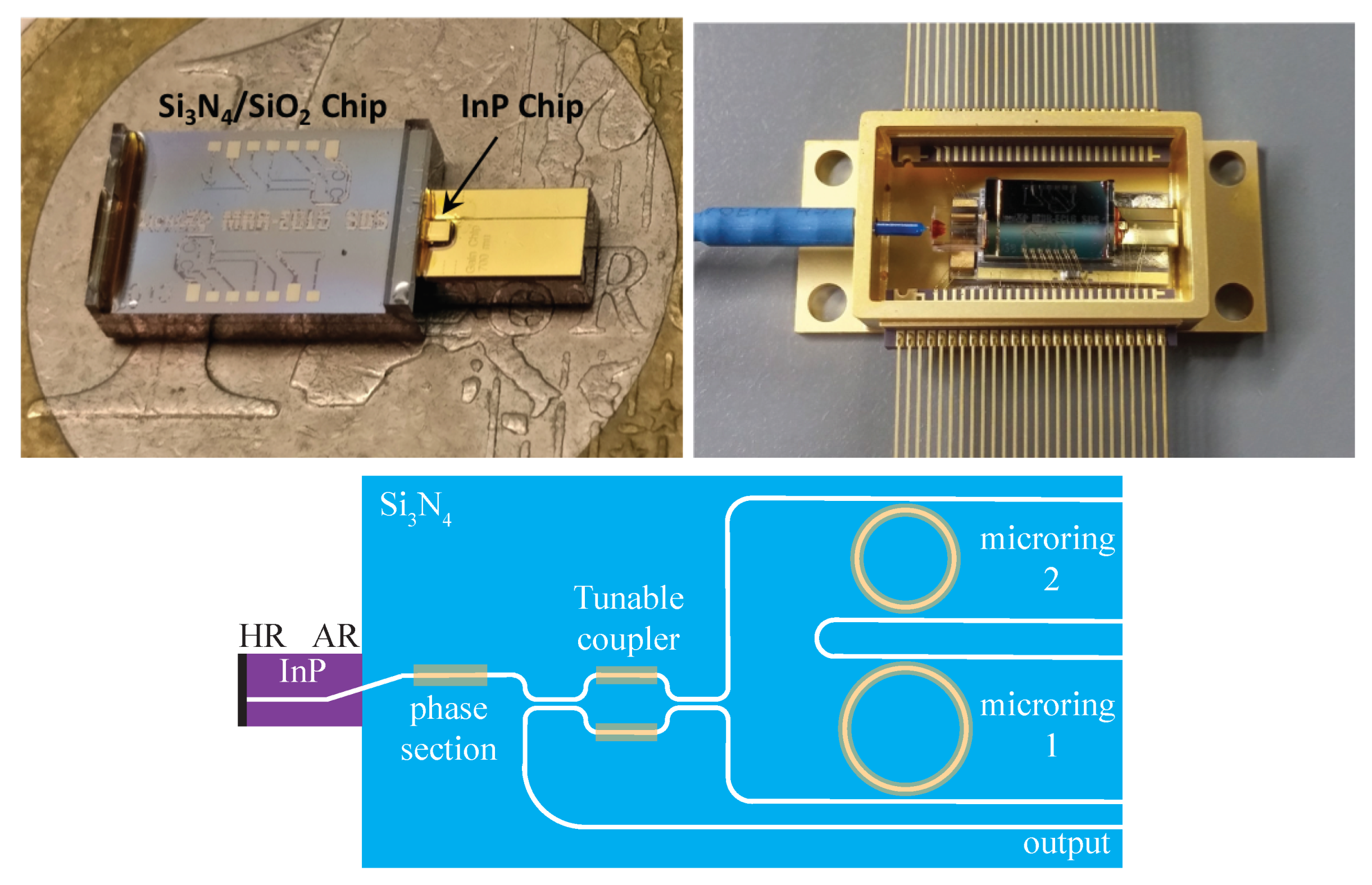
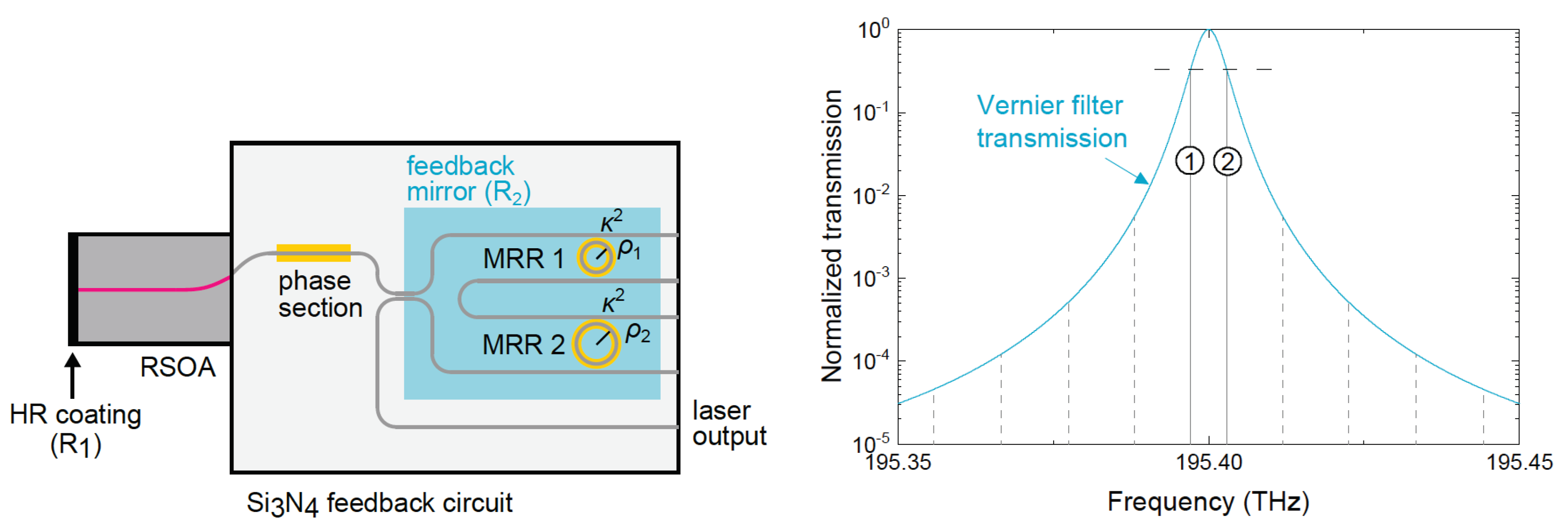
4. Hybrid Lasers with Two Microring Resonators and Single Gain Section
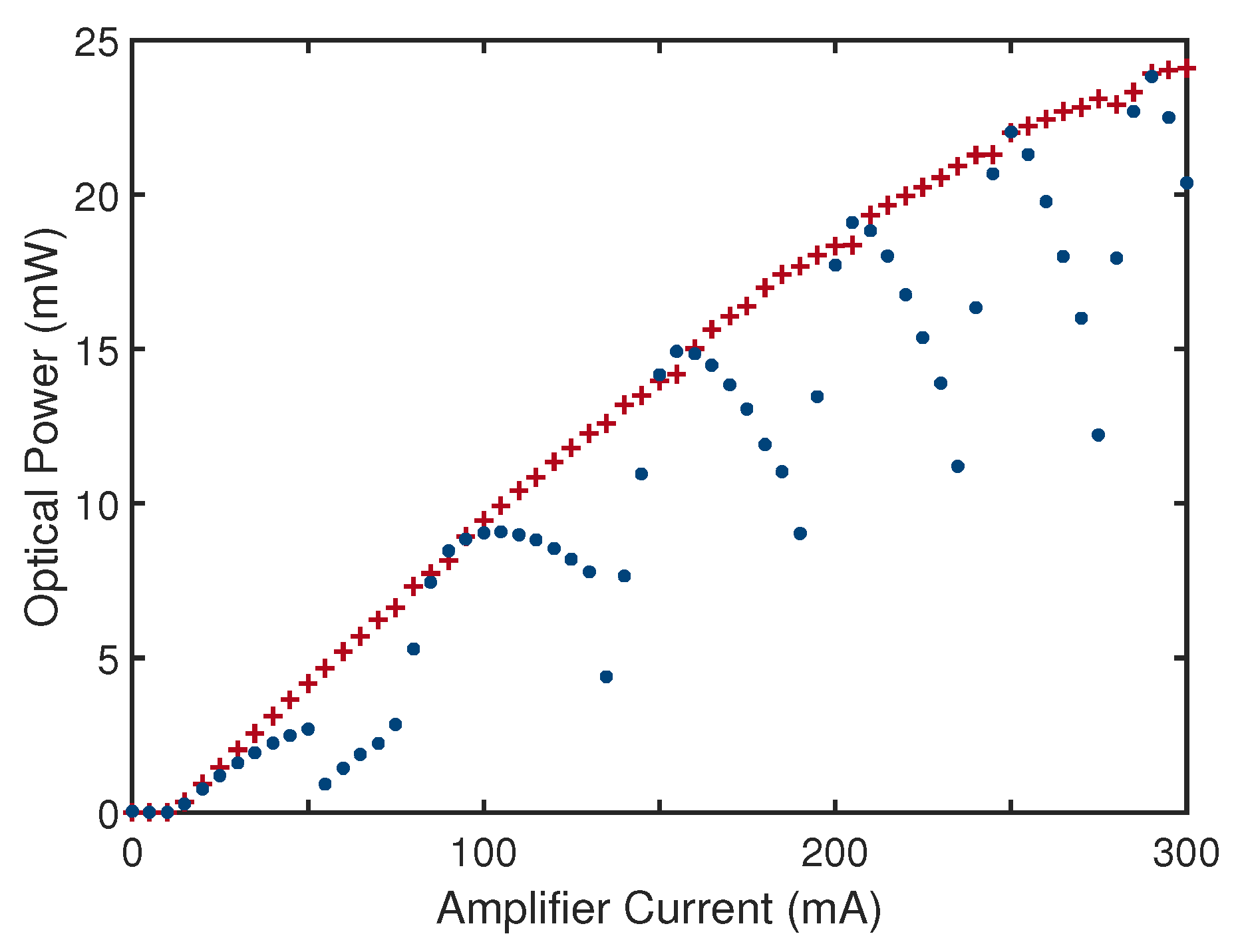
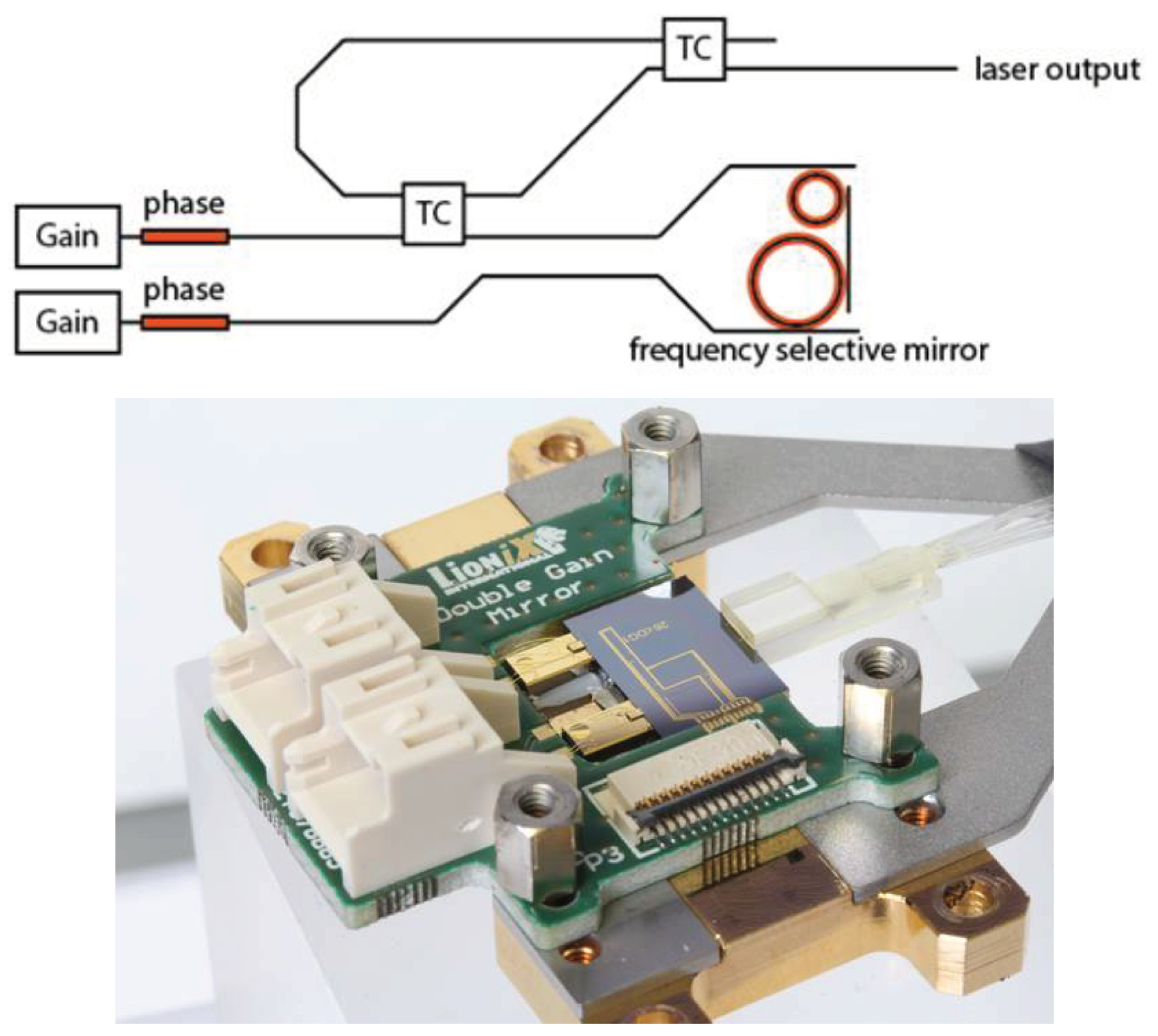
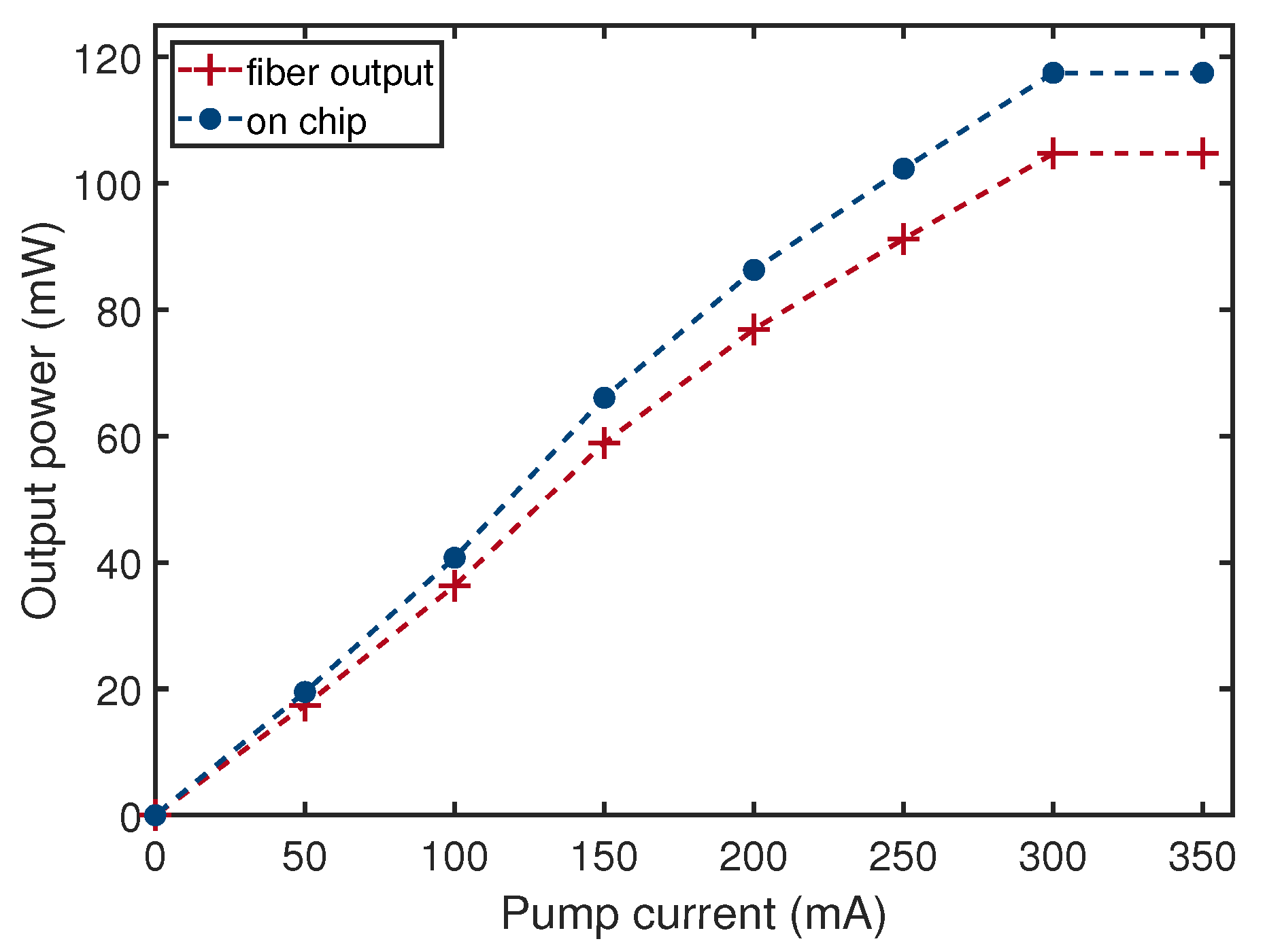
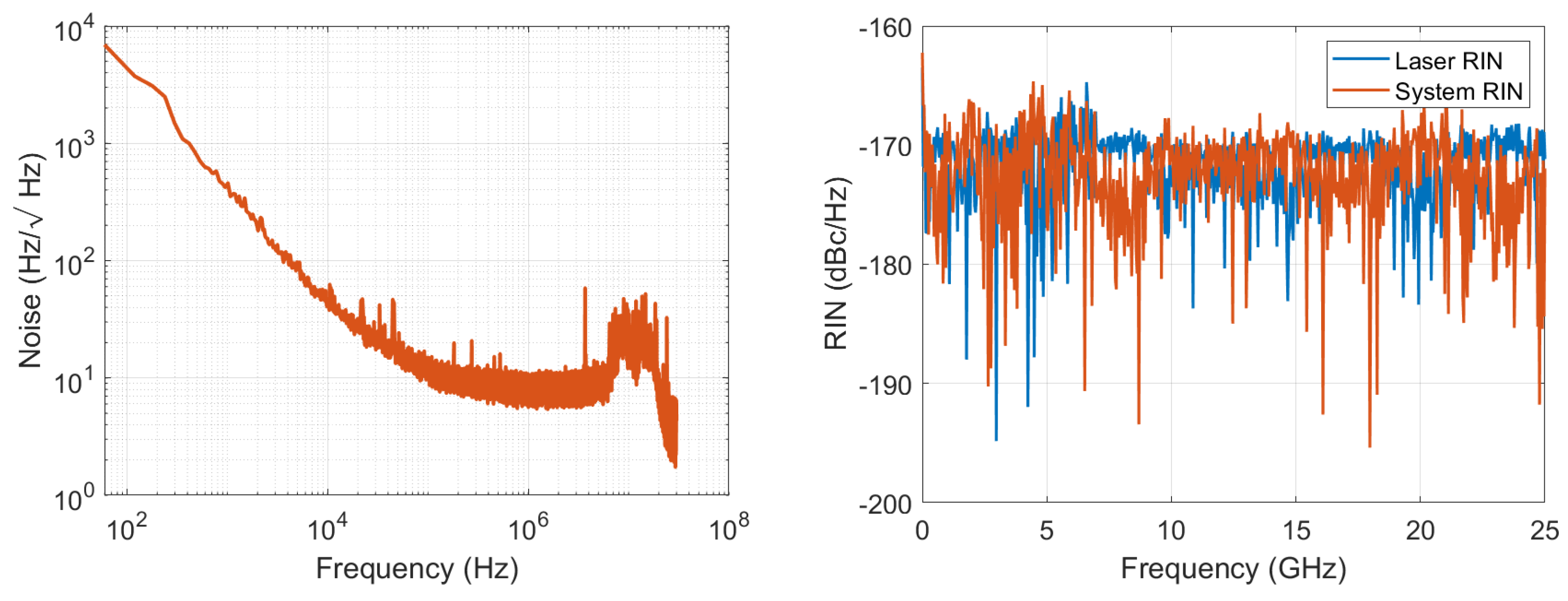
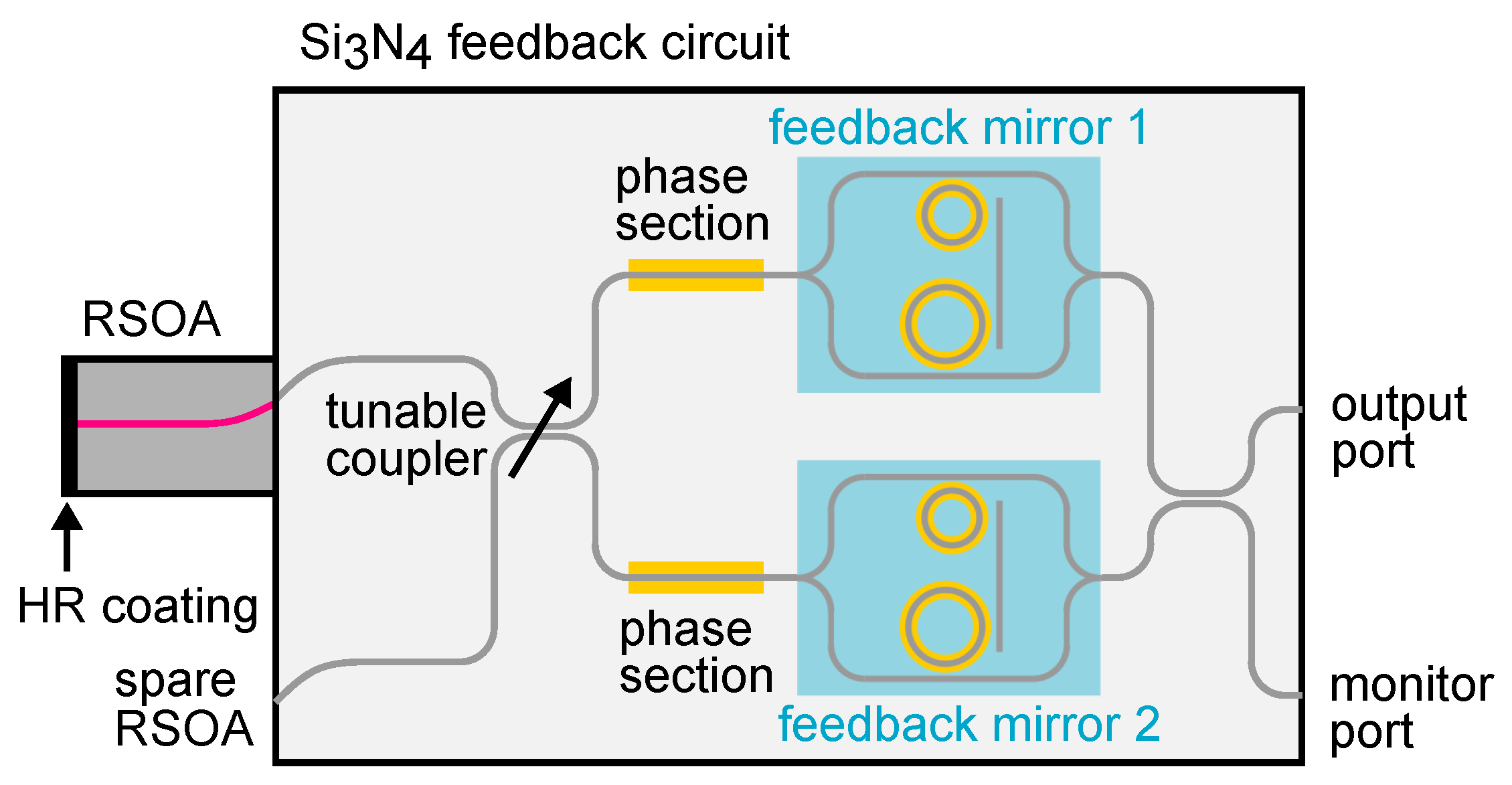
5. High Power Hybrid Integrated Lasers with Two Gain Sections
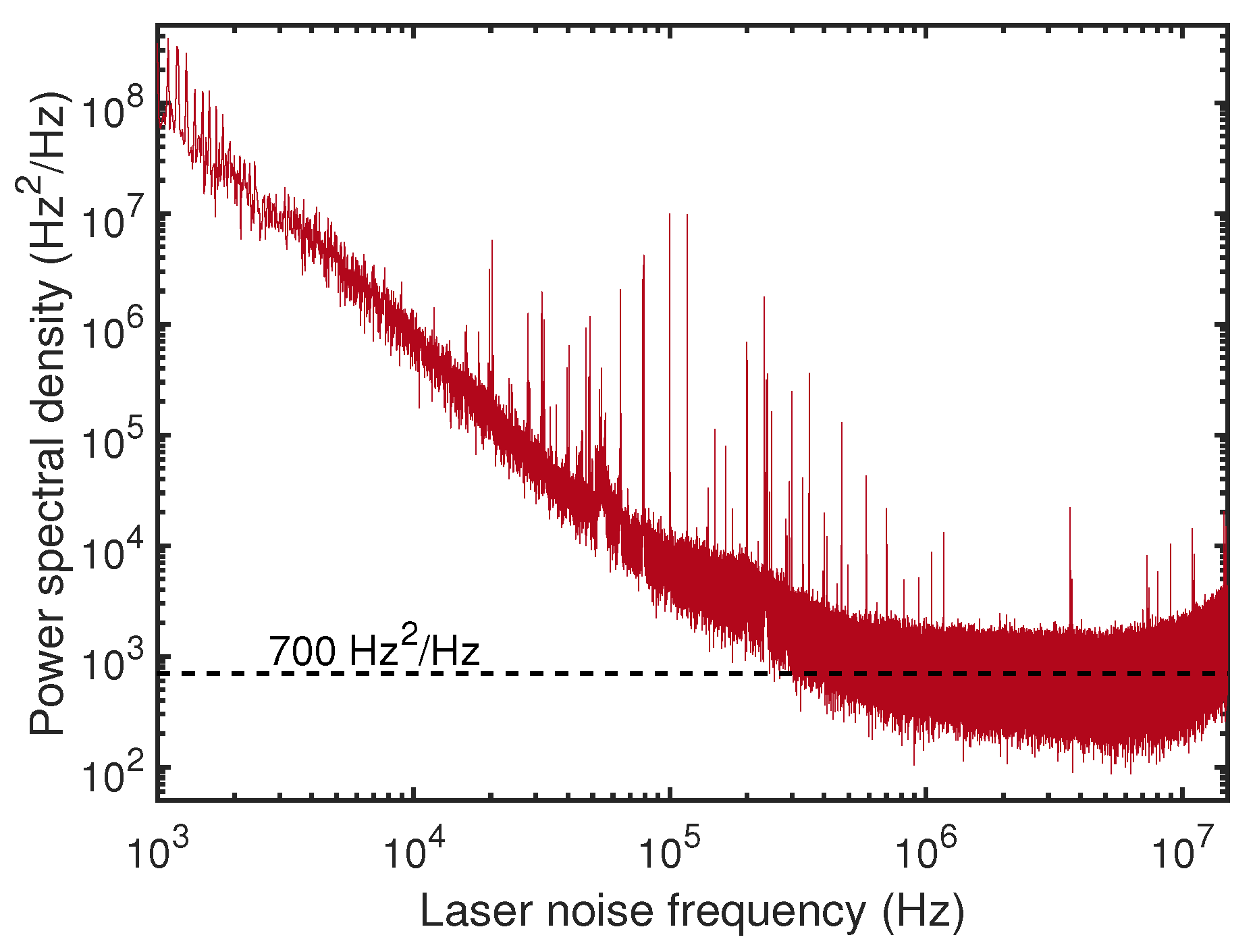
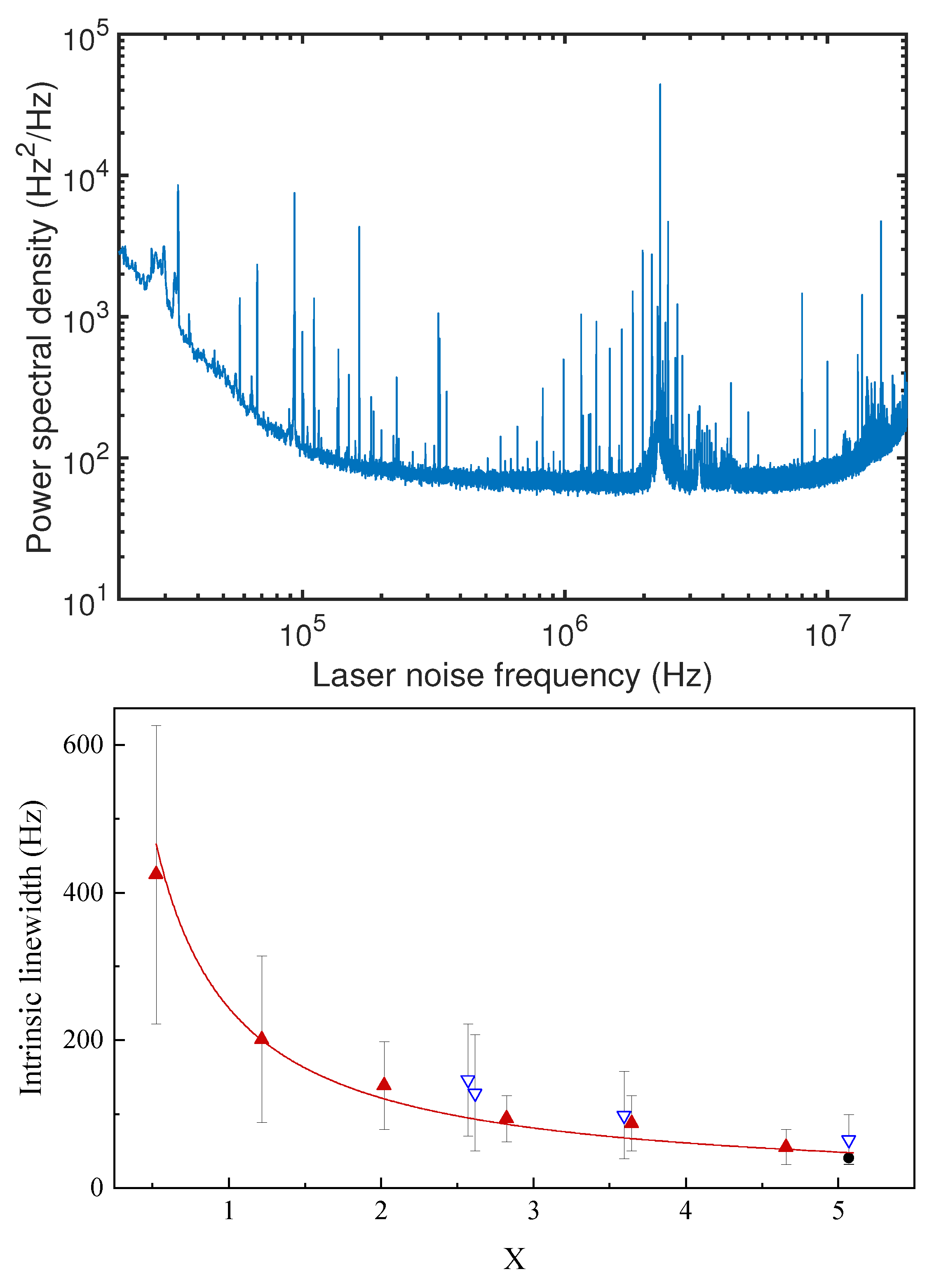
6. Hybrid Integrated Laser with Record-Low Linewidth
7. Dual-Wavelength, Multi-Wavelength and Visible Wavelength Lasers
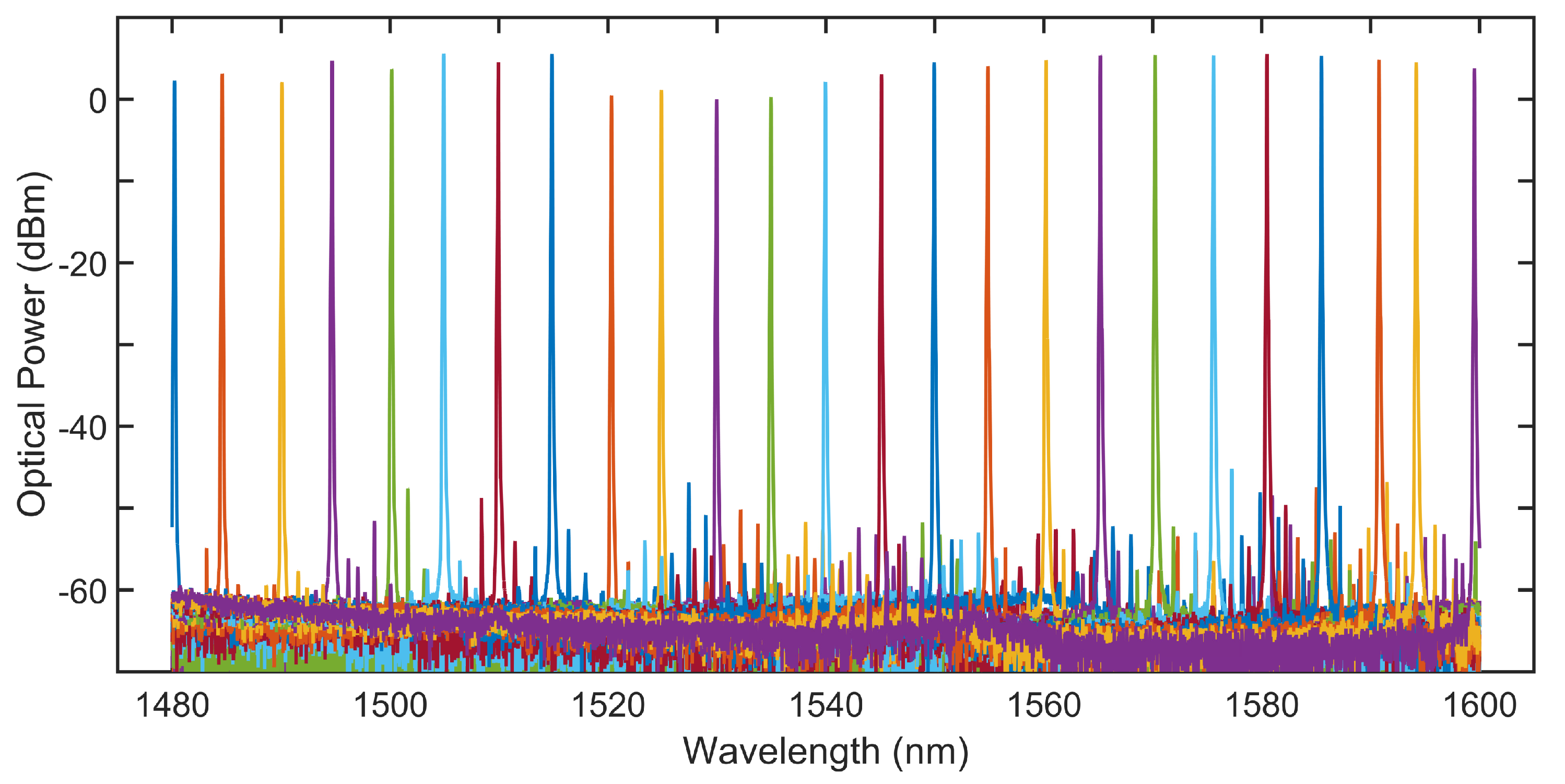
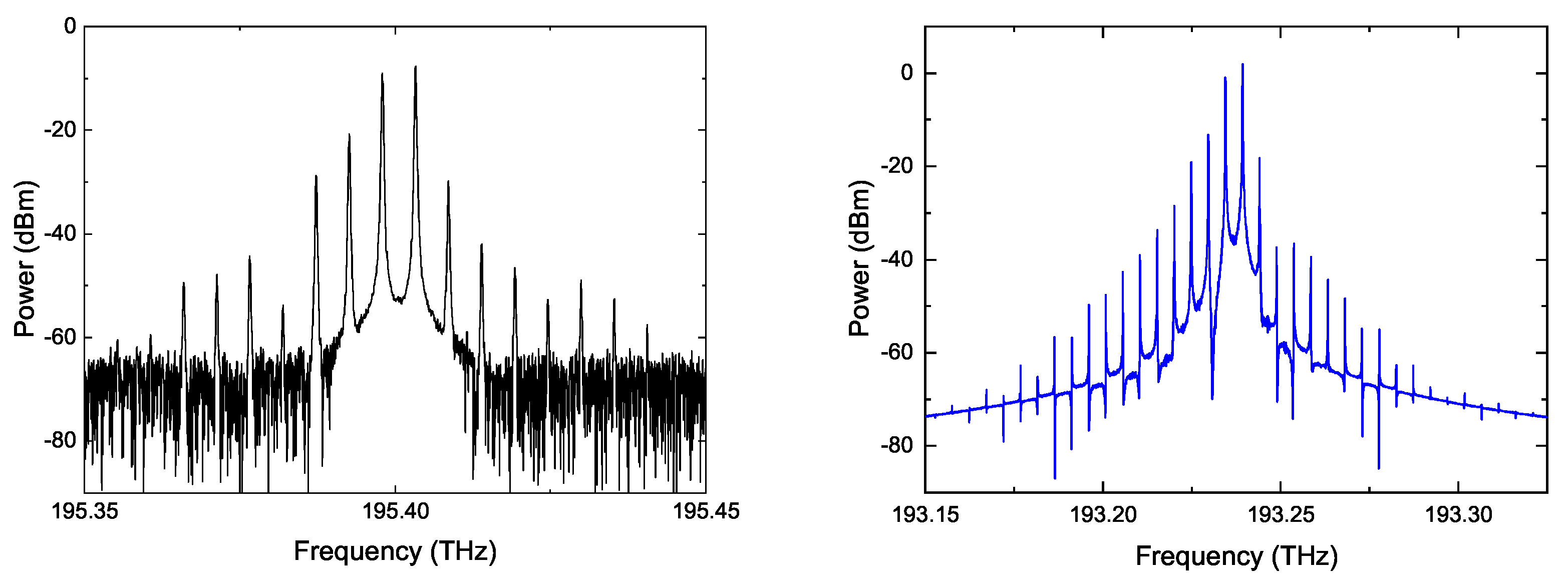
7.1. Diode Comb Lasers
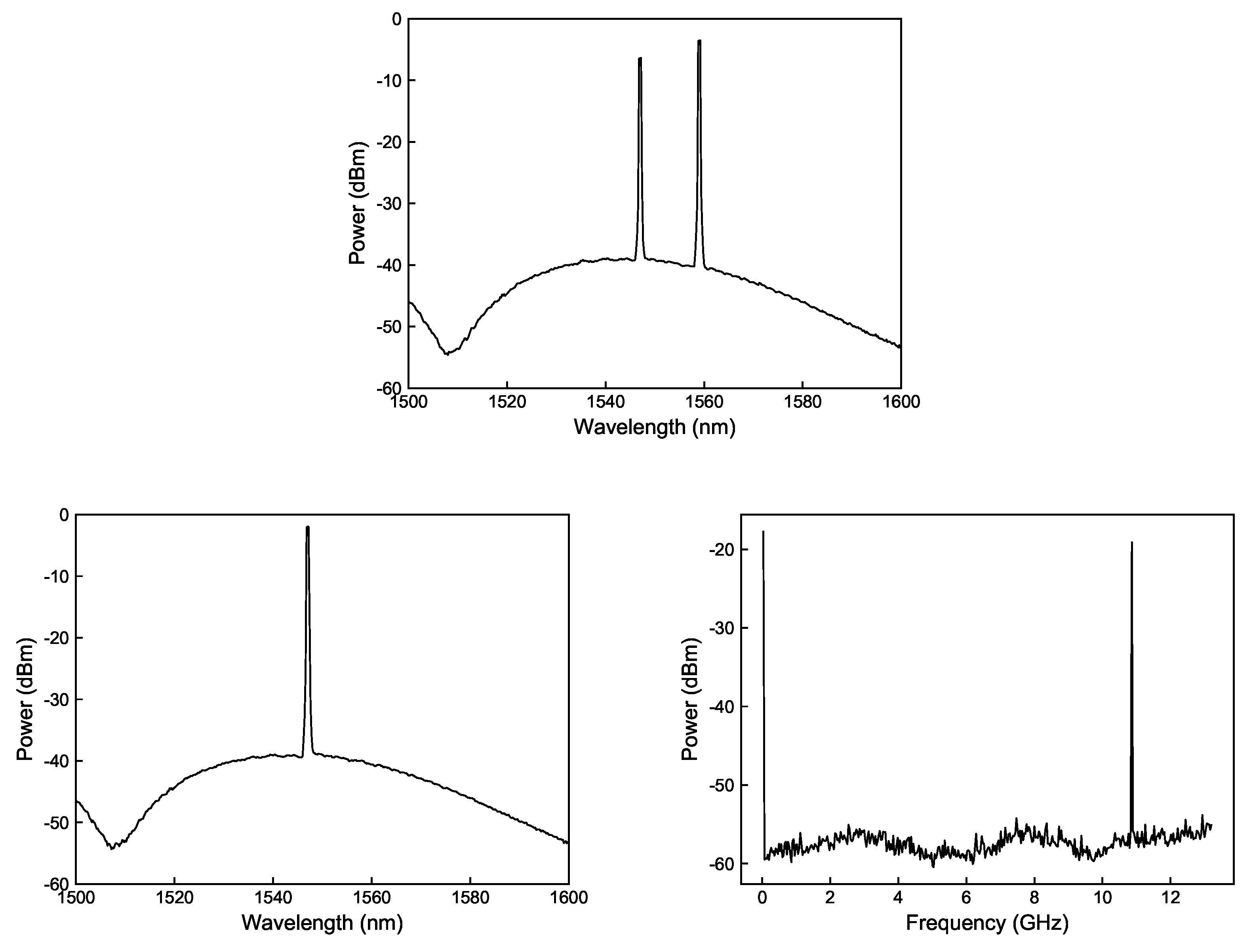
7.2. Dual-Wavelength Lasers
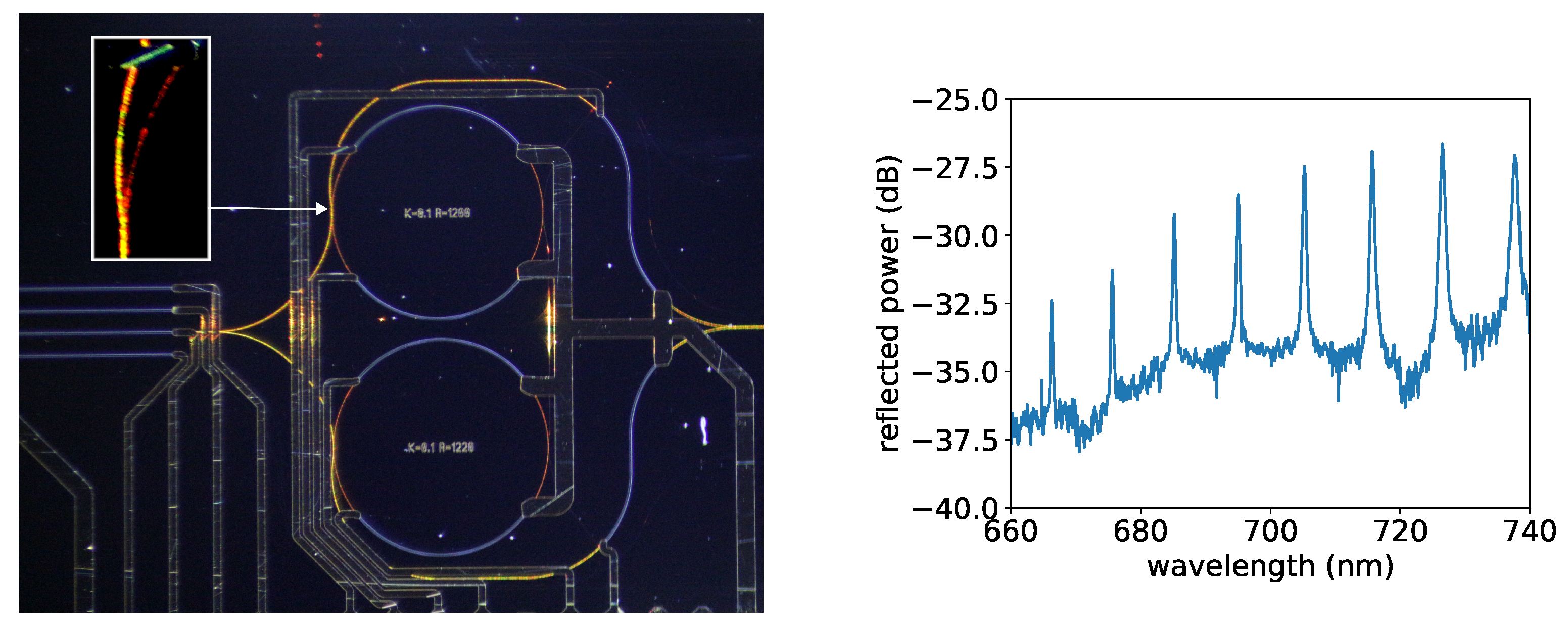
7.3. Visible Wavelength Hybrid Integrated Lasers
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Biesheuvel, J.; Karr, J.P.; Hilico, L.; Eikema, K.S.E.; Ubachs, W.; Koelemeij, J.C.J. Probing QED and fundamental constants through laser spectroscopy of vibrational transitions in HD+. Nat. Commun. 2016, 7, 10385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gabrielse, G.; Bowden, N.S.; Oxley, P.; Speck, A.; Storry, C.H.; Tan, J.N.; Wessels, M.; Grzonka, D.; Oelert, W.; Schepers, G.; et al. Background-free observation of cold antihydrogen with field-ionization analysis of its states. Phys. Rev. Lett. 2002, 89, 213401. [Google Scholar] [CrossRef] [Green Version]
- Hänsch, T.W.; Shahin, I.S.; Schawlow, A.L. Optical resolution of the Lamb shift in atomic hydrogen by laser saturation spectroscopy. Nat. Phys. Sci. 1972, 235, 63–65. [Google Scholar] [CrossRef]
- Bagdonaite, J.; Ubachs, W.; Murphy, M.T.; Whitmore, J.B. Analysis of molecular hydrogen absorption toward QSO B0642-5038 for a varying proton-to-electron mass ratio. Astrophys. J. 2014, 782, 10. [Google Scholar] [CrossRef] [Green Version]
- Crump, P.; Grimshaw, M.; Wang, J.; Dong, W.; Zhang, S.; Das, S.; Farmer, J.; DeVito, M.; Meng, L.S.; Brasseur, J.K. 85% power conversion efficiency 975-nm broad area diode lasers at −50 °C, 76% at 10 °C. In Proceedings of the 2006 Conference on Lasers and Electro-Optics and 2006 Quantum Electronics and Laser Science Conference, Long Beach, CA, USA, 21–26 May 2006; p. JWB24. [Google Scholar] [CrossRef]
- Leong, W.H.; Staszewski, W.J.; Lee, B.C.; Scarpa, F. Structural health monitoring using scanning laser vibrometry: III. Lamb waves for fatigue crack detection. Smart Mater. Struct. 2005, 14, 1387–1395. [Google Scholar] [CrossRef]
- Distributed Fiber Sensing of Pipelines, Oil and Gas Wells, Borders, Railways, Roadways, Power Plants or Utilities. Available online: http://www.optasense.com/wp-cont7nt/uploads/2015/01/FiberOpticAug14.pdf (accessed on 6 October 2019).
- Fiber Sensing in Aerospace, Automotive, High-Tech, Civil, Lifescience, or Pharmaceutical Applications. Available online: http://www.technobis.com (accessed on 6 October 2019).
- He, L.; Özdemir, Ş.; Zhu, J.; Kim, W.; Yang, L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nat. Nanotechnol. 2011, 6, 428–432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alalusi, M.; Brasil, P.; Lee, S.; Mols, P.; Stolpner, L.; Mehnert, A.; Li, S. Low noise planar external cavity laser for interferometric fiber optic sensors. In Proceedings of SPIE; Udd, E., Du, H.H., Wang, A., Eds.; SPIE: Bellingham, WA, USA, 2009; Volume 7316, pp. 235–247. [Google Scholar] [CrossRef]
- Rothberg, S.; Allen, M.; Castellini, P.; Maio, D.D.; Dirckx, J.; Ewins, D.; Halkon, B.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2017, 99, 11–22. [Google Scholar] [CrossRef] [Green Version]
- Hecht, J. Lidar for Self-Driving Cars. Opt. Photonics News 2018, 29, 26–33. [Google Scholar]
- Tran, M.A.; Komljenovic, T.; Hulme, J.C.; Kennedy, M.; Blumenthal, D.J.; Bowers, J.E. Integrated optical driver for interferometric optical gyroscopes. Opt. Express 2017, 25, 3826–3840. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, S.; Moreira, R.; Blumenthal, D.; Bowers, J.E. Design of integrated hybrid silicon waveguide optical gyroscope. Opt. Express 2014, 22, 24988–24993. [Google Scholar] [CrossRef]
- Gundavarapu, S.; Brodnik, G.M.; Puckett, M.; Huffman, T.; Bose, D.; Behunin, R.; Wu, J.; Qiu, T.; Pinho, C.; Chauhan, N.; et al. Sub-Hertz fundamental linewidth photonic integrated Brillouin laser. Nat. Photonics 2019, 13, 60–67. [Google Scholar] [CrossRef] [Green Version]
- Lezius, M.; Wilken, T.; Deutsch, C.; Giunta, M.; Mandel, O.; Thaller, A.; Schkolnik, V.; Schiemangk, M.; Dinkelaker, A.; Kohfeldt, A.; et al. Space-borne frequency comb metrology. Optica 2016, 3, 1381–1387. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Drake, T.; Stone, J.R.; Briles, T.C.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; et al. Architecture for the photonic integration of an optical atomic clock. Optica 2019, 6, 680–685. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Ludlow, A.; Lemke, N.; Fox, R.; Sherman, J.; Ma, L.S.; Oates, C. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nat. Photonics 2011, 5, 158–161. [Google Scholar] [CrossRef] [Green Version]
- GALILEO Begins Serving the Globe. Available online: https://www.esa.int (accessed on 6 October 2019).
- Gill, P. Optical frequency standards. Metrologia 2005, 42, S125–S137. [Google Scholar] [CrossRef]
- Spillane, S.M.; Kippenberg, T.J.; Vahala, K.J. Ultralow-threshold Raman laser using a spherical dielectric microcavity. Nature 2002, 415, 621–623. [Google Scholar] [CrossRef]
- Li, J.; Suh, M.G.; Vahala, K. Microresonator Brillouin gyroscope. Optica 2017, 4, 346–348. [Google Scholar] [CrossRef] [Green Version]
- Stern, B.; Ji, X.; Okawachi, Y.; Gaeta, A.L.; Lipson, M. Battery-operated integrated frequency comb generator. Nature 2018, 562, 401–405. [Google Scholar] [CrossRef] [Green Version]
- Raja, A.S.; Voloshin, A.S.; Guo, H.; Agafonova, S.E.; Liu, J.; Gorodnitskiy, A.S.; Karpov, M.; Pavlov, N.G.; Lucas, E.; Galiev, R.R.; et al. Electrically pumped photonic integrated soliton microcomb. Nat. Commun. 2019, 10, 680. [Google Scholar] [CrossRef]
- Pavlov, N.G.; Koptyaev, S.; Lihachev, G.V.; Voloshin, A.S.; Gorodnitskiy, A.S.; Ryabko, M.V.; Polonsky, S.V.; Gorodetsky, M.L. Narrow-linewidth lasing and soliton Kerr microcombs with ordinary laser diodes. Nat. Photonics 2018, 12, 694–698. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Van Gasse, K.; Moskalenko, V.; Latkowski, S.; Bente, E.; Kuyken, B.; Roelkens, G. A III-V-on-Si ultra-dense comb laser. Light Sci. Appl. 2017, 6, e16260. [Google Scholar] [CrossRef] [Green Version]
- Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and precise absolute distance measurements at long range. Nat. Photonics 2009, 3, 351–356. [Google Scholar] [CrossRef]
- Suh, M.G.; Vahala, K.J. Soliton microcomb range measurement. Science 2018, 359, 884–887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rieker, G.B.; Giorgetta, F.R.; Swann, W.C.; Kofler, J.; Zolot, A.M.; Sinclair, L.C.; Baumann, E.; Cromer, C.; Petron, G.; Sweeney, C.; et al. Frequency-comb-based remote sensing of greenhouse gases over kilometer air paths. Optica 2014, 1, 290–298. [Google Scholar] [CrossRef]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef] [Green Version]
- Bao, C.; Suh, M.G.; Vahala, K. Microresonator soliton dual-comb imaging. Optica 2019, 6, 1110–1116. [Google Scholar] [CrossRef]
- Spencer, D.T.; Drake, T.; Briles, T.C.; Stone, J.; Sinclair, L.C.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; Bluestone, A.; et al. An optical-frequency synthesizer using integrated photonics. Nature 2018, 557, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Reimer, C.; Zhang, Y.; Roztocki, P.; Sciara, S.; Cortés, L.R.; Islam, M.; Fischer, B.; Wetzel, B.; Cino, A.C.; Chu, S.T.; et al. On-chip frequency combs and telecommunications signal processing meet quantum optics. Front. Optoelectron. 2018, 11, 134–147. [Google Scholar] [CrossRef] [Green Version]
- Kikuchi, K. Fundamentals of coherent optical fiber communications. J. Lightwave Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Yue, Y.; Wang, Q.; Anderson, J. Experimental investigation of 400 Gb/s data center interconnect using unamplified high-baud-rate and high-order QAM single-carrier signal. Appl. Sci. 2019, 9, 2455. [Google Scholar] [CrossRef] [Green Version]
- Winzer, P.J.; Essiambre, R.J. Advanced optical modulation formats. Proc. IEEE 2006, 94, 952–985. [Google Scholar] [CrossRef]
- Zhang, S.; Kam, P.Y.; Yu, C.; Chen, J. Laser linewidth tolerance of decision-aided maximum likelihood phase estimation in coherent optical M-ary PSK and QAM systems. IEEE Photonics Technol. Lett. 2009, 21, 1075–1077. [Google Scholar] [CrossRef]
- Beppu, S.; Kasai, K.; Yoshida, M.; Nakazawa, M. 2048 QAM (66 Gbit/s) single-carrier coherent optical transmission over 150 km with a potential SE of 15.3 bit/s/Hz. In Proceedings of the Optical Fiber Communication Conference 2014 (OFC 2014), San Francisco, CA, USA, 9–13 March 2014; p. W1A.6. [Google Scholar] [CrossRef]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seeds, A.J.; Williams, K.J. Microwave photonics. J. Lightwave Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photonics 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Zhuang, L.; Meijerink, A.; Roeloffzen, C.G.H.; Marpaung, D.A.I.; Heideman, R.G.; Hoekman, M.; Leinse, A.; van Etten, W. Novel ring resonator-based optical beamformer for broadband phased array receive antennas. In Proceedings of the 21st Annual Meeting of the IEEE Lasers and Electro-Optics Society (LEOS 2008), Newport Beach, CA, USA, 9–13 November 2008; pp. 20–21. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, L.; Marpaung, D.; Burla, M.; Beeker, W.; Leinse, A.; Roeloffzen, C. Low-loss, high-index-contrast Si3N4/SiO2 optical waveguides for optical delay lines in microwave photonics signal processing. Opt. Express 2011, 19, 23162–23170. [Google Scholar] [CrossRef] [Green Version]
- Burla, M.; Cortés, L.R.; Li, M.; Wang, X.; Chrostowski, L.; Azaña, J. Integrated waveguide Bragg gratings for microwave photonics signal processing. Opt. Express 2013, 21, 25120–25147. [Google Scholar] [CrossRef]
- Marpaung, D.; Morrison, B.; Pagani, M.; Pant, R.; Choi, D.Y.; Luther-Davies, B.; Madden, S.J.; Eggleton, B.J. Low-power, chip-based stimulated Brillouin scattering microwave photonic filter with ultrahigh selectivity. Optica 2015, 2, 76–83. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J. Integrated microwave photonics. Nat. Photonics 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Khilo, A.; Spector, S.J.; Grein, M.E.; Nejadmalayeri, A.H.; Holzwarth, C.W.; Sander, M.Y.; Dahlem, M.S.; Peng, M.Y.; Geis, M.W.; DiLello, N.A.; et al. Photonic ADC: Overcoming the bottleneck of electronic jitter. Opt. Express 2012, 20, 4454–4469. [Google Scholar] [CrossRef]
- Carpintero, G.; Rouvalis, E.; awniczuk, K.; Fice, M.; Renaud, C.C.; Leijtens, X.J.M.; Bente, E.A.J.M.; Chitoui, M.; Dijk, F.V.; Seeds, A.J. 95 GHz millimeter wave signal generation using an arrayed waveguide grating dual wavelength semiconductor laser. Opt. Lett. 2012, 37, 3657–3659. [Google Scholar] [CrossRef] [PubMed]
- Seeds, A.J.; Shams, H.; Fice, M.J.; Renaud, C.C. TeraHertz photonics for wireless communications. J. Lightwave Technol. 2015, 33, 579–587. [Google Scholar] [CrossRef]
- Lang, R.; Vahala, K.; Yariv, A. The effect of spatially dependent temperature and carrier fluctuations on noise in semiconductor lasers. IEEE J. Quantum Electron. 1985, 21, 443–451. [Google Scholar] [CrossRef] [Green Version]
- Rutman, J. Characterization of phase and frequency instabilities in precision frequency sources: Fifteen years of progress. Proc. IEEE 1978, 66, 1048–1075. [Google Scholar] [CrossRef]
- Thomson, D.J. Spectrum estimation and harmonic analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef] [Green Version]
- Domenico, G.D.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef] [PubMed]
- Barnes, J.A.; Chi, A.R.; Cutler, L.S.; Healey, D.J.; Leeson, D.B.; McGunigal, T.E.; Mullen, J.A.; Smith, W.L.; Sydnor, R.L.; Vessot, R.F.C.; et al. Characterization of frequency stability. IEEE Trans. Instrum. Meas. 1971, IM-20, 105–120. [Google Scholar] [CrossRef] [Green Version]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef] [Green Version]
- Fleming, M.W.; Mooradian, A. Fundamental line broadening of single-mode (GaAl)As diode lasers. Appl. Phys. Lett. 1981, 38, 511–513. [Google Scholar] [CrossRef]
- Henry, C. Theory of the linewidth of semiconductor lasers. IEEE J. Quantum Electron. 1982, 18, 259–264. [Google Scholar] [CrossRef]
- Wiseman, H.M. Light amplification without stimulated emission: Beyond the standard quantum limit to the laser linewidth. Phys. Rev. A 1999, 60, 4083–4093. [Google Scholar] [CrossRef] [Green Version]
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Day, T.; Gustafson, E.K.; Byer, R.L. Sub-hertz relative frequency stabilization of two-diode laser-pumped Nd:YAG lasers locked to a Fabry-Pérot interferometer. IEEE J. Quantum Electron. 1992, 28, 1106–1117. [Google Scholar] [CrossRef]
- Lin, Q.; Camp, M.A.V.; Zhang, H.; Jelenković, B.; Vuletić, V. Long-external-cavity distributed Bragg reflector laser with subkilohertz intrinsic linewidth. Opt. Lett. 2012, 37, 1989–1991. [Google Scholar] [CrossRef] [Green Version]
- Ward, A.J.; Robbins, D.J.; Busico, G.; Barton, E.; Ponnampalam, L.; Duck, J.P.; Whitbread, N.D.; Williams, P.J.; Reid, D.C.J.; Carter, A.C.; et al. Widely tunable DS-DBR laser with monolithically integrated SOA: design and performance. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 149–156. [Google Scholar] [CrossRef]
- Lavery, D.; Maher, R.; Millar, D.S.; Thomsen, B.C.; Bayvel, P.; Savory, S.J. Digital coherent receivers for long-reach optical access networks. J. Lightwave Technol. 2013, 31, 609–620. [Google Scholar] [CrossRef]
- Akulova, Y.A.; Fish, G.A.; Koh, P.C.; Schow, C.L.; Kozodoy, P.; Dahl, A.P.; Nakagawa, S.; Larson, M.C.; Mack, M.P.; Strand, T.A.; et al. Widely tunable electroabsorption-modulated sampled-grating DBR laser transmitter. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 1349–1357. [Google Scholar] [CrossRef]
- Okai, M.; Tsuchiya, T.; Uomi, K.; Chinone, N.; Harada, T. Corrugation-pitch-modulated MQW-DFB laser with narrow spectral linewidth (170 kHz). IEEE Photonics Technol. Lett. 1990, 2, 529–530. [Google Scholar] [CrossRef]
- Price, R.K.; Borchardt, J.J.; Elarde, V.C.; Swint, R.B.; Coleman, J.J. Narrow-linewidth asymmetric cladding distributed Bragg reflector semiconductor lasers at 850 nm. IEEE Photonics Technol. Lett. 2006, 18, 97–99. [Google Scholar] [CrossRef]
- Spießberger, S.; Schiemangk, M.; Wicht, A.; Wenzel, H.; Erbert, G.; Tränkle, G. DBR laser diodes emitting near 1064 nm with a narrow intrinsic linewidth of 2 kHz. Appl. Phys. B 2011, 104, 813. [Google Scholar] [CrossRef]
- Tunable Diode Lasers, Toptica Photonics Application Notes. Available online: https://www.toptica.com/fileadmin/Editors_English/11_brochures_datasheets/01_brochures/toptica_BR_Scientific_Lasers.pdf (accessed on 18 October 2019).
- Luvsandamdin, E.; Kürbis, C.; Schiemangk, M.; Sahm, A.; Wicht, A.; Peters, A.; Erbert, G.; Tränkle, G. Micro-integrated extended cavity diode lasers for precision potassium spectroscopy in space. Opt. Express 2014, 22, 7790–7798. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Ilchenko, V.S.; Eliyahu, D.; Savchenkov, A.A.; Matsko, A.B.; Seidel, D.; Maleki, L. Ultralow noise miniature external cavity semiconductor laser. Nat. Commun. 2015, 6, 7371. [Google Scholar] [CrossRef] [PubMed]
- Wei, F.; Yang, F.; Zhang, X.; Xu, D.; Ding, M.; Zhang, L.; Chen, D.; Cai, H.; Fang, Z.; Xijia, G. Subkilohertz linewidth reduction of a DFB diode laser using self-injection locking with a fiber Bragg grating Fabry-Pérot cavity. Opt. Express 2016, 24, 17406–17415. [Google Scholar] [CrossRef] [PubMed]
- Morton, P.A.; Morton, M.J. High-power, ultra-low noise hybrid lasers for microwave photonics and optical sensing. J. Lightwave Technol. 2018, 36, 5048–5057. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Stuhler, J.; Schuricht, G.; Lison, F.; Lu, Z.; Wang, L. Sub-Hertz frequency stabilization of a commercial diode laser. Opt. Commun. 2010, 283, 4696–4700. [Google Scholar] [CrossRef] [Green Version]
- Alnis, J.; Matveev, A.; Kolachevsky, N.; Udem, T.; Hänsch, T.W. Subhertz linewidth diode lasers by stabilization to vibrationally and thermally compensated ultralow-expansion glass Fabry-Pérot cavities. Phys. Rev. A 2008, 77, 053809. [Google Scholar] [CrossRef] [Green Version]
- Stoehr, H.; Mensing, F.; Helmcke, J.; Sterr, U. Diode laser with 1 Hz linewidth. Opt. Lett. 2006, 31, 736–738. [Google Scholar] [CrossRef]
- Roeloffzen, C.G.H.; Zhuang, L.; Taddei, C.; Leinse, A.; Heideman, R.G.; van Dijk, P.W.L.; Oldenbeuving, R.M.; Marpaung, D.A.I.; Burla, M.; Boller, K.J. Silicon nitride microwave photonic circuits. Opt. Express 2013, 21, 22937–22961. [Google Scholar] [CrossRef] [Green Version]
- Marpaung, D.; Roeloffzen, C.; Heideman, R.; Leinse, A.; Sales, S.; Capmany, J. Integrated microwave photonics. Laser Photonics Rev. 2013, 7, 506–538. [Google Scholar] [CrossRef] [Green Version]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Davenport, M.L.; Coldren, L.A.; Bowers, J.E. Hybrid III-V silicon photonic source with integrated 1D free-space beam steering. Opt. Lett. 2012, 37, 4257–4259. [Google Scholar] [CrossRef]
- Matsumoto, T.; Suzuki, A.; Takahashi, M.; Watanabe, S.; Ishii, S.; Suzuki, K.; Kaneko, T.; Yamazaki, H.; Sakuma, N. Narrow spectral linewidth full band tunable laser based on waveguide ring resonators with low power consumption. In Proceedings of the Optical Fiber Communication Conference 2010, San Diego, CA, USA, 21–25 March 2010; Optical Society of America: Washington, DC, USA, 2010; p. OThQ5. [Google Scholar] [CrossRef]
- Nemoto, K.; Kita, T.; Yamada, H. Narrow-spectral-linewidth wavelength-tunable laser diode with Si wire waveguide ring resonators. Appl. Phys. Express 2012, 5, 082701. [Google Scholar] [CrossRef]
- Oldenbeuving, R.M.; Klein, E.J.; Offerhaus, H.L.; Lee, C.J.; Song, H.; Boller, K.J. 25 kHz narrow spectral bandwidth of a wavelength tunable diode laser with a short waveguide-based external cavity. Laser Phys. Lett. 2013, 10, 015804. [Google Scholar] [CrossRef] [Green Version]
- Keyvaninia, S.; Roelkens, G.; Thourhout, D.V.; Jany, C.; Lamponi, M.; Liepvre, A.L.; Lelarge, F.; Make, D.; Duan, G.H.; Bordel, D.; et al. Demonstration of a heterogeneously integrated III-V/SOI single wavelength tunable laser. Opt. Express 2013, 21, 3784–3792. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hulme, J.C.; Doylend, J.K.; Bowers, J.E. Widely tunable Vernier ring laser on hybrid silicon. Opt. Express 2013, 21, 19718–19722. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Y.; Grund, D.W.; Ejzak, G.A.; Liu, Y.; Novack, A.; Prather, D.; Lim, A.E.J.; Lo, G.Q.; Baehr-Jones, T.; et al. A single adiabatic microring-based laser in 220 nm silicon-on-insulator. Opt. Express 2014, 22, 1172–1180. [Google Scholar] [CrossRef]
- Santis, C.T.; Steger, S.T.; Vilenchik, Y.; Vasilyev, A.; Yariv, A. High-coherence semiconductor lasers based on integral high-Q resonators in hybrid Si/III-V platforms. Proc. Natl. Acad. Sci. USA 2014, 111, 2879–2884. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Oldenbeuving, R.M.; Klein, E.J.; Lee, C.J.; Song, H.; Khan, M.R.H.; Offerhaus, H.L.; van der Slot, P.J.M.; Boller, K.J. A hybrid semiconductor-glass waveguide laser. In Proceedings of SPIE; Mackenzie, J.I., Jelínková, H., Taira, T., Ahmed, M.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2014; Volume 9135, p. 91351B. [Google Scholar] [CrossRef] [Green Version]
- Duan, G.; Jany, C.; Liepvre, A.L.; Accard, A.; Lamponi, M.; Make, D.; Kaspar, P.; Levaufre, G.; Girard, N.; Lelarge, F.; et al. Hybrid III-V on silicon lasers for photonic integrated circuits on silicon. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 158–170. [Google Scholar] [CrossRef] [Green Version]
- De Felipe, D.; Zhang, Z.; Brinker, W.; Kleinert, M.; Novo, A.M.; Zawadzki, C.; Moehrle, M.; Keil, N. Polymer-based external cavity Lasers: Tuning efficiency, reliability, and polarization diversity. IEEE Photonics Technol. Lett. 2014, 26, 1391–1394. [Google Scholar] [CrossRef]
- Kita, T.; Nemoto, K.; Yamada, H. Silicon photonic wavelength-tunable laser diode with asymmetric Mach–Zehnder interferometer. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 344–349. [Google Scholar] [CrossRef]
- Dong, P.; Hu, T.C.; Liow, T.Y.; Chen, Y.K.; Xie, C.; Luo, X.; Lo, G.Q.; Kopf, R.; Tate, A. Novel integration technique for silicon/III-V hybrid laser. Opt. Express 2014, 22, 26854–26861. [Google Scholar] [CrossRef]
- Debregeas, H.; Ferrari, C.; Cappuzzo, M.A.; Klemens, F.; Keller, R.; Pardo, F.; Bolle, C.; Xie, C.; Earnshaw, M.P. 2 kHz linewidth C-band tunable laser by hybrid integration of reflective SOA and SiO2 PLC external cavity. In Proceedings of the 2014 International Semiconductor Laser Conference, Palma de Mallorca, Spain, 7–10 September 2014; pp. 50–51. [Google Scholar] [CrossRef]
- Kobayashi, N.; Sato, K.; Namiwaka, M.; Yamamoto, K.; Watanabe, S.; Kita, T.; Yamada, H.; Yamazaki, H. Silicon photonic hybrid ring-filter external cavity wavelength tunable lasers. J. Lightwave Technol. 2015, 33, 1241–1246. [Google Scholar] [CrossRef]
- Tang, R.; Kita, T.; Yamada, H. Narrow-spectral-linewidth silicon photonic wavelength-tunable laser with highly asymmetric Mach–Zehnder interferometer. Opt. Lett. 2015, 40, 1504–1507. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, S.; Davenport, M.; Komljenovic, T.; Hulme, J.; Spencer, D.T.; Bowers, J.E. Coupled-ring-resonator-mirror-based heterogeneous III/V silicon tunable laser. IEEE Photonics J. 2015, 7, 1–8. [Google Scholar] [CrossRef]
- Santis, C.T.; Vilenchik, Y.; Yariv, A.; Satyan, N.; Rakuljic, G. Sub-kHz quantum linewidth semiconductor laser on silicon chip. In Proceedings of the Conference on Applications and Technology 2015 (CLEO), San Jose, CA, USA, 10–15 May 2015; CLEO: 2015 Postdeadline Paper Digest. Optical Society of America: Washington, DC, USA, 2015; p. JTh5A.7. [Google Scholar] [CrossRef]
- Komljenovic, T.; Srinivasan, S.; Norberg, E.; Davenport, M.; Fish, G.; Bowers, J.E. Widely tunable narrow-linewidth monolithically integrated external-cavity semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 214–222. [Google Scholar] [CrossRef]
- Kita, T.; Tang, R.; Yamada, H. Narrow spectral linewidth silicon photonic wavelength tunable laser diode for digital coherent communication system. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 23–34. [Google Scholar] [CrossRef]
- Fan, Y.; Oldenbeuving, R.M.; Roeloffzen, C.G.; Hoekman, M.; Geskus, D.; Heideman, R.G.; Boller, K.J. 290 Hz intrinsic linewidth from an integrated optical chip-based Widely tunable InP-Si3N4 hybrid laser. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 14–19 May 2017; Optical Society of America: Washington, DC, USA, 2017; p. JTh5C.9. [Google Scholar] [CrossRef]
- Komljenovic, T.; Liu, S.; Norberg, E.; Fish, G.A.; Bowers, J.E. Control of widely tunable lasers with high-Q resonator as an integral part of the cavity. J. Lightwave Technol. 2017, 35, 3934–3939. [Google Scholar] [CrossRef]
- Stern, B.; Ji, X.; Dutt, A.; Lipson, M. Compact narrow-linewidth integrated laser based on a low-loss silicon nitride ring resonator. Opt. Lett. 2017, 42, 4541–4544. [Google Scholar] [CrossRef]
- Verdier, A.; de Valicourt, G.; Brenot, R.; Debregeas, H.; Dong, P.; Earnshaw, M.; Carrère, H.; Chen, Y. Ultrawideband wavelength-tunable hybrid external-cavity lasers. J. Lightwave Technol. 2018, 36, 37–43. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Chen, H.; Yang, S.; Chen, M. Tunable self-injected Fabry-Pérot laser diode coupled to an external high-Q Si3N4/SiO2 microring resonator. J. Lightwave Technol. 2018, 36, 3269–3274. [Google Scholar] [CrossRef]
- Tran, M.A.; Huang, D.; Komljenovic, T.; Liu, S.; Liang, L.; Kennedy, M.; Bowers, J.E. Multi-ring mirror-based narrow-linewidth widely-tunable lasers in heterogeneous silicon photonics. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Zhu, Y.; Zeng, S.; Zhao, X.; Zhao, Y.; Zhu, L. Narrow-linewidth, tunable external cavity diode lasers through hybrid integration of quantum-well/quantum-dot SOAs with Si3N4 microresonators. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 13–18 May 2018; Optical Society of America: Washington, DC, USA, 2018; p. SW4B.2. [Google Scholar] [CrossRef]
- Huang, D.; Tran, M.A.; Guo, J.; Peters, J.; Komljenovic, T.; Malik, A.; Morton, P.A.; Bowers, J.E. High-power sub-kHz linewidth lasers fully integrated on silicon. Optica 2019, 6, 745–752. [Google Scholar] [CrossRef] [Green Version]
- Xiang, C.; Morton, P.A.; Bowers, J.E. Ultra-narrow linewidth laser based on a semiconductor gain chip and extended Si3N4 Bragg grating. Opt. Lett. 2019, 44, 3825–3828. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; van Rees, A.; van der Slot, P.J.M.; Mak, J.; Oldenbeuving, R.; Hoekman, M.; Geskus, D.; Roeloffzen, C.G.H.; Boller, K.J. Ultra-Narrow Linewidth Hybrid Integrated Semiconductor Laser. arXiv 2019, arXiv:1910.08141. [Google Scholar]
- Santis, C.T.; Vilenchik, Y.; Satyan, N.; Rakuljic, G.; Yariv, A. Quantum control of phase fluctuations in semiconductor lasers. Proc. Natl. Acad. Sci. USA 2018, 115, E7896–E7904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klein, H.; Wagner, C.; Brinker, W.; Soares, F.; de Felipe, D.; Zhang, Z.; Zawadzki, C.; Keil, N.; Moehrle, M. Hybrid InP-polymer 30 nm tunable DBR laser for 10 Gbit/s direct modulation in the C-band. In Proceedings of the 2012 International Conference on Indium Phosphide and Related Materials, Santa Barbara, CA, USA, 27–30 August 2012; pp. 20–21. [Google Scholar] [CrossRef]
- Numata, K.; Camp, J.; Krainak, M.A.; Stolpner, L. Performance of planar-waveguide external cavity laser for precision measurements. Opt. Express 2010, 18, 22781–22788. [Google Scholar] [CrossRef] [PubMed]
- Numata, K.; Camp, J. Precision laser development for interferometric space missions NGO, SGO, and GRACE Follow-On. J. Phys. Conf. Ser. 2012, 363, 012054. [Google Scholar] [CrossRef] [Green Version]
- Kita, T.; Tang, R.; Yamada, H. Compact silicon photonic wavelength-tunable laser diode with ultra-wide wavelength tuning range. Appl. Phys. Lett. 2015, 106, 111104. [Google Scholar] [CrossRef]
- Tran, M.A.; Huang, D.; Guo, J.; Komljenovic, T.; Morton, P.A.; Bowers, J.E. Ring-resonator based widely-tunable narrow-linewidth Si/InP integrated lasers. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500514. [Google Scholar] [CrossRef]
- Roelkens, G.; Liu, L.; Liang, D.; Jones, R.; Fang, A.; Koch, B.; Bowers, J. III-V/silicon photonics for on-chip and intra-chip optical interconnects. Laser Photonics Rev. 2010, 4, 751–779. [Google Scholar] [CrossRef]
- Yariv, A.; Sun, X. Supermode Si/III-V hybrid lasers, optical amplifiers and modulators: A proposal and analysis. Opt. Express 2007, 15, 9147–9151. [Google Scholar] [CrossRef] [Green Version]
- Vilenchik, Y.; Santis, C.T.; Steger, S.T.; Satyan, N.; Yariv, A. Theory and observation on non-linear effects limiting the coherence properties of high-Q hybrid Si/III-V lasers. In Proceedings SPIE; Belyanin, A.A., Smowton, P.M., Eds.; SPIE: Bellingham, WA, USA, 2015; Volume 9382, p. 93820N. [Google Scholar]
- Kuyken, B.; Leo, F.; Clemmen, S.; Dave, U.; Van Laer, R.; Ideguchi, T.; Zhao, H.; Liu, X.; Safioui, J.; Coen, S.; et al. Nonlinear optical interactions in silicon waveguides. Nanophotonics 2017, 6, 377–392. [Google Scholar] [CrossRef] [Green Version]
- Taballione, C.; Wolterink, T.A.W.; Lugani, J.; Eckstein, A.; Bell, B.A.; Grootjans, R.; Visscher, I.; Geskus, D.; Roeloffzen, C.G.H.; Renema, J.J.; et al. 8×8 reconfigurable quantum photonic processor based on silicon nitride waveguides. Opt. Express 2019, 27, 26842–26857. [Google Scholar] [CrossRef] [PubMed]
- Poberaj, G.; Hu, H.; Sohler, W.; Günter, P. Lithium niobate on insulator (LNOI) for micro-photonic devices. Laser Photonics Rev. 2012, 6, 488–503. [Google Scholar] [CrossRef]
- Chang, L.; Pfeiffer, M.H.P.; Volet, N.; Zervas, M.; Peters, J.D.; Manganelli, C.L.; Stanton, E.J.; Li, Y.; Kippenberg, T.J.; Bowers, J.E. Heterogeneous integration of lithium niobate and silicon nitride waveguides for wafer-scale photonic integrated circuits on silicon. Opt. Lett. 2017, 42, 803–806. [Google Scholar] [CrossRef] [PubMed]
- Belt, M.; Davenport, M.L.; Bowers, J.E.; Blumenthal, D.J. Ultra-low-loss Ta2O5-core/SiO2-clad planar waveguides on Si substrates. Optica 2017, 4, 532–536. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.; Xiong, C.; Fong, K.Y.; Zhang, X.; Tang, H.X. Optical frequency comb generation from aluminum nitride microring resonator. Opt. Lett. 2013, 38, 2810–2813. [Google Scholar] [CrossRef] [Green Version]
- Roeloffzen, C.G.H.; Hoekman, M.; Klein, E.J.; Wevers, L.S.; Timens, R.B.; Marchenko, D.; Geskus, D.; Dekker, R.; Alippi, A.; Grootjans, R.; et al. Low-loss Si3N4 TriPleX optical waveguides: Technology and applications overview. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Fleming, M.; Mooradian, A. Spectral characteristics of external-cavity controlled semiconductor lasers. IEEE J. Quantum Electron. 1981, 17, 44–59. [Google Scholar] [CrossRef]
- Komljenovic, T.; Liang, L.; Chao, R.L.; Hulme, J.; Srinivasan, S.; Davenport, M.; Bowers, J.E. Widely-tunable ring-resonator semiconductor lasers. Appl. Sci. 2017, 7, 732. [Google Scholar] [CrossRef]
- Javaloyes, J.; Balle, S. Freetwm: A Simulation Tool for Semiconductor Lasers. Available online: https://onl.uib.eu/Softwares/Download/ (accessed on 20 October 2019).
- VPI Component Maker Photonics. Available online: https://www.vpiphotonics.com/Tools/PhotonicCircuits/ (accessed on 20 October 2019).
- Fan, Y.; Lammerink, R.E.M.; Mak, J.; Oldenbeuving, R.M.; van der Slot, P.J.M.; Boller, K.J. Spectral linewidth analysis of semiconductor hybrid lasers with feedback from an external waveguide resonator circuit. Opt. Express 2017, 25, 32767–32782. [Google Scholar] [CrossRef] [Green Version]
- Henry, C. Theory of spontaneous emission noise in open resonators and its application to lasers and optical amplifiers. J. Lightwave Technol. 1986, 4, 288–297. [Google Scholar] [CrossRef]
- Patzak, E.; Sugimura, A.; Saito, S.; Mukai, T.; Olesen, H. Semiconductor laser linewidth in optical feedback configurations. Electron. Lett. 1983, 19, 1026–1027. [Google Scholar] [CrossRef]
- Kazarinov, R.; Henry, C. The relation of line narrowing and chirp reduction resulting from the coupling of a semiconductor laser to passive resonator. IEEE J. Quantum Electron. 1987, 23, 1401–1409. [Google Scholar] [CrossRef]
- Koch, T.L.; Koren, U. Semiconductor lasers for coherent optical fiber communications. J. Lightwave Technol. 1990, 8, 274–293. [Google Scholar] [CrossRef]
- Ujihara, K. Phase noise in a laser with output coupling. IEEE J. Quantum Electron. 1984, 20, 814–818. [Google Scholar] [CrossRef]
- Bjork, G.; Nilsson, O. A tool to calculate the linewidth of complicated semiconductor lasers. IEEE J. Quantum Electron. 1987, 23, 1303–1313. [Google Scholar] [CrossRef]
- Vahala, K.; Chiu, L.C.; Margalit, S.; Yariv, A. On the linewidth enhancement factor α in semiconductor injection lasers. Appl. Phys. Lett. 1983, 42, 631–633. [Google Scholar] [CrossRef]
- Vahala, K.; Yariv, A. Detuned loading in coupled cavity semiconductor lasers—Effect on quantum noise and dynamics. Appl. Phys. Lett. 1984, 45, 501–503. [Google Scholar] [CrossRef] [Green Version]
- Newkirk, M.A.; Vahala, K.J. Amplitude-phase decorrelation: A method for reducing intensity noise in semiconductor lasers. IEEE J. Quantum Electron. 1991, 27, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Hao, T.; Li, W.; Domenech, D.; Baños, R.; Muñoz, P.; Zhu, N.; Capmany, J.; Li, M. Integrated optoelectronic oscillator. Opt. Express 2018, 26, 12257–12265. [Google Scholar] [CrossRef]
- Fan, Y.; Epping, J.P.; Oldenbeuving, R.M.; Roeloffzen, C.G.H.; Hoekman, M.; Dekker, R.; Heideman, R.G.; van der Slot, P.J.M.; Boller, K.J. Optically integrated InP-Si3N4 hybrid laser. IEEE Photonics J. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Bauters, J.F.; Heck, M.J.R.; John, D.D.; Barton, J.S.; Bruinink, C.M.; Leinse, A.; Heideman, R.G.; Blumenthal, D.J.; Bowers, J.E. Planar waveguides with less than 0.1 dB/m propagation loss fabricated with wafer bonding. Opt. Express 2011, 19, 24090–24101. [Google Scholar] [CrossRef]
- Taddei, C.; Zhuang, L.; Roeloffzen, C.G.H.; Hoekman, M.; Boller, K. High-selectivity on-chip optical bandpass filter with sub-100-MHz flat-top and under-2 shape factor. IEEE Photonics Technol. Lett. 2019, 31, 455–458. [Google Scholar] [CrossRef]
- Buus, J.; Amann, M.C.; Blumenthal, D.J. Tunable Diode Lasers and Related Optical Sources; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lin, Y.; Browning, C.; Timens, R.B.; Geuzebroek, D.H.; Roeloffzen, C.G.H.; Hoekman, M.; Geskus, D.; Oldenbeuving, R.M.; Heideman, R.G.; Fan, Y.; et al. Characterization of hybrid InP-TriPleX photonic integrated tunable lasers based on silicon nitride (Si3N4/SiO2) microring resonators for optical coherent system. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Latkowski, S.; Hänsel, A.; Bhattacharya, N.; de Vries, T.; Augustin, L.; Williams, K.; Smit, M.; Bente, E. Novel widely tunable monolithically integrated laser source. IEEE Photonics J. 2015, 7, 1–9. [Google Scholar] [CrossRef]
- Stéphan, G.M.; Tam, T.T.; Blin, S.; Besnard, P.; Têtu, M. Laser line shape and spectral density of frequency noise. Phys. Rev. A 2005, 71, 043809. [Google Scholar] [CrossRef] [Green Version]
- Llopis, O.; Merrer, P.H.; Brahimi, H.; Saleh, K.; Lacroix, P. Phase noise measurement of a narrow linewidth CW laser using delay line approaches. Opt. Lett. 2011, 36, 2713–2715. [Google Scholar] [CrossRef] [Green Version]
- Yariv, A. Signal-to-noise considerations in fiber links with periodic or distributed optical amplification. Opt. Lett. 1990, 15, 1064–1066. [Google Scholar] [CrossRef] [Green Version]
- Epping, J.P.; Oldenbeuving, R.M.; Geskus, D.; Visscher, I.; Grootjans, R.; Roeloffzen, C.G.; Heideman, R.G. High power, tunable, narrow linewidth dual gain hybrid laser. In Proceedings of the Laser Congress 2019 (ASSL, LAC, LS&C), Vienna, Austria, 29 September–3 October 2019; Optical Society of America: Washington, DC, USA, 2019; p. ATu1A.4. [Google Scholar] [CrossRef]
- Melnik, S.; Huyet, G.; Uskov, A.V. The linewidth enhancement factor α of quantum dot semiconductor lasers. Opt. Express 2006, 14, 2950–2955. [Google Scholar] [CrossRef]
- Redlich, C.; Lingnau, B.; Huang, H.; Raghunathan, R.; Schires, K.; Poole, P.; Grillot, F.; Lüdge, K. Linewidth rebroadening in quantum dot semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–10. [Google Scholar] [CrossRef]
- Andreou, S.; Williams, K.A.; Bente, E.A.J.M. Monolithically integrated InP-based DBR lasers with an intra-cavity ring resonator. Opt. Express 2019, 27, 26281–26294. [Google Scholar] [CrossRef]
- Krückel, C.J.; Fülöp, A.; Ye, Z.; Andrekson, P.A.; Torres-Company, V. Optical bandgap engineering in nonlinear silicon nitride waveguides. Opt. Express 2017, 25, 15370–15380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Laer, R.; Kuyken, B.; Van Thourhout, D.; Baets, R. Interaction between light and highly confined hypersound in a silicon photonic nanowire. Nat. Photonics 2015, 9, 199–203. [Google Scholar] [CrossRef] [Green Version]
- Gyger, F.; Liu, J.; Yang, F.; He, J.; Raja, A.S.; Wang, R.N.; Bhave, S.A.; Kippenberg, T.J.; Thévenaz, L. Observation of stimulated Brillouin scattering in silicon nitride integrated waveguides. arXiv 2019, arXiv:1908.09815. [Google Scholar]
- Eggleton, B.J.; Poulton, C.G.; Rakich, P.T.; Steel, M.J.; Bahl, G. Brillouin integrated photonics. Nat. Photonics 2019, 13, 664–677. [Google Scholar] [CrossRef]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical frequency metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef]
- Pillet, G.; Morvan, L.; Brunel, M.; Bretenaker, F.; Dolfi, D.; Vallet, M.; Huignard, J.P.; Floch, A.L. Dual-frequency laser at 1.5 μm for optical distribution and generation of high-purity microwave signals. J. Lightwave Technol. 2008, 26, 2764–2773. [Google Scholar] [CrossRef]
- Takamoto, M.; Hong, F.L.; Higashi, R.; Katori, H. An optical lattice clock. Nature 2005, 435, 321–324. [Google Scholar] [CrossRef]
- Wicht, A.; Bawamia, A.; Krüger, M.; Kürbis, C.; Schiemangk, M.; Smol, R.; Peters, A.; Tränkle, G. Narrow linewidth diode laser modules for quantum optical sensor applications in the field and in space. In Components and Packaging for Laser Systems III; Glebov, A.L., Leisher, P.O., Eds.; SPIE: Bellingham, WA, USA, 2017; Volume 10085, pp. 103–118. [Google Scholar] [CrossRef]
- Maze, J.R.; Stanwix, P.L.; Hodges, J.S.; Hong, S.; Taylor, J.M.; Cappellaro, P.; Jiang, L.; Dutt, M.V.G.; Togan, E.; Zibrov, A.S.; et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef]
- Nölleke, C.; Leisching, P.; Blume, G.; Jedrzejczyk, D.; Pohl, J.; Feise, D.; Sahm, A.; Paschke, K. Frequency locking of compact laser-diode modules at 633 nm. In Photonic Instrumentation Engineering V; Soskind, Y.G., Ed.; SPIE: Bellingham, WA, USA, 2018; Volume 10539, pp. 28–33. [Google Scholar] [CrossRef]
- Wang, P.; Chen, W.; Wan, F.; Wang, J.; Hu, J. A review of cavity-enhanced Raman spectroscopy as a gas sensing method. Appl. Spectrosc. Rev. 2019, 1–25. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent multiheterodyne spectroscopy using stabilized optical frequency combs. Phys. Rev. Lett. 2008, 100, 013902. [Google Scholar] [CrossRef] [Green Version]
- Cheung, S.; Baek, J.; Scott, R.P.; Fontaine, N.K.; Soares, F.M.; Zhou, X.; Baney, D.M.; Yoo, S.J.B. 1-GHz monolithically integrated hybrid mode-locked InP laser. IEEE Photonics Technol. Lett. 2010, 22, 1793–1795. [Google Scholar] [CrossRef]
- Srinivasan, S.; Davenport, M.; Heck, M.J.R.; Hutchinson, J.; Norberg, E.; Fish, G.; Bowers, J. Low phase noise hybrid silicon mode-locked lasers. Front. Optoelectron. 2014, 7, 265–276. [Google Scholar] [CrossRef]
- Davenport, M.L.; Liu, S.; Bowers, J.E. Integrated heterogeneous silicon/III-V mode-locked lasers. Photonincs Res. 2018, 6, 468–478. [Google Scholar] [CrossRef]
- Mak, J.; van Rees, A.; Fan, Y.; Klein, E.J.; Geskus, D.; van der Slot, P.J.M.; Boller, K.J. Linewidth narrowing via low-loss dielectric waveguide feedback circuits in hybrid integrated frequency comb lasers. Opt. Express 2019, 27, 13307–13318. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Deng, Z.; Yao, J. Photonic generation of microwave signal using a dual-wavelength single-longitudinal-mode fiber ring laser. IEEE Trans. Microw. Theory Tech. 2006, 54, 804–809. [Google Scholar] [CrossRef]
- Grivas, C. Optically pumped planar waveguide lasers: Part II: Gain media, laser systems, and applications. Prog. Quantum Electron. 2016, 45–46, 3–160. [Google Scholar] [CrossRef]
- Iio, S.; Suehiro, M.; Hirata, T.; Hidaka, T. Two-longitudinal-mode laser diodes. IEEE Photonics Technol. Lett. 1995, 7, 959–961. [Google Scholar] [CrossRef]
- Pozzi, F.; De La Rue, R.M.; Sorel, M. Dual-wavelength InAlGaAs—InP laterally coupled distributed feedback laser. IEEE Photonics Technol. Lett. 2006, 18, 2563–2565. [Google Scholar] [CrossRef]
- Price, R.K.; Verma, V.B.; Tobin, K.E.; Elarde, V.C.; Coleman, J.J. Y-branch surface-etched distributed Bragg reflector lasers at 850 nm for optical heterodyning. IEEE Photonics Technol. Lett. 2007, 19, 1610–1612. [Google Scholar] [CrossRef]
- Kim, N.; Ryu, H.C.; Lee, D.; Han, S.P.; Ko, H.; Moon, K.; Park, J.W.; Jeon, M.Y.; Park, K.H. Monolithically integrated optical beat sources toward a single-chip broadband terahertz emitter. Laser Phys. Lett. 2013, 10, 085805. [Google Scholar] [CrossRef]
- Guzmán, R.; Jimenez, A.; Corral, V.; Carpintero, G.; Leijtens, X.; Lawniczuk, K. Narrow linewidth dual-wavelength laser sources based on AWG for the generation of millimeter wave signals. In Proceedings of the XXIX Simposium Nacional de la Unión Científica Internacional de Radio, Valencia, Spain, 3–5 September 2014. [Google Scholar]
- Zhu, Y.; Zhu, L. Narrow-linewidth, tunable external cavity dual-band diode lasers through InP/GaAs-Si3N4 hybrid integration. Opt. Express 2019, 27, 2354–2362. [Google Scholar] [CrossRef] [PubMed]
- Bovington, J.T.; Heck, M.J.R.; Bowers, J.E. Heterogeneous lasers and coupling to Si3N4 near 1060 nm. Opt. Lett. 2014, 39, 6017–6020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kane, T.J.; Byer, R.L. Monolithic, unidirectional single-mode Nd: YAG ring laser. Opt. Lett. 1985, 10, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, N.; Dekker, R.; Hoekman, M.; Dekkers, M.; Bos, J.; Leinse, A.; Heideman, R. Stress-optic modulator in TriPleX platform using a piezoelectric lead zirconate titanate (PZT) thin film. Opt. Express 2015, 23, 14018–14026. [Google Scholar] [CrossRef] [PubMed]
- Epping, J.P.; Hellwig, T.; Hoekman, M.; Mateman, R.; Leinse, A.; Heideman, R.G.; van Rees, A.; van der Slot, P.J.; Lee, C.J.; Fallnich, C.; et al. On-chip visible-to-infrared supercontinuum generation with more than 495 THz spectral bandwidth. Opt. Express 2015, 23, 19596–19604. [Google Scholar] [CrossRef] [Green Version]
- Fan, T.; Xia, Z.; Adibi, A.; Eftekhar, A.A. Highly-uniform resonator-based visible spectrometer on a Si3N4 platform with robust and accurate post-fabrication trimming. Opt. Lett. 2018, 43, 4887–4890. [Google Scholar] [CrossRef]
- Wang, J.; Chen, S.; Dai, D. Silicon hybrid demultiplexer with 64 channels for wavelength/mode-division multiplexed on-chip optical interconnects. Opt. Lett. 2014, 39, 6993–6996. [Google Scholar] [CrossRef]
- Liu, Y.; Wichman, A.R.; Isaac, B.; Kalkavage, J.; Adles, E.J.; Clark, T.R.; Klamkin, J. Ultra-low-loss silicon nitride optical beamforming network for wideband wireless applications. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–10. [Google Scholar] [CrossRef]
- Visscher, I.; Roeloffzen, C.; Taddei, C.; Hoekman, M.; Wevers, L.; Grootjans, R.; Kapteijn, P.; Geskus, D.; Alippi, A.; Dekker, R.; et al. Broadband true time delay microwave photonic beamformer for phased array antennas. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Oldenbeuving, R.M.; Lee, C.J.; van Voorst, P.D.; Offerhaus, H.L.; Boller, K.J. Modeling of mode locking in a laser with spatially separate gain media. Opt. Express 2010, 18, 22996–23008. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Oldenbeuving, R.M.; Khan, M.R.H.; Roeloffzen, C.G.H.; Klein, E.J.; Lee, C.J.; Offerhaus, H.L.; Boller, K.J. Q-factor measurements through injection locking of a semiconductor-glass hybrid laser with unknown intracavity losses. Opt. Lett. 2014, 39, 1748–1751. [Google Scholar] [CrossRef] [Green Version]
- Kuswandi, B.; Nuriman; Huskens, J.; Verboom, W. Optical sensing systems for microfluidic devices: A review. Anal. Chim. Acta 2007, 601, 141–155. [Google Scholar] [CrossRef] [PubMed]
- Artundo, I. Photonic integration: New applications are visible. Opt. Photonik 2017, 12, 22–25. [Google Scholar] [CrossRef] [Green Version]
- Ymeti, A.; Greve, J.; Lambeck, P.V.; Wink, T.; van Hövell; Beumer; Wijn, R.R.; Heideman, R.G.; Subramaniam, V.; Kanger, J.S. Fast, Ultrasensitive Virus Detection Using a Young Interferometer Sensor. Nano Lett. 2007, 7, 394–397. [Google Scholar] [CrossRef]
- Porcel, M.A.; Hinojosa, A.; Jans, H.; Stassen, A.; Goyvaerts, J.; Geuzebroek, D.; Geiselmann, M.; Dominguez, C.; Artundo, I. Silicon nitride photonic integration for visible light applications. Opt. Laser Technol. 2019, 112, 299–306. [Google Scholar] [CrossRef]
| Parameter | Description | Value | Unit |
|---|---|---|---|
| wavelength | 1.55 | m | |
| output power | 1.0 | mW | |
| linewidth enhancement factor | 5 | ||
| spontaneous emission factor | 2.0 | ||
| Length gain section | 700 | m | |
| Power reflection back facet | 0.9 | ||
| Power reflection loop mirror | 0.5 | ||
| mode coupling loss | 0.9 | ||
| group index gain section | 3.6 | ||
| group index SiN section | 1.715 | ||
| loss gain section | 13 | cm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boller, K.-J.; van Rees, A.; Fan, Y.; Mak, J.; Lammerink, R.E.M.; Franken, C.A.A.; van der Slot, P.J.M.; Marpaung, D.A.I.; Fallnich, C.; Epping, J.P.; et al. Hybrid Integrated Semiconductor Lasers with Silicon Nitride Feedback Circuits. Photonics 2020, 7, 4. https://doi.org/10.3390/photonics7010004
Boller K-J, van Rees A, Fan Y, Mak J, Lammerink REM, Franken CAA, van der Slot PJM, Marpaung DAI, Fallnich C, Epping JP, et al. Hybrid Integrated Semiconductor Lasers with Silicon Nitride Feedback Circuits. Photonics. 2020; 7(1):4. https://doi.org/10.3390/photonics7010004
Chicago/Turabian StyleBoller, Klaus-J., Albert van Rees, Youwen Fan, Jesse Mak, Rob E. M. Lammerink, Cornelis A. A. Franken, Peter J. M. van der Slot, David A. I. Marpaung, Carsten Fallnich, Jörn P. Epping, and et al. 2020. "Hybrid Integrated Semiconductor Lasers with Silicon Nitride Feedback Circuits" Photonics 7, no. 1: 4. https://doi.org/10.3390/photonics7010004
APA StyleBoller, K.-J., van Rees, A., Fan, Y., Mak, J., Lammerink, R. E. M., Franken, C. A. A., van der Slot, P. J. M., Marpaung, D. A. I., Fallnich, C., Epping, J. P., Oldenbeuving, R. M., Geskus, D., Dekker, R., Visscher, I., Grootjans, R., Roeloffzen, C. G. H., Hoekman, M., Klein, E. J., Leinse, A., & Heideman, R. G. (2020). Hybrid Integrated Semiconductor Lasers with Silicon Nitride Feedback Circuits. Photonics, 7(1), 4. https://doi.org/10.3390/photonics7010004






