Abstract
The achievement of wideband high-gain optical parametric amplification has not been shown in micrometer-scale cavities. In this paper we have computationally investigated the optical parametric amplification process in a few micrometer-long dispersive microresonator. By performing a gain medium resonance frequency dependent analysis of optical parametric amplification, we have found that it is possible to achieve a wideband high-gain optical amplification in a dispersive microresonator. In order to account for the effects of dispersion (modeled by the polarization damping coefficient) and the resonance frequency of the gain medium on optical parametric amplification, we have solved the wave equation in parallel with the nonlinear equation of electron cloud motion, using the finite difference time domain method. Then we have determined the resonance frequency values that yield an enhanced or a resonant case of optical parametric amplification, via gain factor optimization. It was observed that if the microresonator is more dispersive (has a lower polarization damping coefficient), then there are more resonance frequencies that yield an optical gain resonance. At these gain resonances, a very wideband, high-gain optical amplification seems possible in the micron scale, which, to our knowledge, has not been previously reported in the context of nonlinear wave mixing theory.
1. Introduction
Parametric amplification has been studied extensively in the context of nonlinear optics. It has been well established that we can amplify a relatively low power input wave, by using another wave of high intensity, which is called the pump wave, in a nonlinear medium [1,2,3,4]. This theory has been mostly investigated experimentally rather than computationally. This is because the concept is almost always studied in the micrometer or nanometer wavelength range, and yet the required medium length to observe any significant nonlinear effect is in the millimeter or centimeter range, which requires an extremely high computational cost for obtaining meaningful results. Furthermore, based on the current concept of parametric amplification, it is impossible to achieve a wideband non-negligible wave amplification in a few micrometer-sized gain medium or a cavity, as the required gain medium length for significant parametric amplification is mostly on the order of centimeters. For this reason, the concept of parametric amplification is not feasible to be used for optical microsystems. However, if it can be achieved in the micrometer scale, super gain optical parametric amplification can lead to much more efficient macroscale high power devices by being engineered to operate in an array form to maximize optical interference, such as laser beam welding machines and petawatt lasers that are used for particle acceleration and fusion reactions. Another potential technological advancement can be in the field of optical antennas via the generation of a supercontinuum for achieving ultra-wideband operation.
In this paper, we have carried out a computational analysis that aims to show that it is possible to amplify a low power input wave by mixing it with an intense pump wave of ultrashort duration, in a wide range of frequencies and with a very large gain coefficient, inside a low-loss microcavity of several micrometers of length. This can be achieved by using a gain medium whose resonance frequency matches with one of the gain resonances of the amplification in a microcavity. The gain resonances of an optical amplification in a microcavity can be determined by solving the wave equation in parallel with the equation of nonlinear electron motion. For this reason, we will start our analysis by investigating wave propagation in nonlinear dispersive media.
2. Wave Propagation in Nonlinear Dispersive Media
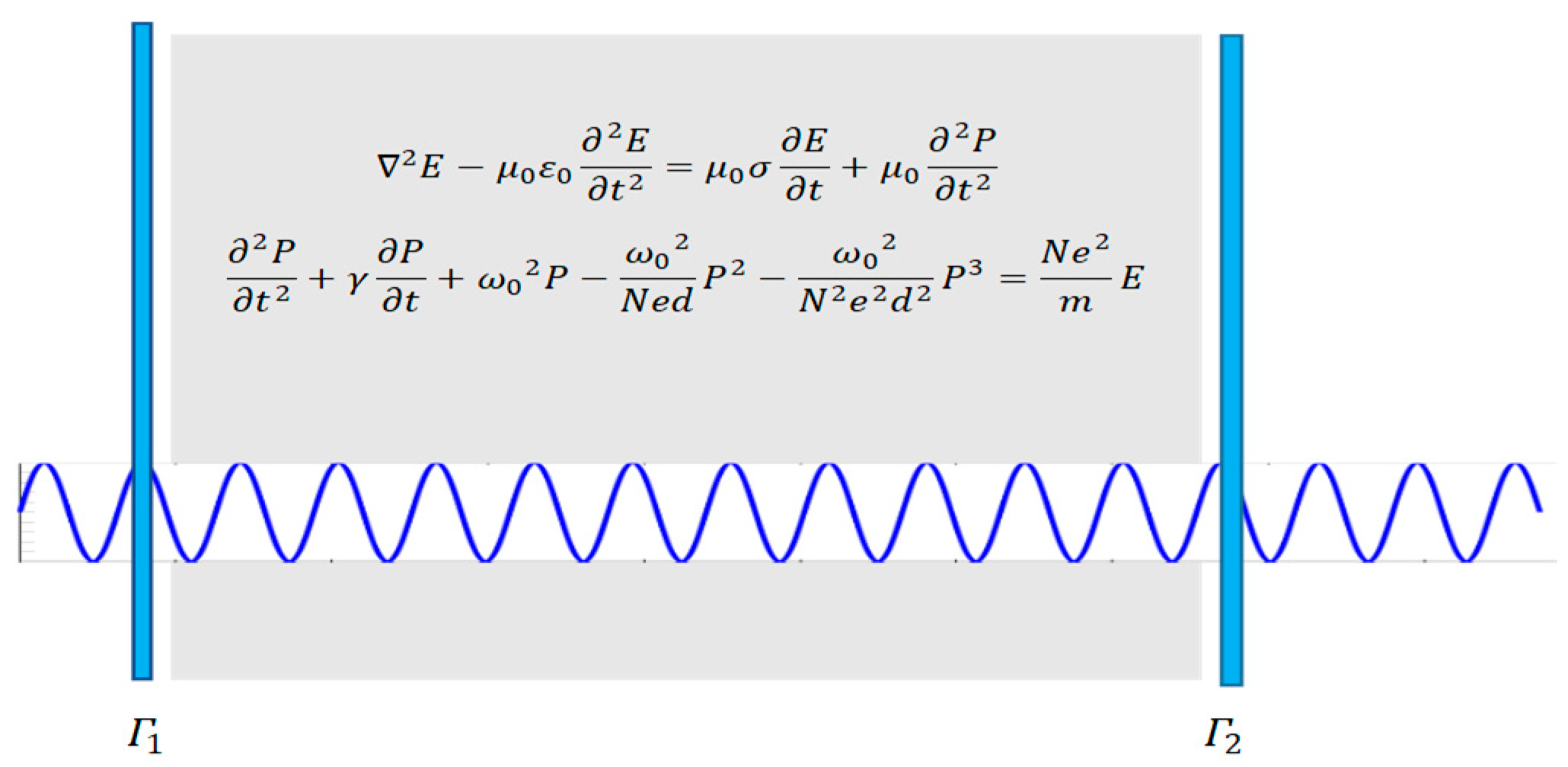
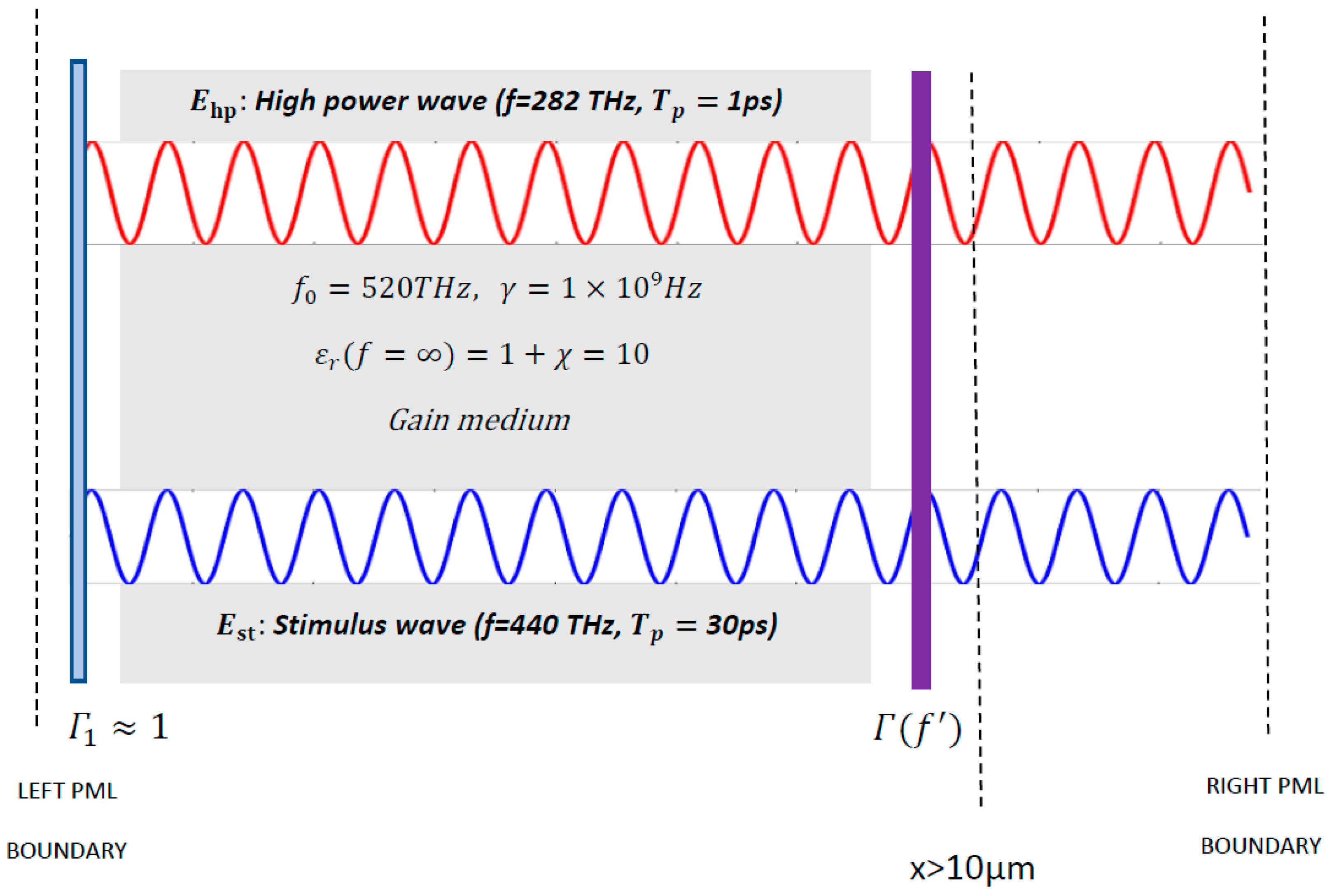
Nonlinearity arises when at least one of the waves that propagate in a medium has a very high intensity. Such high intensities are only possible with very short duration pulses, such as the pulses of a mode locked laser, which have durations on the scale of picoseconds or femtoseconds [5,6]. When high intensity pulses have very short durations, which is almost always the case, we must account for the wave dispersion, as the impulse response of the charge polarization density of many dielectric media last much longer in duration than the pulse durations of such high intensity pulses [7,8,9,10]. One can solve the wave equation in parallel with the nonlinear equation of electron cloud motion for a nonlinear dispersive medium. This is because the parameters such as the resonance frequency, damping coefficient, atom density, and atomic diameter have known values for most solids, which makes the simulation results much more meaningful and precise. In order to determine the time variation of the electric field in a nonlinear dispersive medium, we need to solve the following two equations [1] (see Figure 1):
, .

Figure 1.
A nonlinear dispersive medium placed in a cavity.
In Equation (2) we have made an expansion up to the third order of the nonlinear charge polarization density as higher order terms will be negligibly small. For a dielectric medium, the electrical conductivity can be assumed as negligible Some typical values for solid dielectric media are [1].
Consider the wave that has a very high amplitude, without the presence of the low amplitude wave , the pair of equations that describe the propagation of in a nonlinear dispersive medium is given as
.
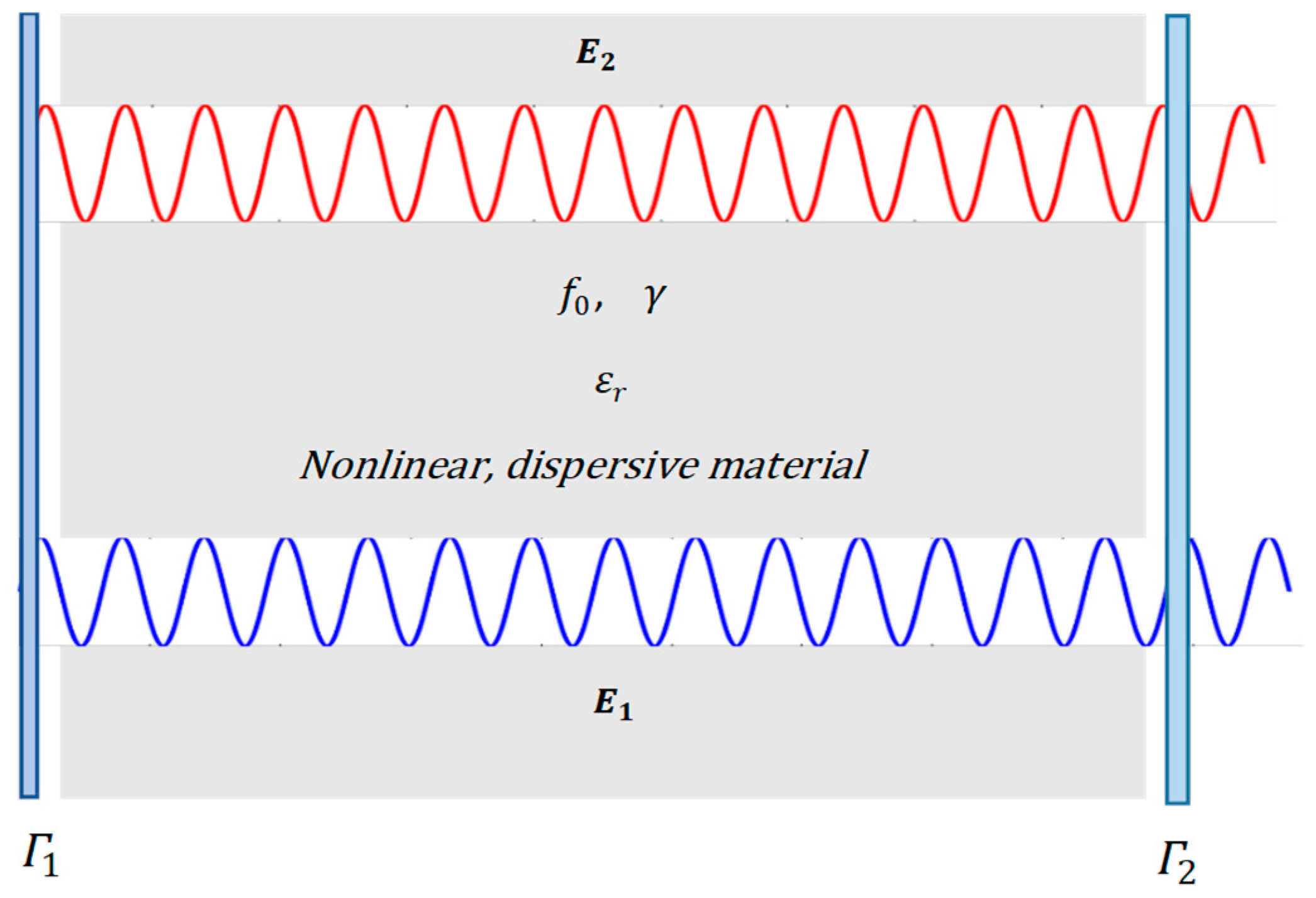
Now assume that and are propagating together in the same nonlinear dispersive medium (see Figure 2). In this case the pair of equations that represent the total electric field propagation is given as

Figure 2.
Two waves are propagating through a nonlinear dispersive medium placed in a cavity.
We want to determine the propagation of the low amplitude wave in the presence of the high amplitude wave ; in other words we want to determine the propagation of when there is an energy coupling from as a result of the nonlinear interaction. In order to do that we subtract Equations (3a) and (3b) from Equations (4a) and (4b) respectively, which gives us
From Equations (3a), (3b), (5a) and (5b) we can see that and are coupled to each other. Based on Equations (5a) and (5b), we will investigate whether it is possible to amplify the low power electric field , by drawing energy from a low loss microcavity that is energized by the high-power electric field
3. Optimization of Optical Parametric Amplification Gain Performance
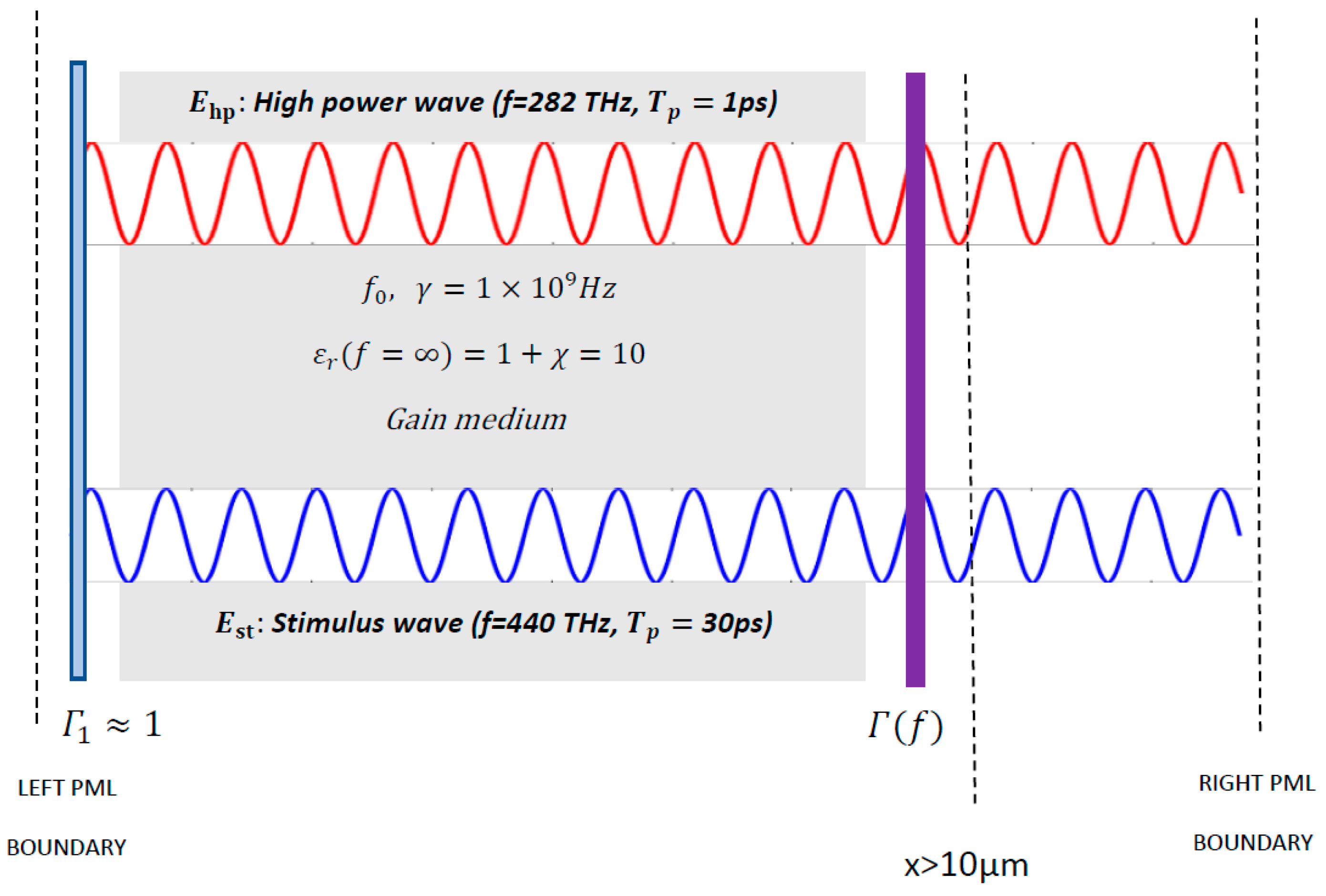
Goal: Maximize the stimulus wave magnitude with respect to the resonance frequency of the interaction medium, with the high power pump wave and the low power stimulus wave time variations at the cavity input (excitations) respectively being (see Figure 3)

Figure 3.
Configuration of the cavity.
The equations that need to be solved at each iteration of the optimization process are given as
At each iteration, we use an update equation based on Newton’s method.
With the step size being updated at each iteration as (optimized by trial and error for fast convergence).
We choose the left cavity wall as an optical isolator and the right cavity wall as an optical bandpass filter.
4. Finite Difference Time Domain Formulation Based Solution of the Gain Factor Optimization Problem in Optical Parametric Amplification
We can discretize Equations (3a), (3b), (5a) and (5b) using the finite difference time domain method as shown in Equations (6a), (6b), (7a) and (7b), at each iteration of the optimization problem. Our first aim is to discretize Equations (3a) and (3b) and solve for i.e., the value of at a given point at the next time step. Since is coupled to , we first solve for and then substitute it into the equation for . We keep on solving these two equations iteratively for all time steps and for all points in the spatial domain of a given one dimensional problem. For a higher accuracy of the resulting solution, we choose and as small as possible [11]. Then we discretize Equations (5a) and (5b) and substitute the value of obtained from Equations (6a) and (6b) to solve for in Equations (7a) and (7b). Finally, we modify the value of the resonance frequency (see Equation (8a)) based on Newton’s method, and we repeat this whole procedure for each iteration of the optimization process until the desired gain factor is attained.
x: Spatial coordinate, t: Time, k: Iteration number,
By solving these six equations simultaneously, along with the initial condition and the boundary conditions of a given optical parametric amplification problem, we can maximize the gain factor. In order to test our computational model, we have compared our computational results with the experimentally verified theoretical results in the well-established context of nonlinear sum frequency generation, in the Appendix A. Now we move on to the discussion of the simulation results.
5. Simulation Results
5.1. Finding the Optimal Resonance Frequency for High Gain Optical Parametric Amplification
Assume that a 440 THz stimulus wave and a high power 282 THz pump wave (Nd:YAG laser field) are propagating inside a low-loss cavity that has two reflecting walls. The reflecting wall on the left side can be thought as an optical isolator and has a reflection coefficient of the one on the right side represents a switch controlled optical band-pass filter with a frequency dependent reflection coefficient Both waves are generated at x = 0 μm and at the time instant t = 0 (see Figure 4)

Figure 4.
Configuration of the cavity.
Problem definition: Find the optimum resonance frequency that maximizes in the cavity, for 10 THz < (THz to UV), for , such that
Initial conditions:
Boundary and excitation conditions:
Absorbing boundary condition (perfectly matched layer (PML)):
Optical isolator condition: Full reflection at
Switch controlled optical bandpass filter condition: Full reflection at for t 30 picoseconds, frequency dependent reflection at after t = 30 picoseconds;
Using the formulation given in Equations (8a) and (8b), the maximum stimulus wave amplitude that has been reached in the cavity (for 0 < t < 30 ps) is determined as , which corresponds to (see Table 1). However, there might be other gain resonances, especially around the major gain resonance Therefore, finding the optimum gain factor and the optimum resonance frequency is not enough by itself. To determine all the other gain resonances, we also need to sweep the resonance frequency from 10 THz to 1000 THz in 10 THz increments, and investigate the reason behind the high gain at this resonance frequency by analyzing the stored electric energy density and the intracavity charge polarization density of the pump wave.

Table 1.
Gain maximization by using Newton’s method.
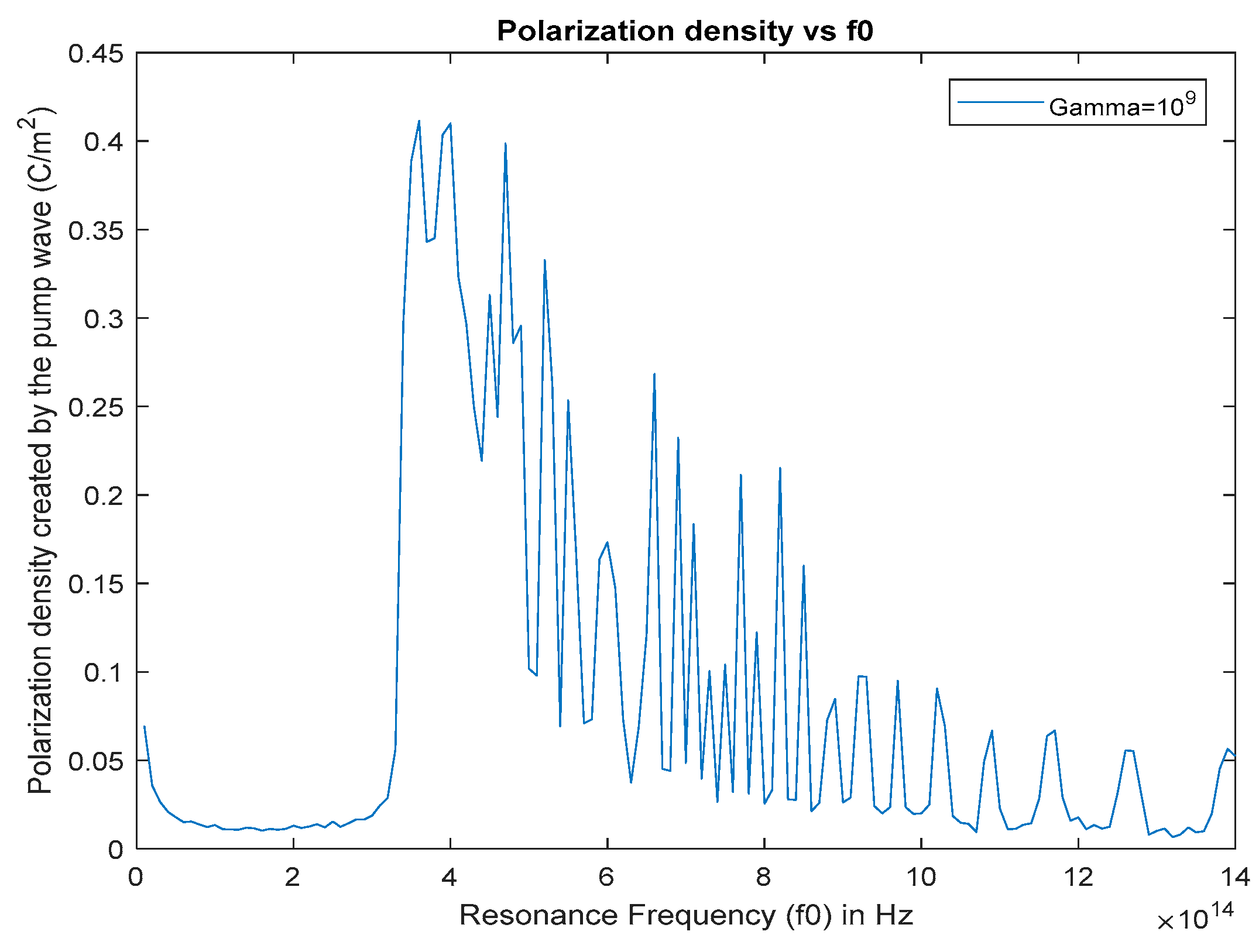
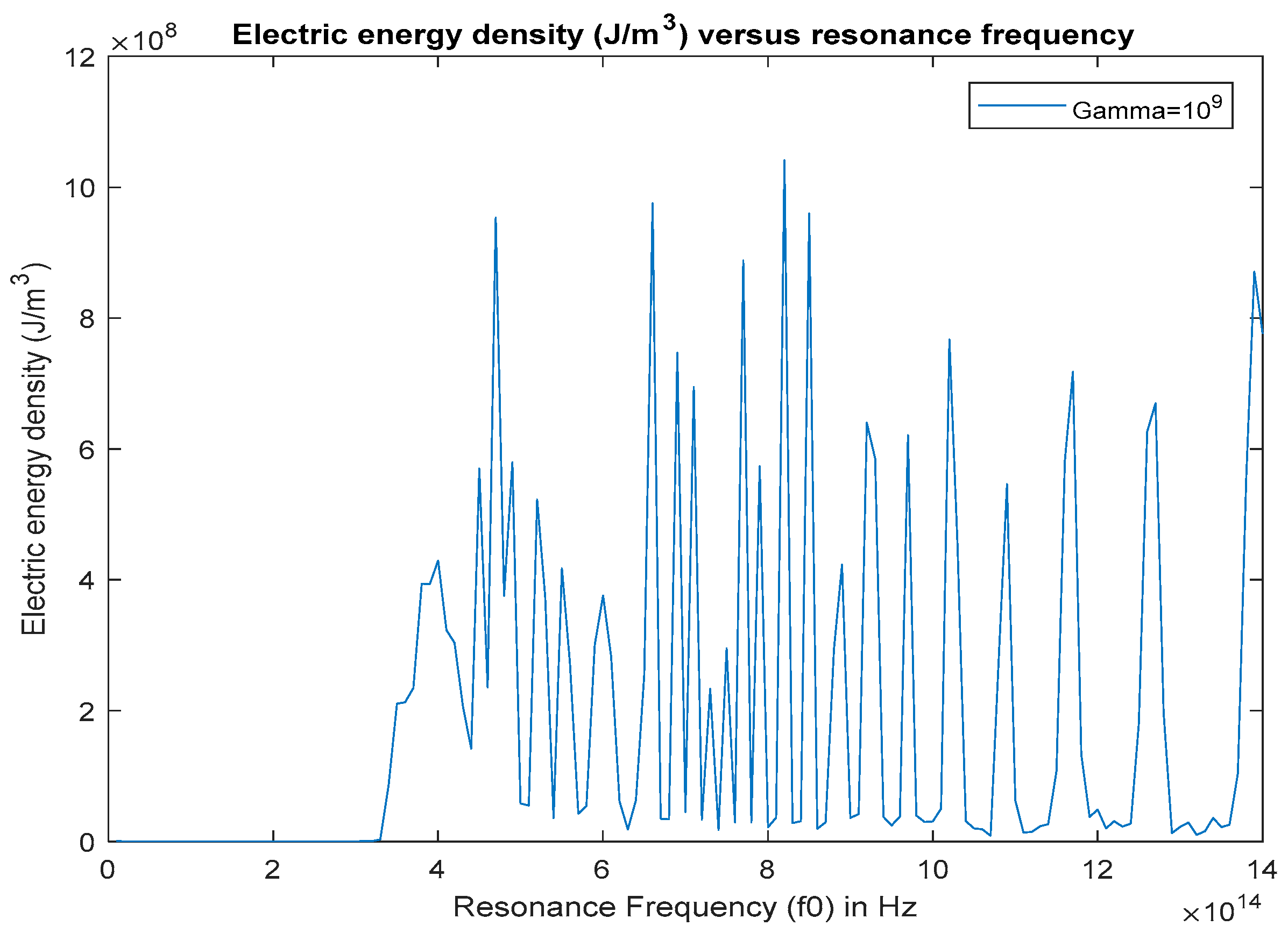
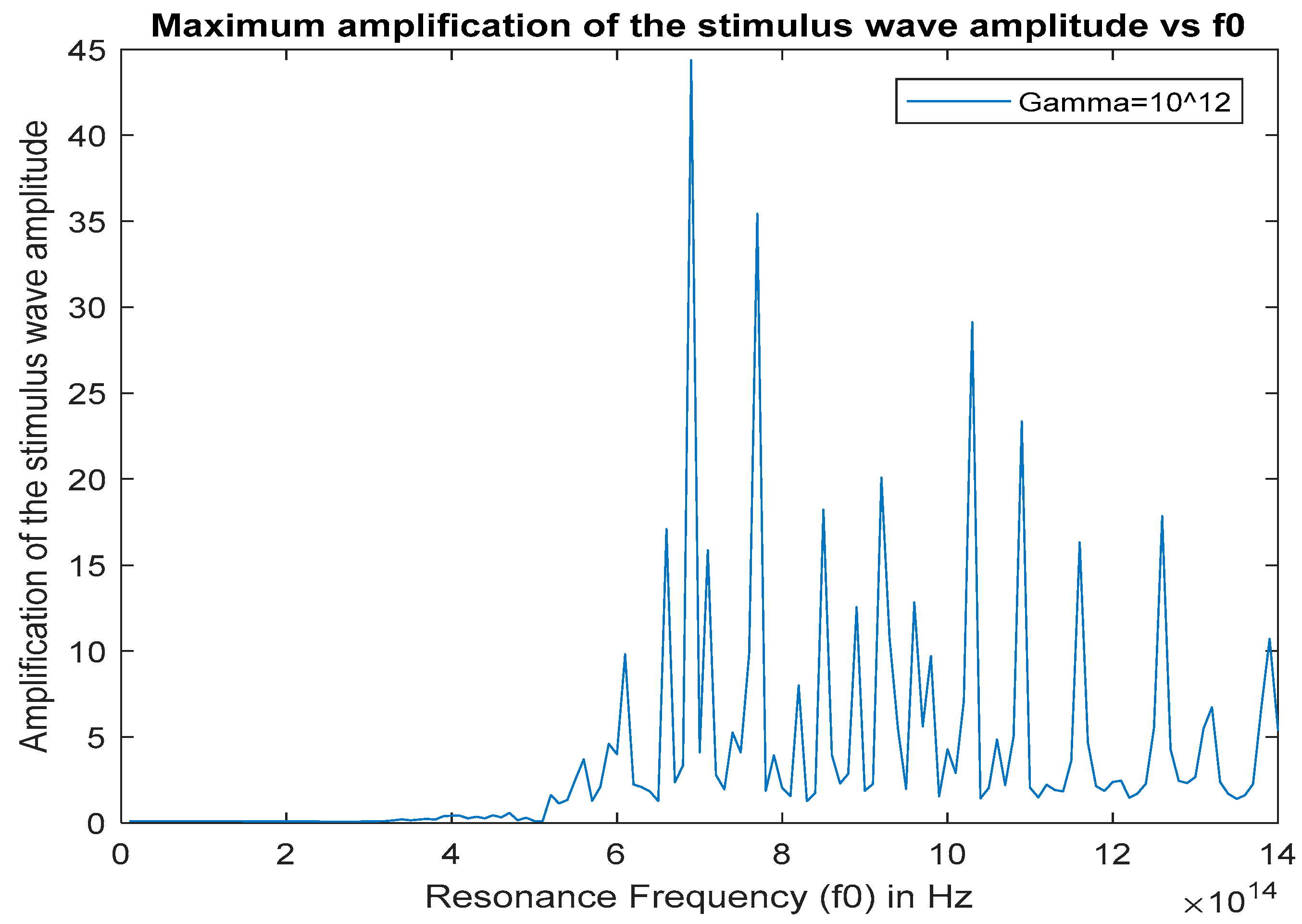
As we can see from Table 2, there are several resonance frequencies that yield a high gain for the stimulus wave, for a 1.064 (282 THz) Nd-YAG pump wave. The amplification peaks occur between the resonance frequencies and . This suggests that we can achieve strong optical parametric amplification in a micrometer sized cavity using a 282 THz pump wave, if we use a gain medium that has the correct or optimal resonance frequency for amplification. In this case the optimal resonance frequencies are as shown in Table 2. The corresponding optimal resonance frequency values of the amplification peaks are especially determined by the intracavity charge polarization density (and to a lesser extent on the electric energy density) created by the pump wave. If we look at Figure 5, the charge polarization density that is created by the pump wave is very high at the gain resonances, and as the charge polarization density decreases at higher frequencies, only less significant (minor) gain peaks are observed. This makes perfect sense because the charge polarization density created by the pump wave couples to the stimulus wave electric field intensity (see Equation (5b)) and acts as a source for the stimulus wave thereby amplifying it. Although the maximum gain factor of the stimulus wave also depends on the stored electric energy density in the cavity, if there is not enough charge polarization density in the cavity to couple this stored electric energy to the stimulus wave, amplification does not occur. This can be seen from Figure 5 and Figure 6. There are many high electric energy density peaks beyond , however, since there is not enough charge polarization density that can transfer this energy density to the stimulus wave, amplification is not significant.

Table 2.
Maximum stimulus wave amplitude (gain factor) inside the cavity at x = 5.73 µm for {0 < t < 30ps, }, versus . Optimum values are indicated in bold.

Figure 5.
Maximum polarization density (created by the pump wave) inside the cavity at x = 5.73 µm for 0 < t < 30 ps, , versus

Figure 6.
Maximum electric energy density inside the cavity at x = 5.73 µm for 0 < t < 30 ps, versus
Since the resonance frequency values that yield a high stimulus wave gain factor is between and , using any dielectric material that has a resonance frequency or an emission peak in this range (especially in the vicinity of the boldly indicated frequencies at Table 2), is suitable for achieving high gain amplification of a stimulus wave of any frequency, under a 282 THz Nd:YAG pump wave, such as the Bithiophene based red fluorescent light emitting material called BTCN [12], which has a resonance frequency value of 470 THz with a FWHM bandwidth of 80 THz. BTCN is recently suggested as a good red-light emitting material for organic light emitting applications.
5.2. Effect of the Damping Coefficient on Stimulus Wave Amplification
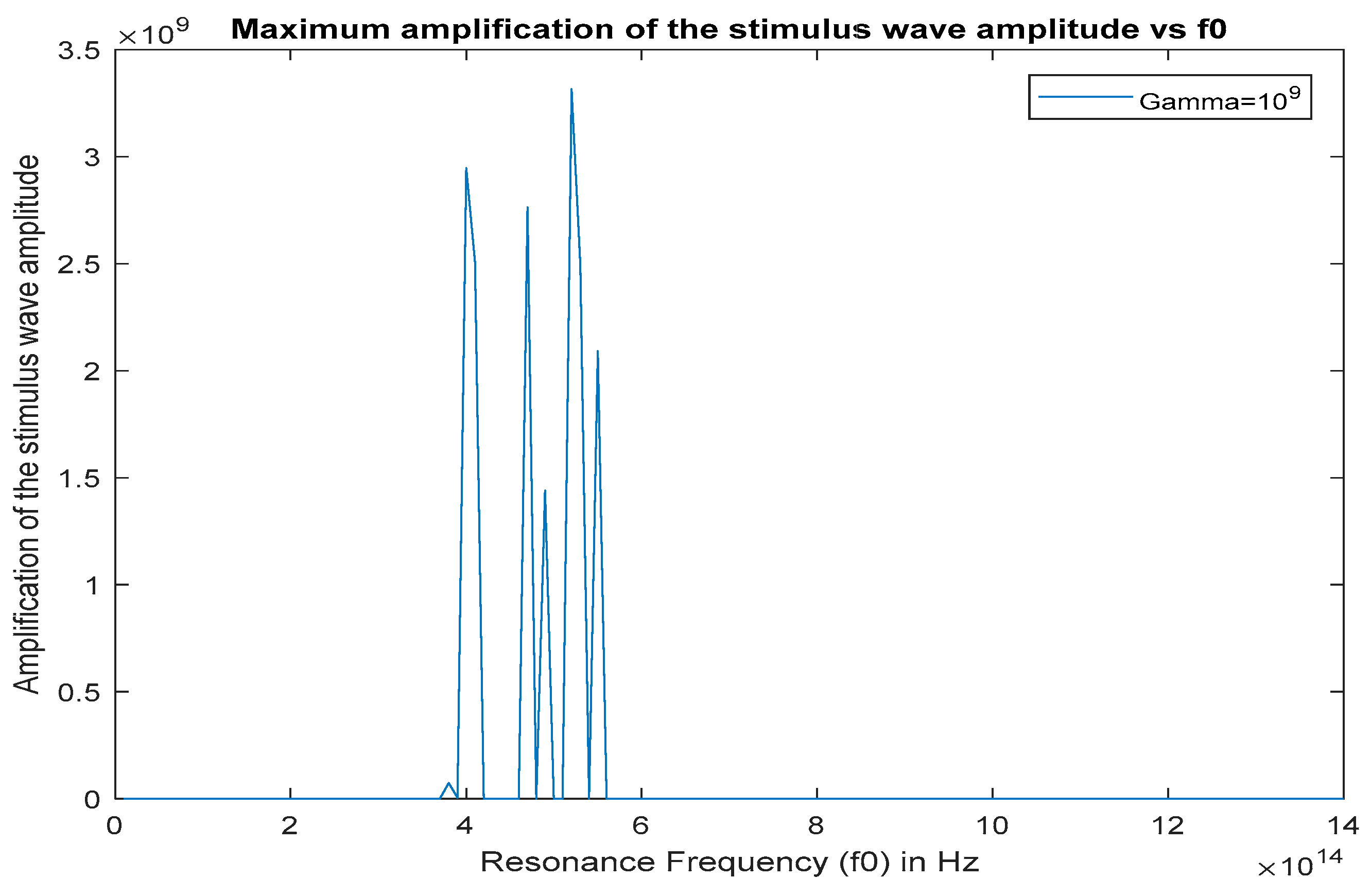
As the damping coefficient (polarization decay rate) increases, the amplification of the stimulus wave gets weaker (Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11). This is because the amount of stored electric energy density in the cavity depends on the damping coefficient. As the charge polarization density decays quicker due to high , the stored electric energy will have less time to accumulate in the cavity and the stimulus wave will have less time to get amplified. If we look at Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, the gain resonances eventually disappear as the damping coefficient is increased. For , the amplification of the stimulus wave becomes insignificant.

Figure 7.
Amplification of the stimulus wave amplitude (gain factor) inside the cavity at x = 5.73 µm for 0 < t < 30 ps, , versus

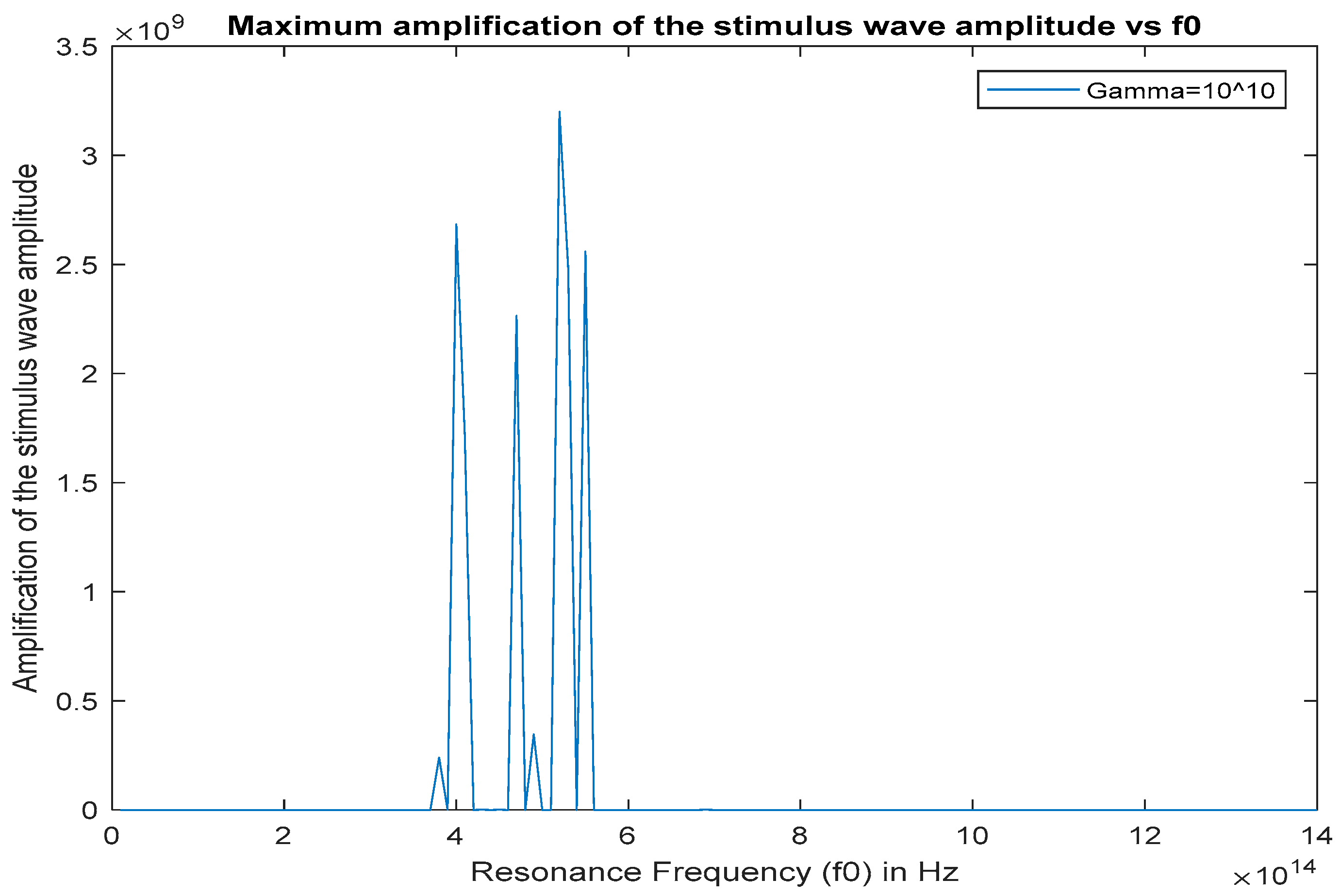
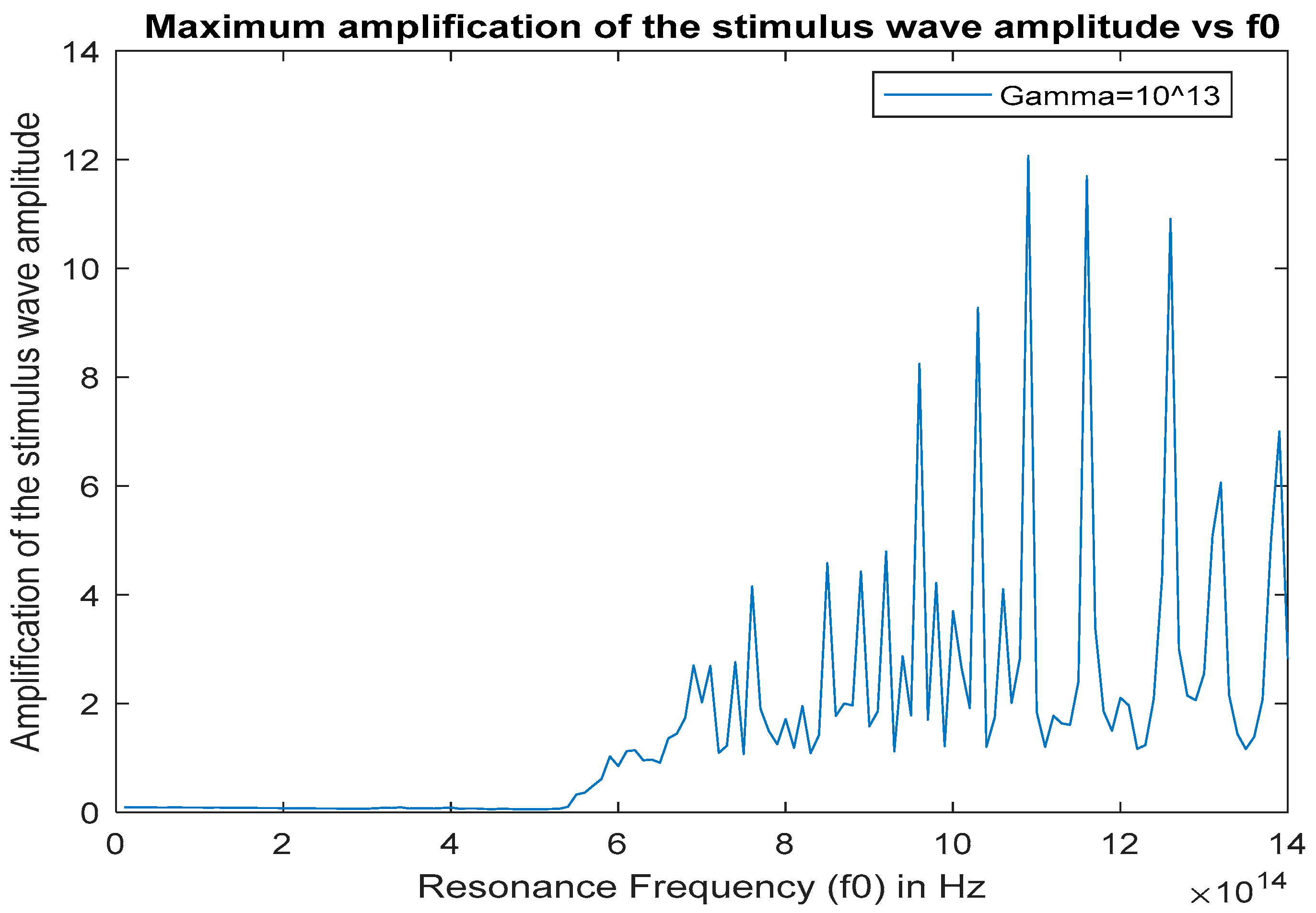
Figure 8.
Maximum stimulus wave amplitude (gain factor) inside the cavity at x = 5.73 µm for 0 < t < 30 ps, , versus

Figure 9.
Maximum stimulus wave amplitude (gain factor) inside the cavity at x = 5.73 µm for 0 < t < 30 ps, , versus

Figure 10.
Maximum stimulus wave amplitude (gain factor) inside the cavity at x = 5.73 µm for 0 < t < 30 ps, , versus

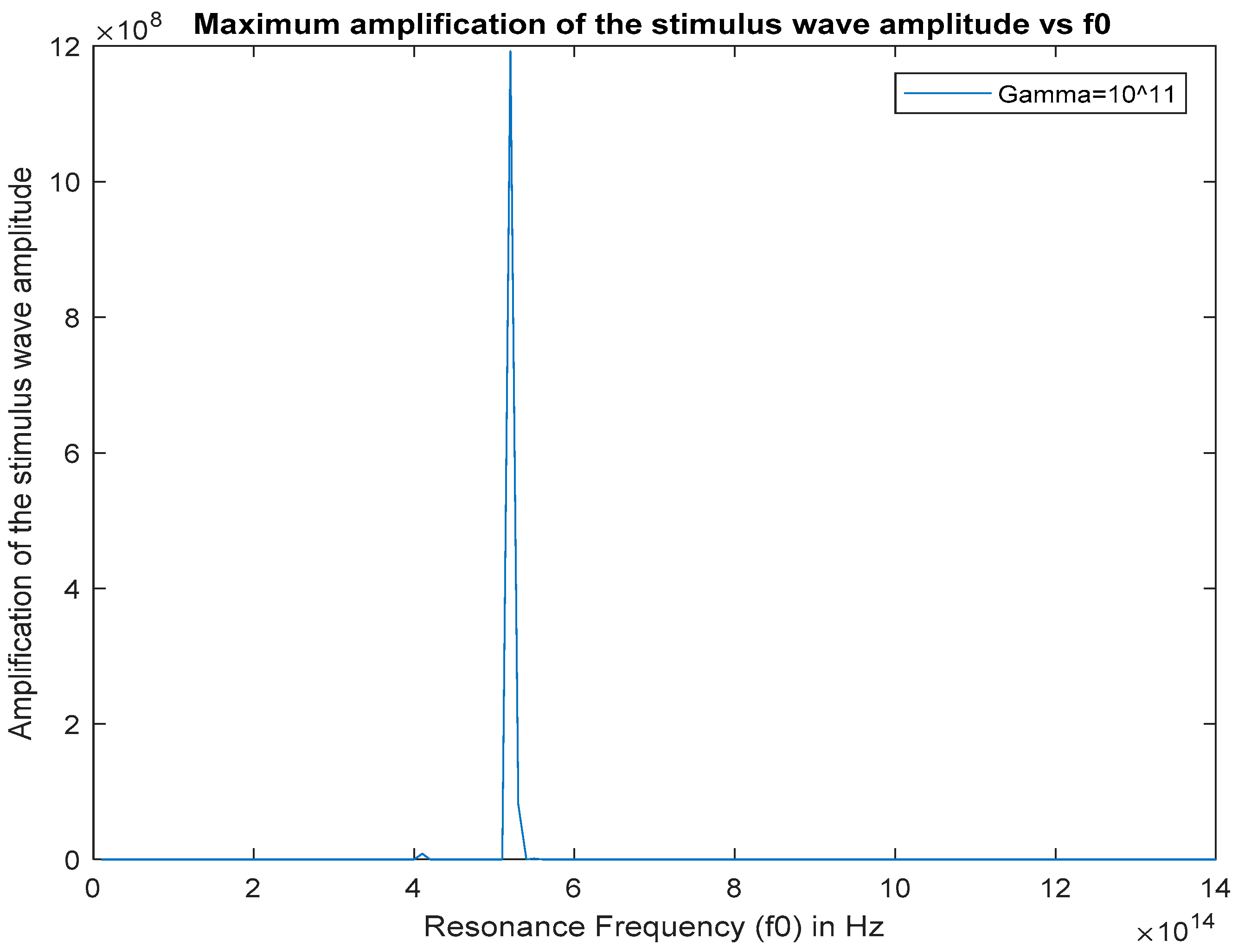
Figure 11.
Maximum stimulus wave amplitude (gain factor) inside the cavity at x = 5.73 µm for 0 < t < 30 ps, , versus
If we compare Figure 7 () and Figure 8 (), we can see that when the damping coefficient is increased from to most gain resonances decrease in amplitude, except the ones at and where there is a minor increase in the amplitudes of the gain peaks. However, if we look at Figure 9 () and Figure 10 (), there is a drastic attenuation of the gain factor from to and from to .
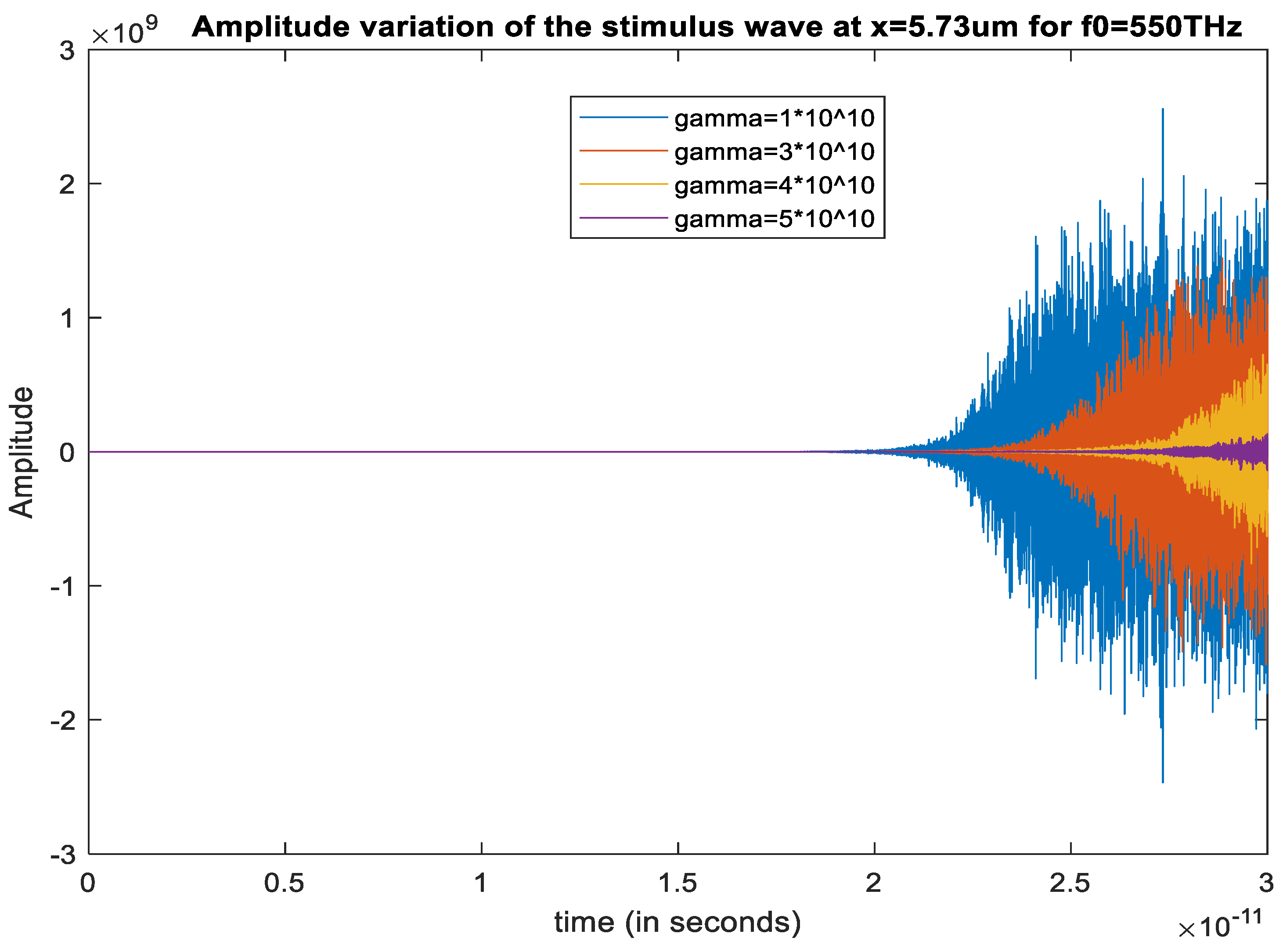
The amplification for is almost insignificant as shown in Figure 11. At this damping rate, the magnitude of the stored electric energy density is not enough to amplify the stimulus wave significantly, as the pump wave magnitude is quickly damped to a level at which nonlinearity is lost and energy coupling does not occur. Figure 12 illustrates the sharp decrease of the gain factor for

Figure 12.
Stimulus wave amplitude variation inside the cavity at x = 5.73 µm, for {, }, for a sample resonance frequency of
5.3. Analyzing the Gain Spectrum of the Stimulus Wave at the Optimal Resonance Frequency
Now let us compute the gain spectrum of the stimulus wave at the optimal resonance frequency of (see Figure 7 and Table 2), for . The configuration is shown in Figure 13:

Figure 13.
The configuration for computing the gain spectrum of the stimulus wave for .
Our problem: For the gain maximizing resonance frequency of 520 THz, find the maximum stimulus wave amplitude (gain factor) in the cavity for each stimulus wave frequency , in the range 10 THz < (THz to UV), for , such that
Initial conditions:
Boundary and excitation conditions:
Absorbing boundary condition (perfectly matched layer):
Optical isolator condition: Full reflection at
Switch controlled optical bandpass filter condition: Full reflection at for t 30 picoseconds, frequency dependent reflection at after t = 30 picoseconds;
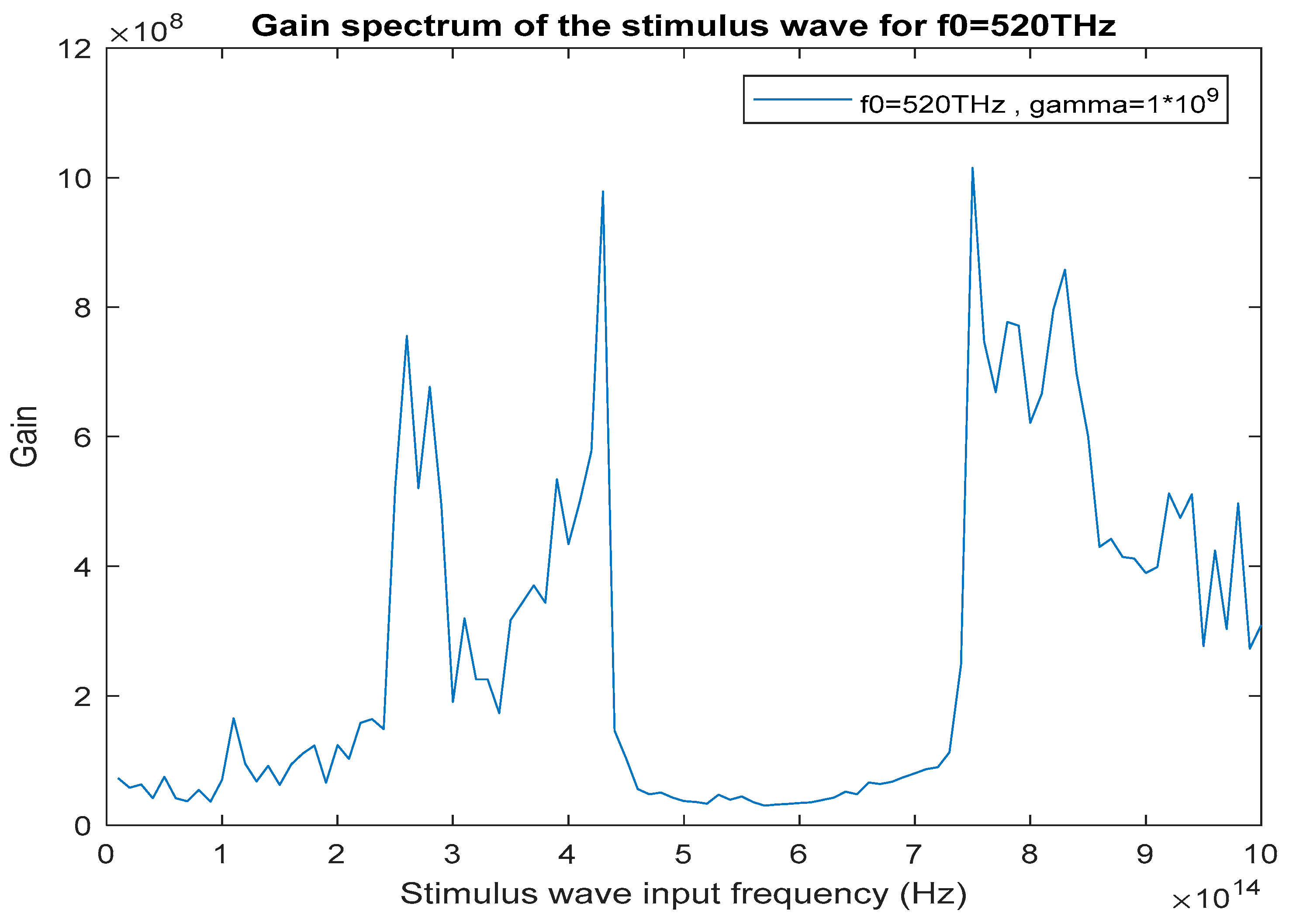
The stimulus wave is supplied to the cavity at t = 0 as a quasi-monochromatic wave. For a given initial (at t = 0 s) stimulus wave frequency, the center frequency of the band-pass filter is adjusted to be at the same frequency with the initial stimulus wave frequency. By doing so, we can observe how much gain can be obtained from the cavity for each initial stimulus wave frequency. Since the resonance frequency of yields the maximum stimulus wave gain, we choose this frequency to compute the gain spectrum of the stimulus wave. Then we sweep the stimulus wave frequency from 10 THz to 1000 THz in 10 THz increments. The amplification (gain) spectrum of the stimulus wave for = 520 THz is plotted below in Figure 14. As evident from Figure 14, the gain spectrum of the stimulus wave extends from the THz region to the UV region of the electromagnetic spectrum. This means that we can obtain strong output radiation at any frequency in the given band. Note that there is relatively low gain around the resonance frequency = 520 THz as the dielectric absorption is strong around the resonance region.

Figure 14.
Gain spectrum of the stimulus wave as measured at x = 11 µm for
Important Notes:
- (1)
- Based on our computations, changing the length of the cavity, or the length of the gain medium, does not change the spectral gain resonance locations.
- (2)
- The amplitude ( of the pump wave is the typical electric field amplitude of a focused 1.064 wavelength ultrashort Nd:YAG laser beam, which corresponds to an optical intensity of . Dielectric breakdown in dispersive media occurs at an optical intensity level of and beyond. Therefore, at this amplitude the pump wave would not induce dielectric breakdown and would not pose an optical hazard to the medium of interaction [13,14,15].
- (3)
- The temporal walk-off between the interacting waves that stems from the dispersion of the medium limits the effective interaction length. To counter-act this effect, we should ensure that the reflection losses at the cavity walls are minimized. The optical isolator that is used as a cavity wall should be of high quality to maximize intracavity reflections (. The bandpass transmission filter reflection coefficient must be maximized at the optical transmission stopband, so that the stored electric energy is retained in the cavity to support the high-gain amplification of the stimulus wave. In this paper we have assumed that the optical isolator (left cavity wall) reflection coefficient is 1 from the inside of the cavity (ideal optical isolator), and the reflection coefficient of the filter (right cavity wall) is close to 1 at the transmission stopband. When the reflection losses are minimized, the number of round trips in the cavity for which the nonlinearity is retained, is maximized and the reduced effective interaction length due to temporal walk-off between the interacting waves is compensated.
Another precaution to counter-act the temporal walk-off effect is to retain the high pump wave amplitude to keep the nonlinearity and nonlinear coupling as high as possible. This can be achieved by choosing an interaction medium with a low polarization damping coefficient. When the polarization damping coefficient is low, the stored electric energy is preserved for longer durations, which increases the number of round trips in the cavity for which the nonlinear energy coupling process is sustained. This also compensates for the reduced effective interaction length. The effect of the polarization damping coefficient on optical parametric amplification will be discussed in more detail in the next section.
5.4. Effect of the Damping Coefficient and the Mean Cavity Wall Reflection Coefficient on Optical Parametric Amplification
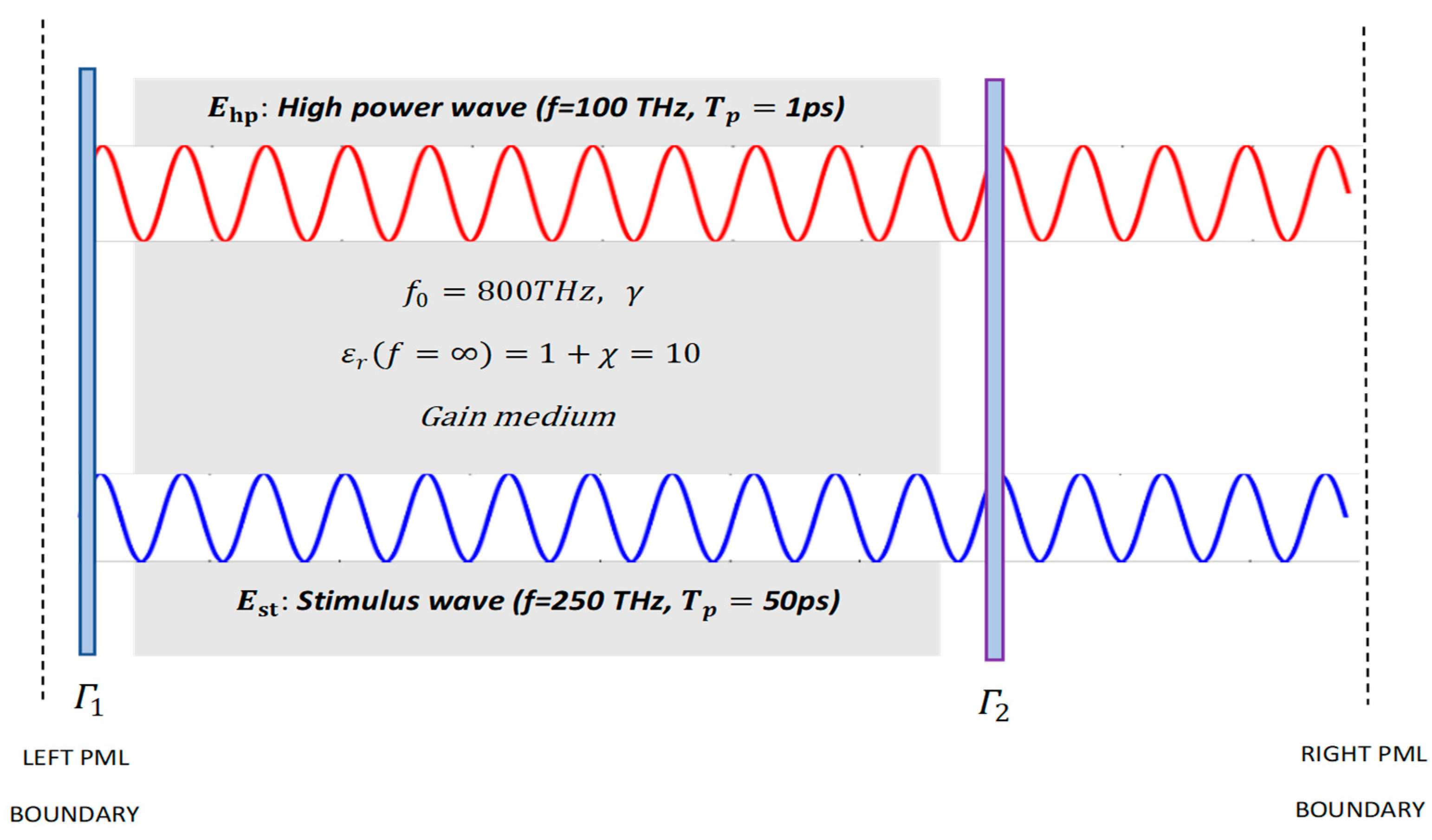
Consider the following resonant optical parametric amplification case, in which is the spectral location of a gain resonance for a 100 THz pump wave. The input wave and the pump wave are propagating inside a cavity that has two reflecting walls on the left and right side. Both waves are generated at x = 0 μm at time t = 0 s (see Figure 15).

Figure 15.
The cavity described along with the given parameters.
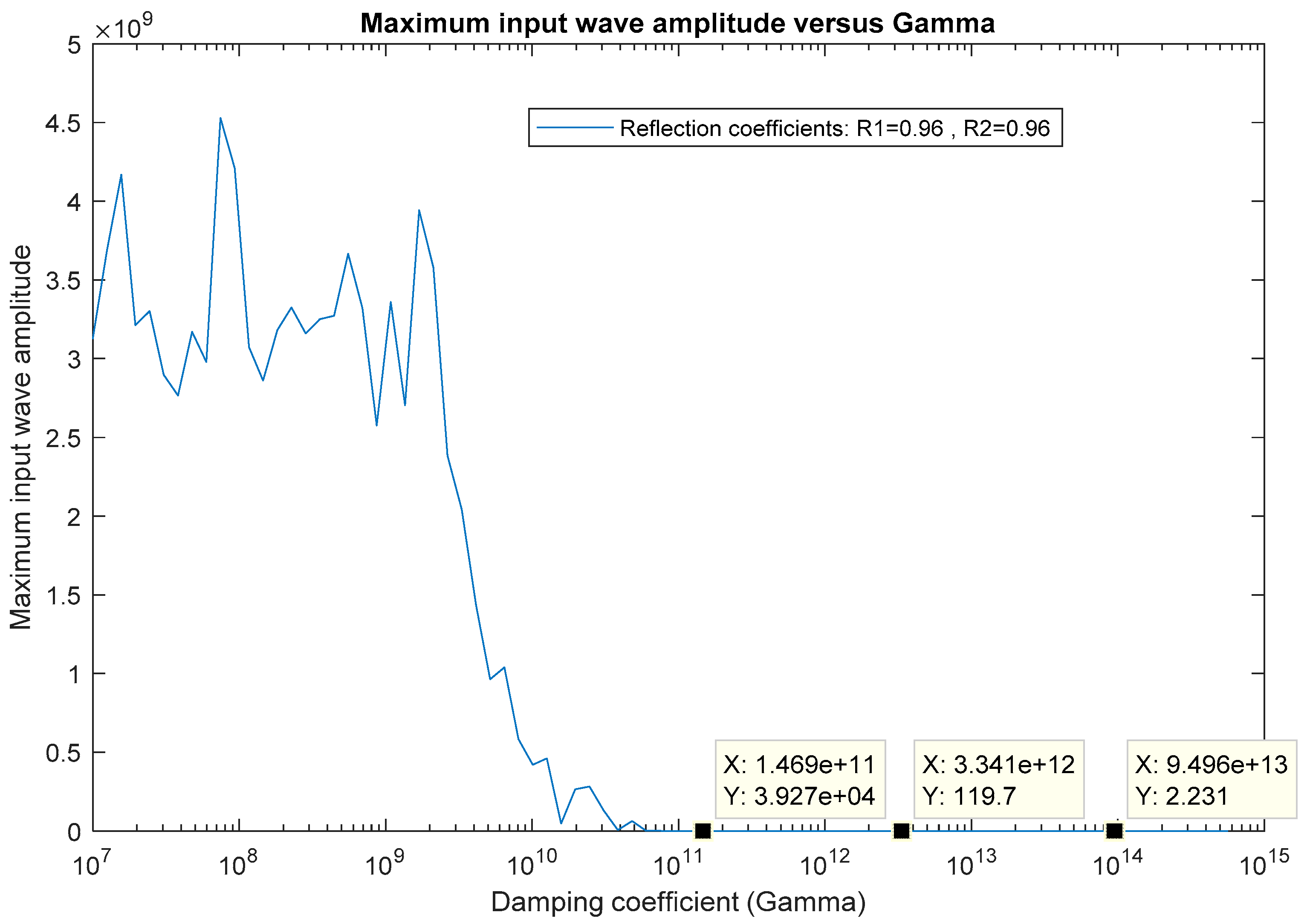
The variation of the maximum input wave amplitude that has been reached between 0 < t < 50 ps is plotted with respect to the damping coefficient and the mean cavity wall reflectivity in Figure 16 and Figure 17. If we look at these figures, it is obvious that as the damping coefficient decreases and/or as the mean cavity wall reflectivity increases, the amplification efficiency improves.

Figure 16.
Maximum input wave amplitude at x = 5.73 µm versus the damping coefficient gamma ().

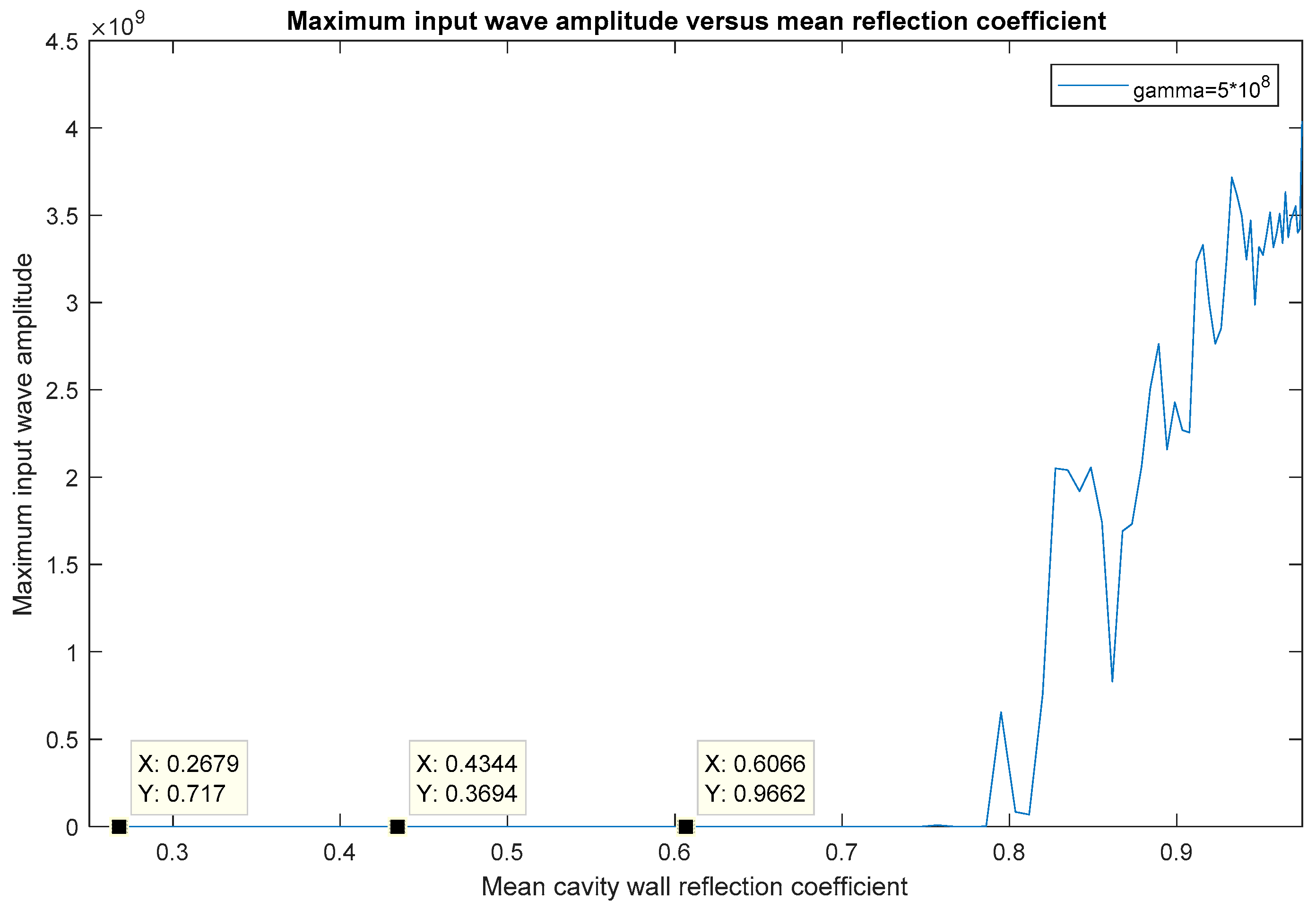
Figure 17.
Maximum input wave amplitude at x = 5.73 µm versus mean cavity wall reflection coefficient for an initial pump wave amplitude of at and for γ =
In Figure 16, we can clearly see that the maximum amplitude of the input (or stimulus) wave decreases sharply for . This means that the gain factor of the input wave to be amplified can be significantly enhanced by choosing an interaction medium with a low damping rate. Moreover, it is interesting to observe that the damping coefficient has a threshold value for high-gain amplification, in this case is the threshold value for high-gain amplification. Around , we can see that the amplification of the input wave has reduced by several orders of magnitude.
In Figure 17, we can see that the mean reflection coefficient of the cavity walls plays a major role in achieving high-gain optical parametric amplification. Below a mean reflection coefficient of = 0.79, the amplification becomes insignificantly small as compared to the amplification for > 0.9, and the gain factor (maximum reached amplitude for 0 < t < 50 ps) of the input wave gradually increases as the mean reflection coefficient of the cavity walls increases. As previously explained, this is because the stored electric energy is better preserved in the cavity for a larger mean reflection coefficient, which enables the amplitude of the pump wave and hence the nonlinearity, to be retained for a longer duration, and a higher gain factor of the input wave to be obtained [15,16,17,18]. The critical (threshold) values of the damping coefficient and the mean reflection coefficient of the cavity walls, for high-gain amplification, are investigated for three different values of the resonance frequency of the interaction medium, the input/stimulus wave frequency, and the pump wave frequency, as shown in Table 3. Based on these critical/threshold values, we suggest the mean reflection coefficient of the cavity walls to be greater than 0.85 ( > 0.85) and the damping coefficient of the dielectric interaction medium to be lower than .

Table 3.
Critical (threshold) values of the polarization damping coefficient and the mean reflection coefficient for high gain amplification of the input (stimulus) wave.
6. Conclusions
Recent studies on achieving high-gain optical parametric amplification in microresonators have focused on materials that display a strong nonlinearity under high intensity excitation. For instance, the recent studies mentioned in [19,20,21] have investigated lithium niobate (LN) for that matter. The study mentioned in [19] has focused on the strong nonlinearity of lithium niobate in a microcavity with a high quality factor, and the study mentioned in [20] has focused on optimal mode matching in a periodically poled waveguide. These studies have reported high harmonic generation and parametric amplification efficiencies. However, none of the recent studies have investigated the possible existence of optimum resonance frequencies for a given pump wave excitation, that can simultaneously maximize the stored electric energy density and the nonlinear coupling coefficient (pump wave polarization density) and may enable ultra high-gain amplification in microresonators with a cavity length of as small as a few micrometers.
Through rigorous computational analysis that involves the maximization of the nonlinear constructive interference and the nonlinear coupling coefficient, we have shown that a very wideband, super-gain optical parametric amplification is possible in a long microcavity. This interaction medium length is even much smaller than the recently suggested parametric amplification waveguide of 300 µm length mentioned in [21], as our analysis directly focuses on maximizing both the nonlinear energy coupling coefficient and the stored electric energy density in the cavity, rather than the stored electric energy (quality factor) alone, which are both critical in achieving a super-gain amplification.
As a summary for resonant optical parametric amplification by nonlinear wave mixing in a microresonator under a 282 THz Nd:YAG pump wave excitation, the following requirements must be met:
- The cavity should be low loss. This is satisfied in our computations by choosing a dielectric gain medium , and by adjusting the reflectivities of the cavity walls to be very high.
- The damping coefficient (polarization decay rate) of the gain medium should be low ().
- The resonance frequency of the gain medium must match with one of the resonance frequencies that are found to maximize the stimulus wave gain inside the cavity. In the case of a 282 THz Nd:YAG pump wave excitation, the resonance frequency of the interaction material should reside between 350 THz and 600 THz (350 THz < .
- Bithiophene based red fluorescent light emitting material called BTCN, which has a resonance frequency value of 470 THz with a FWHM bandwidth of 80 THz, is a suitable interaction medium for resonant optical parametric amplification using a 282 THz Nd:YAG pump wave excitation.
Once these requirements are satisfied, it is possible to amplify a low power input (stimulus) wave with a very large gain coefficient, in a wide range of frequencies, inside a low loss microresonator of several micrometers of length.
Author Contributions
Literature survey, background research, software design, and the interpretation of the results was conducted by Ö.E.A. Supervision of this article was conducted by M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Verification of Our Computational Model
We want to test the accuracy of our computational model by using the experimentally verified theoretical formula in the well-established context of sum frequency generation via nonlinear wave mixing, which is the basis of optical parametric amplification [1,4], in the following example.
Example A1.
Nonlinear sum frequency generation (frequency up-conversion).
This example is about the generation of a higher frequency component , by mixing two monochromatic waves with frequencies and , such that . In order to achieve this, at least one of the waves must have a high intensity, so that nonlinearity arises and wave mixing occurs.
The high amplitude pump wave is generated at x = 2.5 μm. It has an amplitude of V/m and a frequency of 180 THz.
The input wave is generated at x = 2.5 μm. It has an amplitude of V/m and a frequency of 120 THz.
Range of independent simulation variables:

Figure A1.
Configuration for frequency up-conversion.
Figure A1.
Configuration for frequency up-conversion.
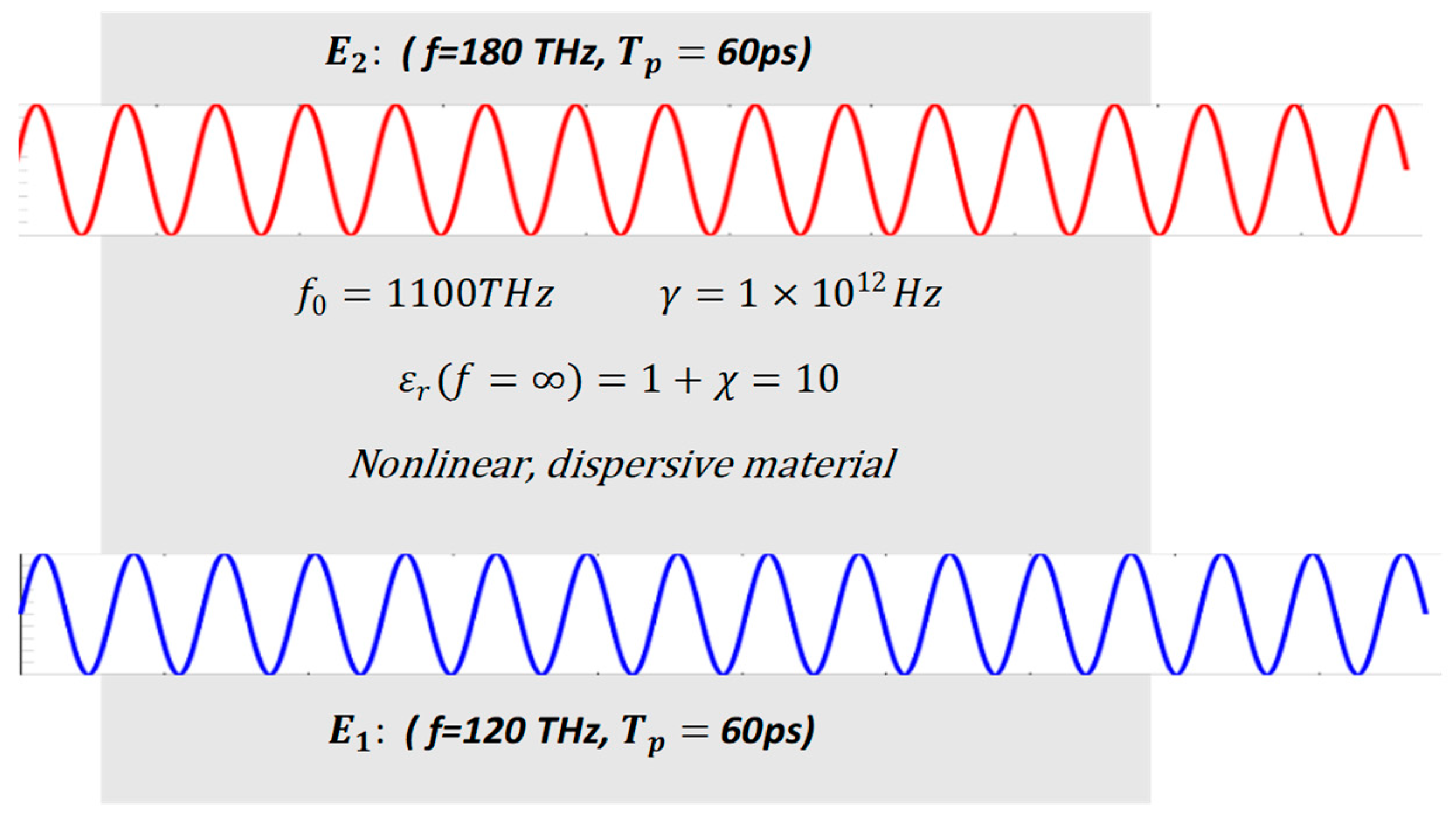
The theoretical formula for frequency up-conversion efficiency, which is derived from the solution of nonlinear wave equation that is based on material nonlinearity coefficient, is given as [4].
, ; d = Material nonlinearity coefficient, n = Refractive index; = Pump wave amplitude, = Input wave amplitude, L = Length of the nonlinear media; .
Our computational model is based on the finite difference time domain discretization of the nonlinear electron motion equation that involves the resonance frequency and the damping coefficient of the interaction medium. Coupled with the wave equation, the total wave can be evaluated from:
For a time interval of , the computational formula for frequency up-conversion efficiency is
In this example, we have used the following values for each efficiency formula
L = Length of the nonlinear dispersive media = 3.33 micrometers (from x = 3.33 to 6.66 );
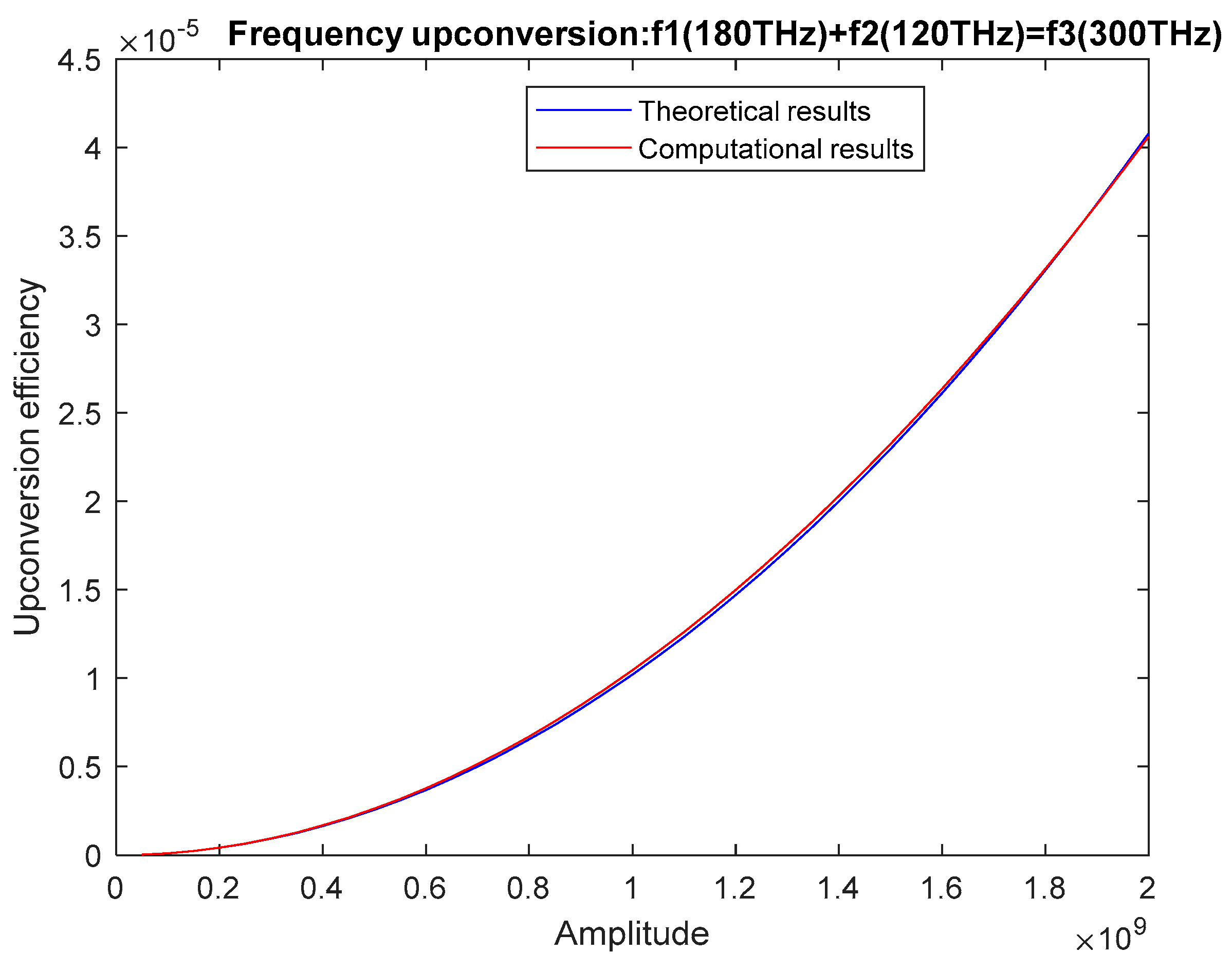
d = Material nonlinearity coefficient = (the theoretical and the computational results agree for this value of d for a sample pump wave amplitude of . Our aim is to see if the results also agree for all of the other pump wave amplitudes for this value of d); = Pump wave amplitude (varied from ); = Input wave amplitude = .

Figure A2.
Comparison of the frequency up-conversion efficiencies for = 300 THz and d = , versus the pump wave amplitude.
Figure A2.
Comparison of the frequency up-conversion efficiencies for = 300 THz and d = , versus the pump wave amplitude.
References
- Boyd Robert, W. Nonlinear Optics; Academic Press: New York, NY, USA, 2008; pp. 105–107. [Google Scholar]
- Mark, F. Optical Properties of Solids; Oxford University Press: New York, NY, USA, 2002; pp. 237–239. [Google Scholar]
- Balanis Constantine, A. Advanced Engineering Electromagnetics; John Wiley & Sons: New York, NY, USA, 1989; pp. 66–67. [Google Scholar]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; Wiley-Interscience: New York, NY, USA, 2007; pp. 885–917. [Google Scholar]
- Silfvast William, T. Laser Fundamentals; Cambridge University Press: New York, NY, USA, 2004; pp. 24–35. [Google Scholar]
- Satsuma, J.; Yajima, N. Initial Value Problems of One-Dimensional Self-Modulation of Nonlinear Waves in Dispersive Media. Prog. Theor. Phys. Suppl. 1974, 55, 284–306. [Google Scholar] [CrossRef]
- Xu, K. Integrated Silicon Directly Modulated Light Source Using p-Well in Standard CMOS Technology. IEEE Sens. J. 2016, 16, 6184–6191. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Boston, MA, USA, 2005; pp. 353–361. [Google Scholar]
- Xu, K. Silicon MOS Optoelectronic Micro-Nano Structure Based on Reverse-Biased PN Junction. Phys. Status Solidi A Appl. Mater. Sci. 2019, 216, 1800868. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Sukhorukov, A.A.; Lavrinenko, A.V.; Kivshar, Y.S. Comparative Study of FDTD-Adopted Numerical Algorithms for Kerr Nonlinearities. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 143–146. [Google Scholar] [CrossRef]
- Ozgun, O.; Kuzuoglu, M. Near-field performance analysis of locally-conformal perfectly matched absorbers via Monte Carlo simulations. J. Comput. Phys. 2007, 227, 1225–1245. [Google Scholar] [CrossRef]
- Mohan, M.; Satyanarayan, M.N.; Trivedi, D.R. Bithiophene based red light emitting material -Photophysical and DFT studies. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2115, p. 030577. [Google Scholar]
- Ciriolo, A.G.; Negro, M.; Devetta, M.; Cinquanta, E.; Faccialà, D.; Pusala, A.; Vozzi, C. Optical Parametric Amplification Techniques for the Generation of High-Energy Few-Optical-Cycles IR Pulses for Strong Field Applications. Appl. Sci. 2017, 7, 265. [Google Scholar] [CrossRef]
- Migal, E.A.; Potemkin, F.V.; Gordienko, V.M. Highly efficient optical parametric amplifier tunable from near-to mid-IR for driving extreme nonlinear optics in solids. Opt. Lett. 2017, 42, 5218–5221. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Fan, J.; Chen, G.; Jia, S. Symmetry-breaking-induced dynamics in a nonlinear microresonator. Opt. Express 2019, 27, 28133–28142. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.B.; Bark, H.S.; Jeon, T. Enhancement of THz resonance using a multilayer slab waveguide for a guided-mode resonance filter. Opt. Express 2019, 27, 29357–29366. [Google Scholar] [CrossRef] [PubMed]
- el Dirani, H.; Youssef, L.; Petit-Etienne, C.; Kerdiles, S.; Grosse, P.; Monat, C.; Pargon, E.; Sciancalepore, C. Ultralow-loss tightly confining Si3N4 waveguides and high-Q microresonators. Opt. Express 2019, 27, 30726–30740. [Google Scholar] [CrossRef] [PubMed]
- Izadi, M.A.; Nouroozi, R. Adjustable Propagation Length Enhancement of the Surface Plasmon Polariton Wave via Phase Sensitive Optical Parametric Amplification. Sci. Rep. 2018, 8, 15495. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Y.; Ma, Z.H.; Sua, Y.M.; Li, Z.; Tang, C.; Huang, Y.P. Ultra-efficient frequency conversion in quasi-phase-matched lithium niobate microrings. Optica 2019, 6, 1244–1245. [Google Scholar] [CrossRef]
- Sua, Y.M.; Chen, J.Y.; Huang, Y.P. Ultra-wideband and high-gain parametric amplification in telecom wavelengths with an optimally mode-matched PPLN waveguide. Opt. Lett. 2018, 43, 2965–2968. [Google Scholar] [CrossRef] [PubMed]
- Luo, R.; He, Y.; Liang, H.; Li, M.; Ling, J.; Lin, Q. Optical Parametric Generation in a Lithium Niobate Microring with Modal Phase Matching. Phys. Rev. Appl. 2019, 11, 034026. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).