Image Processing Operators Based on the Gyrator Transform: Generalized Shift, Convolution and Correlation

Abstract

The gyrator transform (GT) is used for images processing in applications of light propagation. We propose new image processing operators based on the GT, these operators are: Generalized shift, convolution and correlation. The generalized shift is given by a simultaneous application of a spatial shift and a modulation by a pure linear phase term. The new operators of convolution and correlation are defined using the GT. All these image processing operators can be used in order to design and implement new optical image processing systems based on the GT. The sampling theorem for images whose resulting GT has finite support is developed and presented using the previously defined operators. Finally, we describe and show the results for an optical image encryption system using a nonlinear joint transform correlator and the proposed image processing operators based on the GT.

1. Introduction

The usual convolution and correlation operations have been used in some optical systems for image processing, such as filtering, encryption, decryption, comparison, authentication, pattern recognition and classification of images [1,2,3,4,5,6]. Shift operation has also been used in optical systems; for instance, shift operation is utilized at the input plane of the joint transform correlator (JTC) architecture in order to place two non-overlapping data distributions side-by-side [7,8]. The usual shift, convolution and correlation operators have been defined using the fractional Fourier transform [9,10] and these fractional operators were applied to the sampling theorem for fractional bandlimited signal [11], time-variant filtering for non-stationary random signals [12] and prediction, interpolation and filtering of $\alpha$-stationary random signals [13], where $\alpha$ is the fractional order of the fractional Fourier transform [10].

In this paper, we propose to define a new generalized shift, convolution and correlation operators based on the gyrator transform (GT). The GT can be implemented using an optical system [14,15] or a digital algorithm [16]; these implementations are used in applications of filtering and encryption of images, holography, beam characterization, optical mode converter and phase-amplitude retrieval, among other things [17,18]. The generalized shift is the simultaneous application of a spatial shift and a modulation by a pure linear phase term that does not introduce a shift in the gyrator domain (GD). The proposed convolution and correlation operators are generalized versions of the usual convolution and correlation operations and these generalized versions depend on the parameter $\alpha$, which is the rotation angle of the GT. We provide explicit integral equations to compute the new convolution and correlation operators at the spatial domain. The new proposed convolution and correlation operators can also be computed in the GD using two GTs and a pure phase term. We apply the proposed new operators with the purpose of developing and defining the sampling theorem for images whose resulting GT has finite support. This result is important when it is necessary to sample properly the spatial domain or the GD of an optical system based on the GT. Finally, we present the application of the proposed new operators in order to describe and to simulate a nonlinear JTC-based encryption system in the GD [19,20].

2. The Gyrator Transform (GT) Operator

The gyrator transform (GT) operator at parameter $\alpha$, which is the rotation angle, of a two-dimensional function $f(x,y)$ is [14]

$$\begin{array}{c}\hfill f_{\alpha }(u,v)={\mathcal{G}}^{\alpha }\{f(x,y)\}=\underset{-\infty }{\overset{+\infty }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}f(x,y)K_{\alpha }(u,v,x,y)\mathrm{d}x\mathrm{d}y,\end{array}$$

(1)

$$\begin{array}{c}\hfill K_{\alpha }(u,v,x,y)=C_{\alpha }exp\{i2\pi \left[(uv+xy)cot\alpha -(vx+uy)csc\alpha \right]\},C_{\alpha }=\frac{1}{\left|\sin \alpha \right|},\end{array}$$

(2)

where x and y denote the coordinates at the spatial domain, u and v indicate the output coordinates in the gyrator domain (GD), $K_{\alpha }$ is the gyrator kernel and the possible values of the rotation angle are in the following interval $0\le \alpha <2\pi$. For $\alpha =0$, it corresponds to the identity transform. For $\alpha =\pi /2$, it reduces to the direct Fourier transform with rotation of the coordinate at $\pi /2$. For $\alpha =\pi$, the reverse transform is obtained. For $\alpha =3\pi /2$, it corresponds to the inverse Fourier transform with rotation of the coordinate at $\pi /2$ [14]. The inverse GT corresponds to the GT at rotation angle $-\alpha$. There are certain similarities in the properties of the GT and the fractional Fourier transform; however, these transforms are basically different, because the kernel of the GT is a product of the hyperbolic and plane waves, whereas the kernel of the fractional Fourier transform is the product of the spherical and the plane waves [19].

The main properties of the GT, which will be used below in the following sections, are

$$\begin{array}{c}\hfill {\mathcal{G}}^{\alpha }\{{\mathcal{G}}^{\beta }\{f(x,y)\}\}={\mathcal{G}}^{\alpha +\beta }\{f(x,y)\},\end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathcal{G}}^{\alpha }\{f(x-x_0,y-y_0)\}=& e^{i2\pi x_0{y}_0\sin \alpha \cos \alpha }{e}^{-i2\pi (x_{0}v+y_{0}u)\sin \alpha }{f}_{\alpha }(u-x_0\cos \alpha ,v-y_0\cos \alpha ),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\mathcal{G}}^{\alpha }\{e^{i2\pi (u_{0}x+v_{0}y)}f(x,y)\}=& e^{-i2\pi u_0{v}_0\sin \alpha \cos \alpha }{e}^{i2\pi (u_{0}u+v_{0}v)\cos \alpha }{f}_{\alpha }(u-v_0\sin \alpha ,v-u_0\sin \alpha ),\hfill \end{array}$$

(5)

where $x_0$, $y_0$, $u_0$ and $v_0$ are real constants. We can observe in Equations (4) and (5) that a shift or a modulation by a pure linear phase term applied to the function $f(x,y)$ produces a shift of the GT $f_{\alpha }(u,v)$, which is proportional to the parameters $\alpha$, $x_0$, $y_0$, $u_0$ and $v_0$. These properties of the shift or modulation by a pure linear phase term also introduce another modulation by a pure linear phase term in the GD. Other properties of the GT are described in [14].

3. Generalized Shift Operator

We propose a generalized shift operator as the simultaneous application over a function $f(x,y)$ of a spatial shift and a specific modulation by a pure linear phase term. The generalized shift operator at parameters $x_0$, $y_0$ and $\alpha$ is defined as

$$\begin{array}{c}\hfill {\mathrm{GS}}_{x_0,y_0;\alpha }f(x,y)=exp\left\{-i2\pi \left[y_0\left(x-\frac{x_0}{2}\right)+x_0\left(y-\frac{y_0}{2}\right)\right]cot\alpha \right\}f(x-x_0,y-y_0).\end{array}$$

(6)

The generalized shift operator is a commutative group for a given parameter $\alpha$. The composition law is ${\mathrm{GS}}_{x_1,y_1;\alpha }{\mathrm{GS}}_{x_2,y_2;\alpha }={\mathrm{GS}}_{x_1+x_2,y_1+y_2;\alpha }$. When the parameter $\alpha$ is equal to $\pi /2$, the generalized shift operator is reduced to the usual shift operator ${\mathrm{GS}}_{x_0,y_0;\pi /2}f(x,y)=f(x-x_0,y-y_0)$. The GT at parameter $\alpha$ of the generalized shift operator ${\mathrm{GS}}_{x_0,y_0;\alpha }$ is given by

$$\begin{array}{c}\hfill {\mathcal{G}}^{\alpha }\{{\mathrm{GS}}_{x_0,y_0;\alpha }f(x,y)\}=exp\left\{-i2\pi \left(y_{0}u+x_{0}v\right)csc\alpha \right\}{f}_{\alpha }(u,v).\end{array}$$

(7)

From the two previous equations, the parameter $\alpha$ corresponds to the rotation angle of the GT. The generalized shift operator does not produce a shift of the GT $f_{\alpha }(u,v)$ in comparison with Equations (4) and (5). This property is very useful for centred optical systems.

4. Convolution Operator in the GD

We define a new convolution operator at parameter $\alpha$ in the spatial domain by using the following integrals

$$\begin{array}{cc}\hfill f(x,y){\ast }_{\alpha }g(x,y)=C_{\alpha }\underset{-\infty }{\overset{+\infty }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}& f(x^{\prime },y^{\prime })g(x-x^{\prime },y-y^{\prime })\hfill \\ & \times exp\left\{-i2\pi \left[y^{\prime }(x-x^{\prime })+x^{\prime }(y-y^{\prime })\right]cot\alpha \right\}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }.\hfill \end{array}$$

(8)

The GTs of ${\mathcal{G}}^{\alpha }\{f(x,y)\}=f_{\alpha }(u,v)$ and ${\mathcal{G}}^{\alpha }\{g(x,y)\}=g_{\alpha }(u,v)$ allow to write the previous equation in the following form

$$\begin{array}{c}\hfill f(x,y){\ast }_{\alpha }g(x,y)={\mathcal{G}}^{-\alpha }\left\{f_{\alpha }(u,v)g_{\alpha }(u,v)exp\left\{-i2\pi uvcot\alpha \right\}\right\}.\end{array}$$

(9)

The proposed convolution operator at parameter $\alpha$ in the GD can be computed using the product of the resulting GTs at parameter $\alpha$ of the functions $f(x,y)$ and $g(x,y)$ and the pure phase term given by $exp\left\{-i2\pi uvcot\alpha \right\}$. The usual convolution is obtained from Equation (8) when $\alpha =\pi /2$, i.e., $f(x,y){\ast }_{\pi /2}g(x,y)=f(x,y)\ast g(x,y)$. The new convolution of a function $f(x,y)$ and a shifted Dirac delta function $\delta (x-x_0,y-y_0)$ is

$$\begin{array}{c}\hfill f(x,y){\ast }_{\alpha }\delta (x-x_0,y-y_0)=C_{\alpha }exp\left\{-i2\pi \left[y_0(x-x_0)+x_0(y-y_0)\right]cot\alpha \right\}f(x-x_0,y-y_0).\end{array}$$

(10)

Therefore, the generalized shift operator can be expressed in terms of the convolution operator proposed in this work

$$\begin{array}{c}\hfill {\mathrm{GS}}_{x_0,y_0;\alpha }f(x,y)=\frac{1}{C_{\alpha }}\left[f(x,y){\ast }_{\alpha }\delta (x-x_0,y-y_0)\right]exp\left\{-i2\pi x_0{y}_{0}cot\alpha \right\}.\end{array}$$

(11)

The proposed new convolution operator is invariant to the generalized shift operator

$$\begin{array}{c}\hfill {\mathrm{GS}}_{x_0,y_0;\alpha }\left[f(x,y){\ast }_{\alpha }g(x,y)\right]=\left[{\mathrm{GS}}_{x_0,y_0;\alpha }f(x,y)\right]{\ast }_{\alpha }g(x,y)=f(x,y){\ast }_{\alpha }\left[{\mathrm{GS}}_{x_0,y_0;\alpha }g(x,y)\right].\end{array}$$

(12)

5. Correlation Operator in the GD

We propose the definition of a new correlation operator at parameter $\alpha$ in the spatial domain by using the following integrals

$$\begin{array}{cc}\hfill f(x,y){⊛}_{\alpha }g(x,y)=C_{\alpha }\underset{-\infty }{\overset{+\infty }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}& f(x^{\prime },y^{\prime })g^{\ast }(x^{\prime }-x,y^{\prime }-y)\hfill \\ & \times exp\left\{i2\pi \left[y(x^{\prime }-x)+x(y^{\prime }-y)\right]cot\alpha \right\}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }.\hfill \end{array}$$

(13)

Using the GTs ${\mathcal{G}}^{\alpha }\{f(x,y)\}=f_{\alpha }(u,v)$ and ${\mathcal{G}}^{\alpha }\{g(x,y)\}=g_{\alpha }(u,v)$, the integral form of the new correlation operator can be expressed as

$$\begin{array}{c}\hfill f(x,y){⊛}_{\alpha }g(x,y)={\mathcal{G}}^{-\alpha }\left\{f_{\alpha }(u,v)g_{\alpha }^{\ast }(u,v)exp\left\{i2\pi uvcot\alpha \right\}\right\}.\end{array}$$

(14)

The new correlation operator at parameter $\alpha$ in the GD is computed using the product of the GTs $f_{\alpha }(u,v)$ and $g_{\alpha }^{\ast }(u,v)$ and the pure phase term given by $exp\left\{i2\pi uvcot\alpha \right\}$. The new correlation operator is reduced to the usual correlation when $\alpha =\pi /2$, i.e., $f(x,y){⊛}_{\pi /2}g(x,y)=f(x,y)⊛g(x,y)$. The new correlation operator is also invariant to the generalized shift operator

$$\begin{array}{c}\hfill {\mathrm{GS}}_{x_0,y_0;\alpha }\left[f(x,y){⊛}_{\alpha }g(x,y)\right]=\left[{\mathrm{GS}}_{x_0,y_0;\alpha }f(x,y)\right]{⊛}_{\alpha }g(x,y)=f(x,y){⊛}_{\alpha }\left[{\mathrm{GS}}_{-x_0,-y_0;\alpha }g(x,y)\right].\end{array}$$

(15)

6. Sampling Theorem in the GD

Nowadays, the optical implementations of image processing systems are mainly carried out using optoelectronic devices, such as spatial light modulators or cameras. These devices introduce a sampling over the optical wave that it is used in an optical image processing system. Therefore, a right sampling at the spatial domain is necessary for a current optical image processing system when all features of the resulting GT for an image must be preserved by the mentioned optoelectronic devices.

In this section, we use the proposed operators in order to describe the sampling theorem for images whose resulting GT has finite support. We define a new Dirac comb function at parameter $\alpha$ with periods $T_x$ and $T_y$ by

$$\begin{array}{c}\hfill {\displaystyle com{b}_{\alpha }\left(\frac{x}{T_x},\frac{y}{T_y}\right)=T_x{T}_y\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }exp\left\{-i2\pi m{T}_{x}n{T}_{y}cot\alpha \right\}\delta (x-m{T}_x)\delta (y-n{T}_y).}\end{array}$$

(16)

The GT at parameter $\alpha$ of the new Dirac comb function is

$$\begin{array}{c}\hfill {\mathcal{G}}^{\alpha }\left\{com{b}_{\alpha }\left(\frac{x}{T_x},\frac{y}{T_y}\right)\right\}=C_{\alpha }{T}_x{T}_{y}com{b}_{-\alpha }\left(\frac{u}{\sin \alpha /T_y},\frac{v}{\sin \alpha /T_x}\right).\end{array}$$

(17)

Therefore, the GT at parameter $\alpha$ of the new Dirac comb function at parameter $\alpha$ with periods $T_x$ and $T_y$ is another new Dirac comb function at parameter $-\alpha$ with periods $\sin \alpha /T_y$ and $\sin \alpha /T_x$.

In order to describe the sampling theorem in the GD, we consider a function $f(x,y)$ whose GT $f_{\alpha }(u,v)$ has a finite support $[-u_0/2,u_0/2]$ for the horizontal coordinate u and $[-v_0/2,v_0/2]$ for the vertical coordinate v. The following function $S(u,v)$ represents shifted replicas of $f_{\alpha }(u,v)$

$$\begin{array}{cc}\hfill S(u,v)=& f_{\alpha }(u,v){⊛}_{-\alpha }com{b}_{-\alpha }\left(\frac{u}{u_0},\frac{v}{v_0}\right)\hfill \\ \hfill =& {\displaystyle C_{\alpha }{u}_0{v}_0\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }exp\left\{-i2\pi (n{u}_0)(m{v}_0)cot\alpha \right\}exp\left\{i2\pi \left(n{v}_{0}u+m{u}_{0}v\right)cot\alpha \right\}}\hfill \\ & \times f_{\alpha }(u-m{u}_0,v-n{v}_0).\hfill \end{array}$$

(18)

The inverse GT at parameter $-\alpha$ of the previous equation is

$$\begin{array}{c}\hfill {\displaystyle S(x,y)=\frac{1}{C_{\alpha }}\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }f\left(m\frac{\sin \alpha }{v_0},n\frac{\sin \alpha }{u_0}\right)\delta \left(x-m\frac{\sin \alpha }{v_0}\right)\delta \left(y-n\frac{\sin \alpha }{u_0}\right).}\end{array}$$

(19)

Equation (19) is a sampled version of $f(x,y)$ for the sampling periods of the coordinates x and y given by $T_x=\sin \alpha /v_0$ and $T_y=\sin \alpha /u_0$, respectively. The reconstruction of $f(x,y)$ is computed by using the image filtering of the function $S(x,y)$ with a low-pass filter in the GD; this image filtering is described with the proposed convolution operator of Section 4. Thus, the reconstruction of $f(x,y)$ is

$$\begin{array}{cc}\hfill f(x,y)=& S(x,y){⊛}_{-\alpha }{\mathcal{G}}^{-\alpha }\left\{\frac{1}{u_0{v}_0}rect\left(\frac{u}{u_0},\frac{v}{v_0}\right)exp\left\{i2\pi uvcot\alpha \right\}\right\}\hfill \\ \hfill =& {\displaystyle C_{\alpha }exp\left\{-i2\pi xycot\alpha \right\}\sum _{m=-\infty }^{\infty }\sum _{n=-\infty }^{\infty }exp\left\{i2\pi m{T}_{x}n{T}_{y}cot\alpha \right\}f(m{T}_x,n{T}_y)}\hfill \\ & \times \frac{\sin \left(\pi \left(x-m{T}_x\right)/T_x\right)}{\pi \left(x-m{T}_x\right)/T_x}\frac{\sin \left(\pi \left(y-n{T}_y\right)/T_y\right)}{\pi \left(y-n{T}_y\right)/T_y}.\hfill \end{array}$$

(20)

The low-pass filter in the GD is a rectangle whose extension on the horizontal coordinate is $u_0$ and the extension on the vertical coordinate is $v_0$. Therefore, the extension of the low-pass filter in the GD is given by the size of the finite support of the GT $f_{\alpha }(u,v)$. Equation (20) is the sampling theorem in the GD and this equation provides the values of $f(x,y)$ for every x and y in terms of the sampled version of $f(x,y)$ whenever the sampling periods are defined using the following conditions $T_x\le \sin \alpha /v_0$ and $T_y\le \sin \alpha /u_0$. If the previous condition is not fulfilled, the reconstruction of $f(x,y)$ will have aliasing.

7. Optical Image Encryption System Using a Nonlinear Joint Transform Correlator (JTC) in the GD

Several optical image processing systems can be described and analysed using the new operators proposed in this work. The use of these new operators allows for an easy, simple and compact description of the behaviour for some optical image processing systems in the GD.

The proposed operators of the previous sections are used with the purpose of describing and simulating the nonlinear JTC-based encryption system that was presented in the work of references [19,20]. The real-valued image to encrypt $z(x,y)$ has their values in the interval [0, 1] and the two random phase masks (RPMs) $k(x,y)$ and $h(x,y)$ are represented by

$$k(x,y)=exp\{i2\pi m(x,y)\},h(x,y)=exp\{i2\pi n(x,y)\},$$

(21)

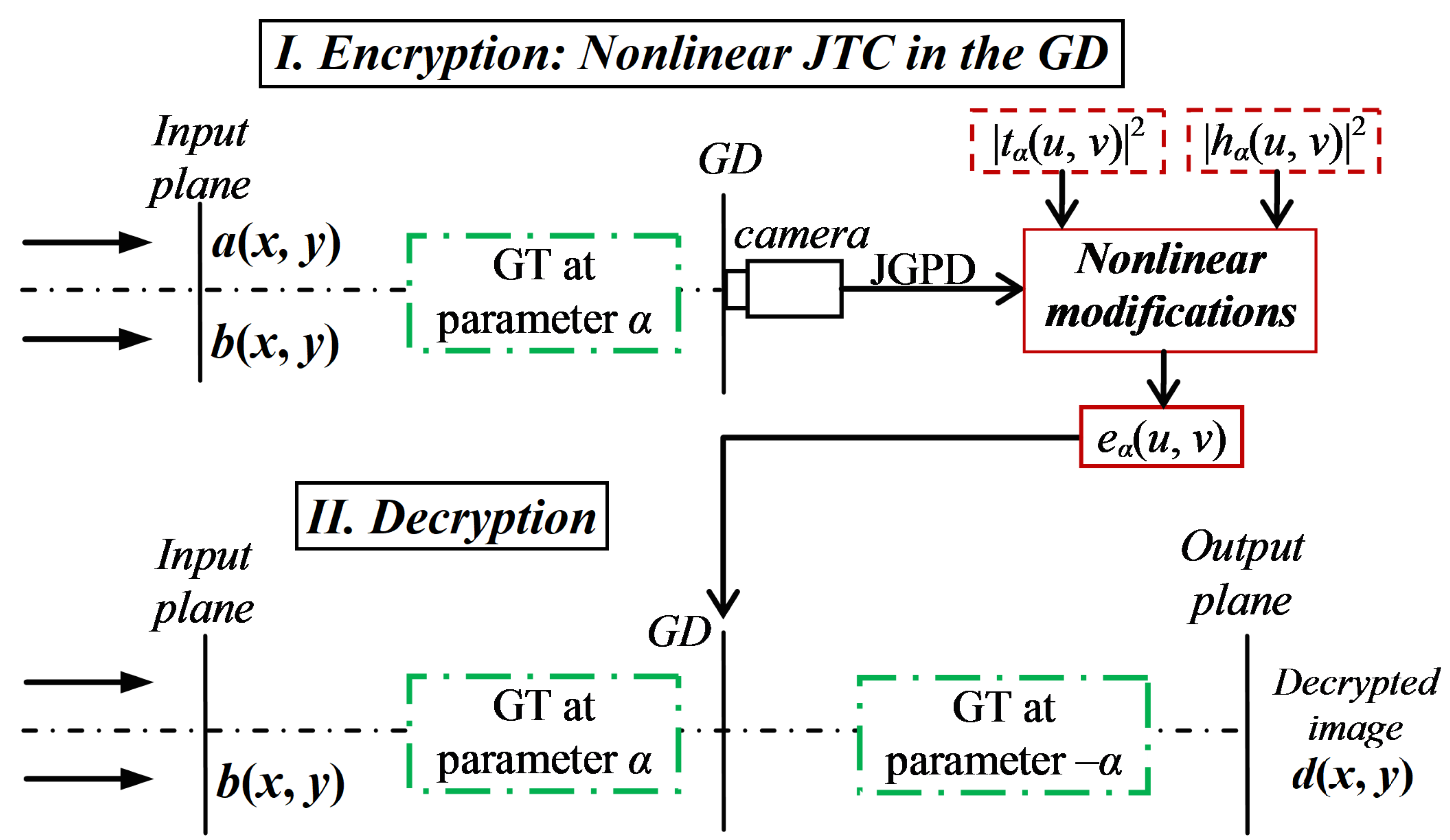
where $m(x,y)$ and $n(x,y)$ are normalized positive functions randomly generated, statistically independent and uniformly distributed in the interval [0, 1]. Figure 1 (part I) depicts the optical encryption scheme based on a nonlinear JTC architecture in the GD. The input plane of the JTC-based encryption system uses two non-overlapping data distributions placed side-by-side. The first data distribution $a(x,y)$ is the result given by the application of the generalized shift operator at parameters $x_0\ne 0$, $y_0=0$ and $\alpha \ne 0$ over the real image to encrypt $z(x,y)$ placed against the RPM $k(x,y)$

$$a(x,y)={\mathrm{GS}}_{x_0,0;\alpha }\left\{k(x,y)z(x,y)\right\}=exp\left\{-i2\pi x_{0}ycot\alpha \right\}z(x-x_0,y)k(x-x_0,y).$$

(22)

The second data distribution $b(x,y)$ of the input plane of the JTC corresponds to the result given by the application of the generalized shift operator at parameters $-x_0\ne 0$, $y_0=0$ and $\alpha \ne 0$ over the RPM $h(x,y)$

$$b(x,y)={\mathrm{GS}}_{-x_0,0;\alpha }\left\{h(x,y)\right\}=exp\left\{i2\pi x_{0}ycot\alpha \right\}h(x+x_0,y).$$

(23)

The GT at parameter $\alpha$ of the distributions $k(x,y)z(x,y)$ and $h(x,y)$ are denoted by

$$t_{\alpha }(u,v)={\mathcal{G}}^{\alpha }\{k(x,y)z(x,y)\},h_{\alpha }(u,v)={\mathcal{G}}^{\alpha }\{h(x,y)\}=\left|h_{\alpha }(u,v)\right|exp\{i2\pi {\varphi }_{\alpha }(u,v)\}.$$

(24)

For the encryption system, the joint gyrator power distribution (JGPD) at parameter $\alpha$ is the intensity of the GT at parameter $\alpha$ applied over the input plane of the JTC [19]

$$\begin{array}{c}\hfill {\mathrm{JGPD}}_{\alpha }(u,v)={\left|{\mathcal{G}}^{\alpha }\left\{a(x,y)+b(x,y)\right\}\right|}^2.\end{array}$$

(25)

The encrypted image is computed using the following nonlinear processing on the JGPD [19]

$$\begin{array}{cc}\hfill e_{\alpha }(u,v)=& \frac{{\mathrm{JGPD}}_{\alpha }(u,v)-{\left|t_{\alpha }(u,v)\right|}^2-{\left|h_{\alpha }(u,v)\right|}^2}{{\left|h_{\alpha }(u,v)\right|}^2}=t_{\alpha }^{\ast }(u,v)\frac{h_{\alpha }(u,v)}{{\left|h_{\alpha }(u,v)\right|}^2}exp\left\{i2\pi (2x_0)vcsc\alpha \right\}\hfill \\ & +t_{\alpha }(u,v)\frac{h_{\alpha }^{\ast }(u,v)}{{\left|h_{\alpha }(u,v)\right|}^2}exp\left\{-i2\pi (2x_0)vcsc\alpha \right\}.\hfill \end{array}$$

(26)

If ${\left|h_{\alpha }(u,v)\right|}^2$ is equal to zero for a particular value of u and v, this intensity value is substituted by a small constant to avoid singularities when computing $e_{\alpha }(u,v)$. The encrypted image is a real-valued image that can be computed using the following three intensity distributions: ${\mathrm{JGPD}}_{\alpha }(u,v)$, ${\left|t_{\alpha }(u,v)\right|}^2$ and ${\left|h_{\alpha }(u,v)\right|}^2$. The security keys of the encryption system are given by the RPM $h(x,y)$ and the rotation angle $\alpha$ of the GT. The RPM $k(x,y)$ is used to spread the information content of the original image $z(x,y)$ onto the encrypted image $e_{\alpha }(u,v)$ [19]. The inverse GT at parameter $-\alpha$ of Equation (26) denotes the encrypted image $e(x,y)$ in the spatial domain

$$\begin{array}{cc}\hfill e(x,y)=& {\mathcal{G}}^{-\alpha }\left\{e_{\alpha }(u,v)\right\}={\mathrm{GS}}_{-2x_0,0;\alpha }\left\{\left[h(x,y){⊛}_{\alpha }\left(k(x,y)z(x,y)\right)\right]{\ast }_{\alpha }{h}_1(x,y)\right\}\hfill \\ & +{\mathrm{GS}}_{2x_0,0;\alpha }\left\{\left[\left(k(x,y)z(x,y)\right){⊛}_{\alpha }h(x,y)\right]{\ast }_{\alpha }{h}_1(x,y)\right\},\hfill \end{array}$$

(27)

where $h_1(x,y)={\mathcal{G}}^{-\alpha }\left\{1/{\left|h_{\alpha }(u,v)\right|}^2\right\}$. Therefore, the encrypted image $e(x,y)$ of reference [19] can be described using the proposed generalized shift, convolution and correlation operators in this work.

For the initial step of the decryption system depicted in Figure 1 (part II), we perform the product of the GT of the second data distribution ${\mathcal{G}}^{\alpha }\left\{b(x,y)\right\}$ and the encrypted image $e_{\alpha }(u,v)$, in order to obtain the following result

$$\begin{array}{cc}\hfill d_{\alpha }(u,v)=& e_{\alpha }(u,v){\mathcal{G}}^{\alpha }\left\{b(x,y)\right\}=e_{\alpha }(u,v)h_{\alpha }(u,v)exp\left\{i2\pi x_{0}vcsc\alpha \right\}\hfill \\ \hfill =& \left[h_{\alpha }(u,v){\left({\mathcal{G}}^{\alpha }\left\{k(x,y)z(x,y)\right\}\right)}^{\ast }exp\left\{i2\pi uvcot\alpha \right\}\right]\frac{1}{h_{\alpha }^{\ast }(u,v)}exp\left\{-i2\pi uvcot\alpha \right\}\hfill \\ & \times exp\left\{i2\pi (3x_0)vcsc\alpha \right\}+{\mathcal{G}}^{\alpha }\left\{k(x,y)z(x,y)\right\}\frac{h_{\alpha }^{\ast }(u,v)h_{\alpha }(u,v)}{{\left|h_{\alpha }(u,v)\right|}^2}exp\left\{-i2\pi x_{0}vcsc\alpha \right\}.\hfill \end{array}$$

(28)

Using the result of Equations (7), (9) and (14), the inverse GT at parameter $-\alpha$ of the previous equation is the output plane $d(x,y)$ of the decryption system

$$\begin{array}{cc}\hfill d(x,y)=& {\mathcal{G}}^{-\alpha }\left\{d_{\alpha }(u,v)\right\}={\mathrm{GS}}_{-3x_0,0;\alpha }\left\{\left[h(x,y){⊛}_{\alpha }\left(k(x,y)z(x,y)\right)\right]{\ast }_{\alpha }{h}_2(x,y)\right\}\hfill \\ & +{\mathrm{GS}}_{x_0,0;\alpha }\left\{k(x,y)z(x,y)\right\},\hfill \end{array}$$

(29)

where $h_2(x,y)={\mathcal{G}}^{-\alpha }\left\{1/h_{\alpha }^{\ast }(u,v)\right\}$. The proposed operators in this work can also be used in order to describe the output plane $d(x,y)$ of the decryption system presented in reference [19]. If we take the absolute value of the second term of the right side of Equation (29), we obtain the decrypted image $\tilde{z}(x,y)$ centred at coordinates $x=x_0$ and $y=0$

$$\tilde{z}(x-x_0,y)=\left|{\mathrm{GS}}_{x_0,0;\alpha }\left\{k(x,y)z(x,y)\right\}\right|.$$

(30)

We perform the numerical simulations of the encryption and decryption systems that were described using the the proposed generalized shift, convolution and correlation operators in this work. Figure 2a,b show the original image to encrypt and the random distribution code $m(x,y)$ of the RPM $k(x,y)$, respectively. The random distribution code $n(x,y)$ of the RPM $h(x,y)$ has a similar appearance to the image presented in Figure 2b but different values for their pixels. The image presented in Figure 2c corresponds to the encrypted image $e_{\alpha }(u,v)$ for the security keys $\alpha =0.727\pi$ and the RPM $h(x,y)$. The decrypted image $\tilde{z}(x,y)$ is shown in Figure 2d when the right values of the security key are used in the decryption system. If a wrong value of the rotation angle $\alpha$ of the GT or an incorrect RPM $h(x,y)$ are used in the decryption process, the obtained decrypted image will be a random distribution image. In reference [19], the authors showed that the sensitivity of the rotation angle of the GT over the resulting decrypted images is much higher than the sensitivity shown by the encryption–decryption system that uses generalized JTC to variations in the fractional order of the fractional Fourier transform.

8. Conclusions

We have proposed new image processing operators based on the GT; these new operators are: Generalized shift and the convolution and correlation operations in the GD. The generalized shift operator allows to use shifted distribution images at the input plane (spatial domain) of an optical system without introducing a shift for the resulting GTs of these shifted distribution images. This feature of the generalized shift operator is very helpful for centred optical systems. The proposed new operators for the convolution and correlation can be computed in the GD using the product of the results of two GTs and a pure phase term. For these new operators of the convolution and correlation, we presented two explicit integrals that permit to perform generalized convolution and correlation operations at the spatial domain using different values of the parameter $\alpha$. The sampling theorem in the GD for images whose resulting GT has finite support was developed and presented by using the new operators proposed in this work. We show that the sampling periods at the spatial domain are directly proportional to the term $\sin \alpha$, where the parameter $\alpha$ is the rotation angle of the GT and inversely proportional to the extension or lengths of the finite support of the image given by the result of the GT. Finally, a nonlinear JTC-based encryption system in the GD was described and simulated by using the new operators proposed in this paper. We expect that the proposed new operators can be used to design, analyse and improve some optical image processing systems, such as imaging systems, diffraction through an aperture, beam focusing, optical tweezers and image filtering system, among others.