Tunable THz Graphene Filter Based on Cross-In-Square-Shaped Resonators Metasurface
Abstract
1. Introduction
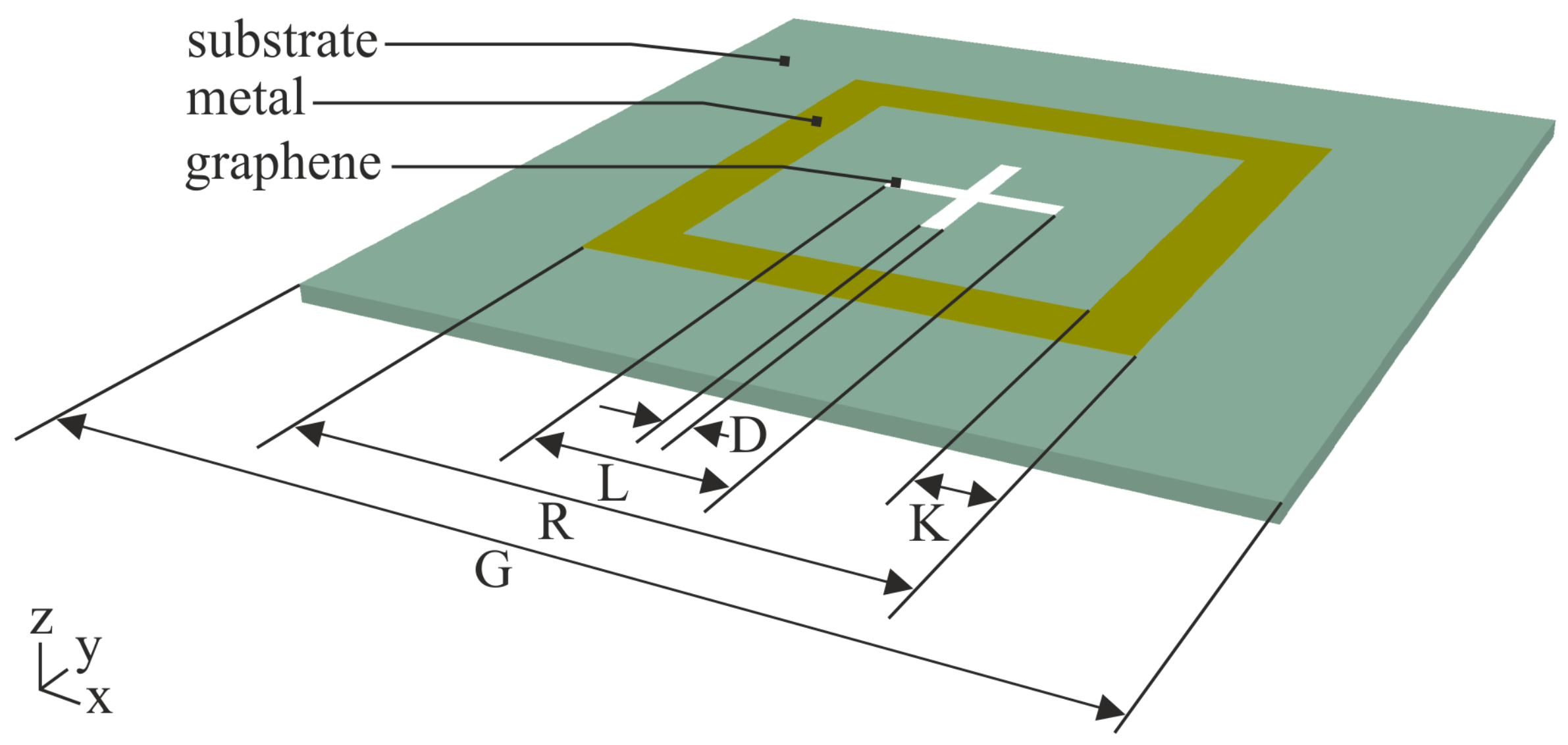
2. Structure Description and Numerical Investigation
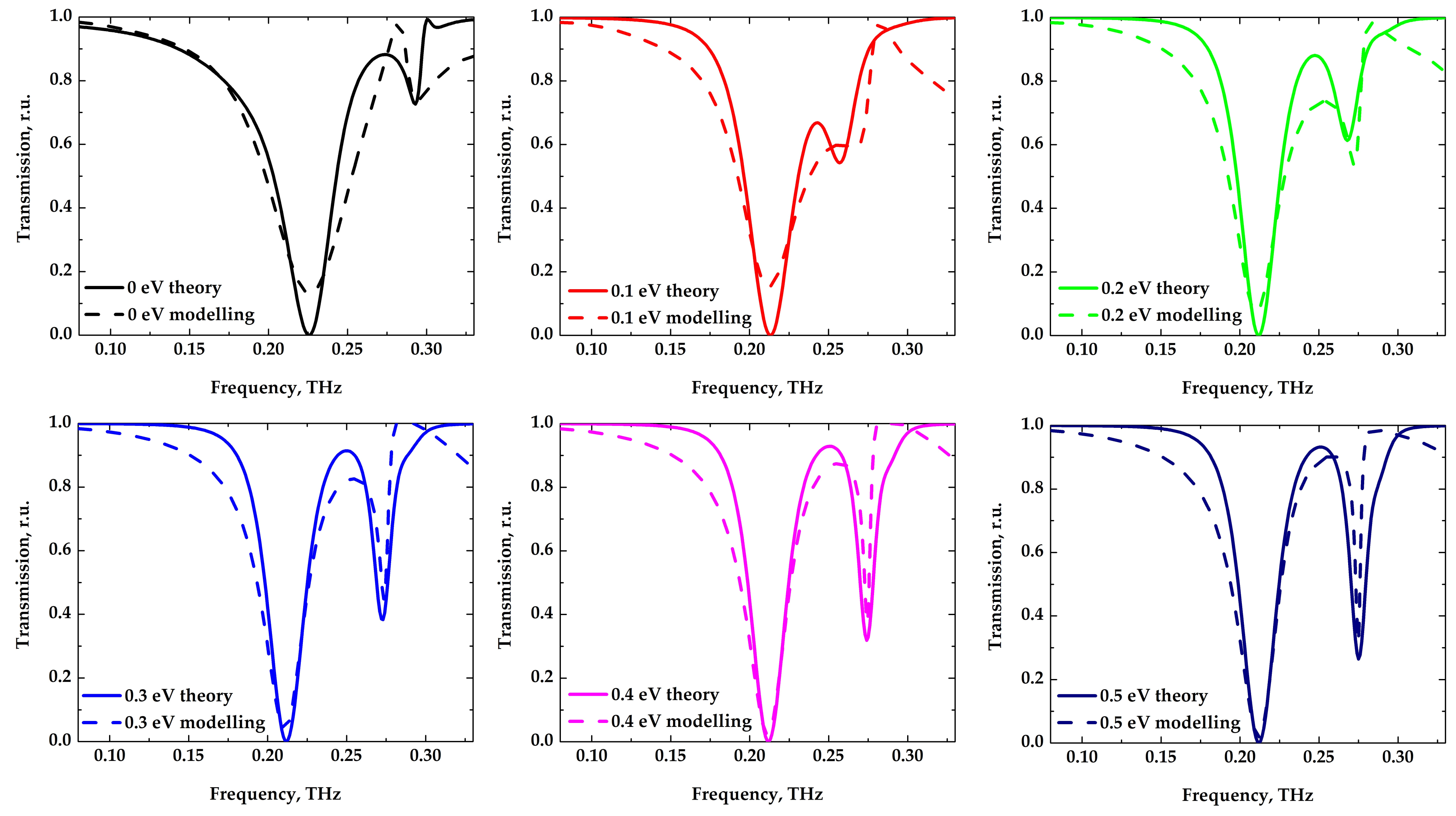
2.1. Conductivity Model of Graphene
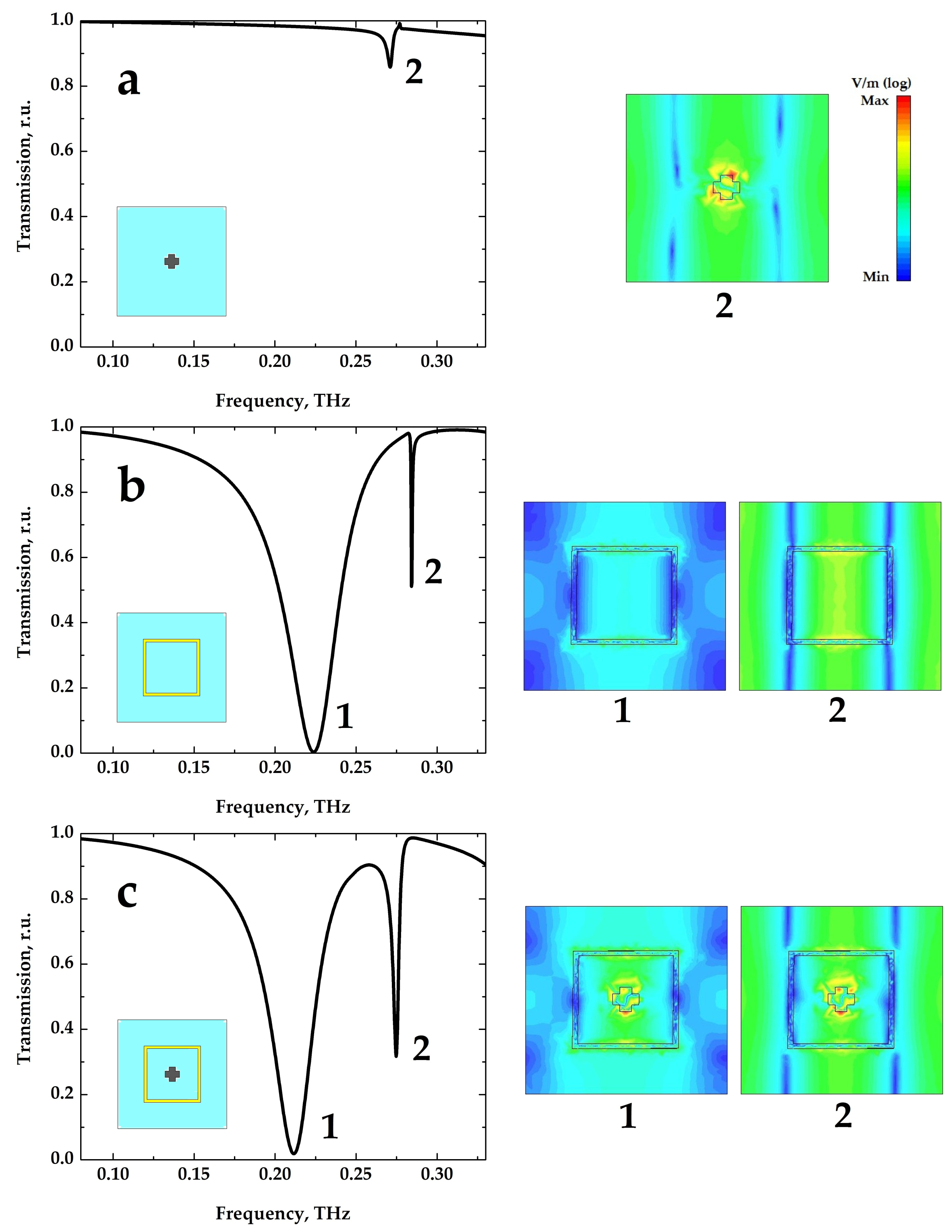
2.2. Numerical Simulation
3. Discussion
3.1. Coupled Oscillators Model Explanation
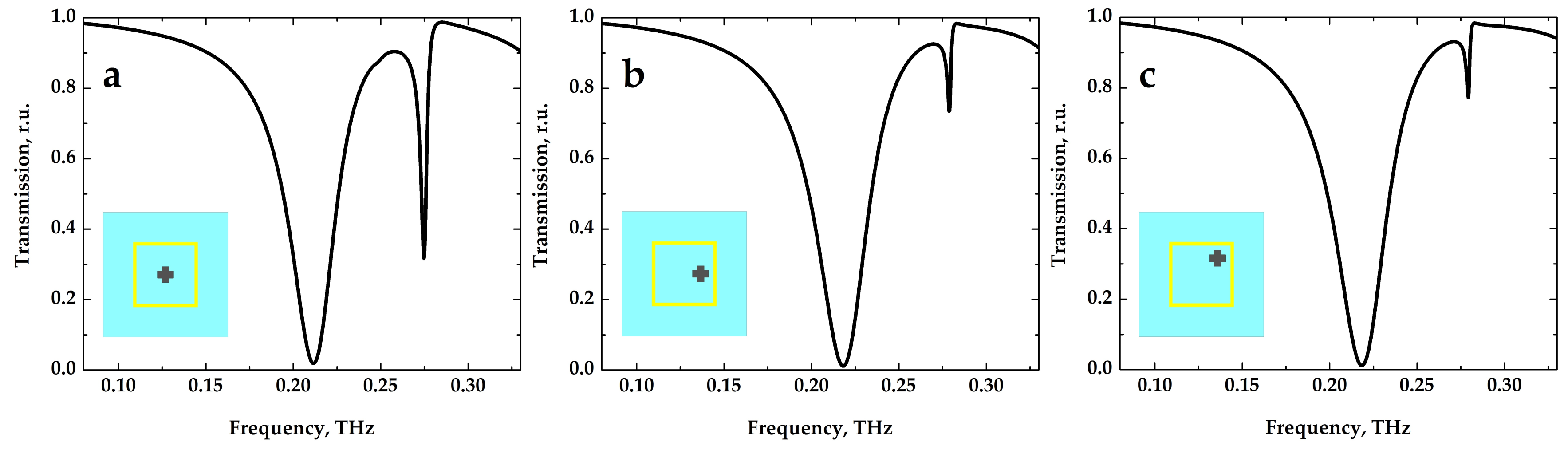
3.2. Influence of Graphene Cross Shift on the Transmission Spectra
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in terahertz communications accelerated by photonics. Nat. Photonics 2016, 10, 371. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef] [PubMed]
- Huq, K.M.S.; Jornet, J.M.; Gerstacker, W.H.; Al-Dulaimi, A.; Zhou, Z.; Aulin, J. THz communications for mobile heterogeneous networks. IEEE Commun. Mag. 2018, 56, 94–95. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef]
- Chen, H.T.; Padilla, W.J.; Zide, J.M.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yang, E.H. THz applications of 2D materials: Graphene and beyond. Nano Struct. Nano Objects 2018, 15, 107–113. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.C.; Bonaccorso, F.; Fal’Ko, V.; Novoselov, K.S.; Roche, S.; Bøggild, P.; Borini, S.; Koppens, F.H.; Palermo, V.; Pugno, N.; et al. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7, 4598–4810. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, R.R.; Kono, J.; Portnoi, M.E. Terahertz science and technology of carbon nanomaterials. Nanotechnology 2014, 25, 322001. [Google Scholar] [CrossRef] [PubMed]
- Jadidi, M.M.; Sushkov, A.B.; Myers-Ward, R.L.; Boyd, A.K.; Daniels, K.M.; Gaskill, D.K.; Fuhrer, M.S.; Drew, H.D.; Murphy, T.E. Tunable terahertz hybrid metal-graphene plasmons. Nano Lett. 2015, 15, 7099–7104. [Google Scholar] [CrossRef] [PubMed]
- Jadidi, M.M.; Sushkov, A.B.; Gaskill, D.K.; Fuhrer, M.; Drew, H.D.; Murphy, T.E. Hybrid Metal-Graphene Terahertz Optoelectronic System with Tunable Plasmonic Resonance and Method of Fabrication. US Patent Application 15/735,662, 1 November 2018. [Google Scholar]
- Lim, W.X.; Singh, R. Universal behaviour of high-Q Fano resonances in metamaterials: terahertz to near-infrared regime. Nano Converg. 2018, 5, 5. [Google Scholar] [CrossRef] [PubMed]
- Grebenchukov, A.N.; Zaitsev, A.D.; Novoselov, M.M.; Kornilov, E.V.; Khodzitsky, M.K. Optically tunable Fano-resonant filter based on graphene. Proc. SPIE 2017, 10343, 103432V. [Google Scholar]
- Weis, P.; Garcia-Pomar, J.L.; Rahm, M. Towards loss compensated and lasing terahertz metamaterials based on optically pumped graphene. Opt. Express 2014, 22, 8473–8489. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Wang, Y.; Schlather, A.E.; Liu, Z.; Ajayan, P.M.; García de Abajo, F.J.; Nordlander, P.; Zhu, X.; Halas, N.J. Active tunable absorption enhancement with graphene nanodisk arrays. Nano Lett. 2013, 14, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Gallinet, B.; Martin, O.J. Ab initio theory of Fano resonances in plasmonic nanostructures and metamaterials. Phys. Rev. B 2011, 83, 235427. [Google Scholar] [CrossRef]
- Taubert, R.; Hentschel, M.; Giessen, H. Plasmonic analog of electromagnetically induced absorption: Simulations, experiments, and coupled oscillator analysis. JOSA B 2013, 30, 3123–3134. [Google Scholar] [CrossRef]

| , eV | , THz | , THz | Q | A | A | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.2192 | 0.0385 | 5.7 | 0.9 | −0.8 | 1.62 | 0.08 | 1 | 0.1 | 0 |
| 0.1 | 0.2632 | 0.0387 | 6.8 | 0.47 | −0.7 | 1.85 | 0.27 | 1 | 0.1 | 0.03 |
| 0.2 | 0.2680 | 0.0112 | 24 | 0.47 | −0.44 | 1.92 | 0.3 | 1 | 0.1 | 0.05 |
| 0.3 | 0.2692 | 0.0088 | 30.6 | 0.47 | −0.34 | 1.93 | 0.32 | 1 | 0.1 | 0.08 |
| 0.4 | 0.2701 | 0.005 | 54 | 0.47 | −0.3 | 1.94 | 0.33 | 1 | 0.1 | 0.1 |
| 0.5 | 0.2712 | 0.0037 | 85 | 0.47 | −0.28 | 1.94 | 0.34 | 1 | 0.1 | 0.12 |
| Offset, m | ||||
|---|---|---|---|---|
| 0–0 | 0.47 | −0.28 | 1.94 | 0.34 |
| 0–100 | 0.3 | −0.32 | 1.94 | 0.51 |
| 100–100 | 0.3 | −0.35 | 1.94 | 0.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaitsev, A.; Grebenchukov, A.; Khodzitsky, M. Tunable THz Graphene Filter Based on Cross-In-Square-Shaped Resonators Metasurface. Photonics 2019, 6, 119. https://doi.org/10.3390/photonics6040119
Zaitsev A, Grebenchukov A, Khodzitsky M. Tunable THz Graphene Filter Based on Cross-In-Square-Shaped Resonators Metasurface. Photonics. 2019; 6(4):119. https://doi.org/10.3390/photonics6040119
Chicago/Turabian StyleZaitsev, Anton, Alexander Grebenchukov, and Mikhail Khodzitsky. 2019. "Tunable THz Graphene Filter Based on Cross-In-Square-Shaped Resonators Metasurface" Photonics 6, no. 4: 119. https://doi.org/10.3390/photonics6040119
APA StyleZaitsev, A., Grebenchukov, A., & Khodzitsky, M. (2019). Tunable THz Graphene Filter Based on Cross-In-Square-Shaped Resonators Metasurface. Photonics, 6(4), 119. https://doi.org/10.3390/photonics6040119





