Image Encryption and Decryption Systems Using the Jigsaw Transform and the Iterative Finite Field Cosine Transform
Abstract
1. Introduction
2. Mathematical Background
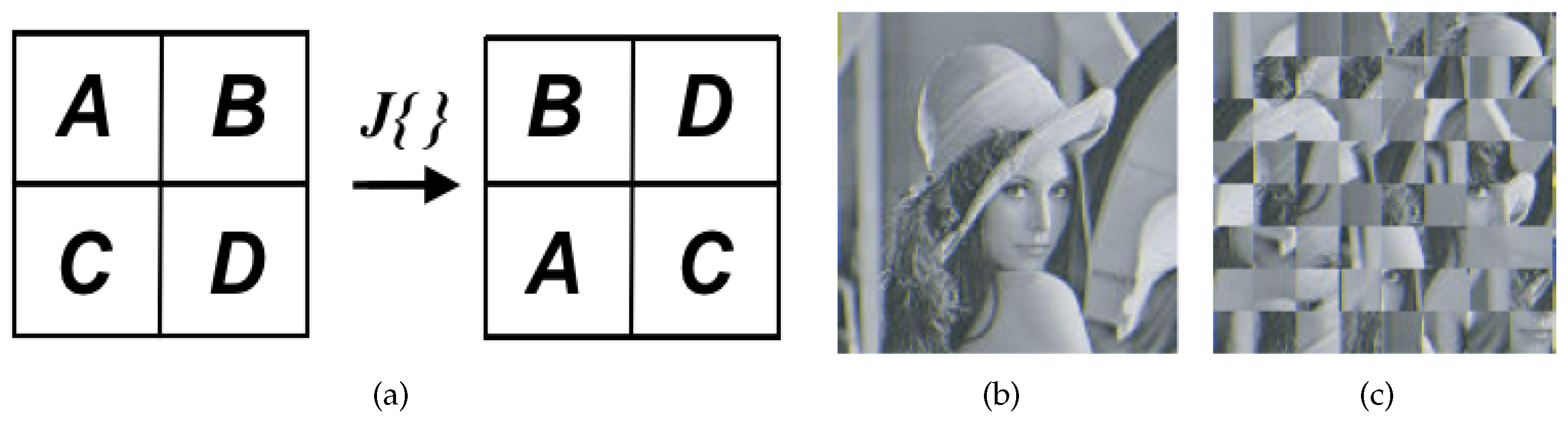
2.1. Jigsaw Transform (JT)
2.2. Finite Field Cosine Transform (FFCT)
3. Image Encryption and Decryption Systems Based on JT and FFCT
4. Numerical Experiments
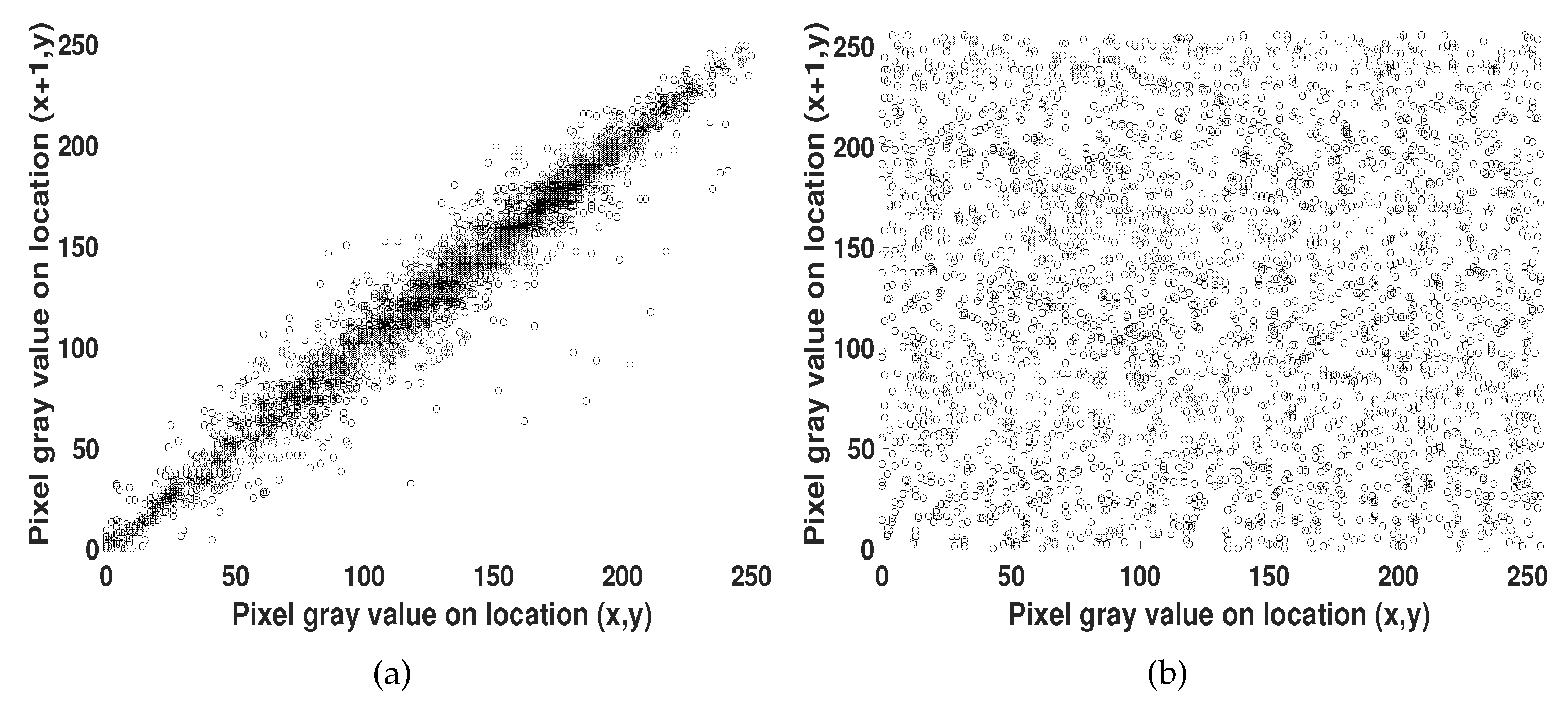
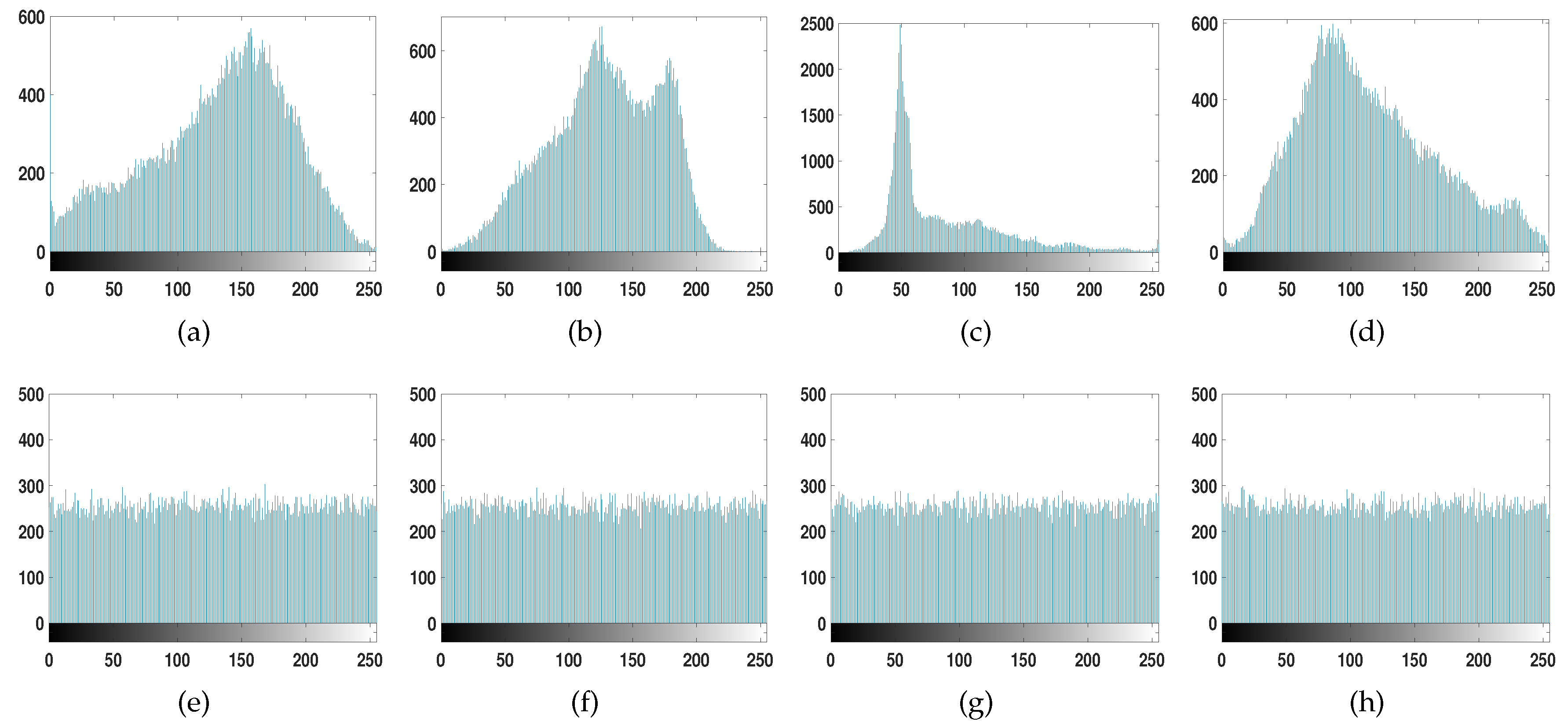
4.1. Statistical Analysis
4.2. Entropy Analysis
4.3. Key Space
4.4. Differential Attack
4.5. Key Sensitivity
4.6. Computing Time
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gu, Z.H.; Leger, J.R.; Lee, S.H. Optical computations of cosine transforms. Opt. Commun. 1981, 39, 137–142. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform: With Applications in Optics and Signal Processing; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Rao, K.; Yip, P. Discrete Cosine Transform: Algorithms, Advantages, Applications; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Krikor, L.; Baba, S.; Arif, T.; Shaaban, Z. Image encryption using DCT and stream cipher. Eur. J. Sci. Res. 2009, 32, 47–57. [Google Scholar]
- Liu, Z.; Xu, L.; Liu, T.; Chen, H.; Li, P.; Lin, C.; Liu, S. Color image encryption by using Arnold transform and color-blend operation in discrete cosine transform domains. Opt. Commun. 2011, 284, 123–128. [Google Scholar] [CrossRef]
- Pan, S.M.; Wen, R.H.; Zhou, Z.H.; Zhou, N.R. Optical multi-image encryption scheme based on discrete cosine transform and nonlinear fractional Mellin transform. Multimed. Tools Appl. 2017, 76, 2933–2953. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Kumar, S.; Panna, B.; Jha, R.K. Medical image encryption using fractional discrete cosine transform with chaotic function. Med. Biol. Eng. Comput. 2019, 57, 2517–2533. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, M. Number Theory in Science and Communication: With Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity; Springer: Berlin, Germany, 2009. [Google Scholar]
- Bhattacharya, M.; Creutzburg, R.; Astola, J. Some historical notes on number theoretic transform. In Proceedings of the International TICS Workshop on Spectral Methods and Multirate Signal Processing, Vienna, Austria, 11–12 September 2004. [Google Scholar]
- Abdallah, E.E.; Hamza, A.B.; Bhattacharya, P. MPEG video watermarking using tensor singular value decomposition. In Proceedings of the International Conference Image Analysis and Recognition, Montreal, QC, Canada, 22–24 August 2007. [Google Scholar]
- Abdallah, E.E.; Hamza, A.B.; Bhattacharya, P. Video watermarking using wavelet transform and tensor algebra. Signal Image Video Process. 2010, 4, 233–245. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Novel image encryption scheme based on Chebyshev polynomial and duffing map. Sci. World J. 2014, 2014, 283639. [Google Scholar] [CrossRef] [PubMed]
- Stoyanov, B.; Kordov, K. Image encryption using Chebyshev map and rotation equation. Entropy 2015, 17, 2117–2139. [Google Scholar] [CrossRef]
- Lima, J.B.; de Souza, R.M.C. Finite field trigonometric transforms. Appl. Algebr. Eng. Commun. 2011, 22, 393–411. [Google Scholar] [CrossRef]
- Lima, J.; Lima, E.; Madeiro, F. Image encryption based on the finite field cosine transform. Signal Process. Image Commun. 2013, 28, 1537–1547. [Google Scholar] [CrossRef]
- Lima, J.; Madeiro, F.; Sales, F. Encryption of medical images based on the cosine number transform. Signal Process. Image Commun. 2015, 35, 1–8. [Google Scholar] [CrossRef]
- Mikhail, M.; Abouelseoud, Y.; ElKobrosy, G. Two-phase image encryption scheme based on FFCT and fractals. Secur. Commun. Netw. 2017, 2017, 7367518. [Google Scholar] [CrossRef]
- Millán, M.S.; Pérez-Cabré, E. Optical data encryption. In Optical and Digital Image Processing: Fundamentals and Applications; Cristóbal, G., Schelkens, P., Thienpont, H., Eds.; Wiley-VCH Verlag GmbH & Co.: Hoboken, NJ, USA, 2011; pp. 739–767. [Google Scholar]
- Millán, M.S.; Pérez-Cabré, E.; Vilardy, J.M. Nonlinear techniques for secure optical encryption and multifactor authentication. In Advanced Secure Optical Image Processing for Communications; Al Falou, A., Ed.; IOP Publishing: Bristol, UK, 2018; pp. 8-1–8-33. [Google Scholar]
- Muniraj, I.; Sheridan, J.T. Optical Encryption and Decryption; SPIE: Bellingham, WA, USA, 2019. [Google Scholar]
- Hennelly, B.; Sheridan, J.T. Optical image encryption by random shifting in fractional Fourier domains. Opt. Lett. 2003, 28, 269–271. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Torres, C.O.; Mattos, L. Image encryption-decryption system based on Gyrator transform and Jigsaw transform. Proc. SPIE 2013, 8785, 87851Q. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilardy O., J.M.; Barba J., L.; Torres M., C.O. Image Encryption and Decryption Systems Using the Jigsaw Transform and the Iterative Finite Field Cosine Transform. Photonics 2019, 6, 121. https://doi.org/10.3390/photonics6040121
Vilardy O. JM, Barba J. L, Torres M. CO. Image Encryption and Decryption Systems Using the Jigsaw Transform and the Iterative Finite Field Cosine Transform. Photonics. 2019; 6(4):121. https://doi.org/10.3390/photonics6040121
Chicago/Turabian StyleVilardy O., Juan M., Leiner Barba J., and Cesar O. Torres M. 2019. "Image Encryption and Decryption Systems Using the Jigsaw Transform and the Iterative Finite Field Cosine Transform" Photonics 6, no. 4: 121. https://doi.org/10.3390/photonics6040121
APA StyleVilardy O., J. M., Barba J., L., & Torres M., C. O. (2019). Image Encryption and Decryption Systems Using the Jigsaw Transform and the Iterative Finite Field Cosine Transform. Photonics, 6(4), 121. https://doi.org/10.3390/photonics6040121